অংকশাস্ত্রে চারটি মৌলিক ক্রিয়ার মধ্যে একটি হলো ভাগ বা বিভাজন ( Division) । ভাগ বা বিভাজন ( Division) প্রক্রিয়াটি “÷” চিহ্ন দ্বারা অথবা ” / ” দ্বারা চিহ্নিত করা হয় ।
সাধারণত সবাই প্রাথমিক বিদ্যালয়েই যোগ, বিয়োগ, গুণের মত ভাগের ধারণাও অর্জন করে ।
>ভাগের গাণিতিক প্রকাশঃ
নির্দিষ্টভাবে বলা যায় যদি 







a ÷ b = c , a/b = c
উদাহরণস্বরূপ, 6÷3=2 যেহেতু, 3×2=6.
দুটি পূর্ণ সংখ্যার একটি অপরটিকে দিয়ে ভাগ করলে তা অনেকসময় নিঃশেষে বিভাজ্য না হয়ে ভাগশেষ নামক অরেকটি সংখ্যা অবশিষ্ট থেকে যায়। ভাগশেষকে পুনরায় ভাজক দ্বারা ভাগ করলে ভাগফলে পূর্ণ সংখ্যার পরিবর্তে দশমিক পাওয়া যায়। তাই দুটি পূর্ণ সংখ্যার ভাগফল অধিকাংশ ক্ষেত্রে পূর্ণ সংখ্যা হয়না। তবে দুটি পূর্ন সংখ্যাের ভাগফল সব সময়ই মূলদ বাস্তব সংখ্যাগুলির মধ্যই অবস্থান করে।
>ভাগঃ বিয়োগের একটি সংক্ষিপ্ত রূপ –
অংকশাস্ত্রে চারটি মৌলিক ক্রিয়ার মধ্যে যেমন একটি হলো ভাগ বা বিভাজন ( Division) তেমনি অপর আর একটি হলো বিয়োগ ।
আমরা দুটি সংখ্যার মধ্যে বিয়োগ করতে গেলে বলি যে,
৭ থেকে ৪ বিয়োগ গাণিতিক ভাষায় লেখা হয় ” ৭ – ৪ “, অথবা![]()
এবার যদি প্রশ্ন করা হয় যে,
৭ থেকে ৪-কে কতো বার বিয়োগ করা যাবে?
তখন আমরা বিয়োগ করবো এবং দেখবো একবার বিয়োগ করে বিয়োগফল কতো হচ্ছে। তারপর বিয়োগফল থেকে আবার বিয়োগ করে দেখতে হবে আর বিয়োগ যাচ্ছে কি না! বিষয়টি উদাহরণের মাধ্যমে বুঝতে চেষ্টা করি।
| উদাহরণ | কতবার বিয়োগ করা যাবে | ভাগঃবিয়োগের সংক্ষিপ্ত রূপ |
| ১৫ থেকে ৪ কে কতবার বিয়োগ করা যাবে? | প্রথম বিয়োগ-> ১৫-৪=১১ ( একবার বিয়োগ হলো ) দ্বিতীয় বিয়োগ -> ১১-৪ = ৭ ( দুই বার বিয়োগ হলো ) তৃতীয় বিয়োগ -> ৭-৪=৩ ( তিনবার বিয়োগ হলো ) তিনবার বিয়োগের পর যেহেতু বিয়োগফল= ৩ , ৪ এর থেকে ছোটো সেহেতু আর বিয়োগ যাবেনা । সুতরাং , ১৫ থেকে ৪ কে তিনবার বিয়োগ করা যাবে এবং তিনবার বিয়োগ করার পরে ৩ অবশিষ্ট থাকবে। | 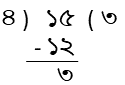 |
| ১২ থেকে ৩ কে কতবার বিয়োগ করা যাবে ? | প্রথম বিয়োগ -> ১২-৩=৯ ( একবার বিয়োগ হলো ) দ্বিতীয় বিয়োগ -> ৯-৩=৬ ( দুইবার বিয়োগ হলো ) তৃতীয় বিয়োগ-> ৬-৩=৩ (তিনবার বিয়োগ হলো ) চতুর্থ বিয়োগ-> ৩-৩=০ ( চারবার বিয়োগ হলো) চারবার বিয়োগের পর যেহেতু বিয়োগফল=০ , সেহেতু আর বিয়োগ যাবেনা । সুতরাং , ১২ থেকে ৩ কে চারবার বিয়োগ করা যাবে এবং চারবার বিয়োগ করার পরে ০ অবশিষ্ট থাকবে। | 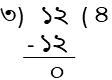 |
উপরের সারণী থেকে আমরা বুঝলাম একটা সংখ্যা থেকে আর একটি সংখ্যা কতবার বিয়োগ করা যাবে সেটা আমরা ভাগের মাধ্যমে খুব সহজেই করে ফেলতে পারবো ।
FAQs
–> ১১ থেকে ৩ বিয়োগ যায় কতবার ?
উত্তর –
১১ থেকে ৩ বিয়োগ কতোবার যাবে সেটার জন্যে আমাকে ১১ কে ৩ দিয়ে ভাগ করতে হবে ।
সুতরাং , ১১ থেকে ৩ আমরা তিনবার বিয়োগ করতে পারবো ।
| ১১ থেকে ৩ বিয়োগ যায় কতবার ? | প্রথম বিয়োগ – ১১ – ৩ = ৮ ( একবার বিয়োগ হলো ) দ্বিতীয় বিয়োগ – ৮ – ৩ = ৫ ( দুইবার বিয়োগ হলো ) তৃতীয় বিয়োগ – ৫- ৩ = ২ ( তিন বার বিয়োগ হলো ) সুতরাং , ১১ থেকে ৩ আমরা তিনবার বিয়োগ করতে পারবো । |


