ত্রিভুজ কাকে বলে?

তিনটি বাহু দ্বারা সীমাবদ্ধ যেকোনো সামতলিক চিত্র কে ত্রিভুজ বলে।
ত্রিভুজের উদাহরণঃ
চিত্রে দেখতে পাচ্ছি একটি ত্রিভুজ ABC.
এই ত্রিভুজ কে গাণিতিক ভাষায় ▲ABC এইভাবে প্রকাশ করা হয় ।
ত্রিভুজ এর প্রকার ভেদঃ | ত্রিভুজ কতো প্রকার ও কি কি?
অভ্যন্তরীণ কোণের পরিমাপে ত্রিভুজের প্রকারভেদঃ
অভ্যন্তরীণ কোণের পরিমাপে ত্রিভুজ তিন প্রকার। যথা-
( i )সূক্ষ্মকোণী ত্রিভুজঃ
যে ত্রিভুজের অভ্যন্তরীণ তিনটি কোণের মধ্যে যে কোনো একটি কোণ সূক্ষ্মকোণ সেই ত্রিভুজ কে সূক্ষ্মকোণী ত্রিভুজ বলে।
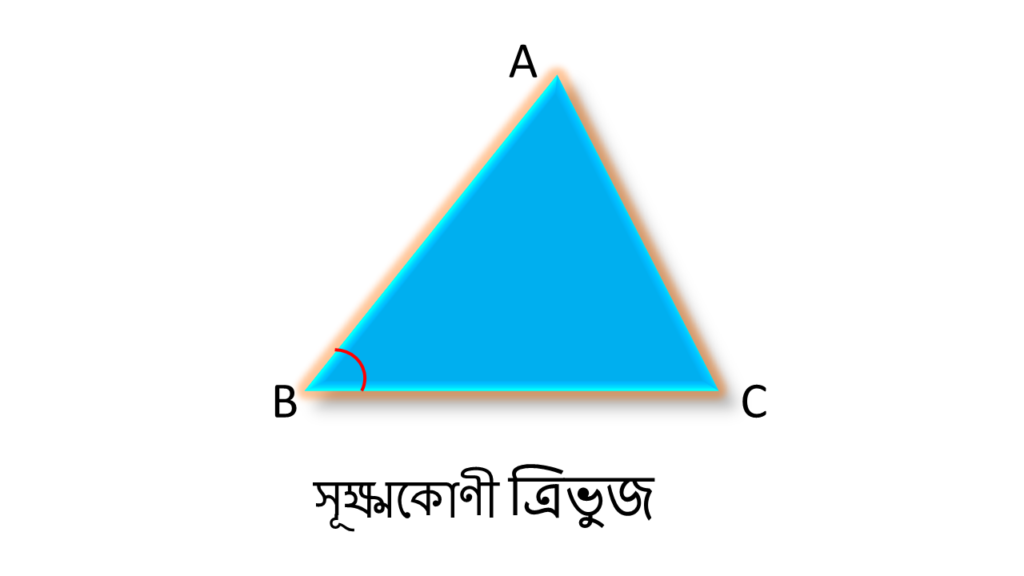
চিত্রে ▲ ABC একটি সূক্ষ্মকোণী ত্রিভুজ ।
( ii ) সমকোণী ত্রিভুজঃ
যে ত্রিভুজের অভ্যন্তরীণ তিনটি কোণের মধ্যে যে কোনো একটি কোণ সমকোণ সেই ত্রিভুজ কে সমকোণী ত্রিভুজ বলে।
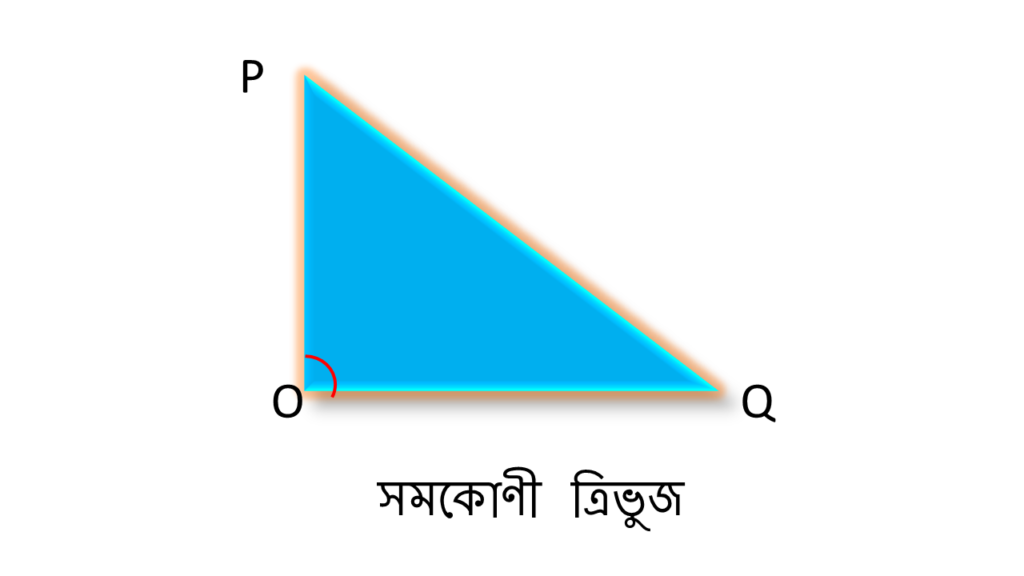
চিত্রে ▲ POQ একটি সমকোণী ত্রিভুজ ।
( iii ) স্থুলকোণী ত্রিভুজঃ
যে ত্রিভুজের অভ্যন্তরীণ তিনটি কোণের মধ্যে যে কোনো একটি কোণ স্থুলকোণ সেই ত্রিভুজ কে স্থুলকোণী ত্রিভুজ বলে।
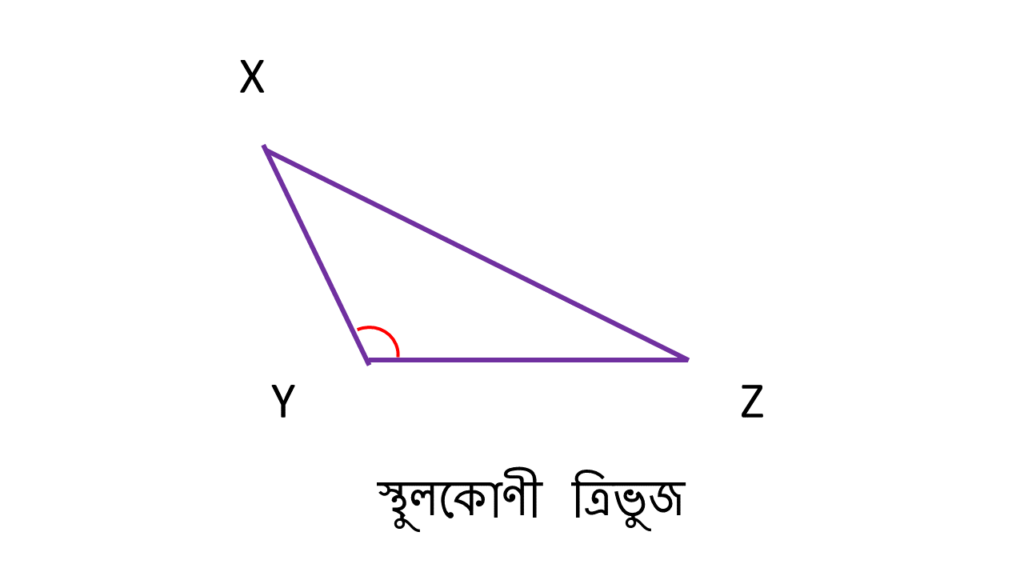
চিত্রে ▲ XYZ একটি স্থুলকোণী ত্রিভুজ ।
বাহুর দৈর্ঘ্যের দ্বারা ত্রিভুজ এর প্রকারভেদঃ
বাহুর দৈর্ঘ্যের ভিত্তিতে ত্রিভুজকে তিন ভাগে ভাগ করা হয়। যথা-
( i ) সমবাহু ত্রিভুজঃ
যে ত্রিভুজের তিনটি বাহু পরস্পর সমান তাকে সমবাহু ত্রিভুজ বলে।
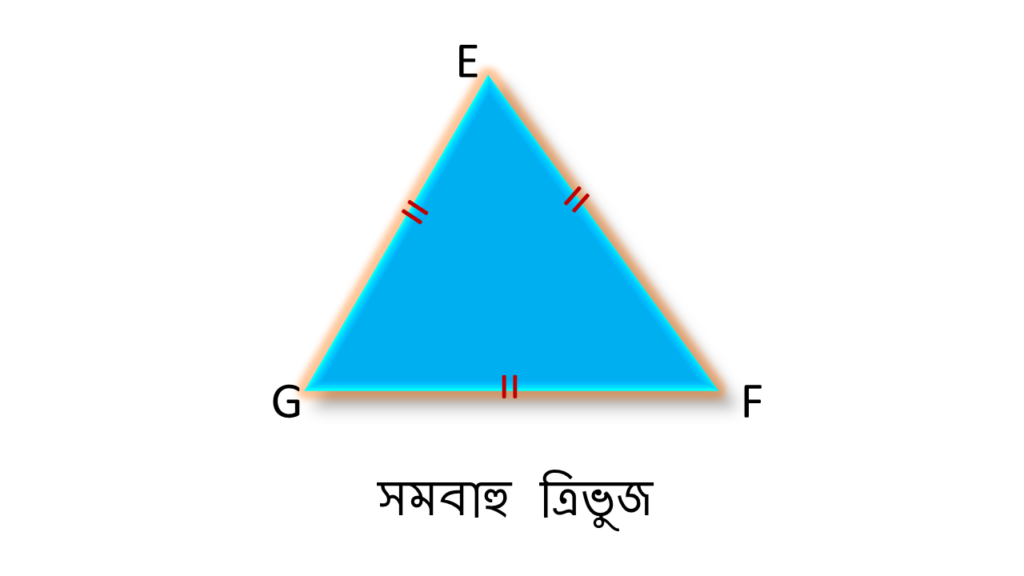
চিত্রে ▲EFG একটি সমবাহু ত্রিভুজ।
( ii )সমদ্বিবাহু ত্রিভুজঃ
যে ত্রিভুজের যে কোনো দুটি বাহু সমান, সেই ত্রিভুজ কে সমদ্বিবাহু ত্রিভুজ বলে ।
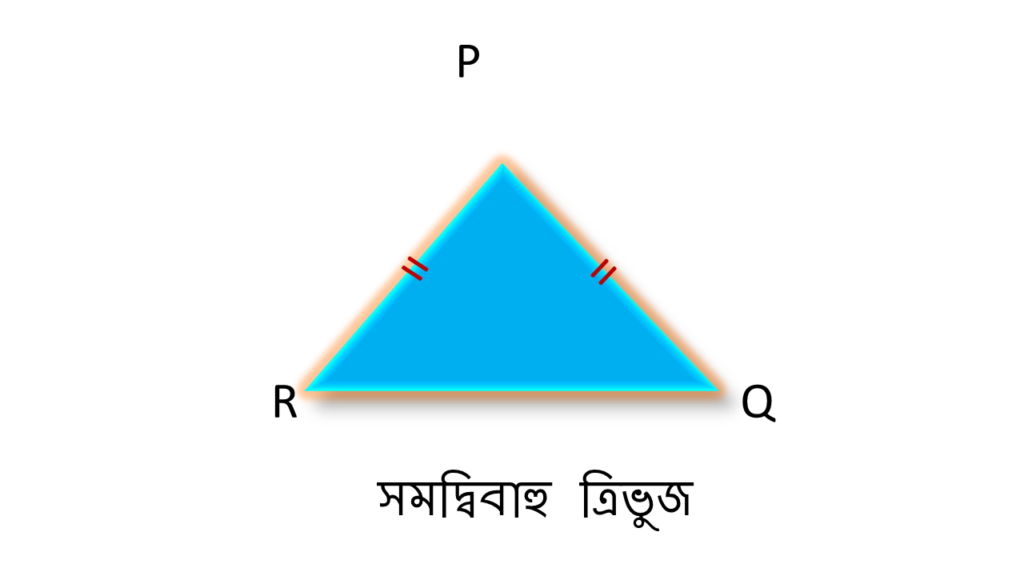
চিত্রে ▲PQR একটি সমদ্বিবাহু ত্রিভুজ ।
( iii ) বিষমবাহু ত্রিভুজঃ
যে ত্রিভুজের তিনটি বাহু সমান নয় অর্থাৎ, তিনটি বাহুর পরিমাপ ভিন্ন ভিন্ন সেই ত্রিভুজকে বিষমবাহু ত্রিভুজ বলে।

চিত্রে ▲TUV একটি বিষমবাহু ত্রিভুজ।
ত্রিভুজ গঠনের শর্তঃ
ত্রিভুজ গঠনে বাহুর শর্তঃ
একটি ত্রিভুজ গঠনের জন্যে ত্রিভুজের বাহুর একটি শর্ত রেয়েছে। সেটি হলো –
ত্রিভুজের যে কোনো দুটি বাহুর দৈর্ঘ্যের সমষ্টি অপর বাহুর দৈর্ঘ্যের অপেক্ষা বেশি হবে।
অর্থাৎ, যদি তিনটি বাহুর দৈর্ঘ্য যথাক্রমে a, b, c হয় তবে শর্ত অনুসারে এই বাহু গুলি দ্বারা ত্রিভুজ গঠন হবে যখন বাহু তিনটি নিম্নের শর্তগুলি পূরণ করবেঃ
| a + b > c |
| b + c > a |
| c + a > b |
সুতরাং একটি ত্রিভুজ এর ক্ষেত্রে যেকোনো দুই বাহুর দৈর্ঘ্যের সমষ্টি কখনোই তৃতীয় বাহুর দৈর্ঘ্যের চেয়ে কম হওয়া সম্ভব নয়।
ত্রিভুজ গঠনে কোণের শর্তঃ
একটি ত্রিভুজ গঠনের ক্ষেত্রে বাহুর দৈর্ঘ্যের পরিমাপের মধ্যে যেমন সম্পর্ক রেয়েছে তেমনি ত্রিভুজ গঠনে অভ্যন্তরীণ কোণ এর পরিমাপ ও একটি গুরুত্ব পূর্ণ ভূমিকা পালন করে। ত্রিভুজ গঠনে কোণের শর্ত হলো –
ত্রিভুজ এর অভ্যন্তরীণ কোণের সমষ্টি সবসময় 180° হবে।
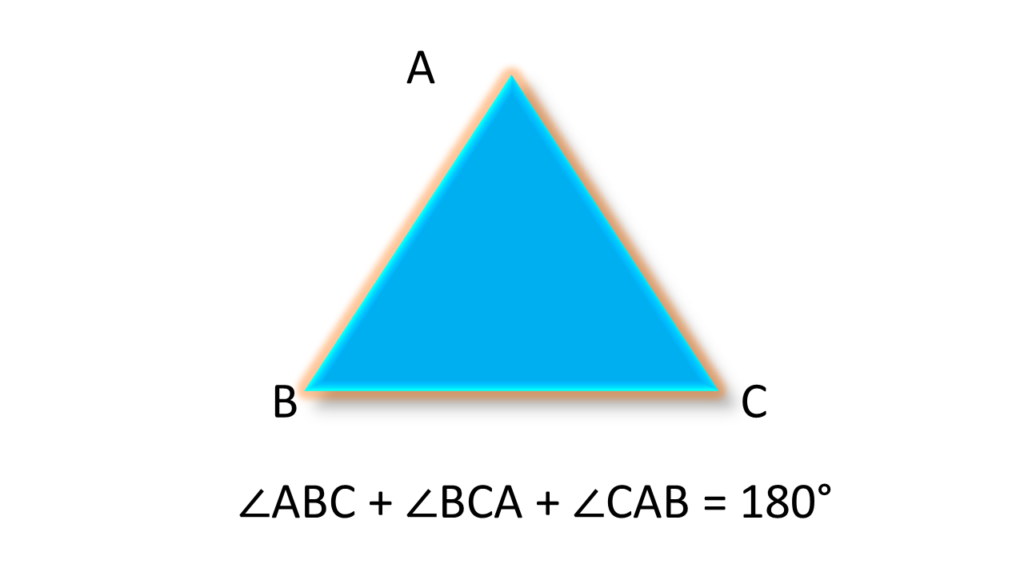
▲ABC এর
∠ABC + ∠BCA + ∠CAB = 180° .
ত্রিভুজ এর মধ্যমাঃ
ত্রিভুজের শীর্ষ বিন্দু ও বিপরীত বাহুর মধ্যবিন্দুর সংযোজক সরলরেখাংশ হলো ত্রিভুজটির মধ্যমা।
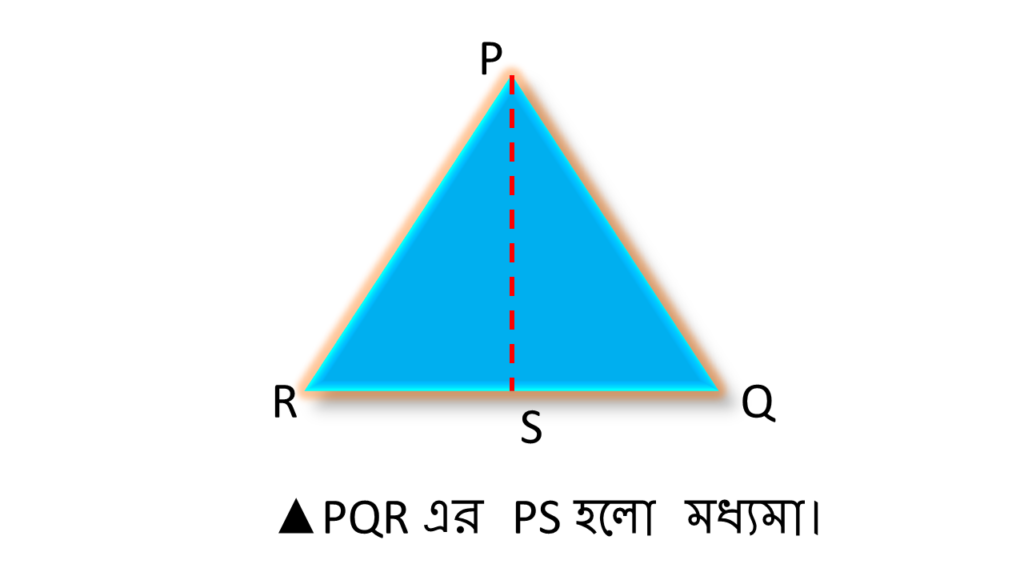
▲PQR এর PS হলো মধ্যমা।
ত্রিভুজ এর উচ্চতাঃ
একটি ত্রিভুজের শীর্ষ বিন্দু থেকে শীর্ষবিন্দুর বিপরীত দিকে বাহুর উপর লম্ব কেই ঐ ত্রিভুজের উচ্চতা বলে।
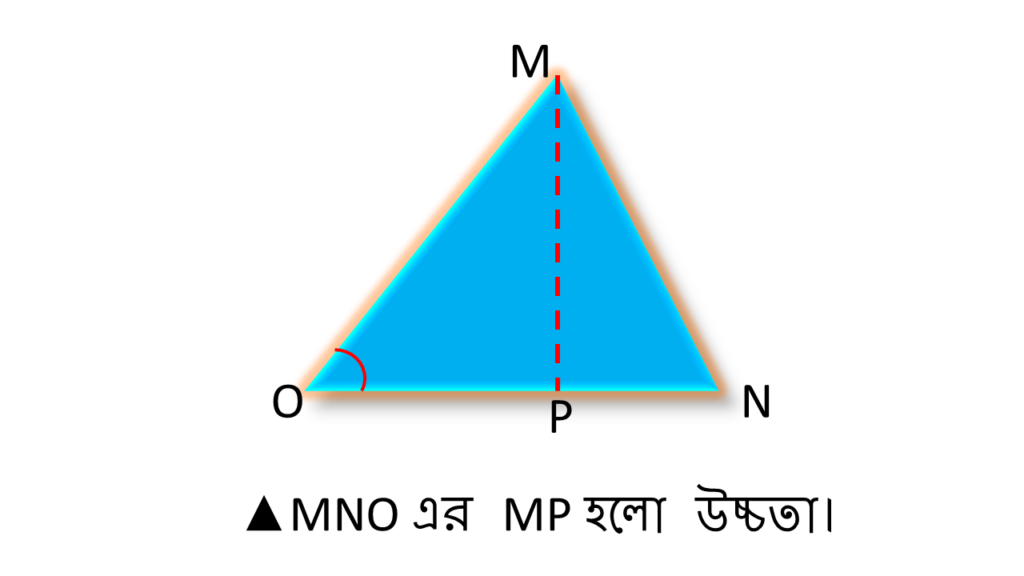
▲MNO এর MP হলো উচ্চতা।
ত্রিভুজের পরিসীমাঃ
ত্রিভুজের তিনটি বাহুর দৈর্ঘ্যের সমষ্টি কে ঐ ত্রিভুজের পরিসীমা বলে।
যেমন-
একটি ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য যথাক্রমে 5 একক , 6 একক ও 7 একক ।
ত্রিভুজটির পরিসীমা = 5 + 6 + 7=18 একক।
ত্রিভুজ এর ক্ষেত্রফলঃ
কোনো জ্যামিতিক আকৃতির ক্ষেত্রফল বলতে আমরা বুঝি ঐ আকৃতি টি কতোটুকু ক্ষেত্র জুড়ে রয়েছে ।
ত্রিভুজ এর ক্ষেত্রফলের সূত্রঃ
ত্রিভুজের ক্ষেত্রফলের সূত্র হলো- ½×ভূমি×উচ্চতা
সর্বসমতাঃ
দুটি জ্যামিতিক চিত্রের একটিকে সরিয়ে বা ঘুরিয়ে বা দু-ভাবে অপরটির সাথে সম্পূর্ণভাবে মিলে যাওয়াকে সর্বসম বলে। আর এই ধর্মকে সর্বসমতা বলে।
দুটি ত্রিভুজ সর্বসম হওয়ার শর্তঃ
যেকোনো দুটি ত্রিভুজ নিম্নের শর্তগুলির মদ্ধ্যে যেকোনো একটি শর্ত পূরণ করলে ত্রিভুজ দুটিকে সর্বসম বলবো।
শর্ত 1ঃ বাহু-বাহু-বাহু বা S-S-S শর্ত-
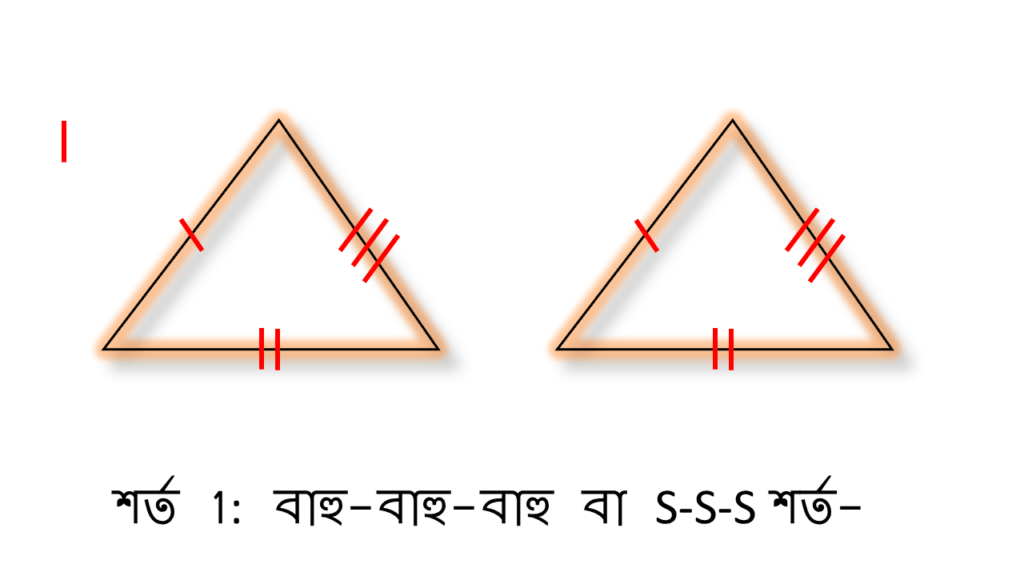
একটি ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য অপর একটি ত্রিভুজের অনুরূপ তিনটি বাহুর দৈর্ঘ্যের সমান হলে ত্রিভুজ দুটি সর্বসম হবে।
শর্ত 2ঃ বাহু-কোণ-বাহু বা S-A-S শর্ত-
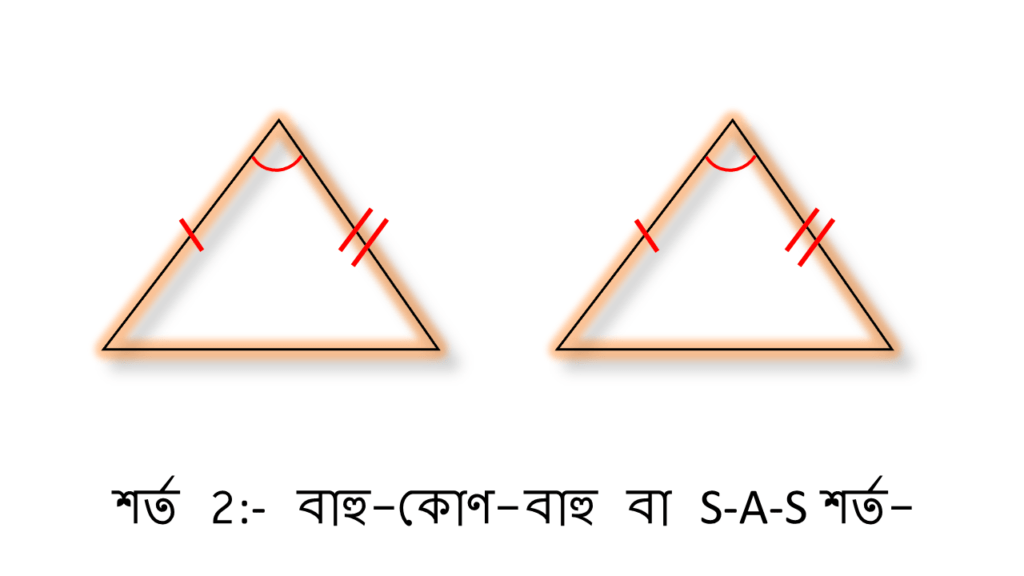
একটি ত্রিভুজের দুটি বাহুর দৈর্ঘ্য ও তাদের অন্তর্ভুক্ত কোণের পরিমাপ অপর একটি ত্রিভুজের অনুরূপ দুটি বাহুর দৈর্ঘ্য ও তাদের অন্তর্ভুক্ত কোণের পরিমাপের সমান হলে ত্রিভুজ দুটি সর্বসম হবে।
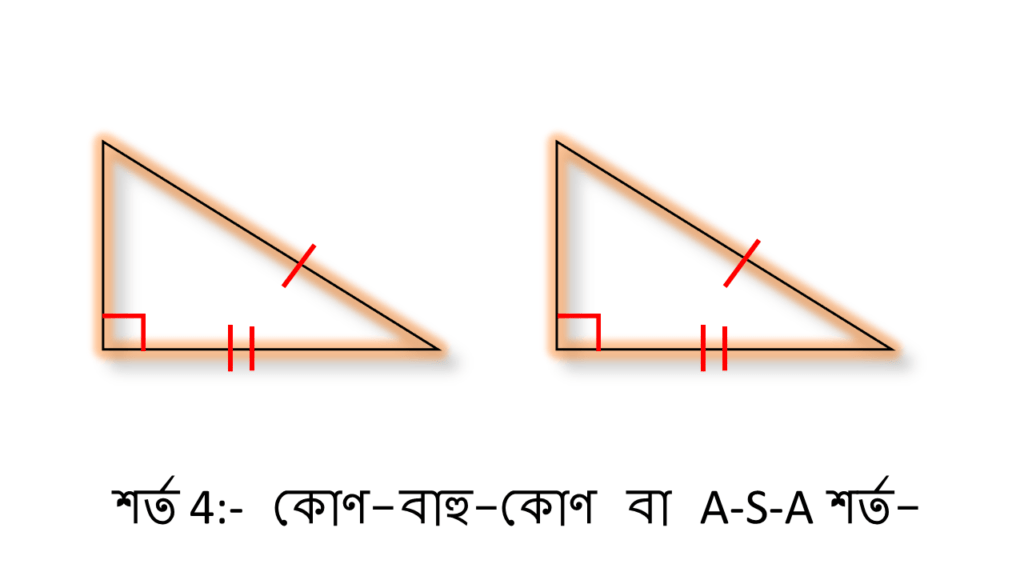
শর্ত 3ঃ কোণ-বাহু-কোণ বা A-S-A শর্ত-
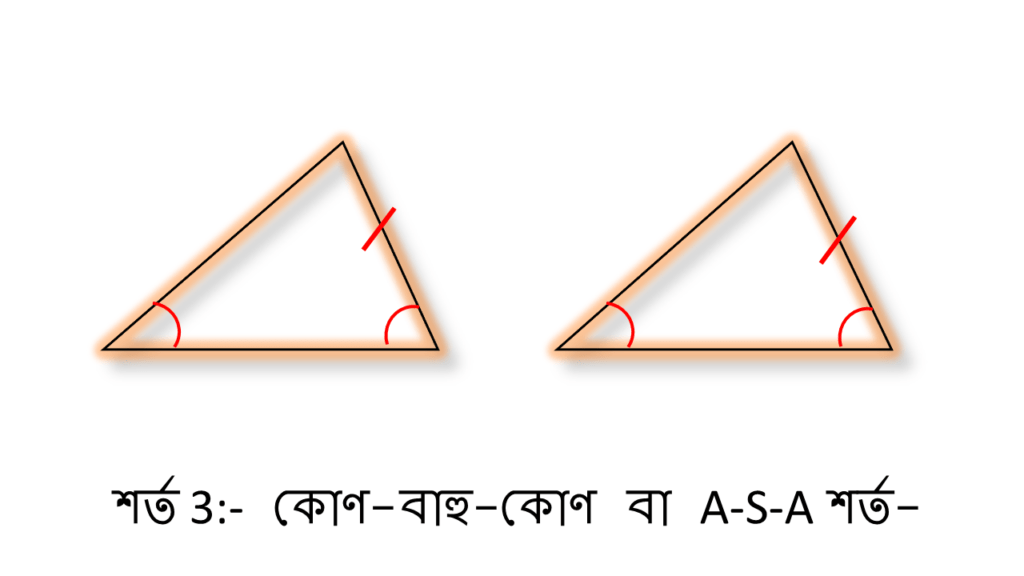
একটি ত্রিভুজের দুটি কোণের পরিমাপ ও একটি বাহুর দৈর্ঘ্য অপর একটি ত্রিভুজের দুটি কোণের পরিমাপ এবং অনুরূপ বাহুর দৈর্ঘ্যের সমান হলে ত্রিভুজ দুটি সর্বসম হবে।
শর্ত 4ঃ সমকোণ-অতিভুজ-বাহু বা R-H-S শর্ত-
একটি সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য ও একটি বাহুর দৈর্ঘ্য অপর একটি সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য ও একটি বাহুর দৈর্ঘ্যের সমান হলে ত্রিভুজ দুটি সর্বসম হবে।
দুটি ত্রিভুজের তিনটি কোণের পরিমাপ সমান হলে ত্রিভুজ দুটিকে সদৃশকোণী ত্রিভুজ বলে। কিন্তু, একটি ত্রিভুজের তিনটি কোণের পরিমাপ অপর একটি ত্রিভুজের তিনটি কোণের পরিমাপের সমান হলে ত্রিভুজ দুটি সর্বসম নাও হতে পারে। সুতরাং দুটি ত্রিভুজের কোণ-কোণ-কোণ বা A-A-A সর্বসমতার শর্ত হতে পারে না। |
ত্রিভুজের দুটি বাহু ও তাদের বিপরীত কোণের সম্পর্কঃ
( i ) একটি ত্রিভুজের দুটি বাহুর দৈর্ঘ্য সমান হলে তাদের বিপরীত কোণগুলির পরিমাপ সমান হবে।
( ii ) একটি ত্রিভুজের দুটি কোণের পরিমাপ সমান হলে তাদের বিপরীত বাহুগুলির দৈর্ঘ্য সমান হবে।
Frequently Asked Questions:
1.কোনের ভিত্তিতে ত্রিভুজ কত প্রকার?
উত্তর- কোণের পরিমাপে ত্রিভুজ তিন প্রকার। সূক্ষ্মকোণী , সমকোণী , স্থুলকোণী ।
2.সকল ত্রিভুজের কি তিনটি কোণ ও তিনটি বাহু আছে?
উত্তর- হ্যাঁ। সকল ত্রিভুজের তিনটি কোণ ও তিনটি বাহু আছে।
3.যে ত্রিভুজের দুইটি বাহু সমান তাকে কি বলে?
উত্তর- যে ত্রিভুজের দুইটি বাহু সমান তাকে সমদ্বিবাহু ত্রিভুজ বলে।
4.ত্রিভুজের তিনটি বাহু কি সবসময় সমান হয়?
উত্তর- ত্রিভুজের তিনটি বাহু সবসময় সমান হয় না ।
ত্রিভুজ নিয়ে এই আলোচনা ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।
তোমাদের জন্যে অষ্টম শ্রেণীর সমস্ত অধ্যায় এর গণিত এবং অধ্যায়টি কিভাবে আয়ত্ত করতে হবে তা খুব সুন্দর করে লেখা হয়েছে যাতে তোমরা খুব সহজেই প্রতিটি অধ্যায় বুঝতে পারো এবং প্রতিটি অংক বুঝে করতে পারো । |


