Class 5 Math Solution WBBSE (Page 75-99) | পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের অন্তর্গত পঞ্চম শ্রেণির শিক্ষার্থীদের জন্য ক্লাস 5 গণিতে ভীতি দূর করার জন্য আমার এই আমার গণিত পঞ্চম শ্রেণির সমাধান Page এ তোমাকে স্বাগত!
গণিত প্রায়শই একটি চ্যালেঞ্জিং বিষয় বলে মনে হতে পারে, কিন্তু সঠিক পদ্ধতি এবং স্পষ্ট ব্যাখ্যা সহ, এটি একটি উপভোগ্য এবং ফলপ্রসূ অভিজ্ঞতা হয়ে উঠতে পারে। এই প্রবন্ধে, আমি ক্লাস 5 এর সিলেবাস থেকে সমস্ত সমস্যার বিশদ সমাধান প্রদান করার চেষ্টা করেছি, যার লক্ষ্য তরুণ শিক্ষার্থীদের জন্য গণিতকে আরও সহজলভ্য এবং কম ভীতিজনক করে তোলা।
আমার লক্ষ্য হল জটিল সমস্যাগুলিকে সহজ, সহজে বোধগম্য ধাপে ভেঙ্গে দিয়ে শিক্ষার্থীদের গণিতে একটি শক্তিশালী ভিত্তি তৈরি করতে সাহায্য করা। এখানে মূল ধারণা এবং সমস্যা সমাধানের কৌশলগুলিতে ফোকাস করা হয়েছে যা শ্রেণীকক্ষে এবং তার বাইরেও সাফল্যের জন্য গুরুত্বপূর্ণ।
Class 5 Math Solution WBBSE Page 75:
ভাজ্য, ভাজক, ভাগফল ও ভাগশেষ ঠিক আছে কিনা সেই সম্পর্ক যাচাই করিঃ
(২) ১২৩১০০÷২৩
উত্তরঃ
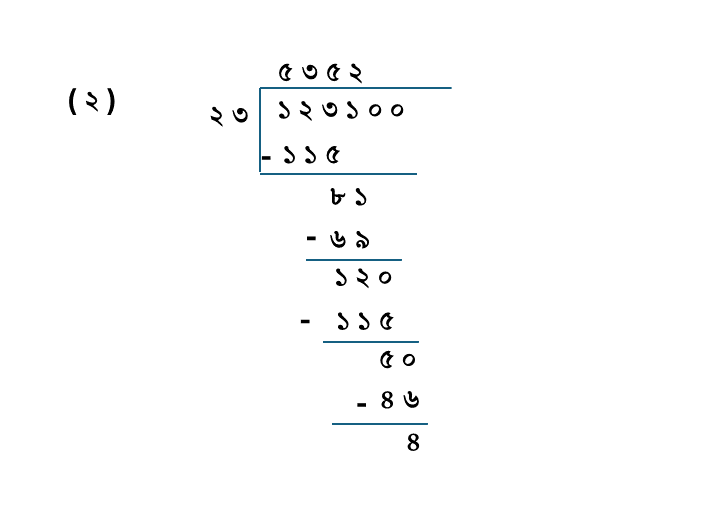
| ভাজ্য = | ১২৩১০০ |
| ভাজক = | ২৩ |
| ভাগফল = | ৫৩৫২ |
| ভাগশেষ = | ৪ |
ভাজক × ভাগফল + ভাগশেষ
২৩×৫৩৫২ + ৪
= ১২৩৯৬ + ৪
= ১২৩১০০
= ভাজ্য
(৩) ৪৭৫৫২০÷৮৪
উত্তরঃ
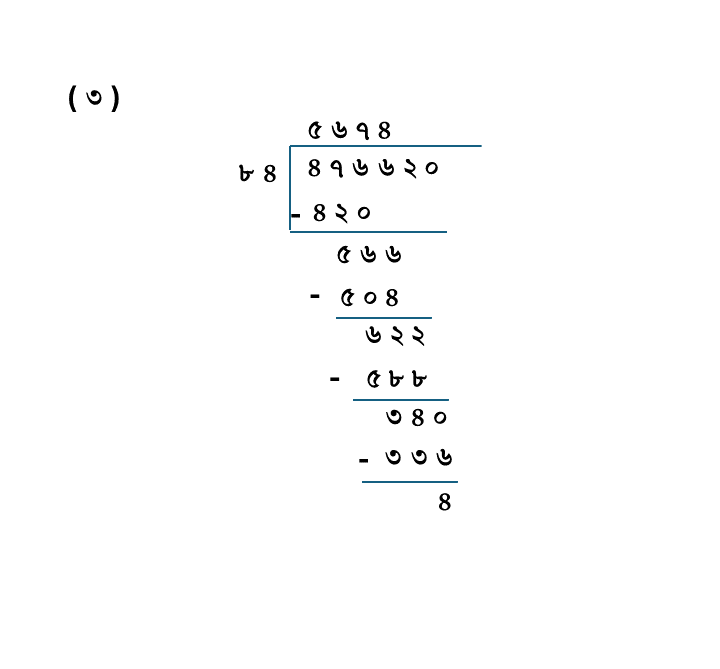
| ভাজ্য = | ৪৭৬৬২০ |
| ভাজক = | ৮৪ |
| ভাগফল = | ৫৬৭৪ |
| ভাগশেষ = | ৪ |
ভাজক × ভাগফল + ভাগশেষ
৮৪×৫৬৭৪ + ৪
= ৪৭৬৬১৬ + ৪
= ৪৭৬৬২০
= ভাজ্য
(৪) ১৩৯৫৯৬÷২৩৭
উত্তরঃ
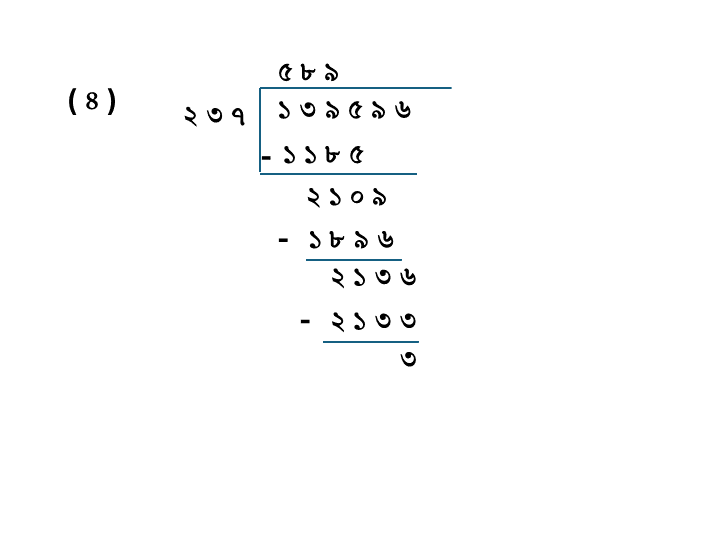
| ভাজ্য = | ১৩৯৫৯৬ |
| ভাজক = | ২৩৭ |
| ভাগফল = | ৫৮৯ |
| ভাগশেষ = | ৩ |
ভাজক × ভাগফল + ভাগশেষ
২৩৭×৫৮৯ + ৩
= ১৩৯৫৯৩ + ৩
= ১৩৯৫৯৬
= ভাজ্য
(৫) ২২৭৪০০÷৩৬৫
উত্তরঃ
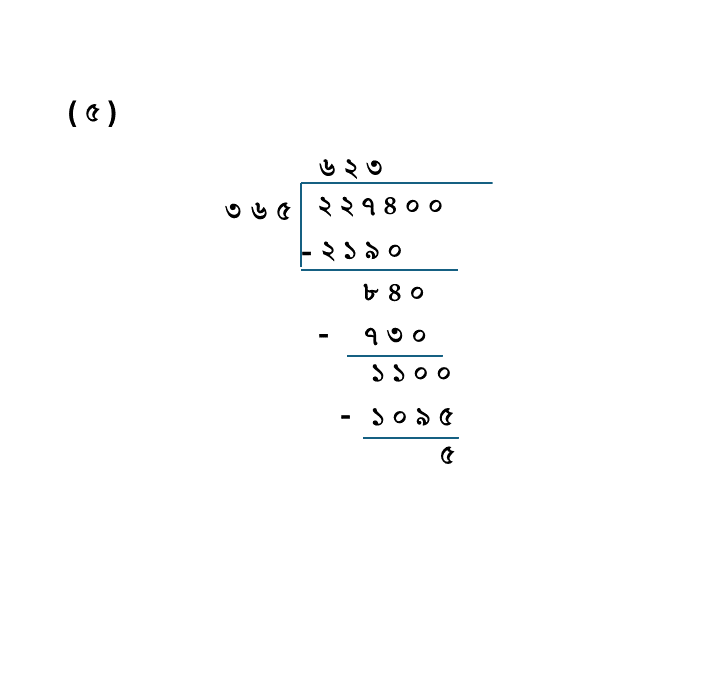
| ভাজ্য = | ২২৭৪০০ |
| ভাজক = | ৩৬৫ |
| ভাগফল = | ৬২৩ |
| ভাগশেষ = | ৫ |
ভাজক × ভাগফল + ভাগশেষ
৩৬৫×৬২৩ + ৫
= ২২৭৩৯৫ + ৫
= ২২৭৪০০
= ভাজ্য
(৬) ৪০০০০০÷২২২
উত্তরঃ
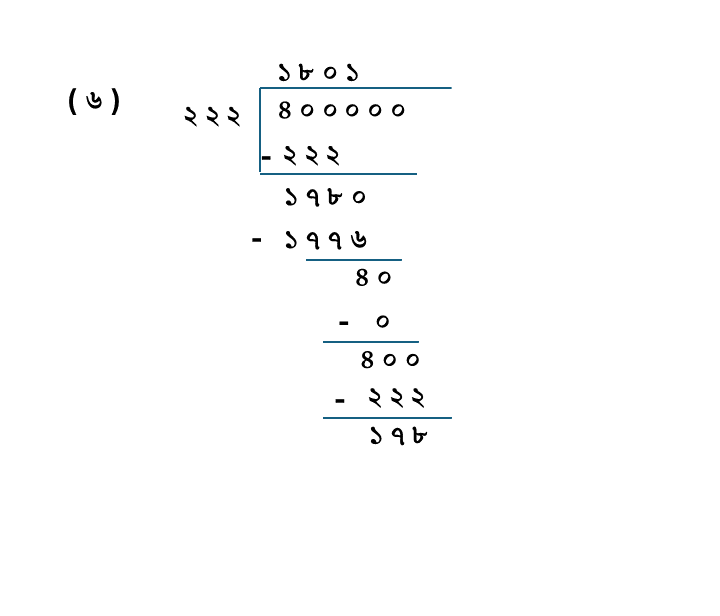
| ভাজ্য = | ৪০০০০০ |
| ভাজক = | ২২২ |
| ভাগফল = | ১৮০১ |
| ভাগশেষ = | ১৭৮ |
ভাজক × ভাগফল + ভাগশেষ
২২২×১৮০১ + ১৭৮
= ৩৯৯৮২২ + ১৭৮
= ৪০০০০০
= ভাজ্য
(৭) ১৪২৬৮৪÷৪৩৫
উত্তরঃ
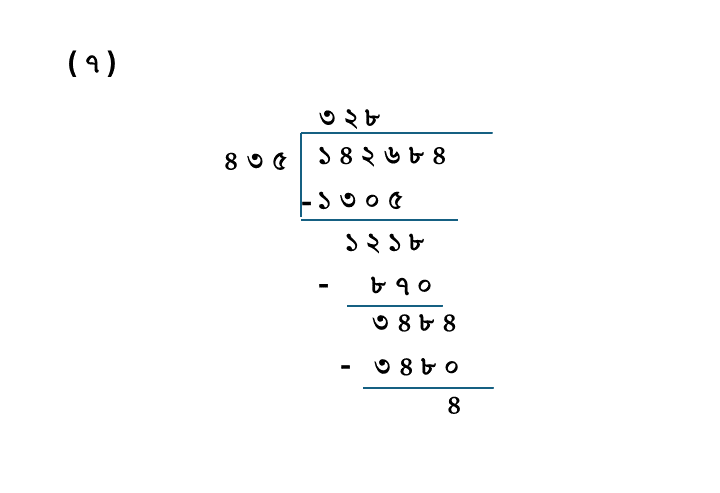
| ভাজ্য = | ১৪২৬৮৪ |
| ভাজক = | ৪৩৫ |
| ভাগফল = | ৩২৮ |
| ভাগশেষ = | ৪ |
ভাজক × ভাগফল + ভাগশেষ
৪৩৫×৩২৮ + ৪
= ১৪২৬৮০ + ৪
= ১৪২৬৮৪
= ভাজ্য
(৮) ১৩৪২০৩÷৩৩৩
উত্তরঃ
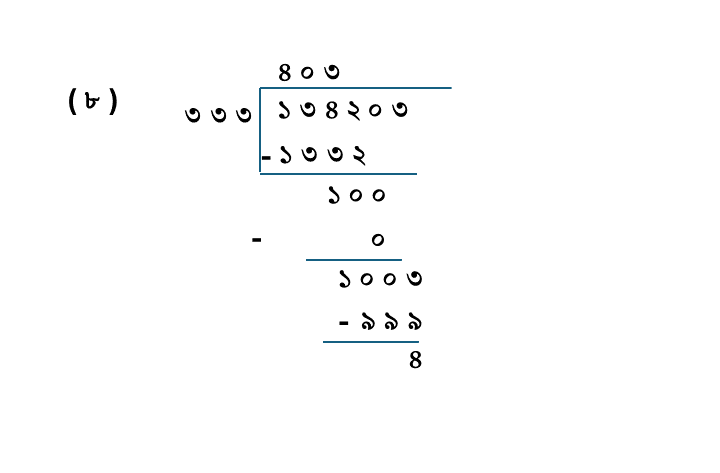
| ভাজ্য = | ১৩৪২০৩ |
| ভাজক = | ৩৩৩ |
| ভাগফল = | ৪০৩ |
| ভাগশেষ = | ৪ |
ভাজক × ভাগফল + ভাগশেষ
৩৩৩×৪০৩ + ৪
= ১৩৪১৯৯ + ৪
= ১৩৪২০৩
= ভাজ্য
(৯) ১৩৫৬২৮÷৩৩৯
উত্তরঃ
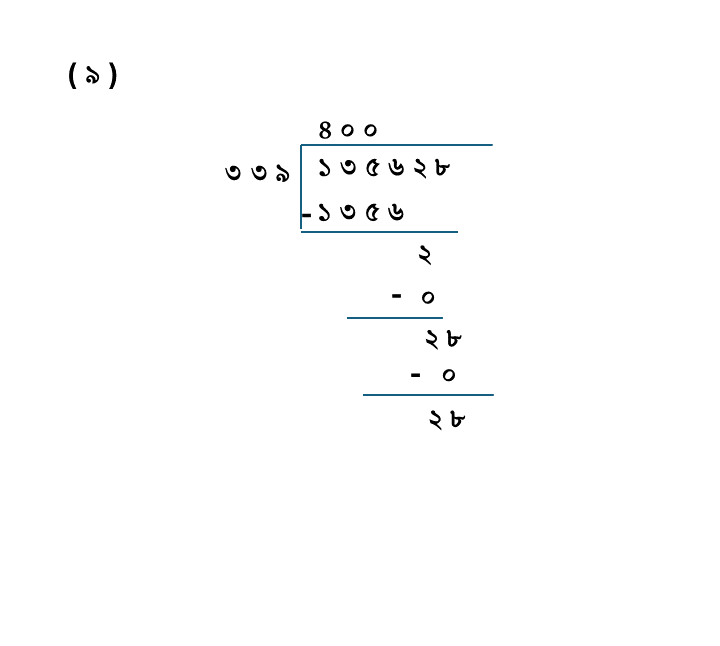
| ভাজ্য = | ১৩৫৬২৮ |
| ভাজক = | ৩৩৯ |
| ভাগফল = | ৪০০ |
| ভাগশেষ = | ২৮ |
ভাজক × ভাগফল + ভাগশেষ
৩৩৯×৪০০ + ২৮
= ১৩৫৬০০ + ২৮
= ১৩৫৬২৮
= ভাজ্য
(১০) ৫৩৮৯১৩÷৩৬৬
উত্তরঃ
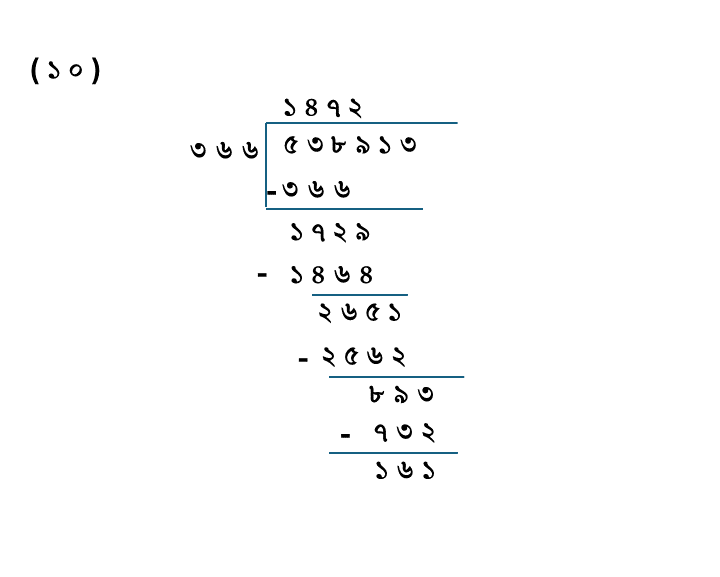
| ভাজ্য = | ৫৩৮৯১৩ |
| ভাজক = | ৩৬৬ |
| ভাগফল = | ১৪৭২ |
| ভাগশেষ = | ১৬১ |
ভাজক × ভাগফল + ভাগশেষ
৩৬৬×১৪৭২ + ১৬১
= ৫৩৮৭৫২ + ১৬১
= ৫৩৮৯১৩
= ভাজ্য
Class V Math Solution WBBSE Page 76:
সমস্যা বুঝে সমাধানের চেষ্টা করি:
১। দুটি সংখ্যার গুণফল ১০৩৫; একটি সংখ্যা ২৩ হলে, অন্যটি কত?
উত্তরঃ
১০৩৫ = ২৩×৪৫
অর্থাৎ, দুটি সংখ্যার গুণফল ১০৩৫ এ একটি সংখ্যা ২৩ হলে অপর সংখ্যাটি হবে ৪৫।
২। ক্রিকেট খেলার টিকিট কেনার জন্য ৩টি সারিতে লোকেরা দাঁড়িয়ে আছে। প্রতিটি সারিতে ৪৮৩০ জন দাঁড়িয়ে আছে। সেখান থেকে ২৫৩৯ জন চলে গেল। এখন কত জন লাইনে দাঁড়িয়ে আছে?
উত্তরঃ
প্রতিটি সারিতে ৪৮৩০ জন দাড়িয়ে আছে
অর্থাৎ, তিনটি সারিতে মোট দাড়িয়ে আছে,
৩×৪৮৩০ = ১৪৪৯০ জন
এখন সেখান থেকে ২৫৩৯ জন চলে গেল।
অর্থাৎ, ১৪৪৯০ জন থেকে ২৫৩৯ জন চলে গেল।
তাহলে (১৪৮৯০-২৫৩৯)=১১৯৫১ জন লাইনে দাঁড়িয়ে আছে।
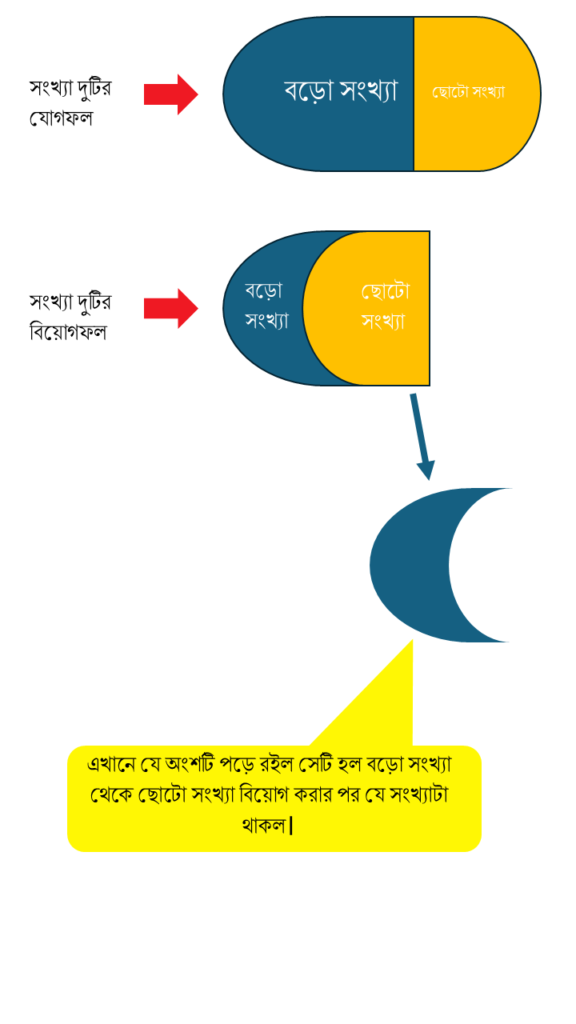
৩। দুটি সংখ্যার যোগফল ২৪২০ এবং তাদের বিয়োগফল ১২২৪ হলে, সংখ্যা দুটি কী কী?
উত্তরঃ
[আমরা অনেকেই জেনেছি যে এরকম অংকের ক্ষেত্রে একটা সূত্র আমরা জানি যে,
বড়োসংখ্যা = (জগফল+বিয়োগফল)/২
কিন্তু, সেটা কেন করবো এখানে সেটা বোঝার চেষ্টা করবো]
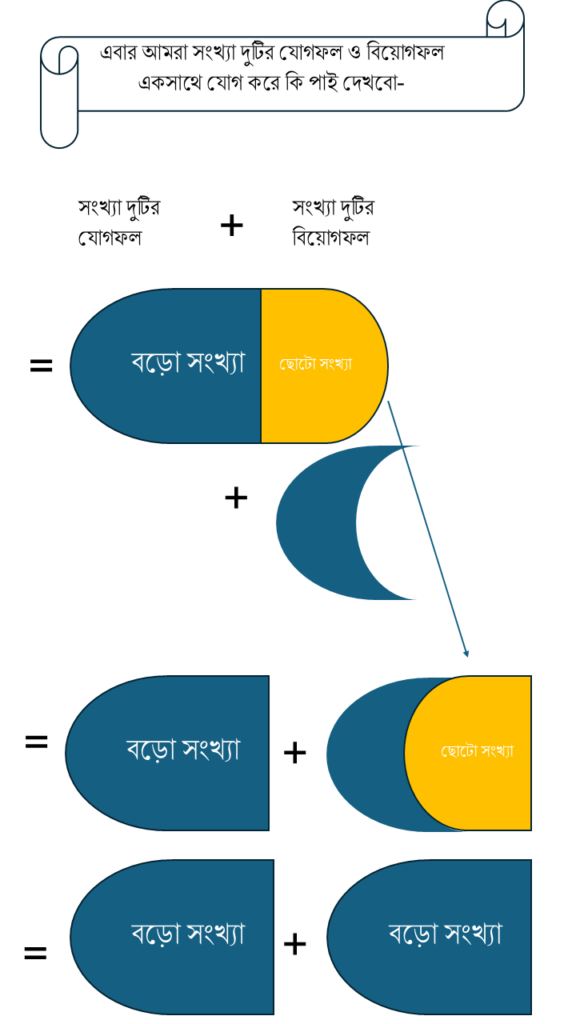

৪। একটি চাকরির পরীক্ষার জন্য ৫০১২৫ জন প্রার্থী এসেছেন। একটি ঘরে ২৫ জন করে বসতে দেওয়া হল। মোট কতগুলি ঘরে সবাই বসল?
উত্তরঃ
একটি চাকরির পরীক্ষার জন্য ৫০১২৫ জন প্রার্থী এসেছেন। একটি ঘরে ২৫ জন করে বসতে দেওয়া হল।
অর্থাৎ, ৫০১২৫ থেকে ২৫ জন করে বাদ দিয়ে ঘরের হিসাব করতে হবে।
[৫০১২৫ কে ২৫ দিয়ে ভাগ করতে হবে]
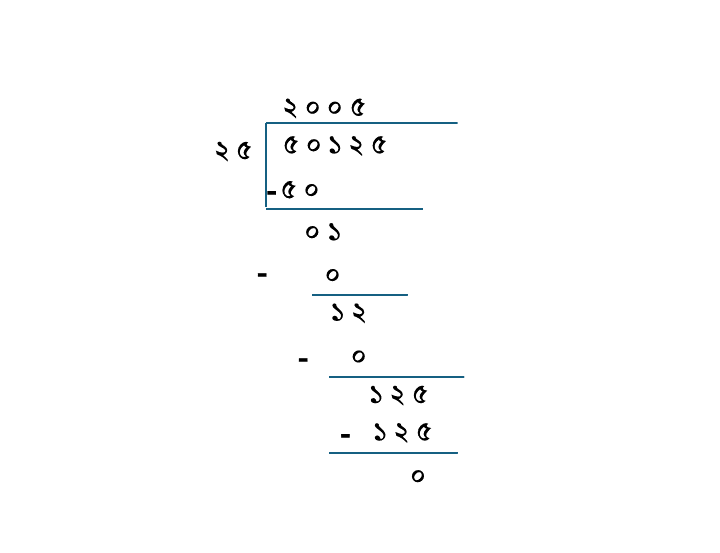
৫০১২৫÷২৫ = ২০০৫ টি ঘরে সবাই বসবে।
৫। বাবা ও ছেলের বর্তমান বয়সের সমষ্টি ৬০ বছর। ১৫ বছর পর তাদের বয়সের সমষ্টি কত হবে?
উত্তরঃ
বাবা ও ছেলের বর্তমান বয়সের সমষ্টি ৬০ বছর
১৫ বছর পর উভয়েরই বয়স ১৫ বছর করে বাড়বে।
সুতরাং, ১৫ বছর পর তাদের বয়সের সমষ্টি হবে,
৬০ + ১৫ + ১৫
= ৯০ বছর
৬। শুভ্রা ও শুভ্রার মায়ের বর্তমান বয়সের সমষ্টি ৫০ বছর। ১০ বছর আগে তাদের বয়সের সমষ্টি কত ছিল?
উত্তরঃ
শুভ্রা ও শুভ্রার মায়ের বর্তমান বয়সের সমষ্টি ৫০ বছর।
১০ বছর আগের বয়সে উভয়েরই বয়স ১০ বছর করে কমবে।
সুতরাং, ১০ বছর আগে তাদের বয়সের সমষ্টি হবে,
৫০ – ১০ – ১০
= ৩০ বছর
৭। এক ব্যক্তির ৬০০০০ টাকা ছিল। তিনি ২৫০০ টাকা স্ত্রীকে ও ১০৫০০ টাকা পুত্রকে দিলেন। বাকি টাকা তিনি দান করলেন। তিনি কত টাকা দান করেছিলেন?
উত্তরঃ
এক ব্যক্তির ৬০০০০ টাকা ছিল।
তিনি ২৫০০ টাকা স্ত্রীকে দিলেন।
অতএব, স্ত্রিকে দেওয়ার পর তিনার কাছে থাকল,
৬০০০০-২৫০০ = ৫৭৫০০ টাকা
এরপর তিনি পুত্রকে দিলেন ১০৫০০ টাকা
পুত্রকে দেওয়ার পর তিনার কাছে থাকল,
৫৭৫০০ – ১০৫০০ = ৪৭০০০ টাকা
অতএব, তিনি ৪৭০০০ টাকা দান করে দিলেন।
৮। ১ এবং ১০ এর মধ্যবর্তী মৌলিক সংখ্যাগুলির যোগফল নির্ণয় করি।
উত্তরঃ
১ ও ১০ এর মধ্যবর্তী মৌলিক সংখ্যাগুলি হল,
২,৩,৫,৭
এদের যোগফল,
২+৩+৫+৭
= ১৭
৯। একটি শ্রেণির ৪২ জন শিশুর গড় বয়স ১১ বছর। তাহলে তাদের বয়সের সমষ্টি কত?
উত্তরঃ
একটি শ্রেণির ৪২ জন শিশুর গড় বয়স ১১ বছর।
তাদের বয়সের সমষ্টি,
৪২×11
= ৪৬২
১০। একটি সৈন্যদলের ২৫৮০ জনকে এক জায়গায় প্রশিক্ষণে পাঠানো হলো। ১২৭০ জনকে আর এক জায়গায় প্রশিক্ষণে পাঠানো হলো। বাকি ৮০০০ জনকে পরে প্রশিক্ষণে পাঠানো হবে। ঐ সৈন্যদলে মোট সৈন্যসংখ্যা কত?
উত্তরঃ
সৈন্যদলে মোট সৈন্যসংখ্যা
= ২৫৮০ + ১২৭০ + ৮০০০
= ১১৮৫০ জন
আমার গণিত পঞ্চম শ্রেণি গণিত সমাধান Page 77:
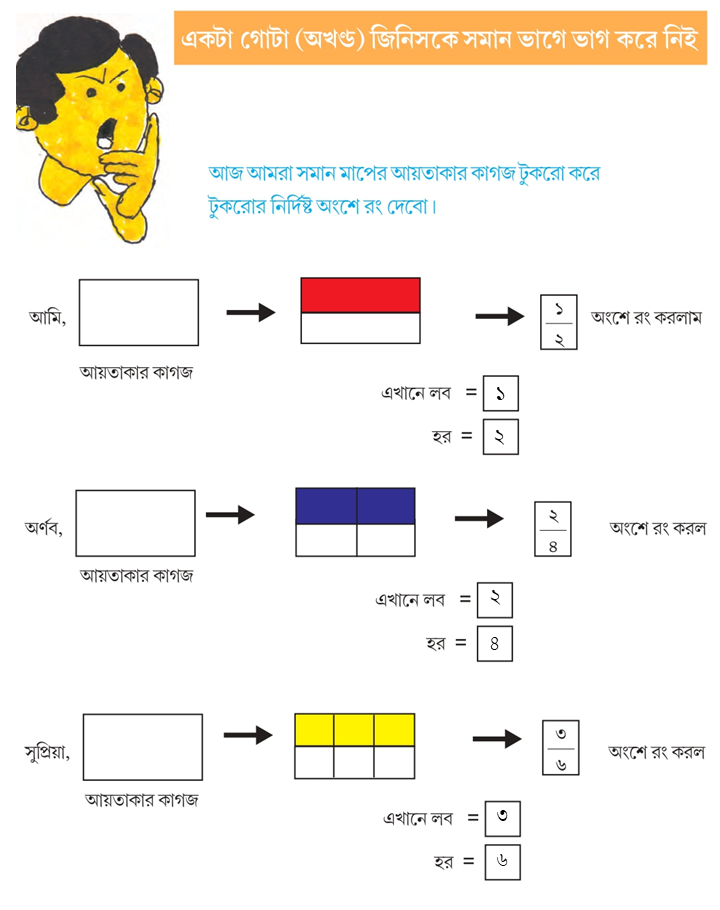
আমার গণিত পঞ্চম শ্রেণি গণিত সমাধান Page 78:
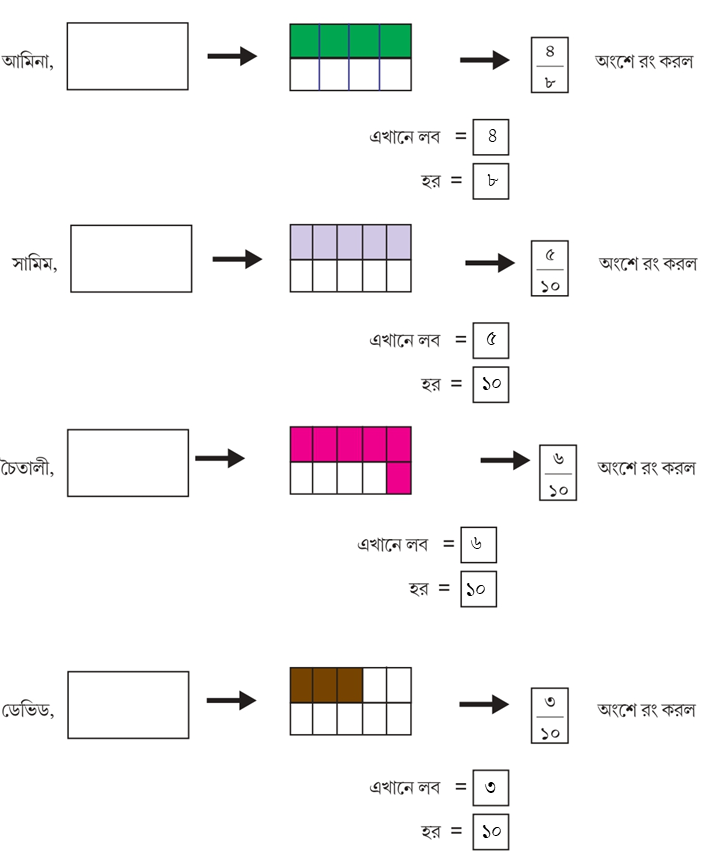
আমার গণিত পঞ্চম শ্রেণি গণিত সমাধান Page 79:
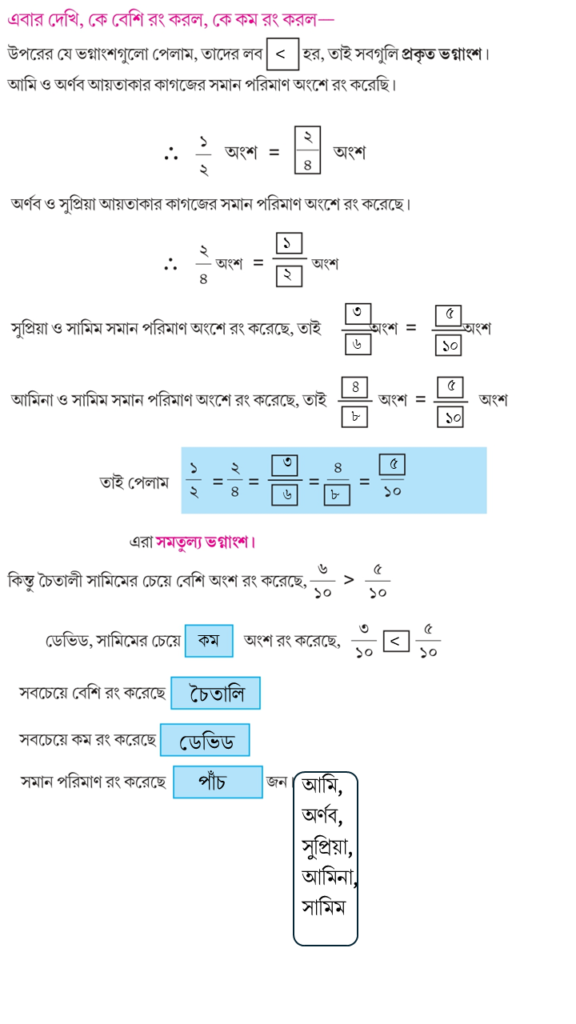
আমার গণিত ক্লাস ৫ এর সমাধান Page 80:
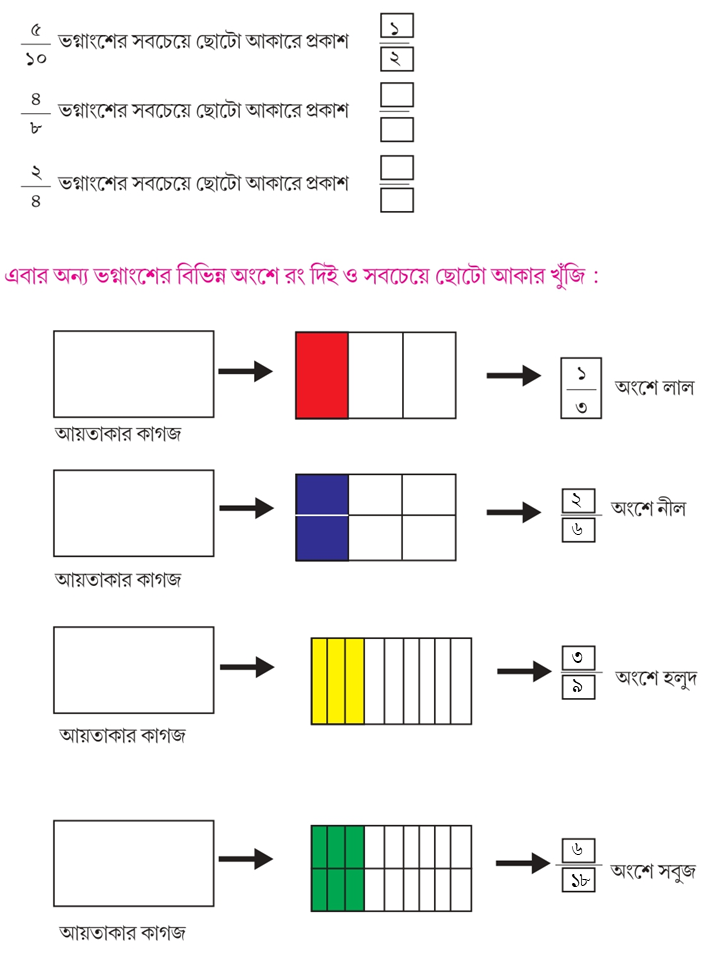
আমার গণিত ক্লাস ৫ এর সমাধান Page 81:

আমার গণিত ক্লাস ৫ এর সমাধান Page 82:

Page 83:
Page 84:
Page 85:
Page 86:
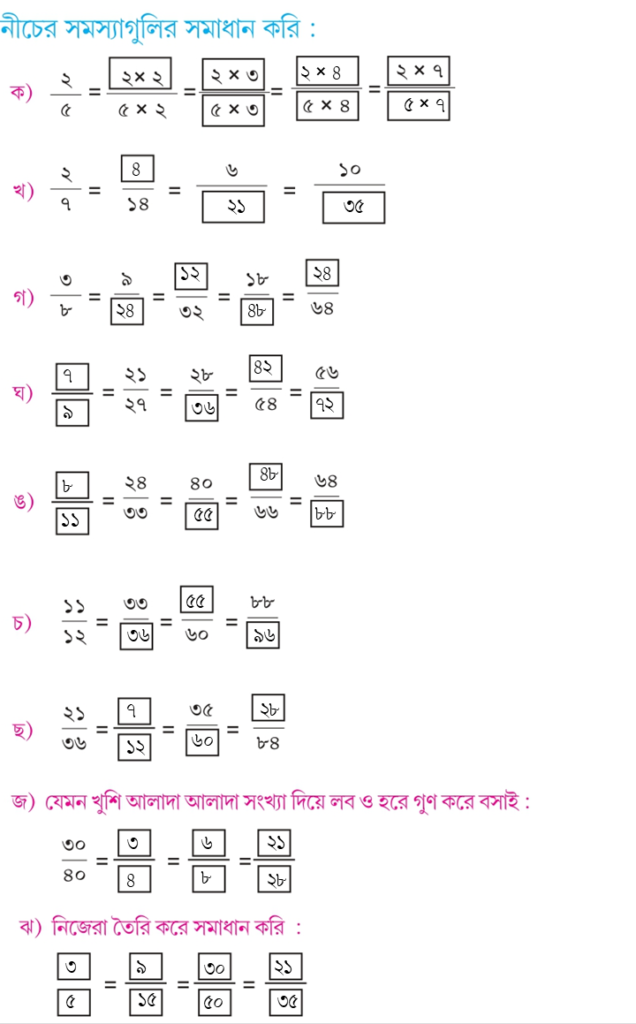
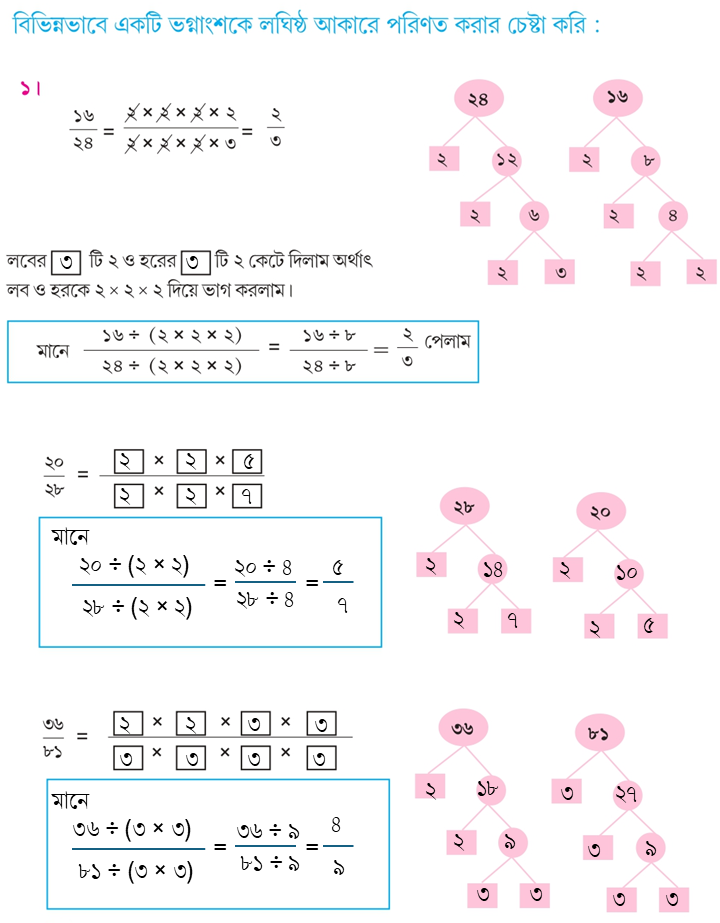
নীচের ভগ্নাংশগুলি লঘিষ্ঠ আকারে প্রকাশ করিঃ
(১) \(\frac{৭২}{৯৯}\)
উত্তরঃ
| \(\frac{৭২}{৯৯}\) |
| = \(\frac{৮\times৩\times৩}{১১\times৩\times৩}\) |
| = \(\frac{৮}{১১}\) |
(২) \(\frac{৭৮}{১০২}\)
উত্তরঃ
| \(\frac{৭৮}{১০২}\) |
| = \(\frac{২\times৩\times১৩}{২\times৩\times১৭}\) |
| = \(\frac{১৩}{১৭}\) |
(৩) \(\frac{৮৪}{১০৮}\)
উত্তরঃ
| \(\frac{৮৪}{১০৮}\) |
| = \(\frac{২\times২\times৩\times৭}{২\times২\times৩\times৩\times৩}\) |
| = \(\frac{৭}{৯}\) |
(৪) \(\frac{১২০}{১৪৪}\)
উত্তরঃ
| \(\frac{১২০}{১৪৪}\) |
| = \(\frac{২\times২\times২\times৩\times৫}{২\times২\times২\times২\times৩\times৩}\) |
| = \(\frac{৫}{৬}\) |
(৫) \(\frac{৮৪}{১০২}\)
উত্তরঃ
| \(\frac{৮৪}{১০২}\) |
| = \(\frac{২\times২\times৩\times৭}{২\times৩\times১৭}\) |
| = \(\frac{১৪}{১৭}\) |
(৬) \(\frac{১৩৮}{১৬২}\)
উত্তরঃ
| \(\frac{১৩৮}{১৬২}\) |
| = \(\frac{২\times৩\times২৩}{২\times৩\times২৭}\) |
| = \(\frac{২৩}{২৭}\) |
(৭) \(\frac{২৪৮}{২৬৪}\)
উত্তরঃ
| \(\frac{২৪৮}{২৬৪}\) |
| = \(\frac{২\times২\times২\times৩১}{২\times২\times২\times৩৩}\) |
| = \(\frac{৩১}{৩৩}\) |
(৮) \(\frac{২১৫}{২৮৫}\)
উত্তরঃ
| \(\frac{২১৫}{২৮৫}\) |
| = \(\frac{৫\times৪৩}{৫\times৫৭}\) |
| = \(\frac{৪৩}{৫৭}\) |
\(\frac{১}{৩}, \frac{১}{৪}, \frac{১}{৫}, \frac{১}{৭}\) কে ১২ লব বিশিষ্ট ভগ্নাংশে পরিণত করিঃ
| \(\frac{১}{৪}\) | \(\frac{১}{৫}\) | \(\frac{১}{৭}\) |
| =\(\frac{১\times১২}{৪\times১২}\) | =\(\frac{১\times১২}{৫\times১২}\) | =\(\frac{১\times১২}{৭\times১২}\) |
| =\(\frac{১২}{৪৮}\) | =\(\frac{১২}{৬০}\) | =\(\frac{১২}{৮৪}\) |
Page 87:
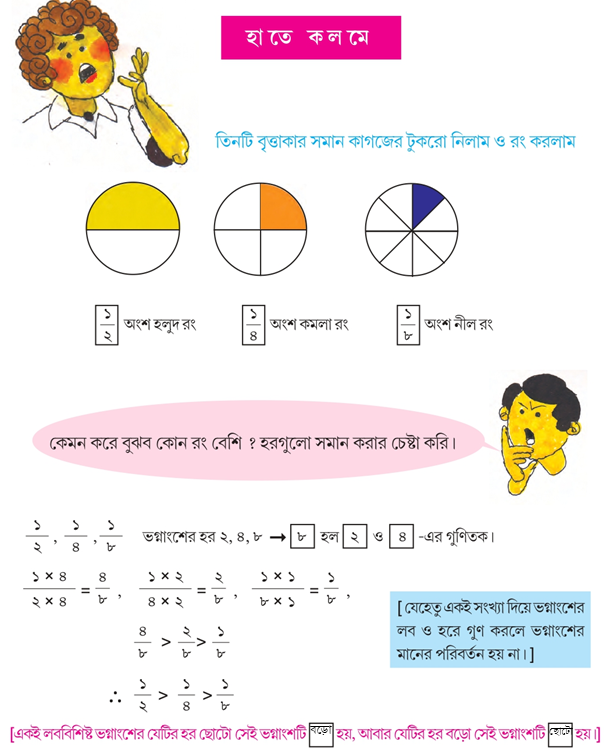
Class 5 Math Solution WBBSE Page 88:

২। একই হরবিশিষ্ট ভগ্নাংশে পরিণত করি :
(ক) \(\frac{২}{৩}\) ও \(\frac{২}{৯}\)
উত্তরঃ
| \(\frac{২}{৩}\) | \(\frac{২}{৯}\) |
| = \(\frac{২\times৩}{৩\times৩}\) | |
| = \(\frac{৬}{৯}\) |
(খ) \(\frac{১}{৪}\) ও \(\frac{৩}{৩২}\)
উত্তরঃ
| \(\frac{১}{৪}\) | \(\frac{৩}{৩২}\) |
| = \(\frac{১\times৮}{৪\times৮}\) | |
| = \(\frac{৮}{৩২}\) |
৩। (ক) \(\frac{২}{৭}\) ও \(\frac{২}{২১}\) এর মধ্যে কোনটি ছোটো ও কোনটি বড়ো লিখি।
উত্তরঃ
| \(\frac{২}{৭}\) | \(\frac{২}{২১}\) |
| = \(\frac{২\times৩}{৭\times৩}\) | |
| = \(\frac{৬}{২১}\) |
অতএব, \(\frac{২}{৭}\) বড়ো এবং \(\frac{২}{২১}\) ছোটো
৩। (খ) \(\frac{১}{৪}\), \(\frac{১}{৮}\) ও \(\frac{১}{১৬}\) কে ছোটো থেকে বড়ো সাজাই।
উত্তরঃ
| \(\frac{১}{৪}\) | \(\frac{১}{৮}\) | \(\frac{১}{১৬}\) |
| = \(\frac{১\times৪}{৪\times৪}\) | = \(\frac{১\times২}{৮\times২}\) | |
| = \(\frac{৪}{১৬}\) | = \(\frac{২}{১৬}\) |
সুতরাং,
\(\frac{১}{১৬}\) < \(\frac{১}{৮}\) < \(\frac{১}{৪}\)
৩। (গ) \(\frac{৩}{৫}\) ও \(\frac{৪}{২৫}\) এর মধ্যে কোনটি ছোটো ও কোনটি বড়ো লিখি।
উত্তরঃ
| \(\frac{৩}{৫}\) | \(\frac{৪}{২৫}\) |
| = \(\frac{৩\times৫}{৫\times৫}\) | |
| = \(\frac{১৫}{২৫}\) |
অতএব, \(\frac{৩}{৫}\) বড়ো এবং \(\frac{৪}{২৫}\) ছোটো
৩। (ঘ) \(\frac{১}{৩}\), \(\frac{১}{৯}\) ও \(\frac{১}{২৭}\) কে ছোটো থেকে বড়ো সাজাই।
উত্তরঃ
| \(\frac{১}{৩}\) | \(\frac{১}{৯}\) | \(\frac{১}{২৭}\) |
| = \(\frac{১\times৯}{৩\times৯}\) | = \(\frac{১\times৩}{৯\times৩}\) | |
| = \(\frac{৯}{২৭}\) | = \(\frac{৩}{২৭}\) |
সুতরাং,
\(\frac{১}{২৭}\) < \(\frac{১}{৯}\) < \(\frac{১}{৩}\)
Page 89:

Page 90:
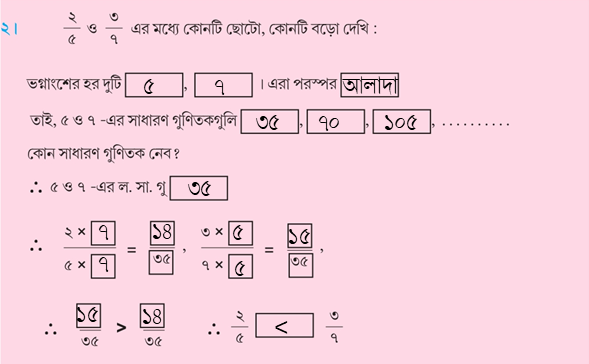
৩। একই হর বিশিষ্ট ভগ্নাংশে পরিণত করি:
(ক) \(\frac{১}{৩}\), \(\frac{১}{৭}\)
উত্তরঃ
৩ ও ৭ এর ল.সা.গু = ২১
| \(\frac{১}{৩}\) | \(\frac{১}{৭}\) |
| = \(\frac{১\times৭}{৩\times৭}\) | = \(\frac{১\times৩}{৭\times৩}\) |
| = \(\frac{৭}{২১}\) | = \(\frac{৩}{২১}\) |
(খ) \(\frac{২}{৫}\), \(\frac{২}{৮}\)
উত্তরঃ
৫ ও ৮ এর ল.সা.গু = ৪০
| \(\frac{২}{৫}\) | \(\frac{২}{৮}\) |
| = \(\frac{২\times৮}{৫\times৮}\) | = \(\frac{২\times৫}{৮\times৫}\) |
| = \(\frac{১৬}{৪০}\) | = \(\frac{১০}{৪০}\) |
৪। (ক) \(\frac{৩}{৫}\) ও \(\frac{৪}{৭}\) এর মধ্যে কোনটি ছোটো কোনটি বড়ো লিখি।
উত্তরঃ
৫ ও ৭ এর ল.সা.গু = ৩৫
| \(\frac{৩}{৫}\) | \(\frac{৪}{৭}\) |
| = \(\frac{৩\times৭}{৫\times৭}\) | = \(\frac{৪\times৫}{৭\times৫}\) |
| = \(\frac{২১}{৩৫}\) | = \(\frac{২০}{৩৫}\) |
অতএব, \(\frac{৩}{৫}\) বড়ো এবং \(\frac{৪}{৭}\) ছোটো
৪। (খ) \(\frac{৩}{৭}\) ও \(\frac{৫}{১১}\) এর মধ্যে কোনটি ছোটো কোনটি বড়ো লিখি।
উত্তরঃ
৭ ও ১১ এর ল.সা.গু = ৭৭
| \(\frac{৩}{৭}\) | \(\frac{৫}{১১}\) |
| = \(\frac{৩\times১১}{৭\times১১}\) | = \(\frac{৫\times৭}{১১\times৭}\) |
| = \(\frac{৩৩}{৭৭}\) | = \(\frac{৩৫}{৭৭}\) |
অতএব, \(\frac{৫}{১১}\) বড়ো এবং \(\frac{৩}{৭}\) ছোটো
৪। (গ) \(\frac{১}{৫}\), \(\frac{১}{২}\), \(\frac{২}{৩}\) ভগ্নাংশগুলি ছোটো থেকে বড়ো সাজাই।
উত্তরঃ
৫,২ ও ৩ এর ল.সা.গু = ৩০
| \(\frac{১}{৫}\) | \(\frac{১}{২}\) | \(\frac{২}{৩}\) |
| = \(\frac{১\times৬}{৫\times৬}\) | = \(\frac{১\times১৫}{২\times১৫}\) | = \(\frac{২\times১০}{৩\times১০}\) |
| = \(\frac{৬}{৩০}\) | = \(\frac{১৫}{৩০}\) | = \(\frac{২০}{৩০}\) |
সুতরাং,
\(\frac{১}{৫}\) < \(\frac{১}{২}\) < \(\frac{২}{৩}\)
8। (ঘ) \(\frac{১}{২}\), \(\frac{১}{৩}\) ও \(\frac{৪}{৫}\) ভগ্নাংশগুলি ছোটো থেকে বড়ো সাজাই।
উত্তরঃ
২,৩ ও ৫ এর ল.সা.গু = ৩০
| \(\frac{১}{৩}\) | \(\frac{১}{২}\) | \(\frac{৪}{৫}\) |
| = \(\frac{১\times১০}{৩\times১০}\) | = \(\frac{১\times১৫}{২\times১৫}\) | = \(\frac{৪\times৬}{৫\times৬}\) |
| = \(\frac{১০}{৩০}\) | = \(\frac{১৫}{৩০}\) | = \(\frac{২৪}{৩০}\) |
সুতরাং,
\(\frac{১}{৩}\) < \(\frac{১}{২}\) < \(\frac{৪}{৫}\)
Page 91:

Page 92:
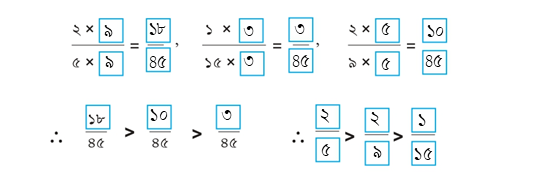
৩। লঘিষ্ঠ সাধারণ হর বিশিষ্ট ভগ্নাংশে পরিণত করিঃ
(ক) \(\frac{২}{৯}\), \(\frac{১}{১৫}\), \(\frac{২}{২৫}\)
উত্তরঃ
ভগ্নাংশের হর গুলি হল ৯, ১৫ ও ২৫
৯, ১৫ ও ২৫ এর ল.সা.গু
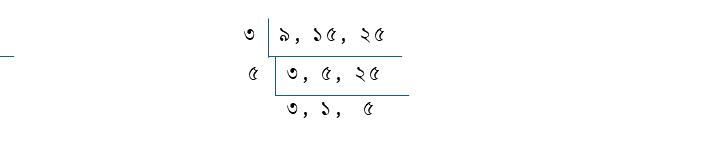
৩×৫×৩×৫ = ২২৫
| \(\frac{২}{৯}\) | \(\frac{১}{১৫}\) | \(\frac{২}{২৫}\) |
| = \(\frac{২\times২৫}{৯\times২৫}\) | = \(\frac{১\times১৫}{১৫\times১৫}\) | = \(\frac{২\times৯}{২৫\times৯}\) |
| = \(\frac{৫০}{২২৫}\) | = \(\frac{১৫}{২২৫}\) | = \(\frac{১৮}{২২৫}\) |
(খ) \(\frac{১}{১৪}\), \(\frac{২}{৭}\), \(\frac{৩}{২১}\)
উত্তরঃ
ভগ্নাংশের হর গুলি হল ১৪, ৭ ও ২১
১৪, ৭ ও ২১ এর ল.সা.গু
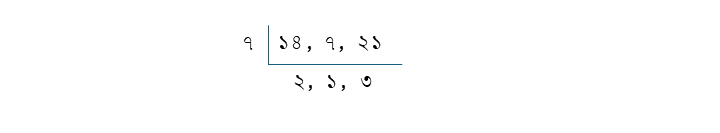
৭×২×৩ = ৪২
| \(\frac{১}{১৪}\) | \(\frac{২}{৭}\) | \(\frac{৩}{২১}\) |
| = \(\frac{১\times৩}{১৪\times৩}\) | = \(\frac{২\times৬}{৭\times৬}\) | = \(\frac{৩\times২}{২১\times২}\) |
| = \(\frac{৩}{৪২}\) | = \(\frac{১২}{৪২}\) | = \(\frac{৬}{৪২}\) |
৪। নীচের ভগ্নাংশগুলি ছোটো থেকে বড়ো সাজাইঃ
(ক) \(\frac{২}{৩}\), \(\frac{৪}{৯}\), \(\frac{৫}{৬}\)
উত্তরঃ
ভগ্নাংশের হর গুলি হল ৩, ৯ ও ৬
৩, ৯ ও ৬ এর ল.সা.গু
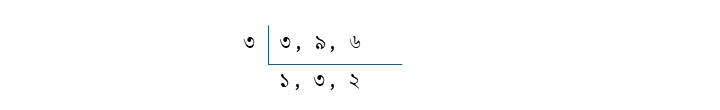
৩×৩×২ = ১৮
| \(\frac{২}{৩}\) | \(\frac{৪}{৯}\) | \(\frac{৫}{৬}\) |
| = \(\frac{২\times৬}{৩\times৬}\) | = \(\frac{৪\times২}{৯\times২}\) | = \(\frac{৫\times৩}{৬\times৩}\) |
| = \(\frac{১২}{১৮}\) | = \(\frac{৮}{১৮}\) | = \(\frac{১৫}{১৮}\) |
অতএব,
\(\frac{৮}{১৮}\) < \(\frac{১২}{১৮}\) < \(\frac{১৫}{১৮}\)
অতএব,
\(\frac{৪}{৯}\) < \(\frac{২}{৩}\) < \(\frac{৫}{৬}\)
(খ) \(\frac{৩}{১০}\), \(\frac{৭}{৫}\), \(\frac{১}{৪}\)
উত্তরঃ
ভগ্নাংশের হর গুলি হল ১০, ৫ ও ৪
১০, ৫ ও ৪ এর ল.সা.গু
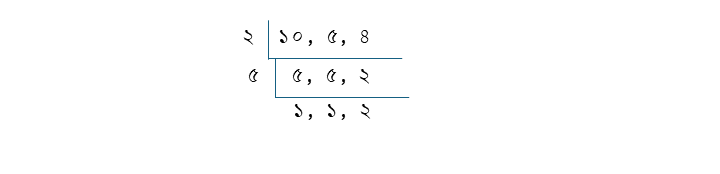
২×৫×২ = ২০
| \(\frac{৩}{১০}\) | \(\frac{৭}{৫}\) | \(\frac{১}{৪}\) |
| = \(\frac{৩\times২}{১০\times২}\) | = \(\frac{৭\times৪}{৫\times৪}\) | = \(\frac{১\times৫}{৪\times৫}\) |
| = \(\frac{৬}{২০}\) | = \(\frac{২৮}{২০}\) | = \(\frac{৫}{২০}\) |
অতএব,
\(\frac{৫}{২০}\) < \(\frac{৬}{২০}\) < \(\frac{২৮}{২০}\)
অতএব,
\(\frac{১}{৪}\) < \(\frac{৩}{১০}\) < \(\frac{৭}{৫}\)
(গ) \(\frac{২}{৩}\), \(\frac{১}{৫}\), \(\frac{৪}{১৫}\)
উত্তরঃ
ভগ্নাংশের হর গুলি হল ৩, ৫ ও ১৫
৩, ৫ ও ১৫ এর ল.সা.গু
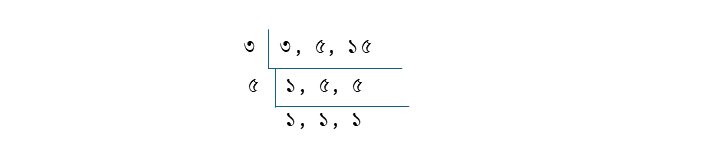
৩×৫ = ১৫
| \(\frac{২}{৩}\) | \(\frac{১}{৫}\) | \(\frac{৪}{১৫}\) |
| = \(\frac{২\times৫}{৩\times৫}\) | = \(\frac{১\times৩}{৫\times৩}\) | |
| = \(\frac{১০}{১৫}\) | = \(\frac{৩}{১৫}\) |
অতএব,
\(\frac{৩}{১৫}\) < \(\frac{৪}{১৫}\) < \(\frac{১০}{১৫}\)
অতএব,
\(\frac{১}{৫}\) < \(\frac{৪}{১৫}\) < \(\frac{২}{৩}\)
(ঘ) \(\frac{১}{৪}\), \(\frac{২}{৩}\), \(\frac{১}{১৮}\)
উত্তরঃ
ভগ্নাংশের হর গুলি হল ৪, ৩ ও ১৮
৪, ৩ ও ১৮ এর ল.সা.গু
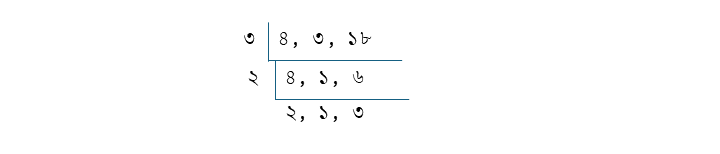
৩×২×২×৩ = ৩৬
| \(\frac{১}{৪}\) | \(\frac{২}{৩}\) | \(\frac{১}{১৮}\) |
| = \(\frac{১\times৯}{৪\times৯}\) | = \(\frac{২\times১২}{৩\times১২}\) | = \(\frac{১\times২}{১৮\times২}\) |
| = \(\frac{৯}{৩৬}\) | = \(\frac{২৪}{৩৬}\) | = \(\frac{২}{৩৬}\) |
অতএব,
\(\frac{২}{৩৬}\) < \(\frac{৯}{৩৬}\) < \(\frac{২৪}{৩৬}\)
অতএব,
\(\frac{১}{১৮}\) < \(\frac{১}{৪}\) < \(\frac{২}{৩}\)
(ঙ) \(\frac{১}{২০}\), \(\frac{২}{১৫}\), \(\frac{৩}{৫}\)
উত্তরঃ
ভগ্নাংশের হর গুলি হল ২০, ১৫ ও ৫
২০, ১৫ ও ৫ এর ল.সা.গু
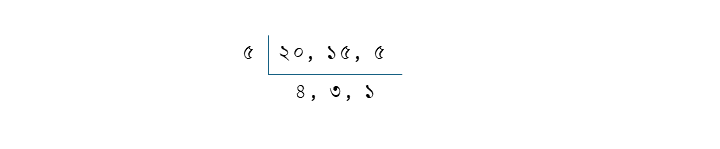
৫×৪×৩ = ৬০
| \(\frac{১}{২০}\) | \(\frac{২}{১৫}\) | \(\frac{৩}{৫}\) |
| = \(\frac{১\times৩}{২০\times৩}\) | = \(\frac{২\times৪}{১৫\times৪}\) | = \(\frac{৩\times১২}{৫\times১২}\) |
| = \(\frac{৩}{৬০}\) | = \(\frac{৮}{৬০}\) | = \(\frac{৩৬}{৬০}\) |
অতএব,
\(\frac{৩}{৬০}\) < \(\frac{৮}{৬০}\) < \(\frac{৩৬}{৬০}\)
অতএব,
\(\frac{১}{২০}\) < \(\frac{২}{১৫}\) < \(\frac{৩}{৫}\)
(চ) \(\frac{১}{১২}\), \(\frac{২}{৩}\), \(\frac{২}{১৮}\)
উত্তরঃ
ভগ্নাংশের হর গুলি হল ১২, ৩ ও ১৮
১২, ৩ ও ১৮ এর ল.সা.গু

৩×২×২×৩ = ৩৬
| \(\frac{১}{১২}\) | \(\frac{২}{৩}\) | \(\frac{২}{১৮}\) |
| = \(\frac{১\times৩}{১২\times৩}\) | = \(\frac{২\times১২}{৩\times১২}\) | = \(\frac{২\times২}{১৮\times২}\) |
| = \(\frac{৩}{৩৬}\) | = \(\frac{২৪}{৩৬}\) | = \(\frac{৪}{৩৬}\) |
অতএব,
\(\frac{৩}{৩৬}\) < \(\frac{৪}{৩৬}\) < \(\frac{২৪}{৩৬}\)
অতএব,
\(\frac{১}{১২}\) < \(\frac{২}{১৮}\) < \(\frac{২}{৩}\)

Page 94:
Page 95:
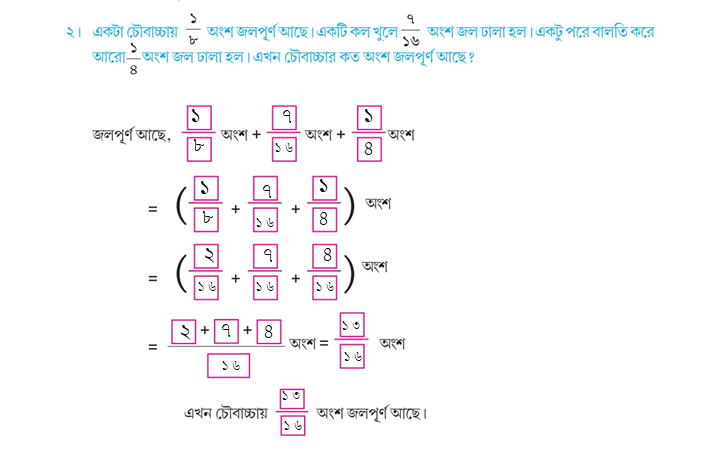
৩। যোগ করিঃ
(ক) \(\frac{১}{২}\) + \(\frac{১}{৪}\) + \(\frac{১}{৮}\)
উত্তরঃ
| \(\frac{১}{২}\) + \(\frac{১}{৪}\) + \(\frac{১}{৮}\) |
| = \(\frac{১\times৪}{২\times৪}\) + \(\frac{১\times২}{৪\times২}\) + \(\frac{১}{৮}\) |
| = \(\frac{৪}{৮}\) + \(\frac{২}{৮}\) + \(\frac{১}{৮}\) |
| = \(\frac{৪+২+১}{৮}\) |
| = \(\frac{৭}{৮}\) |
(খ) \(\frac{১}{৩}\) + \(\frac{২}{২৭}\) + \(\frac{১}{৯}\)
উত্তরঃ
| \(\frac{১}{৩}\) + \(\frac{২}{২৭}\) + \(\frac{১}{৯}\) |
| = \(\frac{১\times৯}{৩\times৯}\) + \(\frac{২}{২৭}\) + \(\frac{১\times৩}{৯\times৩}\) |
| = \(\frac{৯}{২৭}\) + \(\frac{২}{২৭}\) + \(\frac{৩}{২৭}\) |
| = \(\frac{৯+২+৩}{২৭}\) |
| = \(\frac{১৪}{২৭}\) |
(গ) \(\frac{১}{৪}\) + \(\frac{১}{৮}\) + \(\frac{২}{১৬}\)
উত্তরঃ
| \(\frac{১}{৪}\) + \(\frac{১}{৮}\) + \(\frac{২}{১৬}\) |
| = \(\frac{১\times৪}{৪\times৪}\) + \(\frac{১\times২}{৮\times২}\) + \(\frac{২}{১৬}\) |
| = \(\frac{৪}{১৬}\) + \(\frac{২}{১৬}\) + \(\frac{২}{১৬}\) |
| = \(\frac{৪+২+২}{১৬}\) |
| = \(\frac{৮}{১৬}\) |
| = \(\frac{১}{২}\) |
(ঘ) \(\frac{১}{৫}\) + \(\frac{২}{১৫}\) + \(\frac{৪}{২৫}\)
উত্তরঃ
| \(\frac{১}{৫}\) + \(\frac{২}{১৫}\) + \(\frac{৪}{২৫}\) |
| = \(\frac{১\times১৫}{৫\times১৫}\) + \(\frac{২\times৩}{১৫\times৫}\) + \(\frac{৪\times৩}{২৫\times৩}\) |
| = \(\frac{১৫}{৭৫}\) + \(\frac{৬}{৭৫}\) + \(\frac{১২}{৭৫}\) |
| = \(\frac{১৫+৬+১২}{৭৫}\) |
| = \(\frac{৩৩}{৭৫}\) |
Page 97:
৩। হাতে কলমে বোতামের সাহায্যে যোগ করিঃ
(ক) \(\frac{১}{৪}\) + \(\frac{১}{৩}\)
উত্তরঃ
এখানে ১২ টি বোতাম নিতে হবে।
১২ টি বোতামের \(\frac{১}{৪}\) অংশ মানে হচ্ছে, ১২ টি বোতামকে সমান চার ভাগ করে তার ১ অংশ, অর্থাৎ ৩ টি বোতাম।
আবার, ১২ টি বোতামের \(\frac{১}{৩}\) অংশ মানে হচ্ছে, ১২ টি বোতামকে সমান তিন ভাগ করে তার ১ অংশ, অর্থাৎ ৪ টি বোতাম।
অতএব, হাতে কলমে পেলাম,
\(\frac{১}{৪}\) + \(\frac{১}{৩}\) = \(\frac{৭}{১২}\)
(খ) \(\frac{১}{৫}\) + \(\frac{১}{৩}\)
উত্তরঃ
এখানে ১৫ টি বোতাম নিতে হবে।
১৫ টি বোতামের \(\frac{১}{৫}\) অংশ মানে হচ্ছে, ১৫ টি বোতামকে সমান পাঁচ ভাগ করে তার ১ অংশ, অর্থাৎ ৩ টি বোতাম।
আবার, ১৫ টি বোতামের \(\frac{১}{৩}\) অংশ মানে হচ্ছে, ১৫ টি বোতামকে সমান তিন ভাগ করে তার ১ অংশ, অর্থাৎ ৫ টি বোতাম।
অতএব, হাতে কলমে পেলাম,
\(\frac{১}{৫}\) + \(\frac{১}{৩}\) = \(\frac{৮}{১৫}\)
Page 98:
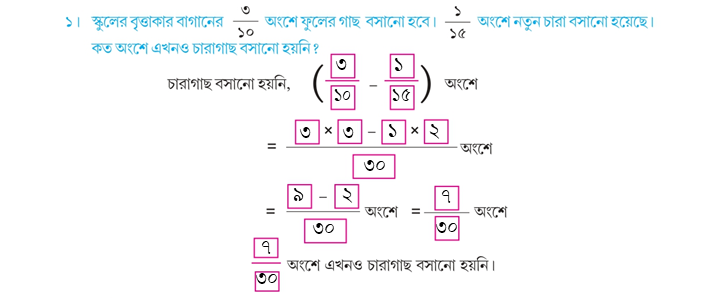
Class 5 Math Solution WBBSE Page 99:
২। বিয়োগ করিঃ
(ক) \(\frac{৭}{১৫}\) – \(\frac{১}{৫}\)
উত্তরঃ
| \(\frac{৭}{১৫}\) – \(\frac{১}{৫}\) |
| = \(\frac{৭ – ১\times৩}{১৫}\) |
| = \(\frac{৭ – ৩}{১৫}\) |
| = \(\frac{৪}{১৫}\) |
(খ) \(\frac{৩}{৭}\) – \(\frac{৫}{১৪}\)
উত্তরঃ
| \(\frac{৩}{৭}\) – \(\frac{৫}{১৪}\) |
| = \(\frac{৩\times২ – ৫}{১৪}\) |
| = \(\frac{৬ – ৫}{১৪}\) |
| = \(\frac{১}{১৪}\) |
(গ) \(\frac{৩}{৭}\) – \(\frac{৩}{৮}\)
উত্তরঃ
| \(\frac{৩}{৭}\) – \(\frac{৩}{৮}\) |
| = \(\frac{৩\times৮ – ৩\times৭}{৫৬}\) |
| = \(\frac{২৪ – ২১}{১৪}\) |
| = \(\frac{৩}{৫৬}\) |
(ঘ) \(\frac{১৩}{১৮}\) – \(\frac{৫}{২৭}\)
উত্তরঃ
| \(\frac{১৩}{১৮}\) – \(\frac{৫}{২৭}\) |
| = \(\frac{১৩\times৩ – ৫\times২}{৫৪}\) |
| = \(\frac{৩৯ – ১০}{৫৪}\) |
| = \(\frac{২৯}{৫৪}\) |
(ঙ) \(\frac{৬}{২০}\) – \(\frac{৭}{৩০}\)
উত্তরঃ
| \(\frac{৬}{২০}\) – \(\frac{৭}{৩০}\) |
| = \(\frac{৬\times৩ – ৭\times২}{৬০}\) |
| = \(\frac{১৮ – ১৪}{৬০}\) |
| = \(\frac{৪}{৬০}\) |
| = \(\frac{১}{১৫}\) |
৩। সিরাজ বাগানের \(\frac{৬}{১৭}\) অংশে ফুলের চারা লাগিয়েছে। মণিকা \(\frac{৩}{৩৪}\) অংশে ফুলের চারা লাগিয়েছে। কে কত বেশি অংশে ফুলের চারা লাগিয়েছে?
উত্তরঃ
ভগ্নাংশের হর গুলি সমান করে পাই,
| \(\frac{৬}{১৭}\) | \(\frac{৩}{৩৪}\) |
| = \(\frac{৬\times২}{১৭\times২}\) | |
| = \(\frac{১২}{৩৪}\) |
সুতরাং, সিরাজের অংশ বেশি।
অতএব,
| \(\frac{৬}{১৭}\) – \(\frac{৩}{৩৪}\) |
| = \(\frac{৬\times২ – ৩}{৩৪}\) |
| = \(\frac{১২ – ৩}{৩৪}\) |
| = \(\frac{৯}{৩৪}\) |
সিরাজ, \(\frac{৯}{৩৪}\) বেশি অংশে ফুলের চারা লাগিয়েছে।
৪। পাড়ায় রাস্তা মেরামত হচ্ছে। প্রথম দিনে \(\frac{৫}{১২}\) অংশ ও দ্বিতীয় দিনে \(\frac{৭}{১৮}\) অংশ মেরামত হয়েছে। কোন দিনে কত বেশি অংশ মেরামত হয়েছে?
উত্তরঃ
ভগ্নাংশের হর গুলি সমান করে পাই,
| \(\frac{৫}{১২}\) | \(\frac{৭}{১৮}\) |
| = \(\frac{৫\times৩}{১২\times৩}\) | = \(\frac{৭\times২}{১৮\times২}\) |
| = \(\frac{১৫}{৩৬}\) | = \(\frac{১৪}{৩৬}\) |
সুতরাং, প্রথম দিনে বেশি অংশ কাজ হয়েছে।
অতএব,
| \(\frac{৫}{১২}\) – \(\frac{৭}{১৮}\) |
| = \(\frac{৫\times৩ – ৭\times২}{৩৬}\) |
| = \(\frac{১৫ – ১৪}{৩৬}\) |
| = \(\frac{১}{৩৬}\) |
প্রথম দিনে দ্বিতীয় দিনের থেকে \(\frac{১}{৩৬}\) অংশ বেশি কাজ হয়েছে।
৫। মিহির বাড়ি থেকে স্টেশনে যাওয়ার সময় \(\frac{৭}{৮}\) অংশ বাসে ও \(\frac{১}{১২}\) অংশ সাইকেলে গেল। মিহির বাকি অংশ পথ হেঁটে গেল। মিহির মোট কত অংশ বাসে ও সাইকেলে গেল? কত অংশ হেঁটে গেল।
উত্তরঃ
| \(\frac{৭}{৮}\) + \(\frac{১}{১২}\) |
| = \(\frac{৭\times৩ + ১\times২}{২৪}\) |
| = \(\frac{২১ + ২}{২৪}\) |
| = \(\frac{২৩}{২৪}\) |
মিহির মোট \(\frac{২৩}{২৪}\) অংশ বাসে ও সাইকেলে গেল।
বাকি থাকে
\(১ – \frac{২৩}{২৪}\)
= \(\frac{২৪-২৩}{২৪}\)
= \(\frac{১}{২৪}\)
অতএব, মিহির \(\frac{১}{২৪}\) অংশ হেঁটে গেল।
Class 5 Math Solution WBBSE এর বাকি সমাধান তোমরা Page ভিত্তিক পেয়ে যাবে।
