Class 5 Math Solution WBBSE Page 100-150 | পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের অন্তর্গত পঞ্চম শ্রেণির শিক্ষার্থীদের জন্য ক্লাস 5 গণিতে ভীতি দূর করার জন্য আমার এই আমার গণিত পঞ্চম শ্রেণির সমাধান Page এ তোমাকে স্বাগত!
গণিত প্রায়শই একটি চ্যালেঞ্জিং বিষয় বলে মনে হতে পারে, কিন্তু সঠিক পদ্ধতি এবং স্পষ্ট ব্যাখ্যা সহ, এটি একটি উপভোগ্য এবং ফলপ্রসূ অভিজ্ঞতা হয়ে উঠতে পারে। এই প্রবন্ধে, আমি ক্লাস 5 এর সিলেবাস থেকে সমস্ত সমস্যার বিশদ সমাধান প্রদান করার চেষ্টা করেছি, যার লক্ষ্য তরুণ শিক্ষার্থীদের জন্য গণিতকে আরও সহজলভ্য এবং কম ভীতিজনক করে তোলা।
আমার লক্ষ্য হল জটিল সমস্যাগুলিকে সহজ, সহজে বোধগম্য ধাপে ভেঙ্গে দিয়ে শিক্ষার্থীদের গণিতে একটি শক্তিশালী ভিত্তি তৈরি করতে সাহায্য করা। এখানে মূল ধারণা এবং সমস্যা সমাধানের কৌশলগুলিতে ফোকাস করা হয়েছে যা শ্রেণীকক্ষে এবং তার বাইরেও সাফল্যের জন্য গুরুত্বপূর্ণ।
Class 5 Math Solution WBBSE Page 102 :
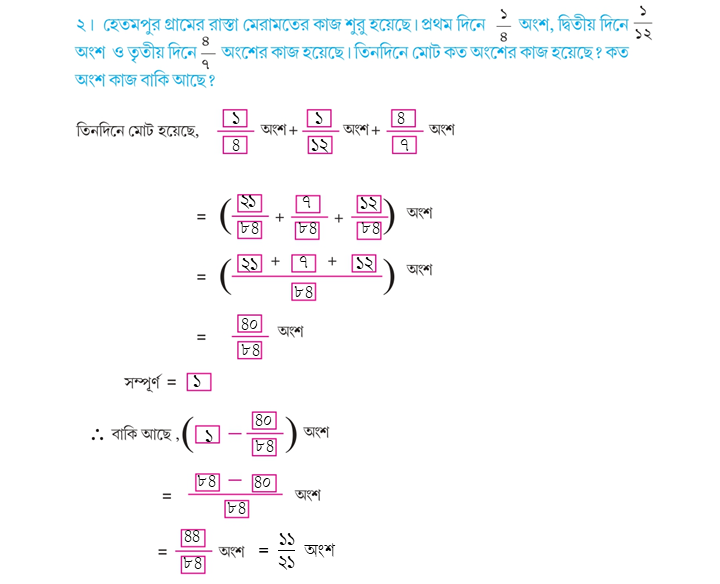
Class 5 Math Solution WBBSE Page 103 :
৩। চৌবাচ্চায় \(\frac{২}{১৫}\) অংশ জল ছিল। আমি চৌবাচ্চায় \(\frac{৩}{২০}\) অংশ জল ঢাললাম ও দাদা \(\frac{৩}{১২}\) অংশ জল ঢালল। এখন চৌবাচ্চায় কত অংশ জল হল? চৌবাচ্চার কত অংশ খালি আছে?
উত্তরঃ
চৌবাচ্চাই মোট জলের পরিমাণ,
| = চৌবাচ্চায় \(\frac{২}{১৫}\) অংশ জল ছিল + আমি চৌবাচ্চায় \(\frac{৩}{২০}\) অংশ জল ঢাললাম + দাদা \(\frac{৩}{১২}\) অংশ জল ঢালল |
| = \(\frac{২}{১৫}\) অংশ + \(\frac{৩}{২০}\) অংশ + \(\frac{৩}{১২}\) অংশ |
| = (\(\frac{২}{১৫}\) + \(\frac{৩}{২০}\) + \(\frac{৩}{১২}\)) অংশ |
| = \(\frac{৮ + ৯ + ১৫}{৬০}\) অংশ |
| = \(\frac{৩২}{৬০}\) |
| = \(\frac{৮}{১৫}\) অংশ |
এখন সম্পূর্ণ চৌবাচ্চা = ১ অংশ
অতএব, চৌবাচ্চাই খালি আছে,
| = সম্পূর্ণ চৌবাচ্চা – জলপূর্ণ অংশ |
| = ১ – \(\frac{৮}{১৫}\) |
| = \(\frac{১৫-৮}{১৫}\) |
| \(\frac{৭}{১৫}\) অংশ |
৪। একটি বাঁশের \(\frac{২}{১৩}\) অংশ লাল, \(\frac{১}{৩}\) অংশ সবুজ ও \(\frac{৮}{৩৯}\) অংশ হলুদ রং করেছি। কত অংশ রং করা বাকি আছে?
উত্তরঃ
সম্পূর্ণ বাশ = ১ অংশ
অতএব, রঙ করা বাকি আছে,
| = সম্পূর্ণ বাঁশ – (বাঁশের \(\frac{২}{১৩}\) অংশ লাল+\(\frac{১}{৩}\) অংশ সবুজ + \(\frac{৮}{৩৯}\) অংশ হলুদ রং ) |
| = ১ – (\(\frac{২}{১৩}\)+\(\frac{১}{৩}\) + \(\frac{৮}{৩৯}\) ) |
| = ১ – \(\frac{৬+১৩+৮}{৩৯}\) |
| = ১ – \(\frac{২৭}{৩৯}\) |
| = ১ – \(\frac{৯}{১৩}\) |
| = \(\frac{১৩-৯}{১৩}\) |
| = \(\frac{৪}{১৩}\) অংশ |
৫। ফুলের বাগানের \(\frac{২}{৩}\) অংশে তৃতীয় শ্রেণির ছাত্ররা, \(\frac{১}{৯}\) অংশে চতুর্থ শ্রেণির ছাত্ররা এবং \(\frac{১}{১২}\) অংশে পঞ্চম শ্রেণির ছাত্ররা ফুলগাছ লাগিয়েছে। মোট কত অংশে ফুলগাছ লাগানো হয়েছে? এখনও কত অংশে ফুল গাছ লাগানো হয়নি?
উত্তরঃ
মোট ফুল গাছ লাগানো হয়েছে,
| = \(\frac{২}{৩}\) অংশে তৃতীয় শ্রেণির ছাত্ররা + \(\frac{১}{৯}\) অংশে চতুর্থ শ্রেণির ছাত্ররা + \(\frac{১}{১২}\) অংশে পঞ্চম শ্রেণির ছাত্ররা |
| = ( \(\frac{২}{৩}\) + \(\frac{১}{৯}\) + \(\frac{১}{১২}\)) অংশ |
| = \(\frac{২৪+৪+৩}{৩৬}\) |
| = \(\frac{৩১}{৩৬}\) অংশ |
এখন সম্পূর্ণ ফুল বাগান = ১ অংশ
ফুল গাছ লাগানো হয়নি,
| = সম্পূর্ণ বাগান – ফুল গাছ লাগানো অংশ |
| = ১ – \(\frac{৩১}{৩৬}\) |
| = \(\frac{৩৬ – ৩১}{৩৬}\) |
| = \(\frac{৫}{৩৬}\) অংশ |
৬। প্রীতমের বাবা বাজার থেকে \(\frac{১}{৪}\) কেজি চাল, \(\frac{২}{৫}\) কেজি ডাল ও \(\frac{১}{৮}\) কেজি আটা কিনেছেন। তিনি মোট কত কেজি জিনিস কিনলেন?
উত্তরঃ
মোট কিনেছেন,
| \(\frac{১}{৪}\) কেজি চাল + \(\frac{২}{৫}\) কেজি ডাল + (\frac{১}{৮}\) কেজি আটা |
| = \(\frac{১}{৪} + \frac{২}{৫} + \frac{১}{৮}\) |
| = \(\frac{১০+১৬+৫}{৪০}\) |
| = \(\frac{৩১}{৪০}\) কেজি |
Class 5 Math Solution WBBSE Page 104 :
সমস্যাগুলির সমাধান করি :
১। বাজার থেকে সকালে বাবা \(\frac{৩}{৪}\) কিগ্রা. চিনি এনেছেন। বাড়িতে \(\frac{১}{৫}\) কিগ্রা. চিনি ছিল। সারাদিনে মা \(\frac{৯}{১০}\) কিগ্রা. চিনি খরচ করেছেন। দিনের শেষে কত কিগ্রা. চিনি পড়ে আছে?
উত্তরঃ
দিনের শেষে চিনি পড়ে থাকবে,
| (সকালে বাবা \(\frac{৩}{৪}\) কিগ্রা. চিনি এনেছেন + বাড়িতে \(\frac{১}{৫}\) কিগ্রা. চিনি ছিল) – সারাদিনে মা \(\frac{৯}{১০}\) কিগ্রা. চিনি খরচ করেছেন |
| = (\(\frac{৩}{৪}\) + \(\frac{১}{৫}\)) – \(\frac{৯}{১০}\) |
| = \(\frac{১৫+৪}{২০}\) – \(\frac{৯}{১০}\) |
| = \(\frac{১৯}{২০}\) – \(\frac{৯}{১০}\) |
| = \(\frac{১৯-১৮}{২০}\) |
| = \(\frac{১}{২০}\) কেজি |
২। চৌবাচ্চায় \(\frac{৩}{৮}\) লিটার জল ছিল। কিছু পরে সেখান থেকে \(\frac{৮}{২৫}\) লিটার জল খরচ হয়েছে। আমি বালতি করে চৌবাচ্চায় \(\frac{৫}{১৬}\) লিটার জল ঢাললাম। এখন চৌবাচ্চায় কত লিটার জল আছে? বেশি কাজ করেছে?
উত্তরঃ
এখন চৌবাচ্চায় জল থাকবে,
| (চৌবাচ্চায় \(\frac{৩}{৮}\) লিটার জল ছিল +আমি বালতি করে চৌবাচ্চায় \(\frac{৫}{১৬}\) লিটার জল ঢাললাম ) – কিছু পরে সেখান থেকে \(\frac{৮}{২৫}\) লিটার জল খরচ হয়েছে |
| = (\(\frac{৩}{৮}\) + \(\frac{৫}{১৬}\)) – \(\frac{৮}{২৫}\) |
| = \(\frac{৬+৫}{১৬}\) – \(\frac{৮}{২৫}\) |
| = \(\frac{১৫০+১২৮}{৪০০}\) |
| = \(\frac{২৭৮}{৪০০}\) |
| = \(\frac{১৩৭}{২০০}\) লিটার জল |
৩। শিবু ও রামু প্রথম দিনে বাগানের যথাক্রমে \(\frac{৮}{৯}\) অংশ ও \(\frac{১}{১৮}\) অংশ পরিষ্কার করেছে। পরের দিন পলি ও মিলি যথাক্রমে বাগানের \(\frac{১১}{২৪}\) অংশ ও \(\frac{১}{৬}\) অংশ পরিষ্কার করেছে। শিবু ও রামু প্রথম দিনে পরের দিন থেকে কত বেশি কাজ করেছে?
উত্তরঃ
প্রথম দিনে কাজ হয়েছে,
| \(\frac{৮}{৯}\) + \(\frac{১}{১৮}\) |
| = \(\frac{১৬+১}{১৮}\) |
| = \(\frac{১৭}{১৮}\) অংশ |
দ্বিতীয় দিন কাজ হয়েছে,
| \(\frac{১১}{২৪}\) + \(\frac{১}{৬}\) |
| = \(\frac{১১+৪}{২৪}\) |
| = \(\frac{১৫}{২৪}\) অংশ |
প্রথম দিনে বেশি কাজ হয়েছে,
| \(\frac{১৭}{১৮}\) – \(\frac{১৫}{২৪}\) |
| = \(\frac{৬৮-৪৫}{৭২}\) |
| = \(\frac{২৩}{৭২}\) অংশ |
৪। সরল করি:
(ক) \(\frac{২}{৫}\) – \(\frac{১}{১০}\) + \(\frac{১}{২}\)
উত্তরঃ
| \(\frac{২}{৫}\) – \(\frac{১}{১০}\) + \(\frac{১}{২}\) |
| = \(\frac{৪-১+৫}{১০}\) |
| = \(\frac{৯-১}{১০}\) |
| = \(\frac{৮}{১০}\) |
| = \(\frac{৪}{৫}\) |
(খ) \(\frac{৩}{৮}\) + \(\frac{৯}{১৬}\) – \(\frac{১}{৮}\)
উত্তরঃ
| \(\frac{৩}{৮}\) + \(\frac{৯}{১৬}\) – \(\frac{১}{৮}\) |
| = \(\frac{৬+৯-২}{১৬}\) |
| = \(\frac{১৫-২}{১৬}\) |
| = \(\frac{১৩}{১৬}\) |
(গ) \(\frac{২}{৩}\) – \(\frac{৩}{৪}\) + \(\frac{১}{৫}\)
উত্তরঃ
| \(\frac{২}{৩}\) – \(\frac{৩}{৪}\) + \(\frac{১}{৫}\) |
| = \(\frac{৪০-৪৫+২০}{৬০}\) |
| = \(\frac{৬০-৪৫}{৬০}\) |
| = \(\frac{১৫}{৬০}\) |
| = \(\frac{১}{৪}\) |
(ঘ) \(\frac{১}{৫}\) + \(\frac{১}{২}\) – \(\frac{১}{৬}\)
উত্তরঃ
| \(\frac{১}{৫}\) + \(\frac{১}{২}\) – \(\frac{১}{৬}\) |
| = \(\frac{৬+১৫-৫}{৩০}\) |
| = \(\frac{২১-৫}{৩০}\) |
| = \(\frac{১৬}{৩০}\) |
| = \(\frac{৮}{১৫}\) |
(ঙ) (\(\frac{১}{৭}\) + \(\frac{৫}{৭}\)) – (\(\frac{১}{৫}\) + \(\frac{২}{৫}\))
উত্তরঃ
| (\(\frac{১}{৭}\) + \(\frac{৫}{৭}\)) – (\(\frac{১}{৫}\) + \(\frac{২}{৫}\)) |
| = (\(\frac{১+৫}{৭}\)) – (\(\frac{১+২}{৫}\)) |
| = \(\frac{৬}{৭}\) – \(\frac{৩}{৫}\) |
| = \(\frac{৩০-২১}{৩৫}\) |
| = \(\frac{৯}{৩৫}\) |
(চ) (\(\frac{১}{২}\) + \(\frac{২}{৯}\)) – \(\frac{৪}{১৫}\) + \(\frac{৫}{১৮}\)
উত্তরঃ
| (\(\frac{১}{২}\) + \(\frac{২}{৯}\)) – \(\frac{৪}{১৫}\) + \(\frac{৫}{১৮}\) |
| = (\(\frac{৯+৪}{১৮}\)) – (\(\frac{২৪+২৫}{৯০}\)) |
| = \(\frac{১৩}{১৮}\) – \(\frac{৪৯}{৯০}\) |
| = \(\frac{৬৫-৪৯}{৯০}\) |
| = \(\frac{১৬}{৯০}\) |
| = \(\frac{৮}{৪৫}\) |
(ছ) \(\frac{৬}{৭}\) – (\(\frac{১}{১৪}\) + \(\frac{৫}{৭}\))
উত্তরঃ
| \(\frac{৬}{৭}\) – (\(\frac{১}{১৪}\) + \(\frac{৫}{৭}\)) |
| = \(\frac{৬}{৭}\) – \(\frac{১+১০}{১৪}\) |
| = \(\frac{৬}{৭}\) – \(\frac{১১}{১৪}\) |
| = \(\frac{১২-১১}{১৪}\) |
| = \(\frac{১}{১৪}\) |
(জ) \(\frac{৯}{১৫}\) – (\(\frac{১}{১০}\)+\(\frac{৩}{১০}\))
উত্তরঃ
| \(\frac{৯}{১৫}\) – (\(\frac{১}{১০}\)+\(\frac{৩}{১০}\)) |
| = \(\frac{৯}{১৫}\) – \(\frac{১+৩}{১০}\) |
| = \(\frac{৯}{১৫}\) – \(\frac{৪}{১০}\) |
| = \(\frac{১৮-১২}{৩০}\) |
| = \(\frac{৬}{৩০}\) |
| = \(\frac{১}{৫}\) |
Page 105:

Page 106:
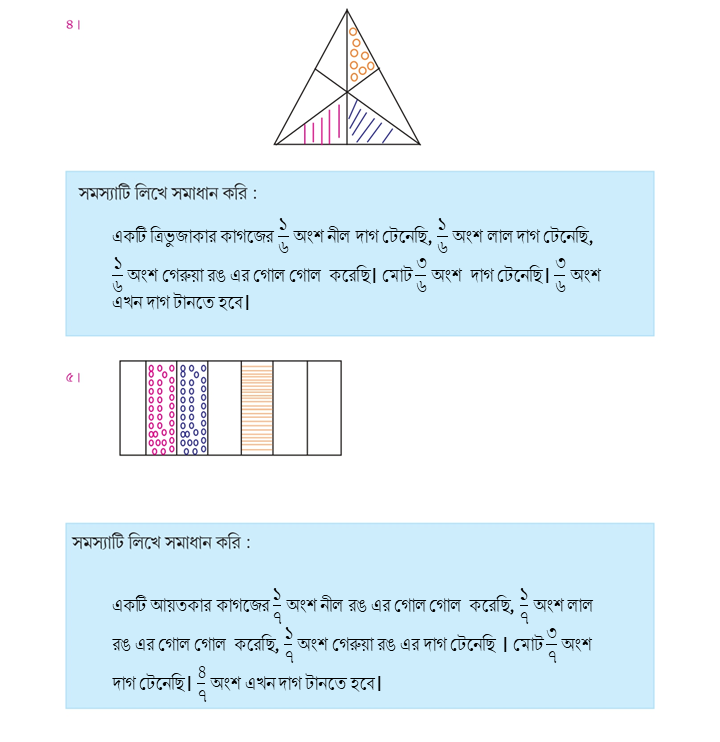
Page 109:

Page 110:
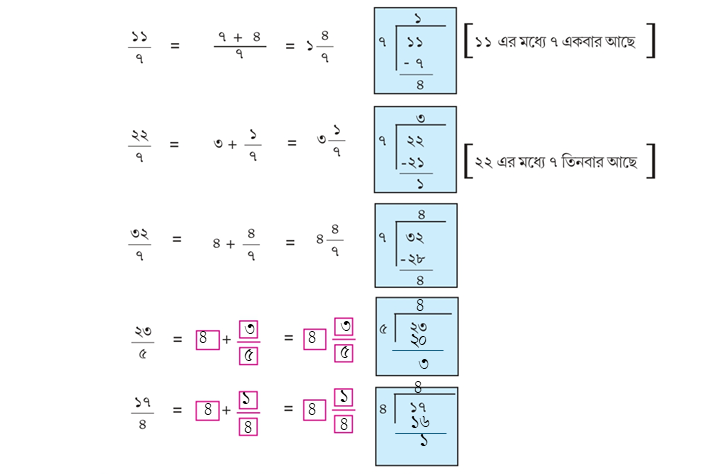
১। নীচের অপ্রকৃত ভগ্নাংশকে মিশ্র ভগ্নাংশে পরিণত করিঃ
(ক) \(\frac{২১}{৪}\)
উত্তরঃ
| \(\frac{২১}{৪}\) |
| = ৫ + \(\frac{১}{৪}\) |
| = ৫\(\frac{১}{৪}\) |
(খ) \(\frac{২৭}{৫}\)
উত্তরঃ
| \(\frac{২৭}{৫}\) |
| = ৫ + \(\frac{২}{৫}\) |
| = ৫\(\frac{২}{৫}\) |
(গ) \(\frac{৩৮}{৫}\)
উত্তরঃ
| \(\frac{৩৮}{৫}\) |
| = ৭ + \(\frac{৩}{৫}\) |
| = ৭\(\frac{৩}{৫}\) |
(ঘ) \(\frac{৫৪}{৭}\)
উত্তরঃ
| \(\frac{৫৪}{৭}\) |
| = ৭ + \(\frac{৫}{৭}\) |
| = ৭\(\frac{৫}{৭}\) |
(ঙ) \(\frac{৫১}{৮}\)
উত্তরঃ
| \(\frac{৫১}{৮}\) |
| = ৬ + \(\frac{৩}{৮}\) |
| = ৬\(\frac{৩}{৮}\) |
Page 111:
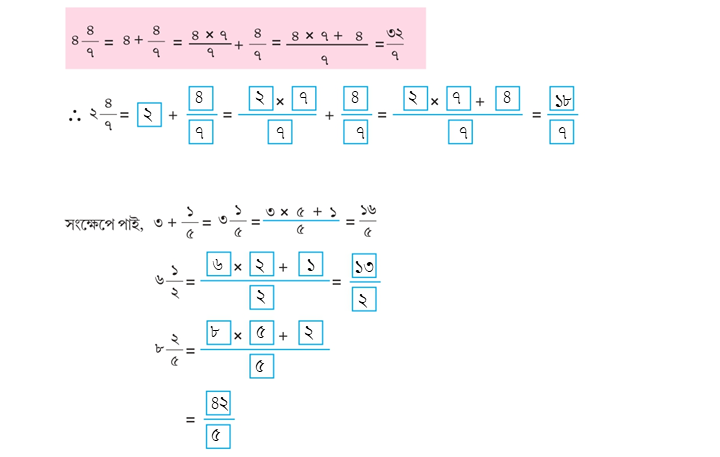
৩। মিশ্র ভগ্নাংশকে অপ্রকৃত ভগ্নাংশে পরিণত করিঃ
(ক) ৩\(\frac{৫}{৭}\)
উত্তরঃ
| ৩\(\frac{৫}{৭}\) |
| = \(\frac{৩\times৭ + ৫}{৭}\) |
| = \(\frac{২৬}{৭}\) |
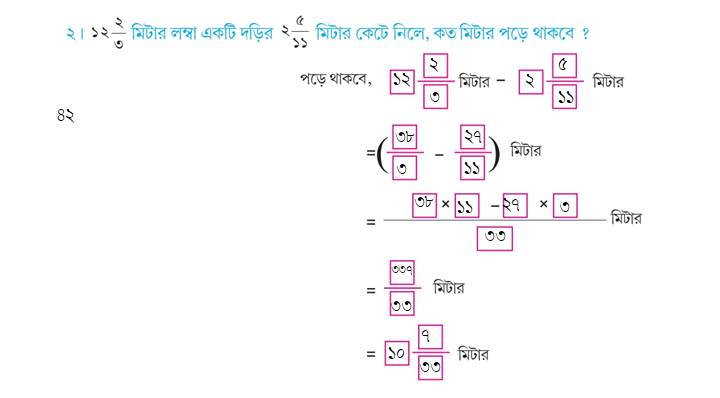
(খ) ১২\(\frac{২}{৩}\)
উত্তরঃ
| ১২\(\frac{২}{৩}\) |
| = \(\frac{১২\times৩ + ২}{৩}\) |
| = \(\frac{৩৮}{৩}\) |
(গ) ৩৩\(\frac{১}{২}\)
উত্তরঃ
| ৩৩\(\frac{১}{২}\) |
| = \(\frac{৩৩\times২ + ১}{২}\) |
| = \(\frac{৬৭}{২}\) |
(ঘ) ৩\(\frac{১}{৩৩}\)
উত্তরঃ
| ৩\(\frac{১}{৩৩}\) |
| = \(\frac{৩\times৩৩ + ১}{৩৩}\) |
| = \(\frac{১০০}{৩৩}\) |
(ঙ) ৬\(\frac{৫}{৩}\)
উত্তরঃ
| ৬\(\frac{৫}{৩}\) |
| = \(\frac{৬\times৩ + ৫}{৩}\) |
| = \(\frac{২৩}{৩}\) |
(চ) ৩\(\frac{৫}{৬}\)
উত্তরঃ
| ৩\(\frac{৫}{৬}\) |
| = \(\frac{৩\times৬ + ৫}{৬}\) |
| = \(\frac{২৩}{৬}\) |
(ছ) ৪\(\frac{৭}{১২}\)
উত্তরঃ
| ৪\(\frac{৭}{১২}\) |
| = \(\frac{৪\times১২ + ৭}{১২}\) |
| = \(\frac{৫৫}{১২}\) |
(জ) ১০\(\frac{৫}{৮}\)
উত্তরঃ
| ১০\(\frac{৫}{৮}\) |
| = \(\frac{১০\times৮ + ৫}{৮}\) |
| = \(\frac{৮৫}{৮}\) |
(ঝ) ১৫\(\frac{৩}{৮}\)
উত্তরঃ
| ১৫\(\frac{৩}{৮}\) |
| = \(\frac{১৫\times৩ + ৩}{৮}\) |
| = \(\frac{৪৮}{৮}\) |
Page 113:
১। যোগ করিঃ
(ক) \(\frac{১২}{৫}\) + \(\frac{১০}{৩}\)
উত্তরঃ
| \(\frac{১২}{৫}\) + \(\frac{১০}{৩}\) |
| = \(\frac{১২\times৩ + ১০\times৫}{১৫}\) |
| = \(\frac{৩৬+৫০}{১৫}\) |
| = \(\frac{৮৬}{১৫}\) |
(খ) ২\(\frac{৪}{৭}\) + ৪\(\frac{৩}{৪}\)
উত্তরঃ
| ২\(\frac{৪}{৭}\) + ৪\(\frac{৩}{৪}\) |
| = \(\frac{১৮}{৭}\) + \(\frac{১৯}{৪}\) |
| = \(\frac{১৮\times৪ + ১৯\times৭}{২৮}\) |
| = \(\frac{৭২+১৩৩}{২৮}\) |
| = \(\frac{২০৫}{২৮}\) |
(গ) \(\frac{২০}{৩}\) + \(\frac{২৫}{২}\) + \(\frac{৭}{৬}\)
উত্তরঃ
| \(\frac{২০}{৩}\) + \(\frac{২৫}{২}\) + \(\frac{৭}{৬}\) |
| = \(\frac{২০\times২ + ২৫\times৩ + ৭}{৬}\) |
| = \(\frac{৪০+৭৫+৭}{৬}\) |
| = \(\frac{১৯২}{৬}\) |
(ঘ) \(\frac{২১}{৭}\) + \(\frac{১২}{৫}\) + \(\frac{১৬}{১৫}\)
উত্তরঃ
| \(\frac{২১}{৭}\) + \(\frac{১২}{৫}\) + \(\frac{১৬}{১৫}\) |
| = \(\frac{২১\times১৫ + ১২\times২১ + ১৬\times৭}{১০৫}\) |
| = \(\frac{৩১৫+২৫২+১১২}{১০৫}\) |
| = \(\frac{৬৭৯}{১০৫}\) |
(ঙ) ২\(\frac{১}{৫}\) + ১\(\frac{৪}{১৫}\) + ১\(\frac{১}{২০}\)
উত্তরঃ
| ২\(\frac{১}{৫}\) + ১\(\frac{৪}{১৫}\) + ১\(\frac{১}{২০}\) |
| = \(\frac{১১}{৫}\) + \(\frac{১৯}{১৫}\) + \(\frac{২১}{২০}\) |
| = \(\frac{১১\times১২ + ১৯\times৪ + ২১\times৩}{৬০}\) |
| = \(\frac{১৩২+৭৬+ ৬৩}{৬০}\) |
| = \(\frac{২৭১}{৬০}\) |
Page 115:
৩। বিয়োগ করিঃ
(ক) ৩\(\frac{২}{১৫}\) – ২\(\frac{৫}{৬}\)
উত্তরঃ
| ৩\(\frac{২}{১৫}\) – ২\(\frac{৫}{৬}\) |
| = \(\frac{৪৭}{১৫}\) – \(\frac{১৭}{৬}\) |
| = \(\frac{৪৭\times২-১৭\times৫}{৩০}\) |
| = \(\frac{৯৪-৮৫}{৩০}\) |
| = \(\frac{৯}{৩০}\) |
| = \(\frac{৩}{১০}\) |
(খ) ৮ – ১\(\frac{৭}{১২}\)
উত্তরঃ
| ৮ – ১\(\frac{৭}{১২}\) |
| = ৮ – \(\frac{১৯}{১২}\) |
| = \(\frac{৮\times১২-১৯}{১২}\) |
| = \(\frac{৯৬-১৯}{১২}\) |
| = \(\frac{৭৭}{১২}\) |
(গ) ৩\(\frac{৫}{২৪}\) – ২
উত্তরঃ
| ৩\(\frac{৫}{২৪}\) – ২ |
| = \(\frac{৭৭}{২৪}\) – ২ |
| = \(\frac{৭৭ – ২\times২৪}{২৪}\) |
| = \(\frac{৭৭-৪৮}{২৪}\) |
| = \(\frac{২৯}{২৪}\) |
(ঘ) \(\frac{৬১}{১৫}\) – \(\frac{৫৩}{২৫}\)
উত্তরঃ
| \(\frac{৬১}{১৫}\) – \(\frac{৫৩}{২৫}\) |
| = \(\frac{৬১\times৫-৫৩\times৩}{৭৫}\) |
| = \(\frac{৩০৫-১৫৯}{৭৫}\) |
| = \(\frac{১৪৬}{৭৫}\) |
(ঙ) \(\frac{৫৩}{১৫}\) – \(\frac{১৩}{১২}\)
উত্তরঃ
| \(\frac{৫৩}{১৫}\) – \(\frac{১৩}{১২}\) |
| = \(\frac{৫৩\times৪-১৩\times৫}{৬০}\) |
| = \(\frac{২১২-৬৫}{৬০}\) |
| = \(\frac{১৪৭}{৬০}\) |
(চ) ৭\(\frac{৮}{৯}\) – ৫\(\frac{১}{৬}\)
উত্তরঃ
| ৭\(\frac{৮}{৯}\) – ৫\(\frac{১}{৬}\) |
| = \(\frac{৭১}{৯}\) – \(\frac{৩১}{৬}\) |
| = \(\frac{৭১\times২-৩১\times৩}{১৮}\) |
| = \(\frac{১৪২-৯৩}{১৮}\) |
| = \(\frac{৪৯}{৬০}\) |
Page 116:

Page 117:

Page 118:

Page 121:

Page 122:
১। আয়তাকার জমির জন্য ফাঁকা ঘরে সঠিক সংখ্যা বসাই :
| দৈর্ঘ্য | প্রস্থ | পরিসীমা |
|---|---|---|
| ৩০ মি | ২০ মি. | ১০০ মি. |
| ৫০ মি. | ২৫মি. | ১৫০ মি. |
| ৬০ মি. | ৪০ মি. | ২০০ মি. |
| ১০০ মি. | ৫০মি. | ৩০০ মি. |
২। একটি বর্গাকার ফুলের বাগানের প্রত্যেক ধারের দৈর্ঘ্য ১০ মিটার। যদি বাগানটির প্রত্যেক ধারের দৈর্ঘ্য ২ মিটার করে বাড়ানো হয়, তবে নতুন বাগানটির পরিসীমা আগের তুলনায় কত বেশি হবে?
উত্তরঃ
আগের পরিসীমা
= ৪ × ১০
= ৪০ মিটার.
প্রত্যেক ধারের দৈর্ঘ্য ২ মিটার করে বাড়ানোর পরের পরিসীমা,
= ৪ × (১০+২)
= ৪ × ১২
= ৪৮ মিটার.
অতএব, নতুন বাগানটির পরিসীমা আগের তুলনায় (৪৮ – ৪০) = ৮ মিটার. বেশি হবে।
৩। একটি আয়তাকার পার্কের দৈর্ঘ্য ২৫ মিটার ও প্রস্থ ১৫ মিটার। যদি পার্কটির প্রত্যেক ধারের দৈর্ঘ্য ২ মিটার করে বাড়ানো হয়, তবে নতুন বাগানটির পরিসীমা আগের থেকে কত বেশি হবে?
উত্তরঃ
আগের পরিসীমা,
= ২ × (২৫ + ১৫)
= ২ × ৪০
= ৮০ মিটার.
পার্কটির প্রত্যেক ধারের দৈর্ঘ্য ২ মিটার করে বাড়ানোর পরের পরিসীমা,
= ২ × {(২৫+২) + (১৫+২)}
= ২ × (২৭+১৭)
= ২ × ৪৪
= ৮৮ মিটার.
অতএব, নতুন বাগানটির পরিসীমা আগের থেকে (৮৮-৮০)=৮ মিটার. বেশি হবে
৪। সমান পরিসীমা বিশিষ্ট একটি আয়তাকার ও একটি বর্গাকার জমি আছে। আয়তাকার জমির দৈর্ঘ্য ৪০ মিটার ও প্রস্থ ২০ মিটার। প্রতি মিটার বেড়ার জন্য ৭ টাকা খরচ হলে, বর্গাকার জমিটির চারপাশে বেড়া দিতে কত খরচ হবে?
উত্তরঃ
আয়তাকার জমির পরিসীমা,
= ২ × (৪০ + ২০)
= ২ × ৬০
= ১২০ মিটার.
প্রতি মিটার বেড়ার জন্য ৭ টাকা খরচ হলে, ১২০ মিটার এ খরচ হবে,
= ৭ × ১২০
= ৮৪০ টাকা
অতএব, বর্গাকার জমিটির চারপাশে বেড়া দিতে ৮৪০ টাকা খরচ হবে।
৫। নীচের জমিটি দেখি
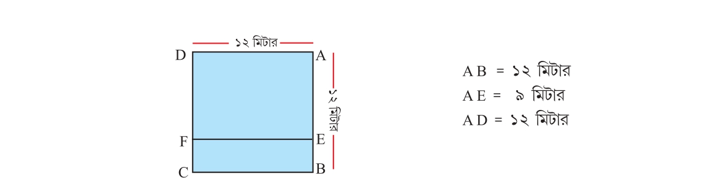
AEFD আয়তাকার জমির পরিসীমা কত?
ABCD জমির পরিসীমা কত?
উত্তরঃ
AEFD আয়তাকার জমির পরিসীমা,
= ২ × (১২ + ৯)
= ২ × ২১
= ৪২ মিটার.
ABCD জমির পরিসীমা ,
= ৪ × ১২
= ৪৮ মিটার.
