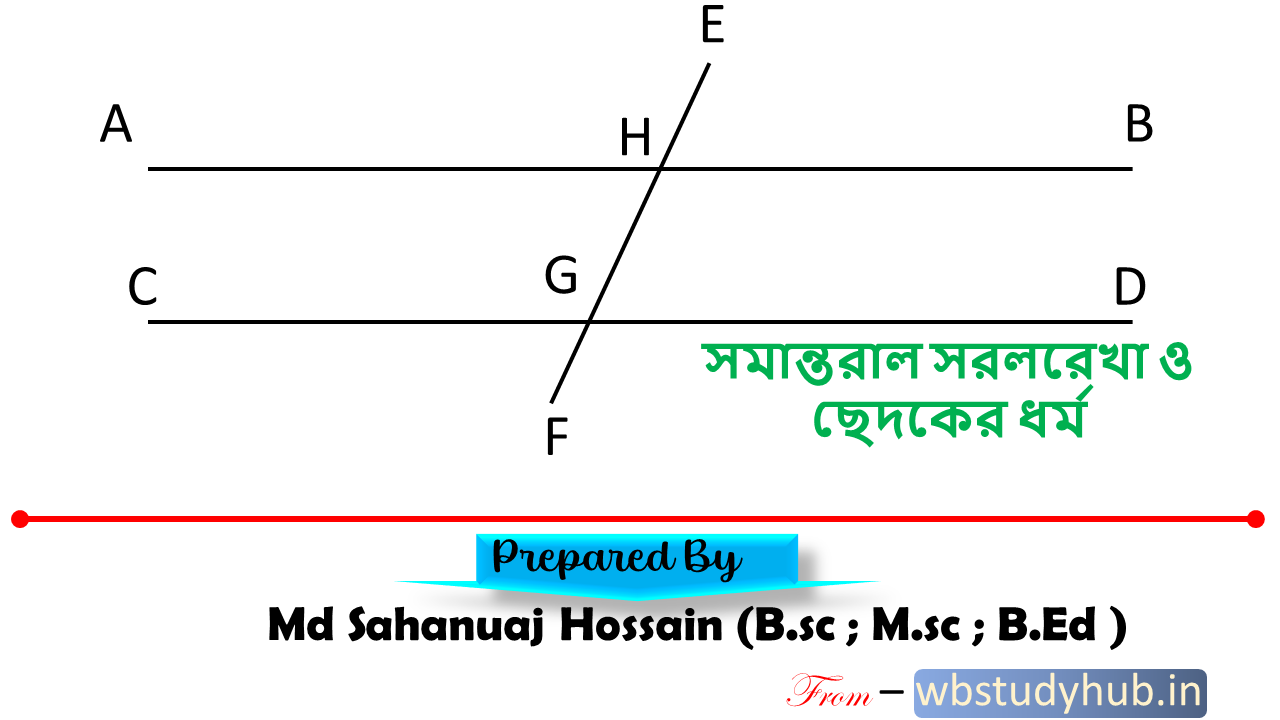
শ্রেণী-অষ্টম ; অধ্যায় – সমান্তরাল সরলরেখা ও ছেদক এর ধর্ম ; অধ্যায়ের সারাংশ
সমান্তরাল সরলরেখা কাকে বলে?
একই সমতলে অবস্থিত দুটি সরলরেখা যখন পরস্পর কখনই মিলিত হয়না তখন ওই দুটি সরলরেখাকে সমান্তরাল সরলরেখা বলা হয়।
সমান্তরাল সরলরেখা কাকে বলে নিশ্চয় তোমরা জেনেছো ! এবার আমরা সমান্তরাল সরলরেখা ও ছেদক নিয়ে কিছু আলোচনা করবো ।
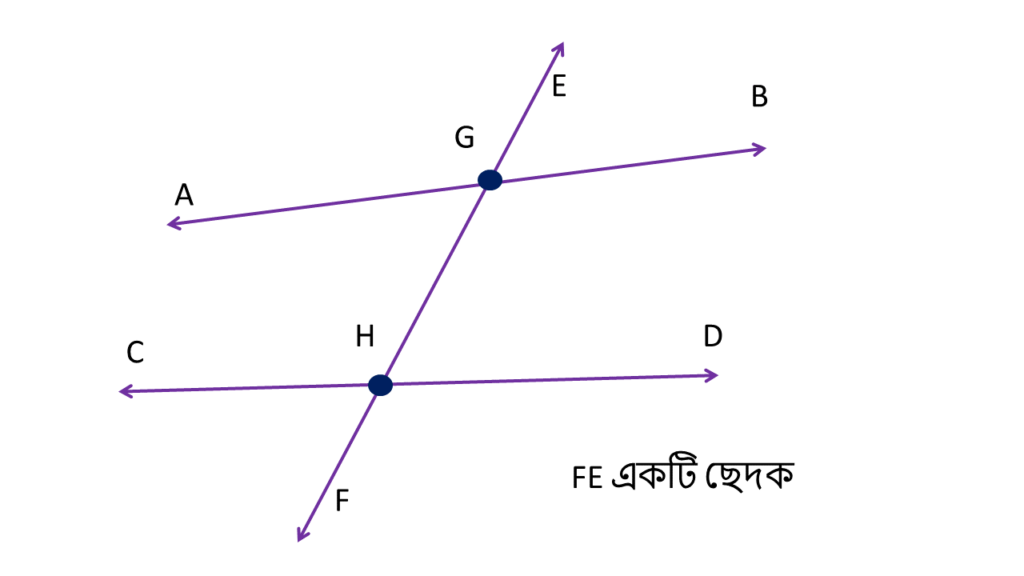
আমরা বাস্তব ক্ষেত্রে অনেক জায়গায় ছেদকের উদাহরণ দেখতে পায় । যেমন ট্রেনের লাইনে , দাগ টানা খাতায় আমাদের বাড়ীর গ্রিলে এরকম অনেক জাইগায় আমরা ছেদক দেখতে পায় । ছেদক তাহলে কাকে বলবো?
ছেদক এর সংজ্ঞাঃ
যদি একটি সরলরেখা দুই বা ততোধিক সরলরেখাকে একাধিক আলাদা বিন্দুতে ছেদ করে, তখন ঐ সরলরেখাকে ছেদক বা ভেদক বলে।
দুটি সমান্তরাল সরলরেখা ও ছেদক এর ফলে উৎপন্ন কোণসমূহঃ
AB ও CD দুটি সমান্তরাল সরলরেখা AB||CD এবং EF একটি ছেদক ।
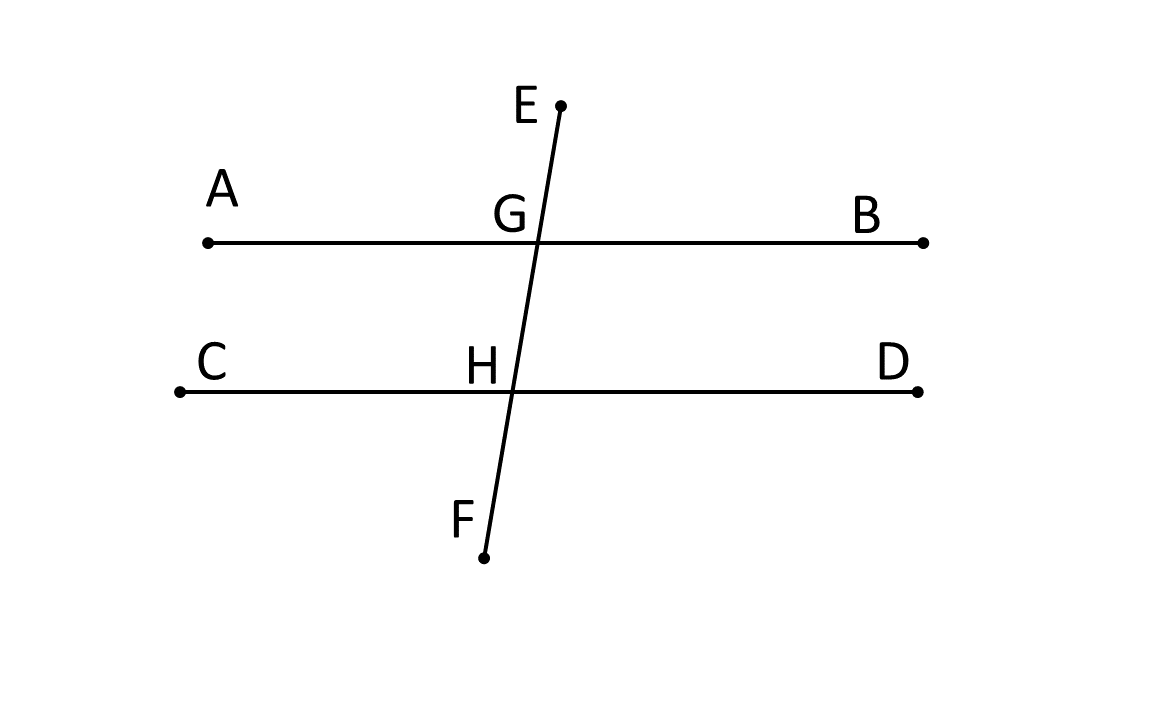
AB ও CD দুটি সমান্তরাল সরলরেখাকে EF যথাক্রমে G ও H বিন্দুতে ছেদ করেছে । এর ফলে যে সমস্ত কোণ উৎপন্ন হয়েছে তা হলো-
চার জোড়া অনুরূপ কোণ যথা-
| ∠BGE এর অনুরূপ কোণ ∠DHG |
| ∠BGF এর অনুরূপ কোণ ∠DHF |
| ∠AGE এর অনুরূপ কোণ ∠CHE |
| ∠AGF এর অনুরূপ কোণ ∠CHF |
2 জোড়া একান্তর কোণ যথা-
| ∠BGE এর একান্তর কোণ ∠CHE |
| ∠AGE এর একান্তর কোণ ∠DHE |
2 জোড়া একই পাশের অন্তঃস্থ কোণ যথা-
| ছেদকের বাম পাশে | ছেদকের ডান পাশে |
|---|---|
| ∠BGF ও ∠DHE | ∠AGF ও ∠CHE |
দুটি সমান্তরাল সরলরেখা ও ছেদক এর মধ্যে সম্পর্কঃ
দুটি সমান্তরাল সরলরেখা এবং একটি ছেদকের ফলে যে অনুরূপ কোণ, একান্তর কোণ ও ছেদকের একই পার্শ্বে অবস্থিত কোণসমূহের মধ্যে কিছু সম্পর্ক আমরা জানবোঃ
( i ) দুটি সমান্তরাল সরলরেখা একটি ছেদক ও অনুরূপ কোণগুলির মধ্যে সম্পর্কঃ
সম্পর্কঃ
দুটি সমান্তরাল সরলরেখাকে একটি সরলরেখা ছেদ করলে প্রতিজোড়া অনুরূপ কোণগুলির পরিমাপ সমান হয় ।
ব্যাখ্যাঃ
AB ও CD দুটি সমান্তরাল সরলরেখা AB||CD এবং EF একটি ছেদক । AB ও CD দুটি সমান্তরাল সরলরেখাকে EF যথাক্রমে G ও H বিন্দুতে ছেদ করেছে ।

উপরোক্ত সম্পর্ক থেকে আমরা পাই,
| ∠BGE = অনুরূপ কোণ ∠DHG |
| ∠BGF = অনুরূপ কোণ ∠DHF |
| ∠AGE = অনুরূপ কোণ ∠CHE |
| ∠AGF = অনুরূপ কোণ ∠CHF |
( ii ) দুটি সমান্তরাল সরলরেখা একটি ছেদক ও একান্তর কোণগুলির মধ্যে সম্পর্কঃ
সম্পর্কঃ
দুটি সমান্তরাল সরলরেখাকে অপর একটি সরলরেখা ছেদ করলে একান্তর কোণগুলির পরিমাপ সমান হয়।
ব্যাখ্যাঃ
AB ও CD দুটি সমান্তরাল সরলরেখা AB||CD এবং EF একটি ছেদক । AB ও CD দুটি সমান্তরাল সরলরেখাকে EF যথাক্রমে G ও H বিন্দুতে ছেদ করেছে । উপরোক্ত সম্পর্ক থেকে আমরা পাই,
| ∠BGE = একান্তর কোণ ∠CHE |
| ∠AGE = একান্তর কোণ ∠DHE |
( iii ) দুটি সমান্তরাল সরলরেখা ,একটি ছেদক ও ছেদকের একই পাশের অন্তঃস্থকোণগুলির মধ্যে সম্পর্কঃ
সম্পর্কঃ
দুটি সমান্তরাল সরলরেখাকে অপর একটি সরলরেখা ছেদ করলে ভেদকের একই পাশে অন্তঃস্থ কোণদুটির পরিমাপের সমষ্টি 180° হয়।
ব্যাখ্যাঃ
AB ও CD দুটি সমান্তরাল সরলরেখা AB||CD এবং EF একটি ছেদক । AB ও CD দুটি সমান্তরাল সরলরেখাকে EF যথাক্রমে G ও H বিন্দুতে ছেদ করেছে । উপরোক্ত সম্পর্ক থেকে আমরা পাই,
| ছেদকের বাম পাশে | ছেদকের ডান পাশে |
|---|---|
| ∠BGF + ∠DHE = 180° | ∠AGF + ∠CHE =180° |
এবার আমরা কিছু সম্পর্ক এর ব্যাপারে জানবো যা দুটি সরলরেখাকে একটি ছেদক ছেদ করলে ঐ ছেদকের ফলে উৎপন্ন কোণ সমূহের পরিমাপের তারতম্যের জন্যে ঐ সরলরেখা দুটি সমান্তরাল হবে, না অসমান্তরাল হবে।
দুটি সরলরেখা ও ছেদকের মধ্যে সম্পর্কঃ
( i ) দুটি সরলরেখাকে একটি সরলরেখা ছেদ করলে যদি একজোড়া অনুরূপ কোণের পরিমাপ সমান হয় তবে ঐ সরলরেখা দুটি পরস্পর সমান্তরাল হয় ।
( ii ) দুটি সরলরেখাকে একটি সরলরেখা ছেদ করলে যদি একজোড়া একান্তর কোণের পরিমাপ সমান হয় তবে ঐ সরলরেখা দুটি পরস্পর সমান্তরাল হয় ।
(iii ) দুটি সরলরেখাকে একটি সরলরেখা ছেদ করলে যদি ছেদকের একই পাশের অন্তঃস্থ কোণদুটির পরিমাপের সমষ্টি 2 সমকোণের সমান হয় তবে ঐ সরলরেখা দুটি পরস্পর সমান্তরাল হয় ।
সমান্তরাল সরলরেখা ও ছেদক বিষয়ে আমার এই আলোচনা ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।
এখানে আগে ভালো করে সমান্তরাল সরলরেখা ও ছেদক এর যে ধর্ম গুলো আলোচনা করা হয়েছে সেগুলো দেখে বুঝবে এবং মুখস্ত করে তারপর এই অধ্যায়ের কষে দেখি শুরু করবে। তাহলে দেখবে কোনো অংকে কোথাও বুঝতে অসুবিধে হবেনা।  |
তোমাদের জন্যে অষ্টম শ্রেণীর সমস্ত অধ্যায় এর গণিত এবং অধ্যায়টি কিভাবে আয়ত্ত করতে হবে তা খুব সুন্দর করে লেখা হয়েছে যাতে তোমরা খুব সহজেই প্রতিটি অধ্যায় বুঝতে পারো এবং প্রতিটি অংক বুঝে করতে পারো । |
এখানে তোমরা তোমাদের অষ্টম শ্রেণীতে কি কি পড়ানো হয়, মানে তোমাদের অষ্টম শ্রেণীর সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।