উপপাদ্য | স্বতঃসিদ্ধ | উপপাদ্য প্রমাণের নিয়ম |Theorem, Axiom, Steps To Prove a Theorem.

---

উপপাদ্য | Theorem

উপপাদ্য হলো এক প্রকারের প্রস্তাবনা, যা কিছু প্রাথমিক ধারণার ভিত্তিতে প্রমাণ করা হয়। গণিতের ভাষায়, উপপাদ্যের দুইটি অংশ রয়েছে –

• আনুষ্ঠানিক ভাবে কিছু প্রাক-ধারণা (assumption) এর উল্লেখ।
• একটি প্রস্তাবনা, যা উপরিউক্ত প্রাক-ধারণার ভিত্তিতে প্রমাণ করতে হবে।

পিথাগোরাসের উপপাদ্যের অন্তত ২৭০টি জানা প্রমাণ আছে

উপপাদ্যকে গাণিতিক সমীকরণের সাহায্যে প্রকাশ করা যায় তবে বাংলা,ইংরেজির মত সাধারণ ভাষাতেও প্রকাশ করা যায়।

বেশিরভাগ উপপাদ্যও পূর্বের কোনো হাইপোথিসিসের উপর নির্ভরশীল। যেমন- “যদি ক সত্য হয় তবে খ সত্য”,এই উপপাদ্যটিতে বলা হয়নি “খ” সত্য,এখানে বলা হয়েছে “খ” সত্য হবেই যদি “ক” সত্য হয়। এখানে ক হলো হাইপোথিসিস এবং খ হলো সিদ্ধান্ত।

উপপাদ্যকে প্রায়ই “তুচ্ছ”,”কঠিন”,”গভীর” এমনকি “সুন্দর” উপাধি দেয়া হয়। এ ধরনের উপাধি মানুষ থেকে মানুষে পরিবর্তিত হয়, এমনকি সময়ের সাথে সাথেও পরিবর্তিত হয়। যেমন আরো সহজ প্রমাণ আবিষ্কৃত হলে একটি “কঠিন” উপপাদ্য “তুচ্ছ” উপাধি পেতে পারে। “গভীর” উপপাদ্যগুলো খুব সাধারণ ভাবে বর্ণনা করা হয় কিন্তু সেগুলোর প্রমাণে আশ্চর্যজনক ভাবে গণিতের বিভিন্ন জটিল অংশের সংযোগ থাকতে পারে, “ফের্মার শেষ উপপাদ্য” এধরনের উপপাদ্যের একটি পরিচিত উদাহরণ।

নোবেল পুরস্কার বিজয়ী পদার্থবিজ্ঞানী রিচার্ড ফেইনম্যানের মতে একটি উপপাদ্য প্রমাণ করা যত কঠিনই হোক না কেনো প্রমাণ করার পর সেটা গণিতবিদদের নিকট তুচ্ছ। ফলে গাণিতিক স্বত্ত্বা দুই রকমেরঃ তুচ্ছ এবং অপ্রমাণিত।

গণিতবিদ রোনাল্ড গ্রাহাম ধারণা করেন প্রতি বছর প্রায় ২ লাখ ৫০ হাজার গাণিতিক উপপাদ্য প্রকাশিত হয় ।

গণিতে একটি সত্য বিবৃতি যাকে ধাপে ধাপে প্রমাণ করতে হয় তাকেই উপপাদ্য বলে ।

স্বতঃসিদ্ধ | Axiom

একটি স্বতঃসিদ্ধ হল এমন একটি বিবৃতি যা সত্য বলে ধরে নেওয়া হয়, আরও যুক্তি এবং যুক্তির জন্য একটি ভিত্তি বা সূচনা বিন্দু হিসাবে পরিবেশন করা হয়। শব্দটি এসেছে প্রাচীন গ্রীক শব্দ ἀξίωμα (axíōma) থেকে, যার অর্থ ‘যা যোগ্য বা উপযুক্ত বলে মনে করা হয়’ বা ‘যা নিজেকে স্পষ্ট বলে প্রশংসা করে’।

সুনির্দিষ্ট সংজ্ঞা অধ্যয়নের ক্ষেত্র জুড়ে পরিবর্তিত হয়। ক্লাসিক দর্শনে, একটি স্বতঃসিদ্ধ একটি বিবৃতি যা এতটাই স্পষ্ট বা সুপ্রতিষ্ঠিত যে এটি বিতর্ক বা প্রশ্ন ছাড়াই গৃহীত হয়। আধুনিক যুক্তিবিদ্যায়, একটি স্বতঃসিদ্ধ হল যুক্তির জন্য একটি ভিত্তি বা সূচনা বিন্দু।

যেকোনো স্বতঃসিদ্ধ একটি বিবৃতি যা একটি সূচনা বিন্দু হিসাবে কাজ করে যেখান থেকে অন্যান্য বিবৃতিগুলি যৌক্তিকভাবে উদ্ভূত হয়। একটি স্বতঃসিদ্ধ “সত্য” হওয়া অর্থপূর্ণ কিনা (এবং, যদি তাই হয় তবে এর অর্থ কী) গণিতের দর্শনে একটি বিতর্কের বিষয়।

যেমন-

স্বতঃসিদ্ধ 1ঃ একটি সরলরেখার উপর একটি রশ্মি দণ্ডায়মান হলে যে দুটি সন্নিহিত কোণ উৎপন্ন হয় তাদের পরিমাপের সমষ্টি দুই সমকোণ ।

---

উপপাদ্য প্রমাণের নিয়ম | Steps To Prove a Theorem:

উপপাদ্য এর নাম শুনলে আমরা ছাত্ররা অনেকে ঘাবড়ে যায় এবং ঘাবড়ে যাওয়ার কারণে আমাদের মাথায় ঢুকে যায় যে উপপাদ্য মানেই একটা কঠিন সমস্যা যা আমরা প্রমাণ করতে পারবোনা না বা কিছুই বুঝতে পারবো না । এই উপপাদ্য প্রমাণের সমস্যা যদি তোমাদেরও হয় বা হয়ে থাকে, তবে এটা স্বাভাবিক ! কারণ আমরাও যখন উপপাদ্য পড়তাম তখন শুনতাম যে উপপাদ্য মানেই বিশাল কঠিন একটা সমস্যা যা নাকি শুধু মুখস্ত করেই পার হওয়া সম্ভব । যা সম্পূর্ণ ভুল একটি ধারণা । আর আমাদের চারিপাশে সবাই এমনকি আমাদের কিছু শিক্ষকও এবিষয়ে সঠিক গাইড না দেওয়ার কারণে আমাদের এই উপপাদ্য জনিত সমস্যা খুব জটিল মনে হয় । আমি Mathematics নিয়ে পড়ে যা এতদূর শিখেছি এবং বুঝেছি তার উপর ভিত্তি করে এখানে তোমাদের উপপাদ্য লেখার কিছু নিয়ম বলে দেবো যাতে করে খুব সহজ ভাবে একটা উপপাদ্য কে ক প্রমানিত করতে পারবে ।

উপপাদ্য হলো এক প্রকারের প্রস্তাবনা, যা কিছু প্রাথমিক ধারণার ভিত্তিতে প্রমাণ করা হয় এবং কিছু নিয়ম মেনে আমরা যদি উপপাদ্য প্রমাণ করি তাহলে খুব সহজেই আমরা একটা উপপাদ্যকে প্রমাণ করতে পারবো । উপপাদ্য প্রমাণ করার জন্যে আমাদের কিছু কিছু স্বতঃসিদ্ধ এর প্রয়োজন হতে পারে ।একটি উদাহরণের মাধ্যমে আমরা বুঝবো যে কিভাবে প্রমাণ করতে হয় । আমরা উপপাদ্য প্রমাণে নিম্নলিখিত ধাপ বা steps অনুসরণ করবো ।

উদাহরণ– দুটি সরলরেখা পরস্পরকে ছেদ করলে যে দু-জোড়া বিপ্রতীপ কোণ উৎপন্ন হয় তাদের প্রতিজোড়া কোণের পরিমাপ পরস্পর সমান ।

Step 1:-( উপপাদ্যটি লেখা )

যে উপপাদ্য টি প্রমাণ করতে হবে সেটি প্রথমে আমরা সুন্দর করে লিখে নেবো ।

যেমন-

Step 1: দুটি সরলরেখা পরস্পরকে ছেদ করলে যে দু-জোড়া বিপ্রতীপ কোণ উৎপন্ন হয় তাদের প্রতিজোড়া কোণের পরিমাপ পরস্পর সমান ।

Step 2:-( চিত্র )

যে উপপাদ্য টি প্রমাণ করতে হবে সেটির হিসাবে একটি সঠিক চিত্র অঙ্কন করতে হবে ।

যেমন উদাহরণে যে উপপাদ্যটি আছে তার চিত্র হবে –

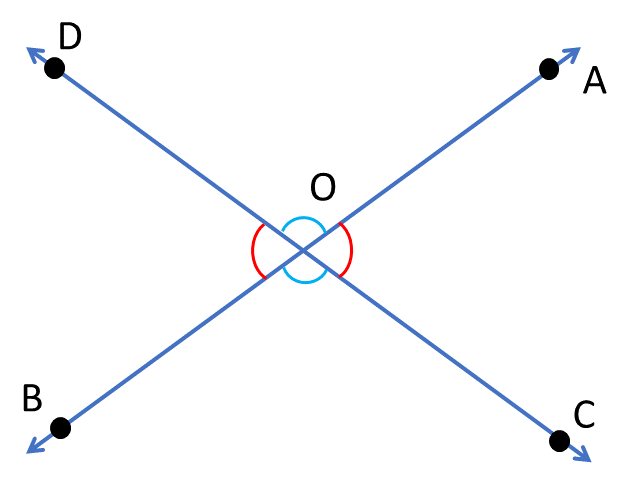
Step 3:-( প্রদত্ত )

যে উপপাদ্যটি দেওয়া আছে তা থেকে আমি কি কি তথ্য পেলাম তা লিখে নেবো ।

উদাহরণের উপপাদ্য টি থেকে আমরা যে যে তথ্য গুলি পেলাম তা হলো –

প্রদত্ত ( দেওয়া আছে ):-

AB ও CD দুটি সরলরেখা পরস্পরকে O বিন্দুতে ছেদ করেছে । এর ফলে দু-জোড়া বিপ্রতীপ কোণ ∠AOD, ∠BOC ও ∠AOC, ∠BOD তৈরি হয়েছে ।

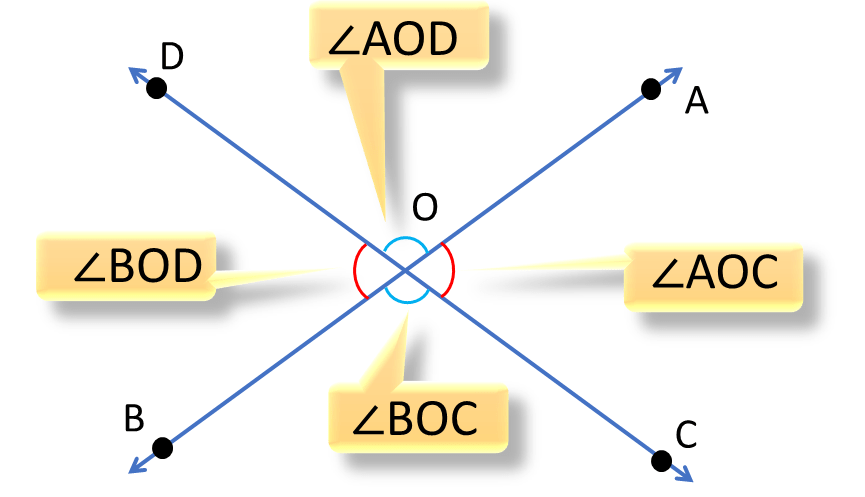
Step 4:( প্রামান্য/কি প্রমাণ করব )

উপপাদ্য টিতে যা প্রমাণ করতে হবে সেটা লিখতে হবে ।

প্রামান্য ( কি প্রমাণ করব ):-

প্রমাণ করতে হবে যে, প্রতিজোড়া বিপ্রতীপ কোণগুলির পরিমাপ সমান অর্থাৎ ∠AOD=∠BOC এবং ∠AOC=∠BOD

Step 5:( অতিরিক্ত অঙ্কন )

উপপাদ্য টি প্রমাণ করতে গিয়ে অতিরিক্ত অঙ্কন করতে হতে পারে ।

উদাহরণে যে উপপাদ্য টি আছে সেটি প্রমাণ করার জন্যে অতিরিক্ত কোনো অঙ্কনের প্রয়োজন নেই ।

Step 6: ( প্রমাণ/যুক্তি দিয়ে প্রমাণ )

এই ধাপে আমরা যুক্তি দিয়ে প্রমাণ করবো ।

উদাহরণের উপপাদ্য টিতে লিখতে হবে-

প্রমানঃ-

∠AOD +∠AOC = 180° [ কারণ CD সরলরেখার উপরে OA রশ্মি দণ্ডায়মান হওয়ায় সন্নিহিত কোণদ্বয়ের সমষ্টি দুই সমকোণ – স্বতঃসিদ্ধ 1 ]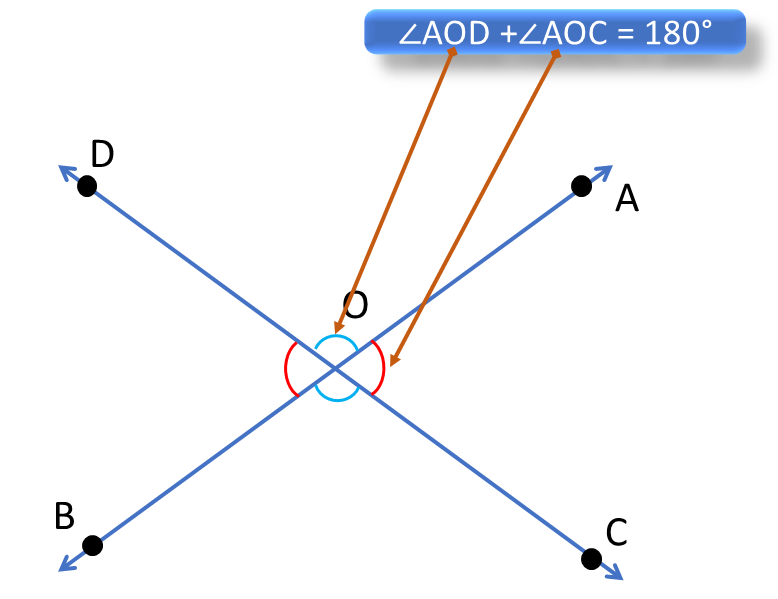

∠AOC + ∠BOC = 180° [ কারণ AB সরলরেখার উপরে OC রশ্মি দণ্ডায়মান হওয়ায় সন্নিহিত কোণদ্বয়ের সমষ্টি দুই সমকোণ – স্বতঃসিদ্ধ 1 ]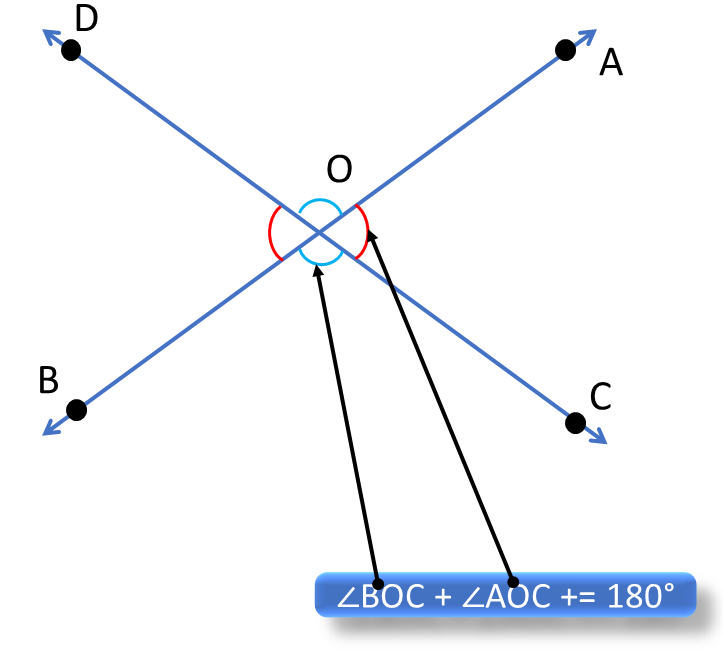

∠AOD +∠AOC =∠AOC + ∠BOC

সুতরাং ∠AOD = ∠BOC ( উভয়দিক থেকে ∠AOC বিয়োগ করে পাই )

আবার একইভাবে লিখতে পারি-

∠BOC + ∠BOD = 180° [ কারণ CD সরলরেখার উপরে OB রশ্মি দণ্ডায়মান হওয়ায় সন্নিহিত কোণদ্বয়ের সমষ্টি দুই সমকোণ – স্বতঃসিদ্ধ 1 ]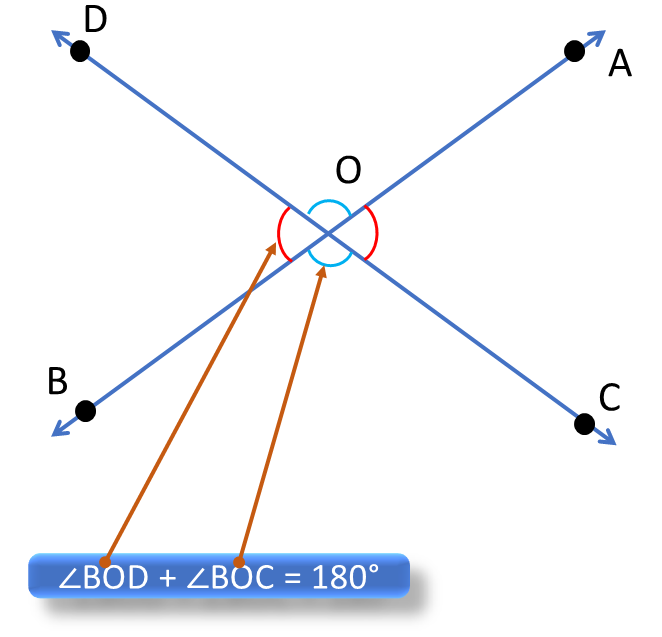

∠BOC + ∠AOC = 180° [ কারণ AB সরলরেখার উপরে OC রশ্মি দণ্ডায়মান হওয়ায় সন্নিহিত কোণদ্বয়ের সমষ্টি দুই সমকোণ – স্বতঃসিদ্ধ 1 ]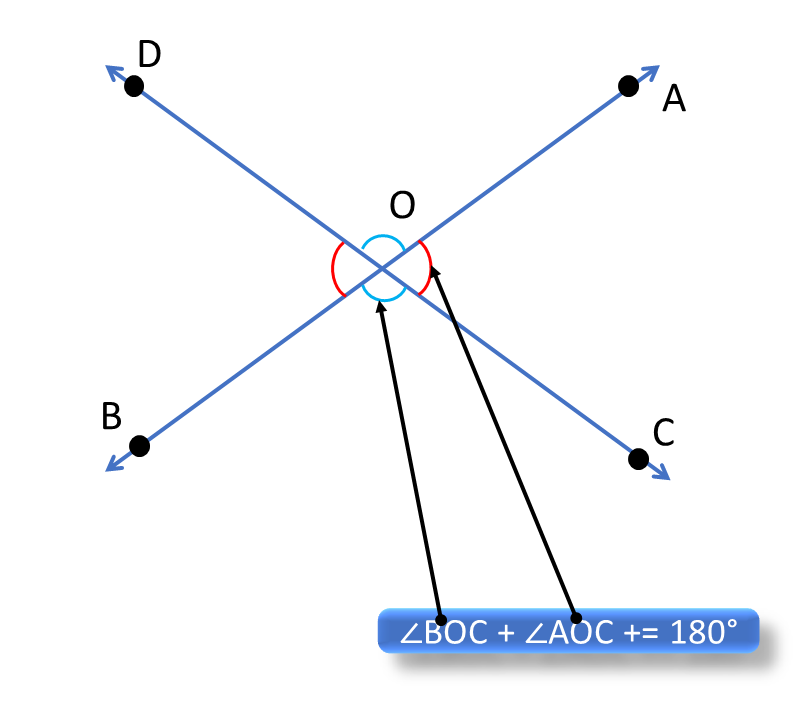

∠BOC + ∠BOD =∠BOC + ∠AOC

সুতরাং ∠BOD = ∠AOC ( উভয়দিক থেকে ∠BOC বিয়োগ করে পাই )

উপরের প্রমাণে ভালো করে লক্ষ্য করে দেখো যে প্রত্যেক লাইন লেখা হয়েছে তা যে যুক্তি থেকে লেখা হয়েছে তা পাশে লেখা হয়েছে কারণ বলে। এটি অবশ্যই খেয়াল করতে হবে যে, আমরা যে লাইন টি লিখবো সেটি কোণ যুক্তিতে লিখলাম সেটা কারণ বলে সেই লাইনের পাশে লিখতে হবে।

Step 7: ( সমাপ্তি/সিদ্ধান্ত )

উপপাদ্য টি প্রমাণ করে আমরা যা পেলাম সেটা লিখতে হবে।

উদাহরণের উপপাদ্য টিতে লিখতে হবে-

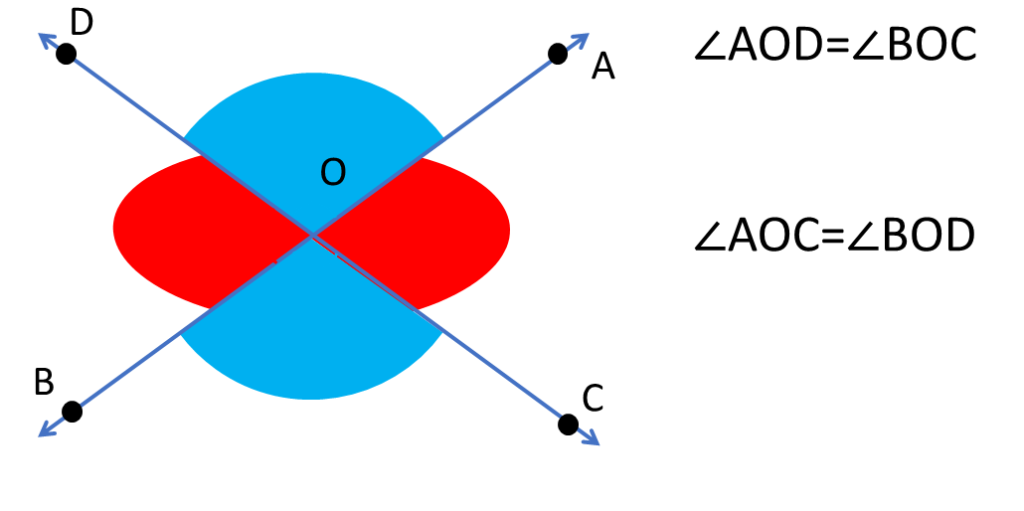
পেলাম AB ও CD দুটি সরলরেখা পরস্পরকে O বিন্দুতে ছেদ করায় বিপ্রতীপ কোণগুলি সমান অর্থাৎ-

∠AOD=∠BOC

এবং ∠AOC=∠BOD

---

এইরকম ভাবে ধাপে ধাপে তোমরা যদি উপপাদ্য প্রমাণ করো তাহলে দেখবে আগের থেকে অনেক সহজ হয়েছে । আর এই উপায়ে করলে যতো STEP তোমরা লিখবে পরীক্ষক তোমাদের খাতা দেখার সময় যতগুলো STEPS তুমি লিখেছো তারউপর তোমাকে নম্বর দেওয়া হবে ।

---