শ্রেনিঃ- অষ্টম ; অধ্যায়ঃ-বিপ্রতীপ কোণের ধারণা ; অধ্যায়ের সারাংশ
বিপ্রতীপ কোণ কাকে বলে?
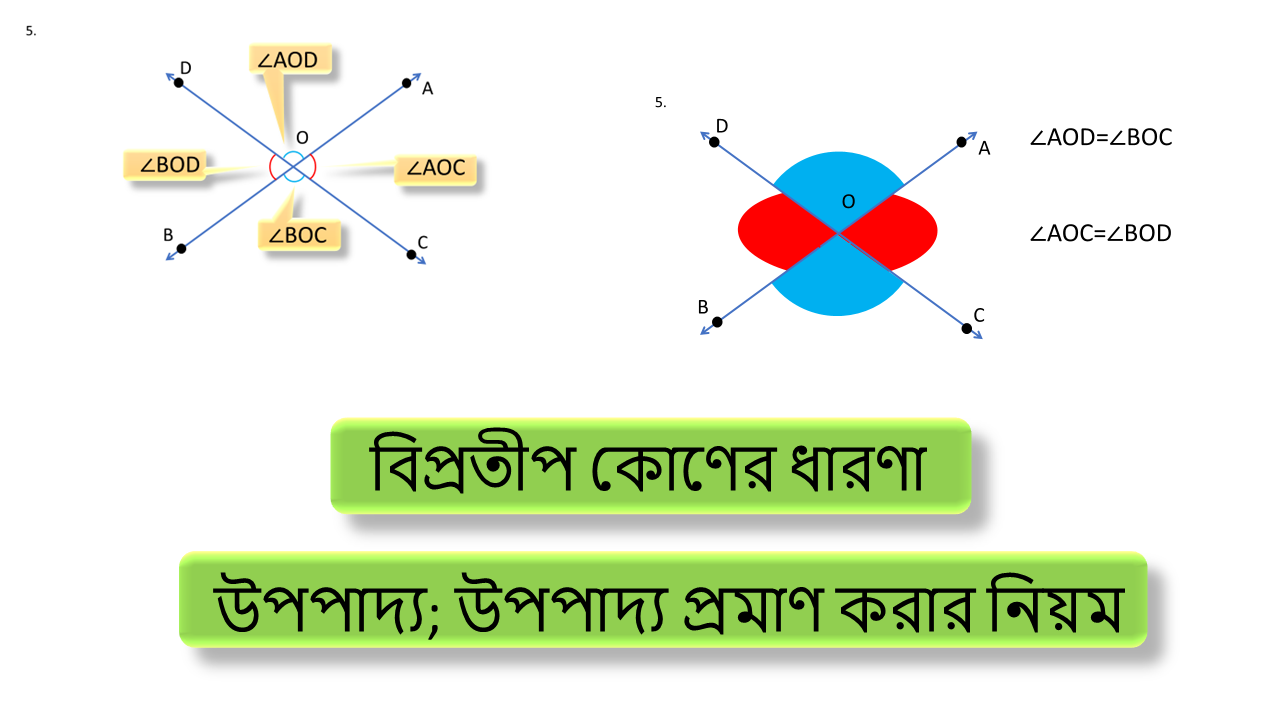
দুটি সরলরেখা পরস্পরকে ছেদ করলে বিপরীত দিকে যে দুই জোড়া কোণ তৈরি হয় তাদের বিপ্রতীপ কোণ বলে ।

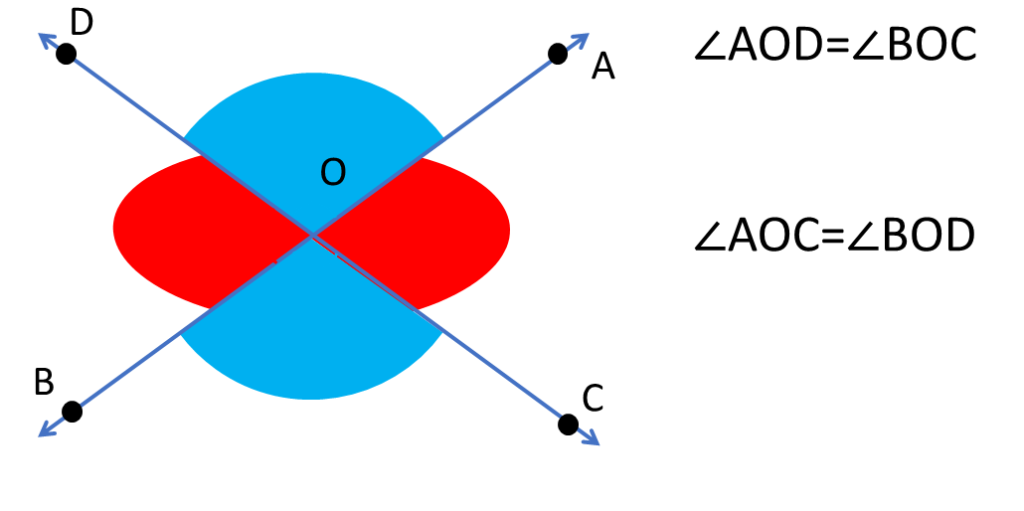
ছবিতে AB ও CD দুটি সরলরেখা O বিন্দুতে পরস্পর মিলিত হয়েছে ।
এখানে ∠AOD এর বিপ্রতীপ ∠BOC
এবং
∠BOD এর বিপ্রতীপ ∠AOC
বিপ্রতীপ কোণ এর এই অধ্যায়টি বোঝার জন্যে আমাকে উপপাদ্য বিষয়ে জানতে হবে। উপপাদ্য বিষয়ে যদি তোমরা না জানো তাহলে এই অধ্যায়ের মতো সমস্ত জ্যামিতিক অধ্যায়( যা আমরা আগামিতে বুঝবো) তা কিছুই বুঝতে পারবেনা। উপপাদ্য বিষয়ক সমস্ত কিছু নিম্নে আলোচনা করা হলঃ
উপপাদ্য এর নাম শুনলে আমরা ছাত্ররা অনেকে ঘাবড়ে যায় এবং ঘাবড়ে যাওয়ার কারণে আমাদের মাথায় ঢুকে যায় যে উপপাদ্য মানেই একটা কঠিন সমস্যা যা আমরা প্রমাণ করতে পারবোনা না বা কিছুই বুঝতে পারবো না । এই উপপাদ্য প্রমাণের সমস্যা যদি তোমাদেরও হয় বা হয়ে থাকে, তবে এটা স্বাভাবিক ! কারণ আমরাও যখন উপপাদ্য পড়তাম তখন শুনতাম যে উপপাদ্য মানেই বিশাল কঠিন একটা সমস্যা যা নাকি শুধু মুখস্ত করেই পার হওয়া সম্ভব । যা সম্পূর্ণ ভুল একটি ধারণা । আর আমাদের চারিপাশে সবাই এমনকি আমাদের কিছু শিক্ষকও এবিষয়ে সঠিক গাইড না দেওয়ার কারণে আমাদের এই উপপাদ্য জনিত সমস্যা খুব জটিল মনে হয় । আমি Mathematics নিয়ে পড়ে যা এতদূর শিখেছি এবং বুঝেছি তার উপর ভিত্তি করে এখানে তোমাদের উপপাদ্য লেখার কিছু নিয়ম বলে দেবো যাতে করে খুব সহজ ভাবে একটা উপপাদ্য কে ক প্রমানিত করতে পারবে । |
উপপাদ্য | Theorem
উপপাদ্য হলো এক প্রকারের প্রস্তাবনা, যা কিছু প্রাথমিক ধারণার ভিত্তিতে প্রমাণ করা হয় এবং কিছু নিয়ম মেনে আমরা যদি উপপাদ্য প্রমাণ করি তাহলে খুব সহজেই আমরা একটা উপপাদ্যকে প্রমাণ করতে পারবো । উপপাদ্য প্রমাণ করার জন্যে আমাদের কিছু কিছু স্বতঃসিদ্ধ এর প্রয়োজন হতে পারে ।একটি উদাহরণের মাধ্যমে আমরা বুঝবো যে কিভাবে প্রমাণ করতে হয় । আমরা উপপাদ্য প্রমাণে নিম্নলিখিত ধাপ বা steps অনুসরণ করবো ।
উদাহরণ– দুটি সরলরেখা পরস্পরকে ছেদ করলে যে দু-জোড়া বিপ্রতীপ কোণ উৎপন্ন হয় তাদের প্রতিজোড়া কোণের পরিমাপ পরস্পর সমান ।
Step 1:-( উপপাদ্যটি লেখা )
| যে উপপাদ্য টি প্রমাণ করতে হবে সেটি প্রথমে আমরা সুন্দর করে লিখে নেবো । |
যেমন-
Step 1: দুটি সরলরেখা পরস্পরকে ছেদ করলে যে দু-জোড়া বিপ্রতীপ কোণ উৎপন্ন হয় তাদের প্রতিজোড়া কোণের পরিমাপ পরস্পর সমান ।
Step 2:-( চিত্র )
| যে উপপাদ্য টি প্রমাণ করতে হবে সেটির হিসাবে একটি সঠিক চিত্র অঙ্কন করতে হবে । |
যেমন উদাহরণে যে উপপাদ্যটি আছে তার চিত্র হবে –
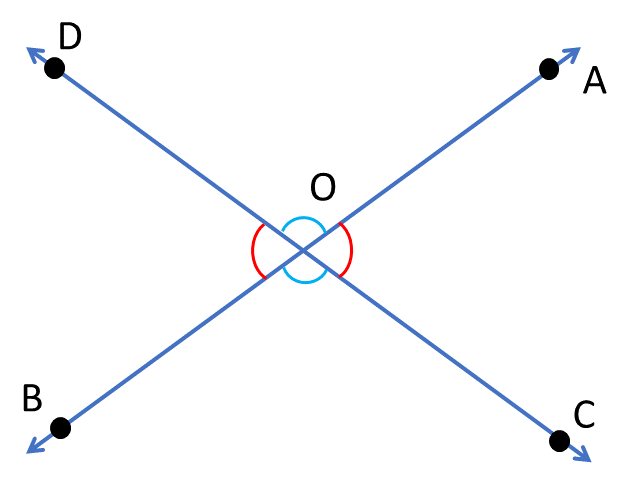
Step 3:-( প্রদত্ত )
| যে উপপাদ্যটি দেওয়া আছে তা থেকে আমি কি কি তথ্য পেলাম তা লিখে নেবো । |
উদাহরণের উপপাদ্য টি থেকে আমরা যে যে তথ্য গুলি পেলাম তা হলো –
প্রদত্ত ( দেওয়া আছে ):-
AB ও CD দুটি সরলরেখা পরস্পরকে O বিন্দুতে ছেদ করেছে । এর ফলে দু-জোড়া বিপ্রতীপ কোণ ∠AOD, ∠BOC ও ∠AOC, ∠BOD তৈরি হয়েছে ।
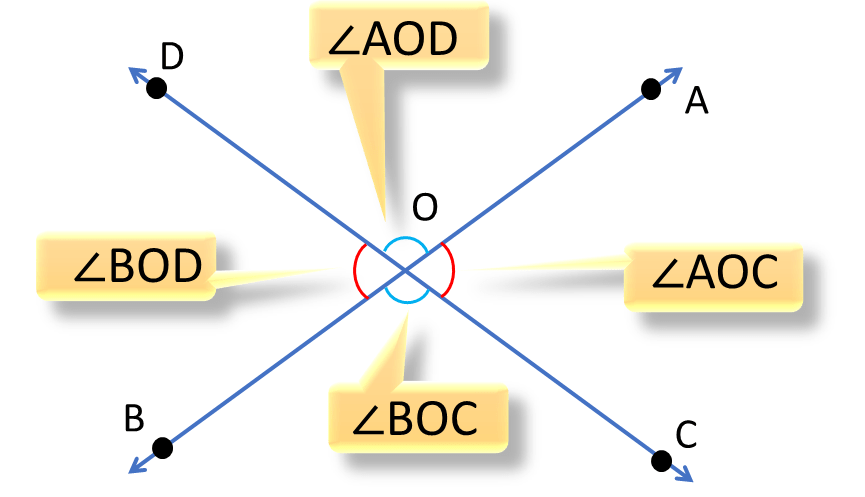
Step 4:( প্রামান্য/কি প্রমাণ করব )
| উপপাদ্য টিতে যা প্রমাণ করতে হবে সেটা লিখতে হবে । |
প্রামান্য ( কি প্রমাণ করব ):-
প্রমাণ করতে হবে যে, প্রতিজোড়া বিপ্রতীপ কোণগুলির পরিমাপ সমান অর্থাৎ ∠AOD=∠BOC এবং ∠AOC=∠BOD
Step 5:( অতিরিক্ত অঙ্কন )
| উপপাদ্য টি প্রমাণ করতে গিয়ে অতিরিক্ত অঙ্কন করতে হতে পারে । |
উদাহরণে যে উপপাদ্য টি আছে সেটি প্রমাণ করার জন্যে অতিরিক্ত কোনো অঙ্কনের প্রয়োজন নেই ।
Step 6: ( প্রমাণ/যুক্তি দিয়ে প্রমাণ )
| এই ধাপে আমরা যুক্তি দিয়ে প্রমাণ করবো । |
উদাহরণের উপপাদ্য টিতে লিখতে হবে-
প্রমানঃ-
∠AOD +∠AOC = 180° [ কারণ CD সরলরেখার উপরে OA রশ্মি দণ্ডায়মান হওয়ায় সন্নিহিত কোণদ্বয়ের সমষ্টি দুই সমকোণ – স্বতঃসিদ্ধ 1 ]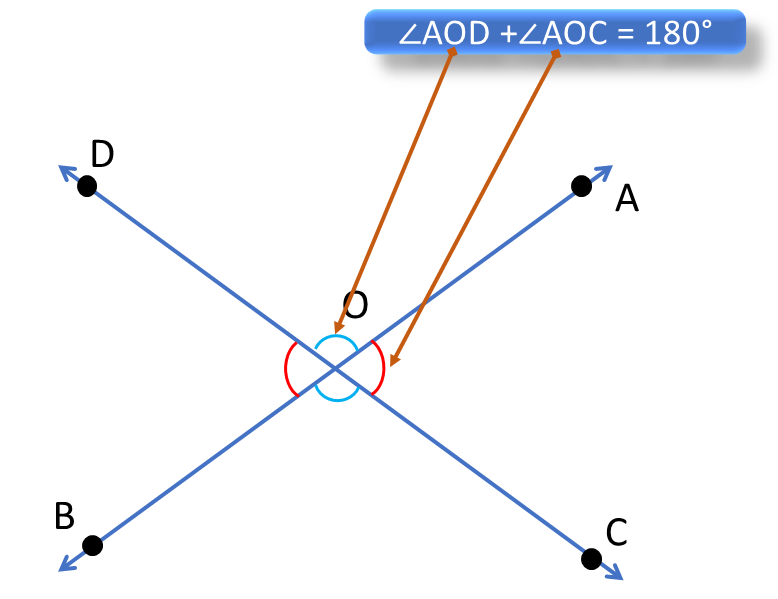 |
∠AOC + ∠BOC = 180° [ কারণ AB সরলরেখার উপরে OC রশ্মি দণ্ডায়মান হওয়ায় সন্নিহিত কোণদ্বয়ের সমষ্টি দুই সমকোণ – স্বতঃসিদ্ধ 1 ]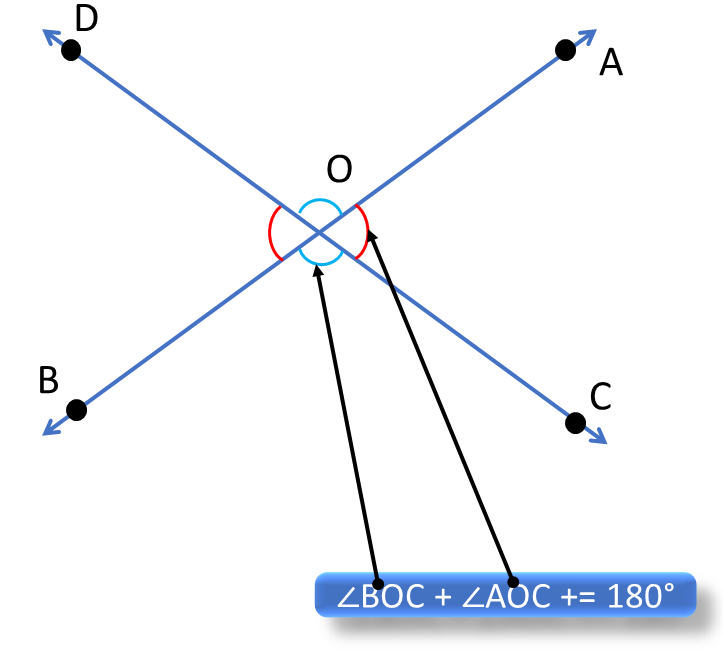 |
| ∠AOD +∠AOC =∠AOC + ∠BOC |
| সুতরাং ∠AOD = ∠BOC ( উভয়দিক থেকে ∠AOC বিয়োগ করে পাই ) |
| আবার একইভাবে লিখতে পারি- |
∠BOC + ∠BOD = 180° [ কারণ CD সরলরেখার উপরে OB রশ্মি দণ্ডায়মান হওয়ায় সন্নিহিত কোণদ্বয়ের সমষ্টি দুই সমকোণ – স্বতঃসিদ্ধ 1 ]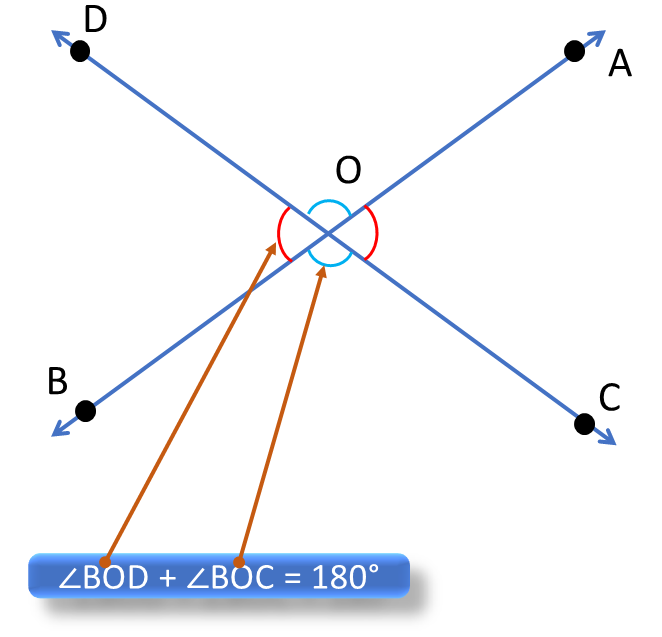 |
∠BOC + ∠AOC = 180° [ কারণ AB সরলরেখার উপরে OC রশ্মি দণ্ডায়মান হওয়ায় সন্নিহিত কোণদ্বয়ের সমষ্টি দুই সমকোণ – স্বতঃসিদ্ধ 1 ]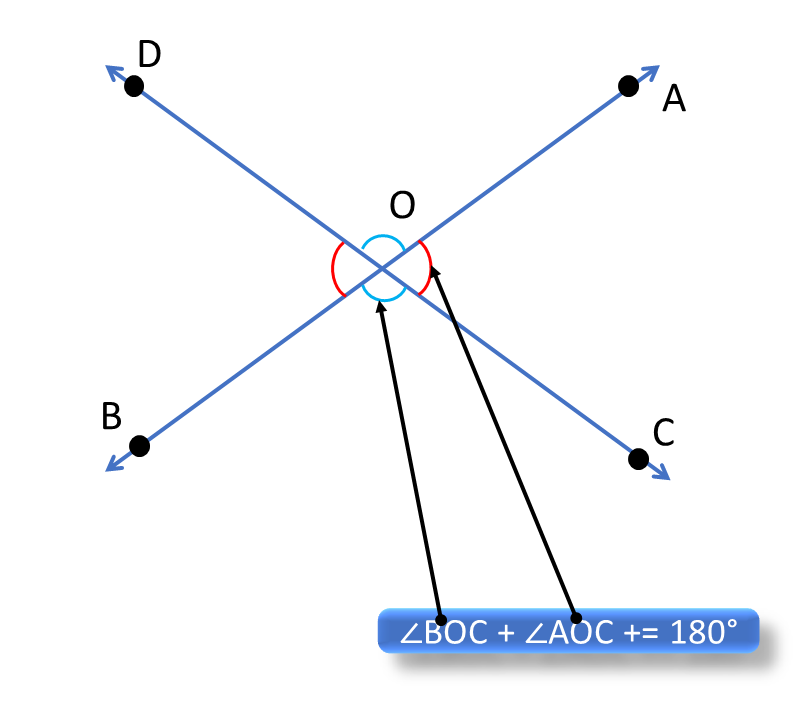 |
| ∠BOC + ∠BOD =∠BOC + ∠AOC |
| সুতরাং ∠BOD = ∠AOC ( উভয়দিক থেকে ∠BOC বিয়োগ করে পাই ) |
উপরের প্রমাণে ভালো করে লক্ষ্য করে দেখো যে প্রত্যেক লাইন লেখা হয়েছে তা যে যুক্তি থেকে লেখা হয়েছে তা পাশে লেখা হয়েছে কারণ বলে। এটি অবশ্যই খেয়াল করতে হবে যে, আমরা যে লাইন টি লিখবো সেটি কোণ যুক্তিতে লিখলাম সেটা কারণ বলে সেই লাইনের পাশে লিখতে হবে।
Step 7: ( সমাপ্তি/সিদ্ধান্ত )
| উপপাদ্য টি প্রমাণ করে আমরা যা পেলাম সেটা লিখতে হবে। |
উদাহরণের উপপাদ্য টিতে লিখতে হবে-
পেলাম AB ও CD দুটি সরলরেখা পরস্পরকে O বিন্দুতে ছেদ করায় বিপ্রতীপ কোণগুলি সমান অর্থাৎ-
∠AOD=∠BOC
এবং ∠AOC=∠BOD
| এইরকম ভাবে ধাপে ধাপে তোমরা যদি উপপাদ্য প্রমাণ করো তাহলে দেখবে আগের থেকে অনেক সহজ হয়েছে । আর এই উপায়ে করলে যতো STEP তোমরা লিখবে পরীক্ষক তোমাদের খাতা দেখার সময় যতগুলো STEPS তুমি লিখেছো তারউপর তোমাকে নম্বর দেওয়া হবে । |
এই কোণ সম্পর্কিত আলোচনা ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।
এই অধ্যায়টি জ্যামিতিক হিসাবে খুবই সোজা ! তোমরা যদি সঠিক পদ্ধতি মেনে এই অধ্যায় এর কষে দেখি তে যে সমস্ত অংক গুলি আছে সেগুলি করো তাহলে কোথাও বুঝতে অসুবিধে হবেনা । এটি পড়ার পর তোমরা পূরক কোণ , সম্পূরক কোণ ও সন্নিহিত কোণ এর কষে দেখি 6 অংক গুলি করলে নিশ্চয় বুঝতে পারবে ।  |
তোমাদের জন্যে অষ্টম শ্রেণীর সমস্ত অধ্যায় এর গণিত এবং অধ্যায়টি কিভাবে আয়ত্ত করতে হবে তা খুব সুন্দর করে লেখা হয়েছে যাতে তোমরা খুব সহজেই প্রতিটি অধ্যায় বুঝতে পারো এবং প্রতিটি অংক বুঝে করতে পারো । |

এখানে তোমরা তোমাদের অষ্টম শ্রেণীতে কি কি পড়ানো হয়, মানে তোমাদের অষ্টম শ্রেণীর সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।