শ্রেণী- দশম ; অধ্যায় – লম্ব বৃত্তাকার শঙ্কু ; কষে দেখি 16
কষে দেখি 16 Class 10 অংকের সূচিপত্র:-
কষে দেখি 16 Class 10 এর অংকের সমাধান গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ
এই কষে দেখি 16, পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদ | WBBSE এর অন্তর্গত দশম শ্রেণি|Class 10 এর 16 নম্বর অধ্যায়|Chapter 16, লম্ব বৃত্তাকার শঙ্কু | Right Circular Cone এর অনুশীলনী।
এই কষে দেখি 16 Class 10 এর অঙ্ক গুলি বোঝার জন্যে যে যে বিষয় জানতে হবে তা আলোচনা করা হলো-
r একক ব্যাসার্ধ , \(l\) একক তির্যক উচ্চতা এবং h একক উচ্চতা বিশিষ্ট একটি লম্ব বৃত্তাকার শঙ্কুর-
- বক্রতলের ক্ষেত্রফল-
= \(πrl\) বর্গ একক

- সমগ্রতলের ক্ষেত্রফল-
= \(πr(r+l)\) বর্গ একক
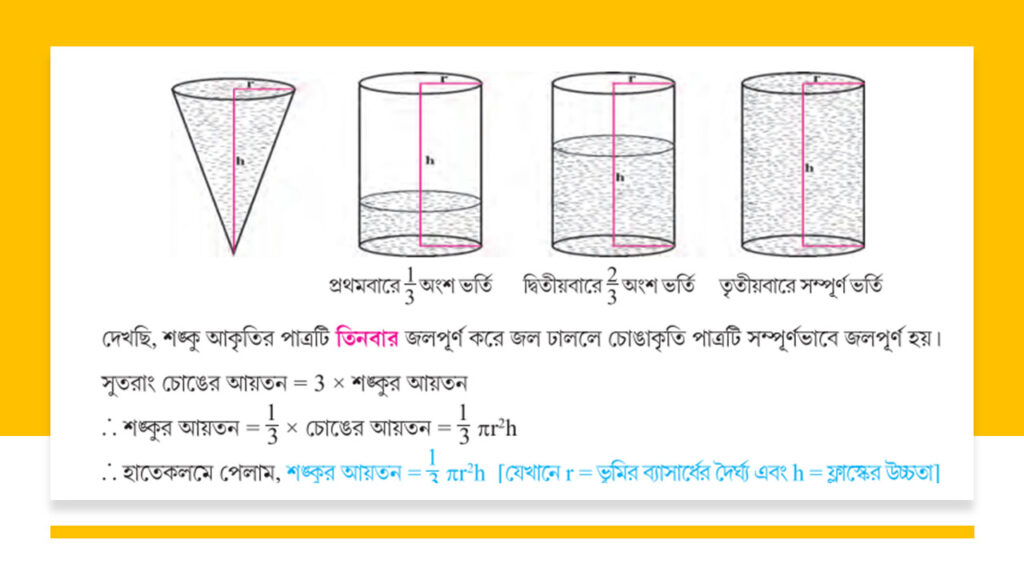
- আয়তন-
= \(\frac{1}{3}πr^2h\) ঘন একক.
আগামিতে এই কষে দেখি 16 Class 10 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| কষে দেখি 16 Class 10 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 16 Class 10 তারপর |
কষে দেখি 16 Class 10|Koshe Dekhi 16 Class 10
1. আমি একটি মুখবন্ধ লম্ব বৃত্তাকার শঙ্কু তৈরি করেছি যার ভূমির ব্যাসার্ধের দৈর্ঘ্য 15 সেমি. এবং তির্যক উচ্চতা 24 সেমি.। ওই শঙ্কুর পার্শ্বতলের ক্ষেত্রফল ও সমগ্রতলের ক্ষেত্রফল হিসাব করে লিখি ।
সমাধানঃ-
শঙ্কুটির,
| ভূমির ব্যাসার্ধ | r = 15 সেমি. |
| তির্যক উচ্চতা | l = 24 সেমি. |
- শঙ্কুর পার্শ্বতলের ক্ষেত্রফল
= πrl
= \(\frac{22}{7}\)×15×24
= 1131.42857 বর্গ সেমি.
= 1131.43 (প্রায়)
- শঙ্কুর সমগ্রতলের ক্ষেত্রফল
= πr(r+l)
= \(\frac{22}{7}\)×15(15 + 24)
= \(\frac{22}{7}\)×15×36
= 1838.5714 বর্গ সেমি.
= 1838.57 বর্গ সেমি. (প্রায়)
2. শঙ্কুর আয়তন নির্ণয় করি যখন,
(i) ভূমির ক্ষেত্রফল 1.54 বর্গ মিটার এবং উচ্চতা 2.4 মিটার,
সমাধানঃ-
ধরি, শঙ্কুর ভূমির ব্যাসার্ধ = r মিটার. ও উচ্চতা h = 2.4 মিটার.
- শঙ্কুর আয়তন
| = \(\frac{1}{3}\)πr2h |
| = \(\frac{1}{3}\)×(ভূমির ক্ষেত্রফল)×উচ্চতা |
| = \(\frac{1}{3}\)×1.54×2.4 |
| = 1.232 ঘন মিটার. |
(ii) ভূমির ব্যাসের দৈর্ঘ্য 21 মিটার এবং তির্যক উচ্চতা 17.5 মিটার।
সমাধানঃ-
মনে করি শঙ্কুর,
| ভূমির ব্যাসার্ধ | r = \(\frac{21}{2}\) = 10.5 মিটার. |
| তির্যক উচ্চতা | \(l\) = 17.5 মিটার. |
অতএব,
| উচ্চতা | h = \(\sqrt{l^2-r^2}\) = \(\sqrt{(17.5)^2}- (10.5)^2\) = \(\sqrt{306.25-110.25}\) = \(\sqrt{196}\) = 14 মিটার. |
- শঙ্কুর আয়তন
| = \(\frac{1}{3}\)πr2h |
| = \(\frac{1}{3}\)π(10.5)2×14 |
| = \(\frac{1}{3}\)×\(\frac{22}{7}\)(10.5)2×14 |
| = 1617 ঘন মিটার. |
3. আমিনা একটি সমকোণী ত্রিভুজ অঙ্কন করেছে যার সমকোণ সংলগ্ন বাহু দুটির দৈর্ঘ্য 15 সেমি. ও 20 সেমি.। 15 সেমি. দীর্ঘ বাহুটিকে অক্ষ ধরে ত্রিভুজটিকে একবার পূর্ণ আবর্তন করলে যে ঘনবস্তু তৈরি হয়, তার পার্শ্বতলের ক্ষেত্রফল, সমগ্রতলের ক্ষেত্রফল এবং আয়তন নির্ণয় করি।
সমাধানঃ-
15 সেমি. দীর্ঘ বাহুটিকে অক্ষ ধরে ত্রিভুজটিকে একবার পূর্ণ আবর্তন করলে একটি লম্ব বৃত্তাকার শঙ্কু তৈরি হয় যার,
| ভূমির দৈর্ঘ্য | r = 20 সেমি. |
| উচ্চতা | h = 15 সেমি . |
| তির্যক উচ্চতা | \(l\) = \(\sqrt{r^2+l^2}\) = \(\sqrt{(20)^2+(15)^2}\) = \(\sqrt{400+225}\) = \(\sqrt{625}\) = 25 সেমি. |
শঙ্কুটির,
- পার্শ্বতলের ক্ষেত্রফল
| = \(πrl\) |
| = \(\frac{22}{7}\)×20×25 |
| = 1571\(\frac{3}{7}\) বর্গ সেমি. |
- সমগ্রতলের ক্ষেত্রফল
| = \(πr(r+l)\) |
| = \(\frac{22}{7} \times 20 (20+25)\) |
| = 2828\(\frac{4}{7}\) বর্গ সেমি. |
- আয়তন
| = \(\frac{1}{3}πr^2h\) |
| = \(\frac{1}{3}\times \frac{22}{7}\times (20)^2\times 15\) |
| = 6285\(\frac{5}{7}\) ঘন সেমি. |
4. কোনো শঙ্কুর উচ্চতা ও তির্যক উচ্চতা যথাক্রমে 6 সেমি. ও 10 সেমি. হলে, শঙ্কুটির সমগ্রতলের ক্ষেত্রফল ও আয়তন নির্ণয় করি।
সমাধানঃ-
শঙ্কুর,
| উচ্চতা | h = 6 সেমি. |
| তির্যক উচ্চতা | \(l\) = 10 সেমি. |
অতএব,
| ভূমির ব্যাসার্ধ | r = \(\sqrt{l^2-h^2}\) = \(\sqrt{(10)^2 – 6^2}\) = \(\sqrt{100-36}\) = \(\sqrt{64}\) = 8 সেমি. |
শঙ্কুটির,
- সমগ্রতলের ক্ষেত্রফল
| = \(πr(r+l)\) |
| = \(\frac{22}{7} \times 8 (8+10)\) |
| = 452\(\frac{4}{7}\) বর্গ সেমি. |
- আয়তন
| = \(\frac{1}{3}πr^2h\) |
| = \(\frac{1}{3}\times \frac{22}{7}\times 8^2\times 6\) |
| = 402\(\frac{2}{7}\) ঘন সেমি. |
5. কোনো লম্ব বৃত্তাকার শঙ্কুর আয়তন (100π) ঘন সেমি. এবং উচ্চতা 12 সেমি. হলে, শঙ্কুর তির্যক উচ্চতা হিসাব করে লিখি।
সমাধানঃ-
শঙ্কুর,
| ব্যাসার্ধ | = r সেমি. (ধরি) |
| উচ্চতা | h = 12 সেমি. |
প্রশ্নানুসারে,
| শঙ্কুর আয়তন = 100π ঘন সেমি. |
| বা, \(\frac{1}{3}πr^2h\) = 100π |
| বা, \(r^2 = \frac{100\times 3}{h}\) |
| বা, \(r^2 = \frac{100\times 3}{12}\) |
| বা, \(r^2 = 25 \) |
| বা, \(r = 5\) |
অতএব,
| তির্যক উচ্চতা |
| = \(\sqrt{r^2+h^2}\) |
| = \(\sqrt{5^2+(12)^2}\) |
| = \(\sqrt{25+144}\) |
| = \(\sqrt{169}\) = 13 সেমি. |
6. লম্ব বৃত্তাকার শঙ্কু আকৃতির একটি তাঁবু তৈরি করতে 77 বর্গ মিটার ত্রিপল লেগেছে। তাঁবুটির তির্যক উচ্চতা যদি 7 মিটার হয়, তবে তাঁবুটির ভূমিতলের ক্ষেত্রফল হিসাব করে লিখি।
সমাধানঃ-
তাবু টির,
| ভূমির ব্যাসার্ধ | = r মিটার. (ধরি) |
| তির্যক উচ্চতা | \(l\) = 7 মিটার. |
প্রশ্নানুসারে,
| তাবু তৈরি করতে ত্রিপল লেগেছে = 77 বর্গ মিটার. |
| বা, তাবুটির পার্শ্বতলের ক্ষেত্রফল = 77 বর্গ মিটার. |
| বা, \(πrl = 77\) |
| বা, \(r = \frac{77}{πl}\) |
| বা, \(r = \frac{77 \times 7}{22 \times 7}\) |
| বা, \(r = 3.5\) |
অতএব,
- তাঁবুটির ভূমিতলের ক্ষেত্রফল
| = \(πr^2\) |
| = \(\frac{22}{7} \times (3.5)^2\) |
| = 38.5 বর্গ মিটার. |
7. একটি লম্ব বৃত্তাকার শঙ্কুর ভূমিতলের ব্যাস 21 মিটার এবং উচ্চতা 14 মিটার। প্রতি বর্গ মিটার 1.50 টাকা হিসাবে পার্শ্বতল রং করতে কত টাকা খরচ পড়বে হিসাব করি।
সমাধানঃ-
লম্ব বৃত্তাকার শঙ্কুর,
| ভূমির ব্যাসার্ধ | r = \(\frac{21}{2}\) = 10.5 মিটার. |
| উচ্চতা | h = 14 মিটার. |
| অতএব, তির্যক উচ্চতা | \(l = \sqrt{(14)^2+(10.5)^2}\) = \(\sqrt{196+110.25}\) = \(\sqrt{306.25}\) = 17.5 মিটার. |
শঙ্কুটির,
- পার্শ্বতলের ক্ষেত্রফল
| = \(πrl\) |
| = \(\frac{22}{7}\)×10.5×17.5 |
| = 577.5 বর্গ সেমি. |
প্রতি বর্গ মিটার 1.50 টাকা হিসাবে পার্শ্বতল অর্থাৎ 577.5 বর্গ সেমি রং করতে খরচ পড়বে
= 577.5×1.5
= 866.25 টাকা.
8. নিরেট শঙ্কু আকৃতির একটি কাঠের খেলনার ভূমিতলের ব্যাসের দৈর্ঘ্য 10 সেমি.। খেলনাটির বক্রতলে প্রতি বর্গ সেমি. 2.10 টাকা হিসাবে পালিশ করতে 429 টাকা খরচ পড়ে। খেলনাটির উচ্চতা কত হিসাব করি। খেলনাটি তৈরি করতে কত ঘন সেমি, কাঠ লেগেছে নির্ণয় করি।
সমাধানঃ-
খেলনাটির বক্রতলে প্রতি বর্গ সেমি. 2.10 টাকা হিসাবে পালিশ করতে 429 টাকা খরচ পড়ে।
অর্থাৎ, খেলনাটির পার্শ্বতলের ক্ষেত্রফল
= \(\frac{429}{2.10}\)
= \(\frac{1430}{7}\) বর্গ সেমি.
খেলনাটির,
| ভূমির ব্যাসার্ধ | r = \(\frac{10}{2}\) = 5 সেমি. |
| তির্যক উচ্চতা | = \(l\) (ধরি) |
এখন,
| খেলনাটির পার্শ্বতলের ক্ষেত্রফল = \(\frac{1430}{7}\) বর্গ সেমি. |
| বা, \(πrl = \frac{1430}{7}\) |
| বা, \(l = \frac{1430}{7πr}\) |
| বা, \(l = \frac{1430 \times 7}{7 \times 22 \times 5}\) |
| বা, \(l = 13\) সেমি. |
অতএব, খেলনাটির উচ্চতা
h = \(\sqrt{(13)^2-5^2}\)
= \(\sqrt{169-25}\)
= \(\sqrt{144}\) = 12 সেমি.
অতএব,
- খেলনাটি তৈরি করতে কাঠ লেগেছে,
| = খেলনাটির আয়তন |
| = \(\frac{1}{3}πr^2h\) |
| = \(\frac{1}{3}\times \frac{22}{7}\times 5^2\times 12\) |
| = 314\(\frac{2}{7}\) ঘন সেমি. |
9. লম্ব বৃত্তাকার শঙ্কু আকৃতির একটি লোহার পাতের বয়া তৈরি করতে 75 \(\frac{3}{7}\) বর্গ মিটার লোহার পাত লেগেছে। বয়াটির তির্যক উচ্চতা যদি 5 মিটার হয়, তবে বয়াটিতে কত বায়ু আছে এবং বয়াটির উচ্চতা কত হিসাব করে লিখি।ওই বয়াটির চারপাশ রং করতে প্রতি বর্গ মিটার 2.80 টাকা হিসাবে কত খরচ পড়বে নির্ণয় করি। [লোহার পাতের বেধ হিসাবের মধ্যে ধরতে হবে না]
সমাধানঃ-
লোহার বয়া টির,
| তির্যক উচ্চতা | \(l\) = 5 মিটার. |
| ভূমির ব্যাসার্ধ | = r (ধরি) |
প্রশ্নানুসারে,
| বয়া তৈরি করতে 75 \(\frac{3}{7}\) বর্গ মিটার লোহার পাত লেগেছে |
| বা, \(πr(r+l) = 75\frac{3}{7}\) |
| বা, \(\frac{22}{7}r(r+5) = \frac{528}{7}\) |
| বা, \(r(r+5) = 24\) |
| বা, \(r^2 + 5r – 24 = 0 |
| বা, \((r+8)(r-3)=0\) |
| অতএব, \(r = 3\) |
h = \(\sqrt{l^2-r^2}\)
= \(\sqrt{5^2-3^2}\)
= \(\sqrt{25-9\)
= \(sqrt{16}\)
= 4 সেমি.
- লোহার বয়া টিতে বাতাস থাকবে
| = বয়াটির আয়তন |
| = \(\frac{1}{3}πr^2h\) |
| = \(\frac{1}{3}\times \frac{22}{7}\times 3^2\times 4\) |
| = 7\(\frac{5}{7}\) ঘন সেমি. |
- বয়াটির বয়াটির চারপাশ রং করতে প্রতি বর্গ মিটার 2.80 টাকা হিসাবে খরচ পড়বে
= \(\frac{528}{7}\times 2.80\)
= 211.20 টাকা
10. লম্ব বৃত্তাকার শঙ্কু আকৃতির একটি তাঁবুতে 11 জন লোক থাকতে পারে। প্রত্যেক লোকের জন্য ভূমিতে 4 বর্গ মিটার জায়গা লাগে এবং 20 ঘন মিটার বাতাসের প্রয়োজন। ঠিক এই 11 জন লোকের জন্য নির্মিত তাবুর উচ্চতা নির্ণয় করি।
সমাধানঃ-
লম্ব বৃত্তাকার শঙ্কু আকৃতির তাবুটির ভূমির ক্ষেত্রফল
= 4 × 11
= 44 বর্গ মিটার.
ধরি, তাঁবুটির
| ভূমির ব্যাসার্ধ | = r মিটার. |
| উচ্চতা | = h মিটার. |
শর্তে,
\(πr^2 = 44\) ——(i)
আবার,
| তাঁবুটির আয়তন = 11×20 ঘন মিটার. |
| বা, \(\frac{1}{3}πr^2h\) = 220 |
| বা, \(h = \frac{220 \times 3}{πr^2}\) |
| বা, \(h = \frac{220 \times 3}{44}\) |
| বা, \(h = 15\) |
11. শোলা দিয়ে তৈরি একটি শঙ্কু আকৃতির মাথার টোপরের ভূমির বাইরের দিকের ব্যাসের দৈর্ঘ্য 21 সেমি. । টোপরটির উপরিভাগ রাংতা দিয়ে মুড়তে প্রতি বর্গ সেমি. 10 পয়সা হিসাবে 57.75 টাকা খরচ পড়ে। টোপরটির উচ্চতা ও তির্যক উচ্চতা হিসাব করে লিখি।
সমাধানঃ-
টোপরটির,
| ভূমির বাইরের ব্যাসার্ধ | r = \(\frac{21}{2}\) = 10.5 সেমি. |
| উচ্চতা | = h (ধরি) |
| তির্যক উচ্চতা | = \(l\)(ধরি) |
টোপরটির উপরিভাগ রাংতা দিয়ে মুড়তে প্রতি বর্গ সেমি. 10 পয়সা হিসাবে 57.75 টাকা খরচ পড়ে।
অর্থাৎ, টোপরটির পার্শ্বতলের ক্ষেত্রফল
= \(\frac{5775}{10}\)
= 577.5 বর্গ সেমি.
শরতে,
| \(πrl = 577.5\) |
| বা, \(l = \frac{577.5}{πr}\) |
| বা, \(l = \frac{577.5 \times 7}{22 \times 10.5}\) |
| বা, \(l = 17.5\) সেমি. |
আবার,
- উচ্চতা h
| = \(\sqrt{l^2-r^2}\) |
| = \(\sqrt{(17.5)^2 – (10.5)^2}\) |
| = \(\sqrt{306.25-110.25}\) |
| = \(\sqrt{196}\) = 14 সেমি. |
12. গমের একটি স্তূপ লম্ব বৃত্তাকার শঙ্কু আকারে আছে, যার ভূমির ব্যাসের দৈর্ঘ্য 9 মিটার এবং উচ্চতা 3.5 মিটার। মোট গমের আয়তন নির্ণয় করি। গমের ওই স্তূপ ঢাকতে কমপক্ষে কত বর্গ মিটার প্লাসটিকের চাদর প্রয়োজন হবে হিসাব করে দেখি। [ ধরি, = 3.14 / 130 = 11.4]
সমাধানঃ-
গমের স্তূপ এর
| ভূমির ব্যাসার্ধ | r = \(\frac{9}{2}\) = 4.5 মিটার. |
| উচ্চতা | h = 3.5 মিটার. |
| তির্যক উচ্চতা | \(l = \sqrt{r^2+h^2}\) = \(\sqrt{(4.5)^2+(3.5)^2}\) = \(\sqrt{(\frac{9}{2})^2+(\frac{7}{2})^2}\) = \(\sqrt{\frac{81}{2}+\frac{49}{4}}\) = \(\sqrt{\frac{81+49}{4}}\) = \(\sqrt{\frac{130}{4}}\) = \(\frac{11.4}{2}\) = \(5.7\) মিটার. |
মোট গমের আয়তন
= \(\frac{1}{3}πr^2h\)
= \(\frac{1}{3}\times 3.14 \times (4.5)^2 \times 3.5\)
= 74.18 ঘন মিটার (প্রায়)
গমের ওই স্তূপ ঢাকতে কমপক্ষে যতো বর্গ মিটার প্লাসটিকের চাদর প্রয়োজন তা হলো-
= \(πrl\)
= 3.14 × 4.5 × 5.7
= 80.541
= 82.54 বর্গ মিটার. (প্রায়)
13. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) :
(i) একটি লম্ব বৃত্তাকার শঙ্কুর তির্যক উচ্চতা 15 সেমি, এবং ভূমিতলের ব্যাসের দৈর্ঘ্য 16 সেমি. হলে, শঙ্কুটির পার্শ্বতলের ক্ষেত্রফল
উত্তরঃ (c) 120π বর্গ সেমি.
সমাধানঃ-
শঙ্কুটির পার্শ্বতলের ক্ষেত্রফল
= πrl
= π×8×15
= 120π বর্গ সেমি.
(ii) দুটি লম্ব বৃত্তাকার শঙ্কুর আয়তনের অনুপাত 1:4 এবং তাদের ভূমিতলের ব্যাসার্ধের দৈর্ঘ্যের অনুপাত 4:5 হলে, তাদের উচ্চতার অনুপাত
উত্তরঃ (d) 25:64
(a) 1:5 (b) 5:4 (c ) 25:16
সমাধানঃ-
শর্তে,
| \(\frac{1}{3}π{r_1}^2h_1 : \frac{1}{3}π{r_2}^2h_2 = 1 : 4 |
| বা, \(\frac{\frac{1}{3}π{r_1}^2h_1}{\frac{1}{3}π{r_2}^2h_2} = \frac{1}{4}\) |
| বা, \((\frac{r_1}{r_2})^2 \times \frac{h_1}{h_2} = \frac{1}{4}\) |
| বা, \((\frac{4}{5})^2 \times \frac{h_1}{h_2} = \frac{1}{4}\) |
| বা, \(\frac{16}{25} \times \frac{h_1}{h_2} = \frac{1}{4}\) |
| বা, \(\frac{h_1}{h_2} = \frac{1 \times 25}{4 \times 16}\) |
| বা, \(\frac{h_1}{h_2} = \frac{25}{64}\) |
(iii) একটি লম্ব বৃত্তাকার শঙ্কুর ব্যাসার্ধের দৈর্ঘ্য একই রেখে উচ্চতা দ্বিগুণ করলে, শঙ্কুটির আয়তন বৃদ্ধি পায়।
উত্তরঃ (a) 100%
(b) 200% (c) 300% (d) 400%
সমাধানঃ-
| লম্ব বৃত্তাকার শঙ্কুর আয়তন- | |
|---|---|
| উচ্চতা দ্বিগুণ করার আগে- | \(\frac{1}{3}πr^2h = V\) |
| উচ্চতা দ্বিগুণ করার পরে- | \(\frac{1}{3}πr^2.2h = 2\frac{1}{3}πr^2h = 2V\) |
আয়তনের শতকরা বৃদ্ধি
= \(\frac{2V-V}{V}\times 100\)
= 100 একক
(iv) একটি শঙ্কুর ব্যাসার্ধের দৈর্ঘ্য এবং উচ্চতা প্রত্যেকটি দ্বিগুণ হলে, শঙ্কুটির আয়তন হয় পূর্বের শঙ্কুর আয়তনের
উত্তরঃ (d) 8 গুণ
(a) 3 গুণ (b) 4 গুণ (c) 6 গুণ
সমাধানঃ-
| শঙ্কুর আয়তন- | |
|---|---|
| ব্যাসার্ধের দৈর্ঘ্য এবং উচ্চতা দ্বিগুণ করার আগে- | \(\frac{1}{3}πr^2h = V\) |
| ব্যাসার্ধের দৈর্ঘ্য এবং উচ্চতা দ্বিগুণ করার পরে- | \(\frac{1}{3}π(2r)^2.2h = 8\frac{1}{3}πr^2h = 8V\) |
(v) একটি লম্ব বৃত্তাকার শঙ্কুর ব্যাসার্ধের দৈর্ঘ্য \(\frac{r}{2}\) একক এবং তির্যক উচ্চতা \(2l\) একক হলে, সমগ্রতলের ক্ষেত্রফল
উত্তরঃ (b) πr(\(l+\frac{r}{4}\)) বর্গ একক
(a) 2nr (l+r) বর্গ একক (c) ar (l+r) বর্গ একক (d) 2nrl বর্গ একক
সমাধানঃ-
- সমগ্রতলের ক্ষেত্রফল
= \(π(\frac{r}{2})(\frac{r}{2}+2l)\)
= πr(\(l+\frac{r}{4}\))
(B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি :
(i) একটি লম্ব বৃত্তাকার শঙ্কুর ভূমিতলের ব্যাসার্ধের দৈর্ঘ্য অর্ধেক এবং উচ্চতা দ্বিগুণ করা হলে শঙ্কটির আয়তন একই থাকে।
উত্তরঃ মিথ্যা
পরের আয়তন হবে-
\(\frac{1}{3}π(\frac{r}{2})^2 \times 2h\)
= \(\frac{1}{2}\times \frac{1}{3}πr^2h\)
যা পূর্বের আয়তনের অর্ধেক।
(ii) একটি লম্ব বৃত্তাকার শঙ্কুর উচ্চতা, ব্যাসার্ধ এবং তির্যক উচ্চতা সর্বদা একটি সমকোণী ত্রিভুজের বাহুত্রয়।
উত্তরঃ সত্য
(C) শূন্যস্থান পূরণ করি:
(i) ABC সমকোণী ত্রিভুজের AC অতিভুজ। AB বাহুকে অক্ষ করে ত্রিভুজটির একবার পূর্ণ আবর্তনের জন্য যে লম্ব বৃত্তাকার শঙ্কু উৎপন্ন হয় তার ব্যাসার্ধ _________।
উত্তরঃ BC
সমাধানঃ-
(ii) একটি লম্ব বৃত্তাকার শঙ্কুর আয়তন V ঘন একক এবং ভূমিতলের ক্ষেত্রফল A বর্গ একক হলে, উচ্চতা ___________।
উত্তরঃ \(\frac{3V}{A}\)
সমাধানঃ-
| A | = \(πr^2\) |
| V | = \(\frac{1}{3}πr^2h\) |
অতএব,
V = \(\frac{1}{3}πr^2h\)
বা, V = \(\frac{1}{3}Ah\)
বা, \(h = \frac{3V}{A}\)
(iii) একটি লম্ব বৃত্তাকার চোঙ এবং লম্ব বৃত্তাকার শঙ্কুর ভূমিতলের ব্যাসার্থের দৈর্ঘ্য সমান এবং তাদের উচ্চতা সমান। তাদের আয়তনের অনুপাত ________।
উত্তরঃ 3 : 1
সমাধানঃ-
| \(V_1 : V_2\) |
| = \(πr^2h : \frac{1}{3}πr^2h\) |
| = \(1 : \frac{1}{3}\) |
| = 3 : 1 |
14. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)
(i) একটি লম্ব বৃত্তাকার শঙ্কুর উচ্চতা 12 সেমি. এবং আয়তন 100π ঘন সেমি। শঙ্কুটির ব্যাসার্ধের দৈর্ঘ্য কত তা লিখি।
সমাধানঃ-
ধরি, ব্যাসার্ধ = r সেমি.
শর্তে,
| \(\frac{1}{3}πr^2h = 100π\) |
| বা, \(r^2 = \frac{100 \times 3}{12}\) |
| বা, \(r^2 = 25\) |
| বা, \(r = 5\) |
(ii) একটি লম্ব বৃত্তাকার শঙ্কুর পার্শ্বতলের ক্ষেত্রফল ভূমিতলের ক্ষেত্রফলের √5 গুণ। শঙ্কটির উচ্চতা ও ব্যাসার্ধের দৈর্ঘ্যের অনুপাত কত তা লিখি।
সমাধানঃ-
ধরি, শঙ্কুর তির্যক উচ্চতা = \(l\) একক, উচ্চতা = h একক, ভূমির ব্যাসার্ধ = r একক।
| শঙ্কুর পার্শ্বতলের ক্ষেত্রফল ভূমিতলের ক্ষেত্রফলের √5 গুণ |
| বা, \(πrl = \sqrt5 πr^2\) |
| বা, \(l = r\sqrt5\) |
| বা, \(l^2 = 5r^2\) |
| বা, \(r^2 + h^2 = 5r^2\) |
| বা, \( h^2 = 4r^2\) |
| বা, \(h = 2r\) |
| বা, \(h : r = 2 : 1\) |
(iii) একটি লম্ব বৃত্তাকার শঙ্কুর আয়তন V ঘন একক, ভূমিতলের ক্ষেত্রফল A বর্গ একক এবং উচ্চতা H একক হলে, \(\frac{AH}{V}\)-এর মান কত তা লিখি।
সমাধানঃ-
| A | = \(πr^2\) |
| V | = \(\frac{1}{3}πr^2h\) |
অতএব,
V = \(\frac{1}{3}πr^2H\)
বা, V = \(\frac{1}{3}AH\)
বা, \(\frac{AH}{V} = 3\)
(iv) একটি লম্ব বৃত্তাকার শঙ্কুর আয়তন এবং পার্শ্বতলের ক্ষেত্রফলের সাংখ্যমান সমান। শঙ্কুটির উচ্চতা এবং ব্যাসার্ধের দৈর্ঘ্য যথাক্রমে h একক এবং r একক হলে, \(\frac{1}{h^2}+\frac{1}{r^2}\) -এর মান কত তা লিখি ।
সমাধানঃ-
ধরি, তির্যক উচ্চতা = \(l\) একক
| \(\frac{1}{3}πr^2h = πrl\) |
| বা, \(\frac{r}{3} = \frac{l}{h}\) |
| বা, \((\frac{r}{3})^2 = (\frac{l}{h})^2\) |
| বা, \(\frac{r^2}{9} = \frac{l^2}{h^2}\) |
| বা, \(\frac{r^2}{9} = \frac{r^2 + h^2}{h^2}\) |
| বা, \(\frac{r^2}{9} = \frac{r^2 }{h^2}+1\) |
| বা, \(\frac{1}{9} = \frac{1}{h^2}+\frac{1}{r^2}\) |
(v) একটি লম্ব বৃত্তাকার চোঙ এবং লম্ব বৃত্তাকার শঙ্কুর ভূমিতলের ব্যাসার্ধের দৈর্ঘ্যের অনুপাত 3:4 এবং তাদের উচ্চতার অনুপাত 2:3; চোঙ এবং শঙ্কুর আয়তনের অনুপাত কত তা লিখি।
সমাধানঃ-
ধরি, চোঙের ব্যাসার্ধ = \(r_1\) এবং উচ্চতা=\(h_1\) একক
এবং
শঙ্কুর ব্যাসার্ধ = \(r_2\) এবং উচ্চতা=\(h_2\) একক
| চোঙ এবং শঙ্কুর আয়তনের অনুপাত |
| = \(π{r_1}^2h_1 : \frac{1}{3}π{r_2}^2h_2\) |
| = \(3\times (\frac{r_1}{r_2})^2 \times \frac{h_1}{h_2}\) |
| = \(3\times (\frac{3}{4})^2 \times \frac{2}{3}\) |
| = \(3\times \frac{9}{16} \times \frac{2}{3}\) |
| = \(\frac{9}{8}\) |
| = 9 : 8 |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  |
এই কষে দেখি 16 Class 10|Koshe Dekhi 16 Class 10 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।

এখানে তোমরা তোমাদের দশম শ্রেণীতে| Class 10 এ কি কি পড়ানো হয়, মানে তোমাদের দশম শ্রেণীতে| Class 10 সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

