| কোণ সম্পর্কে কিছু সাধারণ আলোচনাঃ |
দুটি রশ্মি যখন কোনো এক বিন্দুতে মিলিত হয় তখন কোণ উৎপন্ন হয় । অন্যভাবে বলা যায় যে , দুটি রশ্মি পরস্পর মিলনের ফলে বা দুটি রশ্মি একে অপরকে ছেদ করলে যে আকৃতি তৈরি হয় সেটাই হলো কোণ ।
আবার , দুটি রেখাংশ তার প্রান্তবিন্দুতে মিলিত হলে যে সামতলিক চিত্র উৎপন্ন হয় তাকে কোণ বলে ।
তাহলে সহজ করে বুঝলে , দুইটি সরলরেখা পরস্পর ছেদ করলে কোণ উৎপন্ন হয় এবং ছেদ বিন্দুতে চারটি কোণ উৎপন্ন হয় ।
অতএব , দুটি সরলরেখা তির্যকভাবে পরস্পরের সাথে মিলিত হলে যে জ্যামিতিক আকার ধারন করে তাকে কোণ বলে ।
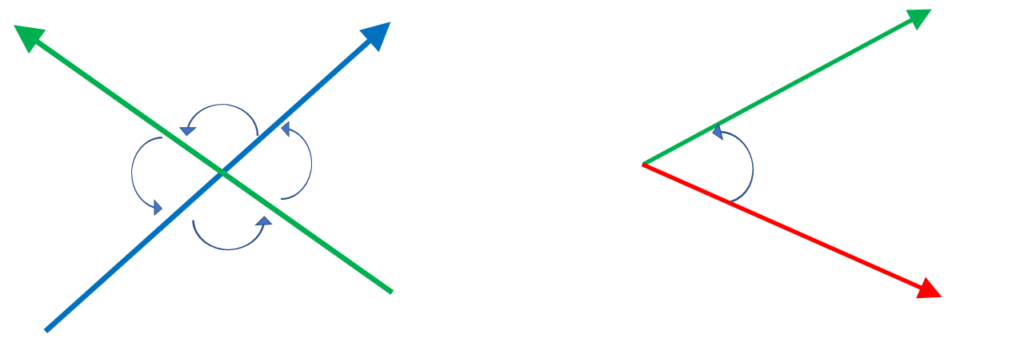
সমতল জ্যামিতিতে, একই প্রান্তবিন্দু বিশিষ্ট দুইটি রশ্মি দ্বারা গঠিত জ্যামিতিক আকৃতিকে কোণ বলে। রশ্মি দুইটি দ্বারা সৃষ্ট কোণটি এদের সাধারণ প্রান্তবিন্দুতে উৎপন্ন হয়। রশ্মি দুইটিকে কোণের বাহু বলা হয়। আর সাধারণ প্রান্তবিন্দুটিকে কোণের শীর্ষ বলে। কোণের রশ্মিদ্বয় একই সমতলে অবস্থিত হতে পারে; আবার ভিন্ন সমতলেও অবস্থিত হতে পারে। রশ্মি দুইটি একই সমতলে অবস্থিত হলে সেই সমতলটিকে ইউক্লিডিও সমতলই হতে হবে – এমন কোনো শর্ত নেই। তাছাড়া ইউক্লিডিও জগত ও অন্যান্য জগতের দুইটি সমতল পরস্পর ছেদ করলেও কোণ উৎপন্ন হয়। এ ধরণের কোণকে ডাইহেড্রাল কোণ (dihedral angle) বলে।
কোণ কে ডিগ্রি বা ” ° ” এককে পরিমাপ করা হয় ।
| কোণের প্রকাশঃ |
গাণিতিক বাক্যগুলোতে, কোণের মান প্রকাশ করতে সাধারণত গ্রিক অক্ষরগুলো (α, β, γ, θ, φ, . . . ) ব্যবহার করা হয়। দ্বার্থতা এড়াতে গ্রিক অক্ষর π কে একাজে ব্যবহার করা হয় না। ছোট হাতের রোমান অক্ষরগুলোকেও (a, b, c, . . . ) কোণের মান হিসেবে প্রকাশ করা হয়। বড় হাতের অক্ষরগুলো বহুভুজ এর ক্ষেত্রে ব্যবহার করা হয়।
জ্যামিতির চিত্র যে তিনটি বিন্দু দিয়ে কোণটি গঠিত হয়েছে সেগুলো দিয়ে কোণটিকে প্রকাশ করা হয়।
উদাহরণস্বরূপ,
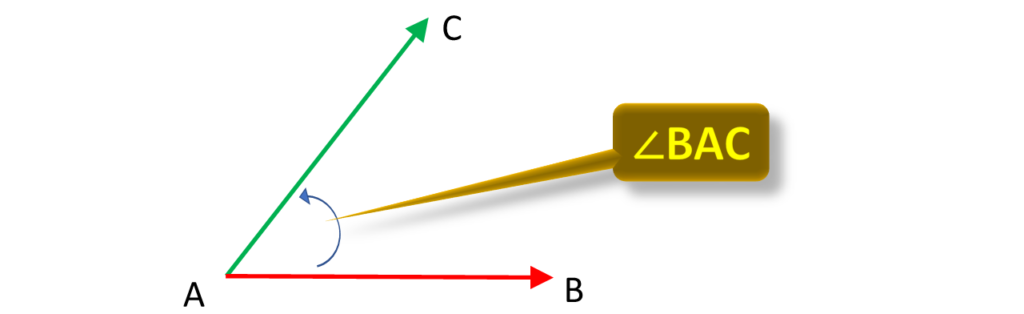
A শীর্ষবিন্দুতে AB এবং AC রশ্মি দ্বারা গঠিত কোণকে ∠BAC বলা হয়। যেখানে কোন দ্ব্যর্থতার সুযোগ নেই, সেখানে শুধুমাত্র শীর্ষবিন্দুটি দিয়ে কোণটিকে প্রকাশ করা হয় (এক্ষেত্রে কোণ A)।
কোণ কাকে বলে?
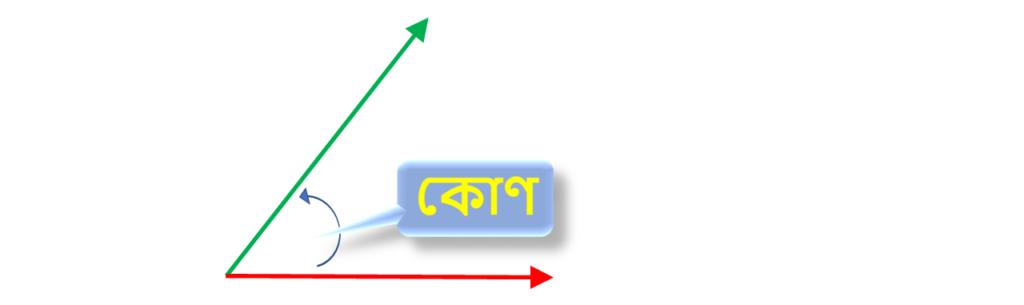
দুটি সরলরেখা তির্যকভাবে পরস্পরের সাথে মিলিত হলে যে জ্যামিতিক আকার ধারন করে তাকে কোণ বলে ।
কোণ কতো প্রকার ও কি কি ?
কোণ চার প্রকার ।
- শূন্য কোণ
- সূক্ষ্মকোন
- সমকোণ
- স্থুলকোণ
- সরলকোণ
শূন্য কোণ কি?
যে কোণের মাপ 0° , তাকে শূন্য কোণ বলে।
সূক্ষ্মকোন ( Acute Angle ) কাকে বলে ?
যে কোণের মাপ শূন্য ডিগ্রি / 0° অপেক্ষা বড়ো কিন্তু 90° অপেক্ষা ছোটো তাকে সূক্ষ্মকোন বলে ।
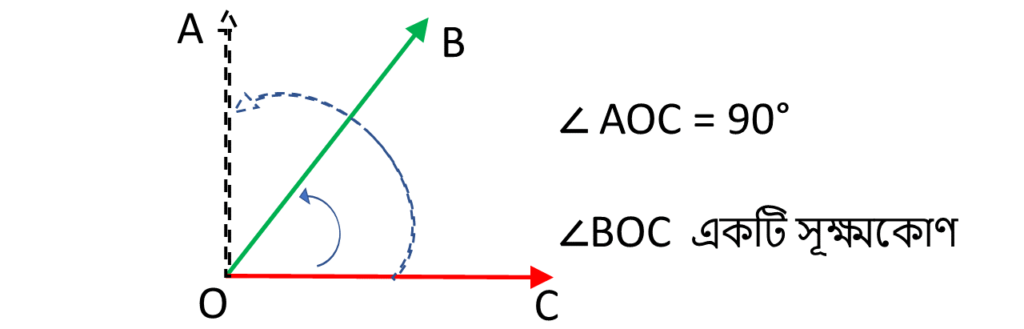
ছবিতে আমরা দেখতে পাচ্ছি যে ,
∠AOC = 90°
এবং ∠BOC একটি সূক্ষ্মকোণ ।
কারণ,
0° < ∠BOC < 90°
অর্থাৎ, ∠BOC শূন্য ডিগ্রি অপেক্ষা বড়ো এবং 90° অপেক্ষা ছোটো ।
সূক্ষ্মকোন এর উদাহরণ –
45° কোণ একটি সূক্ষ্মকোন ।
সূক্ষ্মকোন এর বৈশিষ্ট্য-
- সূক্ষ্মকোন এ কোণের মাপ 90° অপেক্ষা ছোটো
- সূক্ষ্মকোন এর বাহু দুটি পরস্পর লম্বভাবে অবস্থান করেনা
সমকোণ ( Right Angle )/ সমকোণ কাকে বলে?
যে কোণের মাপ 90° হয় তাকে সমকোণ বলে ।
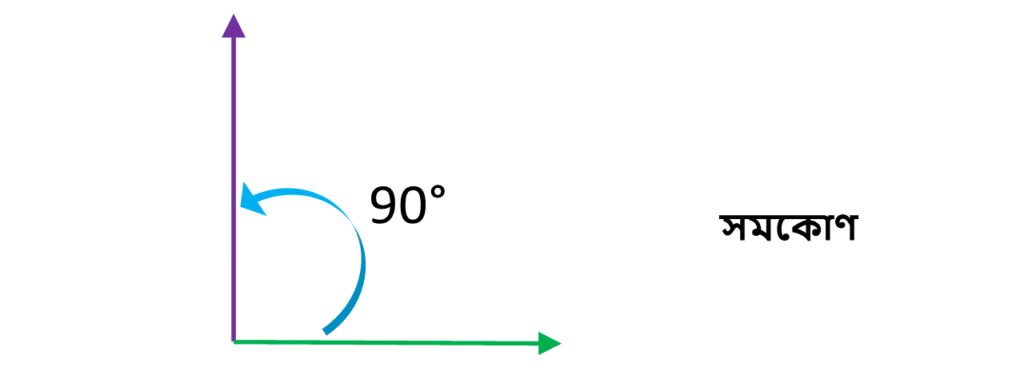
সমকোণ এর উদাহরণ-
যে কোনো 90° কোণই হলো সমকোণের উদাহরণ ।
সমকোণের বৈশিষ্ট্য-
- সমকোণ এর মধ্যে কোণের পরিমাপ হবে 90 ডিগ্রি।
- সমকোণের বাহু দুটি পরস্পর লম্বভাবে অবস্থান করে
- এক সমকোণ সমান 90 ভাগ করলে প্রতিভাকে ১ ডিগ্রী বলা হয়।
- চারটি সমকোণ মিলে ৩৬০ ডিগ্রি তৈরি হয়।
স্থুলকোণ ( Obtuse Angle ) / স্থুলকোণ কাকে বলে?
যে কোণের মাপ 90 ডিগ্রি / 90° অপেক্ষা বড়ো কিন্তু 180° অপেক্ষা ছোটো তাকে স্থুলকোণ বলে ।
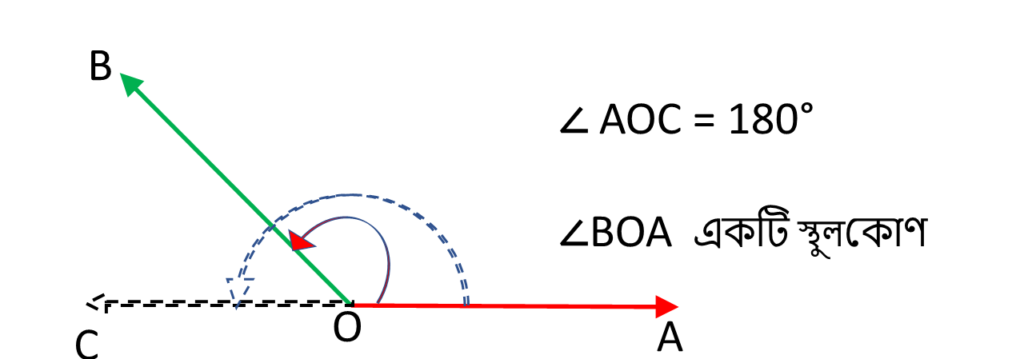
ছবিতে আমরা দেখতে পাচ্ছি যে ,
∠AOC = 180°
এবং ∠BOC একটি স্থুলকোণ ।
কারণ,
90° < ∠BOA < 180°
অর্থাৎ, ∠BOA 90° অপেক্ষা বড়ো এবং 180° অপেক্ষা ছোটো ।
স্থুলকোণ এর উদাহরণ –
145° কোণ হলো একটি স্থুলকোণ এর উদাহরণ ।
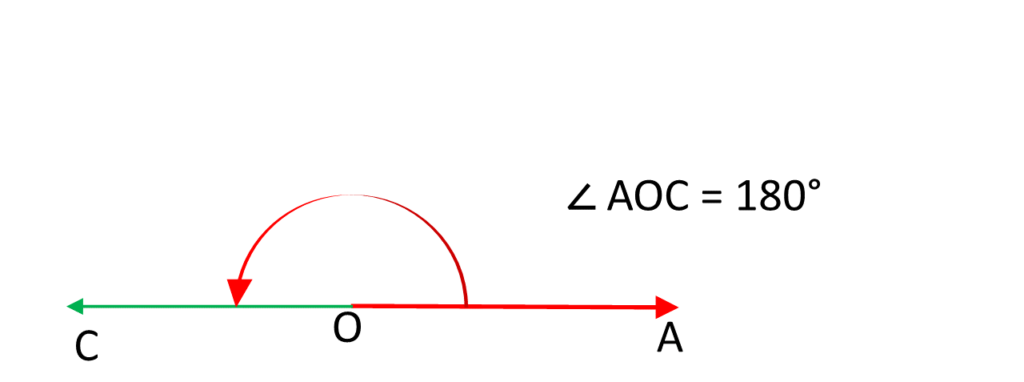
সরলকোণ ( Straight Angle ) /সরলকোণ কাকে বলে ?
যে কোণের মাপ 180° হয় তাকে সরলকোণ বলে ।
Frequently asked questions:
>দুটি রশ্মি একটি সাধারণ প্রান্তবিন্দুতে মিলিত হলে কোন জ্যামিতিক চিত্র গঠিত হয়?
উত্তর – কোণ উৎপন্ন হয় ।
> কোণ পরিমাপের একক কে কি বলে ?
উত্তর- কোণ পরিমাপের একক কে ডিগ্রি বলে ।
> 0 থেকে বড় কিন্তু 90 এর ছোট কোণ কোনটি?
উত্তর – 0 থেকে বড় কিন্তু 90 এর ছোট কোণ হলো সূক্ষ্মকোন ।
> সমকোনের চেয়ে ছোট কোণকে কি বলে?
উত্তর- সমকোনের চেয়ে ছোট কোণকে সূক্ষ্মকোন বলে ।
> সূক্ষ্মকোন এর মান কতো ?
উত্তর – শূন্য ডিগ্রি / 0° অপেক্ষা বড়ো কিন্তু 90° অপেক্ষা ছোটো ।
> সূক্ষ্মকোন কতো ডিগ্রি ?
উত্তর- শূন্য ডিগ্রি / 0° অপেক্ষা বড়ো কিন্তু 90° অপেক্ষা ছোটো ।
> 0 কি সূক্ষকোণ?
উত্তর- না , এটি শূন্যকোণ ।
> এক সমকোণ অপেক্ষা ছোট কোণকে কি বলে?
উত্তর- এক সমকোণ অপেক্ষা ছোট কোণকে সূক্ষ্মকোন বলে ।
> কোন কোণের পরিমাপ 90°?
উত্তর– সমকোণের পরিমাপ 90° ।
> 2 সমকোণ কত ডিগ্রি?
উত্তর – 2 সমকোণ= 180° ।
> এক সমকোণ সমান কত?
উত্তর- এক সমকোণ সমান 90° ।
> এক সরল কোণ সমান কত ডিগ্রি?
উত্তর- এক সরল কোণ সমান 180° ।
আরও দেখো–
> গুণ
> ভাগ

