বীজগাণিতিক সংখ্যামালার গুণ ও ভাগ Class 8 | Bijganitik Sonkhya Malar Gun Vag .

শ্রেণি- অষ্টম ; অধ্যায়- বীজগাণিতিক সংখ্যামালার গুণ ও ভাগ ; অধ্যায়ের সারাংশ

---

বীজগাণিতিক সংখ্যামালার গুণ ও ভাগ হলো অষ্টম শ্রেণির একটি অধ্যায় ।

বীজগাণিতিক সংখ্যা বলতে আমরা বুঝি x , xy , z , x² , y² … ইত্যাদি । এগুলো হলো সব একপদি বীজগাণিতিক সংখ্যা । কিন্তু একের বেশী যেমন- x + y +z , xy² + z , z + x³ ইত্যাদি গুলি হলো বহুপদী বীজগাণিতিক সংখ্যামালা ।

5x + 2y	দ্বি-পদী বীজগাণিতিক সংখ্যামালা
-6y	একপদী বীজগাণিতিক সংখ্যামালা
4y	একপদী বীজগাণিতিক সংখ্যামালা
a + b + c	ত্রি-পদী বীজগাণিতিক সংখ্যামালা
-7y – 3x	দ্বি- পদী বীজগাণিতিক সংখ্যামালা
a + b – c	ত্রি – পদী বীজগাণিতিক সংখ্যামালা
3x2	এক-পদী বীজগাণিতিক সংখ্যামালা
-11x3 + 2x2 + 8x	ত্রি – পদী বীজগাণিতিক সংখ্যামালা
7x2	এক- পদী বীজগাণিতিক সংখ্যামালা
0	এক-পদী বীজগাণিতিক সংখ্যামালা
2y4 + 5y3 – 10y2 – 8	চার-পদী বীজগাণিতিক সংখ্যামালা

এক বা একের বেশী পদবিশিষ্ট বীজগাণিতিক সংখ্যামালাকে বহুপদী বীজগাণিতিক সংখ্যামালা বলে ।

অষ্টম শ্রেণিতে আমরা বীজগাণিতিক সংখ্যামালার গুণ ও ভাগ পড়বো ।

>বীজগাণিতিক সংখ্যামালার গুণঃ

বীজগাণিতিক সংখ্যামালার গুণ আমরা কিছু উদাহরণের মাধ্যমে বুঝবো ।

উদাহরণ 1 :-

ধরি ( 3x² – x + 12 ) এবং ( 12x + 5 ) দুটি বীজগাণিতিক সংখ্যামালা ।

STEP 1 :-

আমরা উপরের দুটি বীজগাণিতিক সংখ্যামালা কে p =3x² – x + 12 এবং q=12x + 5 দ্বারা চিহ্নিত করবো । ( এই step টি সবসময় করার দরকার পড়বে না , তোমরা যখন শিখে যাবে তখন আর এই step টি লাগবেনা )

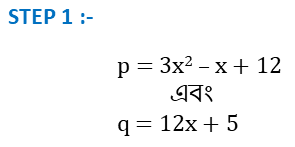
STEP 1 – p =3x2 – x + 12 এবং q=12x + 5

STEP 2 :-

সংখ্যামালা দুটিকে পাশাপাশি গুণ আকারে লিখবো । যেমন-

p × q = ( 3x² – x + 12 ) × ( 12x + 5 )

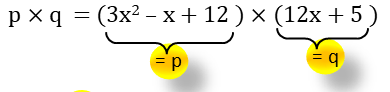
STEP 1	p =3x2 – x + 12 এবং q=12x + 5
STEP 2	p × q = ( 3x2 – x + 12 ) × ( 12x + 5 )

STEP 3 :-

এবার দুটি পদ্ধতিতে গুণ করতে পারি ।

প্রথম পদ্ধতিঃ-

p এর প্রতিটি সংখ্যা কে q দ্বারা গুণ ।

অর্থাৎ –

( 3x² – x + 12 ) × ( 12x + 5 )

= 3x² q – x q + 12q [ q = 12x + 5 ]

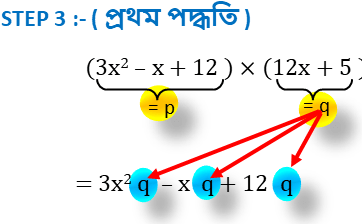
STEP 1	p =3x2 – x + 12 এবং q=12x + 5
STEP 2	p × q = ( 3x2 – x + 12 ) × ( 12x + 5 )
STEP 3	= 3x2 q – x q + 12q [ q = 12x + 5 ]

দ্বিতীয় পদ্ধতিঃ-

q এর প্রতিটি সংখ্যা কে p দ্বারা গুণ ।

অর্থাৎ –

( 3x² – x + 12 ) × ( 12x + 5 )

= 12xp + 5p [ p = 3x² – x + 12 ]

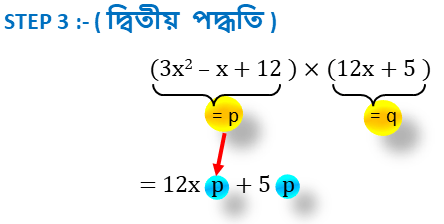
STEP 1	p =3x2 – x + 12 এবং q=12x + 5
STEP 2	p × q = ( 3x2 – x + 12 ) × ( 12x + 5 )
STEP 3	= 12xp + 5p [ p = 3x2 – x + 12 ]

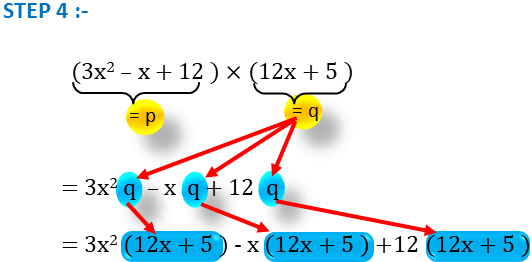
STEP 4 :-

( STEP 3 তে আমারা যে দুটি পদ্ধতি দেখলাম , এই দুটির মধ্যে যে কোনো একটি উপায়ে করলেই হবে। দুই ক্ষেত্রেই উত্তর একই আসবে। আমরা এখানে STEP 3 এর প্রথম পদ্ধতি টা অনুসরণ করে তারপরের STEP গুলো বুঝবো । তোমরা চাইলে নিজে নিজে করে দেখতে পারো । কোথাও অসুবিধে হলে অবশ্যই কমেন্টে যানাবে । )

এরপরে q এর মান বসাবো ।

( 3x² – x + 12 ) × ( 12x + 5 )

= 3x² q – x q + 12q [ q = 12x + 5 ]

= 3x² ( 12x + 5 ) – x ( 12x + 5 ) + 12 ( 12x + 5 )

STEP 1	p =3x2 – x + 12 এবং q=12x + 5
STEP 2	p × q = ( 3x2 – x + 12 ) × ( 12x + 5 )
STEP 3	= 3x2 q – x q + 12q [ q = 12x + 5 ]
STEP 4	= 3x2 ( 12x + 5 ) – x ( 12x + 5 ) + 12 ( 12x + 5 )

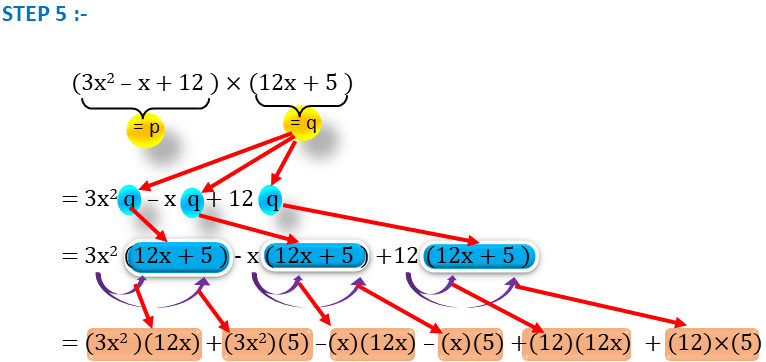
STEP 5 :-

p এর প্রতিটি সংখ্যার সাথে q এর গুণ হবে ।

এখানে যেমন p এর তিনটি সংখ্যা আছে যথাক্রমে -> 3x² , x এবং 12

আবার q এর দুটি সংখ্যা আছে যেমন -> 12x এবং 5

এখন 3x² এর সঙ্গে 12x এবং 5 গুণ করে যোগ হবে। এই গুণ টি করার সময় আমরা যে দুটি সংখ্যা গুণ করছি তাদের আগে কি চিহ্ন আছে সেটা অবশ্যই খেয়াল রাখবো এবং সংখ্যাদুটি গুণ করার আগে, সংখ্যাদুটির আগে যে চিহ্ন আছে তাদের গুণ করবো এবং সেটা লিখবো ।

>চিহ্ন এর গুণ এবং গুণফলঃ

চিহ্ন-এর গুণ		গুণফল
( + ) × ( + )	=	+
( – ) × ( + )	=	–
( + ) × ( – )	=	–
( – ) × ( – )	=	+

অর্থাৎ – দুটি সংখ্যার গুণ করার সময় আমরা আগে সংখ্যা দুটির আগে যে চিহ্ন আছে তাদের গুণ করবো এবং গুণফলটি আগে লিখবো । তারপর সংখ্যাদুটির গুণ করবো ।

( 3x² – x + 12 ) × ( 12x + 5 )

= 3x² q – x q + 12q [ q = 12x + 5 ]

= 3x² ( 12x + 5 ) – x ( 12x + 5 ) + 12 ( 12x + 5 )

= ( 3x² ) ( 12x ) + ( 3x² ) (5) – ( x ) ( 12x ) – ( x ) ( 5 ) + ( 12 ) (12x) + ( 12 ) (5)

STEP 1	p =3x2 – x + 12 এবং q=12x + 5
STEP 2	p × q = ( 3x2 – x + 12 ) × ( 12x + 5 )
STEP 3	= 3x2 q – x q + 12q [ q = 12x + 5 ]
STEP 4	= 3x2 ( 12x + 5 ) – x ( 12x + 5 ) + 12 ( 12x + 5 )
STEP 5	= ( 3x2 ) ( 12x ) + ( 3x2 ) (5) – ( x ) ( 12x ) – ( x ) ( 5 ) + ( 12 ) (12x) + ( 12 ) (5)

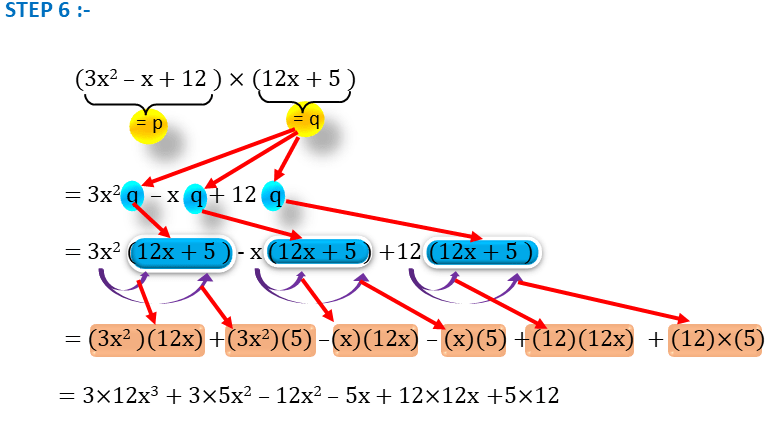
STEP 6 :-

এই ধাপে আমরা আগে চলরাশি গুলির গুণ করে নেবো ।

( 3x² – x + 12 ) × ( 12x + 5 )

= 3x² q – x q + 12q [ q = 12x + 5 ]

= 3x² ( 12x + 5 ) – x ( 12x + 5 ) + 12 ( 12x + 5 )

= ( 3x² ) ( 12x ) + ( 3x² ) (5) – ( x ) ( 12x ) – ( x ) ( 5 ) + ( 12 ) (12x) + ( 12 ) (5)

= 3 × 12 x²⁺¹ + 3 × 5 x² – 12 x¹⁺¹ – 5x + 12 × 12x + 12 × 5

= 3 × 12 x³ + 3 × 5 x² – 12 x² – 5x + 12 × 12x + 12 × 5

STEP 1	p =3x2 – x + 12 এবং q=12x + 5
STEP 2	p × q = ( 3x2 – x + 12 ) × ( 12x + 5 )
STEP 3	= 3x2 q – x q + 12q [ q = 12x + 5 ]
STEP 4	= 3x2 ( 12x + 5 ) – x ( 12x + 5 ) + 12 ( 12x + 5 )
STEP 5	= ( 3x2 ) ( 12x ) + ( 3x2 ) (5) – ( x ) ( 12x ) – ( x ) ( 5 ) + ( 12 ) (12x) + ( 12 ) (5)
STEP 6	= 3 × 12 x2+1 + 3 × 5 x2 – 12 x1+1 – 5x + 12 × 12x + 12 × 5 = 3 × 12 x3 + 3 × 5 x2 – 12 x2 – 5x + 12 × 12x + 12 × 5

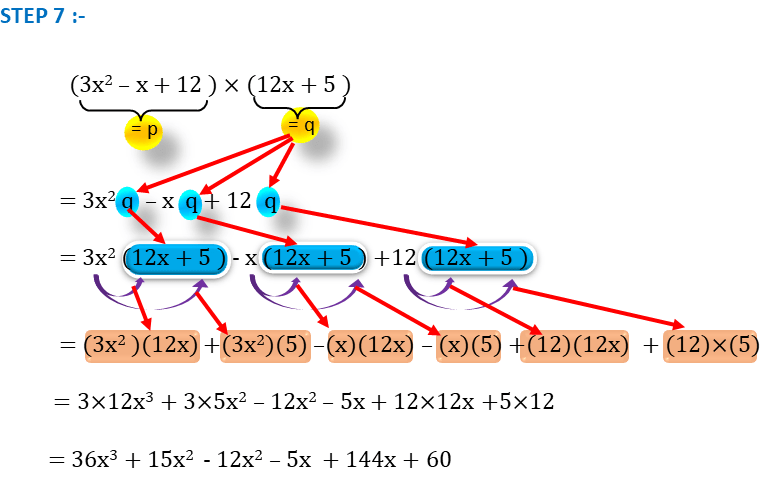
STEP 7 –

এরপর আমরা ধ্রুবক সংখ্যা গুলি গুণ করে নেবো ।

( 3x² – x + 12 ) × ( 12x + 5 )

= 3x² q – x q + 12q [ q = 12x + 5 ]

= 3x² ( 12x + 5 ) – x ( 12x + 5 ) + 12 ( 12x + 5 )

= ( 3x² ) ( 12x ) + ( 3x² ) (5) – ( x ) ( 12x ) – ( x ) ( 5 ) + ( 12 ) (12x) + ( 12 ) (5)

= 3 × 12 x²⁺¹ + 3 × 5 x² – 12 x¹⁺¹ – 5x + 12 × 12x + 12 × 5

= 3 × 12 x³ + 3 × 5 x² – 12 x² – 5x + 12 × 12x + 12 × 5

= 36x³ + 15x² – 12x² – 5x + 144x + 60

STEP 1	p =3x2 – x + 12 এবং q=12x + 5
STEP 2	p × q = ( 3x2 – x + 12 ) × ( 12x + 5 )
STEP 3	= 3x2 q – x q + 12q [ q = 12x + 5 ]
STEP 4	= 3x2 ( 12x + 5 ) – x ( 12x + 5 ) + 12 ( 12x + 5 )
STEP 5	= ( 3x2 ) ( 12x ) + ( 3x2 ) (5) – ( x ) ( 12x ) – ( x ) ( 5 ) + ( 12 ) (12x) + ( 12 ) (5)
STEP 6	= 3 × 12 x2+1 + 3 × 5 x2 – 12 x1+1 – 5x + 12 × 12x + 12 × 5 = 3 × 12 x3 + 3 × 5 x2 – 12 x2 – 5x + 12 × 12x + 12 × 5
STEP 7	= 36x3 + 15x2 – 12x2 – 5x + 144x + 60

STEP 8 –

এরপর আমরা চলরাশি গুলির ঘাত লক্ষ্য করবো । যে সমস্ত চলরাশির ঘাত সমান সেই সংখ্যার আগের চিহ্ন অনুযায়ী যোগ/বিয়োগ করতে হবে ।

এখানে যেমন -> x এর দুই ঘাতের সংখ্যা দুটি আছে , 15x² এবং 12x² । আমরা এদের আগে কি চিহ্ন আছে তা খেয়াল করবো । এখানে 15x² এর আগে আছে ” + ” ( যোগ চিহ্ন ) এবং 12x² এর আগে আছে ” – ” ( বিয়োগ চিহ্ন ) । সুতরাং , 15x² এবং 12x² এর মধ্যে বিয়োগ হবে । এবং যে সংখ্যা টা বড়ো তার আগে যে চিহ্ন টি আছে সেই চিহ্নটি বিয়োগফলের আগে বসবে । এখানে যেহেতু 15x² > 12x² সেহেতু বিয়োগফল = 3x² এর আগে ” + ” ( যোগ ) চিহ্ন বসবে ।

একইরকম ভাব এখানে x এর এক ঘাতের সংখ্যা দুটি আছে, 5x এবং 144x . এদের মধ্যে বড়ো এবং ছোটো ; সংখ্যার আগে কি চিহ্ন তা হিসাব করে বিয়োগফল হবে 139x .

আবার যেহেতু x এর তিন ঘাতের সংখ্যা কেবলমাত্র একটিই আছে 36x³ , সেহেতু এটির সাথে আর কারোর যোগ-বিয়োগ হবেনা ।

( 3x² – x + 12 ) × ( 12x + 5 )

= 3x² q – x q + 12q [ q = 12x + 5 ]

= 3x² ( 12x + 5 ) – x ( 12x + 5 ) + 12 ( 12x + 5 )

= ( 3x² ) ( 12x ) + ( 3x² ) (5) – ( x ) ( 12x ) – ( x ) ( 5 ) + ( 12 ) (12x) + ( 12 ) (5)

= 3 × 12 x²⁺¹ + 3 × 5 x² – 12 x¹⁺¹ – 5x + 12 × 12x + 12 × 5

= 3 × 12 x³ + 3 × 5 x² – 12 x² – 5x + 12 × 12x + 12 × 5

= 36x³ + 15x² – 12x² – 5x + 144x + 60

= 36x³ + 3x² + 139x + 60

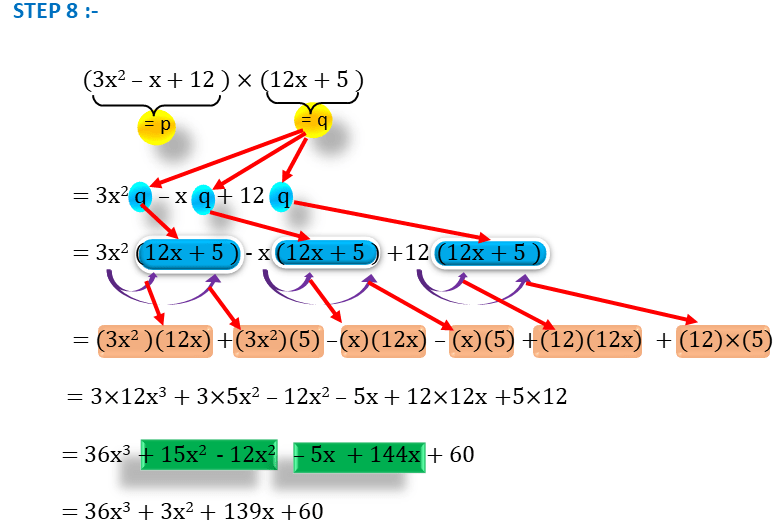
STEP 1	p =3x2 – x + 12 এবং q=12x + 5
STEP 2	p × q = ( 3x2 – x + 12 ) × ( 12x + 5 )
STEP 3	= 3x2 q – x q + 12q [ q = 12x + 5 ]
STEP 4	= 3x2 ( 12x + 5 ) – x ( 12x + 5 ) + 12 ( 12x + 5 )
STEP 5	= ( 3x2 ) ( 12x ) + ( 3x2 ) (5) – ( x ) ( 12x ) – ( x ) ( 5 ) + ( 12 ) (12x) + ( 12 ) (5)
STEP 6	= 3 × 12 x2+1 + 3 × 5 x2 – 12 x1+1 – 5x + 12 × 12x + 12 × 5 = 3 × 12 x3 + 3 × 5 x2 – 12 x2 – 5x + 12 × 12x + 12 × 5
STEP 7	= 36x3 + 15x2 – 12x2 – 5x + 144x + 60
STEP 8	= 36x3 + 3x2 + 139x + 60

STEP 9 –

সবশেষে পুরো গুণ প্রক্রিয়াটি একবার দেখে নেবো ।

উদাহরণ 2 :–

ধরি ( 9 – 8x³ + 2x² ) এবং ( x² – x +12 ) দুটি বীজগাণিতিক সংখ্যামালা ।

এই ধরনের সংখ্যামালার ক্ষেত্রে আমরা সংখ্যামালা গুলি কে x এর ঘাতের অধঃক্রমে সাজিয়ে নেবো ।

অতএব সংখ্যামালা গুলিকে x এর ঘাতের অধঃক্রমে সাজালে হবে –

(- 8x³ + 2x² + 9 ) এবং ( x² – x +12 )

STEP 1 :-

p = (- 8x³ + 2x² + 9 ) এবং q = ( x² – x +12 )

STEP 1

p = (- 8x3 + 2x2 + 9 ) এবং q = ( x2 – x +12 )

STEP 2 :-

p × q = (- 8x³ + 2x² + 9 )×( x² – x +12 )

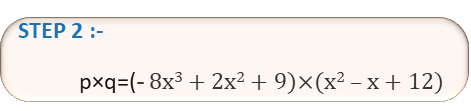
STEP 1	p = (- 8x3 + 2x2 + 9 ) এবং q = ( x2 – x +12 )
STEP 2	p × q = (- 8x3 + 2x2 + 9 )×( x2 – x +12 )

STEP 3:-

p × q = (- 8x³ + 2x² + 9 )×( x² – x +12 )

= -8x³ q + 2x² q + 9q

STEP 1	p = (- 8x3 + 2x2 + 9 ) এবং q = ( x2 – x +12 )
STEP 2	p × q = (- 8x3 + 2x2 + 9 )×( x2 – x +12 )
STEP 3	= -8x3 q + 2x2 q + 9q

STEP 4 :-

p × q = (- 8x³ + 2x² + 9 )×( x² – x +12 )

= -8x³ q + 2x² q + 9q

= -8x³ ( x² – x +12 ) + 2x² ( x² – x +12 ) + 9( x² – x +12 )

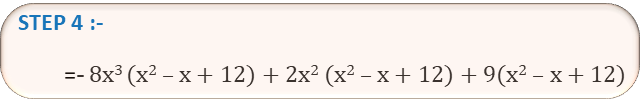
STEP 1	p = (- 8x3 + 2x2 + 9 ) এবং q = ( x2 – x +12 )
STEP 2	p × q = (- 8x3 + 2x2 + 9 )×( x2 – x +12 )
STEP 3	= -8x3 q + 2x2 q + 9q
STEP 4	= -8x3 ( x2 – x +12 ) + 2x2 ( x2 – x +12 ) + 9( x2 – x +12 )

STEP 5:-

p × q = (- 8x³ + 2x² + 9 )×( x² – x +12 )

= -8x³ q + 2x² q + 9q

= -8x³ ( x² – x +12 ) + 2x² ( x² – x +12 ) + 9( x² – x +12 )

= (-8x³ )(x²) + ( -8x³)(-x) + (-8x³)(12) + (2x²)(x²) + (2x²)(-x) + (2x²)(12) + (9)(x²) + (9)(-x) + 9×12

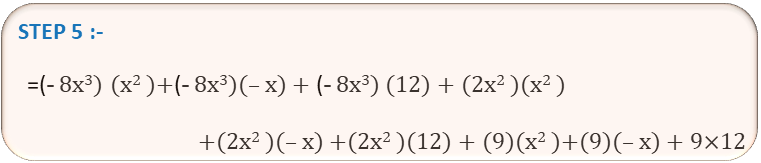
STEP 1	p = (- 8x3 + 2x2 + 9 ) এবং q = ( x2 – x +12 )
STEP 2	p × q = (- 8x3 + 2x2 + 9 )×( x2 – x +12 )
STEP 3	= -8x3 q + 2x2 q + 9q
STEP 4	= -8x3 ( x2 – x +12 ) + 2x2 ( x2 – x +12 ) + 9( x2 – x +12 )
STEP 5	= (-8x3 )(x2) + ( -8x3)(-x) + (-8x3)(12) + (2x2)(x2) + (2x2)(-x) + (2x2)(12) + (9)(x2) + (9)(-x) + 9×12

STEP 6:-

p × q = (- 8x³ + 2x² + 9 )×( x² – x +12 )

= -8x³ q + 2x² q + 9q

= -8x³ ( x² – x +12 ) + 2x² ( x² – x +12 ) + 9( x² – x +12 )

= (-8x³ )(x²) + ( -8x³)(-x) + (-8x³)(12) + (2x²)(x²) + (2x²)(-x) + (2x²)(12) + (9)(x²) + (9)(-x) + 9×12

= -8x³⁺² + 8x³⁺¹ – 8×12x³ + 2x²⁺² – 2x²⁺¹ + 2×12x² + 9x² – 9x + 9×12

= -8x⁵ + 8x⁴ – 8×12x³ + 2x⁴ – 2x³ + 2×12x² + 9x² – 9x + 9×12

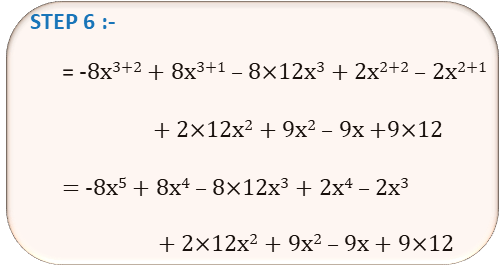
STEP 1	p = (- 8x3 + 2x2 + 9 ) এবং q = ( x2 – x +12 )
STEP 2	p × q = (- 8x3 + 2x2 + 9 )×( x2 – x +12 )
STEP 3	= -8x3 q + 2x2 q + 9q
STEP 4	= -8x3 ( x2 – x +12 ) + 2x2 ( x2 – x +12 ) + 9( x2 – x +12 )
STEP 5	= (-8x3 )(x2) + ( -8x3)(-x) + (-8x3)(12) + (2x2)(x2) + (2x2)(-x) + (2x2)(12) + (9)(x2) + (9)(-x) + 9×12
STEP 6	= -8x3+2 + 8x3+1 – 8×12x3 + 2x2+2 – 2x2+1 + 2×12x2 + 9x2 – 9x + 9×12 = -8x5 + 8x4 – 8×12x3 + 2x4 – 2x3 + 2×12x2 + 9x2 – 9x + 9×12

STEP 7:-

p × q = (- 8x³ + 2x² + 9 )×( x² – x +12 )

= -8x³ q + 2x² q + 9q

= -8x³ ( x² – x +12 ) + 2x² ( x² – x +12 ) + 9( x² – x +12 )

= (-8x³ )(x²) + ( -8x³)(-x) + (-8x³)(12) + (2x²)(x²) + (2x²)(-x) + (2x²)(12) + (9)(x²) + (9)(-x) + 9×12

= -8x³⁺² + 8x³⁺¹ – 8×12x³ + 2x²⁺² – 2x²⁺¹ + 2×12x² + 9x² – 9x + 9×12

= -8x⁵ + 8x⁴ – 8×12x³ + 2x⁴ – 2x³ + 2×12x² + 9x² – 9x + 9×12

= -8x⁵ + 8x⁴ – 96x³ + 2x⁴ – 2x³ + 24x² + 9x² – 9x + 108

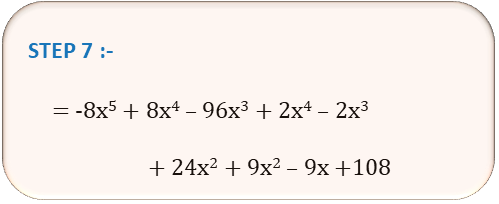
STEP 1	p = (- 8x3 + 2x2 + 9 ) এবং q = ( x2 – x +12 )
STEP 2	p × q = (- 8x3 + 2x2 + 9 )×( x2 – x +12 )
STEP 3	= -8x3 q + 2x2 q + 9q
STEP 4	= -8x3 ( x2 – x +12 ) + 2x2 ( x2 – x +12 ) + 9( x2 – x +12 )
STEP 5	= (-8x3 )(x2) + ( -8x3)(-x) + (-8x3)(12) + (2x2)(x2) + (2x2)(-x) + (2x2)(12) + (9)(x2) + (9)(-x) + 9×12
STEP 6	= -8x3+2 + 8x3+1 – 8×12x3 + 2x2+2 – 2x2+1 + 2×12x2 + 9x2 – 9x + 9×12 = -8x5 + 8x4 – 8×12x3 + 2x4 – 2x3 + 2×12x2 + 9x2 – 9x + 9×12
STEP 7	= -8x5 + 8x4 – 96x3 + 2x4 – 2x3 + 24x2 + 9x2 – 9x + 108

STEP 8:-

p × q = (- 8x³ + 2x² + 9 )×( x² – x +12 )

= -8x³ q + 2x² q + 9q

= -8x³ ( x² – x +12 ) + 2x² ( x² – x +12 ) + 9( x² – x +12 )

= (-8x³ )(x²) + ( -8x³)(-x) + (-8x³)(12) + (2x²)(x²) + (2x²)(-x) + (2x²)(12) + (9)(x²) + (9)(-x) + 9×12

= -8x³⁺² + 8x³⁺¹ – 8×12x³ + 2x²⁺² – 2x²⁺¹ + 2×12x² + 9x² – 9x + 9×12

= -8x⁵ + 8x⁴ – 8×12x³ + 2x⁴ – 2x³ + 2×12x² + 9x² – 9x + 9×12

= -8x⁵ + 8x⁴ – 96x³ + 2x⁴ – 2x³ + 24x² + 9x² – 9x + 108

= -8x⁵ + 10x⁴ – 98x³ + 33x² – 9x + 108

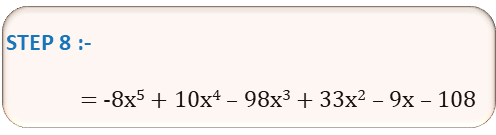
STEP 1	p = (- 8x3 + 2x2 + 9 ) এবং q = ( x2 – x +12 )
STEP 2	p × q = (- 8x3 + 2x2 + 9 )×( x2 – x +12 )
STEP 3	= -8x3 q + 2x2 q + 9q
STEP 4	= -8x3 ( x2 – x +12 ) + 2x2 ( x2 – x +12 ) + 9( x2 – x +12 )
STEP 5	= (-8x3 )(x2) + ( -8x3)(-x) + (-8x3)(12) + (2x2)(x2) + (2x2)(-x) + (2x2)(12) + (9)(x2) + (9)(-x) + 9×12
STEP 6	= -8x3+2 + 8x3+1 – 8×12x3 + 2x2+2 – 2x2+1 + 2×12x2 + 9x2 – 9x + 9×12 = -8x5 + 8x4 – 8×12x3 + 2x4 – 2x3 + 2×12x2 + 9x2 – 9x + 9×12
STEP 7	= -8x5 + 8x4 – 96x3 + 2x4 – 2x3 + 24x2 + 9x2 – 9x + 108
STEP 8	= -8x5 + 10x4 – 98x3 + 33x2 – 9x + 108

উপরের যে দুটি উদাহরণ আমরা দেখলাম step by step কিভাবে বীজগাণিতিক সংখ্যামালার গুণ খুব সহজেই আমরা করতে পারি । এভাবে step by step অংক গুলো করলে আস্তে আস্তে যখন অভ্যাস হয়ে যাবে তখন আর এতো step করা লাগবেনা । তখন নিজেরাই বুঝতে পারবে এবং খুব short-cut এ গুণ গুলো করতে পারবে।

> বীজগাণিতিক সংখ্যামালার ভাগঃ

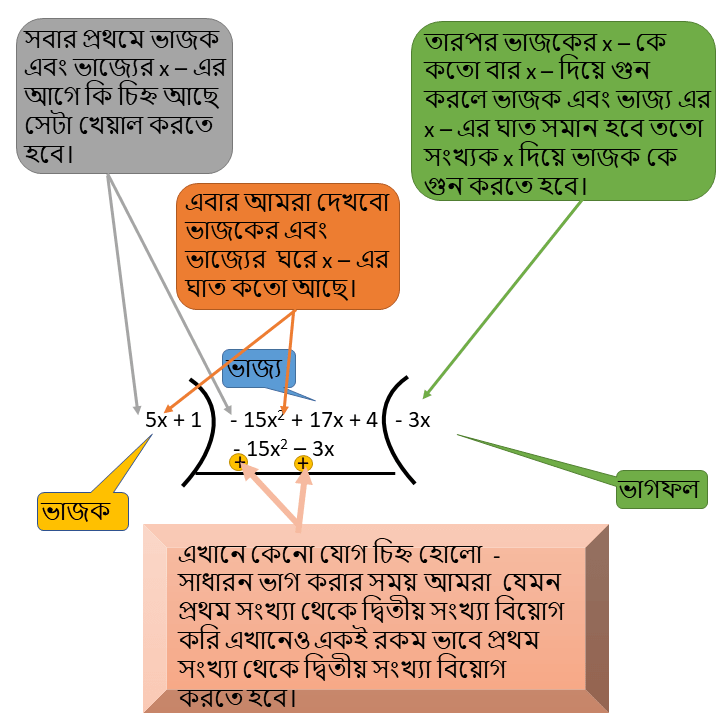
ধরি ( 4 + 17x – 15x²) সংখ্যাকে ( 1 + 5x ) দিয়ে ভাগ করতে হবে ।

প্রথমেই আমরা সংখ্যাগুলো কে x এর ঘাতের অধঃক্রমে সাজিয়ে নেবো ।

তাহলে সংখ্যাদুটি হবে –

( -15x² + 17x + 4 ) এবং ( 5x + 1 )

বীজগাণিতিক সংখ্যামালার গুণ ও ভাগ কেমন লাগলো অবশ্যই কমেন্ট করে জানাবে । এবার তোমরা এই অধ্যায়ের কষে দেখি গুলো ভালো করে করবে এবং যেখানে সমস্যা হবে সেই অংক টা তোমরা এখানে এসে দেখে নেবে। কষে দেখি – 4.1 কষে দেখি – 4.2 তোমাদের জন্যে অষ্টম শ্রেণীর সমস্ত অধ্যায় এর গণিত এবং অধ্যায়টি কিভাবে আয়ত্ত করতে হবে তা খুব সুন্দর করে লেখা হয়েছে যাতে তোমরা খুব সহজেই প্রতিটি অধ্যায় বুঝতে পারো এবং প্রতিটি অংক বুঝে করতে পারো । সমস্ত অধ্যায়ের সমাধান এবং অধ্যায়ের খুঁটিনাটি

---

এখানে তোমরা তোমাদের অষ্টম শ্রেণীতে কি কি পড়ানো হয়, মানে তোমাদের অষ্টম শ্রেণীর সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

---