কষে দেখি 15.1 Class 10।বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য কষে দেখি Class 10| Koshe Dekhi 15.1 Class 10 WBBSE.

শ্রেণী- দশম ; অধ্যায় – বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য ; কষে দেখি 15.1

---

কষে দেখি 15.1 Class 10 অংকের সূচিপত্র:-

কষে দেখি 15.1 Class 10 এর অংকের সমাধান গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ

এই কষে দেখি 15.1, পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদ | WBBSE এর অন্তর্গত দশম শ্রেণি|Class 10 এর 15 নম্বর অধ্যায়|Chapter 15, বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য | Theorems Related To Tangent Of a Circle এর প্রথম অনুশীলনী।

এই কষে দেখি 15.1 Class 10 এর অঙ্ক গুলি বঝার জন্যে যে যে বিষয় জানতে হবে তা আলোচনা করা হলো-

---

আগামিতে এই কষে দেখি 15.1 Class 10 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?

কষে দেখি 15.1 Class 10 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 15.1 Class 10 তারপর এই চিহ্ন দেখে Click করলে আবার তোমরা এখানে এসে যাবে।

---

কষে দেখি 15.1 Class 10|Koshe Dekhi 15.1 Class 10

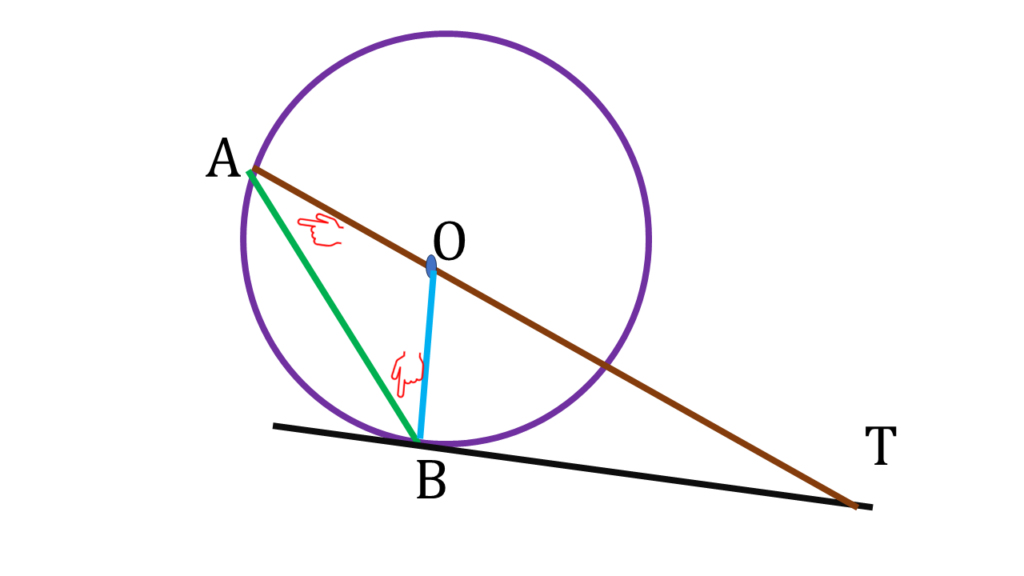
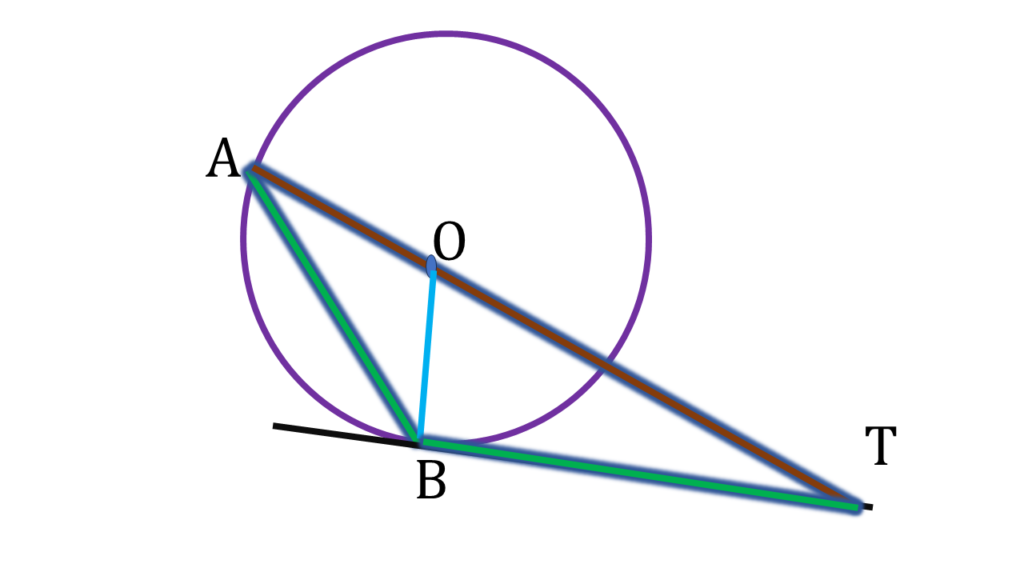
1. মাসুম O কেন্দ্রীয় একটি বৃত্ত অঙ্কন করেছে যার AB একটি জ্যা। B বিন্দুতে একটি স্পর্শক অঙ্কন করেছি যা বর্ধিত AO-কে T বিন্দুতে ছেদ করল। ∠BAT = 21° হলে, ∠BTA-এর মান হিসাব করে লিখি।

সমাধানঃ-

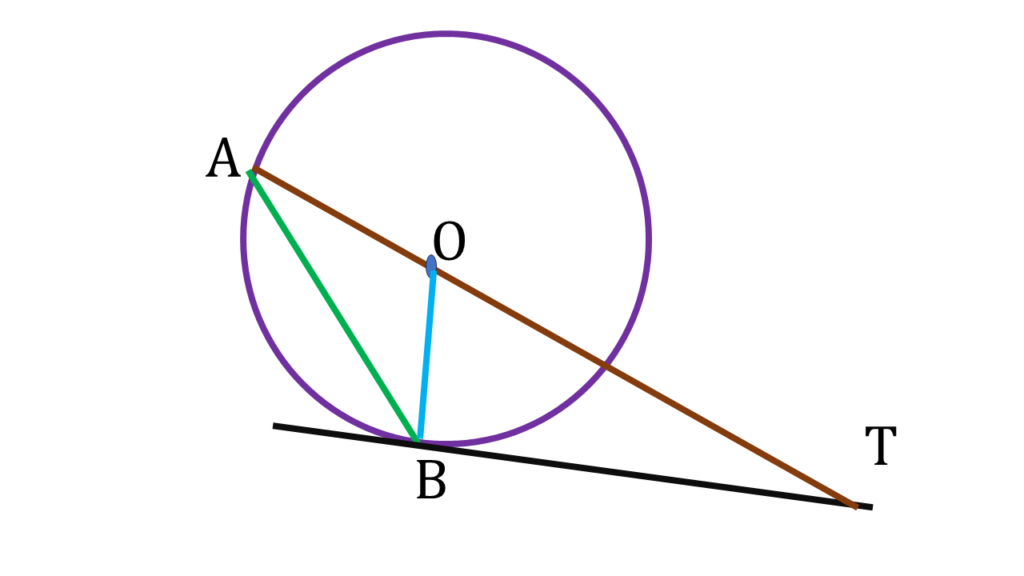
O, B যুক্ত করলাম।

B বিন্দুতে BT স্পর্শক।

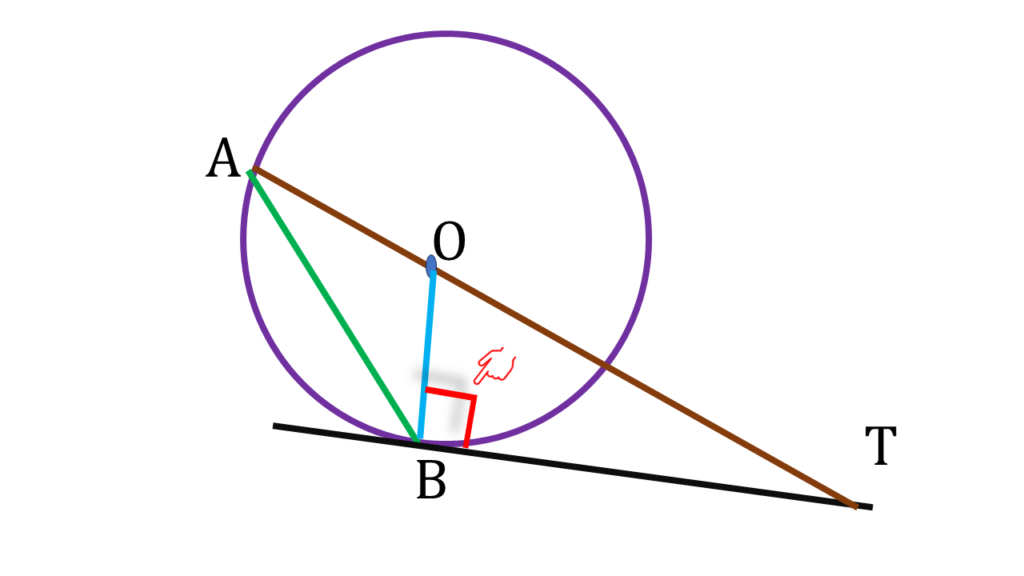
⇒ ∠OBT = 90° —–(i)

আবার, ▲OAB এর OA=OB (একই বৃত্তের ব্যাসার্ধ)

⇒ ∠OBA = ∠BAO = 21° ——-(ii)

অতএব, ▲ABT এর

∠BAT + ∠ABT + ∠BTA = 180°

বা, ∠BAT + ∠ABO + ∠OBT + ∠BTA = 180°

বা, 21° + 21° + 90° + ∠BTA = 180° [(i) ও (ii) নং থেকে পাই]

বা, 132° + ∠BTA = 180°

বা, ∠BTA = 48°

---

2 . কোনো বৃত্তের XY একটি ব্যাস। বৃত্তটির উপর অবস্থিত A বিন্দুতে PAQ বৃত্তের স্পর্শক। X বিন্দু থেকে বৃত্তের স্পর্শকের উপর অঙ্কিত লম্ব PAQ-কে Z বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, XA, ∠YXZ-এর সমদ্বিখণ্ডক।

সমাধানঃ-

প্রদত্তঃ

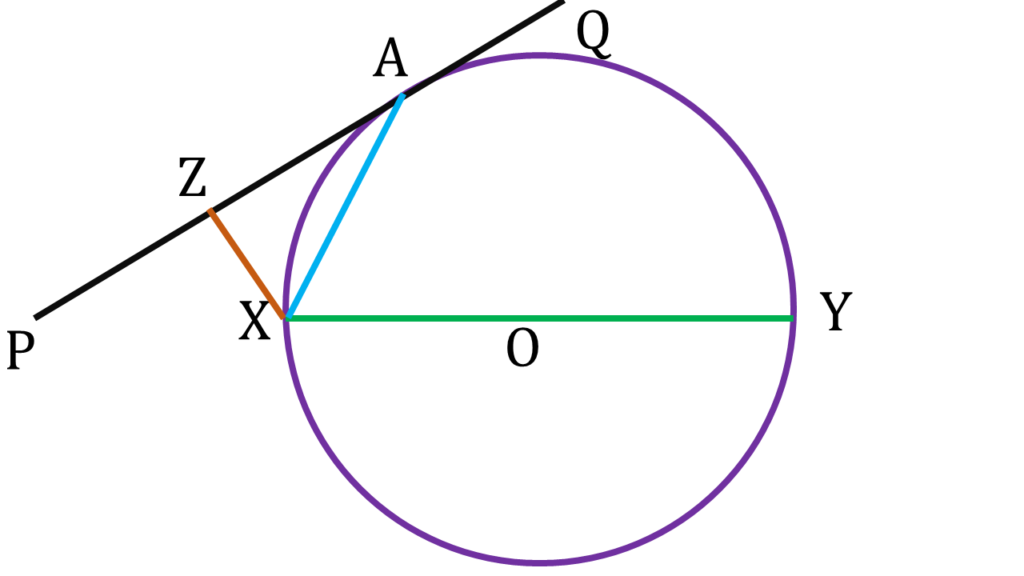
O কেন্দ্রীয় বৃত্তের XY একটি ব্যাস। বৃত্তটির উপর অবস্থিত A বিন্দুতে PAQ বৃত্তের স্পর্শক। X বিন্দু থেকে বৃত্তের স্পর্শকের উপর অঙ্কিত লম্ব PAQ-কে Z বিন্দুতে ছেদ করেছে।

প্রামাণ্যঃ

প্রমাণ করতে হবে যে,

XA, ∠YXZ-এর সমদ্বিখণ্ডক।

অঙ্কনঃ

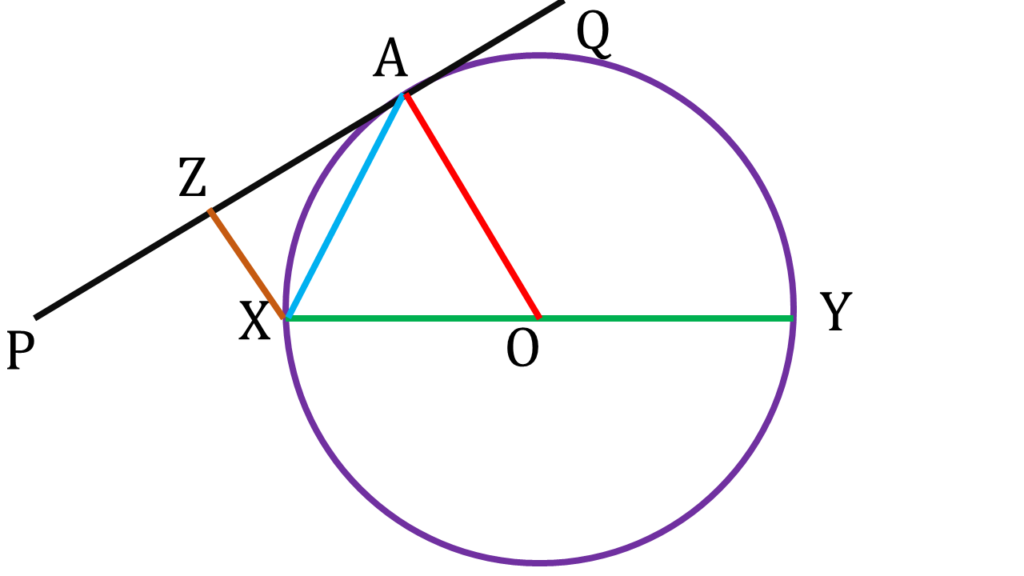
O, A যুক্ত করলাম।

প্রমাণঃ

A বিন্দুতে PAQ স্পর্শক

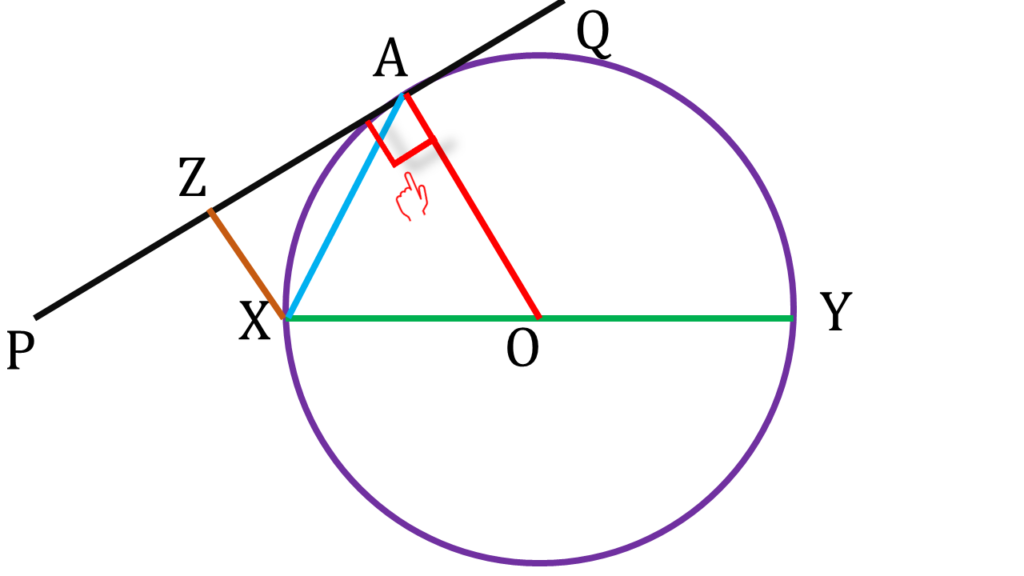
সুতরাং, OA⊥PQ —–(i)

আবার, XZ ⊥ PQ (প্রদত্ত) ——(ii)

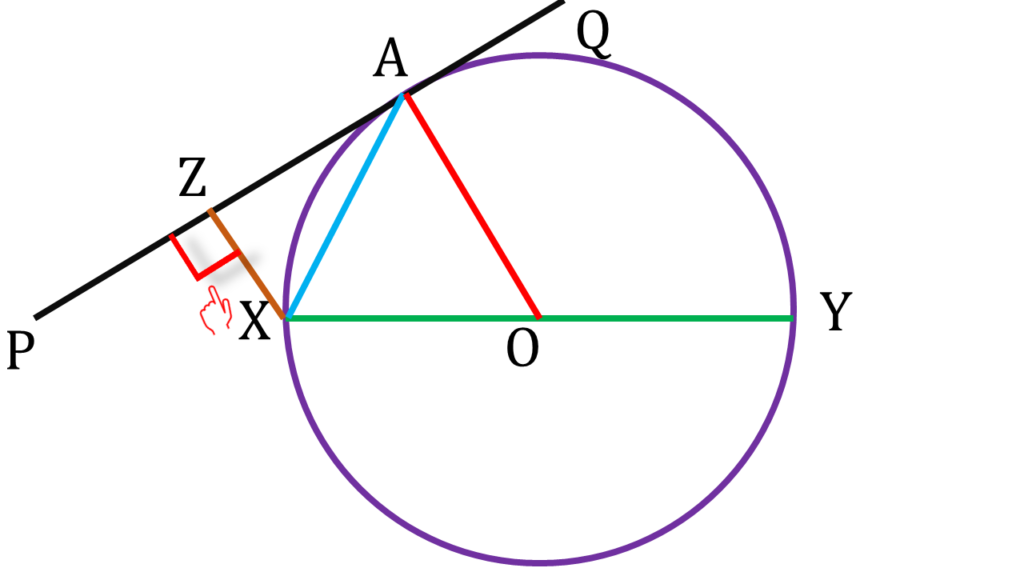
(i) ও (ii) নং থেকে পাই,

OA || XZ

এখন, OA || XZ এবং XE ভেদক

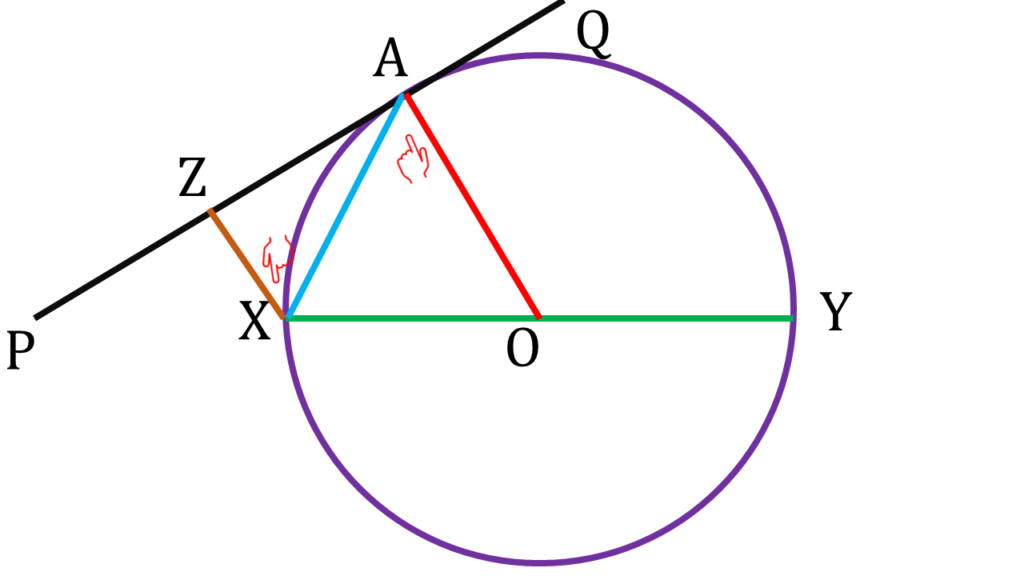
⇒ ∠ZXA = একান্তর ∠OAX —-(iii)

আবার, ▲XOA এর OA = OX(একই বৃত্তের ব্যাসার্ধ)

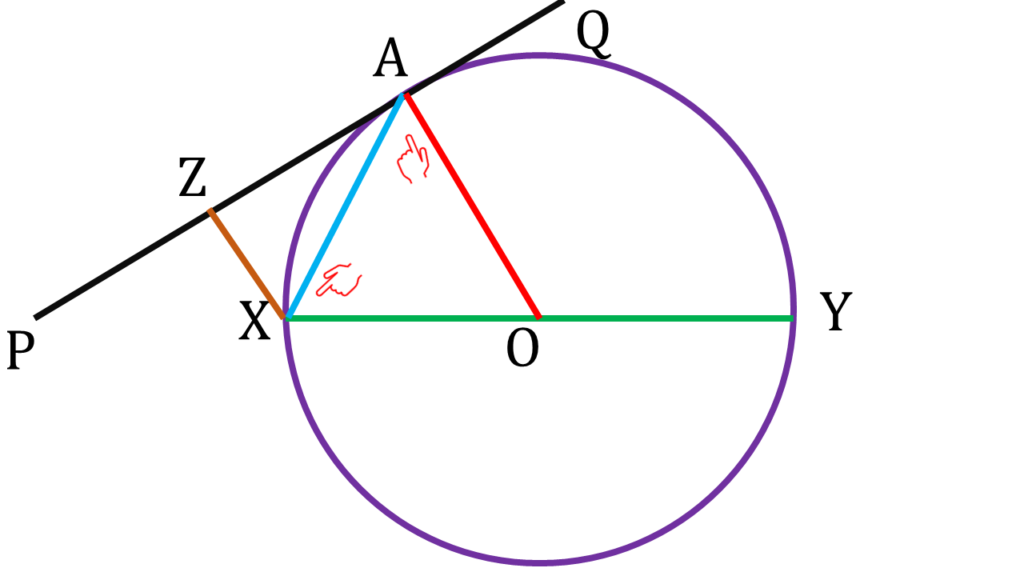
⇒ ∠OXA = ∠OAX —–(iv)

(iii) ও (iv) নং থেকে পাই,

∠ZXA = ∠OXA

সুতরাং, XA, ∠YXZ-এর সমদ্বিখণ্ডক।

---

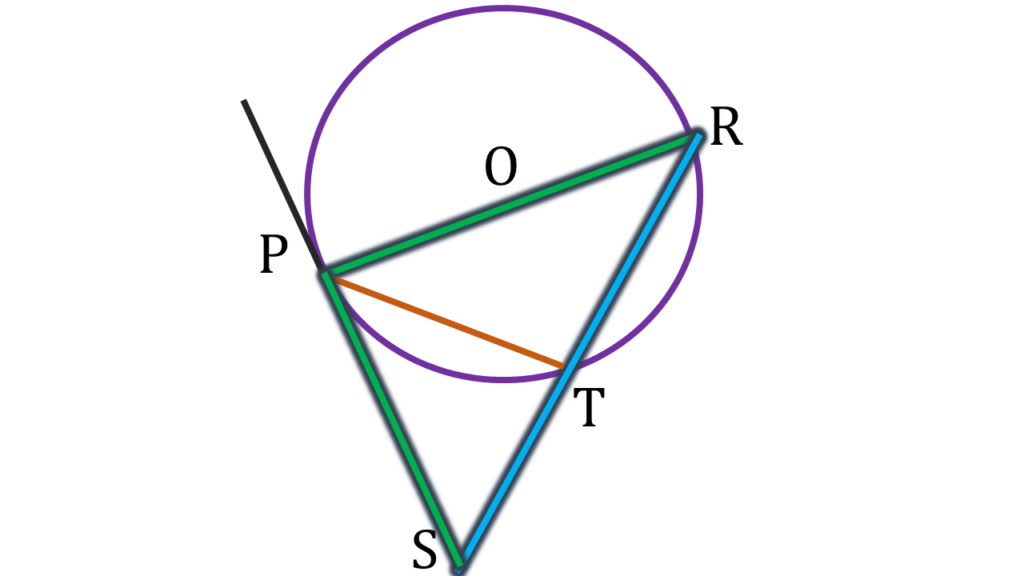
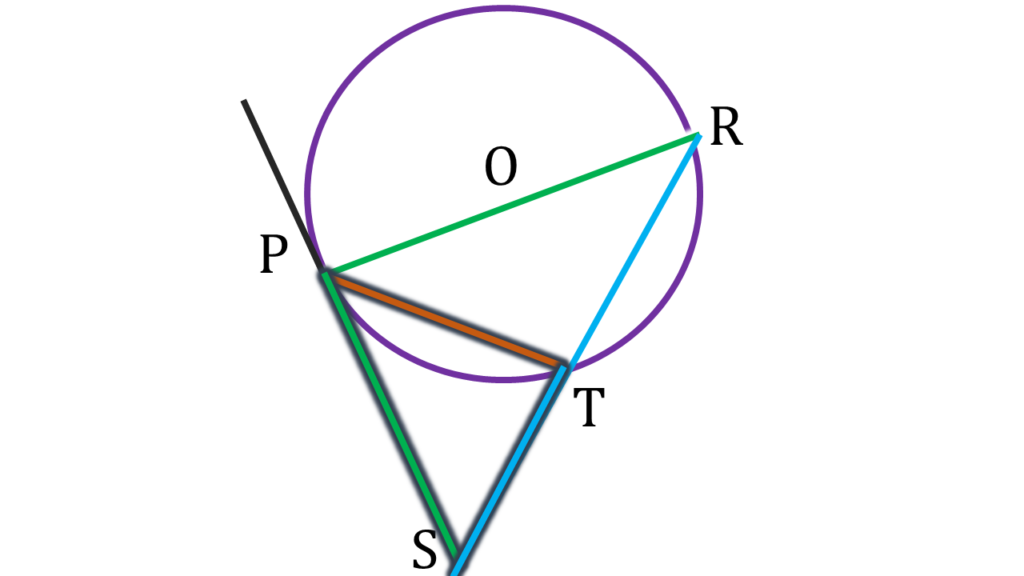
3. একটি বৃত্ত অঙ্কন করলাম যার PR একটি ব্যাস। P বিন্দুতে একটি স্পর্শক অঙ্কন করলাম এবং এই স্পর্শকের উপরে S এমন একটি বিন্দু নিলাম যাতে PR = PS হয়। RS, বৃত্তকে T বিন্দুতে ছেদ করলে, প্রমাণ করি যে, ST = RT = PT.

সমাধানঃ-

প্রদত্তঃ

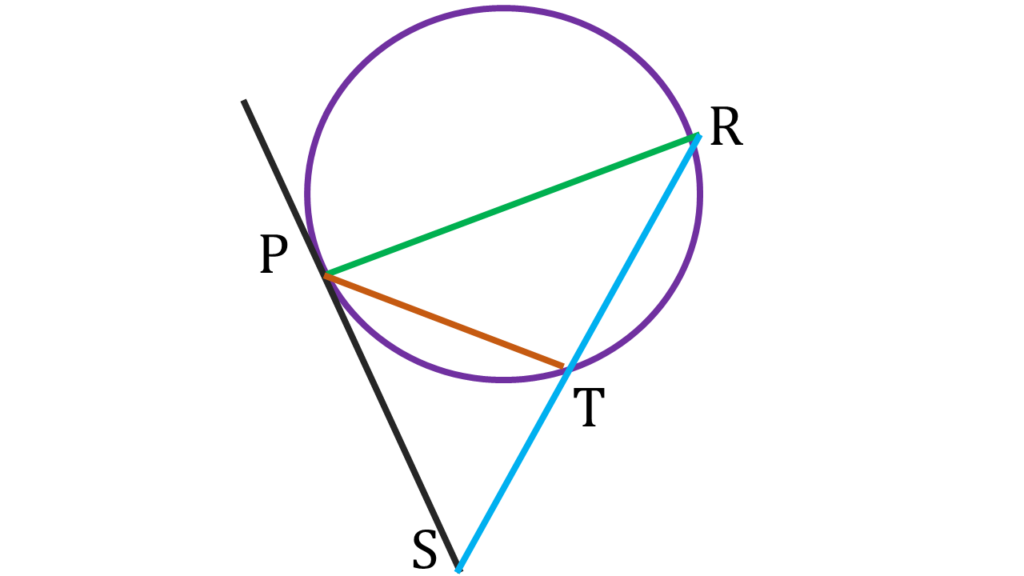
একটি বৃত্ত অঙ্কন করলাম যার PR একটি ব্যাস। P বিন্দুতে একটি স্পর্শক অঙ্কন করলাম এবং এই স্পর্শকের উপরে S এমন একটি বিন্দু নিলাম যাতে PR = PS হয়। RS, বৃত্তকে T বিন্দুতে ছেদ করেছে।

প্রামাণ্যঃ

প্রমাণ করতে হবে যে,

ST = RT = PT.

অঙ্কনঃ

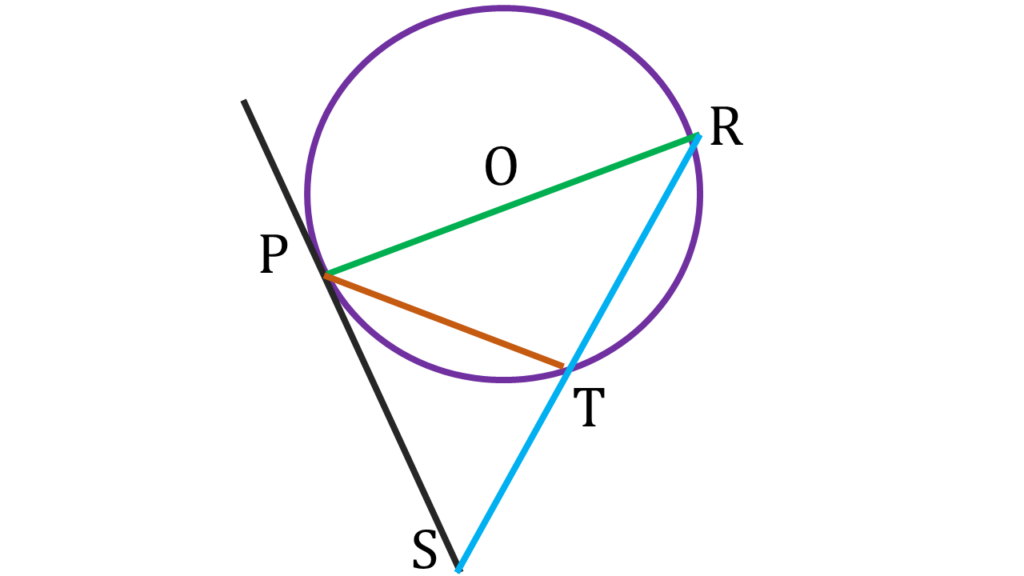
ধরি, বৃত্তের কেন্দ্র O.

প্রমাণঃ

PS, P বিন্দুতে স্পর্শক

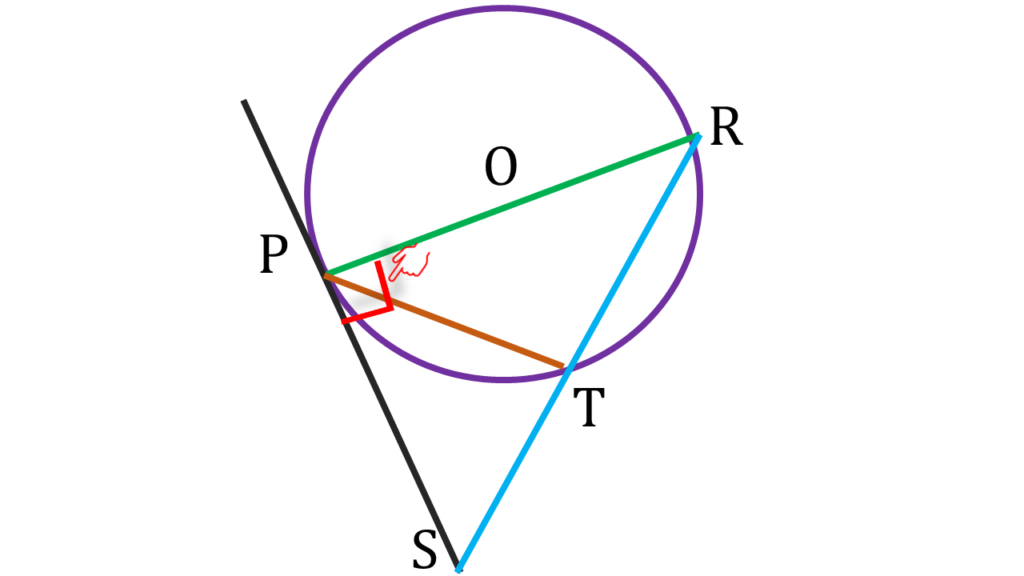
সুতরাং ∠RPS = 90° —–(i)

আবার, ∠PTR একটি অর্ধবৃত্তস্থ কোণ।

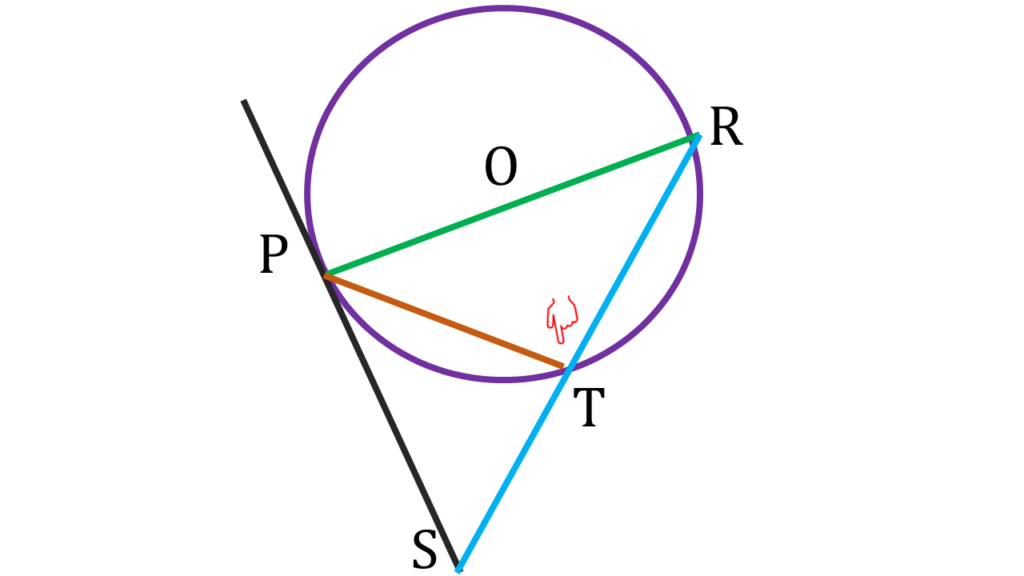
⇒ ∠PTR = 90° —–(ii)

⇒ ∠PTS = 90° —–(iii)

এখন ▲PSR এর,

∠PSR + ∠PRS + ∠SPR = 180°

বা, ∠PSR + ∠PSR = 180° – 90° [∵ PS = PR এবং (i) নং থেকে মান বসিয়ে পাই]

বা, 2∠PSR = 90°

বা, ∠PSR = 45° = ∠PRS —–(iv)

আবার, ▲PTS এর

∠PST + ∠PTS + ∠SPT = 180°

বা, 45°° + 90° + ∠SPT = 180°[∵ PS = PR এবং (iii) ও (iv) নং থেকে পাই]

বা, ∠SPT = 45°

⇒ ∠SPT = ∠PST = 45°

⇒ PT = ST

একইরকমভাবে ▲PTR থেকে পাই,

PT = RT

সুতরাং , ST = RT = PT.

---

4. একটি O কেন্দ্রীয় বৃত্ত অঙ্কন করি যার দুটি ব্যাসার্ধ OA ও OB পরস্পর লম্বভাবে অবস্থিত। A ও B বিন্দুতে অঙ্কিত স্পর্শকদ্বয় পরস্পরকে T বিন্দুতে ছেদ করলে, প্রমাণ করি যে, AB = OT এবং তারা পরস্পরকে লম্বভাবে সমদ্বিখণ্ডিত করে।

সমাধানঃ-

প্রদত্তঃ

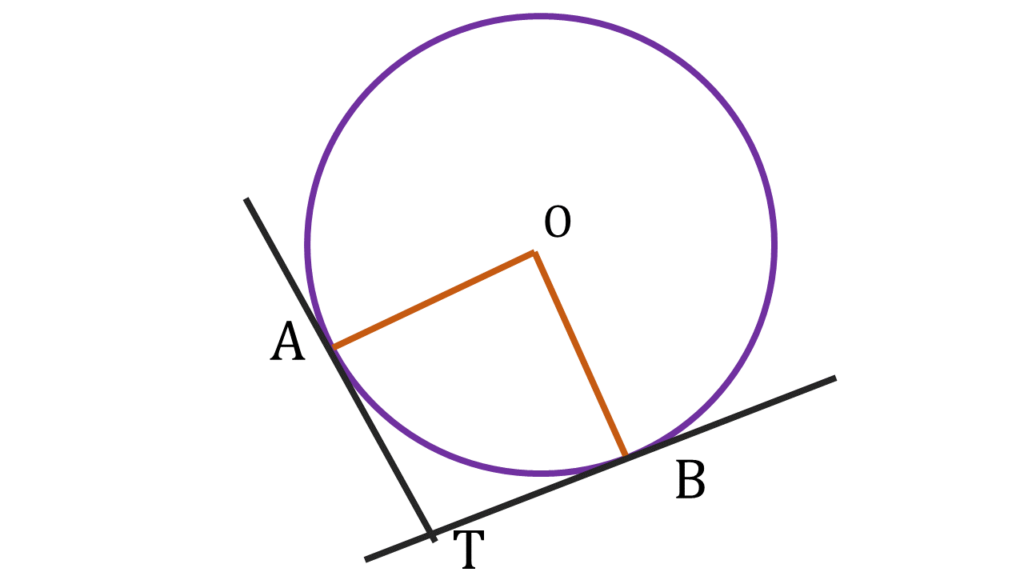
O কেন্দ্রীয় বৃত্ত অঙ্কন করেছি যার দুটি ব্যাসার্ধ OA ও OB পরস্পর লম্বভাবে অবস্থিত। A ও B বিন্দুতে অঙ্কিত স্পর্শকদ্বয় পরস্পরকে T বিন্দুতে ছেদ করেছে।

প্রামাণ্যঃ

প্রমাণ করতে হবে যে,

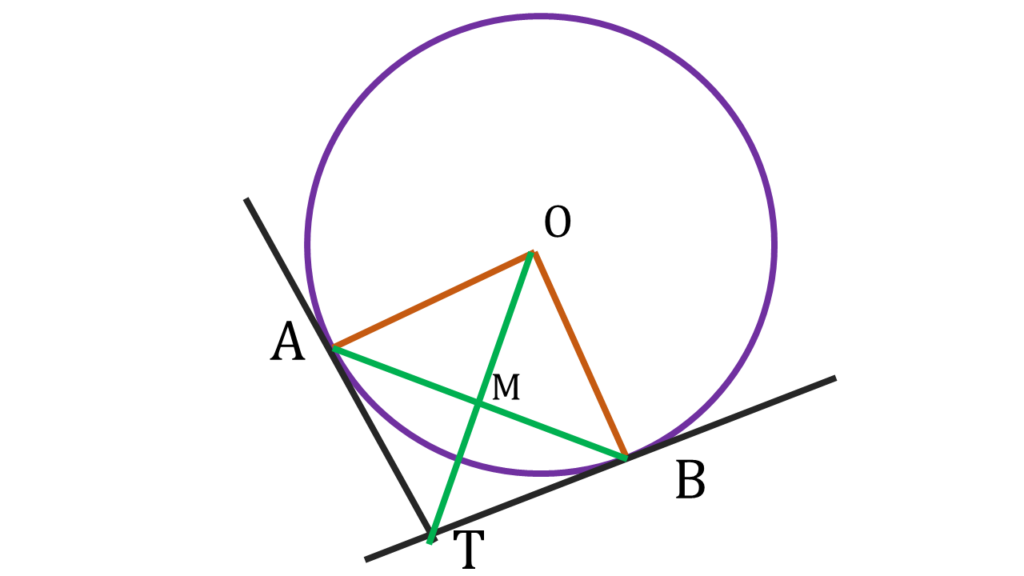
AB = OT এবং তারা পরস্পরকে লম্বভাবে সমদ্বিখণ্ডিত করে।

প্রমাণঃ

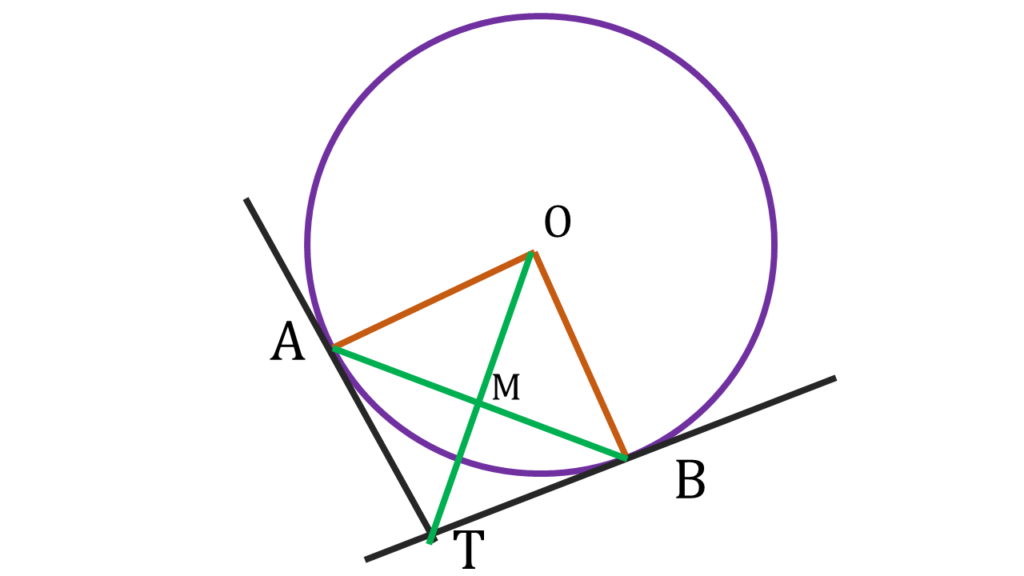
মনে করি, OT, AB বাহুকে M বিন্দুতে ছেদ করেছে।

এখন চতুর্ভুজ OATB এর,

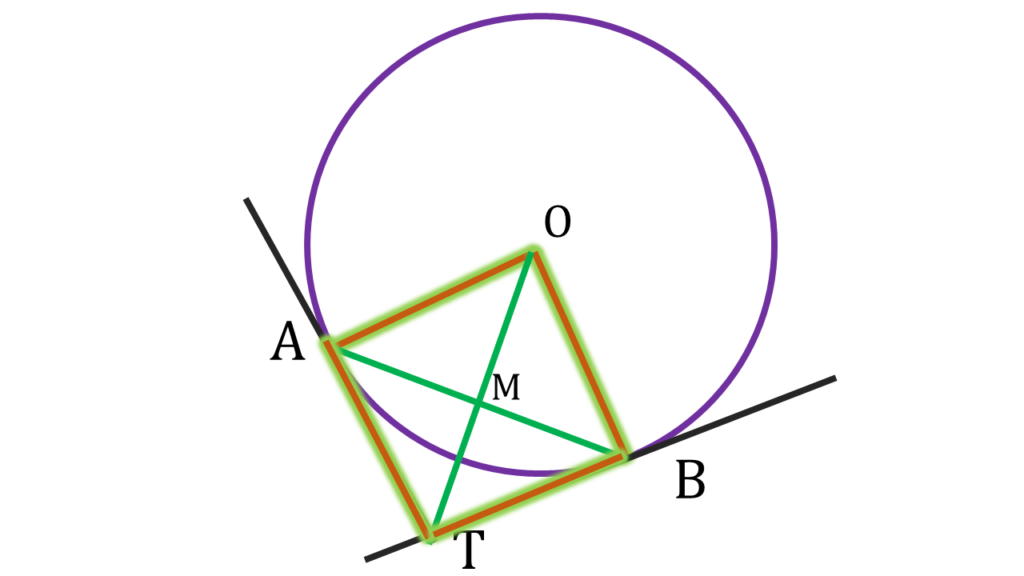
∠OBT = 90° [∵ OB ব্যাসার্ধের B বিন্দুতে BT স্পর্শক]

∠OAT = 90° [∵ OA ব্যাসার্ধের A বিন্দুতে AT স্পর্শক]

∠AOB = 90° [প্রদত্ত]

অতএব,

∠OAT + ∠ATB + ∠OBT + ∠AOB = 360° থেকে পাই,

∠ATB = 360° – ∠OAT – ∠OBT – ∠AOB

বা, ∠ATB = 360° – 90° – 90° – 90° = 90°

সুতরাং, চতুর্ভুজ OATB এর চারটি কোণ সমকোণ

⇒ চতুর্ভুজ OATB একটি আয়তক্ষেত্র।

⇒ আয়তক্ষেত্র OATB এর কর্ণদ্বয় যথা AB ও OT পরস্পর সমান এবং পরস্পরকে সমদ্বিখণ্ডিত করে।

⇒ AB = OT

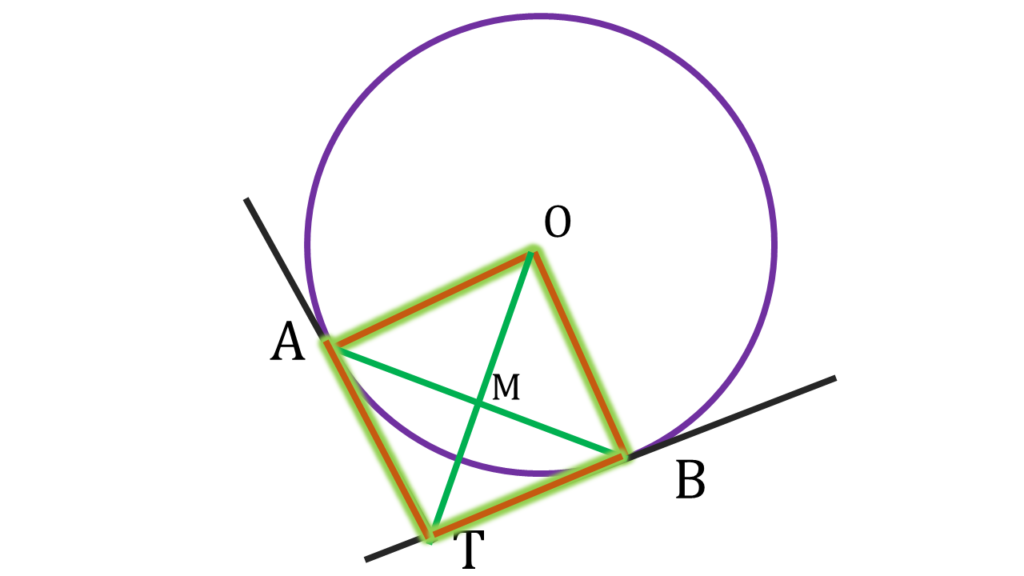
আবার, কোনো জ্যা এর সমদ্বিখণ্ডক কেন্দ্রগামী হলে ঐ কেন্দ্রগামী সরলরেখা জ্যা টিকে লম্বভাবে সমদ্বিখণ্ডিত করে।

সুতরাং, AB = OT এবং তারা পরস্পরকে লম্বভাবে সমদ্বিখণ্ডিত করে।

---

5 . দুটি এককেন্দ্রীয় বৃত্তের বৃহত্তরটির AB ও AC জ্যা দুটি অপর বৃত্তকে যথাক্রমে P ও Q বিন্দুতে স্পর্শ করলে, প্রমাণ করি যে, PQ = \(\frac{1}{2}\)BC.

সমাধানঃ-

প্রদত্তঃ

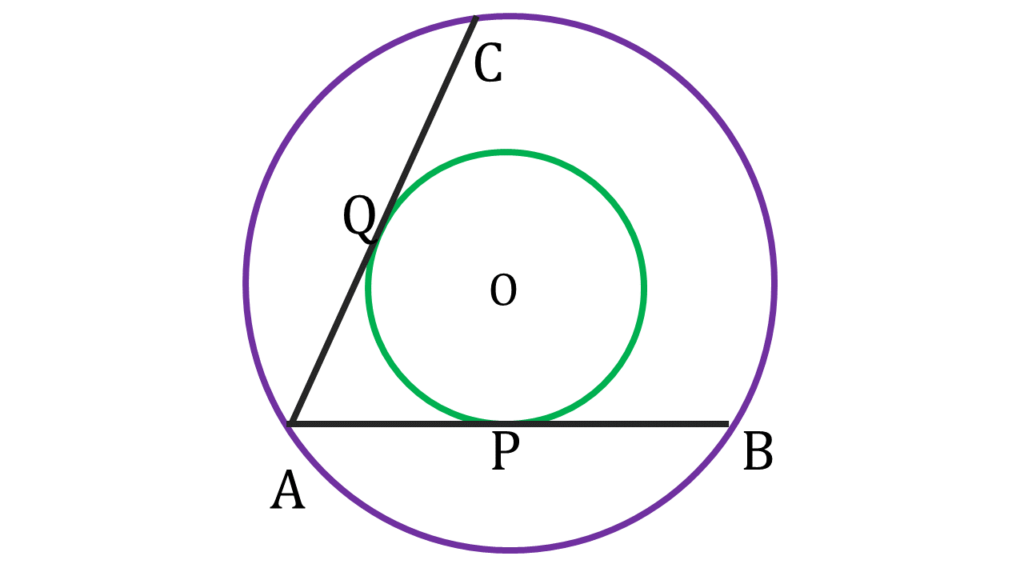
দুটি এককেন্দ্রীয় বৃত্তের বৃহত্তরটির AB ও AC জ্যা দুটি অপর বৃত্তকে যথাক্রমে P ও Q বিন্দুতে স্পর্শ করেছে।

প্রামাণ্যঃ

প্রমাণ করতে হবে যে,

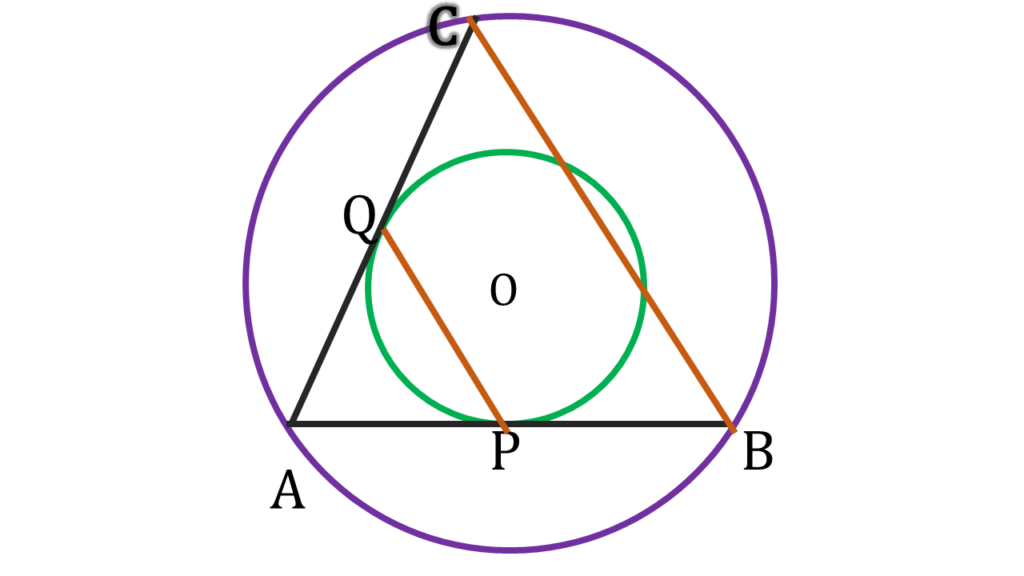
PQ = \(\frac{1}{2}\)BC.

অঙ্কনঃ

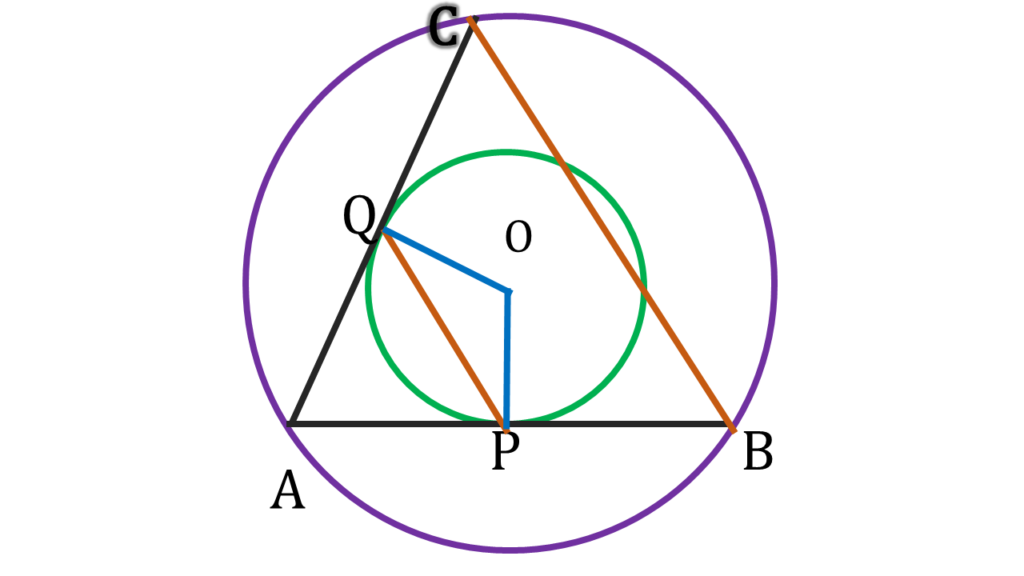
O, Q; O, P যুক্ত করলাম।

প্রমাণঃ

O কেন্দ্রীয় ছোটো বৃত্তের,

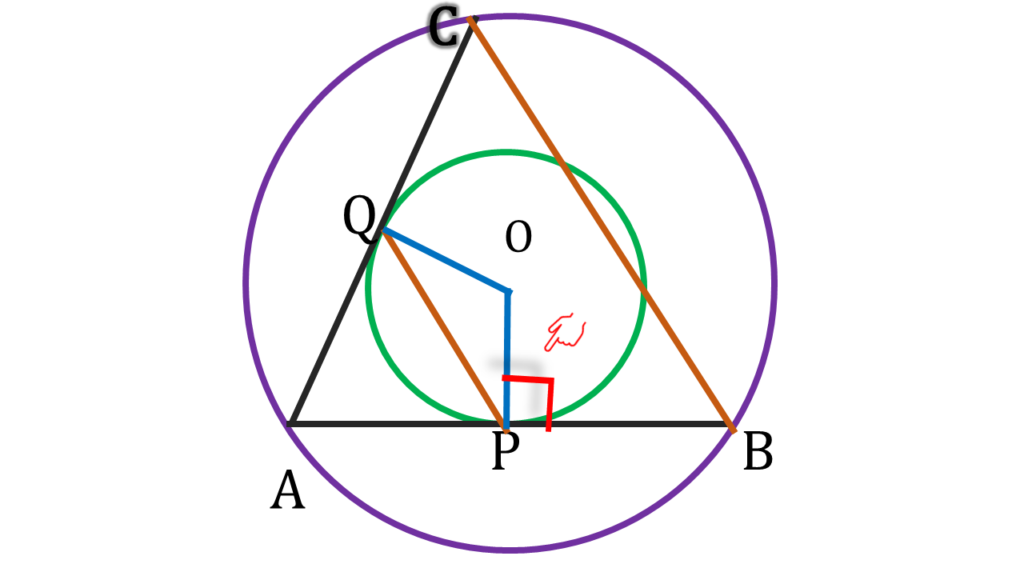
OP ব্যাসার্ধের P বিন্দুতে AB স্পর্শক

⇒ OP, AB এর উপর লম্ব

আবার, বৃহত্তর বৃত্তের AB জ্যা এর উপর OP লম্ব

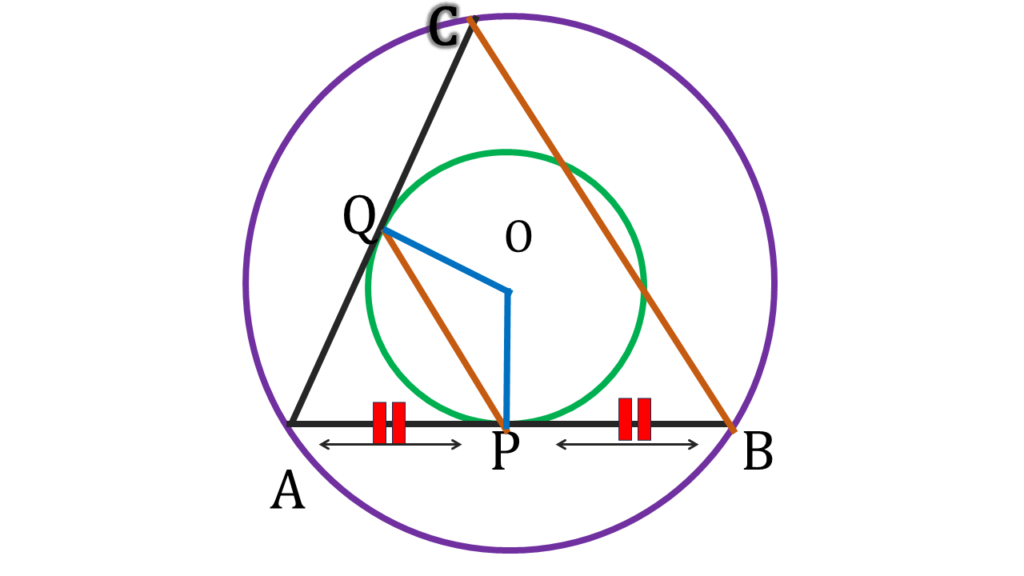
সুতরাং, OP, AB কে সমদ্বিখণ্ডিত করে।

একইরকমভাবে, 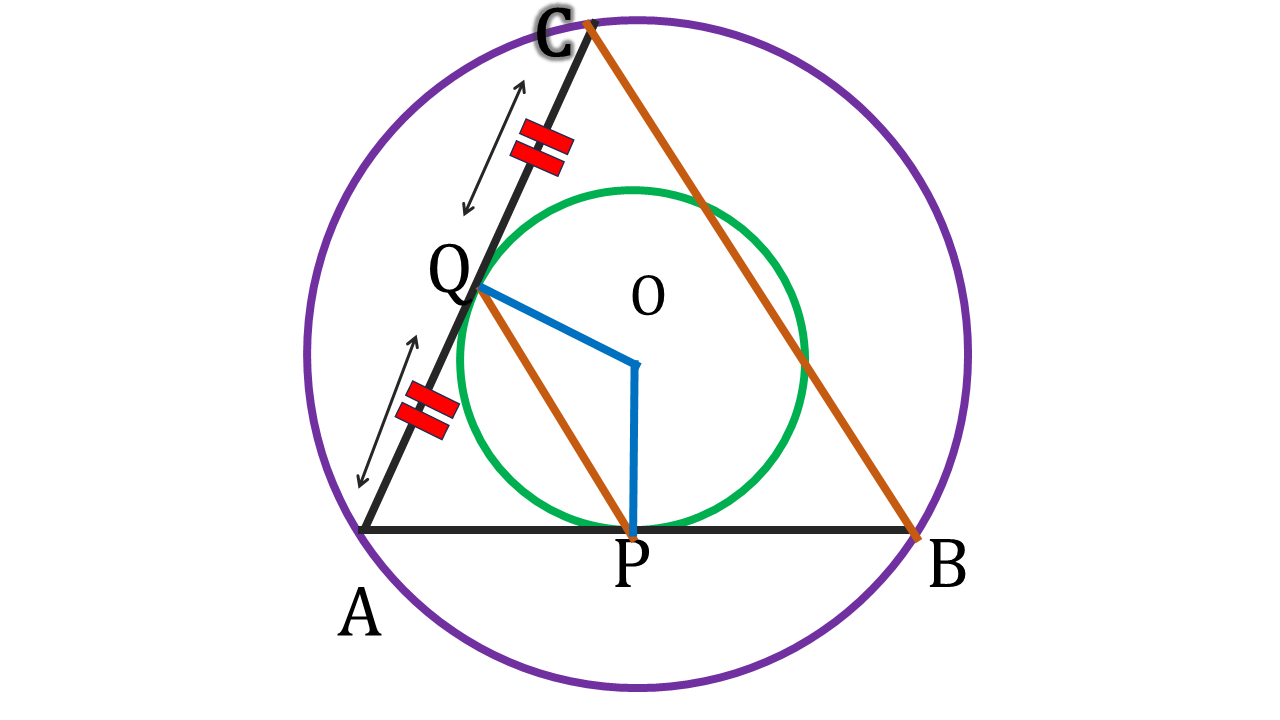OQ, AC কে লম্বসমদ্বিখণ্ডিত করে।

এখন, ▲ABC এর P ও Q যথাক্রমে AB ও AC বাহুর মধ্যবিন্দু

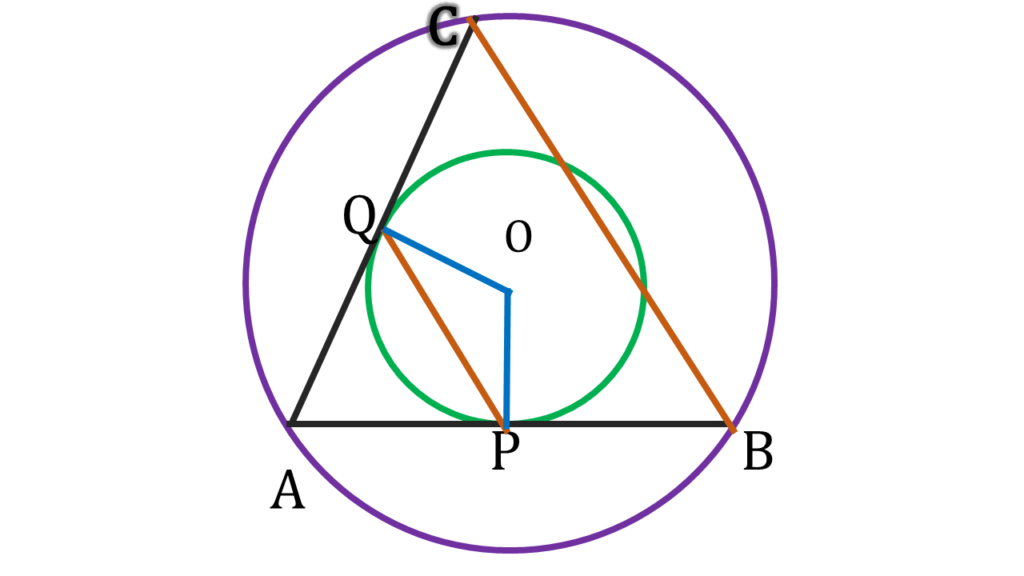
সুতরাং, PQ = \(\frac{1}{2}\)BC.

যেহেতু, একটি ত্রিভুজের দুটি বাহুর মধ্যবিন্দুর সংযোজক সরলরেখা তৃতীয় বাহুর অর্ধেক হয়।

---

6. O কেন্দ্রীয় কোনো বৃত্তের উপর অবস্থিত A বিন্দুতে স্পর্শকের উপর X যে-কোনো একটি বিন্দু। X বিন্দু থেকে অঙ্কিত একটি ছেদক বৃত্তকে Y ও Z বিন্দুতে ছেদ করে। YZ-এর মধ্যবিন্দু P হলে, প্রমাণ করি যে, XAPO বা XAOP একটি বৃত্তস্থ চতুর্ভুজ।

সমাধানঃ-

প্রদত্তঃ

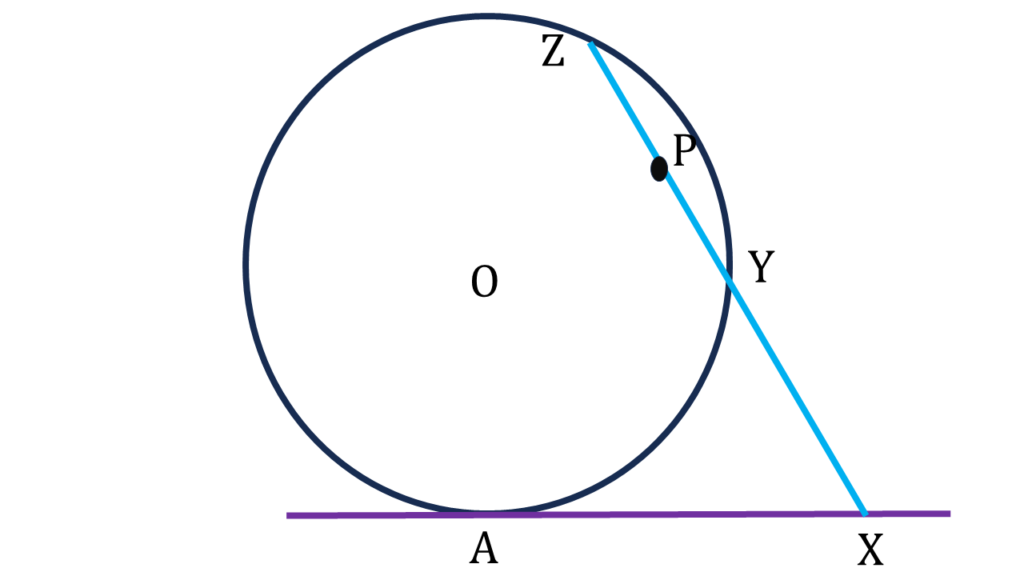
O কেন্দ্রীয় কোনো বৃত্তের উপর অবস্থিত A বিন্দুতে স্পর্শকের উপর X যে-কোনো একটি বিন্দু। X বিন্দু থেকে অঙ্কিত একটি ছেদক বৃত্তকে Y ও Z বিন্দুতে ছেদ করে। YZ-এর মধ্যবিন্দু P।

প্রামাণ্যঃ

প্রমাণ করতে হবে যে,

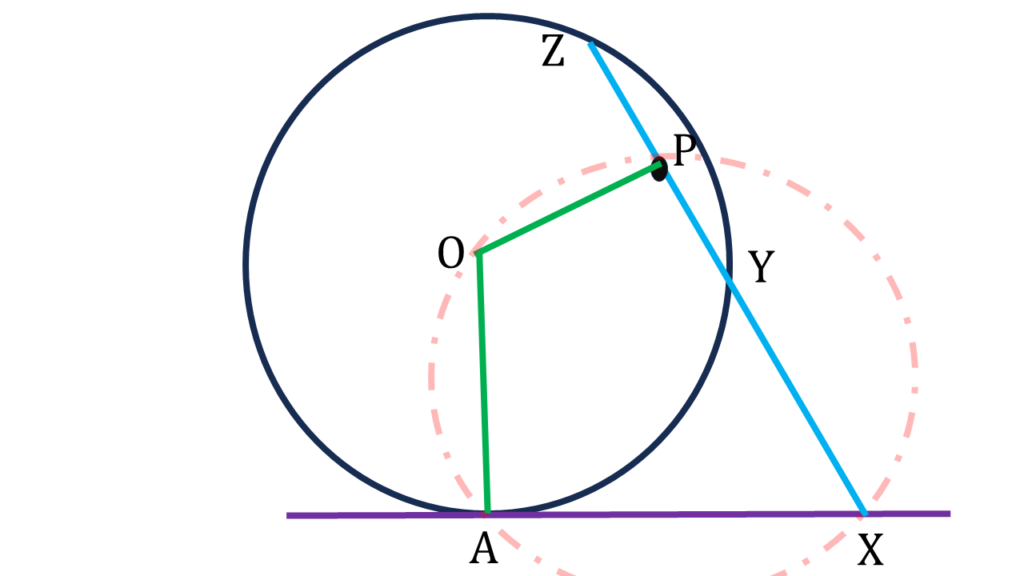
XAOP একটি বৃত্তস্থ চতুর্ভুজ।

প্রমাণঃ

OA ব্যাসার্ধ এবং AX, A বিন্দুতে স্পর্শক।

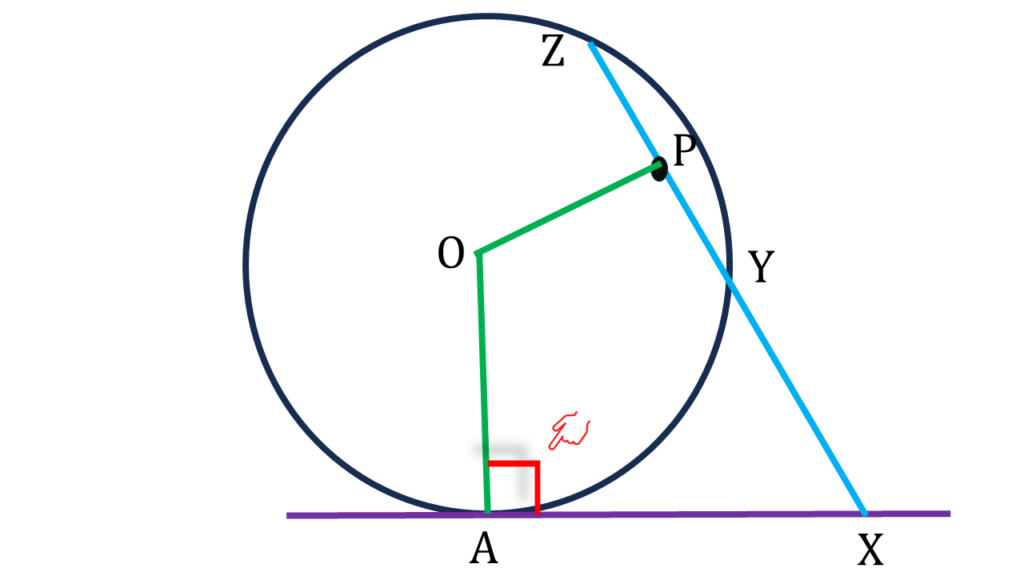
সুতরাং, ∠OAX = 90°

আবার, YZ, O কেন্দ্রীয় বৃত্তের জ্যা এবং P, YZ জ্যা এর মধ্যবিন্দু।

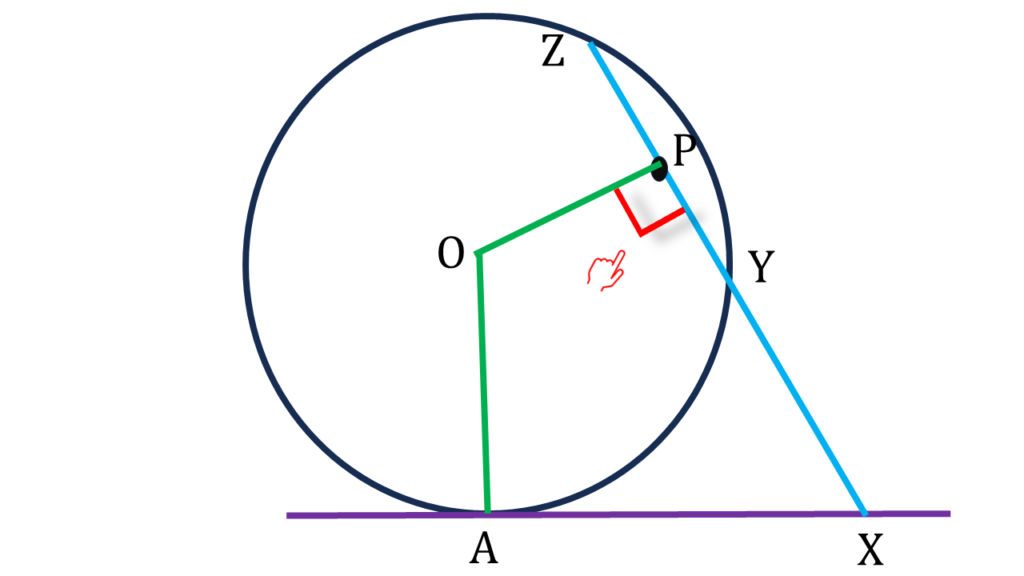
সুতরাং, ∠OPY = 90°

অতএব,

∠OAX + ∠OPY = 90° + 90° = 180° —–(i)

এখন,

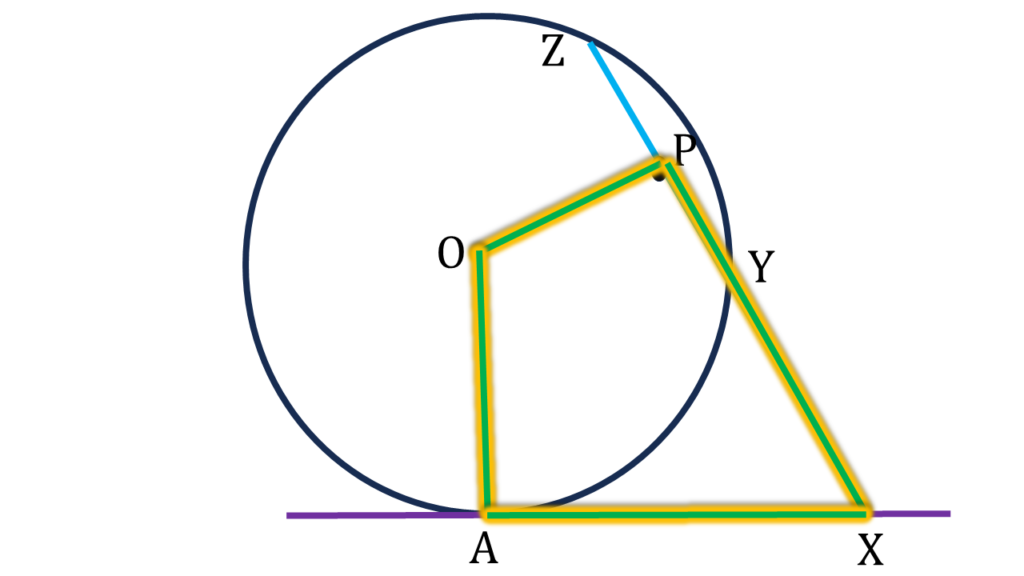
চতুর্ভুজ XAOP এর
∠POA + ∠OAX + ∠AXP + ∠XPO = 360°
বা, ∠POA + ∠AXP + ∠OAX + ∠OPY = 360°
বা, ∠POA + ∠AXP + 180° = 360° [(i) নং থেকে পাই]
বা, ∠POA + ∠AXP = 180°

সুতরাং, আমরা পেলাম চতুর্ভুজ XAOP এর বিপরীত বাহুগুলি পরস্পর সমপূরক।

অতএব, XAOP একটি বৃত্তস্থ চতুর্ভুজ।

---

7. O কেন্দ্রীয় কোনো বৃত্তের একটি ব্যাসের উপর P যে-কোনো একটি বিন্দু। ওই ব্যাসের উপর O বিন্দুতে অঙ্কিত লম্ব বৃত্তকে Q বিন্দুতে ছেদ করে। বর্ধিত QP বৃত্তকে R বিন্দুতে ছেদ করে। R বিন্দুতে অঙ্কিত স্পর্শক বর্ধিত OP-কে S বিন্দুতে ছেদ করে। প্রমাণ করি যে, SP=SR.

সমাধানঃ-

প্রদত্তঃ

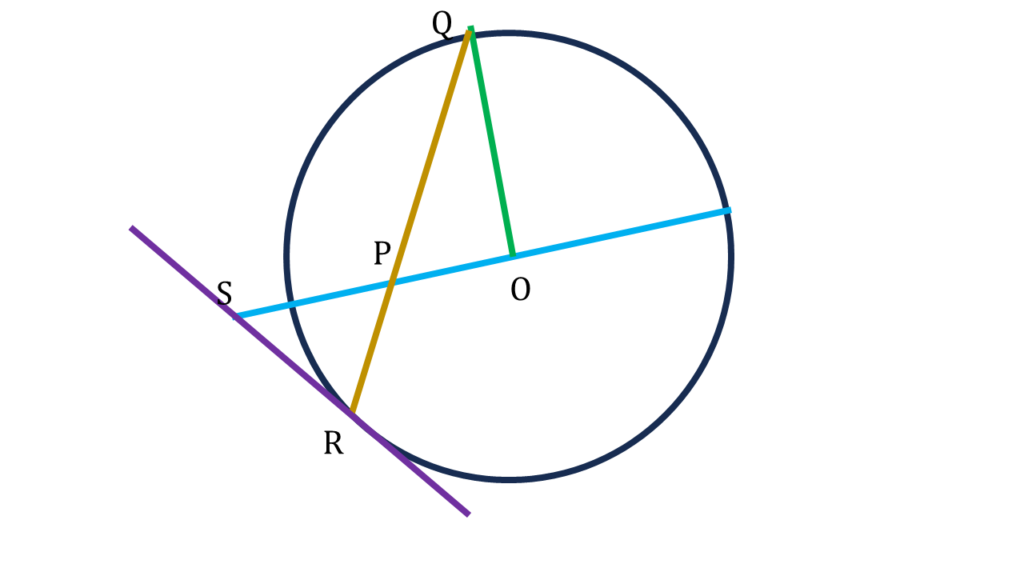
O কেন্দ্রীয় কোনো বৃত্তের একটি ব্যাসের উপর P যে-কোনো একটি বিন্দু। ওই ব্যাসের উপর O বিন্দুতে অঙ্কিত লম্ব বৃত্তকে Q বিন্দুতে ছেদ করে। বর্ধিত QP বৃত্তকে R বিন্দুতে ছেদ করে। R বিন্দুতে অঙ্কিত স্পর্শক বর্ধিত OP-কে S বিন্দুতে ছেদ করেছে।

প্রামাণ্যঃ

প্রমাণ করতে হবে যে,

SP=SR.

অঙ্কনঃ

O, R যুক্ত করলাম।

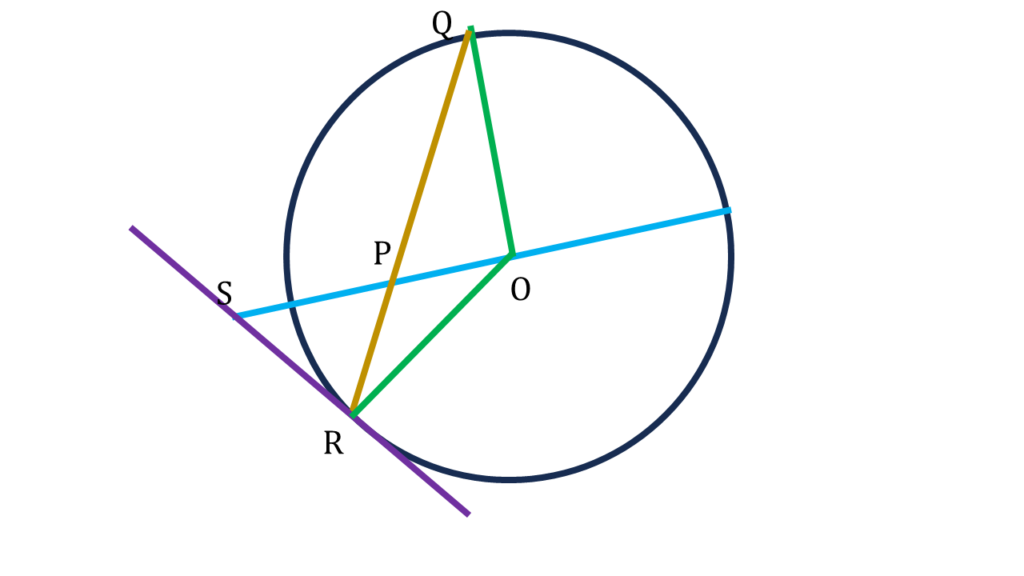
প্রমাণঃ

O কেন্দ্রীয় বৃত্তের OR ব্যাসার্ধ এবং R বিন্দুতে RS স্পর্শক।

সুতরাং,

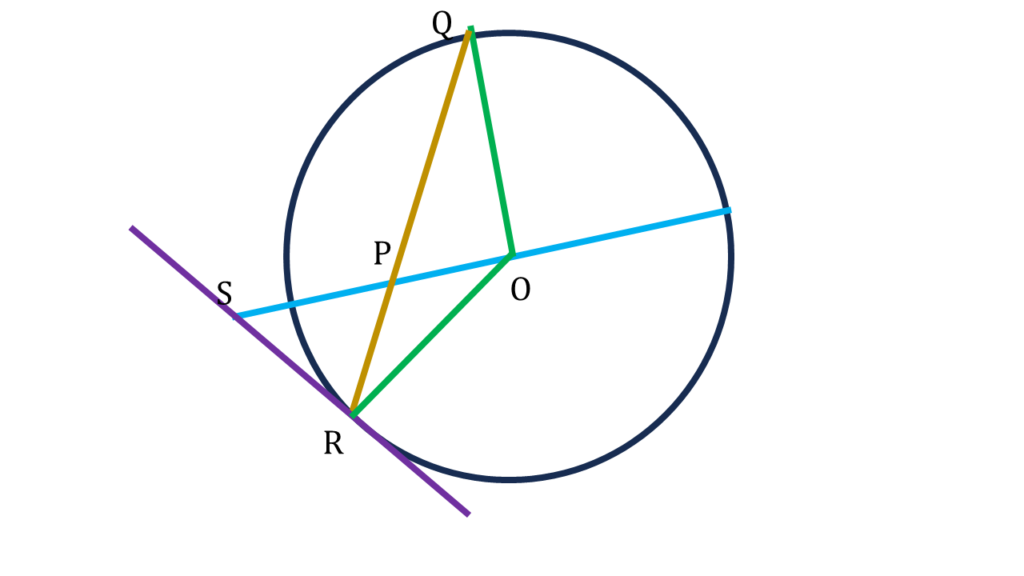
∠ORS = 90°

বা, ∠PRS + ∠ORP = 90°

বা, ∠PRS = 90° – ∠ORP

বা, ∠PRS = 90° – ∠OQP [∵ ▲ORQ এর OQ=OR একই বৃত্তের ব্যাসার্ধ]

বা, ∠PRS = 90° – (180° – ∠QOP – ∠OPQ) [∵ ▲OPQ এর ∠OQP+∠OPQ+∠POQ = 180°]

বা, ∠PRS = 90° – (180° – 90° – ∠OPQ) [∵ QO⊥PO]

বা, ∠PRS = 90° – 90° + ∠OPQ

বা, ∠PRS = ∠OPQ = বিপ্রতীপ∠SPR

বা, ∠PRS = ∠SPR

সুতরাং, SR = SP

---

8. রুমেলা O কেন্দ্রীয় একটি বৃত্ত অঙ্কন করেছে যার QR একটি জ্যা। Q ও R বিন্দুতে দুটি স্পর্শক অঙ্কন করেছি যারা পরস্পরকে P বিন্দুতে ছেদ করেছে। QM বৃত্তের একটি ব্যাস হলে, প্রমাণ করি যে, ∠QPR = 2∠RQM.

সমাধানঃ-

প্রদত্তঃ

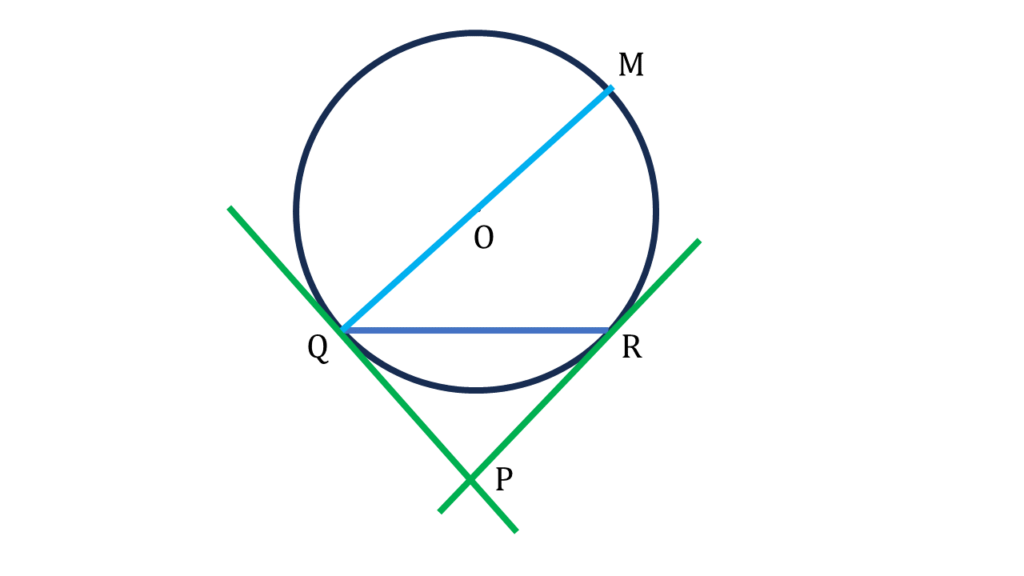
O কেন্দ্রীয় একটি বৃত্ত অঙ্কন করা হয়েছে যার QR একটি জ্যা। Q ও R বিন্দুতে দুটি স্পর্শক অঙ্কন করা হয়েছে যারা পরস্পরকে P বিন্দুতে ছেদ করেছে। QM বৃত্তের একটি ব্যাস।

প্রামাণ্যঃ

প্রমাণ করতে হবে যে,

∠QPR = 2∠RQM

অঙ্কনঃ

O, R যুক্ত করলাম।

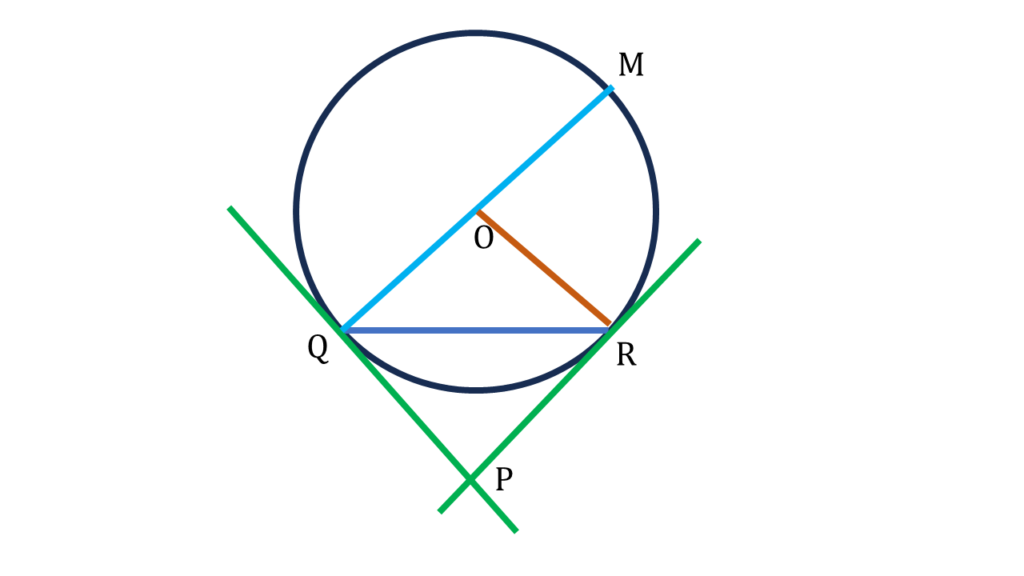
প্রমাণঃ

O কেন্দ্রীয় বৃত্তের OQ ও OR ব্যাসার্ধ এবং QP ও RP যথাক্রমে Q ও R বিন্দুতে স্পর্শক।

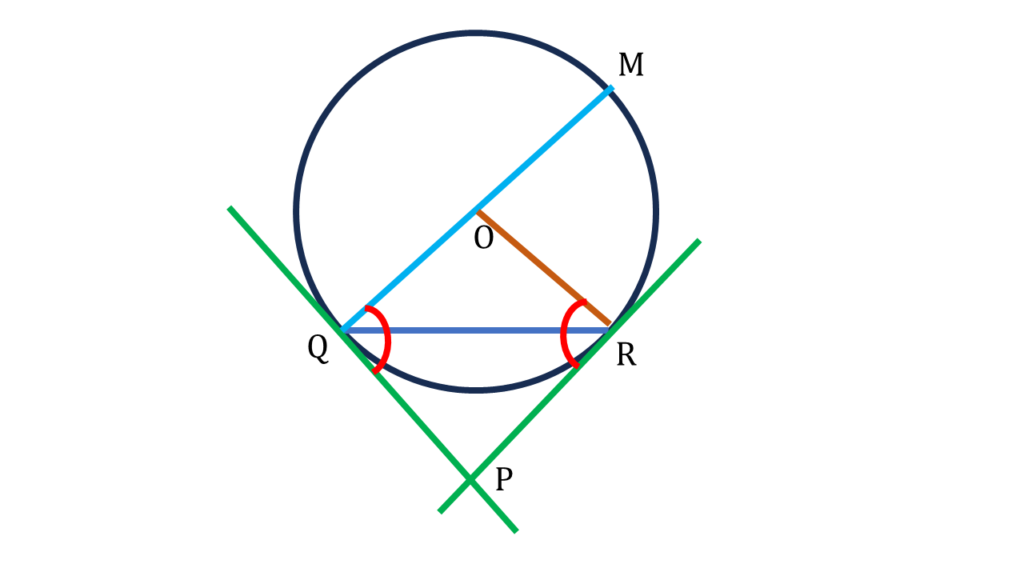
সুতরাং, ∠OQP = ∠ORP = 90°

অতএব, চতুর্ভুজ QPRO এর

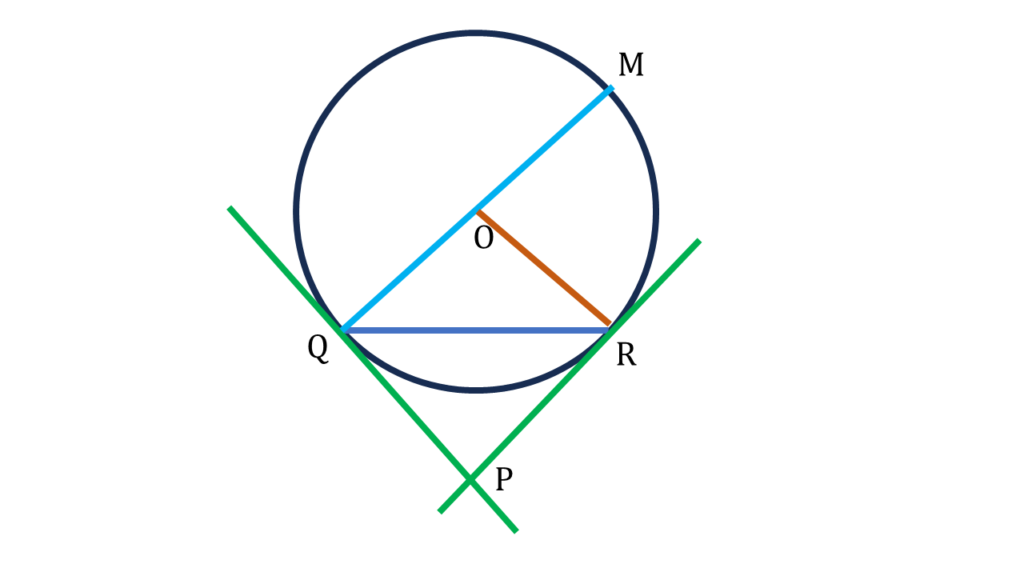
∠OQP + ∠QPR + ∠PRO + ∠ROQ = 360°

বা, 90° + ∠QPR + 90° + ∠ROQ = 360°

বা, ∠QPR + ∠ROQ = 180°

বা, ∠QPR = 180° – ∠ROQ

বা, ∠QPR = ∠OQR + ∠ORQ [∵ ▲QOR এর ∠QOR + ∠OQR + ∠ORQ = 180°]

বা, ∠QPR = ∠OQR + ∠OQR [∵ ▲QOR এর OQ = OR একই বৃত্তের ব্যাসার্ধ]

বা, ∠QPR = 2∠OQR

বা, ∠QPR = 2∠RQM

---

9. কোনো বৃত্তের AC ও BD দুটি জ্যা পরস্পরকে O বিন্দুতে ছেদ করেছে। A ও B বিন্দুতে অঙ্কিত স্পর্শক দুটি পরস্পরকে P বিন্দুতে এবং C ও D বিন্দুতে অঙ্কিত স্পর্শক দুটি পরস্পরকে Q বিন্দুতে ছেদ করলে, প্রমাণ করি যে, ∠P + ∠Q = 2∠BOC.

সমাধানঃ-

প্রদত্তঃ

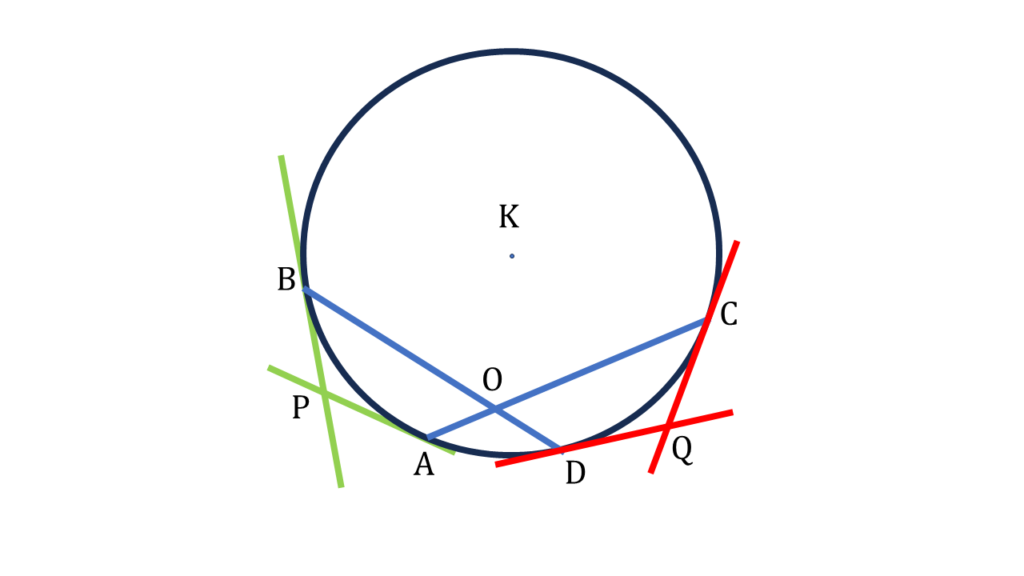
K কেন্দ্রীয় বৃত্তের AC ও BD দুটি জ্যা পরস্পরকে O বিন্দুতে ছেদ করেছে। A ও B বিন্দুতে অঙ্কিত স্পর্শক দুটি পরস্পরকে P বিন্দুতে এবং C ও D বিন্দুতে অঙ্কিত স্পর্শক দুটি পরস্পরকে Q বিন্দুতে ছেদ করেছে।

প্রামাণ্যঃ

প্রমাণ করতে হবে যে, ∠P + ∠Q = 2∠BOC.

অঙ্কনঃ

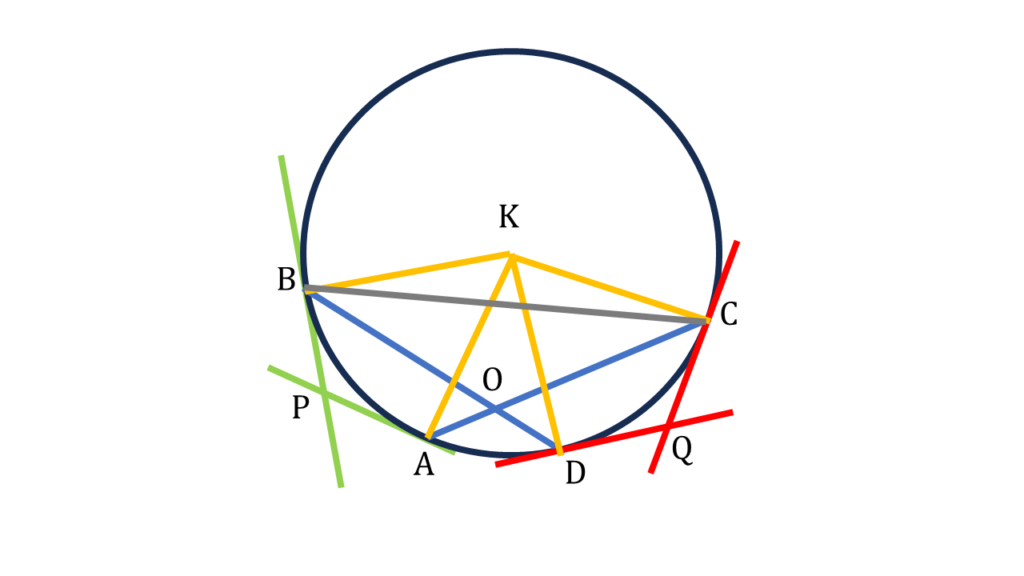
K, B; K, A; K, D; K, C এবং B, C যুক্ত করলাম।

প্রমাণঃ

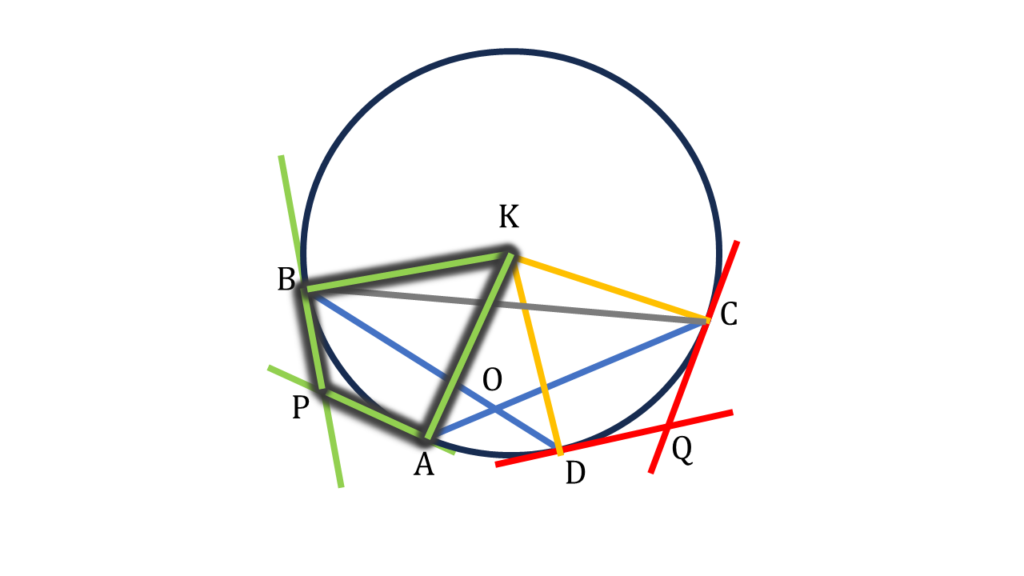
চতুর্ভুজ APBK এর ,
∠PBK = 90° [∵ KB বৃত্তের ব্যাসার্ধ এবং BP স্পর্শক ]
∠PAK = 90° [∵ KA বৃত্তের ব্যাসার্ধ এবং AP স্পর্শক ]
সুতরাং,
∠KBP + ∠BPA + ∠PAK + ∠AKB = 360° থেকে পাই,
∠P + ∠AKB = 360° – ∠KBP – ∠PAK
বা, ∠P + ∠AKB = 360° – 90° – 90°
বা, ∠AKB = 180° – ∠P ——(i)

আবার, K কেন্দ্রীয় বৃত্তের ∠AKB কেন্দ্রস্থ কোণ এবং ∠ACB বৃত্তস্থ কোণ

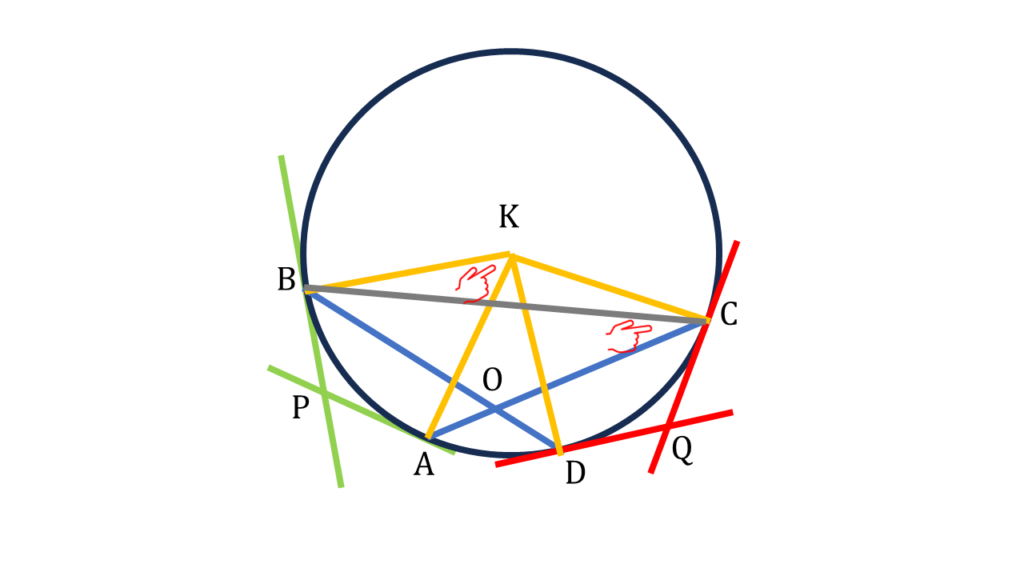
⇒ ∠AKB = 2∠ACB —-(ii)

(i) ও (ii) নং সমান করে পাই,

2∠ACB = 180° – ∠P —–(iii)

একইরকম ভাবে,

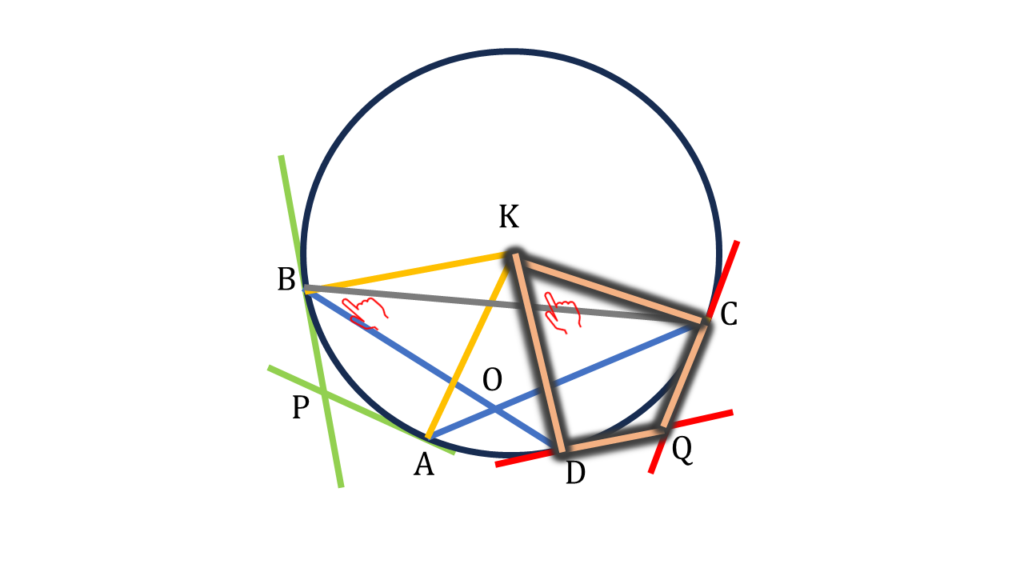
চতুর্ভুজ KDQC থেকে পাই –	∠DKC = 180° – ∠Q —–(iv)
এবং K কেন্দ্রীয় বৃত্তের ∠DKC কেন্দ্রস্থ কোণ এবং ∠DBC বৃত্তস্থ কোণ থেকে পাই –	∠DKC = 2∠DBC ——(v)
(iv) ও (v) সমান করে পাই-
2∠DBC = 180° – ∠Q —–(vi)

এখন

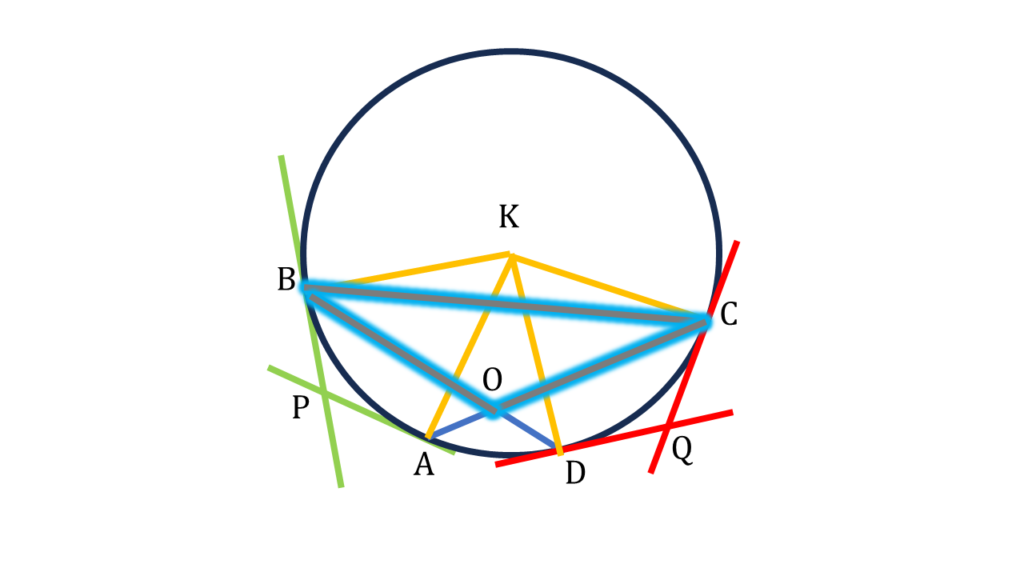
▲BOC থেকে পাই,
∠OBC + ∠OCB + ∠BOC = 180°
বা, ∠DBC + ∠ACB + ∠BOC = 180°
বা, ∠BOC = 180° – (∠DBC + ∠ACB)
বা, 2∠BOC = 360° – (2∠DBC + 2∠ACB)
বা, 2∠BOC = 360° – (180° – ∠Q + 180° – ∠P)
বা, 2∠BOC = 360° – 360° + ∠P + ∠Q
বা, ∠P + ∠Q = 2∠BOC

---

Request For Share
সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….

---

এই কষে দেখি 15.1 Class 10|Koshe Dekhi 15.1 Class 10 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।

---

এখানে তোমরা তোমাদের দশম শ্রেণীতে| Class 10 এ কি কি পড়ানো হয়, মানে তোমাদের দশম শ্রেণীতে| Class 10 সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

---