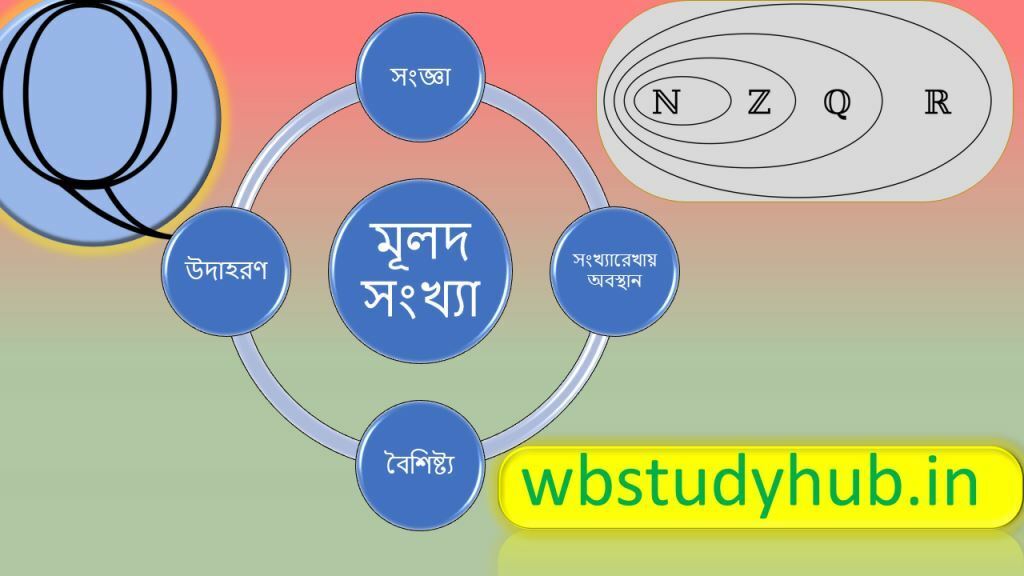
মূলদ সংখ্যা, যাকে ইংরাজিতে বলে Rational Number.
(Ratio)nal – ব্র্যাকেট এর মধ্যের অংশ টুকু দেখলে বোঝা যাচ্ছে যে Ratio/ভগ্নাংশ বিষয়ক কিছু হবে !
ঠিকই! ভগ্নাংশ /Ratio আকারে যে সমস্ত সংখ্যা আছে তাদের বলা হয় মূলদ সংখ্যা/Rational Number.
মূলদ সংখ্যা কাকে বলে ( সংজ্ঞা ) ? | What is Rational Number ( Definition)
সংজ্ঞাঃ–
যে সমস্ত বাস্তব সংখ্যাকে p/q আকারে প্রকাশ করা যায় এবং যেখানে ,
(i) p এবং q উভয়েই পূর্ণসংখ্যা
(ii) q ≠0
মূলদ সংখ্যা এর উদাহরণঃ | Example of Rational Number :
যেকোন পূর্ণসংখ্যা একটি মূলদ সংখ্যা। মূলদ সংখ্যা হচ্ছে সেই সংখ্যা যে সংখ্যাকে দুইটি পূর্ণ সংখ্যার অনুপাত হিসেবে (শূন্য দিয়ে ভাগ করা ছাড়া) প্রকাশ করা যায়। মূলদ সংখ্যাকে দশমিক আকারেও প্রকাশ করা যায় এবং তা হয় সসীম ঘর দশমিক (যেমন: ১.২৯, ৫.৬৯৮৭, ৮.৯৭৯৮৭) অথবা পৌনঃপুনিক (recurrent) দশমিক (যেমন: ১.৬৩৬৩৬৩৬৩৬৩, ৪.৬৯৬৯৬৯৬৯৬৯, .১০১১০১১০১১০১)।
সব পূর্ণসংখ্যাই মূলদ সংখ্যা (কারণ 


এছাড়াও সমস্ত ভগ্নাংশ গুলোও হচ্ছে মূলদ সংখ্যা।
অতএব মূলদ সংখ্যা বলতে আমরা দেখছি ,
| ধরণ | ব্যাখ্যা |
| পূর্ণসংখ্যা যেমন- -3,-2,-1,0,1,2,3 | n যদি একটি পূর্ণসংখ্যা হয় তবে n কে n/1 আকারে লেখা যাবে। যেমন- -3/1, -2/1 ,0/1, 1/1,2/1,3/1 |
| সসীম দশমিক সংখ্যা যেমন- .5 , 2.8 , 3.7 | .5= 1/2 2.8=14/5 3.7=37/10 |
| ভগ্নাংশ যেমন – 2/5 , 5/4 3/5 | প্রতিটি ভগ্নাংশ কেই p/q আকারে প্রকাশ করা যায় । |
Understand মূলদ সংখ্যা By Video-
> মূলদ সংখ্যা এর প্রয়োজনীয়তা | মূলদ সংখ্যার গুরুত্বঃ | Importance of Rational Numbers:
মূলদ সংখ্যা হলো স্বাভাবিক সংখ্যার একটি প্রকারভেদ। এই সংখ্যার গুরুত্ব অসীম। যেমন-
- সমীকরণ সমাধানের ক্ষেত্রে –
ধরি, আমি নিম্নলিখিত সমীকরণটি সমাধান করবো,
2x + 15 = 32
বা, 2x = 32 – 15
বা, 2x = 17
বা, x = 17/2
উপরোক্ত সমীকরণের যে বীজটি আমরা পেলাম সেটি হলো একটি মূলদ সংখ্যা।
- ভগ্নাংশের যোগ-বিয়োগ –
তাছাড়াও 1 থেকে অর্ধেক বাদ দিতে গেলেও 1/2 একটি মূলদ সংখ্যার প্রয়োজন।
1 – 1/2 = 1/2 , 3/4 – 1/4 = 1/2
>মূলদ সংখ্যার বৈশিষ্ট্য | মূলদ সংখ্যা চেনার উপায়ঃ | Properties Of Rational Numbers :
সংখ্যার পরিসরে মূলদ সংখ্যা একটি গুরুত্বপূর্ণ ভূমিকা পালন করে থাকে। মূলদ সংখ্যার বৈশিষ্ট্যগুলি হলোঃ
- প্রত্যেক পূর্ণসংখ্যা( Integer) যেমন- 1 , 2,3, 4, -1 , -6 , -7 ইত্যাদি একটি মূলদ সংখ্যা ।
- কারণ- 1 , 2,3, 4, -1 , -6 , -7 প্রত্যেক সংখ্যাকে দুটি পূর্ণসংখ্যার ভগ্নাংশ যথা p/q আকারে (1=1/1 , 2= 2/1 , 3=3/1 , -1= -1/1 , -6= -6/1 , -7=-7/1) প্রকাশ করা যায় ।
- প্রত্যেক স্বাভাবিক সংখ্যা একটি মূলদ সংখ্যা ।যেমন- 1 , 2 , 3 , 4 …..
- কারণ- 1 , 2,3, 4, প্রত্যেক সংখ্যাকে দুটি পূর্ণসংখ্যার ভগ্নাংশ যথা p/q আকারে( 1=1/1 , 2=2/1 , 3=3/1 , 4=4/1) প্রকাশ করা যায় ।
- সকল প্রকার ভগ্নাংশ একটি মূলদ সংখ্যা ।
- ” 0 ” (শূন্য) একটি মূলদ সংখ্যা।
- কারণ- ” 0 ” (শূন্য) কে দুটি পূর্ণসংখ্যার ভগ্নাংশ যথা p/q আকারে 0=0/1 , 0=0/2 , 0=0/6 , 0=0/4 প্রকাশ করা যায় ।
- সকল পৌণপৌনিক সংখ্যা মূলদ সংখ্যা।
- সসীম দশমিক ভগ্নাংশ সংখ্যা অর্থাৎ দশমিকের পরের অংক সংখ্যা যদি সসীম হয় তাহলে তা মূলদ সংখ্যা । যেমন – 5.3 , 8.227 ইত্যাদি ।
- যেকোন পূর্নবর্গ সংখ্যা মূলদ সংখ্যা। যেমনঃ √9=3=3/1 , √25=5=5/1, √100=10=10/1 ইত্যাদি ।
- দশমিকের পরের অংক গুলো যদি অভিন্ন আকারে অসীম হয় বা আবৃত হয়, তাহলে তা মূলদ সংখ্যা । অর্থাৎ যে কোন আবৃত দশমিক ভগ্নাংশ ই মূলদ সংখ্যা। যেমন- 33.333333 , 5.343434…. ইত্যাদি ।
>মূলদ সংখ্যার মধ্যে সম্পর্কঃ | Relation Between Rational Numbers:
যোগ | Addition
ধরি 5/7 ও 3/5 দুটি মূলদ সংখ্যা । এদের যোগফল হলো –
5/7 + 3/5 = (25+21)/35 = 46/35
বিয়োগ | Substract
ধরি 5/7 ও 3/5 দুটি মূলদ সংখ্যা । এদের বিয়োগফল হলো –
5/7 – 3/5 = (25 – 21)/35 = 4/35
গুণ | Multiplication
ধরি 5/7 ও 3/5 দুটি মূলদ সংখ্যা । এদের গুণফল হলো –
5/7 × 3/5 = 3/7
ভাগ | Division
ধরি 5/7 ও 3/5 দুটি মূলদ সংখ্যা . ( 5/7 ) ÷ ( 3/5) = 5/7 × 5/3 = 25/21
>সংখ্যারেখায় মূলদ সংখ্যার অবস্থানঃ | Position of Rational Number in Number Line :

মূলদ সংখ্যাকে জ্যামিতিক আকারে প্রকাশ করার উপায় হলো সংখ্যারেখা ( সংখ্যারেখা কি?) । সংখ্যারেখায় মূলদ সংখ্যাকে বসানোর আগে মূলদ সংখ্যা কে আমরা দুটি ভাগে ভাগ করে দেখবো।
(i) মূলদ সংখ্যা<1 এবং > -1
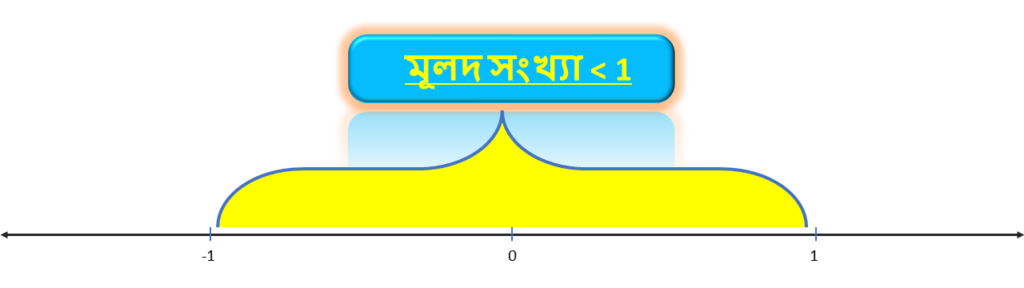
1 এর থেকে ছোটো মূলদ সংখ্যা বলতে সাধারণত যে সমস্ত ভগ্নাংশের লব হরের থেকে ছোটো তাদেরকে বোঝায় । যেমন- 1/2 , 2/3 , 4/5 , 6/7 , 11/16 ইত্যাদি ।
-1 এর থেকে বড়ো মূলদ সংখ্যা বলতে সাধারণত যে সমস্ত ভগ্নাংশের লব হরের থেকে ছোটো এবং সংখ্যারেখায় “0” থেকে বাম দিকে থাকে তাদেরকে বোঝায় । যেমন- -1/2 , -2/3 , -4/5 , -6/7 , -11/16 ইত্যাদি ।
সংখ্যারেখায় মুলদ সংখ্যা(<1) বসানোর সময় যে যে নিয়ম গুলো অনুসরণ করতে হবে তা হলো –
- প্রথমেই আমারা দেখছি যে এই ধরনের মূলদ সংখ্যা( যেমন- 1/2 , 2/3 , 4/5 , 6/7 , 11/16 ) যেহেতু 1 এর থেকে ছোটো, সুতরাং এই সংখ্যা সংখ্যারেখায় ” 0 ” থেকে ” 1 ” এর মধ্যে থাকবে।
- এরপর হরে যে সংখ্যা টা থাকবে ( 1/2 এর 2) ততোভাগে সংখ্যারেখায় ” 0 ” থেকে ” 1 ” এর মধ্যের দূরত্বকে সমানভাগে ভাগ করতে হবে । 1/2 এর ক্ষেত্রে ” 0 ” থেকে ” 1 ” এর মধ্যের দূরত্বকে সমান দুই ভাগে ভাগ করতে হবে ।
- এরপর লবে যে সংখ্যাটি থাকবে ( 1/2 এর 1) ” 0 ” থেকে ততো নাম্বার দাগটি হবে উল্লিখিত মূলদ সংখ্যা ।
এবার আমরা কিছু উদাহরণের মাধ্যমে বুঝবো ।
উদাহরণ 1: 3/5
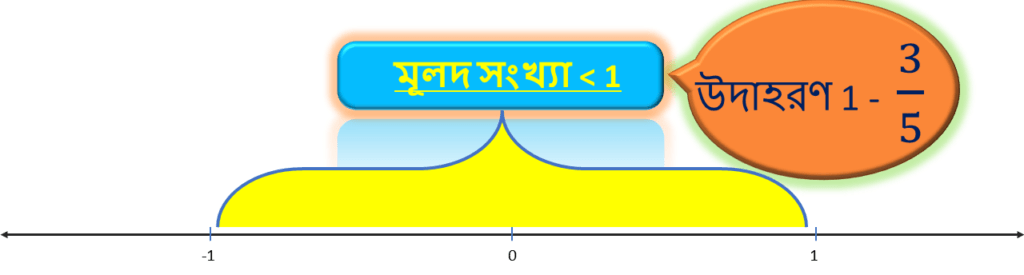
প্রথমেই আমরা দেখতে পাচ্ছি মূলদ সংখ্যাটি 1 এর থেকে ছোটো । সুতরাং , এই সংখ্যা সংখ্যারেখায় ” 0 ” থেকে ” 1 ” এর মধ্যে থাকবে
STEP – 1
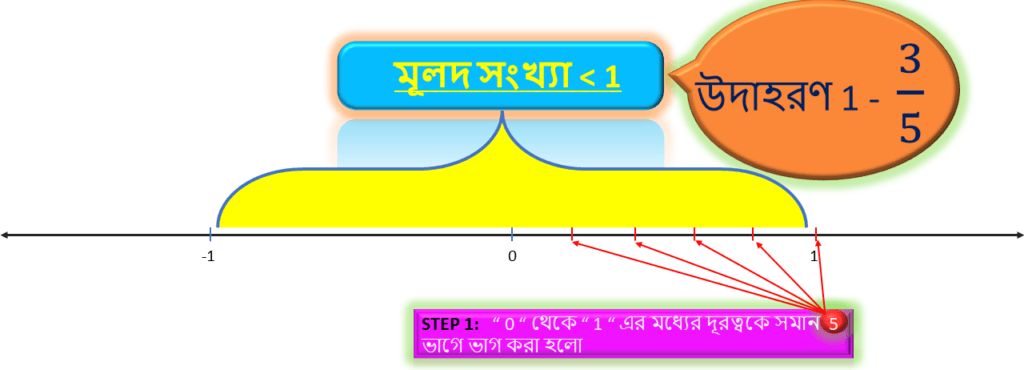
| সংখ্যা | লব | হর |
| 3/5 | 3 | 5 |
যেহেতু সংখ্যাটিতে হর = 5 , সেহেতু সংখ্যারেখায় ” 0 ” থেকে ” 1 ” এর মধ্যের দূরত্বকে সমান ” 5 ” ভাগে ভাগ করে উল্লিখিত ভাগ গুলি দাগ দ্বারা চিহ্নিত করতে হবে।
STEP – 2
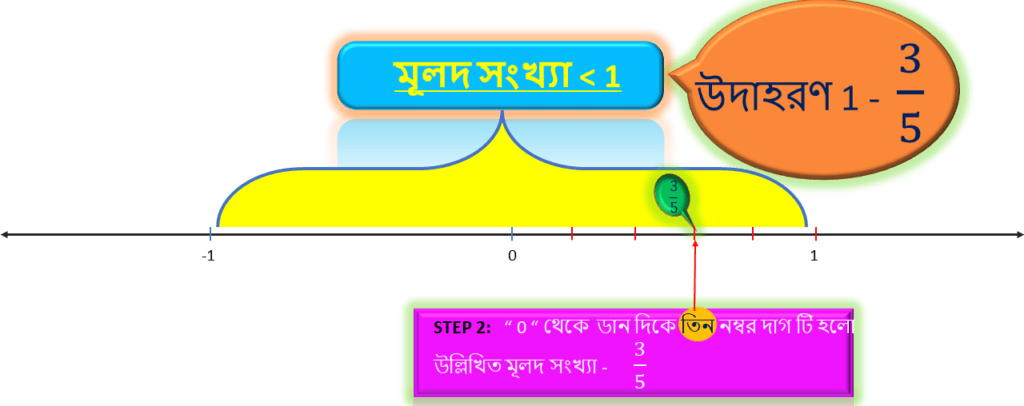
এরপর সংখ্যাটিতে দেখতে পাচ্ছি লব = 3 , অতএব এর আগে যে আমরা ” 0 ” থেকে ” 1 ” এর মধ্যের দূরত্বকে সমান ” 5 ” ভাগে ভাগ করেছি তার মধ্যে ” 0 ” থেকে ডান দিকে তিন নাম্বার দাগ টি হবে উল্লিখিত মূলদ সংখ্যা 3/5 .
উদাহরণ 2: -3/5
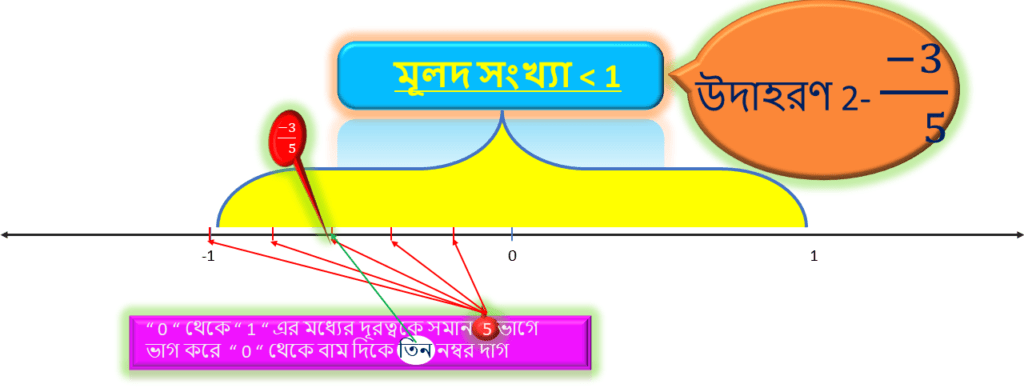
এই উদাহরণ টি আগের মতোই হবে। এর আগের উদাহরণে আমরা ” 0 ” থেকে ডান দিকে বসিয়েছি , এই উদাহরণে একই ভাবে করতে হবে শুধু এটা ” 0 ” থেকে বাম দিকে বসবে।
উদাহরণ 3: – 7/9
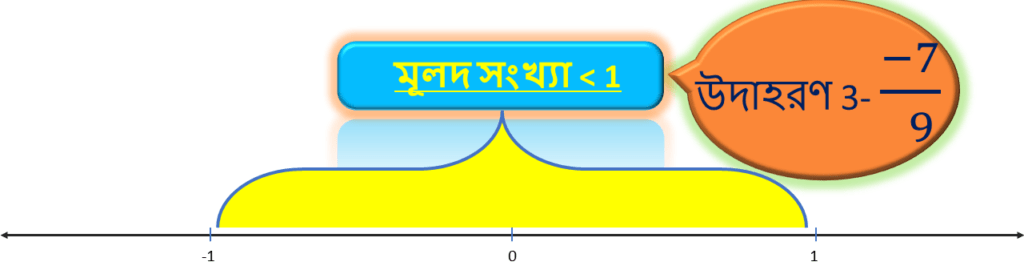
প্রথমেই আমরা দেখতে পাচ্ছি মূলদ সংখ্যাটি -1 এর থেকে বড়ো এবং ঋনাত্বক । সুতরাং , এই সংখ্যা সংখ্যারেখায় ” 0 ” থেকে ” – 1 ” এর মধ্যে থাকবে ।
STEP -1
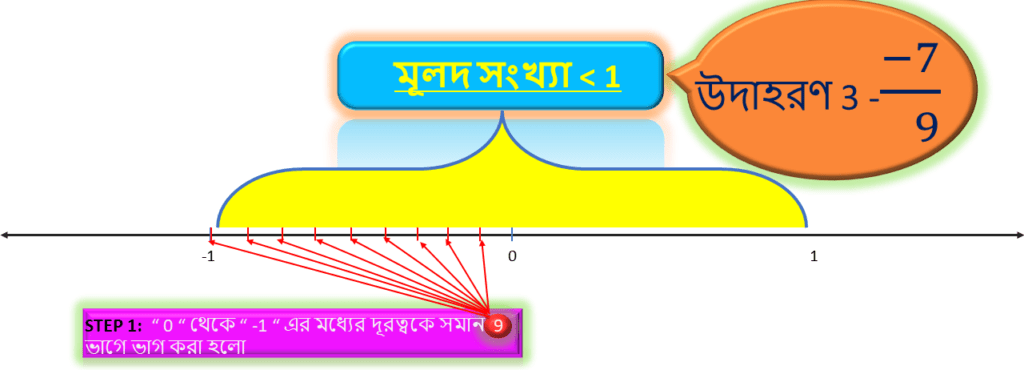
| সংখ্যা | লব | হর |
| – 7/9 | 7 | 9 |
যেহেতু সংখ্যাটিতে হর = 9 , সেহেতু সংখ্যারেখায় ” 0 ” থেকে ” -1 ” এর মধ্যের দূরত্বকে সমান ” 9 ” ভাগে ভাগ করে উল্লিখিত ভাগ গুলি দাগ দ্বারা চিহ্নিত করতে হবে।
STEP – 2
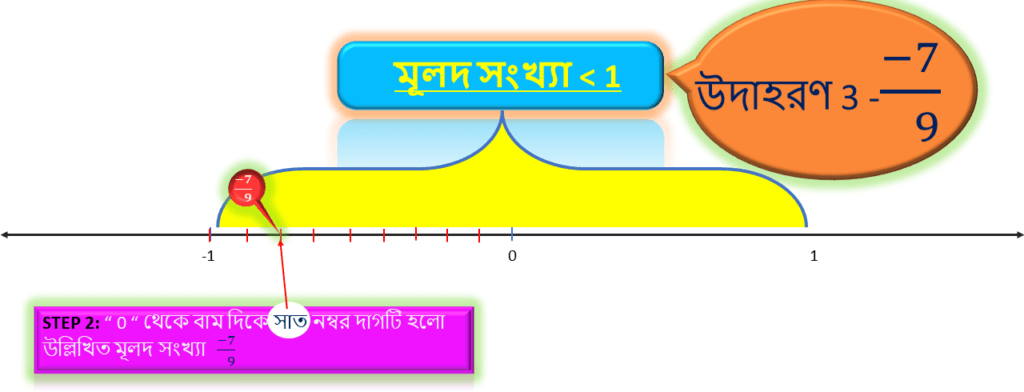
এরপর সংখ্যাটিতে দেখতে পাচ্ছি লব = 7 , অতএব এর আগে যে আমরা ” 0 ” থেকে ” -1 ” এর মধ্যের দূরত্বকে সমান ” 9 ” ভাগে ভাগ করেছি তার মধ্যে ” 0 ” থেকে বাম দিকে ছয় নাম্বার দাগ টি হবে উল্লিখিত মূলদ সংখ্যা -7/9 .
(ii) মূলদ সংখ্যা >1 এবং < -1 :
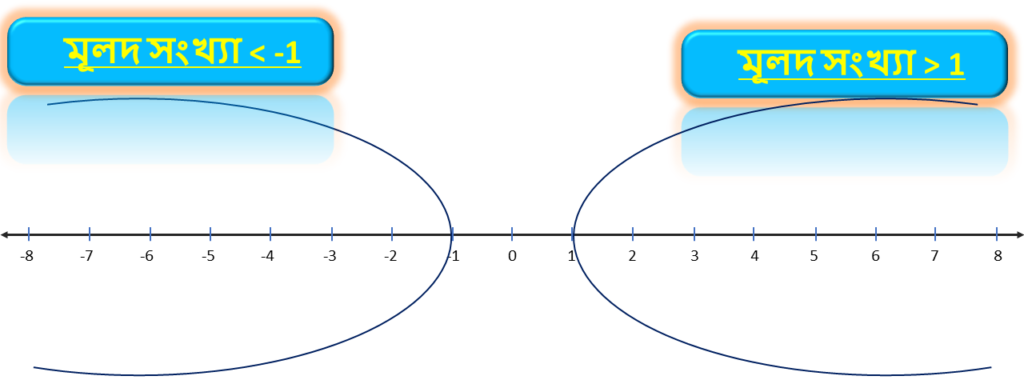
1 এর থেকে বড়ো মূলদ সংখ্যা বলতে সাধারণত যে সমস্ত ভগ্নাংশের লব হরের থেকে বড়ো তাদেরকে বোঝায় । যেমন- 3/2 , 5/3 , 7/5 , 11/7 , 19/16 ইত্যাদি ।
-1 এর থেকে ছোটো মূলদ সংখ্যা বলতে সাধারণত যে সমস্ত ভগ্নাংশের লব হরের থেকে বড়ো এবং সংখ্যারেখায় “0” থেকে বাম দিকে থাকে তাদেরকে বোঝায় । যেমন- 3/2 , 5/3 , 7/5 , 11/7 , 19/16 ইত্যাদি ।
সংখ্যারেখায় মুলদ সংখ্যা(>1) বসানোর সময় যে যে নিয়ম গুলো অনুসরণ করতে হবে তা হলো –
- প্রথমেই আমারা দেখছি যে এই ধরনের মূলদ সংখ্যা( যেমন- 3/2 , 4/3 , 7/5 , 11/7 , 19/16 ) যেহেতু 1 এর থেকে বড়ো , সুতরাং এই সংখ্যা সংখ্যারেখায় ” 0 ” থেকে ” 1 ” এর বাইরে থাকবে।
- এরপর উক্ত মূলদ সংখ্যাকে ভেঙ্গে লিখতে হবে। যেমন – 3/2=1+1/2 , 4/3= 1 + 1/3 , 7/5= 1 + 2/7 , 8/3 = 2 + 2/3 ইত্যাদি ।
- এরপর আমরা লক্ষ্য করি, প্রত্যেক সংখ্যাকে আমরা দুটি সংখ্যার যোগফল হিসাবে লিখতে পেরেছি। । তারমধ্যে একটি হচ্ছে পূর্ণসংখ্যা এবং অপর সংখ্যাটি হলো একটি মূলদ সংখ্যা যা “1” এর থেকে ছোটো।
| ” 1″ এর থেকে বড়ো মূলদ সংখ্যা | পূর্ণ সংখ্যা | মূলদ সংখ্যা , যেটি ” 1 ” এর থেকে ছোটো | |
| 3/2 = | 1 | + | 1/2 |
| 5/2 = | 2 | + | 1/2 |
| 10/3 = | 3 | + | 1/3 |
| 24/7 = | 3 | + | 3/7 |
- সংখ্যাটিকে ভেঙ্গে যে পূর্ণসংখ্যা টি পেলাম, সংখ্যারেখায় ততোঘর এগিয়ে যেতে হবে। মানে যদি 1 থাকে তবে 1 ঘর এগিয়ে যাবো , যদি 2 থাকে তবে 2 ঘর এগিয়ে যাবো।
- এরপর ” 1 ” এর থেকে ছোটো যে মুলদ সংখ্যাটি থাকবে সেটার ক্ষেত্রে ,
- যে পূর্ণসংখ্যাটি পর্যন্ত আমরা এগিয়ে এলাম, সেটি এবং তারপরের পূর্ণসংখ্যার মধ্যের দূরত্ব কে বিবেচনা করতে হবে ।
- এরপর হরে যে সংখ্যা মানে ” 1 ” এর থেকে ছোটো মূলদ সংখ্যা টা থাকবে সেটির হর যতো থাকবে (যেমন- 1/2 এর 2) ততোভাগে সংখ্যারেখায় উপরোক্ত দূরত্বের মধ্যের দূরত্বকে সমানভাগে ভাগ করতে হবে এবং দাগ দিয়ে চিহ্নিত করতে হবে । 1/2 এর ক্ষেত্রে উপরোক্ত দূরত্ব এর মধ্যের দূরত্বকে সমান দুই ভাগে ভাগ করতে হবে ।
- এরপর লবে যে সংখ্যাটি থাকবে ( 1/2 এর 1) উপরে যে ভাগ করে দাগ দিয়ে চিহ্নিত করেছিলাম , ততো নাম্বার দাগটি হবে উল্লিখিত মূলদ সংখ্যা ।
এবার আমরা কিছু উদাহরণের মাধ্যমে বুঝবোঃ
উদাহরণ 1 – 8/7

প্রথমেই আমরা দেখতে পাচ্ছি মূলদ সংখ্যাটি 1 এর থেকে বড়ো । সুতরাং , এই সংখ্যা সংখ্যারেখায় ” 0 ” থেকে ” 1 ” এর বাইরে থাকবে।
| মূলদ সংখ্যা > 1 | পূর্ণ সংখ্যা | মূলদ সংখ্যা, যেটি 1 এর থেকে ছোটো | ||
| 8/7 | = | 1 | + | 1/7 |
STEP 1 :
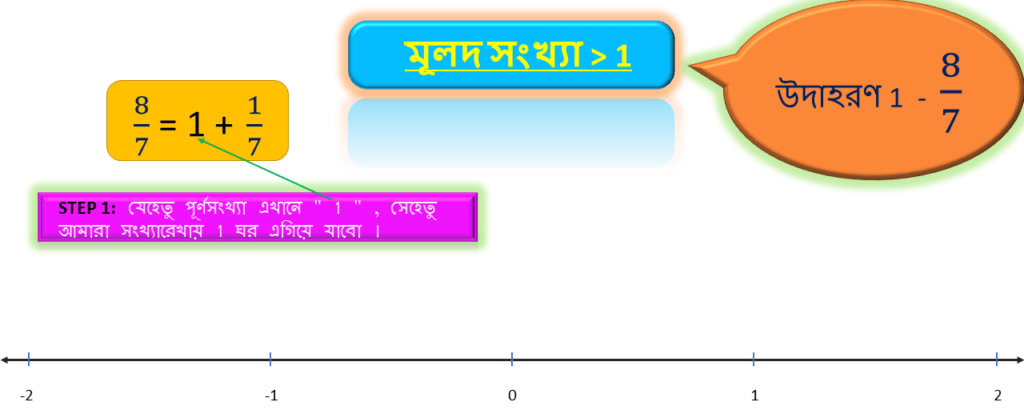
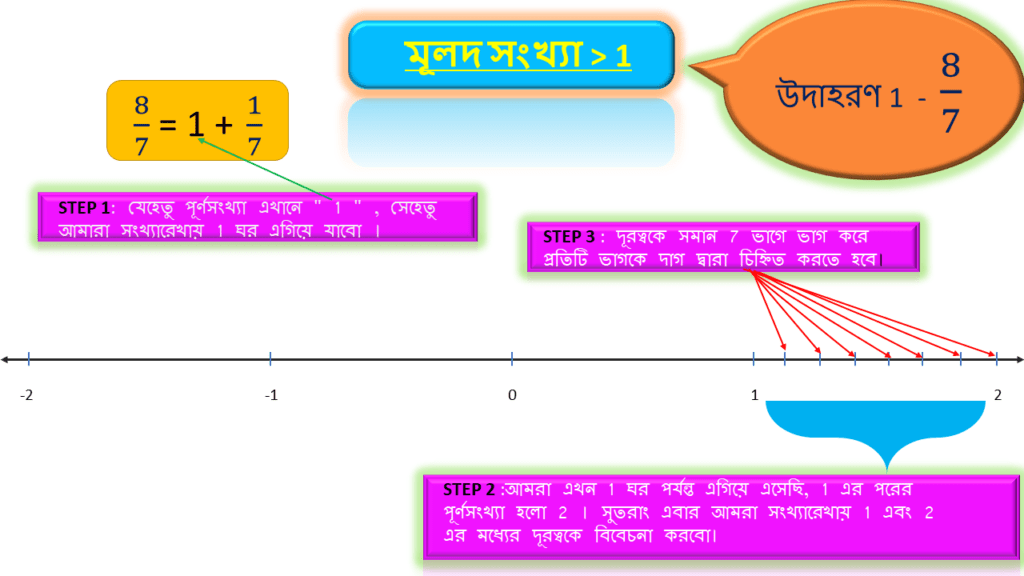
যেহেতু পূর্ণসংখ্যা এখানে ” 1 ” , সেহেতু আমারা সংখ্যারেখায় 1 ঘর এগিয়ে যাবো ।
STEP 2 :
আমরা এখন 1 ঘর পর্যন্ত এগিয়ে এসেছি, 1 এর পরের পূর্ণসংখ্যা হলো 2 । সুতরাং এবার আমরা সংখ্যারেখায় 1 এবং 2 এর মধ্যের দূরত্বকে বিবেচনা করবো।
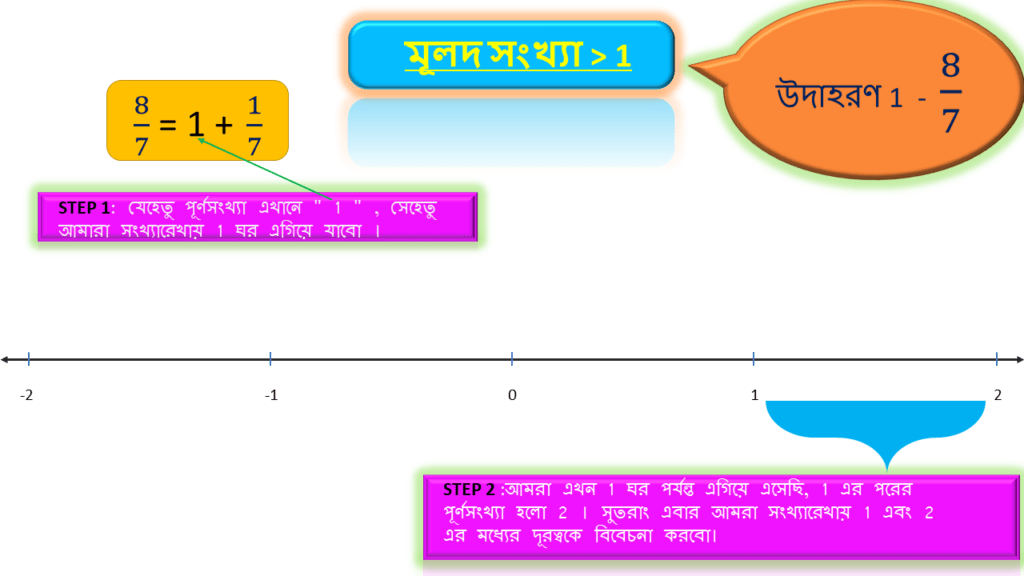
STEP 3 :
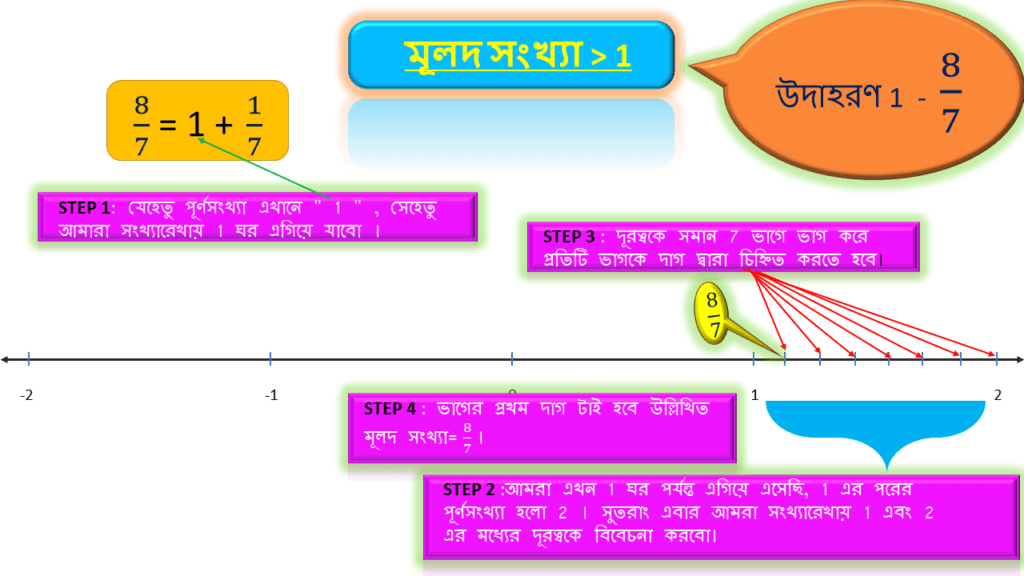
উল্লিখিত মূলদ সংখ্যাটি ভেঙ্গে আর একটি যে 1 এর থেকে ছোটো মূলদ সংখ্যা=1/7 পেয়েছি তার হর=7। অতএব উপরোক্ত দূরত্বকে সমান 7 ভাগে ভাগ করে প্রতিটি ভাগকে দাগ দ্বারা চিহ্নিত করতে হবে।
STEP 4 :
1 এর থেকে ছোটো মূলদ সংখ্যা=1/7 , তার লব=1 । অতএব উপরোক্ত ভাগের প্রথম দাগ টাই হবে উল্লিখিত মূলদ সংখ্যা=8/7 ।
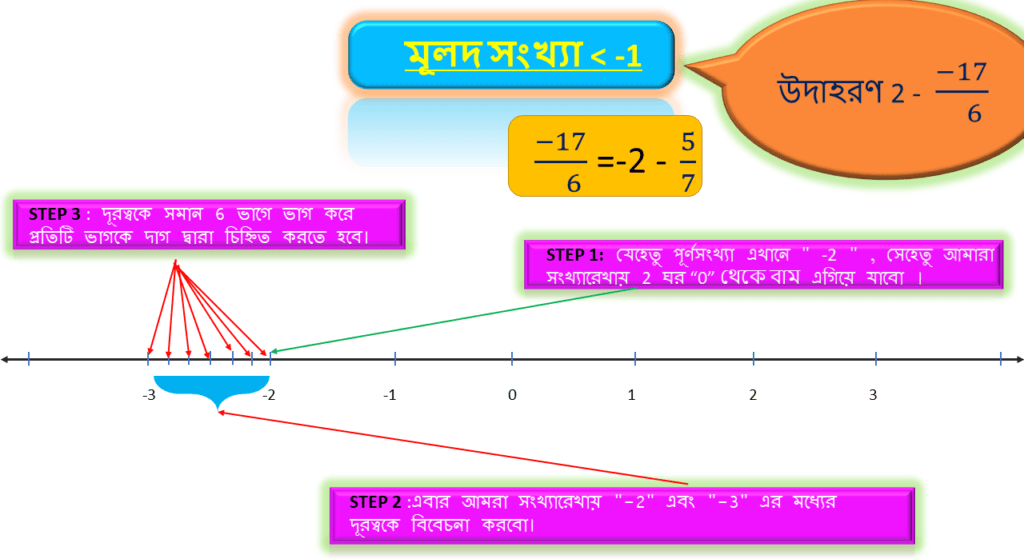
উদাহরণ 2 – -17/6
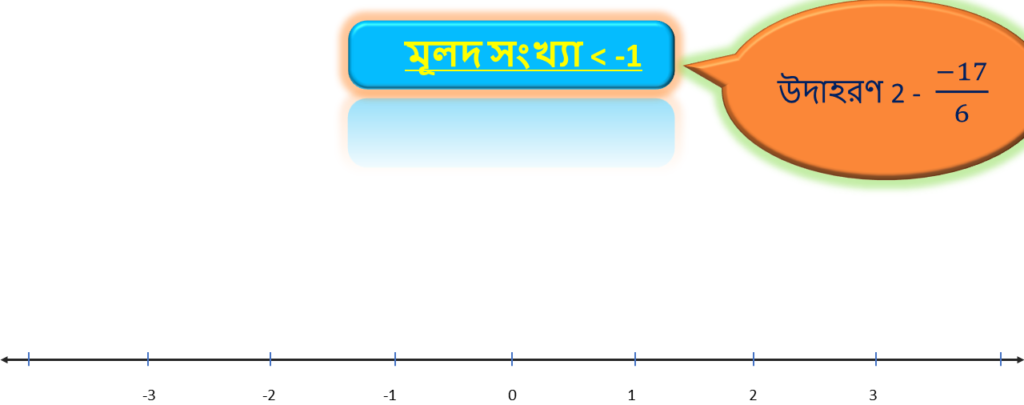
প্রথমেই আমরা দেখতে পাচ্ছি মূলদ সংখ্যাটি -1 এর থেকে ছোটো । সুতরাং , এই সংখ্যা সংখ্যারেখায় ” 0 ” থেকে ” -1 ” এর বাইরে থাকবে ( মানে ” 0 ” থেকে বাম দিকে ) ।
| মূলদ সংখ্যা > 1 | পূর্ণ সংখ্যা | মূলদ সংখ্যা, যেটি 1 এর থেকে ছোটো | ||
| -17/6 | = | -2 | + | -5/6 |
STEP 1 :
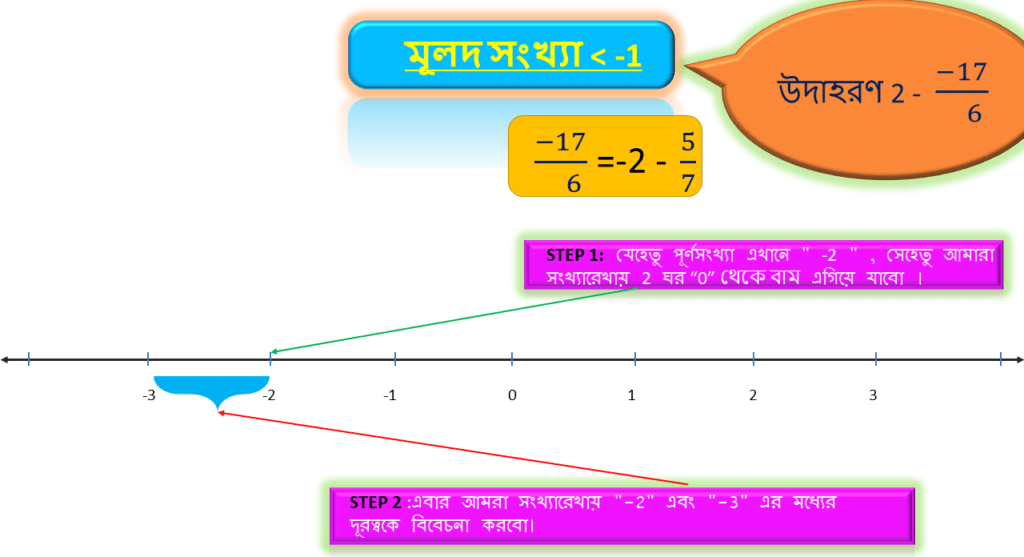
যেহেতু পূর্ণসংখ্যা এখানে ” -2 ” , সেহেতু আমারা সংখ্যারেখায় বাম দিকে -2 ঘর এগিয়ে যাবো ।

STEP 2 :
আমরা এখন বাম দিকে -2 ঘর পর্যন্ত এগিয়ে এসেছি, -2 এর পরের পূর্ণসংখ্যা হলো -3 । সুতরাং এবার আমরা সংখ্যারেখায় “-2” এবং “-3” এর মধ্যের দূরত্বকে বিবেচনা করবো।
STEP 3 :
উল্লিখিত মূলদ সংখ্যাটি ভেঙ্গে আর একটি যে 1 এর থেকে ছোটো মূলদ সংখ্যা=-5/6 পেয়েছি তার হর=6। অতএব উপরোক্ত দূরত্বকে সমান 6 ভাগে ভাগ করে প্রতিটি ভাগকে দাগ দ্বারা চিহ্নিত করতে হবে।
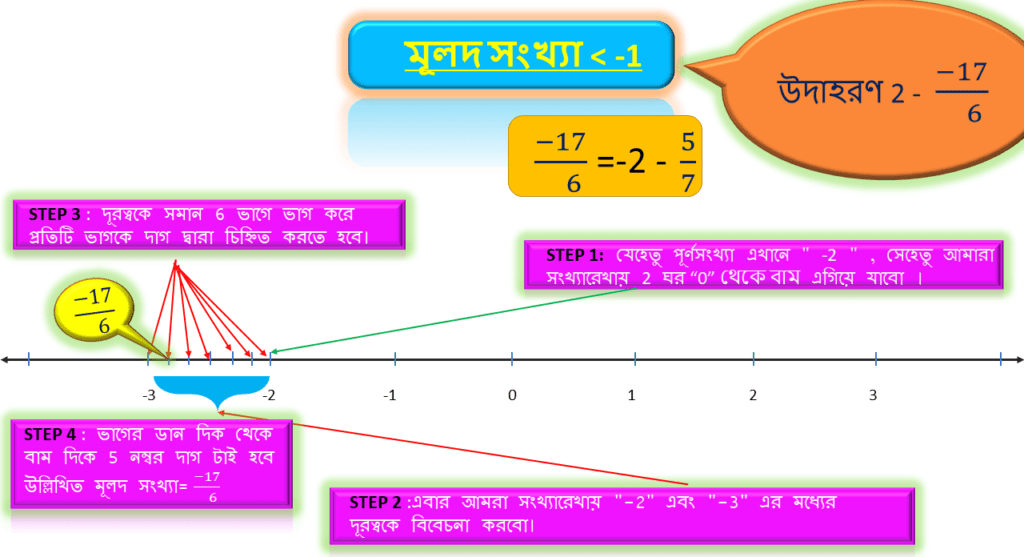
STEP 4 :
1 এর থেকে ছোটো মূলদ সংখ্যা=-5/6 , তার লব=5 । অতএব উপরোক্ত ভাগের ডান দিক থেকে বাম দিকে 5 নম্বর দাগ টাই হবে উল্লিখিত মূলদ সংখ্যা=-17/6 ।
>মূলদ সংখ্যা কোন কোন শ্রেণীতে পড়ানো হয়?
মূলদ সংখ্যার পরিসর প্রচুর । তবুও পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের অন্তর্গত অষ্টম শ্রেণীতে কিছু সাধারন বিষয়ে আলোকপাত করা হয়েছে । বাকি বড়ো পরিসরে এটি স্নাতকস্তরে ভালো করে পড়ানো হয় ।
| এই অধ্যায় টি ভালো করে বুঝতে হবে, কারণ মূলদ সংখ্যা সংখ্যারেখায় অবস্থান কিরকম তা আমরা এই অধ্যায় তে জানতে পারলাম । তোমরা যদি এই অধ্যায়ের সারাংশ না পড়ো তাহলে সংখ্যারেখায় মূলদ সংখ্যার অবস্থান আমরা বুঝতে পারবোনা । সুতরাং তোমাদের বলবো তোমরা আগে অধ্যায়ের সারাংশ দেখে নিয়ে তারপর কষে দেখি 3 শুরু করো । তোমাদের জন্যে অষ্টম শ্রেণীর সমস্ত অধ্যায় এর গণিত এবং অধ্যায়টি কিভাবে আয়ত্ত করতে হবে তা খুব সুন্দর করে লেখা হয়েছে যাতে তোমরা খুব সহজেই প্রতিটি অধ্যায় বুঝতে পারো এবং প্রতিটি অংক বুঝে করতে পারো । |
Frequently Asked Questions:
√4 কি মূলদ সংখ্যা?
উত্তর- √4=2 যা একটি মূলদ সংখ্যা।
৭ কি মূলদ সংখ্যা?
উত্তর- ৭ একটি মূলদ সংখ্যা।
মূলদ সংখ্যা কাকে বলে উদাহরণ দাও
উত্তর-
যে সমস্ত বাস্তব সংখ্যাকে p/q আকারে প্রকাশ করা যায় এবং যেখানে ,
(i) p এবং q উভয়েই পূর্ণসংখ্যা
(ii) q ≠0
মূলদ সংখ্যার উদাহরণ হলো 7/5 ।
3√7 সংখ্যাটি মূলদ নাকি অমূলদ?
উত্তর- 3√7 সংখ্যাটি একটি মূলদ সংখ্যা ।
মূলদ সংখ্যা কয়টি ?
উত্তর- মূলদ সংখ্যা হচ্ছে অসীম । কারণ যে কোনো দুটি মূলদ সংখ্যার মধ্যে অসংখ্য মূলদ এবং অমূলদ সংখ্যা আছে।
সকল মূলদ সংখ্যা কি পূর্ণসংখ্যা?
উত্তর-
না, সকল মূলদ সংখ্যা পূর্ণসংখ্যা নয়। যেমন – 3/5 একটি মূলদ স্নখ্যা,কিন্তু এটি একটি পূর্ণসংখ্যা নয়।
মূলদ সংখ্যা চেনার উপায়?
” 0 ” ( শূন্য) কি মূলদ সংখ্যা ?
উত্তর-
হ্যাঁ। ” 0 ” ( শূন্য) একটি মূলদ সংখ্যা ।
কারণ- ” 0 ” (শূন্য) কে দুটি পূর্ণসংখ্যার ভগ্নাংশ যথা p/q আকারে 0=0/1 , 0=0/2 , 0=0/6 , 0=0/4 প্রকাশ করা যায় ।
” 0 ” ( শূন্য) কে কেনো মূলদ সংখ্যা বলে?
উত্তর-
কারণ- ” 0 ” (শূন্য) কে দুটি পূর্ণসংখ্যার ভগ্নাংশ যথা p/q আকারে 0=0/1 , 0=0/2 , 0=0/6 , 0=0/4 প্রকাশ করা যায় ।
সব স্বাভাবিক সংখ্যা কি মূলদ সংখ্যা?
উত্তর-
না। সব স্বাভাবিক সংখ্যা মূলদ সংখ্যা নয় ।
কারণ- √3 একটি স্বাভাবিক সংখ্যা কিন্তু √3 কে দুটি পূর্ণসংখ্যার ভগ্নাংশ যথা p/q আকারে প্রকাশ করা যায়না ।
√২৫ মূলদ সংখ্যা না অমূলদ সংখ্যা ?
উত্তর– √২৫=৫ একটি মূলদ সংখ্যা। কারণ ৫=৫/১ ।
2/5 এবং 3/7-এর মধ্যে মূলদ সংখ্যা কয়টি?
উত্তর- 2/5 এবং 3/7 এর মধ্যে অসংখ্য মূলদ সংখ্যা আছে।
0 কোন ধরনের সংখ্যা, মূলদ নাকি অমূলদ?
উত্তর- 0(শূন্য) একটি মূলদ সংখ্যা । কারণ- 0= 0/9 .
এখানে তোমরা তোমাদের অষ্টম শ্রেণীতে কি কি পড়ানো হয়, মানে তোমাদের অষ্টম শ্রেণীর সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।