এই কষে দেখি 15.2 পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদ | WBBSE এর অন্তর্গত Class 9 | নবম শ্রেণীর গণিত বই এর 15 নম্বর অধ্যায় ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল এর দ্বিতীয় অনুশীলনী।
কষে দেখি 15.2 | Koshe Dekhi 15.2
1. নীচের ছবিগুলির ক্ষেত্রের ক্ষেত্রফল হিসাব করে লিখি
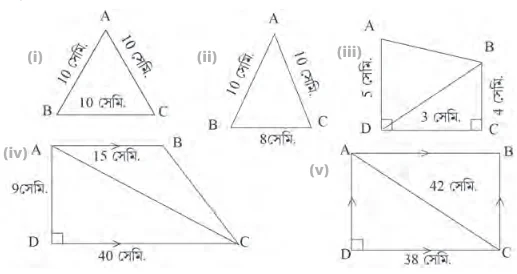
(i) এটি একটি সমবাহু ত্রিভুজ।
ক্ষেত্রফল
= \(\frac{\sqrt3}{4}\) ×10×10
= 25√3 বর্গ সেমি.
(ii) এটি একটি সমদ্বিবাহু ত্রিভুজ।
ক্ষেত্রফল
= ½ × 8 × \(\sqrt{10^2 – 4^2}\)
= 4 × \(\sqrt{100-16}\)
= 4 × \(\sqrt{84}\)
= 4 × 2\(\sqrt{21}\)
= 8\(\sqrt{21}\) বর্গ সেমি.
(iii) এটি একটি ট্রাপিজিয়াম।
ক্ষেত্রফল
= ½ × 3 × (4+5)
= \(\frac{27}{2}\)
= 13.5 বর্গ সেমি.
(iv) এটি একটি ট্রাপিজিয়াম।
ক্ষেত্রফল
= $\frac{1}{2}$ × 9 × (15+40)
= \(\frac{9 \times 55}{2}\)
= \(\frac{495}{2}\)
= 247.5 বর্গ সেমি.
(v) ABCD আয়তক্ষেত্রের,
AD2 +CD2 = AC2
বা, AD2 + (38)2 = (42)2
বা, AD2 = (42)2 –(38)2
বা, AD2 = (42+38) (42-38)
বা, AD2 = 80 ✕ 4
বা, AD2 = 320
বা, AD = 8√5
ক্ষেত্রফল
= 2×$\frac{1}{2}$ × 38 × 8 √5
= 304√5 বর্গ সেমি.
2. কোনো সমবাহু ত্রিভুজের পরিসীমা 48 সেমি. হলে, তার ক্ষেত্রফল হিসাব করে লিখি।
ধরি,
সমবাহু ত্রিভুজটির একটি বাহুর দৈর্ঘ্য =a সেমি.
| ∴ 3a = 48 |
| বা, a = 16 |
| ক্ষেত্রফল |
| = \(\frac{\sqrt3}{4}\)× (16)2 |
| = 64√3 বর্গ সেমি. |
3. ABC সমবাহু ত্রিভুজের উচ্চতা 5√3 সেমি. হলে, ত্রিভুজটির পরিসীমা ও ক্ষেত্রফল হিসাব করে লিখি।
সমাধানঃ-
ধরি,
সমবাহু ত্রিভুজটির একটি বাহুর দৈর্ঘ্য =a সেমি.
| ∴\(\frac{\sqrt3}{2}\)a = 5√3 |
| বা, a = 10 |
| পরিসীমা |
| = 3×10 |
| = 30 সেমি. |
| ক্ষেত্রফল |
| = \(\frac{\sqrt3}{4}\) × (10)2 |
| = 25√3 বর্গ সেমি. |
4. ▲ABC সমদ্বিবাহু ত্রিভুজের সমান বাহুদুটির প্রত্যেকটির দৈর্ঘ্য 10 সেমি. এবং ভূমির দৈর্ঘ্য 4 সেমি, হলে, ▲ABC-এর ক্ষেত্রফল হিসাব করে লিখি।
সমাধানঃ-
| = ½ × 4 × \(\sqrt{(10)^2 – 2^2}\) |
| = 2 × \(\sqrt{100 – 4}\) |
| = 2 \(\sqrt{96}\) |
| = 8√6 বর্গ সেমি. |
5. যদি কোনো সমদ্বিবাহু ত্রিভুজের ভূমির দৈর্ঘ্য 12 সেমি এবং সমান বাহুর প্রত্যেকটির দৈর্ঘ্য 10 সেমি হয়, তবে ওই সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল হিসাব করে লিখি।
সমাধানঃ-
| = ½ × 12 × \(\sqrt{10^2 – 6^2}\) |
| = 6 × \(\sqrt{100 – 36}\) |
| = 6\(\sqrt{64}\) |
| = 48 বর্গ সেমি. |
6. কোনো সমদ্বিবাহু ত্রিভুজের পরিসীমা 544 সেমি. এবং সমান বাহুর প্রত্যেকটির দৈর্ঘ্য ভূমির দৈর্ঘ্যের \(\frac{5}{6}\) অংশ: ত্রিভুজটির ক্ষেত্রফল হিসাব করে লিখি।
সমাধানঃ-
ধরি,
সমদ্বিবাহু ত্রিভুজটির ভূমির দৈর্ঘ্য = \(a\) সেমি.
সমান বাহুর প্রত্যেকটির দৈর্ঘ্য ভূমির দৈর্ঘ্যের \(\frac{5}{6}\) অংশ
অতএব,
সমান বাহুর প্রত্যেকটির দৈর্ঘ্য = \(\frac{5a}{6}\)
| ∴ \(\frac{5a}{6} + \frac{5a}{6} + a\) = 544 |
| বা, \(\frac{5a+5a+6a}{6}\) = 544 |
| বা, 16a = 544 × 6 |
| বা, a = \(\frac{544 \times 6}{16}\) |
| বা, a = 204 |
অতএব, সমদ্বিবাহু ত্রিভুজটির,
| ভূমির দৈর্ঘ্য | = 204 সেমি. |
| সমান বাহুর প্রত্যেকটির দৈর্ঘ্য | = \(\frac{5}{6}\)×204= 170 সেমি. |
| সমদ্বিবাহু ত্রিভুজটির ক্ষেত্রফল |
| = ½ × 204 × \(\sqrt{(170)^2 – (102)^2}\) |
| = 102 × \(\sqrt{28900 – 10404}\) |
| = 102\(\sqrt{18496}\) |
| = 102×136 |
| = 13872 বর্গ সেমি. |
7. একটি সমকোণী সমদ্বিবাহু ত্রিভুজের অতিভুজের দৈর্ঘ্য 12√2 সেমি. হলে, ত্রিভুজটির ক্ষেত্রফল হিসাব করে লিখি।
সমাধানঃ-
ধরি, ▲ABC একটি সমকোণী সমদ্বিবাহু ত্রিভুজ যার অতিভুজের দৈর্ঘ্য 12√2 সেমি.
এবং ধরি, AB = BC = x সেমি.
| পিথাগোরাসের সূত্রানুসারে, |
| ∴ (12√2)2 = x2 + x2 |
| বা, 2x2 = 12×12×2 |
| বা, x2 = 12×12 |
| বা, x = 12 |
এখন
| ▲ABC ক্ষেত্রফল |
| = ½ × 12 × 12 |
| = 6 × 12 |
| = 72 বর্গ সেমি. |
8. পৃথা একটি সামান্তরিক এঁকেছে যার কর্ণদ্বয়ের দৈর্ঘ্য যথাক্রমে 6 সেমি. ও 8 সেমি. এবং কর্ণদ্বয়ের মধ্যবর্তী কোণগুলির প্রত্যেকটি 90°: সামান্তরিকের বাহুগুলির দৈর্ঘ্য লিখি ও সামান্তরিকটির বৈশিষ্ট্য লিখি।
সমাধানঃ-
ধরি, পৃথা ABCD একটি সামান্তরিক এঁকেছে যার কর্ণদ্বয় AC ও BD এর দৈর্ঘ্য যথাক্রমে 6 সেমি. ও 8 সেমি. এবং কর্ণদ্বয়ের মধ্যবর্তী কোণগুলির প্রত্যেকটি 90°
অর্থাৎ,
| ∠AOD = | 90° |
| ∠DOC = | 90° |
| ∠BOC = | 90° |
| ∠AOB = | 90° |
এবং
| AO = OC | = 3 সেমি. |
| BO = OD | = 4 সেমি. |
সমকোণী ▲AOD এর
| ∴ AD2 = AO2 + OD2 |
| বা, AD2 = 32 + 42 |
| বা, AD2 = 25 |
| বা, AD = 5 |
একই ভাবে সমকোণী ▲DOC থেকে পাই DC=5
সুতরাং ABCD সামান্তরিকটি একটি রম্বস যার প্রতিটি বাহুর দৈর্ঘ্য = 5 সেমি.
9. আমাদের পাড়ার ত্রিভুজাকৃতি একটি পার্কের বাহুগুলির দৈর্ঘ্যের অনুপাত 2:3:4; পার্কটির পরিসীমা 216 মিটার।
(i) হিসাব করে পার্কটির ক্ষেত্রফল লিখি।
(ii) পার্কটির বৃহত্তম বাহুর বিপরীত কৌণিক বিন্দু থেকে এই বাহুতে সোজাসুজি যেতে কত পথ হাঁটতে হবে হিসাব করে লিখি।
সমাধানঃ-
পার্কের বাহুগুলির দৈর্ঘ্যের অনুপাত 2:3:4
ধরি, বাহুগুলির দৈর্ঘ্য 2x মিটার, 3x মিটার, 4x মিটার
| ∴ 2x + 3x + 4x = 216 |
| বা, 9x = 216 |
| বা, x = \(\frac{216}{9}\) |
| বা, x = 24 |
অতএব, বাহুগুলির দৈর্ঘ্য 48 মিটার, 72 মিটার, 96 মিটার
| অর্ধ পরিসীমা s |
| s = 216/2 = 108 |
| আমরা জানি, |
| ∴ ক্ষেত্রফল |
| = \(\sqrt{108(108 – 48)(108 – 72)(108 – 96)}\) |
| = \(\sqrt{108×60×36×12}\) |
| = 432\(\sqrt{15}\) |
∴ ত্রিভুজটির ক্ষেত্রফল=432\(\sqrt{15}\) বর্গ মিটার.
ধরি, পার্কটির বৃহত্তম বাহু যার দৈর্ঘ্য = 96 মিটার তার বিপরীত কৌণিক বিন্দু থেকে এই বাহুতে সোজাসুজি যেতে x মিটার পথ হাঁটতে হবে , যেটি ওই ত্রিভুজের উচ্চতা।
সুতরাং ,
| ½ × ভূমি × উচ্চতা = ত্রিভুজের ক্ষেত্রফল |
| বা, \(\frac{96x}{2}\) = 432\(\sqrt{15}\) |
| বা, x = 9\(\sqrt{15}\) |
∴ 9\(\sqrt{15}\) মিটার পথ হাটতে হবে।
10. পহলমপুর গ্রামের ত্রিভুজাকৃতি মাঠের তিনদিকের দৈর্ঘ্য যথাক্রমে 26 মিটার, 28 মিটার ও 30 মিটার।
(i) প্রতি বর্গমিটারে 5 টাকা হিসাবে ত্রিভুজাকৃতি মাঠে ঘাস লাগাতে মোট কত টাকা খরচ হবে হিসাব করে লিখি।
সমাধানঃ-
অতএব, বাহুগুলির দৈর্ঘ্য 26 মিটার, 28 মিটার, 30 মিটার
| অর্ধ পরিসীমা s |
| s = \(\frac{26+28+30}{2}\) = 42 |
| আমরা জানি, |
| ∴ ক্ষেত্রফল |
| = \(\sqrt{42(42 – 26)(42 – 28)(42 – 30)}\) |
| = \(\sqrt{42×16×14×12}\) |
| = 432\(\sqrt{15}\) |
| = 336 বর্গ মিটার. |
প্রতি বর্গমিটারে 5 টাকা হিসাবে 336 বর্গ মিটার. ত্রিভুজাকৃতি মাঠে ঘাস লাগাতে মোট খরচ হবে
= 336×5 = 1680 টাকা
(ii) ওই ত্রিভুজাকৃতি মাঠে প্রবেশের গেট তৈরির জন্য 5 মিটার জায়গা ছেড়ে বাকি চারধার বেড়া দিয়ে ঘিরতে প্রতি মিটার 18 টাকা হিসাবে মোট কত টাকা খরচ হবে হিসাব করে লিখি।
সমাধানঃ-
ত্রিভুজটির পরিসীমা = 84 মিটার।
ওই ত্রিভুজাকৃতি মাঠে প্রবেশের গেট তৈরির জন্য 5 মিটার জায়গা ছেড়ে বাকি চারধারে জায়গা থাকে (84 – 5) = 79 মিটার
অতএব, 79 মিটার চারধার বেড়া দিয়ে ঘিরতে প্রতি মিটার 18 টাকা হিসাবে মোট খরচ হবে
= 79×18 = 1422 টাকা
11. শাকিল একটি সমবাহু ত্রিভুজ PQR এঁকেছে। আমি ওই সমবাহু ত্রিভুজের অন্তস্থঃ কোনো বিন্দু থেকে ত্রিভুজের বাহুগুলির উপর তিনটি লম্ব অঙ্কন করেছি যাদের দৈর্ঘ্য যথাক্রমে 10 সেমি., 12 সেমি. ও ৪ সেমি.। হিসাব করে ▲PQR-এর ক্ষেত্রফল লিখি।
সমাধানঃ-
শাকিল একটি সমবাহু ত্রিভুজ PQR এঁকেছে
আমি ওই সমবাহু ত্রিভুজের অন্তস্থঃ বিন্দু O থেকে ত্রিভুজের বাহুগুলি QR, PR ও PQ এর উপর তিনটি লম্ব যথাক্রমে OA, OB ও OC
অঙ্কন করেছি যাদের দৈর্ঘ্য যথাক্রমে 10 সেমি., 12 সেমি. ও 8 সেমি.
আমরা জানি, সমবাহু ত্রিভুজের ক্ষেত্রফল
= \(\frac{\sqrt3}{4}\)×(PR)2
এখন ▲PQR এর ক্ষেত্রফল
| = ▲POR + ▲QOR + ▲POQ |
| = ½×PR×OB+½×QR×OA+½×PQ×OC |
| = ½×PR×OB+½×PR×OA+½×PR×OC |
| = ½×PR (OB + OA + OC) |
| = ½×PR (12 + 10 + 8) |
| = ½×PR × 30 = 15×PR |
অতএব,
| \(\frac{\sqrt3}{4}\)×(PR)2 = 15×PR |
| বা, PR = \(\frac{4 \times 15}{\sqrt3}\) = 20√3 |
▲PQR এর ক্ষেত্রফল
= 15×20√3 = 300√3 বর্গ সেমি.
12. একটি সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য 20 সেমি, এবং এই বাহুদ্বয়ের অন্তর্ভুক্ত কোণ 45° হলে, ত্রিভুজটির ক্ষেত্রফল হিসাব করে লিখি।
সমাধানঃ-
▲PQR একটি সমদ্বিবাহু ত্রিভুজ যার PQ=PR = 20 সেমি. এবং এই বাহুদ্বয়ের অন্তর্ভুক্ত কোণ অর্থাৎ ∠QPR=45°
Q বিন্দু থেকে PR বাহুর উপর লম্ব যা PR বাহুকে A বিন্দুতে ছেদ করেছে।
▲APQ এর
| ∠AQP + ∠QPA + ∠PAQ = 180° |
| বা, ∠AQP + 45° + 90° = 180° |
| বা, ∠AQP = 180° – 90° – 45° |
| বা, ∠AQP = 45° |
অতএব ▲APQ একটি সমকোণী সমদ্বিবাহু ত্রিভুজ যার AP=AQ=x(ধরি)
x2 + x2 = 202
বা, 2x2 = 400
বা, x = 10√2
▲PQR এর ক্ষেত্রফল
= ½×ভূমি×উচ্চতা
= ½×PR×AQ
= \(\frac{1}{2}\)×20×10√2
= 100√2 বর্গ সেমি.
13. একটি সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য 20 সেমি, এবং ওই বাহুদ্বয়ের অন্তর্ভুক্ত কোণ 30° হলে, ত্রিভুজটির ক্ষেত্রফল হিসাব করে লিখি।
▲ABC একটি সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য 20 সেমি, এবং ওই বাহুদ্বয়ের অন্তর্ভুক্ত কোণ 30°
B বিন্দু থেকে AC বাহুর উপর লম্ব অঙ্কন করলাম এবং D বিন্দু পর্যন্ত বর্ধিত করলাম এমনভাবে যাতে BE=ED হয়।
| ▲AEB ও ▲AED এর মধ্যে, |
| BE = ED[অঙ্কন] |
| ∠BEA = ∠AED = 90° |
| AE সাধারণ বাহু |
| ∴ ▲AEB ≅ ▲AED |
| ⇒ ∠BAE = ∠EAD[সর্বসম ত্রিভুজের অনুরূপ কোন ]———–(i) |
| এবং |
| ⇒ ∠ABE = ∠ADE[সর্বসম ত্রিভুজের অনুরূপ কোন ]———–(ii) |
| এবং |
| ⇒ AB=AD[সর্বসম ত্রিভুজের অনুরূপ বাহু ]————–(iii) |
এখন ▲AEB এর
| ∠BAE + ∠AEB + ∠ABE = 180° |
| বা, 30° + 90° + ∠ABE = 180° |
| বা, ∠ABE = 60° |
(ii) নং থেকে পাই ∠ABE = ∠ADE = 60°
সুতরাং ▲ABD একটি সমবাহু ত্রিভুজ যার
AB = BD = AD
∴ BE = ½BD=½AB = 10 সেমি.
এখন ▲ABC এর ক্ষেত্রফল
= ½ × AC × BE
= ½×20×10
= 100 বর্গ সেমি.
14. একটি সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমা (√2 + 1 ) সেমি. হলে, ত্রিভুজটির অতিভুজের দৈর্ঘ্য ও ক্ষেত্রফল হিসাব করে লিখি।
সমাধানঃ-▲ABC একটি সমকোণী সমদ্বিবাহু ত্রিভুজ যার AB=BC এবং ∠ABC = 90°
ধরি, AB = BC = x সেমি. এবং AC = y সেমি.
| ∴ y2 = x2 + x2 |
| বা, y2 = 2×2 |
| বা, y = x√2 |
আবার, পরিসীমা = (√2 + 1) সেমি.
| ∴ x + x + y = √2 + 1 |
| বা, 2x + x√2 = √2 + 1 [ y = x√2 বসিয়ে পেলাম ] |
| বা, x√2(√2 + 1) = √2 + 1 |
| বা, x√2 = 1 |
| বা, x = \(\frac{1}{\sqrt2}\) |
অতএব, y = x√2 = √2× \(\frac{1}{\sqrt2}\)1 = 1 সেমি.
= ½ × BC × AB
= ½ × \(\frac{1}{\sqrt2}\) × \(\frac{1}{\sqrt2}\)
= ¼ = 0.25 বর্গ সেমি.
15. মারিয়া ঘন্টায় 18 কিমি. বেগে সাইকেল চালিয়ে 10 মিনিটে একটি সমবাহু ত্রিভুজাকার মাঠের পরিসীমা বরাবর ঘুরে এল। ত্রিভুজটির একটি কৌণিক বিন্দু থেকে বিপরীত বাহুর মধ্যবিন্দু পর্যন্ত সোজা যেতে মারিয়ার কত সময় লাগবে হিসাব করে লিখি। (√3 = 1.732)
সমাধানঃ-
সমাধানঃ-
| মারিয়া 60 মিনিটে যায় 18 কিমি |
| মারিয়া 10 মিনিটে যায় = \(\frac{18 \times 10}{60}\) = 3 কিমি. |
অতএব, সমবাহু ত্রিভুজের পরিসীমা = 3 কিমি.
⇒ একটি বাহুর দৈর্ঘ্য = 1 কিমি. = 1000 মি.
সমবাহু ত্রিভুজের উচ্চতা
= \(\frac{\sqrt3}{2}\)×1000
= \(\frac{1.732 \times 1000}{2}\)
= \(\frac{1732}{2}\) মি.
| মারিয়া 18000 মিটার যায় 60 মিনিটে |
| মারিয়া \(\frac{1732}{2}\) মিটার যায়= \(\frac{60 \times 1732}{18000 \times 2}\)= 2.886≈ 2.89 মিনিটে |
16. একটি সমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য 1 মিটার বৃদ্ধি করলে ত্রিভুজটির ক্ষেত্রফল √3 বর্গমিটার বৃদ্ধি পায়। সমবাহু ত্রিভুজটির বাহুর দৈর্ঘ্য হিসাব করে লিখি।
সমাধানঃ-
ধরি, সমবাহু ত্রিভুজটির বাহুর দৈর্ঘ্য = a মিটার.
| বাহুর দৈর্ঘ্য(মিটার.) | ক্ষেত্রফল(বর্গ মিটার.) |
| a | \(\frac{\sqrt3}{4}\) × a2 |
| a + 1 | \(\frac{\sqrt3}{4}\) × (a+1)2 |
শর্তে,
| \(\frac{\sqrt3}{4}\) × (a+1)2 – \(\frac{\sqrt3}{4}\) × a2= √3 |
| বা, ¼ {(a+1)2 – a2} = 1 |
| বা, a2 + 2a + 1 – a2 = 4 |
| বা, 2a + 1 = 4 |
| বা, a = \(\frac{4-1}{2}\) = \(\frac{3}{2}\) = 1.5 |
∴সমবাহু ত্রিভুজটির বাহুর দৈর্ঘ্য=1.5 মিটার.
17. একটি সমবাহু ত্রিভুজ এবং বর্গক্ষেত্রের ক্ষেত্রফলের অনুপাত √3:2; বর্গক্ষেত্রটির কর্ণের দৈর্ঘ্য 60 সেমি. হলে, সমবাহু ত্রিভুজটির পরিসীমা হিসাব করে লিখি।
সমাধানঃ-
18. একটি সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য এবং পরিসীমা যথাক্রমে 13 সেমি. এবং 30 সেমি.। ত্রিভুজটির ক্ষেত্রফল হিসাব করে লিখি।
সমাধানঃ-
ধরি, অতিভুজ বাদে অপর দুই বাহুর দৈর্ঘ্য যথাক্রমে x সেমি. ও y সেমি.
অতএব,
| x + y + 13 = 30 |
| বা, x + y = 17 ——-(i) |
| x2 + y2 = 132 |
| বা, (x + y)2 – 2xy = 169 |
| বা, 2xy = 172 – 169 |
| বা, 2xy = 289 – 169 |
| বা, xy = \(\frac{120}{2}\) |
| বা, xy = 60 |
| বা, \(\frac{1}{2}\)xy = 30 |
| ∴ ত্রিভুজ টির ক্ষেত্রফল = 30 বর্গ সেমি. |
19. একটি সমকোণী ত্রিভুজের সমকোণ সংলগ্ন বাহু দুটির দৈর্ঘ্য যথাক্রমে 12 সেমি এবং 5 সেমি.। সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্বের দৈর্ঘ্য হিসাব করে লিখি (3 দশমিক স্থান পর্যন্ত আসন্নমান)
সমাধানঃ-
সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য
= \(\sqrt{12^2 + 5^2}\)
= \(\sqrt{144+25}\)
=\(\sqrt{169}\)
= 13 সেমি.
সমকোণী ত্রিভুজের ক্ষেত্রফল
= ½ × 12 × 5
= 30 বর্গ সেমি.
ধরি, সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্বের দৈর্ঘ্য = a সেমি.
এখন অতিভুজকে ভূমি হিসাবে ধরে সমকোণী ত্রিভুজের ক্ষেত্রফল
= ½ × 13 × a = \(\frac{13a}{2}\) বর্গ সেমি.
শর্তে,
| \(\frac{13a}{2}\) = 30 |
| বা, a = \(\frac{60}{13}\) |
| বা, a = 4.615 সেমি. |
20. 3 সেমি., 4সেমি. ও 5 সেমি. দৈর্ঘ্যের বাহুবিশিষ্ট একটি সমকোণী ত্রিভুজাকার ক্ষেত্র থেকে একটি সর্ববৃহৎ বর্গাকারক্ষেত্র এমনভাবে কেটে নেওয়া হলো যার একটি শীর্ষবিন্দু ত্রিভুজটির অতিভুজের উপর অবস্থিত। বর্গাকারক্ষেত্রটির বাহুর দৈর্ঘ্য হিসাব করে লিখি।
সমাধানঃ-
3 সেমি., 4সেমি. ও 5 সেমি. দৈর্ঘ্যের বাহুবিশিষ্ট ▲ABC একটি সমকোণী ত্রিভুজাকার ক্ষেত্র থেকে একটি সর্ববৃহৎ বর্গাকারক্ষেত্র BEDF কেটে নেওয়া হলো যার একটি শীর্ষবিন্দু D ত্রিভুজটির অতিভুজ AC এর উপর অবস্থিত।
ধরি, বর্গাকারক্ষেত্রটির বাহুর দৈর্ঘ্য = a সেমি.
| ▲ABC = ▲BDC + ▲ABD |
| বা, ½×BC×AB = ½×BC×DE + ½×AB×FD |
| বা, ½×4×3 = ½×4×a + ½×3×a |
| বা, 12 = 4a + 3a |
| বা, 7a = 12 |
| বা, a = \(\frac{12}{7}\) |
বহু বিকল্পীয় প্রশ্ন (M.C.Q.):
(i) একটি সমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য 4 সেমি. হলে, ত্রিভুজটির উচ্চতার পরিমাপ
উত্তরঃ- (d) 2√3 সেমি.
(ii) একটি সমকোণী সমদ্বিবাহু ত্রিভুজ যার সমান বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য a একক। ত্রিভুজটির পরিসীমা
উত্তরঃ- (b) (2+ √2) a একক
সমাধানঃ-
অতিভুজের দৈর্ঘ্য
= \(\sqrt{a^2 + a^2}\) = a√2 একক
পরিসীমা
= a + a + a√2
= 2a + a√2
= a(2 + √2) একক
(iii) একটি সমবাহু ত্রিভুজের ক্ষেত্রফল, পরিসীমা এবং উচ্চতা যথাক্রমে a, s এবং h হলে, \(\frac{2a}{sh}\) এর মান
উত্তরঃ- (c) \(\frac{1}{3}\)
সমাধানঃ-
ধরি, সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য = x একক
| a = | \(\frac{\sqrt3}{4}\)x2 |
| s = | 3x |
| h = | \(\frac{\sqrt3}{2}\)x |
(iv) একটি সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয়ের দৈর্ঘ্য 5 সেমি এবং ভূমির দৈর্ঘ্য 6 সেমি.। ত্রিভুজটির ক্ষেত্রফল
উত্তরঃ- (b) 12 বর্গ সেমি.
সমাধানঃ-
(v) ABC ত্রিভুজের AC বাহুর উপর D এমন একটি বিন্দু যে AD:DC=3:2; ABC ত্রিভুজের ক্ষেত্রফল 40 বর্গসেমি. হলে BDC ত্রিভুজের ক্ষেত্রফল
উত্তরঃ- (a) 16 বর্গ সেমি.
সমাধানঃ-
AD:DC = 3:2
বা, AD = \(\frac{3}{2}\)DC
| AC = AD + DC |
| বা, AC = \(\frac{3}{2}\)DC + DC |
| বা, AC = \(\frac{5}{2}\)DC |
| বা, DC = \(\frac{2}{5}\)AC ——–(i) |
AC বাহুকে ভূমি ধরলে ▲ABC ও ▲BDC এর উচ্চতা একই হবে। ধরি, ওই উচ্চতা = a সেমি.
এখন AC বাহুকে ভূমি ধরে ▲ABC এর ক্ষেত্রফল
= ½×AC×a বর্গ সেমি।
অতএব, ½×AC×a = 40
বা, AC×a = 80 ——(ii)
এখন ▲BDC এর ক্ষেত্রফল
= ½×DC×a
= ½×\(\frac{2}{5}\)AC ×a
= AC×\(\frac{a}{5}\)
= \(\frac{80}{5}\) [(ii) নং থেকে মান বসিয়ে পাই ]
= 16 বর্গ সেমি।
(vi) একটি ত্রিভুজের অর্ধপরিসীমা থেকে প্রতিটির বাহুর দৈর্ঘ্যের অন্তর যথাক্রমে 8 সেমি., 7 সেমি. ও 5 সেমি.। ত্রিভুজটির ক্ষেত্রফল
উত্তরঃ- (c) 20\(\sqrt{14}\) বর্গ সেমি.
সমাধানঃ-
| s – a = | 8 |
| s – b = | 7 |
| s – c = | 5 |
| s – a + s – b + s – c = 8 + 7 + 5 | |
| বা, 3s – (a + b + c) = 20 | |
| বা, s = 20 | |
ক্ষেত্রফল
= \(\sqrt{20×8×7×5} = 20\sqrt{14}\) বর্গ সেমি.
21. সংক্ষিপ্ত উত্তর ভিত্তিক প্রশ্ন:
(i) একটি সমবাহু ত্রিভুজের ক্ষেত্রফল ও উচ্চতার সাংখ্যমান সমান। ত্রিভুজের বাহুর দৈর্ঘ্য কত?
সমাধানঃ-
ধরি, সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য = a একক
| \(\frac{\sqrt3}{4}\)a2 = \(\frac{\sqrt3}{2}\)a |
| বা, a = 2 |
(ii) একটি ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য দ্বিগুণ করলে, ত্রিভুজটির ক্ষেত্রফল শতকরা কত বৃদ্ধি হয়?
সমাধানঃ-
একটি ত্রিভুজের বাহুর দৈর্ঘ্য যথাক্রমে a একক, b একক ও c একক
| প্রথম ক্ষেত্রে | দ্বিতীয় ক্ষেত্রে দৈর্ঘ্য দ্বিগুণ করার পর |
| s = \(\frac{a+b+c}{2}\) | s’ = \(\frac{2a+2b+2c}{2}\)= a + b+ c = 2s |
| s-a | s’-2a = 2s-2a = 2(s-a) |
| s-b | s’-2b = 2s-2b = 2(s-b) |
| s-c | s’-2c = 2s-2c = 2(s-c) |
যেখানে s = প্রথম ক্ষেত্রের অর্ধপরিসীমা এবং
s’ = দ্বিতীয় ক্ষেত্রের অর্ধপরিসীমা।
এখন,
| ক্ষেত্রফল | ||
| প্রথম ক্ষেত্রে | \(\sqrt{s(s-a)(s-b)(s-c)}\)=∆(ধরি) | |
| দ্বিতীয় ক্ষেত্রে | \(\sqrt{s'(s’-2a)(s’-2b)(s’-2c)}\)=\(\sqrt{2s×2(s-a)×2(s-b)×2(s-c)}\)= 4\(\sqrt{s(s-a)(s-b)(s-c)}\)= 4∆ | |
| ক্ষেত্রফলের বৃদ্ধি = 4∆ – ∆ = 3∆ | ||
| শতকরা বৃদ্ধি = \(\frac{3∆ \times 100}{∆}\) = 300 বর্গ একক | ||
(iii) একটি ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য তিনগুণ করলে, ত্রিভুজটির ক্ষেত্রফল শতকরা কত বৃদ্ধি হয়?
সমাধানঃ-
একটি ত্রিভুজের বাহুর দৈর্ঘ্য যথাক্রমে a একক, b একক ও c একক
| প্রথম ক্ষেত্রে | দ্বিতীয় ক্ষেত্রে দৈর্ঘ্য তিনগুন করার পর |
| s =\(\frac{a+b+c}{2}\) | s’ = \(\frac{3a+3b+3c}{2}\)= a + b+ c = 3s |
| s-a | s’-3a = 3s-3a = 3(s-a) |
| s-b | s’-3b = 3s-3b = 3(s-b) |
| s-c | s’-3c = 3s-3c = 3(s-c) |
যেখানে s = প্রথম ক্ষেত্রের অর্ধপরিসীমা এবং
s’ = দ্বিতীয় ক্ষেত্রের অর্ধপরিসীমা।
এখন,
| ক্ষেত্রফল | ||
| প্রথম ক্ষেত্রে | \(\sqrt{s(s-a)(s-b)(s-c)}\)=∆(ধরি) | |
| দ্বিতীয় ক্ষেত্রে | \(\sqrt{s'(s’-3a)(s’-3b)(s’-3c)}\)=\(\sqrt{3s×3(s-a)×3(s-b)×3(s-c)}\)= 9\(\sqrt{s(s-a)(s-b)(s-c)}\)= 9∆ | |
| ক্ষেত্রফলের বৃদ্ধি = 9∆ – ∆ = 8∆ | ||
| শতকরা বৃদ্ধি = \(\frac{8∆×100}{∆}\) = 800 বর্গ একক | ||
(iv) একটি সমকোণী ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য (x-2) সেমি. x সেমি. এবং (x+2) সেমি.। ত্রিভুজটির অতিভুজের দৈর্ঘ্য কত?
সমাধানঃ-
| x2 + (x – 2)2 = (x + 2)2 |
| বা, x2 + x2 – 4x + 4 = x2 + 4x + 4 |
| বা, x2 – 4x – 4x = 0 |
| বা, x2 – 8x = 0 |
| বা, x(x – 8) = 0 |
| বা, x = 0 নতুবা, x = 8 |
| এখানে x = 8 |
অতিভুজ = 8 + 2 = 10 সেমি.
(v) একটি সমবাহু ত্রিভুজের উচ্চতার উপর একটি বর্গক্ষেত্র অঙ্কন করা হলো। ত্রিভুজ ও বর্গক্ষেত্রের ক্ষেত্রফলের অনুপাত কত ?
সমাধানঃ-
ধরি, সমবাহু ত্রিভুজের বাহু = a একক
সমবাহু ত্রিভুজের উচ্চতা
= \(\frac{\sqrt3}{2}\)a = বর্গক্ষেত্রের বাহুর দৈর্ঘ্য