কষে দেখি 14 Class 8।বীজগাণিতিক সংখ্যামালার গ.সা.গু ও ল.সা.গু কষে দেখি 14| Koshe Dekhi 14 Class 8 WBBSE.

শ্রেণী-অষ্টম; অধ্যায়- বীজগাণিতিক সংখ্যামালার গ.সা.গু ও ল.সা.গু ; কষে দেখি 14

---

গনিতপ্রভা বীজগাণিতিক সংখ্যামালার গ.সা.গু ও ল.সা.গু কষে দেখি 14 এর সমাধান গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ

বীজগাণিতিক সংখ্যামালার গ.সা.গু ও ল.সা.গু হলো অষ্টম শ্রেণীর গণিত বই এর 14 নম্বর অধ্যায়। এই অধ্যায় টি বীজগাণিতিক সংখ্যামালার উৎপাদকে বিশ্লেষণের পরের অধ্যায়। তাই তোমরা যদি আগের অধ্যায়টি না করে থাকো তাহলে তোমাদের এই অধ্যায়টি বুঝতে একটু অসুবিধে হতে পারে। কারন বীজগাণিতিক সংখ্যামালার গ.সা.গু ও ল.সা.গু অধ্যায়ের কষে দেখি 14 এর অংক গুলি করতে গেলে বীজগাণিতিক সংখ্যামালাকে কিভাবে ভাঙতে হয় সেটা আগে তোমাদের জানতে হবে। কারন দুই বা ততোধিক সংখ্যা কে না ভাঙলে ওই সংখ্যা গুলির মধ্যে কোন কোন উৎপাদক সাধারণ উৎপাদক সেটা বুঝতে পারবেনা। তাই তোমাদের বলবো এর আগের অধ্যায় বীজগাণিতিক সংখ্যামালার উৎপাদকে বিশ্লেষণের অংক গুলি ভালো করে করবে।

আর যদি না করে থাকো তাহলে তোমরা Google এ গিয়ে Search করবে-

“কষে দেখি 13 Class 8 wbstudyhub.in”

এই কষে দেখি 14 এর অংক গুলি তোমরা যাতে ভালো ভাবে বুঝতে পারো তারজন্যে তোমাদের কিছু point মাথায় রাখতে হবে। তা হলো-

( i )

Point I
কষে দেখি 14 তে প্রায় সমস্ত অংক তে তোমাকে উৎপাদকে বিশ্লেষণের নিয়ম জানতে হবে। যদি উৎপাদকে বিশ্লেষণের নিয়ম না দেখে থাকো তাহলে এখান থেকে দেখে নিও। উৎপাদকে বিশ্লেষণ করার নিয়ম

( ii )

Point II
এই অংক গুলি করার সময় সংখ্যা মালা দেখে ঘাবড়ে গেলে চলবে না।সংখ্যামালা যাই থাক একটু শান্ত মাথায় চিন্তা করতে হবে।

( iii )

Point III
প্রতিটি সংখ্যামালাতে তার যতগুলি উৎপাদক আছে সবগুলি ভেঙ্গে বার করতে হবে। এটি প্রথম প্রথম একটু সময় লাগতে পারে কিন্তু Practice করলে একটি সংখ্যামালা দেখলে আপনা আপনিই মাথায় চলে আসবে যে এটা কি করে ভাঙতে হবে।

( iv )

Point IV
অংক করার সময় তাড়াহুড়ো করবে না এতে করে যোগ বিয়োগ চিহ্নের ভুল হওয়ার সম্ভাবনা বেড়ে যায়।

---

আগামিতে এই কষে দেখি 14 Class 8 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?

আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে?
কষে দেখি 14 Class 8 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 14 Class 8 তারপর 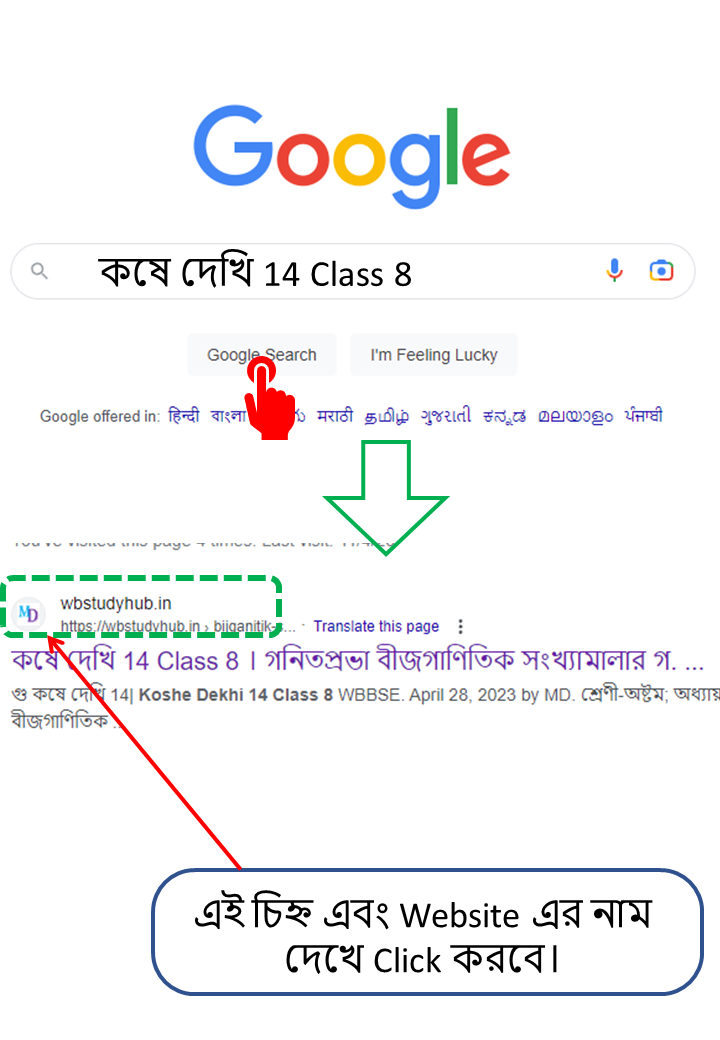এই চিহ্ন দেখে Click করলে আবার তোমরা এখানে এসে যাবে।

---

কষে দেখি 14 | Koshe Dekhi 14

1. নীচের বীজগাণিতিক সংখ্যামালাগুলির গ.সা.গু নির্ণয় করি-

( i ) 4a²b², 20ab²

সমাধানঃ-

প্রথম সংখ্যামালা,

4a²b²

= 2×2×a×a×b×b

দ্বিতীয় সংখ্যামালা,

20ab²

=2×2×5×a×b×b

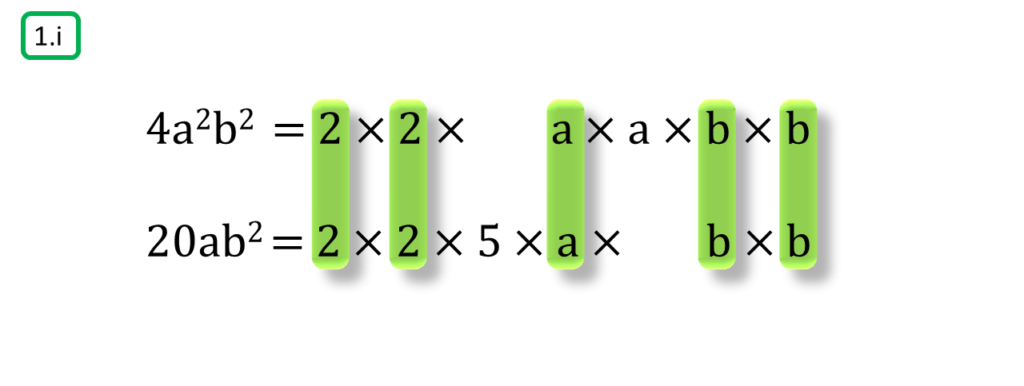
অতএব

নির্ণেয় গ.সা.গু =2×2×a×b×b =4ab2

---

( ii ) 5p²q², 10p²q², 25p⁴q³

সমাধানঃ-

প্রথম সংখ্যামালা,

5p²q²

=5×p×p×q×q

দ্বিতীয় সংখ্যামালা,

10p²q²

=2×5×p×p×q×q

তৃতীয় সংখ্যামালা,

25p⁴q³

=5×5×p×p×p×p×q×q×q

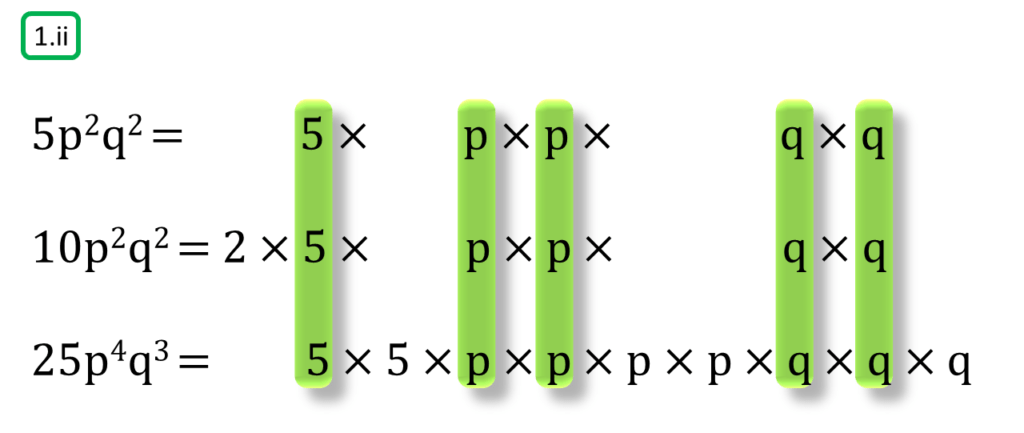
অতএব

নির্ণেয় গ.সা.গু =5×p×p×q×q =5p2q2

---

Request For Share
সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share]

---

( iii ) 7y³z⁶, 21y², 14z²

সমাধানঃ-

প্রথম সংখ্যামালা

7y³z⁶

=7×y×y×y×z×z×z×z×z

দ্বিতীয় সংখ্যামালা,

21y²

=3×7×y×y

তৃতীয় সংখ্যামালা,

14z²

=2×7×z×z

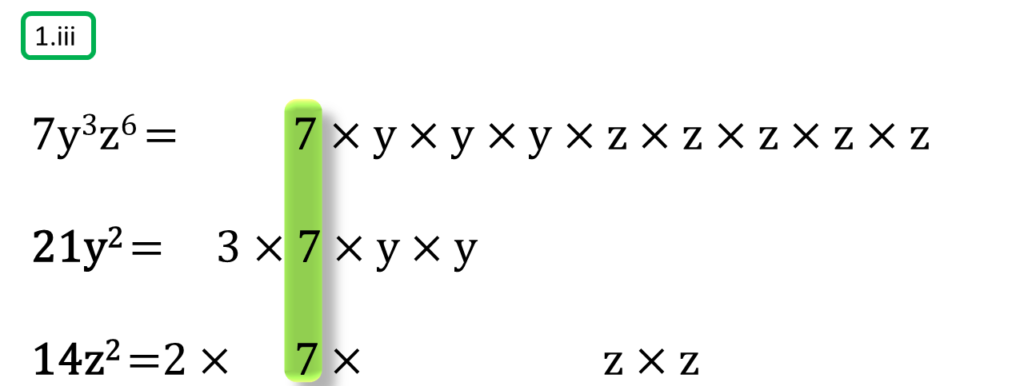
অতএব

নির্ণেয় গ.সা.গু =7

---

পড়াতে মন বসানোর Study Table

---

( iv ) 3a²b²c, 12a²b⁴c², 9a⁵b⁴

সমাধানঃ-

প্রথম সংখ্যামালা,

3a²b²c

=3×a×a×b×b×c

দ্বিতীয় সংখ্যামালা,

12a²b⁴c²

=2×2×3×a×a×b×b×b×b×c×c

তৃতীয় সংখ্যামালা,

9a⁵b⁴

=3×3×a×a×a×a×a×b×b×b×b

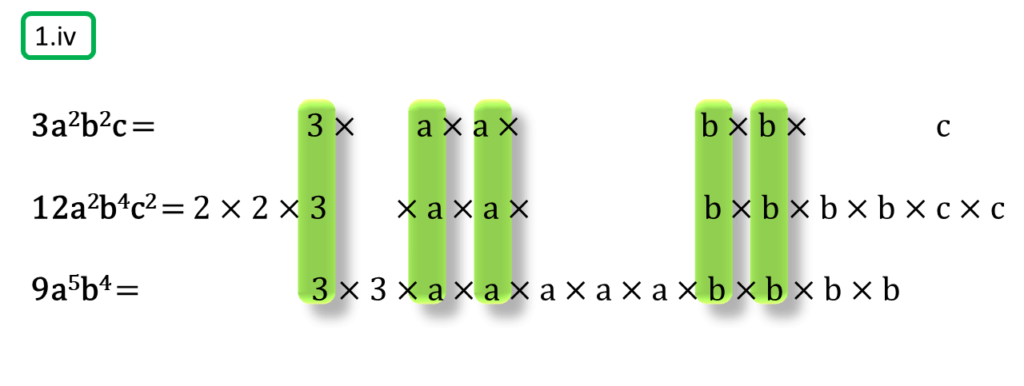
অতএব

নির্ণেয় গ.সা.গু =3×a×a×b×b =3a2b2

---

Request For Share
সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share]

---

2. নীচের বীজগাণিতিক সংখ্যামালাগুলির ল.সা.গু নির্ণয় করি-

( i ) 2x²y³, 10x³y

সমাধানঃ-

প্রথম সংখ্যামালা,

2x²y³

=2×x×x×y×y×y

দ্বিতীয় সংখ্যামালা,

10x³y

=2×5×x×x×x×y

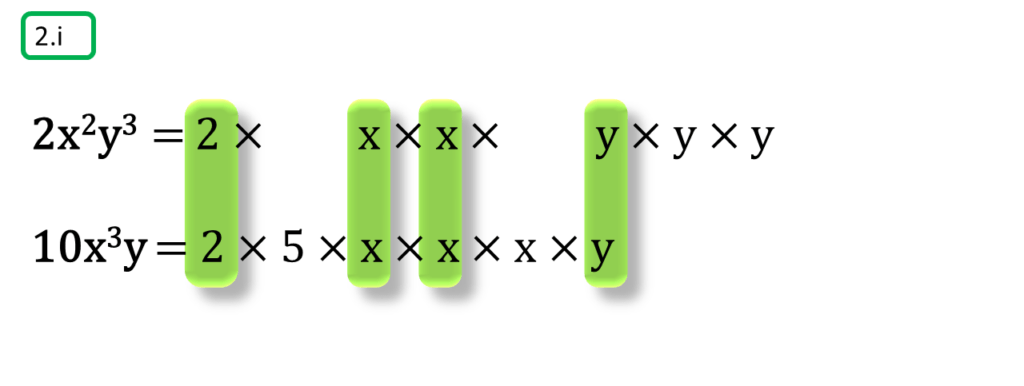
অতএব

নির্ণেয় ল.সা.গু =2×5×x×x×x×y×y×y =10x3y3

---

( ii ) 7p²q³, 35p³q, 42pq⁴

সমাধানঃ-

প্রথম সংখ্যামালা,

7p²q³

=7×p×p×q×q×q

দ্বিতীয় সংখ্যামালা,

35p³q

=5×7×p×p×p×q

তৃতীয় সংখ্যামালা,

42pq⁴

=2×3×7×p×q×q×q×q

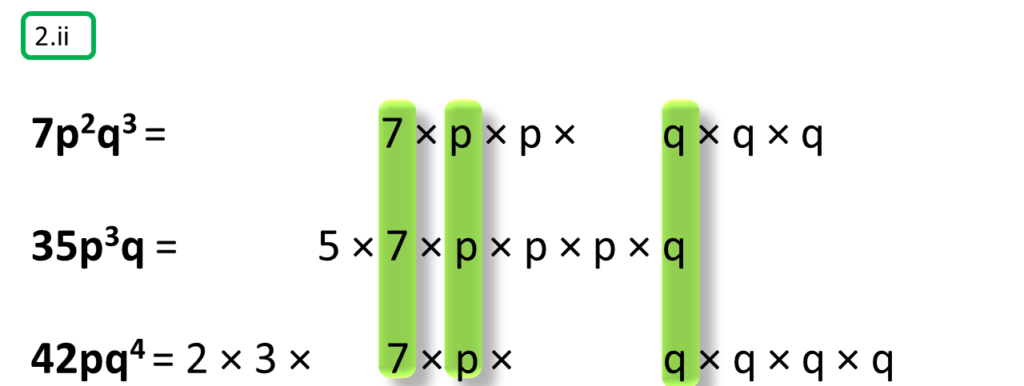
অতএব

নির্ণেয় ল.সা.গু =2×3×5×7×p×p×p×q×q×q×q =210p3q4

---

( iii ) 5a⁵b, 15ab²c, 25a²b²c²

সমাধানঃ-

প্রথম সংখ্যামালা,

5a⁵b

=5×a×a×a×a×a×b

দ্বিতীয় সংখ্যামালা,

15ab²c

=3×5×a×b×b×c

তৃতীয় সংখ্যামালা,

25a²b²c²

=5×5×a×a×b×b×c×c

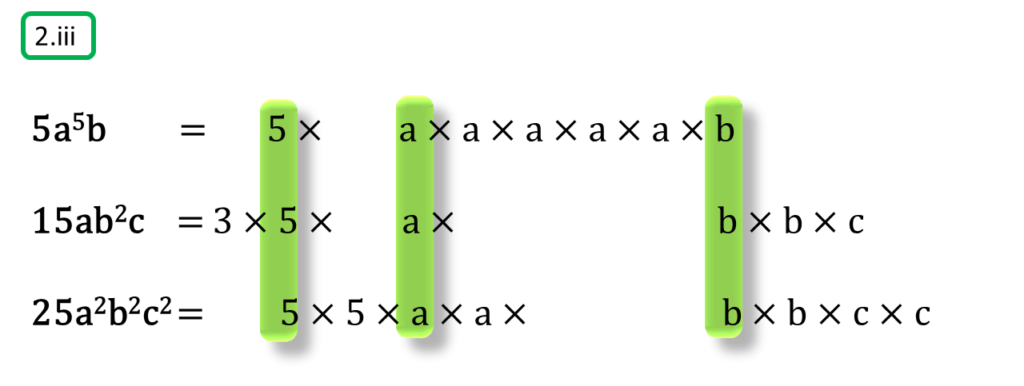
অতএব

নির্ণেয় ল.সা.গু =3×5×5×a×a×a×a×a×b×b×c×c =75a5b2c2

---

( iv ) 11a²bc², 33a²b²c, 55a²bc²

সমাধানঃ-

প্রথম সংখ্যামালা,

11a²bc²

=11×a×a×b×c×c

দ্বিতীয় সংখ্যামালা,

33a²b²c

=3×11×a×a×b×b×c

তৃতীয় সংখ্যামালা,

55a²bc²

=5×11×a×a×b×c×c

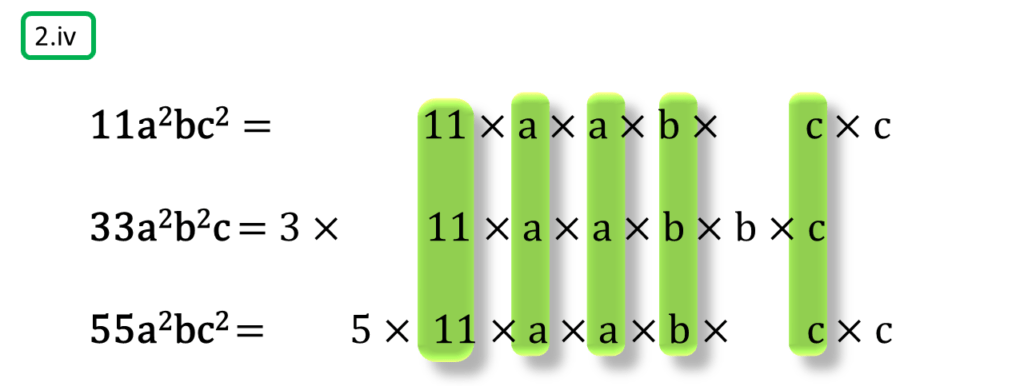
অতএব

নির্ণেয় ল.সা.গু =3×5×11×a×a×b×b×c×c =165a2b2c2

---

পড়াতে মন বসানোর Study Table

---

Request For Share
সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share]

---

3. নীচের বীজগাণিতিক সংখ্যামালাগুলির গ.সা.গু নির্ণয় করি-

( i ) 5x (x + y), x³ – xy²

সমাধানঃ-

প্রথম সংখ্যামালা,

5x (x + y)

=5×x (x + y)

দ্বিতীয় সংখ্যামালা,

x³ – xy²

=x (x² – y²)

=x (x + y) (x – y)

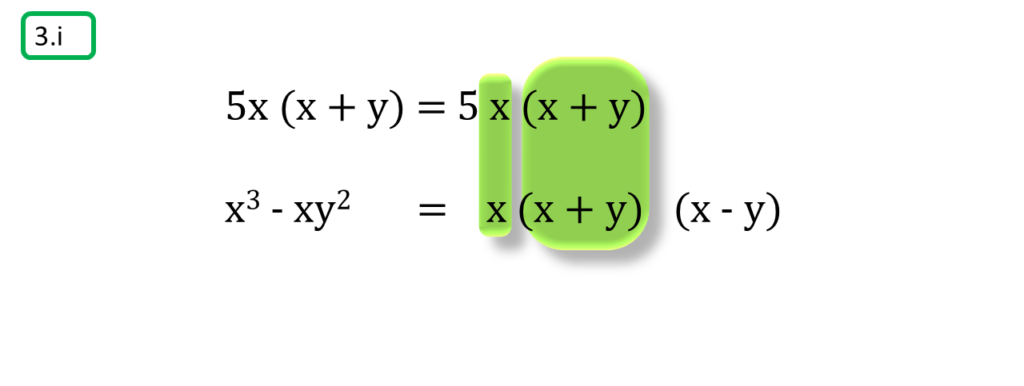
অতএব

নির্ণেয় গ.সা.গু =x (x + y)

---

( ii ) x³ – 3x²y, x² – 9y²

সমাধানঃ-

প্রথম সংখ্যামালা,

x³ – 3x²y

=x² (x – 3y)

দ্বিতীয় সংখ্যামালা,

x² – 9y²

={(x)² – (3y)²}

= (x + 3y) (x – 3y)

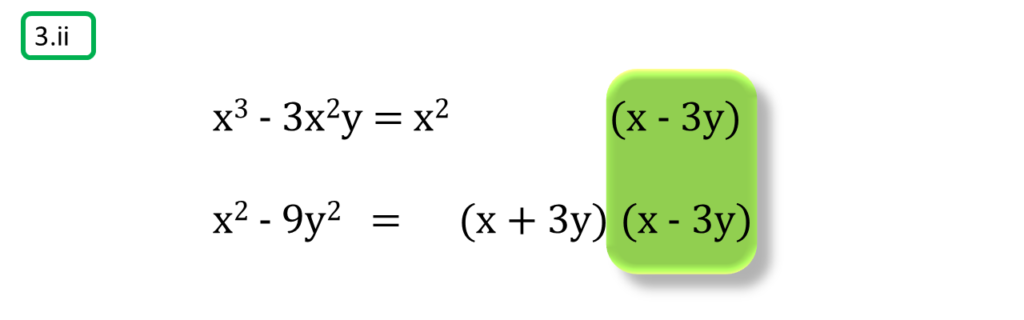
অতএব

নির্ণেয় গ.সা.গু = (x – 3y)

---

( iii ) 2ax(a – x)², 4a²x(a – x)³

সমাধানঃ-

প্রথম সংখ্যামালা,

2ax(a – x)²

= 2ax(a – x) (a – x)

দ্বিতীয় সংখ্যামালা,

4a²x(a – x)³

= 2a.2ax (a – x) (a – x) (a – x)

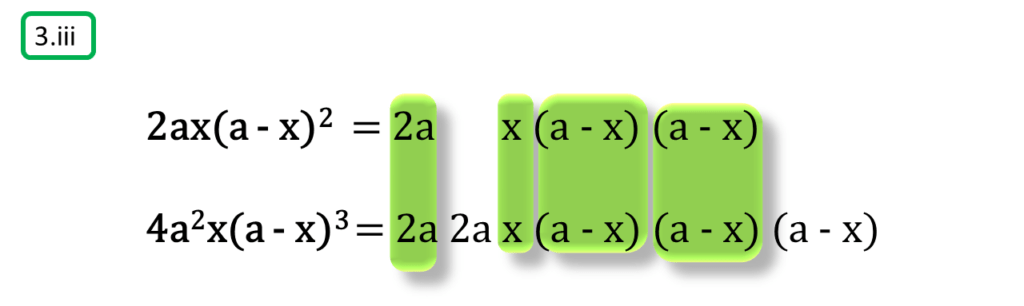
অতএব

নির্ণেয় গ.সা.গু = 2ax (a – x) (a – x) = 2ax (a – x)2

---

Request For Share
সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share]

---

পড়ার টেবিল সাজানোর সুন্দর কিছু Table Organizer

---

( iv ) x² – 1, x² – 2x + 1, x³ + x² – 2x

সমাধানঃ-

প্রথম সংখ্যামালা,

x² – 1

= {(x)² – 1²}

= (x + 1) (x – 1)

দ্বিতীয় সংখ্যামালা,

x² – 2x + 1

= (x – 1)²

= (x – 1) (x – 1)

তৃতীয় সংখ্যামালা,

x³ + x² – 2x

= x (x² + x – 2)

= x {x² +(2 – 1) x – 2}

= x (x² +2x – x – 2)

= x {x(x + 2) – 1(x + 2)}

=x (x – 1) (x + 2)

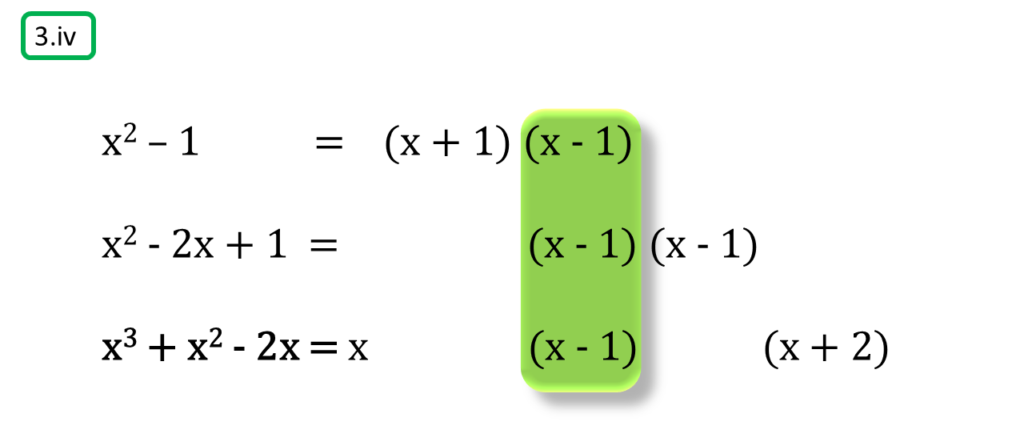
অতএব

নির্ণেয় গ.সা.গু = (x – 1)

---

Request For Share
সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share]

---

( v ) a² – 1, a³ – 1, a² + a – 2

সমাধানঃ-

প্রথম সংখ্যামালা,

a² – 1

= (a + 1) (a – 1)

দ্বিতীয় সংখ্যামালা,

a³ – 1

= (a – 1) (a² + a + 1)

তৃতীয় সংখ্যামালা,

a² + a – 2

= a² + (2 – 1)a – 2

= a² + 2a – a – 2

= a (a + 2) – 1(a + 2)

= (a – 1) (a + 2)

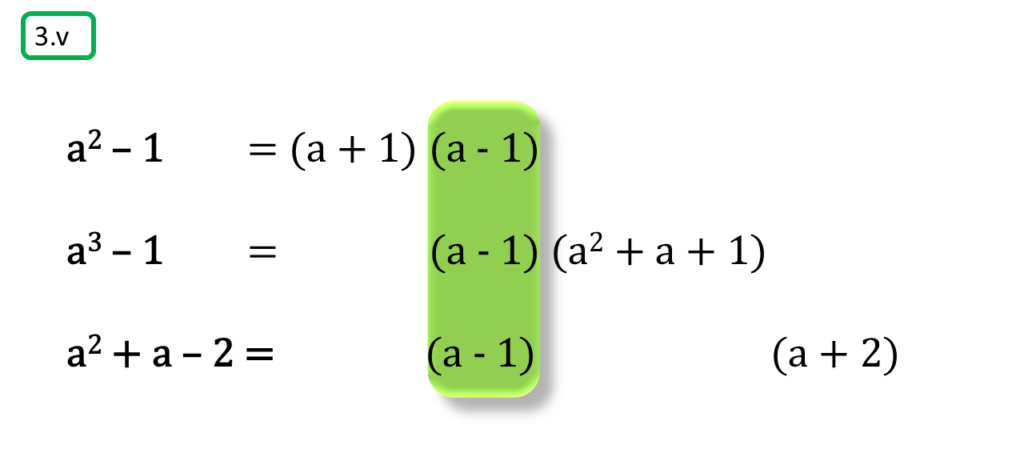
অতএব

নির্ণেয় গ.সা.গু = (a – 1)

---

( vi ) x² + 3x + 2, x² + 4x + 3, x² + 5x + 6

সমাধানঃ-

প্রথম সংখ্যামালা,

x² + 3x + 2

= x² + (2 + 1)x + 2

= x² + 2x + x + 2

= x(x + 2) + 1(x + 2)

= (x + 1) (x + 2)

দ্বিতীয় সংখ্যামালা,

x² + 4x + 3

= x² + (3 + 1)x + 3

= x² + 3x + x + 3

= x(x + 3) + 1(x + 3)

= (x + 1) (x + 3)

তৃতীয় সংখ্যামালা,

x² + 5x + 6

= x² + (3 + 2)x + 6

= x² + 3x + 2x + 6

= x (x + 3) + 2 (x + 3)

= (x + 2) (x + 3)

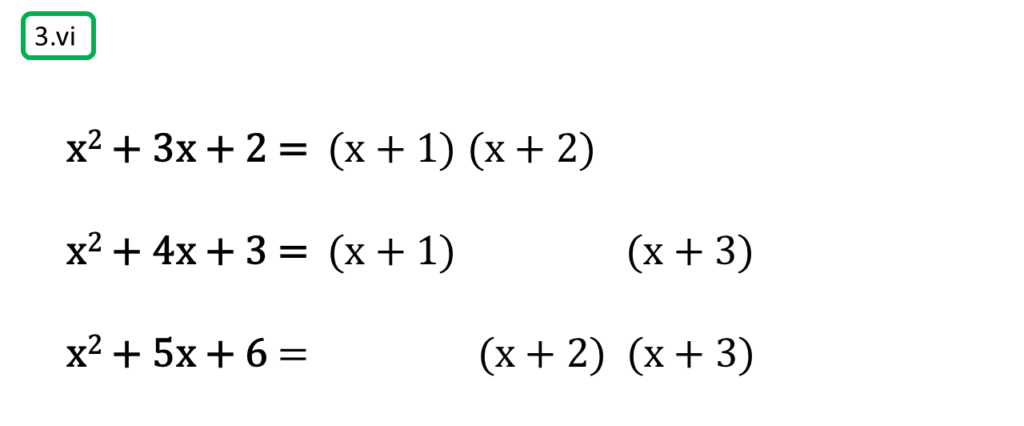
অতএব

নির্ণেয় গ.সা.গু = 1

---

পড়াতে মন বসানোর Study Table

---

Request For Share
সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share]

---

( vii ) x² + xy, xz + yz, x² + 2xy + y²

সমাধানঃ-

প্রথম সংখ্যামালা,

x² + xy

= x (x + y)

দ্বিতীয় সংখ্যামালা,

xz + yz

= z (x + y)

তৃতীয় সংখ্যামালা,

x² + 2xy + y²

= (x + y)²

= (x + y) (x + y)

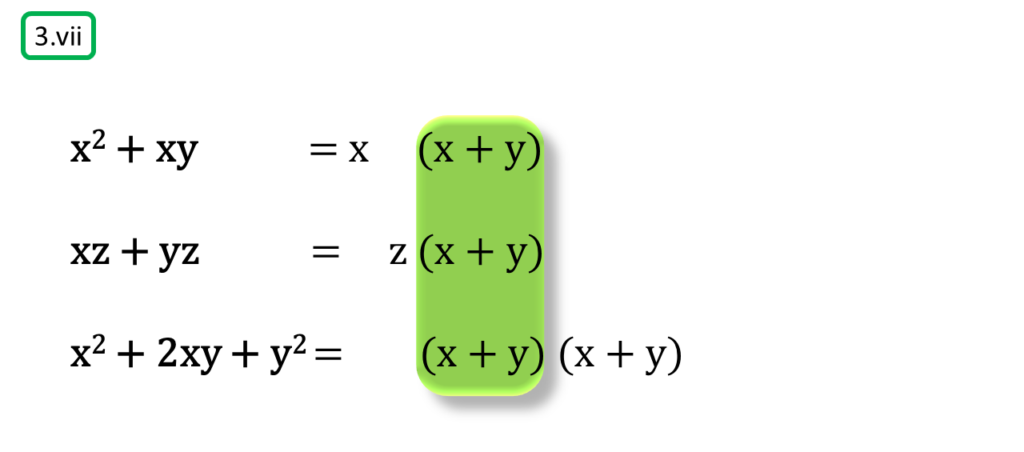
অতএব

নির্ণেয় গ.সা.গু = (x + y)

---

( viii ) 8(x² – 4), 12(x³+ 8), 36(x² – 3x – 10)

সমাধানঃ-

প্রথম সংখ্যামালা,

8(x² – 4)

= 2×4(x² – 2²)

= 2×4 (x + 2) (x – 2)

দ্বিতীয় সংখ্যামালা,

12(x³+ 8)

= 3×4 (x³ + 2³)

= 3×4 (x + 2) (x² – 2x + 4)

তৃতীয় সংখ্যামালা,

36(x² – 3x – 10)

= 9×4{x² – (5 – 2) x – 10}

= 9×4 (x² – 5x + 2x – 10)

= 9×4{x (x – 5) + 2(x – 5)}

= 9×4 (x + 2) (x – 5)

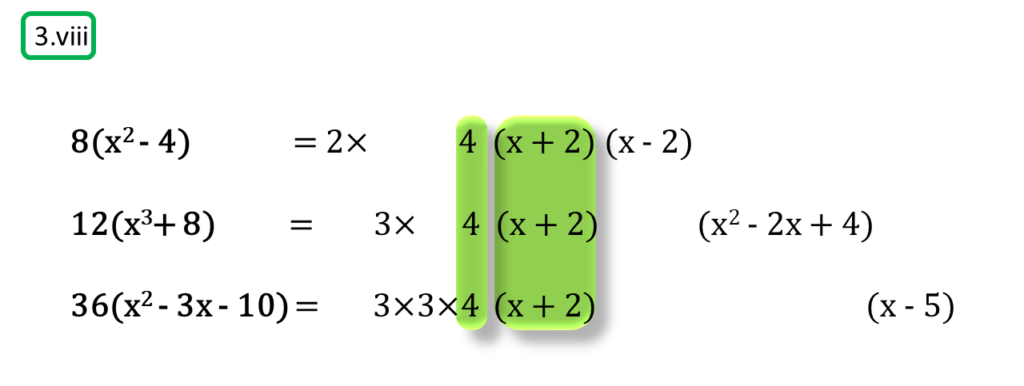
অতএব

নির্ণেয় গ.সা.গু = 4 (x + 2)

---

পড়ার টেবিল সাজানোর সুন্দর কিছু Table Organizer

---

( ix ) a² – b² – c² + 2bc, b² – c² – a² + 2ac, c² – a² – b² + 2ab

সমাধানঃ-

প্রথম সংখ্যামালা,

a² – b² – c² + 2bc

= a² – (b² – 2bc + c²)

= a² – (b – c)²

= {a + (b – c)} {a – (b – c)}

= (a + b – c) (a – b + c)

দ্বিতীয় সংখ্যামালা,

b² – c² – a² + 2ac

= b² – (c² – 2ac + a²)

= b² – (c – a)²

= {b + (c – a)} {b – (c – a)}

= (b + c – a) (b – c + a)

তৃতীয় সংখ্যামালা,

c² – a² – b² + 2ab

= c² – (a² – 2ab + b²)

= c² – (a – b)²

= {c + (a – b)} {c – (a – b)}

= (c + a – b) (c – a + b)

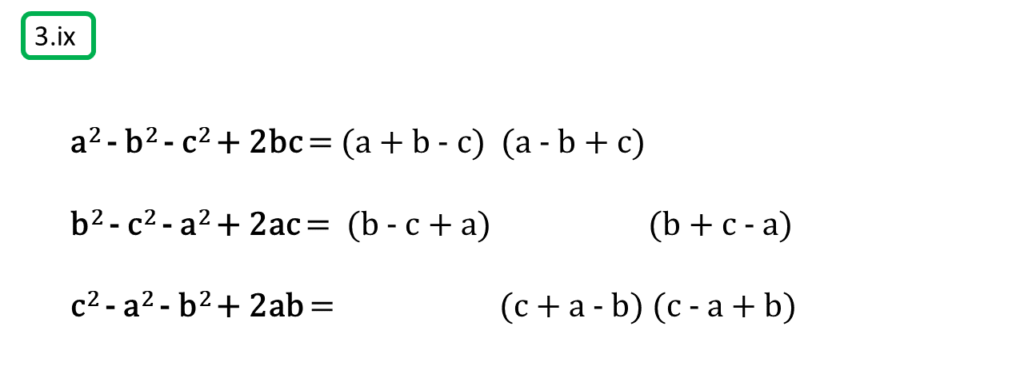
অতএব

নির্ণেয় গ.সা.গ = 1

---

Request For Share
সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share]

---

( x ) x³ – 16x, 2x³ + 9x² + 4x, 2x³ + x² – 28x

সমাধানঃ-

প্রথম সংখ্যামালা,

x³ – 16x

= x (x² – 4²)

= x (x + 4) (x – 4)

দ্বিতীয় সংখ্যামালা,

2x³ + 9x² + 4x

= x {2x² + (8 + 1) x + 4}

= x (2x² + 8x + x + 4)

= x {2x (x + 4) + 1(x + 4)}

= x (2x + 1) (x + 4)

তৃতীয় সংখ্যামালা,

2x³ + x² – 28x

=x {2x² + (8 – 7) x – 28}

= x (2x² + 8x – 7x – 28)

= x {2x (x + 4) – 7 (x + 4)}

= x (x + 4) (2x – 7)

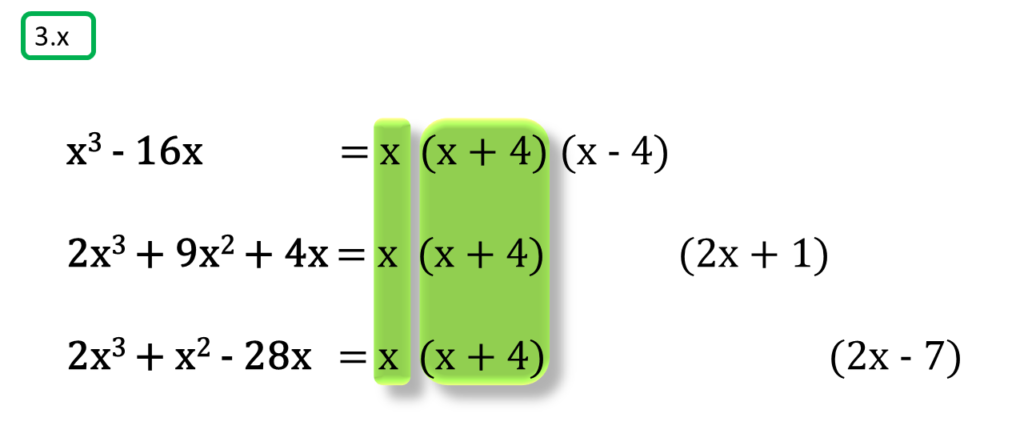
অতএব

নির্ণেয় গ.সা.গু = x (x + 4)

---

( xi ) 4x² – 1, 8x³ – 1, 4x² – 4x + 1

সমাধানঃ-

প্রথম সংখ্যামালা,

4x² – 1

= (2x)² – 1²

= (2x + 1) (2x – 1)

দ্বিতীয় সংখ্যামালা,

8x³ – 1

= (2x)³ – 1³

= (2x – 1) {(2x)² + 2x + 1}

= (2x – 1) (4x² + 2x + 1)

তৃতীয় সংখ্যামালা,

4x² – 4x + 1

= (2x)² – 2.2x.1 + 1²

= (2x – 1)²

= (2x – 1) (2x – 1)

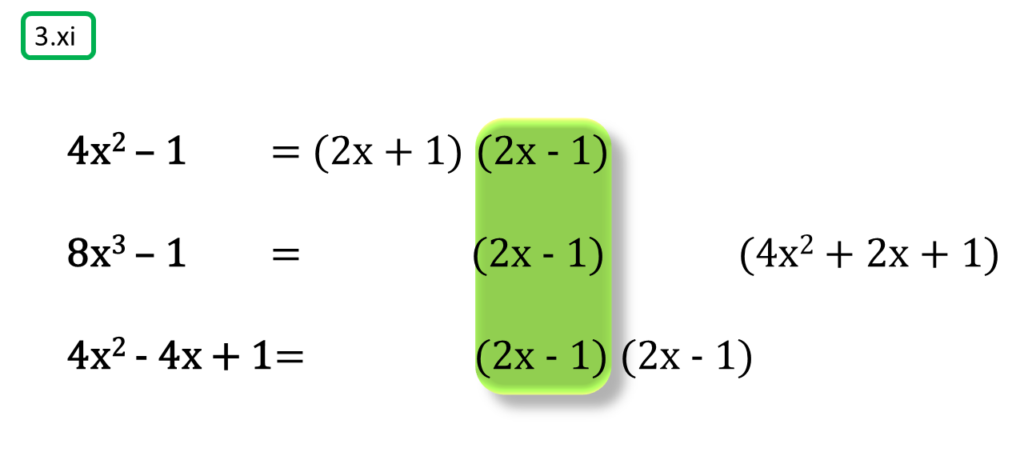
অতএব

নির্ণেয় গ.সা.গু = 2x – 1

---

পড়াতে মন বসানোর Study Table

---

( xii ) x³ – 3x² – 10x, x³ + 6x² + 8x, x⁴ – 5x³ – 14x²

সমাধানঃ-

প্রথম সংখ্যামালা,

x³ – 3x² – 10x

= x (x² – 3x – 10)

= x {x² – (5 – 2) x – 10}

= x (x² – 5x + 2x – 10)

= x {x (x – 5) + 2 (x – 5)}

= x (x – 5) (x + 2)

দ্বিতীয় সংখ্যামালা,

x³ + 6x² + 8x

= x (x² + 6x + 8)

= x {x² + (4 + 2) x + 8}

= x (x² + 4x + 2x + 8)

= x {x (x + 4) + 2 (x + 4)}

= x (x + 4) (x + 2)

তৃতীয় সংখ্যামালা,

x⁴ – 5x³ – 14x²

= x² (x² – 5x – 14)

= x² {x² – (7 – 2) x – 14}

= x² (x² – 7x + 2x – 14)

= x² {x (x – 7) + 2 (x – 7)}

= x² (x + 2) (x – 7)

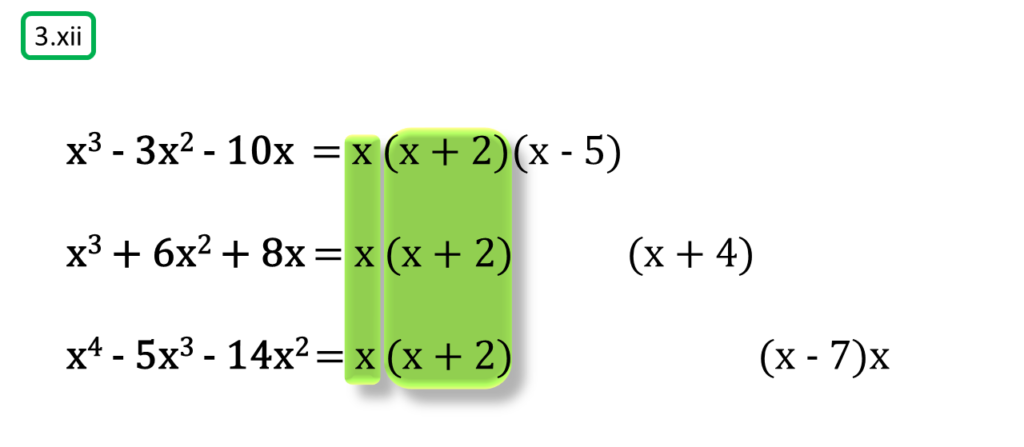
অতএব

নির্ণেয় গ.সা.গু = x (x + 2)

---

ঘরে বসে অনলাইনে পড়ার জন্যে তোমাদের জন্য উপযুক্ত কিছু TAB

---

( xiii ) 6x² – 13xa + 6a², 6x² + 2xa – 4a²

সমাধানঃ-

প্রথম সংখ্যামালা,

6x² – 13xa + 6a²

= 6x² – (9 + 4)xa + 6a²

= 6x² – 9xa – 4xa + 6a²

= 3x (2x – 3a) – 2a (2x – 3a)

= (2x – 3a) (3x – 2a)

দ্বিতীয় সংখ্যামালা,

6x² + 2xa – 4a²

= 2 (3x² + xa – 2a²)

= 2 {3x² + (3 – 2)xa – 2a²}

= 2 (3x² + 3xa – 2xa – 2a²)

= 2 {3x (x + a) – 2a (x + a)}

= 2 (x + a) (3x – 2a)

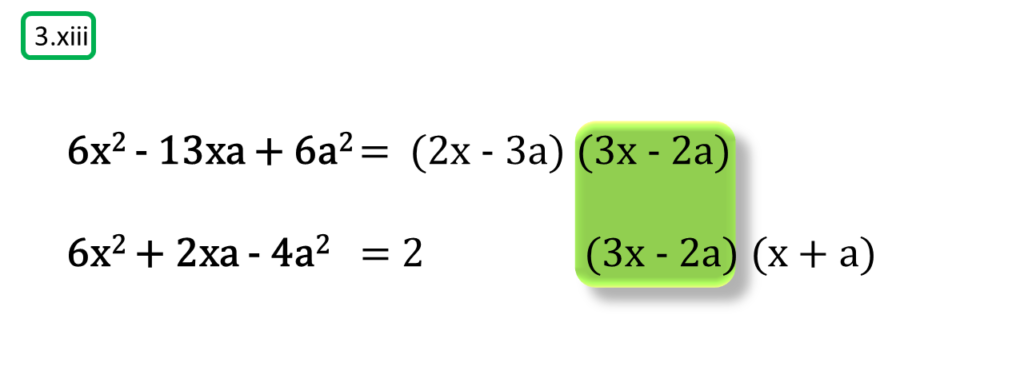
অতএব

নির্ণেয় গ.সা.গু = 3x – 2a

---

4. নীচের বীজগাণিতিক সংখ্যামালাগুলির ল.সা.গু নির্ণয় করি-

( i ) p² – q², (p + q)²

সমাধানঃ-

প্রথম সংখ্যামালা,

p² – q²

= (p + q) (p – q)

দ্বিতীয় সংখ্যামালা,

(p + q)²

= (p + q) (p + q)

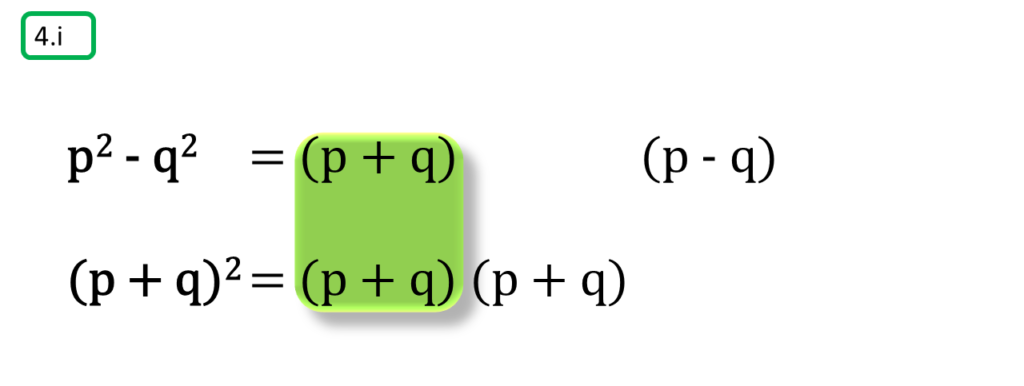
অতএব

নির্ণেয় ল.সা.গু = (p + q) (p2 – q2) বা, = (p – q) (p + q)2

---

পড়ার টেবিল সাজানোর সুন্দর কিছু Table Organizer

---

( ii ) (x²y² – x²), (xy² – 2xy + x)

সমাধানঃ-

প্রথম সংখ্যামালা,

(x²y² – x²)

= x² (y² – 1)

= x² (y + 1) (y – 1)

দ্বিতীয় সংখ্যামালা,

(xy² – 2xy + x)

= x (y² – 2y + 1)

= x (y – 1)²

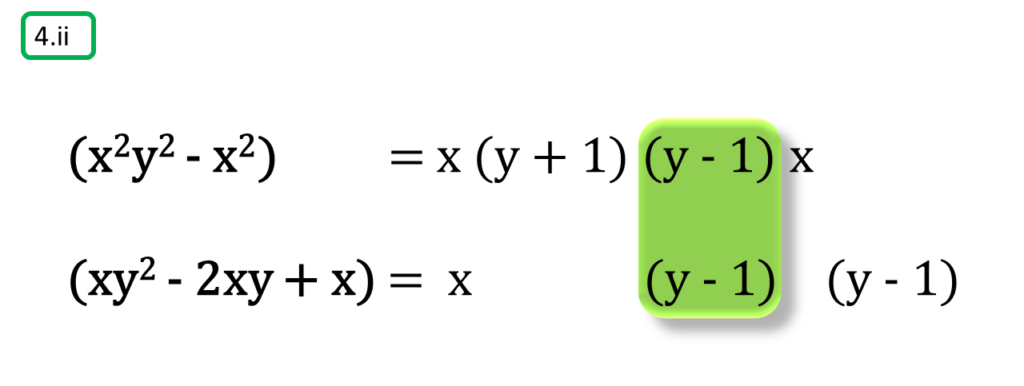
অতএব

নির্ণেয় ল.সা.গু = x2 (y + 1) (y – 1)2

---

( iii ) (p + q) (q + r), (q + r) (r + p), (r + p) (p + q)

সমাধানঃ-

প্রথম সংখ্যামালা,

(p + q) (q + r)

দ্বিতীয় সংখ্যামালা,

(q + r) (r + p)

তৃতীয় সংখ্যামালা,

(r + p) (p + q)

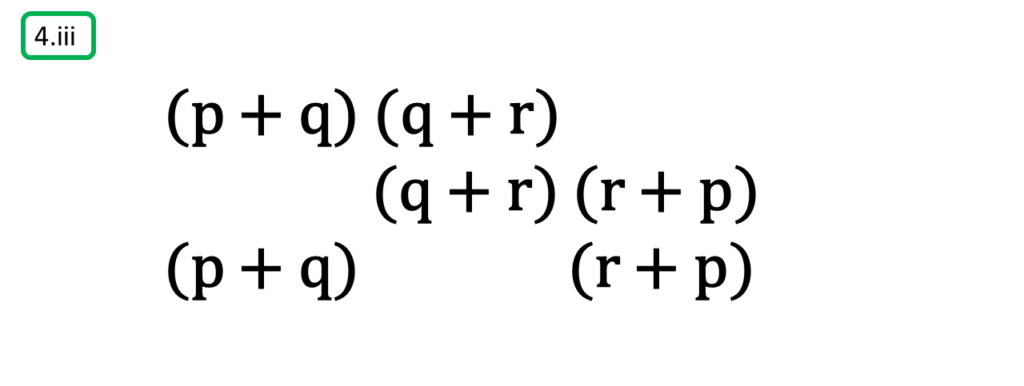
অতএব

নির্ণেয় ল.সা.গু = (p + q) (q + r) (r + p)

---

Request For Share
সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share]

---

( iv ) ab⁴ – 8ab, a²b⁴ + 8a²b, ab⁴ – 4ab²

সমাধানঃ-

প্রথম সংখ্যামালা,

ab⁴ – 8ab

= ab (b³ – 8)

= ab (b³ – 2³)

= ab (b – 2) (b² + 2b + 4)

দ্বিতীয় সংখ্যামালা,

a²b⁴ + 8a²b

= a²b (b³ + 8)

= a²b (b³ – 2³)

= a²b (b – 2) (b² + 2b + 4)

তৃতীয় সংখ্যামালা,

ab⁴ – 4ab²

= ab² (b² – 4)

= ab² (b² – 2²)

= ab² (b + 2) (b – 2)

অতএব

নির্ণেয় ল.সা.গু = a2b2 (b + 2) (b – 2) (b2 + 2b + 4)

---

( v ) x⁴ + x²y² + y⁴, x³y + y⁴, (x² – xy)³

সমাধানঃ-

প্রথম সংখ্যামালা,

x⁴ + x²y² + y⁴

= (x²)² + (y²)² + x²y²

= (x² + y²)² – 2x²y² + x²y²

= (x² + y²)² – x²y²

= (x² + y² + xy) (x² + y² – xy)

দ্বিতীয় সংখ্যামালা,

x³y + y⁴

= y (x³ + y³)

= y (x + y) (x² – xy + y²)

তৃতীয় সংখ্যামালা,

(x² – xy)³

= x³ (x – y)³

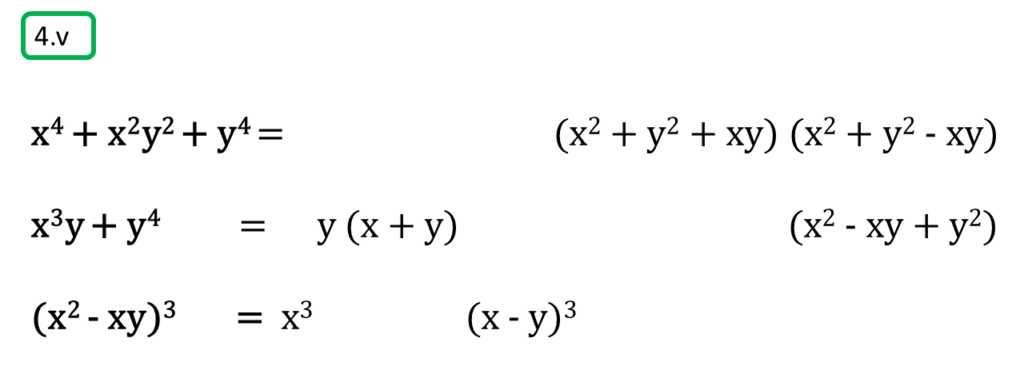
অতএব

নির্ণেয় ল.সা.গু = x3y (x + y) (x – y)3 (x2 – xy + y2) (x2 + xy + y2)

---

( vi ) p² + 2p, 2p⁴ + 3p³ – 2p², 2p³ – 3p² – 14p

সমাধানঃ-

প্রথম সংখ্যামালা,

p² + 2p

= p (p + 2)

দ্বিতীয় সংখ্যামালা,

2p⁴ + 3p³ – 2p²

= p² (2p² + 3p – 2)

= p² {2p² + (4 – 1) p – 2}

= p² (2p² + 4p – p – 2)

= p² {2p (p + 2) – 1(p + 2)}

= p² (p + 2) (2p – 1)

তৃতীয় সংখ্যামালা,

2p³ – 3p² – 14p

= p (2p² – 3p – 14)

= p {2p² – (7 – 4) p – 14}

= p (2p² – 7p + 4p – 14)

= p {p (2p – 7) + 2 (2p – 7)}

= p (2p – 7) (p + 2)

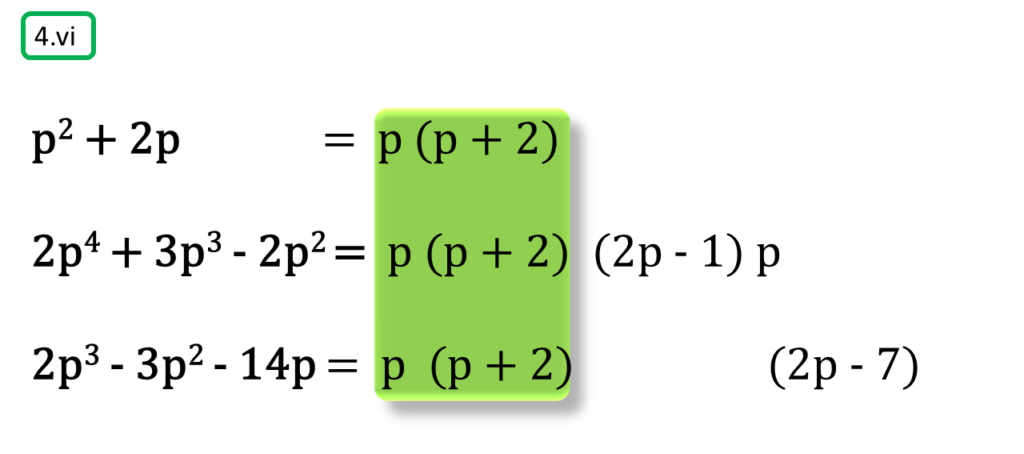
অতএব

নির্ণেয় ল.সা.গু = p2 (p + 2) (2p – 1) (2p – 7)

---

Request For Share
সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share]

---

( vii ) x² – y² + z² – 2xz, x² – y² – z² + 2yz, xy + zx + y² – z²

সমাধানঃ-

প্রথম সংখ্যামালা,

x² – y² + z² – 2xz

= x² – 2xz + z² – y²

= (x – z)² – y²

= (x – z + y) (x – z – y)

দ্বিতীয় সংখ্যামালা,

x² – y² – z² + 2yz

= x² – (z² – 2yz + y²)

= x² – (z – y)²

= (x + z – y) (x – z + y)

তৃতীয় সংখ্যামালা,

xy + zx + y² – z²

= x (y + z) + (y + z) (y – z)

= (y + z) (x + y – z)

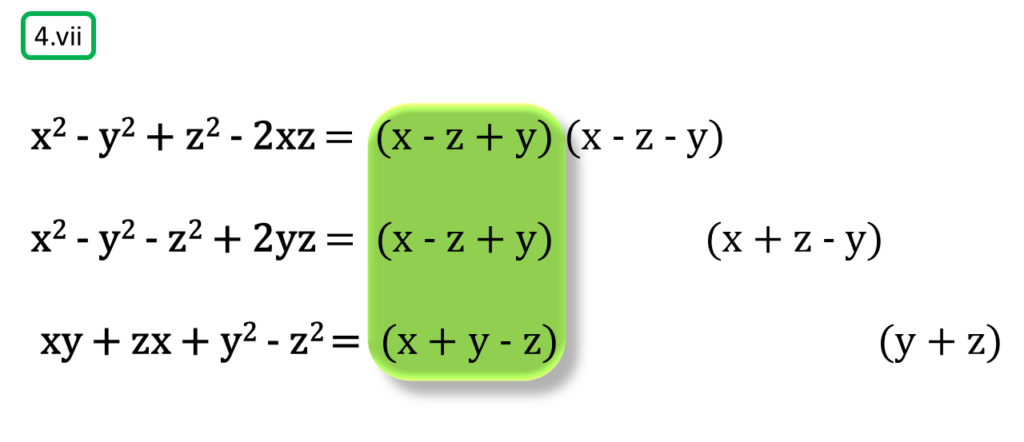
অতএব

নির্ণেয় ল.সা.গু = (y + z) (x + y – z) (x + z – y) (x – z – y)

---

( viii ) x² – xy – 2y², 2x² – 5xy + 2y², 2x² + xy – y²

সমাধানঃ-

প্রথম সংখ্যামালা,

x² – xy – 2y²

= x² – (2 – 1)xy – 2y²

= x² – 2xy + xy – 2y²

= x (x – 2y) + y (x – 2y)

= (x – 2y) (x + y)

দ্বিতীয় সংখ্যামালা,

2x² – 5xy + 2y²

= 2x² – (4 + 1)xy + 2y²

= 2x² – 4xy – xy + 2y²

= 2x (x – 2y) – y (x – 2y)

= (x – 2y) (2x – y)

তৃতীয় সংখ্যামালা,

2x² + xy – y²

= 2x² + (2 – 1) xy – y²

= 2x² + 2xy – xy – y²

= 2x (x + y) – y (x + y)

= (x + y) (2x – y)

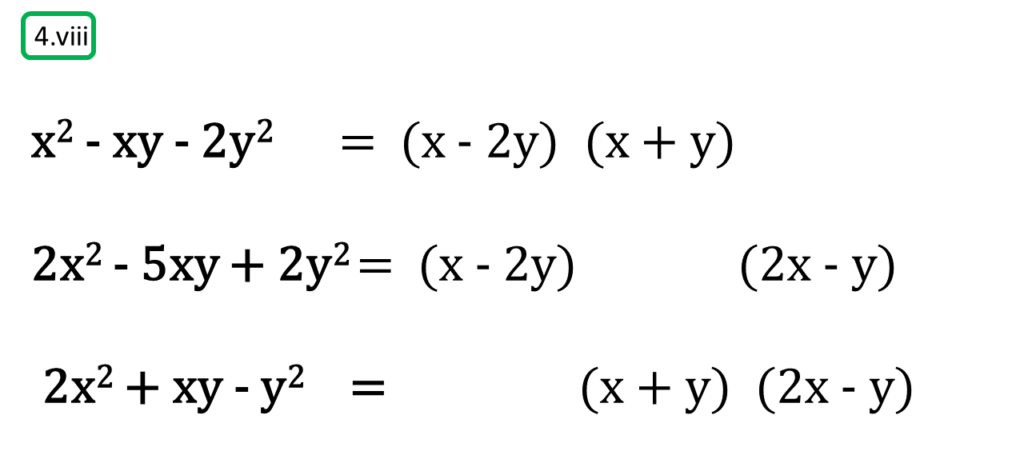
অতএব

নির্ণেয় ল.সা.গু = (x + y) (2x – y) (x – 2y)

---

পড়াতে মন বসানোর Study Table

---

( ix ) 3x² – 15x + 18, 2x² + 2x – 24, 4x² + 36x + 80

সমাধানঃ-

প্রথম সংখ্যামালা,

3x² – 15x + 18

= 3 (x² – 5x + 6)

= 3 {x² – (3 + 2) x + 6}

= 3 (x² – 3x – 2x + 6)

= 3 {x (x – 3) – 2 (x – 3)}

= 3 (x – 3) (x – 2)

দ্বিতীয় সংখ্যামালা,

2x² + 2x – 24

= 2 (x² + x – 12)

= 2 {x² + (4 – 3) x – 12}

= 2 (x² + 4x – 3x – 12)

= 2 {x (x + 4) – 3 (x + 4)}

= 2 (x + 4) (x – 3)

তৃতীয় সংখ্যামালা,

4x² + 36x + 80

= 4 (x² + 9x + 20)

= 4 {x² + (5 + 4) x + 20}

= 4 (x² + 5x + 4x + 20)

= 4 {x (x + 5) + 4 (x + 5)}

= 4 (x + 5) (x + 4)

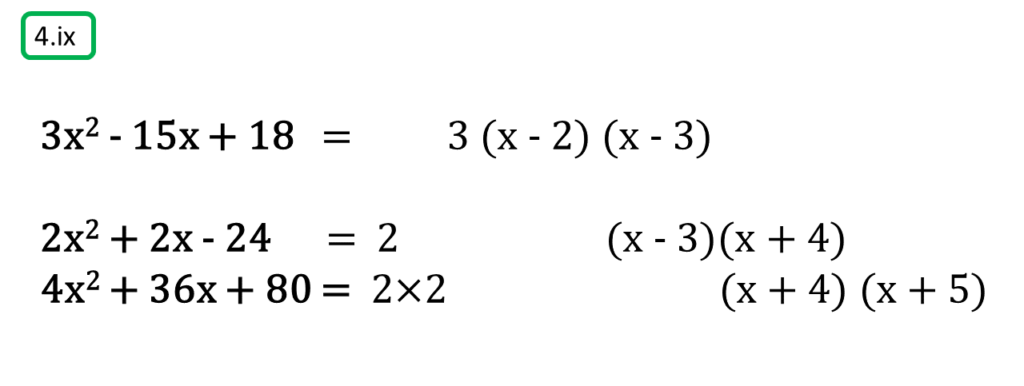
অতএব

নির্ণেয় ল.সা.গু = 4×3 (x + 4) (x – 3) (x – 2) (x + 5) = 12(x + 4) (x – 3) (x – 2) (x + 5)

---

Request For Share
সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share]

---

পড়ার টেবিল সাজানোর সুন্দর কিছু Table Organizer

---

( x ) (a² + 2a)², 2a³ + 3a² – 2a, 2a⁴ – 3a³ – 14a²

সমাধানঃ-

প্রথম সংখ্যামালা,

(a² + 2a)²

= a²(a + 2)²

দ্বিতীয় সংখ্যামালা,

2a³ + 3a² – 2a

= a (2a² + 3a – 2)

= a {2a² + (4 – 1) a – 2}

= a (2a² + 4a – a – 2)

= a {2a (a + 2) – 1(a + 2)}

= a (a + 2) (2a – 1)

তৃতীয় সংখ্যামালা,

2a⁴ – 3a³ – 14a²

= a² (2a² – 3a – 14)

= a² {2a² – (7 – 4) a – 14}

= a² (2a² – 7a + 4a – 14)

= a² {a (2a – 7) + 2 (2a – 7)}

= a² (2a – 7) (a + 2)

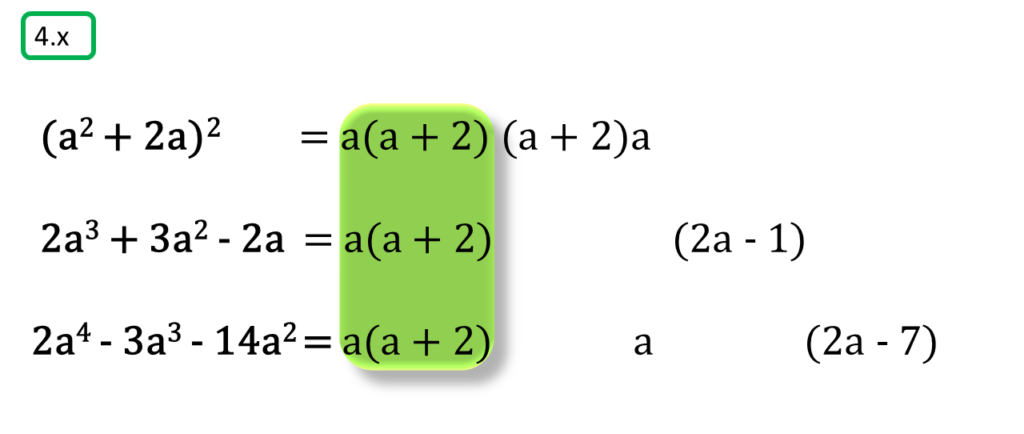
অতএব

নির্ণেয় ল.সা.গু = a2(a + 2)2 (2a – 1) (2a – 7)

---

( xi ) 3a² – 5ab – 12², a⁵ – 27a²b³, 9a² + 24ab + 16b²

সমাধানঃ-

প্রথম সংখ্যামালা,

3a² – 5ab – 12b²

=3a² – (9 – 4)ab – 12b²

= 3a² – 9ab + 4ab – 12b²

= 3a (a – 3b) + 4b (a – 3b)

= (a – 3b) (3a + 4b)

দ্বিতীয় সংখ্যামালা,

a⁵ – 27a²b³

= a² (a³ – 27b³)

= a² {a³ – (3b)³}

= a² (a – 3b) (a² + 3ab + 9b²)

তৃতীয় সংখ্যামালা,

9a² + 24ab + 16b²

= (3a)² + 2.3a.4b + (4b)²

= (3a + 4b)²

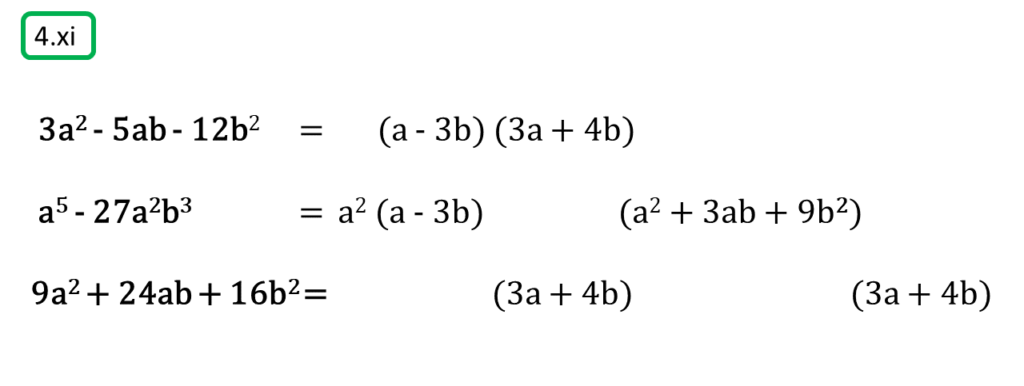
অতএব

নির্ণেয় ল.সা.গু = a2 (a – 3b) (3a + 4b)2 (a2 + 3ab + 9b2)

---

5. নীচের বীজগাণিতিক সংখ্যামালাগুলির গ.সা.গু ও ল.সা.গু নির্ণয় করি-

( i ) x³ – 8, x² + 3x – 10, x³ + 2x² – 8x

সমাধানঃ-

প্রথম সংখ্যামালা,

x³ – 8

= x³ – 2³

= (x – 2) (x² + 2x + 4)

দ্বিতীয় সংখ্যামালা,

x² + 3x – 10

= x² + (5 – 2) x – 10

= x² + 5x – 2x – 10

= x (x + 5) – 2 (x + 5)

= (x + 5) (x – 2)

তৃতীয় সংখ্যামালা,

x³ + 2x² – 8x

= x (x² + 2x – 8)

= x {x² + (4 – 2)x – 8}

= x (x² + 4x – 2x – 8)

= x {x (x + 4) – 2 (x + 4)}

= x (x + 4) (x – 2)

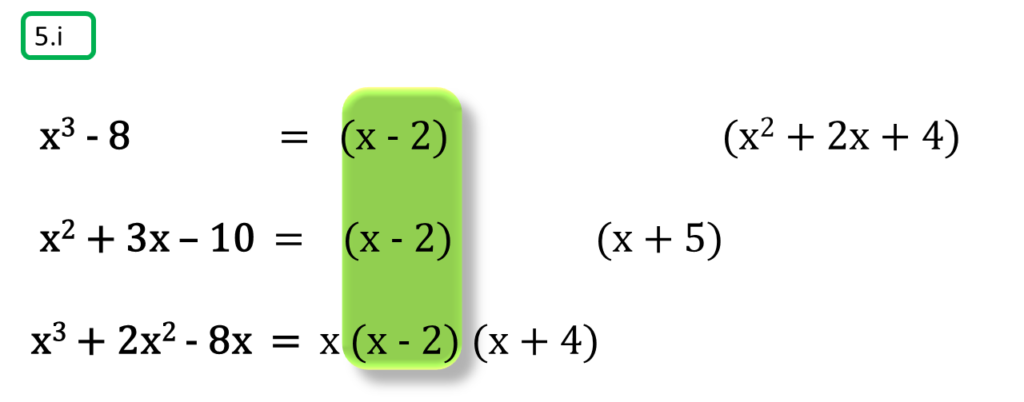
অতএব

নির্ণেয় গ.সা.গু =	x – 2
নির্ণেয় ল.সা.গু =	x (x – 2) (x + 4) (x + 5) (x2 + 2x + 4)

---

পড়ার টেবিল সাজানোর সুন্দর কিছু Table Organizer

---

( ii ) 3y² – 15y + 18, 2y² + 2y – 24, 4y² + 36y + 80

সমাধানঃ-

প্রথম সংখ্যামালা,

3y² – 15y + 18

= 3 (y² – 5y + 6)

= 3 {y² – (3 + 2) y + 6}

= 3 (y² – 3y – 2y + 6)

= 3 {y (y – 3) – 2 (y – 3)}

= 3 (y – 3) (y – 2)

দ্বিতীয় সংখ্যামালা,

2y² + 2y – 24

= 2 (y² + y – 12)

= 2 {y² + (4 – 3) y – 12}

= 2 (y² + 4y – 3y – 12)

= 2 {y (y + 4) – 3 (y + 4)}

= 2 (y + 4) (y – 3)

তৃতীয় সংখ্যামালা,

4y² + 36y + 80

= 4 (y² + 9y + 20)

= 4 {y² + (5 + 4) y + 20}

= 4 (y² + 5y + 4y + 20)

= 4 {y (y + 5) + 4 (y + 5)}

= 4 (y + 5) (y + 4)

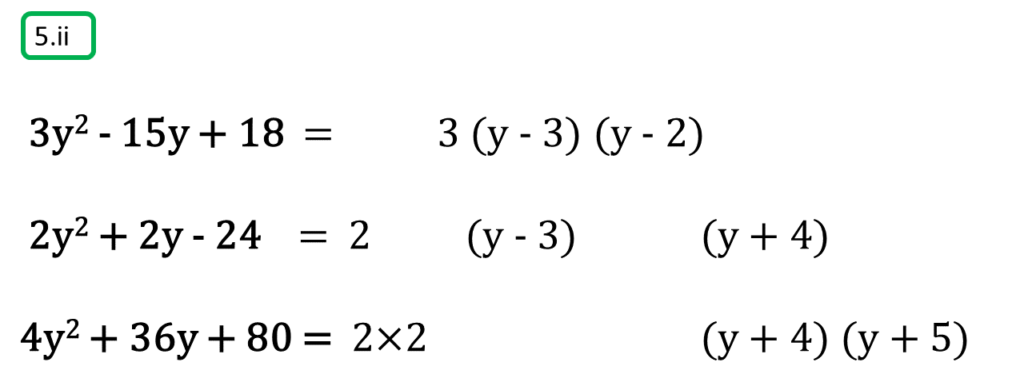
অতএব

নির্ণেয় গ.সা.গু =	1
নির্ণেয় ল.সা.গু =	12 (y + 4) (y – 3) (y + 5) (y – 2)

---

Request For Share
সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share]

---

( iii ) a³ – 4a² + 4a, a² + a – 6, a³ – 8

সমাধানঃ-

প্রথম সংখ্যামালা,

a³ – 4a² + 4a

= a (a² – 4a + 4)

= a (a² – 2.2.a + 2²)

= a (a – 2)²

দ্বিতীয় সংখ্যামালা,

a² + a – 6

= a² + (3 – 2) a – 6

= a² + 3a – 2a – 6

= a (a + 3) – 2 (a + 3)

= (a + 3) (a – 2)

তৃতীয় সংখ্যামালা,

a³ – 8

= a³ – 2³

= (a – 2) (a² + 2a + 4)

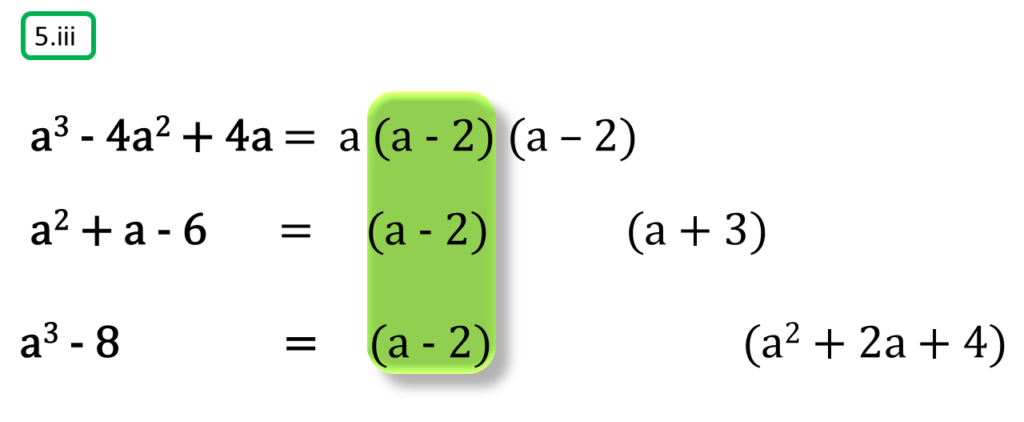
অতএব

নির্ণেয় গ.সা.গু =	a – 2
নির্ণেয় ল.সা.গু =	a (a – 2)2 (a + 3) (a2 + 2a + 4)

---

( iv ) a² + b² – c² + 2ab, c² + a² – b² + 2ca, b² + c² – a² + 2bc

সমাধানঃ-

প্রথম সংখ্যামালা,

a² + b² – c² + 2ab

= a² + 2ab + b² – c²

= (a + b)² – c²

= (a + b + c) (a + b – c)

দ্বিতীয় সংখ্যামালা,

c² + a² – b² + 2ca

= a² + 2ca + c² – b²

= (a + c)² – b²

= (a + c + b) (a + c – b)

তৃতীয় সংখ্যামালা,

b² + c² – a² + 2bc

= b² + 2bc + c² – a²

= (b + c)² – a²

= (b + c + a) (b + c – a)

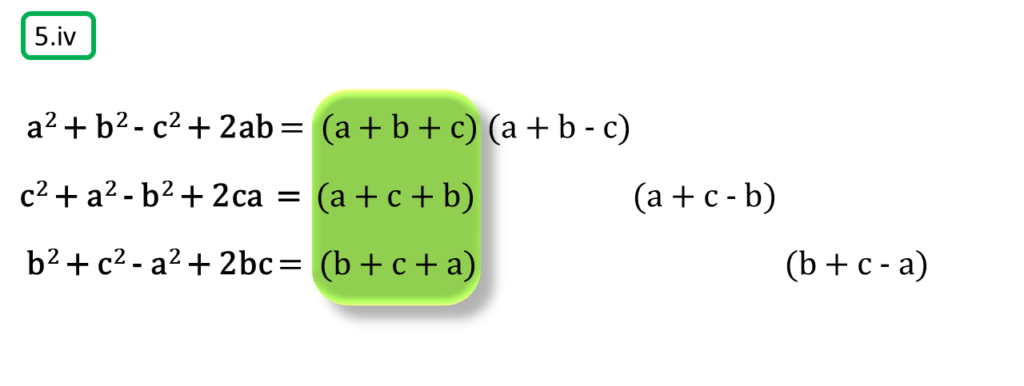
অতএব

নির্ণেয় গ.সা.গু =	a + b + c
নির্ণেয় ল.সা.গু =	(a + b + c) (a + b – c) (a + c – b) (b + c – a)

---

পড়ার টেবিল সাজানোর সুন্দর কিছু Table Organizer

---

( v ) x³ – 4x, 4(x² – 5x +6), (x² – 4x + 4)

সমাধানঃ-

প্রথম সংখ্যামালা,

x³ – 4x

= x (x² – 4)

= x (x² – 2²)

= x (x + 2) (x – 2)

দ্বিতীয় সংখ্যামালা,

4(x² – 5x +6)

= 4 {x² – (3 + 2) x + 6}

= 4 (x² – 3x – 2x + 6)

= 4 {x (x – 3) – 2 (x – 3)}

= 4 (x – 3) (x – 2)

তৃতীয় সংখ্যামালা,

(x² – 4x + 4)

= x² – 2.2.x + 2²

= (x – 2)²

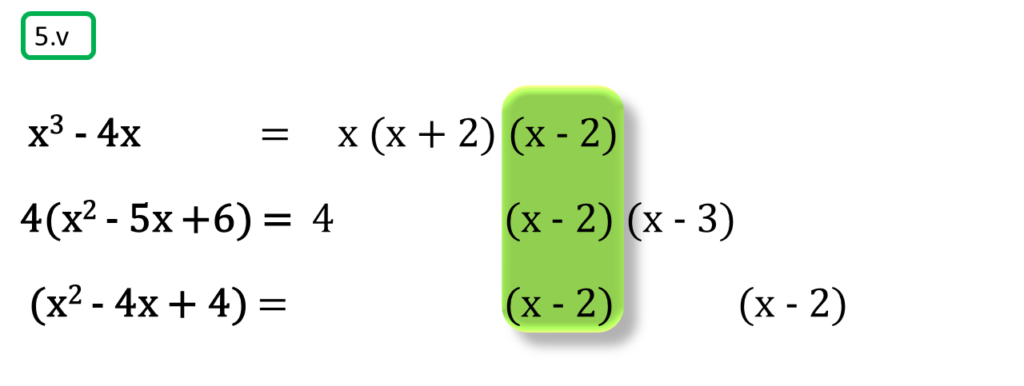
অতএব

নির্ণেয় গ.সা.গু =	x – 2
নির্ণেয় ল.সা.গু =	4x (x + 2) (x – 3) (x – 2)2

---

এই কষে দেখি 14 Class 8|Koshe Dekhi 14 Class 8 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।

---

আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে?
কষে দেখি 14 Class 8 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 14 Class 8 তারপর এই চিহ্ন দেখে Click করলে আবার তোমরা এখানে এসে যাবে।

---

গনিতপ্রভা অষ্টম শ্রেণীর সমস্ত অধ্যায়ের সমাধান-
অধ্যায়	সমাধান
2. পাই চিত্র	কষে দেখি 2
3. মূলদ সংখ্যার ধারণা	অধ্যায়ের সারাংশ
	কষে দেখি 3
4. বীজগাণিতিক সংখ্যামালার গুণ ও ভাগ	অধ্যায়ের সারাংশ
	কষে দেখি 4.1
	কষে দেখি 4.2
5. ঘনফল নির্ণয়	অধ্যায়ের সারাংশ
	কষে দেখি 5.1
	কষে দেখি 5.2
	কষে দেখি 5.3
6. পূরক কোণ, সম্পূরক কোণ ও সন্নিহিত কোণ	অধ্যায়ের সারাংশ
	কষে দেখি 6
7. বিপ্রতীপ কোণের ধারণা	অধ্যায়ের সারাংশ
	কষে দেখি 7.1
8. সমান্তরাল সরলরেখা ও ছেদকের ধর্ম	অধ্যায়ের সারাংশ
	কষে দেখি 8
9. ত্রিভুজের দুটি বাহু ও তাদের বিপরীত কোণের সম্পর্ক	অধ্যায়ের সারাংশ
	কষে দেখি 9
10. ত্রৈরাশিক	কষে দেখি 10.1
	কষে দেখি 10.2
11. শতকরা	কষে দেখি 11
12. মিশ্রণ	কষে দেখি 12
13. বীজগাণিতিক সংখ্যামালার উৎপাদকে বিশ্লেষণ	কষে দেখি 13.1
	কষে দেখি 13.2
14. বীজগাণিতিক সংখ্যামালার গ.সা.গু ও ল.সা.গু	কষে দেখি 14
15. বীজগাণিতিক সংখ্যামালার সরলীকরণ	কষে দেখি 15
16. ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই	কষে দেখি 16.1
	কষে দেখি 16.2
17. সময় ও কার্য	কষে দেখি 17.1
	কষে দেখি 17.2
18. লেখচিত্র	কষে দেখি 18
19. সমীকরণ গঠন ও সমাধান	কষে দেখি 19
20. জ্যামিতিক প্রমাণ	কষে দেখি 20.1
	কষে দেখি 20.2
	কষে দেখি 20.3

---

---

এখানে তোমরা তোমাদের অষ্টম শ্রেণীতে কি কি পড়ানো হয়, মানে তোমাদের অষ্টম শ্রেণীর সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

---