শ্রেণী-অষ্টম ; অধ্যায় – ঘনফল নির্ণয় ; কষে দেখি – 5.1
ঘনফল নির্ণয় অধ্যায় থেকে অধ্যায়ের সারাংশতে আমরা জেনেছি –
-> ঘনক কি ?
-> ঘনফল কাকে বলে?
-> ঘনকের আয়তনের সূত্র কী?/ঘনকের ঘনফলের সূত্র
-> পূর্ণঘনসংখ্যা কাকে বলে?
-> ঘনমূল কি?
-> কিছু সূত্র ।
যদি তোমরা অধ্যায়ের সারাংশ না দেখে থাকো তাহলে একবার দেখে নিও ।
আমাদের শুধু অধ্যায়ের সারাংশ বুঝলেই হবেনা , তারসাথে আমি কতোটা শিখলাম , নিজে কতোটা বুঝলাম এবং নিজে নিজে কারোর সাহাজ্য ছাড়ায় কতোটা অংক সমাধান করতে পারবো তা ঘনফল নির্ণয় কষে দেখি 5.1 থেকে অংক করলে তবেই বুঝতে পারবো।
শুধু তায় নয়, অংক যতো সমাধান করা যাবে ( নিজে নিজে ) ততো নিজের প্রতি বিশ্বাস টা শক্ত হবে। এমনকি এই বিষয়ে নতুন অংক সামনে পেলে সেটা করতে সাহস পাবে ।

পাঠ ক্রম হল কয়েকটি বিষয়ের এবং পরিকল্পিত অভিজ্ঞতার শৃঙ্খলাবদ্ধ সমষ্টি।
কার্টার ভি গুড
এবার ঘনফল নির্ণয় কষে দেখি 5.1 Class 8 (Koshe Dekhi – 5.1 Class 8) আমরা শুরু করবো। । এখানে প্রতিটি অঙ্ক সুন্দর করে STEP BY STEP গুছিয়ে লেখা হয়েছে এবং সহজ ভাষায় উপস্থাপন করা হয়েছে যাতে তোমরা সহজেই এই কষে দেখি 5.1 Class 8 এর প্রতিটি অঙ্ক বুঝতে পারো তারসাথে ভবিষ্যতে এরকম অংক পরীক্ষায় আসলে তা যেনো সহজেই করে উঠতে পারো।
আগে তোমরা নিজেরা অংক গুলি করবে, তারপর যেখানে আটকে যাবে এখান থেকে দেখে নেবে ।
এখানে করে দেওয়া অংক গুলি ভালো ভাবে বোঝার জন্যে নিম্নে কিছু নির্দেশিকা তোমাদের জন্যে থাকলোঃ
কিছু উপদেশঃ-
- প্রথমত প্রতিটি অংক খুবই সহজ ভাবে করা হয়েছে
- প্রতিটি অঙ্কে এক লাইন থেকে আর এক লাইন কি কারনে হলো সেটা বলা হয়েছে এবং সেটা আলাদা box এর মধ্যে লিখে দেখানো হয়েছে।
- তারসাথে arrow চিহ্ন প্রয়োগ করেও দেখানো হয়েছে
- প্রতিটি লাইনে কি সুত্র প্রয়োগ করে অঙ্কটি সমাধান করা হয়েছে সেটা আলাদা করে পাশে উল্লেখ করা হয়েছে।
- প্রতিটি প্রশ্নের উত্তর কিভাবে লিখতে হবে তা সমাধানের শেষে আলাদা ভাবে box এর মধ্যে লিখে দেওয়া হয়েছে
আগামিতে এই কষে দেখি 5.1 Class 8 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 5.1 Class 8 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 5.1 Class 8 তারপর  |
কষে দেখি 5.1 | Koshe Dekhi 5.1


1. দুটি ঘনক তৈরি করি যার একটি বাহুর দৈর্ঘ্য যথাক্রমে 5 সেমি . ও 1 সেমি. ।
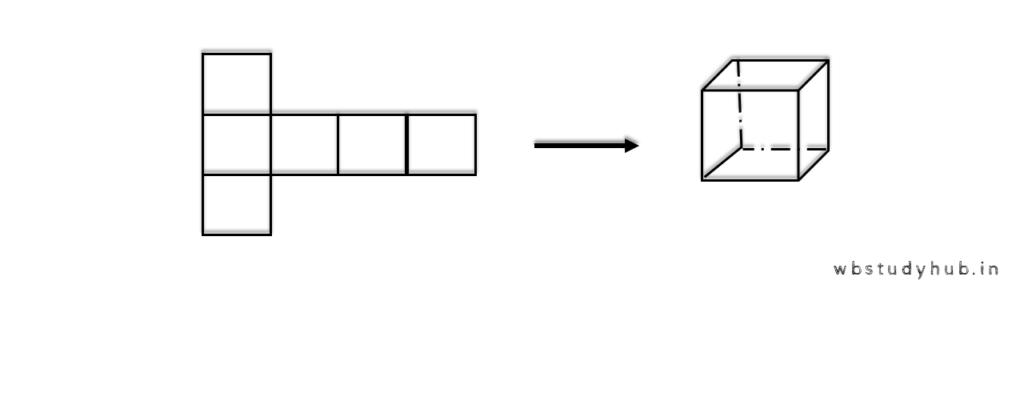
কতগুলি 1 সেমি. দৈর্ঘ্যের বাহুবিশিষ্ট ঘনক জুড়ে এই বড়ো ঘনক পাব হিসাব করে লিখি ।
সমাধানঃ-
আমরা দেখছি এখানে যে বড়ো ঘনক টি তৈরি হবে তার প্রতিটি বাহুর দৈর্ঘ্য 5 সেমি. , আর এই বড়ো ঘনক টি তৈরি হবে কিছু ছোটো ঘনক সজিয়ে, সেই ছোটো ঘনক গুলির প্রত্যেকটির বাহুর দৈর্ঘ্য হচ্ছে 1 সেমি ।
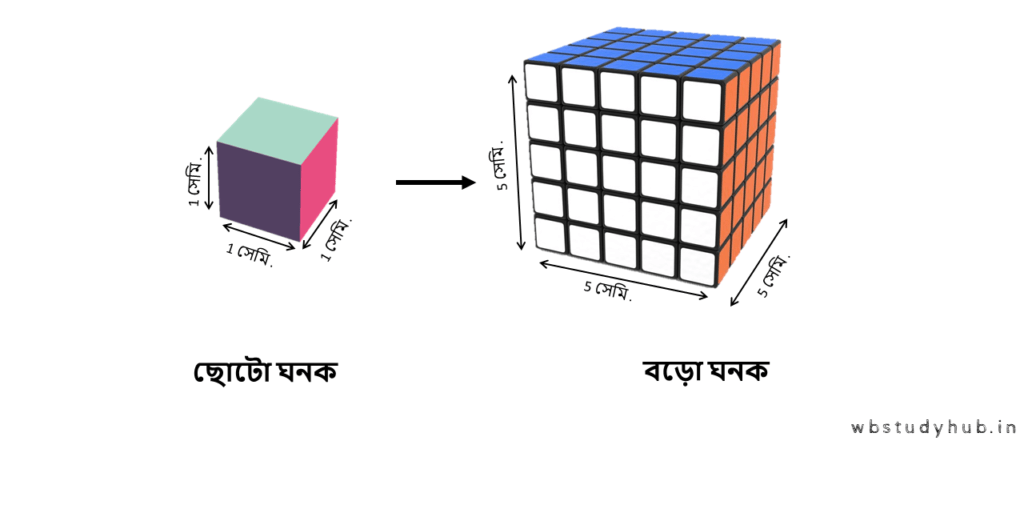
∴ 5 সেমি দৈর্ঘ্যের বাহুবিশিষ্ট বড়ো ঘনক তৈরি করতে ,
| (5)3 = 125 টি 1 সেমি. দৈর্ঘ্যের বাহুবিশিষ্ট ঘনক লাগবে। |
2. সুমন্ত অনেকগুলি 1 সেমি. দৈর্ঘ্যের বাহুবিশিষ্ট ঘনক তৈরি করেছে। মনামী সেই ঘনকগুলি জোড়া লাগিয়ে বড়ো ঘনক তৈরির চেষ্টা করছে । হিসাব করে দেখি নীচের কোন সংখ্যক ঘনকের ক্ষেত্রে মনামী বড়ো ঘনক তৈরি করতে পারবে ।
( i ) 100
সমাধানঃ-
| 100 |
| = 2× 50 |
| = 2×2×25 |
| = 2×2×5×5 ≠ ( কোন পূর্ণসংখ্যা )3 |
| ∴ 100 সংখ্যক 1 সেমি. দৈর্ঘ্যের বাহুবিশিষ্ট ঘনক দিয়ে মনামী বড়ো ঘনক তৈরি করতে পারবেনা। |
( ii ) 1000
সমাধানঃ-
| 1000 |
| = 2×500 |
| = 2×2×250 |
| = 2×2×2×125 |
| = 2×2×2×5×25 |
| = 2×2×2×5×5×5 |
| = 23×53 |
| = (2×5)3 = 103 = ( একটি পূর্ণসংখ্যা)3 |
| ∴ 1000 সংখ্যক 1 সেমি. দৈর্ঘ্যের বাহুবিশিষ্ট ঘনক দিয়ে মনামী বড়ো ঘনক তৈরি করতে পারবে। |
( iii ) 1331
সমাধানঃ-
| 1331 |
| = 11×121 |
| = 11×11×11 |
| = 113 = (একটি পূর্ণসংখ্যা )3 |
| ∴ 1331 সংখ্যক 1 সেমি. দৈর্ঘ্যের বাহুবিশিষ্ট ঘনক দিয়ে মনামী বড়ো ঘনক তৈরি করতে পারবে। |
( iv ) 1210
সমাধানঃ-
| 1210 |
| = 2×605 |
| = 2×5×121 |
| = 2×5×11×11≠ (কোন পূর্ণসংখ্যা)3 |
| ∴ 1210 সংখ্যক 1 সেমি. দৈর্ঘ্যের বাহুবিশিষ্ট ঘনক দিয়ে মনামী বড়ো ঘনক তৈরি করতে পারবে না । |
( v ) 3375
সমাধানঃ-
| 3375 |
| = 5×675 |
| = 5×5×135 |
| = 5×5×5×27 |
| = 5×5×5×3×9 |
| = 5×5×5×3×3×3 |
| = 53 × 33 |
| = (5×3)3 = 153 = ( একটি পূর্ণসংখ্যা)3 |
| ∴ 3375 সংখ্যক 1 সেমি. দৈর্ঘ্যের বাহুবিশিষ্ট ঘনক দিয়ে মনামী বড়ো ঘনক তৈরি করতে পারবে। |
( vi ) 2700
সমাধানঃ-
| 2700 |
| = 27 × 100 |
| = 3×3×3×10×10×10 |
| = 33 × 103 |
| = (30)3= ( একটি পূর্ণসংখ্যা)3 |
| ∴ 2700 সংখ্যক 1 সেমি. দৈর্ঘ্যের বাহুবিশিষ্ট ঘনক দিয়ে মনামী বড়ো ঘনক তৈরি করতে পারবে। |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
3.নীচের সংখ্যাগুলির মধ্যে কোনটি পূর্ণঘনসংখ্যা নয় লিখি ।
(i) 216
সমাধানঃ-
| 216 |
| = 2×108 |
| = 2×2×54 |
| = 2×2×2×27 |
| = 2×2×2×3×9 |
| = 2×2×2×3×3×3 |
| = 23 × 33 |
| = (2×3)3 = 63 = (একটি পূর্ণসংখ্যা)3 |
| ∴ 216 একটি পূর্ণঘনসংখ্যা । |
(ii) 343
সমাধানঃ-
| 343 |
| = 7×49 |
| = 7×7×7 |
| = 73= (একটি পূর্ণঘনসংখ্যা)3 |
| ∴ 343 একটি পূর্ণঘনসংখ্যা । |
(iii) 1024
সমাধানঃ-
| 1024 |
| =2×512 |
| = 2×2×256 |
| = 2×2×2×128 |
| = 2×2×2×2×64 |
| = 2×2×2×2×2×32 |
| = 2×2×2×2×2×2×16 |
| = 2×2×2×2×2×2×2×8 |
| = 2×2×2×2×2×2×2×2×4 |
| = 2×2×2×2×2×2×2×2×2×2 |
| = (2×2×2)×(2×2×2)×(2×2×2)×2 |
| = 23×23×23×2 |
| = 83×2 ≠( কোন পূর্ণসংখ্যা)3 |
| ∴ 1024 একটি পূর্ণঘনসংখ্যা নয় । |
(iv) 324
সমাধানঃ-
| 324 |
| = 2×162 |
| = 2×2× 81 |
| = 2×2×3×27 |
| = 2×2×3×3×9 |
| = 2×2×3×3×3×3 |
| = 22×33×3 ≠ (কোন পূর্ণসংখ্যা)3 |
| ∴ 324 একটি পূর্ণঘনসংখ্যা নয় । |
(v) 1744
সমাধানঃ-
| 1744 |
| =2×872 |
| = 2×2×436 |
| = 2×2×2×218 |
| = 2×2×2×2×109 |
| = 23×2×109= (একটি পূর্ণসংখ্যা)3 |
| ∴ 1744 একটি পূর্ণঘনসংখ্যা নয় । |
(vi) 1372
সমাধানঃ-
| 1372 |
| = 2×686 |
| = 2×2×343 |
| = 2×2×7×49 |
| = 2×2×7×7×7 |
| = 22×73≠ (কোন পূর্ণসংখ্যা)3 |
| ∴ 1372 একটি পূর্ণঘনসংখ্যা নয়। |
4. দেবনাথ একটি আয়তঘন তৈরি করেছে যার দৈর্ঘ্য, প্রস্থ, ও উচ্চতা যথাক্রমে 4 সেমি., 3 সেমি., ও 3 সেমি.। হিসাব করে দেখি এইরকম কতগুলি আয়তঘন জুড়ে দেবনাথ ঘনক তৈরি করতে পারবে।
সমাধানঃ-
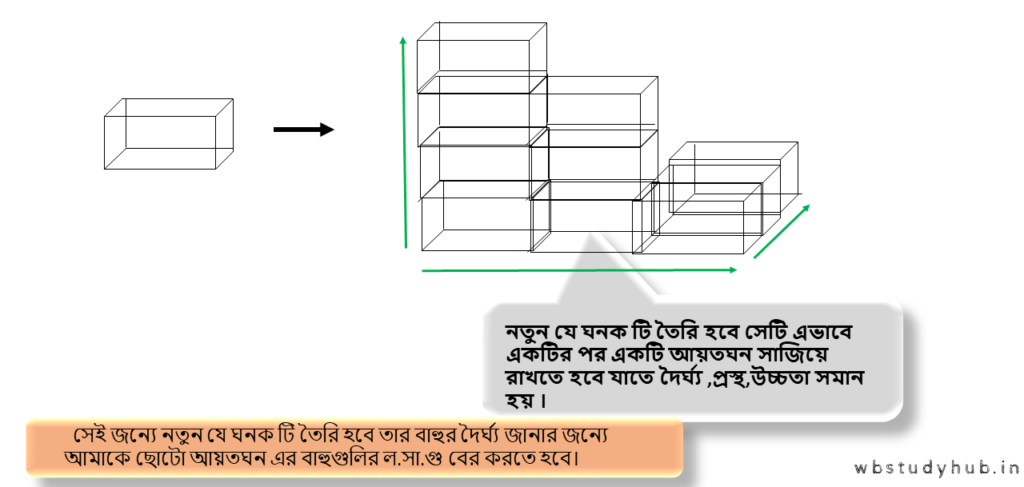
∴ বড়ো ঘনক টির প্রতিটি বাহুর দৈর্ঘ্য হবে-
ল.সা.গু ( 4,3,3) = 12 সেমি.
∴ বড়ো ঘনকটির আয়তন = 123=1728 ঘনসেমি
ছোটো আয়তঘন এর আয়তন = 4×3×3=36 ঘনসেমি
∴ বড়ো ঘনকটির মধ্যে ছোটো আয়তঘন এর সংখ্যা = 1728÷36 = 48 টি ।
| ∴ 48 টি আয়তঘন জুড়ে দেবনাথ ঘনক তৈরি করতে পারবে। |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
5. নীচের সংখ্যাগুলিকে ক্ষুদ্রতম কোন ধনাত্মক সংখ্যা দিয়ে গুণ করলে গুণফল পূর্ণঘন সংখ্যা হবে হিসাব করে লিখি ।
(i) 675
সমাধানঃ-
| 675 |
| = 3×225 |
| = 3 ×3 ×75 |
| = 3×3 ×3 ×25 |
| = 3 ×3 ×3 ×5 ×5 |
| = 33 ×52 [ এখানে আমরা দেখতে পাচ্ছি যে, আর একটি 5 থাকলে সংখ্যা টি পূর্ণঘনসংখ্যা হয়ে যাবে। |
| ∴ 5 ×675 |
| = 5 ×52 ×33 |
| = 53 ×33 |
| = (5 ×3)3 = 153= (একটি পূর্ণসংখ্যা)3 |
| ∴ 5 দিয়ে গুণ করলে গুণফল একটি পূর্ণঘনসংখ্যা হবে। |
(ii) 200
সমাধানঃ-
| 200 |
| = 2 ×100 |
| = 2 ×2 ×50 |
| = 2 ×2 ×2 ×25 |
| = 2 ×2 ×2 ×5 ×5 [ এখানে আমরা দেখতে পাচ্ছি যে, আর একটি 5 থাকলে সংখ্যা টি পূর্ণঘনসংখ্যা হয়ে যাবে। ] |
| ∴ 5 ×200 |
| = 23 ×52 ×5 |
| = 23 ×53 |
| = (2 ×5)3 = 103= (একটি পূর্ণসংখ্যা )3 |
| ∴ 5 দিয়ে গুণ করলে গুণফল একটি পূর্ণঘনসংখ্যা হবে। |
(iii) 108
সমাধানঃ-
| 108 |
| = 3 ×36 |
| = 3 ×3 ×12 |
| = 3 ×3 ×3 ×4 |
| = 3 ×3 ×3 ×2 ×2 |
| = 33 ×22 [ এখানে আমরা দেখতে পাচ্ছি যে, আর একটি 2 থাকলে সংখ্যা টি পূর্ণঘনসংখ্যা হয়ে যাবে। ] |
| ∴ 2 ×108 |
| = 33 ×22 ×2 |
| = 33 ×23 |
| = (3 ×2)3 = 63 = (একটি পূর্ণঘনসংখ্যা)3 |
| ∴ 2 দিয়ে গুণ করলে গুণফল একটি পূর্ণঘনসংখ্যা হবে। |
(iv) 121
সমাধানঃ-
| 121 |
| = 11 ×11 |
| = 112 [ এখানে আমরা দেখতে পাচ্ছি যে, আর একটি 11 থাকলে সংখ্যা টি পূর্ণঘনসংখ্যা হয়ে যাবে ] |
| ∴ 11× 121 |
| = 112 ×11 |
| = 113= (একটি পূর্ণসংখ্যা)3 |
| ∴ 11 দিয়ে গুণ করলে গুণফল একটি পূর্ণঘনসংখ্যা হবে। |
(v) 1225
সমাধানঃ-
| 1225 |
| = 5 ×245 |
| = 5 ×5 ×49 |
| = 5 ×5 ×7 ×7 |
| = 52 ×72 [ এখানে আমরা দেখতে পাচ্ছি যে,একটি 7 ও একটি 5 থাকলে সংখ্যা টি পূর্ণঘনসংখ্যা হয়ে যাবে। ] |
| ∴ 5 ×7 ×1225 |
| = 5 ×7 ×52 ×72 |
| = 5 ×52 ×7 ×72 |
| = 53 ×73 |
| = (5 ×7)3 = 353= (একটি পূর্ণসংখ্যা)3 |
| ∴ 35 দিয়ে গুণ করলে গুণফল একটি পূর্ণঘনসংখ্যা হবে। |
6. নীচের সংখ্যাগুলিকে ক্ষুদ্রতম কোন ধনাত্মক সংখ্যা দিয়ে ভাগ করলে ভাগফল পূর্ণঘন সংখ্যা হবে হিসাব করে লিখি।
(i) 7000
সমাধানঃ-
| 7000 |
| = 10×700 |
| = 10×10×70 |
| = 10×10×10×7 |
| = 103×7 [ আমরা এখানে দেখতে পাচ্ছি যে, সংখ্যাটিকে পূর্ণঘনসংখ্যা হতে হলে 7 কে বাদ দিতে হবে। সুতরাং 7 দিয়ে ভাগ করতে হবে। ] |
∴ সংখ্যাটিকে 7 দিয়ে ভাগ করে পায় ,
| 7000 ÷ 7 |
| = (103×7)÷7 |
| = 103=(একটি পূর্ণসংখ্যা)3 |
| ∴ সংখ্যাটিকে 7 দিয়ে ভাগ করলে ভাগফল একটি পূর্ণঘনসংখ্যা হবে। |
(ii) 2662
সমাধানঃ-
| 2662 |
| = 2×1331 |
| = 2×11×121 |
| = 2×11×11×11 |
| = 2×113 [ আমরা এখানে দেখতে পাচ্ছি যে, সংখ্যাটিকে পূর্ণঘনসংখ্যা হতে হলে 2 কে বাদ দিতে হবে। সুতরাং 2 দিয়ে ভাগ করতে হবে। ] |
∴ সংখ্যাটিকে 2 দিয়ে ভাগ করে পায় ,
| 2662÷2 |
| = (2×113)÷2 |
| = 113= (একটি পূর্ণসংখ্যা)3 |
| ∴ সংখ্যাটিকে 2 দিয়ে ভাগ করলে ভাগফল একটি পূর্ণঘনসংখ্যা হবে । |
(iii) 4394
সমাধানঃ-
| 4394 |
| = 2 ×2197 |
| = 2 ×13 ×169 |
| = 2 ×13 ×13 ×13 |
| = 2 ×133 [ আমরা এখানে দেখতে পাচ্ছি যে, সংখ্যাটিকে পূর্ণঘনসংখ্যা হতে হলে 2 কে বাদ দিতে হবে। সুতরাং 2 দিয়ে ভাগ করতে হবে। ] |
∴ সংখ্যাটিকে 2 দিয়ে ভাগ করে পায়,
| 4394÷2 |
| =(2 ×133)÷2 |
| = 133 = (একটি পূর্ণসংখ্যা)3 |
| ∴ সংখ্যাটিকে 2 দিয়ে ভাগ করলে ভাগফল একটি পূর্ণঘনসংখ্যা হবে । |
(iv) 6750
সমাধানঃ-
| 6750 |
| =5×1350 |
| = 5×5×270 |
| = 5×5×5×54 |
| = 5×5×5×27×2 |
| = 5×5×5×3×3×3×2 |
| = 53×33×2 [ আমরা এখানে দেখতে পাচ্ছি যে, সংখ্যাটিকে পূর্ণঘনসংখ্যা হতে হলে 2 কে বাদ দিতে হবে। সুতরাং 2 দিয়ে ভাগ করতে হবে। ] |
∴ সংখ্যাটিকে 2 দিয়ে ভাগ করে পায়,
| 6750÷2 |
| = (53×33×2)÷2 |
| = 53×33 |
| = (5×3)3 = 153 = (একটি পূর্ণসংখ্যা)3 |
| ∴ সংখ্যাটিকে 2 দিয়ে ভাগ করলে ভাগফল একটি পূর্ণঘনসংখ্যা হবে । |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
(v) 675
সমাধানঃ-
| 675 |
| = 5×135 |
| = 5×5×27 |
| = 5×5×3×9 |
| = 5×5×3×3×3 |
| = 25×33 [ আমরা এখানে দেখতে পাচ্ছি যে, সংখ্যাটিকে পূর্ণঘনসংখ্যা হতে হলে 25 কে বাদ দিতে হবে। সুতরাং 25 দিয়ে ভাগ করতে হবে। ] |
∴ সংখ্যাটিকে 25 দিয়ে ভাগ করে পায়,
| 675÷25 |
| =(25×33)÷25 |
| = 33 = (একটি পূর্ণসংখ্যা)3 |
| ∴ সংখ্যাটিকে 25 দিয়ে ভাগ করলে ভাগফল একটি পূর্ণঘনসংখ্যা হবে । |
7. নীচের পূর্ণঘনসংখ্যাগুলি মৌলিক উৎপাদকে বিশ্লেষণ করি ও ঘনমূল লিখি ।
(i) 512
সমাধানঃ-
| 512 |
| =2×256 |
| =2×2×128 |
| = 2×2×2×64 |
| = 2×2×2×2×32 |
| = 2×2×2×2×2×16 |
| = 2×2×2×2×2×2×8 |
| = 2×2×2×2×2×2×2×4 |
| = 2×2×2×2×2×2×2×2×2 |
| = (2×2×2)×(2×2×2)×(2×2×2) |
| = 23×23×23 |
| = (2×2×2)3 |
| = 83 |
| ∴ 512 এর ঘনমূল হলো 8 . |
(ii) 1728
সমাধানঃ-
| 1728 |
| = 2×864 |
| = 2×2×432 |
| = 2×2×2×216 |
| = 2×2×2×2×108 |
| = 2×2×2×2×2×54 |
| = 2×2×2×2×2×2×27 |
| = 2×2×2×2×2×2×3×9 |
| = 2×2×2×2×2×2×3×3×3 |
| =(2×2×2)×(2×2×2)×(3×3×3) |
| = 23×23×33 |
| = (2×2×3)3 |
| =123 |
| ∴ 1728 এর ঘনমূল হলো 12 । |
(iii) 5832
সমাধানঃ-
| 5832 |
| = 2×2916 |
| = 2×2×1458 |
| = 2×2×2×729 |
| = 2×2×2×9×81 |
| = 2×2×2×9×9×9 |
| = (2×2×2)×(9×9×9) |
| = 23×93 |
| = (2×9)3 |
| = 183 |
| ∴ 15625 এর ঘনমূল হলো 25 । |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
(iv) 15625
সমাধানঃ-
| 15625 |
| = 5×3125 |
| = 5×5×625 |
| = 5×5×5×125 |
| = 5×5×5×5×25 |
| = 5×5×5×5×5×5 |
| = (5×5×5)×(5×5×5) |
| = 53×53 |
| = (5×5)3 |
| = 253 |
| ∴ 15625 এর ঘনমূল হলো 25 । |
(v) 10648
সমাধানঃ-
| 10648 |
| = 2×5324 |
| = 2×2×2662 |
| = 2×2×2×1331 |
| = 2×2×2×11×121 |
| = 2×2×2×11×11×11 |
| = (2×2×2)×(11×11×11) |
| = 23×113 |
| = (2×11)3 |
| = 223 |
| ∴ 10648 এর ঘনমূল হলো 22 । |
এই কষে দেখি 5.1 Class 8|Koshe Dekhi 5.1 Class 8 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 5.1 Class 8 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 5.1 Class 8 তারপর  |
| ঘনফল নির্ণয় অধ্যায়ের- | |
|---|---|
 |  কষে দেখি 5.2 কষে দেখি 5.2 |
 |  কষে দেখি-5.3 কষে দেখি-5.3 |
| গনিতপ্রভা অষ্টম শ্রেণীর সমস্ত অধ্যায়ের সমাধান- | |
|---|---|
| অধ্যায় | সমাধান |
| 2. পাই চিত্র | কষে দেখি 2 |
| 3. মূলদ সংখ্যার ধারণা | অধ্যায়ের সারাংশ |
| কষে দেখি 3 | |
| 4. বীজগাণিতিক সংখ্যামালার গুণ ও ভাগ | অধ্যায়ের সারাংশ |
| কষে দেখি 4.1 | |
| কষে দেখি 4.2 | |
| 5. ঘনফল নির্ণয় | অধ্যায়ের সারাংশ |
| কষে দেখি 5.1 | |
| কষে দেখি 5.2 | |
| কষে দেখি 5.3 | |
| 6. পূরক কোণ, সম্পূরক কোণ ও সন্নিহিত কোণ | অধ্যায়ের সারাংশ |
| কষে দেখি 6 | |
| 7. বিপ্রতীপ কোণের ধারণা | অধ্যায়ের সারাংশ |
| কষে দেখি 7.1 | |
8. সমান্তরাল সরলরেখা ও ছেদকের ধর্ম | অধ্যায়ের সারাংশ |
| কষে দেখি 8 | |
9. ত্রিভুজের দুটি বাহু ও তাদের বিপরীত কোণের সম্পর্ক | অধ্যায়ের সারাংশ |
| কষে দেখি 9 | |
| 10. ত্রৈরাশিক | কষে দেখি 10.1 |
| কষে দেখি 10.2 | |
| 11. শতকরা | কষে দেখি 11 |
| 12. মিশ্রণ | কষে দেখি 12 |
13. বীজগাণিতিক সংখ্যামালার উৎপাদকে বিশ্লেষণ | কষে দেখি 13.1 |
| কষে দেখি 13.2 | |
14. বীজগাণিতিক সংখ্যামালার গ.সা.গু ও ল.সা.গু | কষে দেখি 14 |
15. বীজগাণিতিক সংখ্যামালার সরলীকরণ | কষে দেখি 15 |
16. ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই | কষে দেখি 16.1 |
| কষে দেখি 16.2 | |
17. সময় ও কার্য | কষে দেখি 17.1 |
| কষে দেখি 17.2 | |
18. লেখচিত্র | কষে দেখি 18 |
19. সমীকরণ গঠন ও সমাধান | কষে দেখি 19 |
| 20. জ্যামিতিক প্রমাণ | কষে দেখি 20.1 |
| কষে দেখি 20.2 | |
| কষে দেখি 20.3 | |

এখানে তোমরা তোমাদের অষ্টম শ্রেণীতে কি কি পড়ানো হয়, মানে তোমাদের অষ্টম শ্রেণীর সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।



