কষে দেখি 5.3 Class 8।ঘনফল নির্ণয় কষে দেখি 5.3 | Koshe Dekhi 5.3 Class 8 WBBSE

শ্রেণী-অষ্টম ; অধ্যায় – ঘনফল নির্ণয় ; কষে দেখি – 5.3

---

ঘনফল নির্ণয় অধ্যায় থেকে অধ্যায়ের সারাংশতে আমরা জেনেছি –

-> ঘনক কি ?

-> ঘনফল কাকে বলে?

-> ঘনকের আয়তনের সূত্র কী?/ঘনকের ঘনফলের সূত্র

-> পূর্ণঘনসংখ্যা কাকে বলে?

-> ঘনমূল কি?

-> কিছু সূত্র ।

যদি তোমরা অধ্যায়ের সারাংশ না দেখে থাকো তাহলে একবার দেখে নিও ।

আমাদের শুধু অধ্যায়ের সারাংশ বুঝলেই হবেনা , তারসাথে আমি কতোটা শিখলাম , নিজে কতোটা বুঝলাম এবং নিজে নিজে কারোর সাহাজ্য ছাড়ায় কতোটা অংক সমাধান করতে পারবো তা বীজগাণিতিক সংখ্যামালার গুণ ও ভাগ ঘনফল নির্ণয় কষে দেখি 5.3 Class 8 | Koshe Dekhi 5.3 Class 8 থেকে অংক করলে তবেই বুঝতে পারবো।

শুধু তায় নয়, অংক যতো সমাধান করা যাবে ( নিজে নিজে ) ততো নিজের প্রতি বিশ্বাস টা শক্ত হবে। এমনকি এই বিষয়ে নতুন অংক সামনে পেলে সেটা করতে সাহস পাবে ।

পাঠ ক্রম হল কয়েকটি বিষয়ের এবং পরিকল্পিত অভিজ্ঞতার শৃঙ্খলাবদ্ধ সমষ্টি।

কার্টার ভি গুড

এবার ঘনফল নির্ণয় কষে দেখি 5.3 Class 8 | Koshe Dekhi 5.3 Class 8 আমরা শুরু করবো। । এখানে প্রতিটি অঙ্ক সুন্দর করে STEP BY STEP গুছিয়ে লেখা হয়েছে এবং সহজ ভাষায় উপস্থাপন করা হয়েছে যাতে তোমরা সহজেই এই কষে দেখি 5.3 Class 8 এর প্রতিটি অঙ্ক বুঝতে পারো তারসাথে ভবিষ্যতে এরকম অংক পরীক্ষায় আসলে তা যেনো সহজেই করে উঠতে পারো।

আগে তোমরা নিজেরা অংক গুলি করবে, তারপর যেখানে আটকে যাবে এখান থেকে দেখে নেবে ।

এখানে করে দেওয়া অংক গুলি ভালো ভাবে বোঝার জন্যে নিম্নে কিছু নির্দেশিকা তোমাদের জন্যে থাকলোঃ

কিছু উপদেশঃ-

• প্রথমত প্রতিটি অংক খুবই সহজ ভাবে করা হয়েছে

• প্রতিটি অঙ্কে এক লাইন থেকে আর এক লাইন কি কারনে হলো সেটা বলা হয়েছে এবং সেটা আলাদা box এর মধ্যে লিখে দেখানো হয়েছে।
  • তারসাথে arrow চিহ্ন প্রয়োগ করেও দেখানো হয়েছে

• প্রতিটি লাইনে কি সুত্র প্রয়োগ করে অঙ্কটি সমাধান করা হয়েছে সেটা আলাদা করে পাশে উল্লেখ করা হয়েছে।

• প্রতিটি প্রশ্নের উত্তর কিভাবে লিখতে হবে তা সমাধানের শেষে আলাদা ভাবে box এর মধ্যে লিখে দেওয়া হয়েছে

---

আগামিতে এই কষে দেখি 5.3 Class 8 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?

আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে?
কষে দেখি 5.3 Class 8 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 5.3 Class 8 তারপর 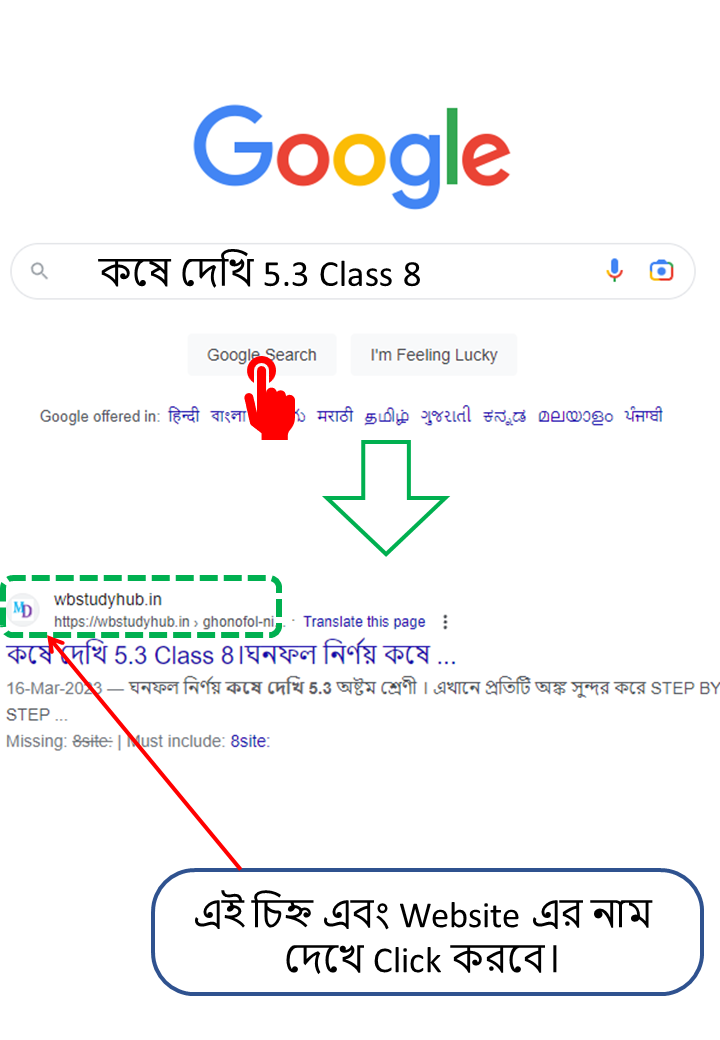এই চিহ্ন দেখে Click করলে আবার তোমরা এখানে এসে যাবে।

---

কষে দেখি 5.3 | Koshe Dekhi 5.3

---

1. ফাঁকা ঘরে বুঝে লিখি :

---

( i )

প্রথম বীজগাণিতিক সংখ্যামালা	দ্বিতীয় বীজগাণিতিক সংখ্যামালা	অভেদের সাহায্যে প্রথম ও দ্বিতীয়ের গুণফল
x + 9	x2 – 9x + 81

সমাধানঃ-

প্রথম ও দ্বিতীয় বীজগাণিতিক সংখ্যামালা গুণ করে পায় ,

                   (x + 9)(x² – 9x + 81)

এখানে দেখো  a= x  এবং  b = 9 ধরলে a3 + b3 = (a + b)(a2 – ab + b2) সূত্রের গঠনে চলে আসছে ।

(x + 9)(x2 – 9x + 81)

= x3 + 93 [ ∵  a3 + b3 = (a + b)(a2 – ab + b2) ]

= x3  + 729

∴ গুণফল = x3  + 729

( ii )

প্রথম বীজগাণিতিক সংখ্যামালা	দ্বিতীয় বীজগাণিতিক সংখ্যামালা	অভেদের সাহায্যে প্রথম ও দ্বিতীয়ের গুণফল
2a – 1		8a3 – 1 =  (2a)3 – (1)3 = (2a – 1){(2a)2+2a×1+(1)2} = (2a – 1)( 4a2 + 2a + 1)

সমাধানঃ-

             দেওয়া আছে,

গুণফল = 8a³ – 1

8a3 – 1

= (2a – 1)( 4a2 + 2a + 1 )

∴ দ্বিতীয় বীজগাণিতিক সংখ্যামালাটি হলো  – 4a2 + 2a + 1

---

Request For Share
সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share]

---

( iii )

প্রথম বীজগাণিতিক সংখ্যামালা	দ্বিতীয় বীজগাণিতিক সংখ্যামালা	অভেদের সাহায্যে প্রথম ও দ্বিতীয়ের গুণফল
3 – 5c		27 – 125c3

সমাধানঃ-

বীজগাণিতিক সংখ্যামালাদ্বয়ের গুণফল = 27 – 125c³

27 – 125c3

= (3)3 – (5c)3

= (3 – 5c) {(3)2 + 3×5c + (5c)2} [ ∵  a3 + b3= (a + b)(a2 – ab + b2) ]

= (3 – 5c)(9 + 15c + 25c2)

∴ দ্বিতীয় বীজগাণিতিক সংখ্যামালাটি হলো -(9 + 15c + 25c2)

---

( iv )

প্রথম বীজগাণিতিক সংখ্যামালা	দ্বিতীয় বীজগাণিতিক সংখ্যামালা	অভেদের সাহায্যে প্রথম ও দ্বিতীয়ের গুণফল
(a + b + c)	(a+b)2-(a+b)c+c2

সমাধানঃ-

সংখ্যাদ্বয়ের গুণফল = (a + b + c){(a+b)² – (a+b)c + c²}

(a + b + c){(a+b)2 – (a+b)c + c2}

= {(a+b)+c} {(a+b)2 – (a+b)c + c2}

[ এখানে দেখো  p= a+b  এবং  q = c ধরলে p3 + q3 = (p + q)(p2 – pq + q2) সূত্রের গঠনে চলে আসছে । ]

= (a+b)3 + c3

∴ সংখ্যাদ্বয়ের গুণফল   = (a+b)3 + c3

---

( v )

প্রথম বীজগাণিতিক সংখ্যামালা	দ্বিতীয় বীজগাণিতিক সংখ্যামালা	অভেদের সাহায্যে প্রথম ও দ্বিতীয়ের গুণফল
3x	(2x-1)2 – (2x-1)(x+1)+(x+1)2

সমাধানঃ-

সংখ্যাদ্বয়ের গুণফল = (3x) {(2x-1)² – (2x-1)(x+1)+(x+1)²}

(3x) {(2x-1)2 – (2x-1)(x+1)+(x+1)2}

= {(2x – 1)+(x+1)} {(2x-1)2 – (2x-1)(x+1)+(x+1)2}

[ এখানে দেখো  a= 2x – 1  এবং  b =x + 1 ধরলে a3 + b3 = (a + b)(a2 – ab + b2) সূত্রের গঠনে চলে আসছে । ]

= (2x – 1)3 + (x + 1)3

∴ গুণফল = (2x – 1)3 + (x + 1)3

---

( vi )

প্রথম বীজগাণিতিক সংখ্যামালা	দ্বিতীয় বীজগাণিতিক সংখ্যামালা	অভেদের সাহায্যে প্রথম ও দ্বিতীয়ের গুণফল
x/y  + 1	x2/y2   – x/y  + 1

সমাধানঃ-

সংখ্যামালাদ্বয়ের গুণফল =   ( x/y  + 1 )(x²/y²  – x/y  + 1 )

( x/y  + 1 )(x2/y2  – x/y  + 1 )

= ( x/y  + 1 ){ x2/y2  – (x/y)×1  + 1 }

[ এখানে দেখো  a= x/y   এবং  b =  1 ধরলে a3 + b3 = (a + b)(a2 – ab + b2) সূত্রের গঠনে চলে আসছে । ]

= x3/y3  + 13

= x3/y3  + 1

∴ গুণফল = x3/y3  + 1

---

( vii )

প্রথম বীজগাণিতিক সংখ্যামালা	দ্বিতীয় বীজগাণিতিক সংখ্যামালা	অভেদের সাহায্যে প্রথম ও দ্বিতীয়ের গুণফল
4a  – 5b	16a2 + 20ab +25b2

সমাধানঃ-

সংখ্যাদ্বয়ের গুনফল = (4a  – 5b)(16a² + 20ab +25b²)

(4a  – 5b)(16a2 + 20ab +25b2)

= (4a – 5b){(4a)2 + 4a × 5b + (5b)2}

[ এখানে দেখো  p= 4a  এবং  q = 5b ধরলে p3 – q3 = (p – q)(p2 + pq + q2) সূত্রের গঠনে চলে আসছে । ]

= (4a)3 – (5b)3

= 16a3 – 125b3

∴ গুণফল = 16a3 – 125b3

---

( viii )

প্রথম বীজগাণিতিক সংখ্যামালা	দ্বিতীয় বীজগাণিতিক সংখ্যামালা	অভেদের সাহায্যে প্রথম ও দ্বিতীয়ের গুণফল
	a2b2  + abcd + c2d2	a3b3 – c3d3

সমাধানঃ-

সংখ্যামালাদ্বয়ের গুণফল =  a³b³ – c³d³

a3b3 – c3d3

= (ab)3 – (cd)3

[ এখানে দেখো  p= ab  এবং  q = cd ধরলে p3 – q3 = (p – q)(p2 + pq + q2) সূত্রের গঠনে চলে আসছে । ]

= (ab – cd){(ab)2 + (ab)(cd) + (cd)2}

=(ab – cd)(a2b2  + abcd + c2d2)

∴ প্রথম বীজগাণিতিক সংখ্যামালা= ab – cd

---

( ix )

প্রথম বীজগাণিতিক সংখ্যামালা	দ্বিতীয় বীজগাণিতিক সংখ্যামালা	অভেদের সাহায্যে প্রথম ও দ্বিতীয়ের গুণফল
1 – 4y	1 – 64y3

সমাধানঃ-

সংখ্যামালাদ্বয়ের গুণফল = 1 – 64y³

1 – 64y3

= (1)3 – (4y)3

[ এখানে দেখো  p= 1  এবং  q = 4y ধরলে p3- q3= (p – q)(p2 + pq + q2) সূত্রের গঠনে চলে আসছে । ]

= (1 – 4y){(1)2 + 1×4y + (4y)2}

= (1 – 4y)(1+4y+16y2)

∴ দ্বিতীয় বীজগাণিতিক সংখ্যামালা = 1+4y+16y2

---

Request For Share
সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share]

---

( x )

প্রথম বীজগাণিতিক সংখ্যামালা	দ্বিতীয় বীজগাণিতিক সংখ্যামালা	অভেদের সাহায্যে প্রথম ও দ্বিতীয়ের গুণফল
(2p+1)		8(p – 3)3 + 343

সমাধানঃ-

সংখ্যামালাদ্বয়ের গুণফল = 8(p – 3)³ + 343

8(p – 3)3 + 343

= {2(p – 3)}3 + (7)3

[ এখানে দেখো  a= 2(p – 3) এবং  b = 7 ধরলে a3– b3 = (a – b)(a2 + ab + b2) সূত্রের গঠনে চলে আসছে । ]

= {2(p – 3) + 7}[{2(p – 3)}2 + {2(p – 3)}×7 + (7)2]

= (2p – 6 +7){4(p – 3)2 + 14(p – 3) + 49}

= (2p + 1){4(p2 – 2×p×3 +32 )+ 14p – 3×14 + 49 }

= (2p + 1)(4p2 – 4×2×3×p + 4×32 + 14p – 42 + 49)

= (2p+1)(4p2 – 24p + 36 + 14p – 42 + 49)

= (2p + 1)(4p2 – 10p + 29)

∴ দ্বিতীয় বীজগাণিতিক সংখ্যামালা = 4p2 – 10p + 29 [ বই – এ যে উত্তর টা আছে সেটাকে ভাঙ্গলে এটাই আসবে , তোমাদের যেটা ইচ্ছে সেটা লিখবে/রেখে দেবে । ]

---

( xi )

প্রথম বীজগাণিতিক সংখ্যামালা	দ্বিতীয় বীজগাণিতিক সংখ্যামালা	অভেদের সাহায্যে প্রথম ও দ্বিতীয়ের গুণফল
(m – p)	(m+n)2 + (m+n)(n+p)+(n+p)2

সমাধানঃ-

সংখ্যাদ্বয়ের গুণফল = (m – p){(m+n)² + (m+n)(n+p)+(n+p)²}

(m – p){(m+n)2 + (m+n)(n+p)+(n+p)2}

= {(m+n) – (n+p)}{(m+n)2 + (m+n)(n+p)+(n+p)2}  [ ∵ m – p =(m+n) – (n+p) ]

[ এখানে দেখো  a=m+n  এবং  b =n+p ধরলে a3 – b3 = (a + b)(a2 + ab + b2) সূত্রের গঠনে চলে আসছে । ]

= {(m+n)3 – (n+p)3}

∴ সংখ্যাদ্বয়ের গুণফল = (m+n)3 – (n+p)3

---

( xii )

প্রথম বীজগাণিতিক সংখ্যামালা	দ্বিতীয় বীজগাণিতিক সংখ্যামালা	অভেদের সাহায্যে প্রথম ও দ্বিতীয়ের গুণফল
(3a – 2b)2 +(3a-2b)×(2a-3b) +(2a-3b)2	a + b

সমাধানঃ-

সংখ্যামালাদ্বয়ের গুণফল = {(3a – 2b)²+(3a-2b)×(2a-3b)+(2a-3b)²}(a + b)

{(3a – 2b)2+(3a-2b)×(2a-3b)+(2a-3b)2}(a + b)

= (a + b) {(3a – 2b)2+(3a-2b)×(2a-3b)+(2a-3b)2}

= {(3a – 2b) – (2a – 3b)} {(3a – 2b)2+(3a-2b)×(2a-3b)+(2a-3b)2}  [ ∵  a+b= (3a – 2b) – (2a – 3b) ]

[ এখানে দেখো  p=3a-2b  এবং  q = 2a-3b ধরলে p3– q3 = (p – q)(p2 + pq + q2) সূত্রের গঠনে চলে আসছে । ]

= {(3a – 2b)3 – (2a – 3b)3 }

∴ সংখ্যামালাদ্বয়ের গুণফল = (3a – 2b)3 – (2a – 3b)3

---

Request For Share
সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share]

---

2. সরল করি [ সূত্রের সাহায্যে ]

---

( i )  (a+b) (a – b) (a²+ab+b²) (a² – ab+b²)

সমাধানঃ-

(a+b) (a – b) (a2+ab+b2) (a2 – ab+b2)

= (a+b) (a2 – ab+b2) (a – b) (a2+ab+b2)

= (a3 + b3)(a3 – b3) [ ∵  a3 + b3 = (a + b)(a2 – ab + b2) এবং   a3 – b3 = (a – b)(a2 + ab + b2) ]

= (a3)2 – (b3)2            [∵ (a+b)(a – b)=a2 – b2 ]

= a6 – b6

∴ উত্তর – a6 – b6

---

( ii ) (a – 2b) (a² + 2ab +4b²) (a³+8b³)

সমাধানঃ-

(a – 2b) (a2 + 2ab +4b2) (a3+8b3)

= (a – 2b){a2 + 2ab + (2b)2}(a3+8b3)

এখানে দেখো  p=a  এবং  q = 2b ধরলে p3 – q3 = (p – q)(p2 + pq + q2) সূত্রের গঠনে চলে আসছে ।

= {(a)3 – (2b)3}(a3 + 8b3)

= (a3 – 8b3)(a3 + 8b3)

= {(a3)2 – (8b3)2}             [ ∵ (a+b)(a-b)=a2 – b2 ]

= a6 – 64b6

∴ উত্তর – a6 – 64b6

---

( iii ) ( 4a² – 9 )( 4a² – 6a + 9 )( 4a² + 6a +9 )

সমাধানঃ-

(4a2 – 9)(4a2 – 6a + 9)(4a2 + 6a +9)

= {(2a)2–(3)2}{(2a)2–2a×3+(3)2}{(2a)2 +2a×3+(3)2}

= (2a+3)(2a–3){(2a)2–2a×3+(3)2}{(2a)2 +2a×3+(3)2}

= (2a+3){(2a)2–2a×3+(3)2}(2a–3){(2a)2 +2a×3+(3)2}

[ এখানে দেখো  p=2a  এবং  q =3  ধরলে p3 – q3 = (p – q)(p2 + pq + q2) এবং  p3 + q3 = (p – q)(p2 + pq + q2) সূত্রের গঠনে চলে আসছে ]

= (8a3 + 27)(8a3 – 27)

= {(8a3)2 – (27)2}      [ ∵ (a+b)(a-b)=a2 – b2 ]

= (64a6 – 729)

∴ উত্তর – 64a6 – 729

---

( iv ) ( x – y ) ( x² + xy + y² ) + ( y – z )( y² + yz + z² ) + ( z – x )( z² + ax + x² )

সমাধানঃ-

(x-y)(x2+xy+y2)+(y-z)(y2+yz+z2)+(z-x)(z2+ax+x2)

= (x3 – y3) + (y3 – z3) + (z3 – x3 ) [ ∵  a3 – b3 = (a – b)(a2 + ab + b2) ]

= x3 – y3 + y3 – z3 + z3 – x3

= 0

∴ উত্তর – 0

---

( v ) ( x + 1 ) (x² – x + 1 ) + ( 2x – 1 )( 4x² + 2x + 1 ) – ( x – 1 )( x² + x + 1 )

সমাধানঃ-

(x+1)(x2-x+1)+(2x-1)(4x2+2x+1)-(x-1)(x2+x+1)

= (x+1)(x2-x+1)+(2x-1){(2x)2+(2x)×1 + (1)2} – (x-1)(x2+x+1)

= {x3 + (1)3} +{(2x)3 – (1)3} – {x3 – (1)3}

= x3 + 1 + 8x3 – 1 – x3 + 1

= 8x3 + 1

∴       উত্তর –   8x3 + 1

---

Request For Share
সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share]

---

3.

সমাধানঃ-

---

4. a + 9/a = 3  হলে  (a³ + 27)  -এর মান কি হবে হিসাব করে লিখি ।

সমাধানঃ-

দেওয়া আছে ,

a + 9/a = 3

⇒  a2 + 9/a = 3

⇒ a2 + 9 = 3a

⇒ a2 – 3a + 9 = 0     —-(i)

a3 + 27

= a3 + (3)3

= (a+3)(a2 – 3a + 9) [ ∵  a3 + b3 = (a + b)(a2 – ab + b2) ]

= (a + 3)× 0      [  (i)নং থেকে মান বসিয়ে পাই ]

= 0

∴    a + 9/a = 3  হলে  (a3 + 27) = 0 .

---

5. a/b + b/a = 1  হলে  ( a³ + b³) – এর মান কি হবে হিসাব করে লিখি ।

সমাধানঃ-

                 দেওয়া আছে,

a/b + b/a = 1

⇒  ( a2+b2)/(ab)   = 1

⇒  a2 + b2 = ab

⇒ a2 – ab + b2 = 0   ——(i)

a3 + b3

= (a + b)(a2 – ab + b2 )

= (a + b)×0 [ ( i ) থেকে মান বসিয়ে পায় ]

= 0

∴    a/b + b/a = 1  হলে  ( a3 + b3) = 0 ।

---

6. নীচের বীজগাণিতিক সংখ্যামালাগুলিকে উৎপাদকে বিশ্লেষণ করি ।

---

( i ) 1000a³ + 27b⁶

সমাধানঃ-

1000a3 + 27b6

= (10a)3 + (3b2 )3

= (10a + 3b2){(10a)2 – 10a×3b2 +(3b2)2 }  [ ∵  a3 + b3 = (a + b)(a2 – ab + b2) ]

=  (10a + 3b2)(100a2 – 30ab2 + 9b4)

∴       উত্তর = (10a + 3b2)(100a2 – 30ab2 + 9b4)

---

( ii ) 1 – 216z³

সমাধানঃ-

1 – 216z3

= (1)3 – (6z)3

= (1 – 6z){(1)2 + 1×6z + (6z)2}  [ ∵  a3 – b3 = (a – b)(a2 + ab + b2) ]

= (1 – 6z)(1 + 6z + 36z2)

∴       উত্তর= (1 – 6z)(1 + 6z + 36z2)

---

( iii ) m⁴ – m

সমাধানঃ-

m4 – m

= m(m3 – 1)

= m{(m)3 – (1)3 }

= m(m – 1)(m2 + m ×1 + 12)   [ ∵  a3 – b3= (a – b)(a2 + ab + b2) ]

= m(m – 1)(m2 + m + 1)

∴       উত্তর = m(m – 1)(m2 + m + 1)

---

( iv ) 192a³ + 3

সমাধানঃ-

192a3 + 3

= 3( 64a3 + 1)

= 3 {(4a)3 + (1)3}

= 3 (4a + 1){(4a)2 – 4a×1 + (1)2}  [ ∵  a3 + b3 = (a + b)(a2 – ab + b2) ]

= 3 (4a + 1)(16a2 – 4a + 1)

∴       উত্তর = 3 (4a + 1)(16a2 – 4a + 1)

---

Request For Share
সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share]

---

( v ) 16a⁴x³ + 54ay³

সমাধানঃ-

16a4x3 + 54ay3

= 2a(8a3x3 + 27y3)

= 2a{(2ax)3 + (3y)3}

= 2a ( 2ax + 3y){(2ax)2 – (2ax)×(3y) + (3y)2}  [ ∵  a3 + b3 = (a + b)(a2 – ab + b2) ]

= 2a (2ax + 3y)( 4a2x2 – 6axy + 9y2)

∴       উত্তর = 2a (2ax + 3y)( 4a2x2 – 6axy + 9y2)

---

( vi ) 729a³b³c³ – 125

সমাধানঃ-

729a3b3c3 – 125

= (9abc)3 – (5)3

= ( 9abc – 5){(9abc)2 + (9abc)×5 + (5)2}  [ ∵ a3 – b3 = (a – b)(a2 + ab + b2) ]

= (9abc – 5)( 81a2b2c2 + 45abc + 25)

∴       উত্তর= (9abc – 5)( 81a2b2c2 + 45abc + 25)

---

( vii ) 27/a³  –  1/(27b³)

সমাধানঃ-

27/a3  –  1/(27b3)

=  ( 3/a )3  –  { 1/(3b) }3

= { 3/a   –  1/(3b) } [( 3/a )2 +3/a  ×1/(3b)   + {1/(3b)}2]  [ ∵  a3 – b3 = (a – b)(a2 + ab + b2) ]

= { 3/a   –  1/(3b)} { 9/a2 + 1/(ab) + 1/(9b)2}

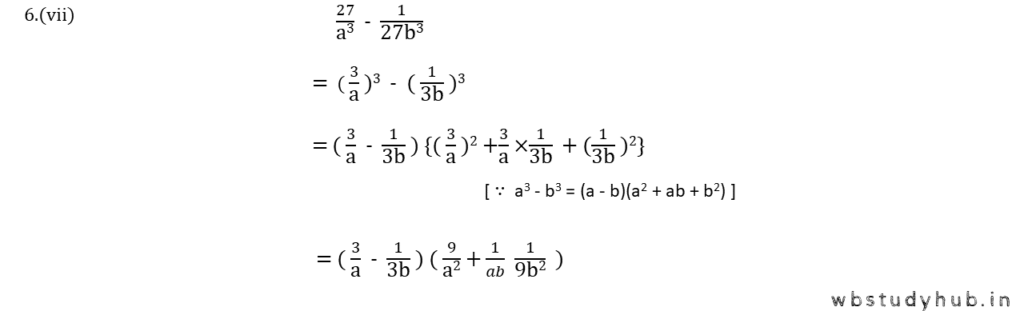
∴       উত্তর = { 3/a   –  1/(3b)} { 9/a2 + 1/(ab) + 1/(9b)2}

---

( viii ) x³/64 –  64/x³

সমাধানঃ-

x3/64 –  64/x3

= ( x/4 )3 – ( 4/x  )3

= ( x/4  – 4/x ) { ( x/4 )2 +  x/4  × 4/x  + ( 4/x )2 }  [ ∵  a3 + b3 = (a + b)(a2 – ab + b2) ]

= ( x/4  –  4/x ) (  x2/16  + 1 + 16/x2  )

∴       উত্তর = ( x/4  –  4/x ) (  x2/16  + 1 + 16/x2  )

---

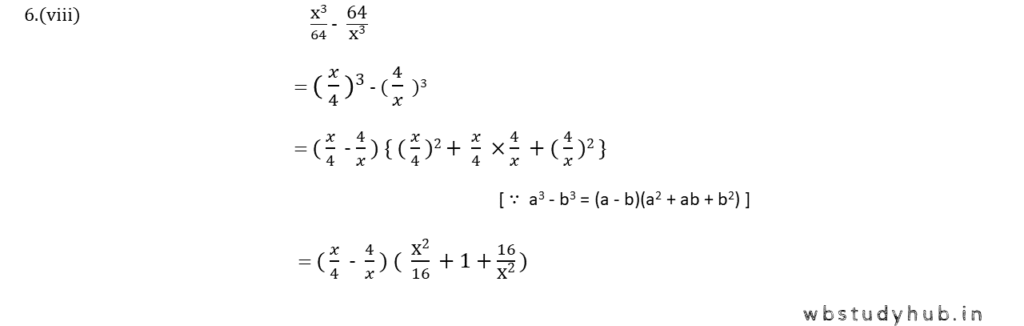
( ix )  x³ + 3x²y + 3xy² + 2y³

সমাধানঃ-

x3 + 3x2y + 3xy2 + 2y3

= x3 + 3x2y + 3xy2 + y3 + y3

= (x + y)3 + y3      [ ∵ a3 +3a2b+3ab2+b3=(a+b)3]

এখানে দেখো  p=x+y  এবং  q=y ধরলে  a3 + b3 = (a + b)(a2 – ab + b2) সূত্রের গঠনে চলে আসছে ।

= ( x+y+y){(x+y)2 – (x+y)y + y2 }

= (x+2y) ( x2 +2xy + y2 – xy – y2 + y2 }

= (x+2y) (x2 + xy +y2 )

∴ উত্তর = (x+2y) (x2 + xy +y2 )

---

Request For Share
সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share]

---

( x ) 1 + 9x + 27x² + 28x³

সমাধানঃ-

1 + 9x + 27x2 + 28x3

= 1 + 9x + 27x2 + 27x3 + x3

= (1)3 + 3×(1)2 ×(3x) + 3 ×1 ×(3x)2 + (3x)3 + x3  [ ∵  (a+b)3 = a3+3a2b+3ab2 + b3 ]

= ( 1 + 3x)3 + x3

= ( 1 + 3x + x) { (1+3x)2 – (1+3x)x + x2 }  [ ∵  a3 + b3 = (a + b)(a2 – ab + b2) ]

= ( 1 + 4x ) { (1)2 + 2 ×1 ×3x + (3x)2 – x – 3x2 + x2 }

= ( 1 + 4x ) ( 1 +6x + 9x2 – x – 3x2 + x2 )

= ( 1 + 4x)( 1 + 5x + 7x2 )

∴ উত্তর = ( 1 + 4x)( 1 + 5x + 7x2 )

---

( xi ) x³ – 9y³ – 3xy (x – y)

সমাধানঃ-

x3 – 9y3 – 3xy (x – y)

= x3 – y3 – 3xy(x – y) – 8y3  [ ∵  (a-b)3 = a3 – b3 – 3ab(a – b) ]

= (x – y)3 – 8y3

= (x – y)3 – (2y)3

এখানে দেখো  a=x – y  এবং  b = 2y ধরলে  a3 – b3 = (a – b)(a2 + ab + b2) সূত্রের গঠনে চলে আসছে ।

= (x – y – 2y) {(x – y)2 + (x – y)2y + (2y)2 }

= ( x – 3y)( x2 – 2xy + y2 + 2xy – 2y2 + 4y2 )

= ( x – 3y) ( x2 + 3y2 )

∴ উত্তর= ( x – 3y) ( x2 + 3y2 )

---

( xii ) 8 – a³ + 3a²b – 3ab² + b³

সমাধানঃ-

8 – a3 + 3a2b – 3ab2 + b3

= (2)3 – (a3 – 3a2b + 3ab2 –  b3 )

= (2)3 – ( a – b)3  [ ∵  (a-b)3 = a3– 3a2b+3ab2 – b3 ]

= { 2 – ( a – b)} { (2)2 + 2 (a – b) + ( a – b)2}  [ ∵  a3 – b3 = (a – b)(a2 + ab + b2) ]

= ( 2 – a + b) ( 4 + 2a – 2b + a2 – 2ab + b2 )

= ( 2 – a + b) ( a2 – 2ab + 2a – 2b + 4)

∴ উত্তর= ( 2 – a + b) ( a2 – 2ab + 2a – 2b + 4)

---

( xiii ) x⁶ + 3x⁴b² + 3x²b⁴ + b⁶ + a³b³

সমাধানঃ-

x6 + 3x4b2 + 3x2b4 + b6 + a3b3

= (x2)3 + 3 (x2)2b2 + 3 x2(b2)2 + (b2)3 + a3b3

এখানে দেখো  p=x2  এবং  q =b2 ধরলে   (p+q)3 = p3+3p2q+3pq2 + q3 সূত্রের গঠনে চলে আসছে ।

= ( x2 + b2 )3 + a3b3

= ( x2 + b2 )3 + (ab)3

= ( x2 + b2 + ab ) { (x2  + b2 )2 – ( x2 + b2 )ab + (ab)2}  [ ∵  a3 + b3 = (a + b)(a2 – ab + b2) ]

= ( x2 + b2 + ab ) { (x2)2 + 2x2b2 + (b2)2 – abx2 – ab3 + a2b2 }

= ( x2 + b2 + ab )( x4 + 2x2b2 + b4 – abx2 – ab3 + a2b2)

∴ উত্তর= ( x2 + b2 + ab )( x4 + 2x2b2 + b4 – abx2 – ab3 + a2b2)

---

( xiv ) x⁶ + 27

সমাধানঃ-

x6 + 27

= (x2)3 + 33

= ( x2 + 3 ) { (x2)2 – 3x2 + 32 }

= ( x2 + 3 ) (x4– 3x2 + 9 )

∴ উত্তর = ( x2 + 3 ) (x4– 3x2 + 9 )

---

( xv ) x⁶ – y⁶

সমাধানঃ-

x6 – y6

= ( x3 )2 – ( y3 )2

= ( x3 – y3 ) (x3 + y3 )

= ( x – y ) ( x2 + xy + y2 )( x + y ) ( x2 – xy + y2 )

∴ উত্তর= ( x – y ) ( x2 + xy + y2 )( x + y ) ( x2 – xy + y2 )

---

Request For Share
সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share]

---

( xvi ) x¹² – y¹²

সমাধানঃ-

x12 – y12

= ( x6 )2 – ( y6 )2

= ( x6 + y6 ) ( x6 – y6 )

= { ( x2 )3 + ( y2 )3 } { ( x2 )3 – ( y2 )3 }

= ( x2 + y2 ) { ( x2 )2 – x2y2 + ( y2 )2 }( x2 – y2 ) { ( x2 )2 + x2y2 + ( y2 )2 }

= ( x2 + y2 )( x2 – y2 )( x4 – x2y2 + y4 )( x4 + x2y2 + y4 )

= ( x2 + y2 )( x + y )( x – y )( x4 – x2y2 + y4 )( x4 + x2y2 + y4 )

∴ উত্তর = ( x2 + y2 )( x + y )( x – y )( x4 – x2y2 + y4 )( x4 + x2y2 + y4 )

---

( xvii ) m³ – n³ – m( m² – n² ) + n( m – n )²

সমাধানঃ-

m3 – n3 – m( m2 – n2 ) + n( m – n )2

= (m – n)(m2 + mn + n2 ) – m( m+n )( m – n ) + n( m – n )2

= ( m – n ) { (m2 + mn + n2 ) – m ( m + n ) + n( m – n ) }

= ( m – n ) ( m2 + mn + n2 – m2 – mn + mn – n2 )

= ( m – n )mn

∴ উত্তর= ( m – n )mn

---

এই কষে দেখি 5.3 Class 8|Koshe Dekhi 5.3 Class 8 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।

---

আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে?
কষে দেখি 5.3 Class 8 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 5.3 Class 8 তারপর এই চিহ্ন দেখে Click করলে আবার তোমরা এখানে এসে যাবে।

---

এই অধ্যায়টি থেকে ঘনফল এবং ঘনমূল নির্ণয় করা অনেকের কাছে খুব জটিল মনে হয় ! কিন্তু তোমরা যদি সঠিক পদ্ধতি মেনে ঘনফল নির্ণয় এর কষে দেখি তে যে সমস্ত অংক গুলি আছে সেগুলি করো তাহলে কোথাও বুঝতে অসুবিধে হবেনা । সেজন্যে তোমাদের বলবো তোমরা ঘনফল ও ঘনমূল করার সঠিক পদ্ধতিটি নিচের লিংক থেকে জানো এবং তারপর কষে দেখি এর অংক গুলি করলে নিশ্চয় কিছু পার্থক্য বুঝতে পারবে ।

ঘনফল নির্ণয় অধ্যায়ের-
	কষে দেখি 5.1
	কষে দেখি 5.2

---

গনিতপ্রভা অষ্টম শ্রেণীর সমস্ত অধ্যায়ের সমাধান-
অধ্যায়	সমাধান
2. পাই চিত্র	কষে দেখি 2
3. মূলদ সংখ্যার ধারণা	অধ্যায়ের সারাংশ
	কষে দেখি 3
4. বীজগাণিতিক সংখ্যামালার গুণ ও ভাগ	অধ্যায়ের সারাংশ
	কষে দেখি 4.1
	কষে দেখি 4.2
5. ঘনফল নির্ণয়	অধ্যায়ের সারাংশ
	কষে দেখি 5.1
	কষে দেখি 5.2
	কষে দেখি 5.3
6. পূরক কোণ, সম্পূরক কোণ ও সন্নিহিত কোণ	অধ্যায়ের সারাংশ
	কষে দেখি 6
7. বিপ্রতীপ কোণের ধারণা	অধ্যায়ের সারাংশ
	কষে দেখি 7.1
8. সমান্তরাল সরলরেখা ও ছেদকের ধর্ম	অধ্যায়ের সারাংশ
	কষে দেখি 8
9. ত্রিভুজের দুটি বাহু ও তাদের বিপরীত কোণের সম্পর্ক	অধ্যায়ের সারাংশ
	কষে দেখি 9
10. ত্রৈরাশিক	কষে দেখি 10.1
	কষে দেখি 10.2
11. শতকরা	কষে দেখি 11
12. মিশ্রণ	কষে দেখি 12
13. বীজগাণিতিক সংখ্যামালার উৎপাদকে বিশ্লেষণ	কষে দেখি 13.1
	কষে দেখি 13.2
14. বীজগাণিতিক সংখ্যামালার গ.সা.গু ও ল.সা.গু	কষে দেখি 14
15. বীজগাণিতিক সংখ্যামালার সরলীকরণ	কষে দেখি 15
16. ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই	কষে দেখি 16.1
	কষে দেখি 16.2
17. সময় ও কার্য	কষে দেখি 17.1
	কষে দেখি 17.2
18. লেখচিত্র	কষে দেখি 18
19. সমীকরণ গঠন ও সমাধান	কষে দেখি 19
20. জ্যামিতিক প্রমাণ	কষে দেখি 20.1
	কষে দেখি 20.2
	কষে দেখি 20.3

---

এখানে তোমরা তোমাদের অষ্টম শ্রেণীতে কি কি পড়ানো হয়, মানে তোমাদের অষ্টম শ্রেণীর সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

---