শ্রেণী-অষ্টম ; অধ্যায় – জ্যামিতিক প্রমাণ ; কষে দেখি 20.1
কষে দেখি 20.1 Class 8 এর অংকের সমাধান গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ
কষে দেখি 20.1 | Koshe Dekhi 20.1 তোমাদের অষ্টম শ্রেণীর | Class 8 এর জ্যামিতিক প্রমাণের একটি অনুশীলনী। এই কষে দেখি 20.1 | Koshe Dekhi 20.1 এর অংক গুলি করার ক্ষেত্রে আমরা দেখতে পাবো এর আগের জ্যামিতিক অধ্যায় এর মতই কিছু পদ্ধতি।
সুতরাং এই অধ্যায় নিয়ে বেশী চিন্তিত হবার কোনো কারন নেই। যারা একদমই বুঝতে পারছনা তাদের বলবো আগে তোমরা তোমাদের Class 8 এর জ্যামিতির অধ্যায় গুলি একটু দেখে নেবে।
এই কষে দেখি 20.1 এর অংক করতে গেলে আমাদের কিছু উপপাদ্য আগে জেনে নিতে হবে। যেমন-
| উপপাদ্য 11 |
|---|
| ত্রিভুজের যেকোনো দুটি বাহুর দৈর্ঘ্যের সমষ্টি তৃতীয় বাহুর দৈর্ঘ্যের অপেক্ষা বৃহত্তর । |
এই উপপাদ্যকে কাজে লাগিয়ে আমাদের কষে দেখি 20.1 এর অংক করতে হবে এবং কিছু প্রয়োগ ও করতে হবে।
আগামিতে এই কষে দেখি 20.1 Class 8 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 20.1 Class 8 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 20.1 Class 8 তারপর  |

কষে দেখি 20.1 | Koshe Dekhi 20.1
1. ▲ABC এর BC বাহুর উপর D যেকোনো একটি বিন্দু। প্রমাণ করি যে, AB + BC + CA > 2AD
সমাধানঃ-
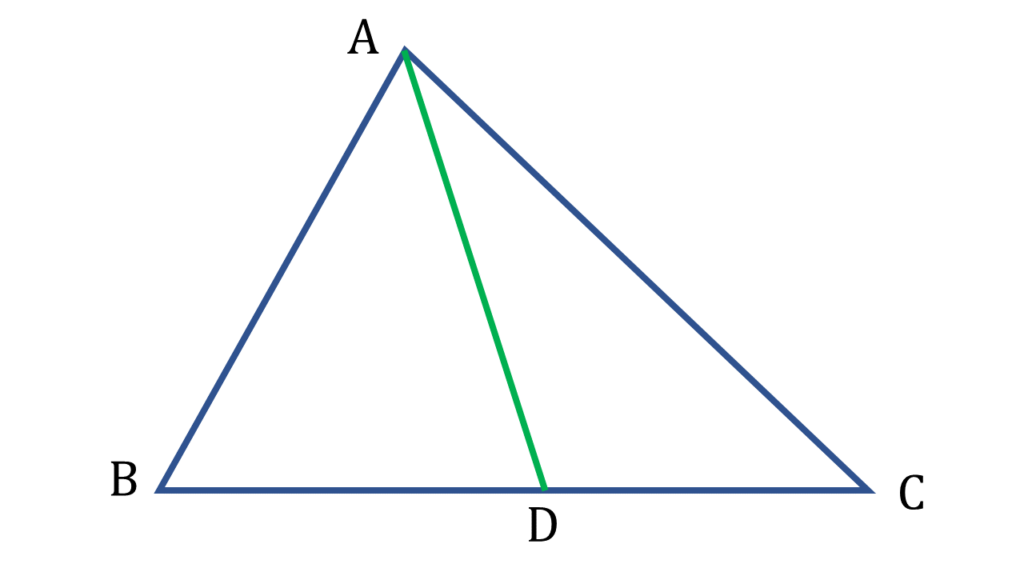
প্রদত্তঃ
▲ABC এর BC বাহুর উপর D যেকোনো একটি বিন্দু।
প্রামাণ্যঃ
প্রমাণ করতে হবে AB + BC + CA > 2AD
প্রমাণঃ
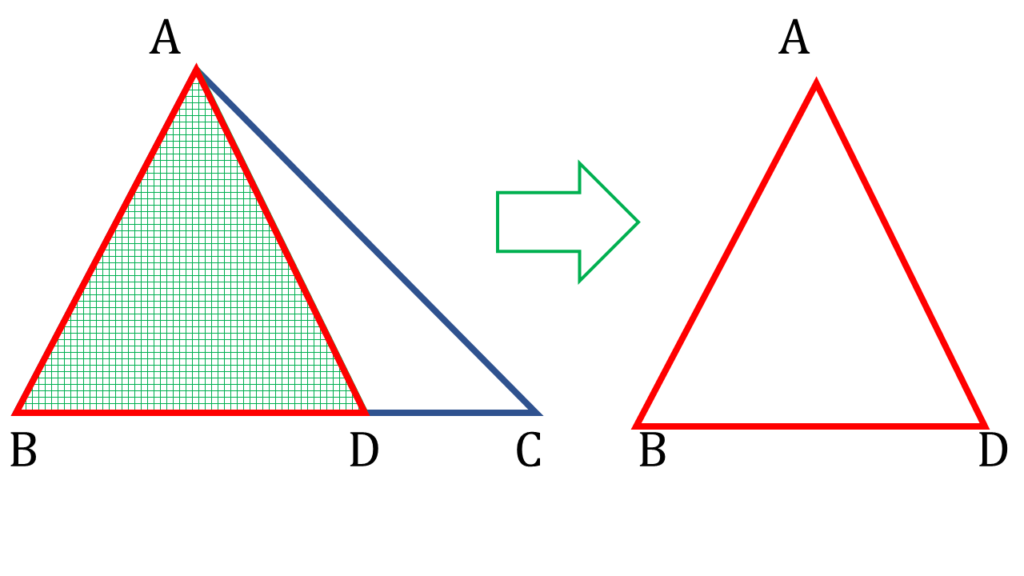
| ▲ABD থেকে পাই, |
|---|
| AB + BD > AD ——-( i ) |
আবার,
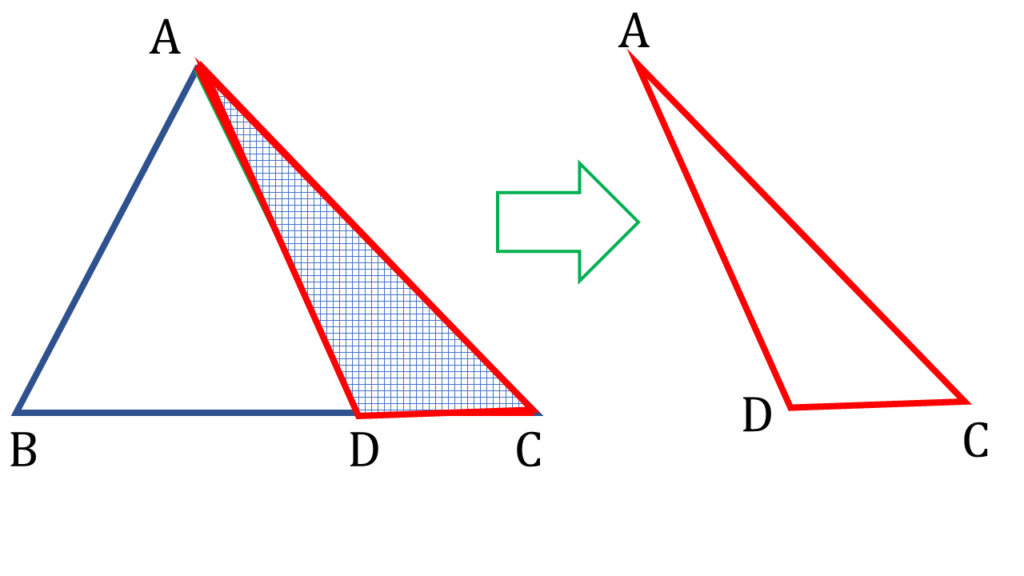
| ▲ADC থেকে পাই, |
|---|
| AC + DC > AD ——-( ii ) |
( i ) ও ( ii ) নং যোগ করে পাই ,
AB +BD + AC + DC > AD + AD
বা, AB + AC + BD + DC > 2AD
বা, AB + AC + BC > 2AD
| ∴ AB + BC + CA > 2AD প্রমাণিত । |
2. ▲ABC এর ভিতরে O যেকোনো একটি বিন্দু। প্রমাণ করি যে,
(i) AB + AC > OB + OC
সমাধানঃ-
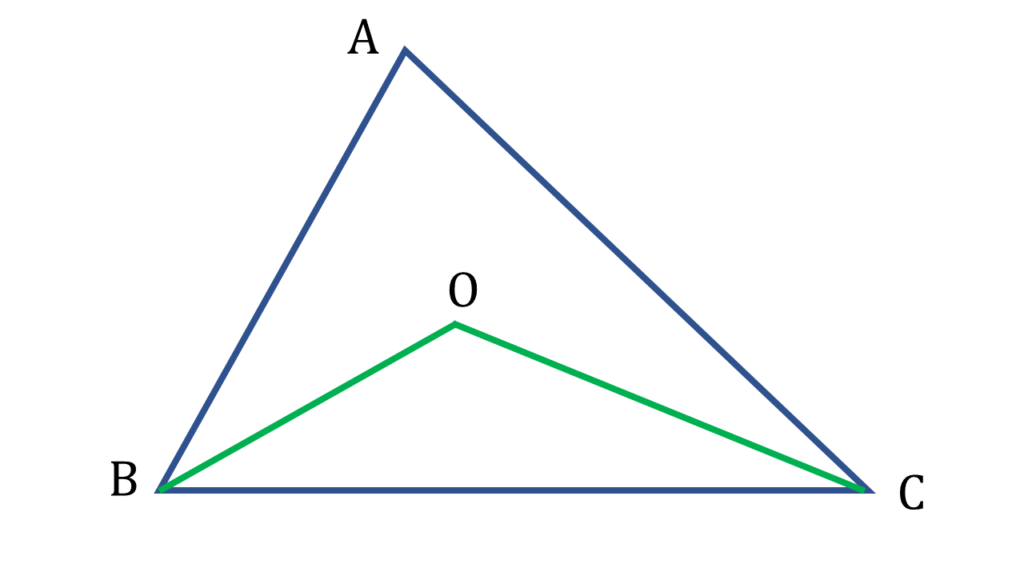
প্রদত্তঃ
▲ABC এর ভিতরে O যেকোনো একটি বিন্দু ।
প্রামাণ্যঃ
প্রমাণ করতে হবে AB + AC > OB + OC
অঙ্কনঃ
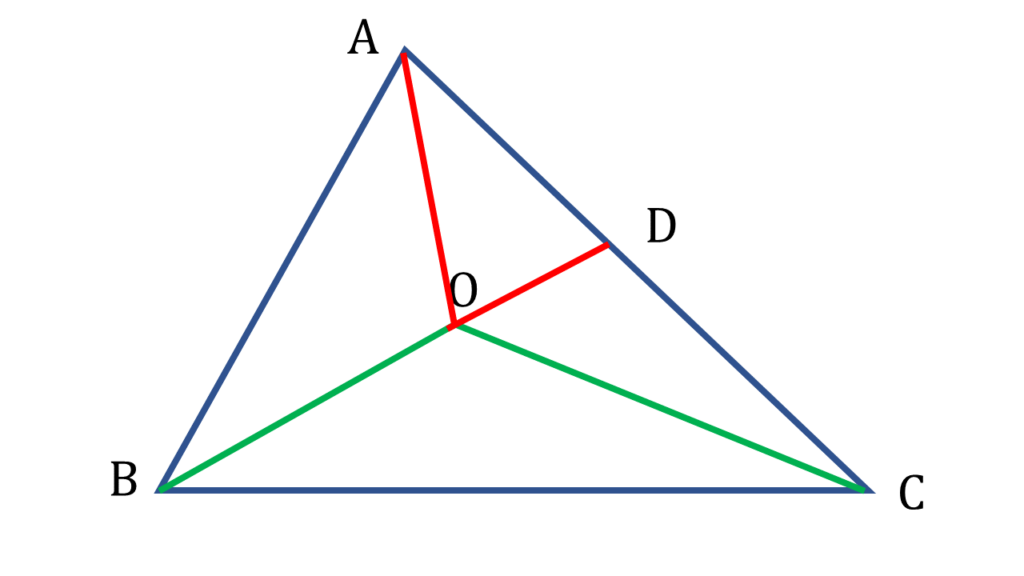
BO বাহুকে বর্ধিত করলাম যা AC বাহুকে D বিন্দুতে ছেদ করেছে এবং A, O যুক্ত করলাম।
প্রমাণঃ
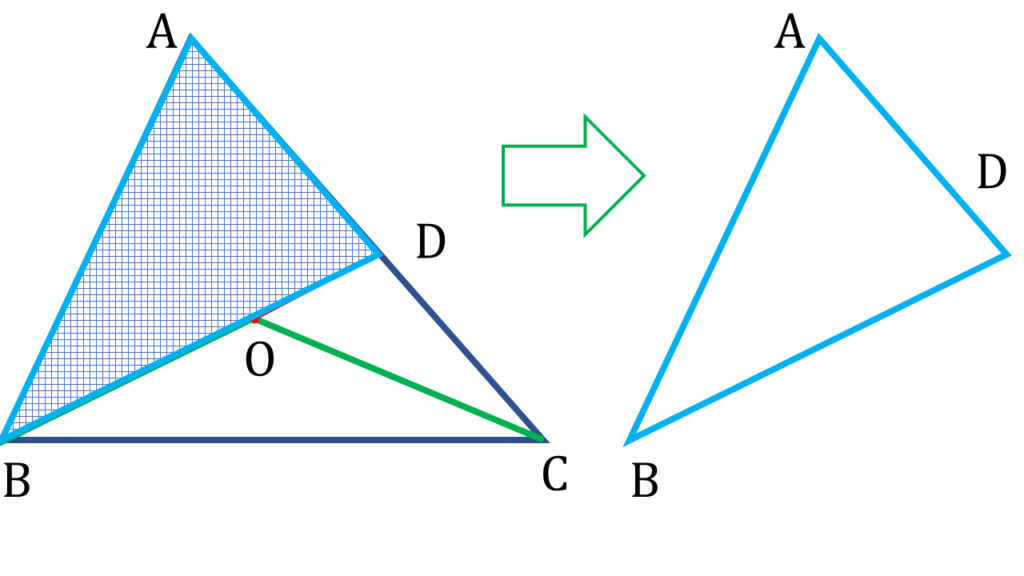
| ▲ABD থেকে পাই, |
|---|
| AB + AD > BD |
| বা, AB + AD > OB + OD ——( i ) |
আবার,
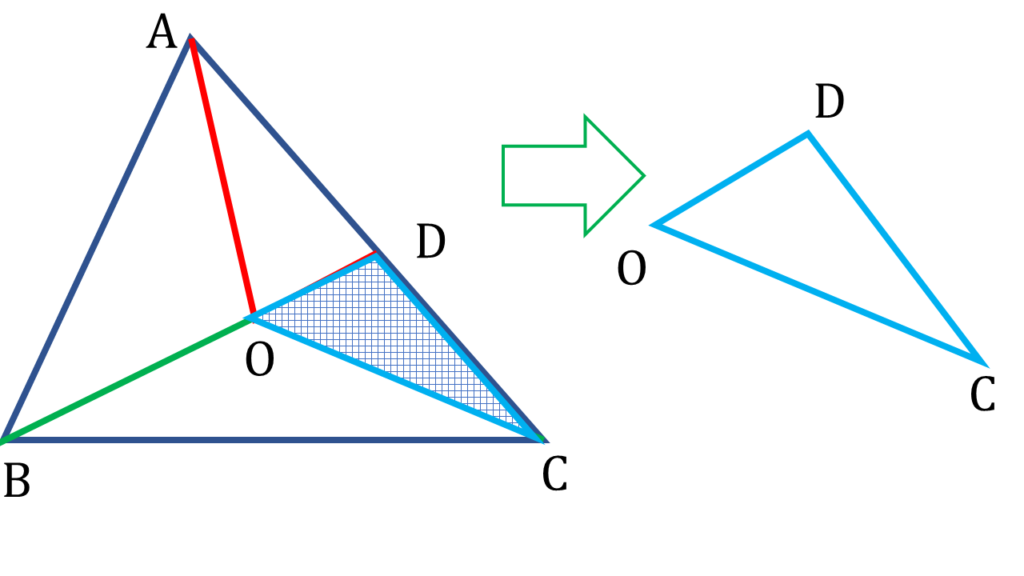
| ▲ODC থেকে পাই, |
|---|
| CD + OD > OC ——( ii ) |
( i ) ও ( ii ) নং যোগ করে পাই ,
AB + AD + CD + OD > OB + OD + OC
বা, AB + AC > OB + OC
| ∴ AB + AC > OB + OC প্রমাণিত । |
(ii) AB + BC + AC > OA + OB + OC
সমাধানঃ-
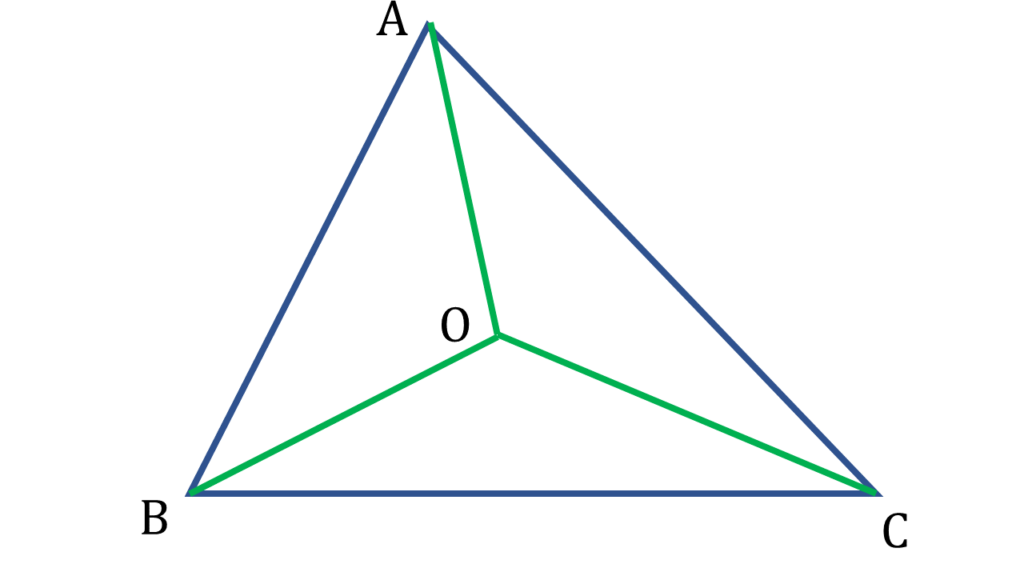
প্রদত্তঃ
▲ABC এর ভিতরে O যেকোনো একটি বিন্দু ।
প্রামাণ্যঃ
প্রমাণ করতে হবে AB + BC + AC > OA + OB + OC
প্রমাণঃ
আগের প্রমাণ থেকে আমরা একই ভাবে প্রমাণ করতে পারবো,
AB + AC > OB + OC —( i )
AB + BC > OA + OC —( ii )
BC + AC > OA + OB —( iii )
( i ), ( ii ) ও (iii) নং যোগ করে পাই ,
AB + AC + AB + BC + BC + AC > OB + OC + OA + OC + OA + OB
বা, 2(AB + BC + AC) > 2(OA + OB + OC)
বা, (AB + BC + AC) > (OA + OB + OC)
| ∴ AB + BC + AC > OA + OB + OC প্রমাণিত । |
3. প্রমাণ করি যে, একটি চতুর্ভুজের পরিসীমা যেকোনো কর্ণের দৈর্ঘ্যের দ্বিগুণ অপেক্ষা বৃহত্তর।
সমাধানঃ-
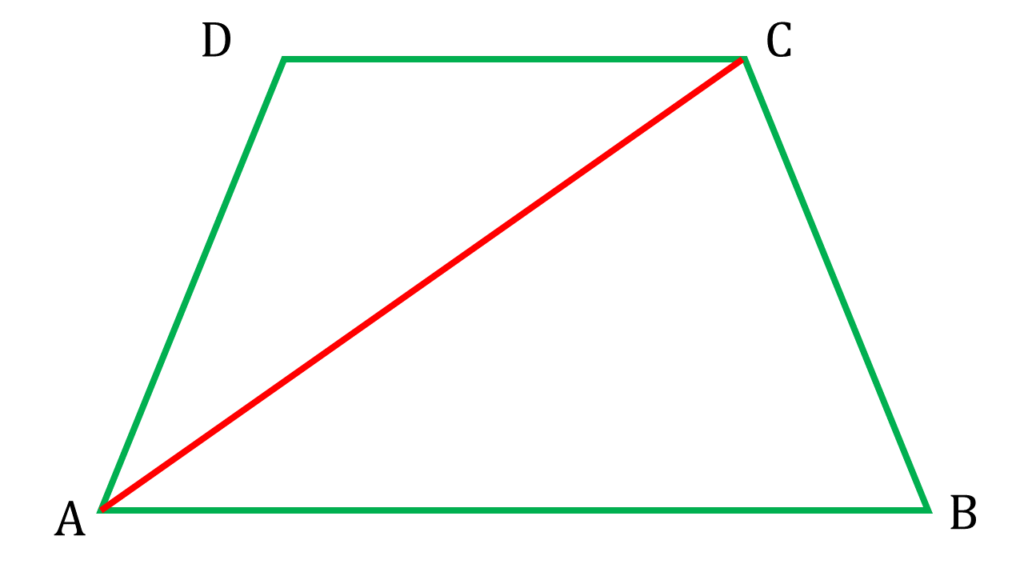
প্রদত্তঃ
ABCD একটি চতুর্ভুজ।
প্রামাণ্যঃ
প্রমাণ করতে হবে
AB + BC + CD + AD > 2AC
প্রমাণঃ
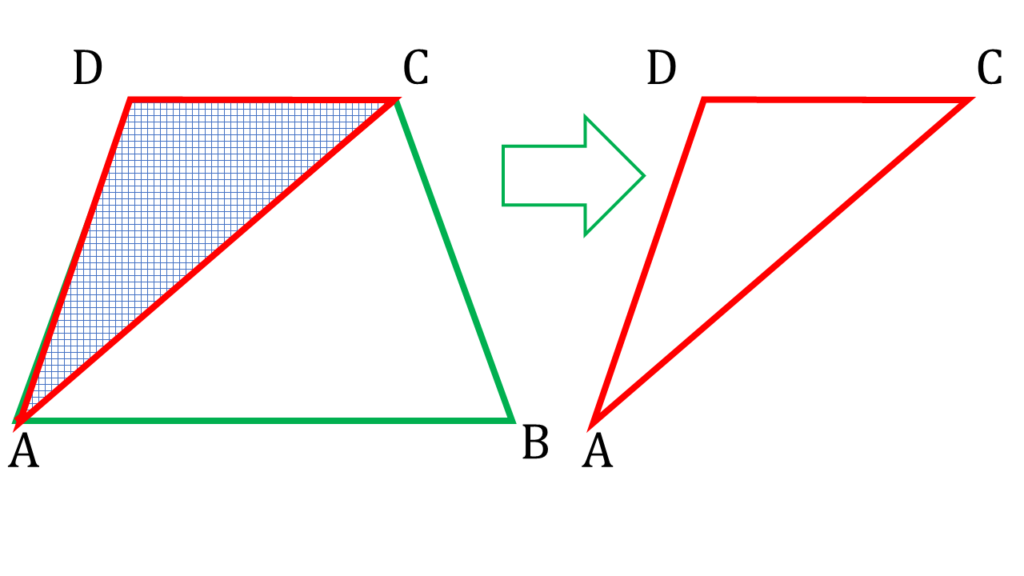
| ▲ADC থেকে পাই, |
|---|
| AD + DC > AC —-( i ) |
আবার,
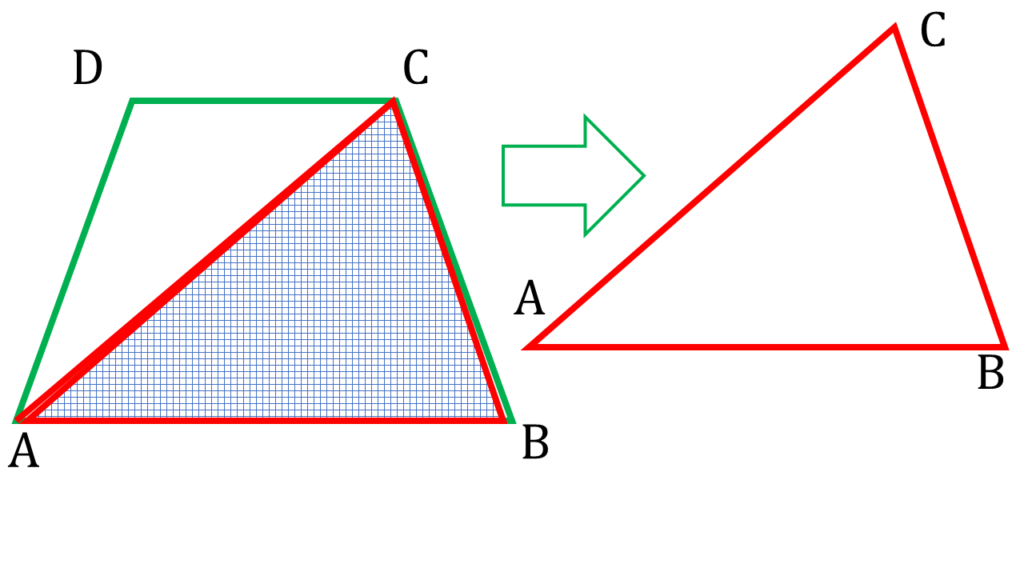
| ▲ABC থেকে পাই, |
|---|
| AB + BC > AC —-( ii ) |
( i ) ও ( ii ) নং যোগ করে পাই ,
AB + BC + CD + AD > AC + AC
বা, AB + BC + CD + AD > 2AC
| ∴ AB + BC + CD + AD > 2AC প্রমাণিত । |
4. ▲ABC এর ভিতরে P যেকোনো একটি বিন্দু। প্রমাণ করি যে,
(i) AP + BP >AB
সমাধানঃ-
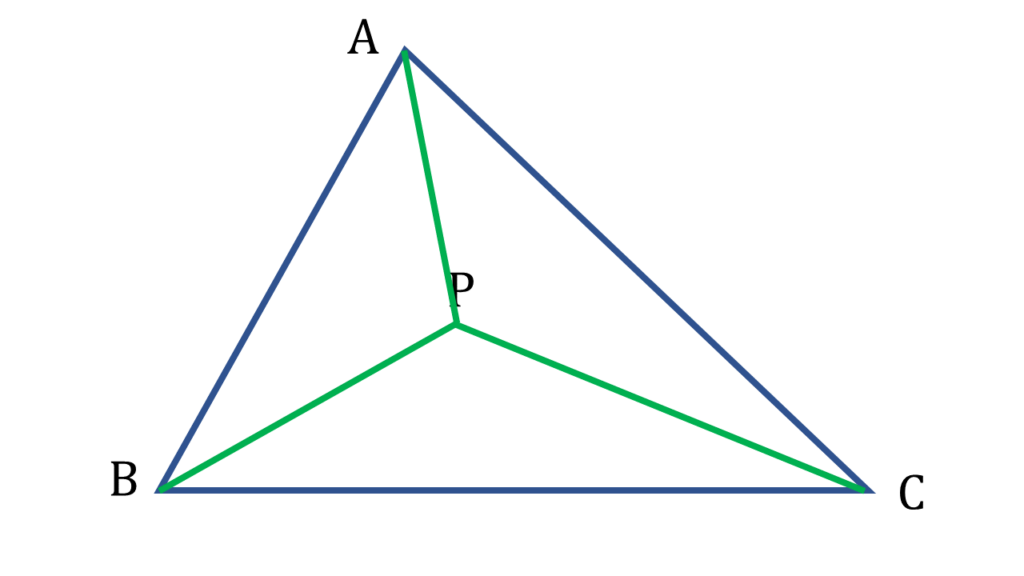
প্রদত্তঃ
▲ABC এর ভিতরে P যেকোনো একটি বিন্দু
প্রামাণ্যঃ
প্রমাণ করতে হবে
AP + BP >AB
প্রমাণঃ
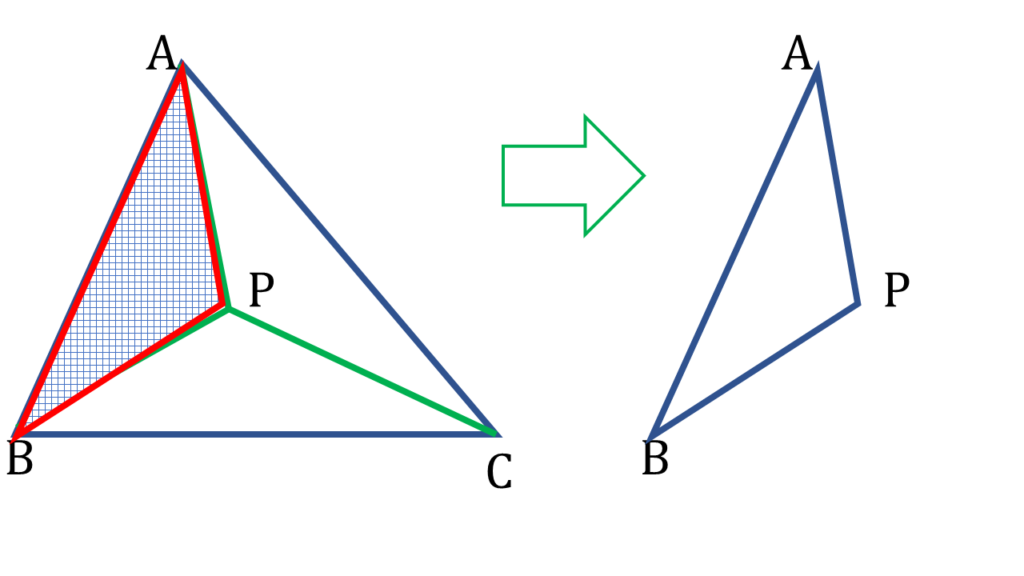
| ▲APB থেকে পাই, |
|---|
| AP + BP > AB |
| ∴ AP + BP > AB প্রমাণিত । |
(ii) AB + BC + AC < 2 ( AP + BP + CP)
সমাধানঃ-
প্রদত্তঃ
▲ABC এর ভিতরে P যেকোনো একটি বিন্দু
প্রামাণ্যঃ
প্রমাণ করতে হবে
AB + BC + AC < 2 ( AP + BP + CP)
প্রমাণঃ
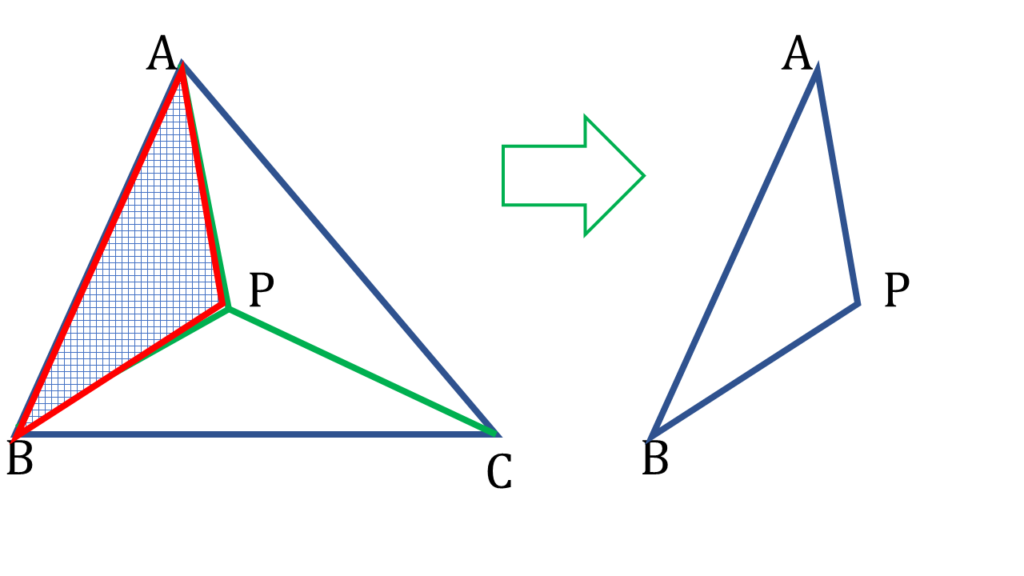
| ▲APB থেকে পাই, |
|---|
| AP + BP > AB —( i ) |
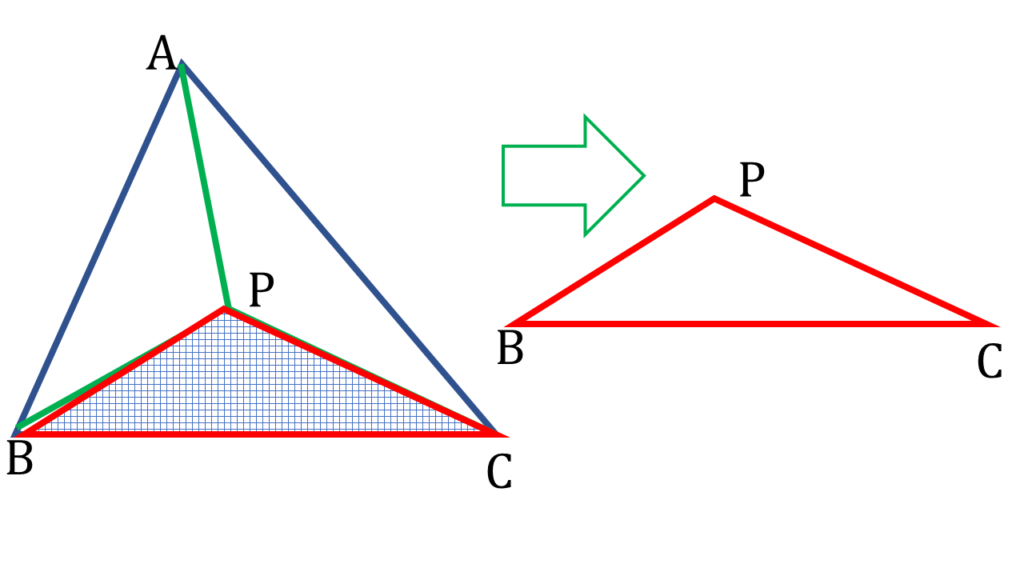
| ▲PBC থেকে পাই, |
|---|
| BP + PC > BC —( ii ) |
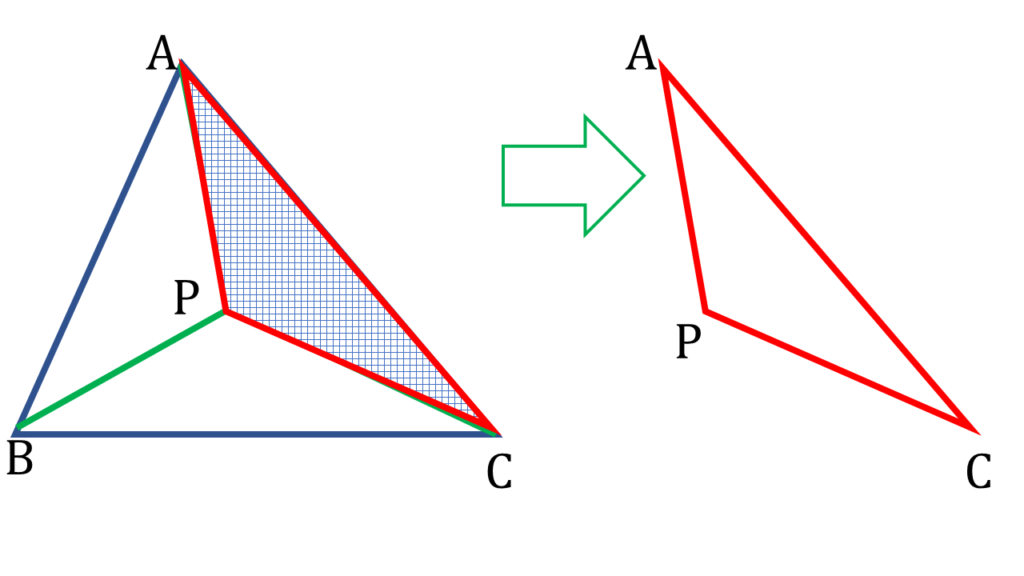
| ▲APC থেকে পাই, |
|---|
| AP + PC > AC —( iii ) |
( i ), ( ii ) ও (iii) নং যোগ করে পাই ,
AP + BP + BP + PC + AP + PC > AB + BC + AC
বা, 2(AP + BP + CP) > AB + BC + AC
| ∴ AB + BC + AC < 2 ( AP + BP + CP) প্রমাণিত । |
5. প্রমাণ করি যে, ত্রিভুজের পরিসীমা ত্রিভুজটির মধ্যমা তিনটির দৈর্ঘ্যের সমষ্টির চেয়ে বড়ো।
সমাধানঃ-
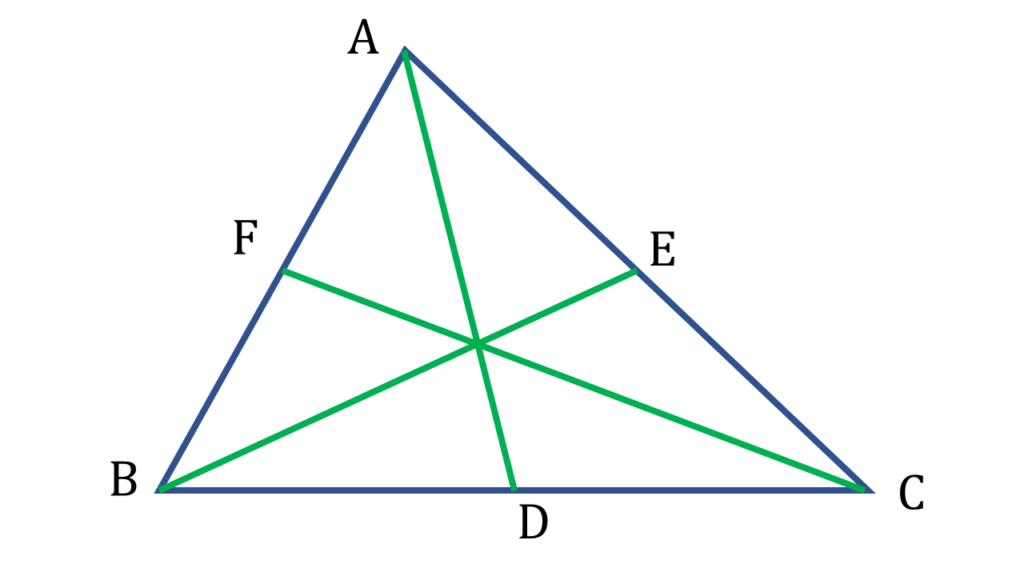
প্রদত্তঃ
ABC একটি ত্রিভুজ যার AD, BE ও CF তিনটি মধ্যমা।
প্রামাণ্যঃ
প্রমাণ করতে হবে
AB + BC + AC > AD + BE + CF
অঙ্কনঃ
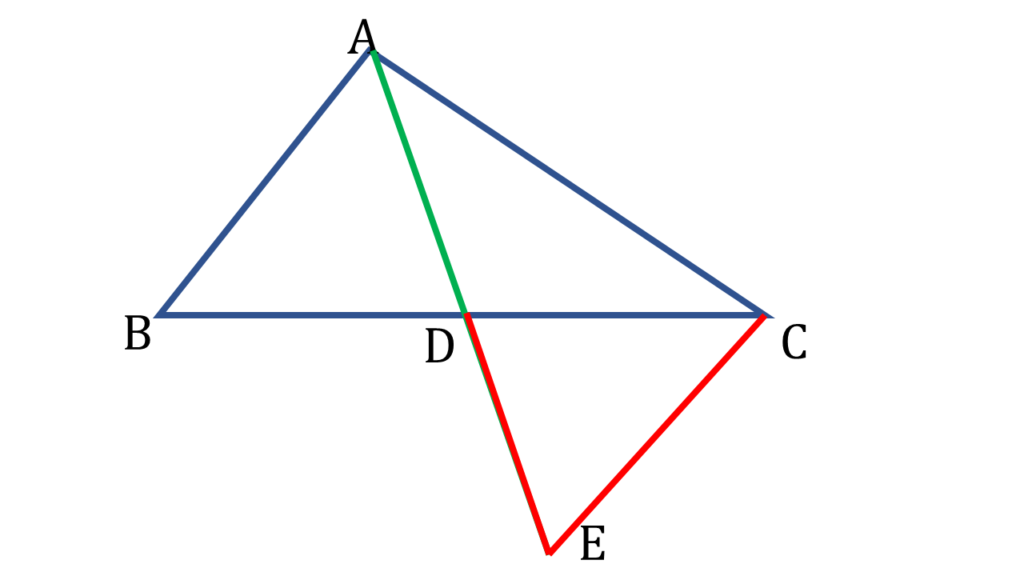
মধ্যমা AD কে E পর্যন্ত বর্ধিত করলাম যাতে AD = ED হয় এবং C ও এ যুক্ত করলাম।
প্রমাণঃ
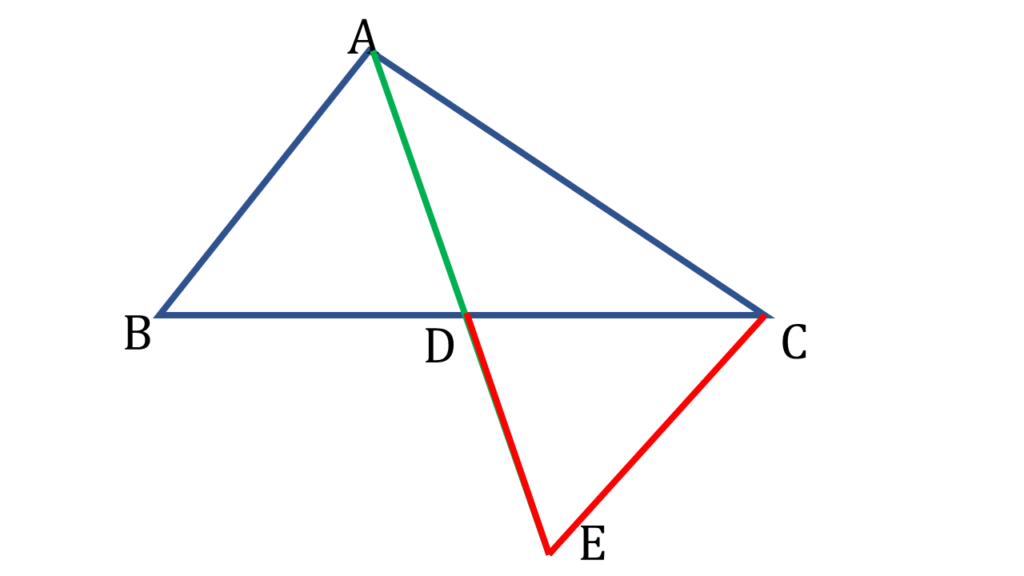
▲ABD ও ▲DEC থেকে পাই,
AD=DE
BD = DC
∠EDC = বিপ্রতীপ ∠ADB
∴ ▲ABD ≅ ▲DEC
অতএব,
AD = DE
এখন
▲ACE থেকে পাই,
EC + AC > AE
বা, AB + AC > 2AD —(i)
একই রকম ভাবে আমরা পাবো,
AC + BC > 2CE —-(ii)
এবং
AB + BC > 2BE —(iii)
( i ), ( ii ) ও (iii) নং যোগ করে পাই ,
AB + AC + AC + BC + AB + BC > 2AD + 2CE + 2BE
বা, 2(AB + BC + CA) > 2 (AD + CE + BE)
বা, AB + BC + CA > AD + CE + BE
| ∴ ত্রিভুজের পরিসীমা ত্রিভুজটির মধ্যমা তিনটির দৈর্ঘ্যের সমষ্টির চেয়ে বড়ো প্রমাণিত । |
6. প্রমাণ করি যে, একটি চতুর্ভুজের কর্ণদ্বয়ের দৈর্ঘ্যের সমষ্টি চতুর্ভুজের যেকোনো দুটি বিপরীত বাহুর দৈর্ঘ্যের সমষ্টির চেয়ে বড়ো।
সমাধানঃ-
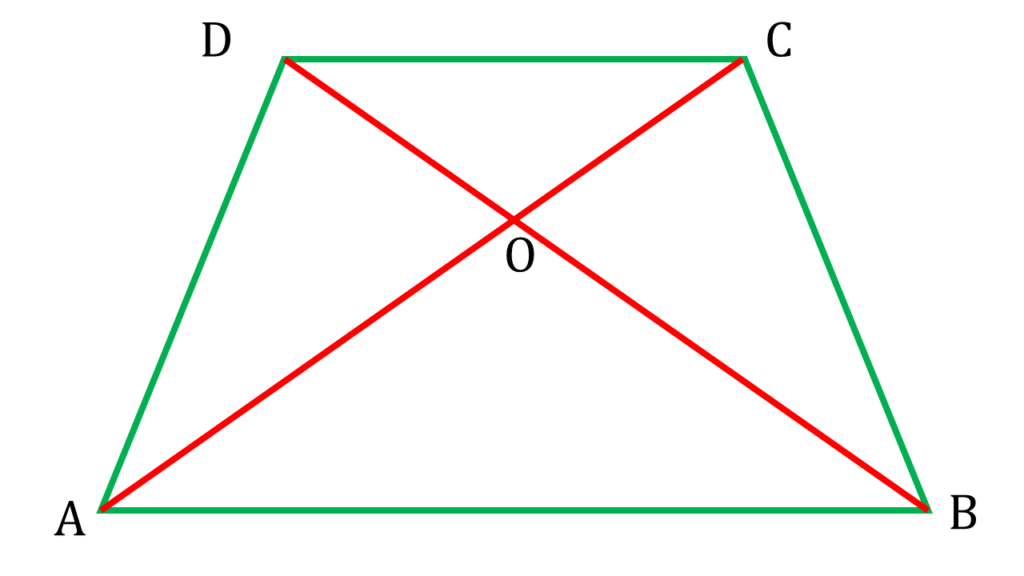
প্রদত্তঃ
ABCD একটি চতুর্ভুজ এবং AC ও BD চতুর্ভুজের দুটি কর্ণ।
প্রামাণ্যঃ
প্রমাণ করতে হবে
AC + BD > AD + BC
অথবা
AC + BD > DC + AB
প্রমাণঃ
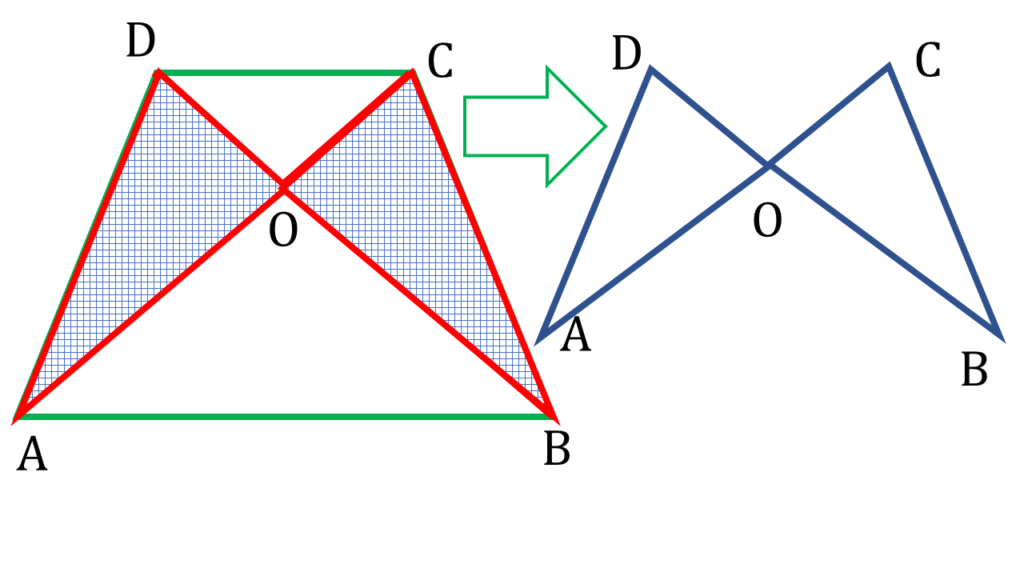
▲AOD এবং ▲BOC থেকে পাই,
AO + OD > AD—(i)
এবং
OC + OB > BC—(ii)
(i) ও (ii) নং যোগ করে পাই,
AO + OD + OC + OB > AD + BC
বা, AO + OC + OD + OB > AD + BC
বা, AC + BD > AD + BC
একইরকম ভাবে
▲DOC ও ▲AOB থেকে পাই,
AC + BD > CD + AB
| ∴ প্রমাণিত |
7. প্রমাণ করি যে, একটি চতুর্ভুজের কর্ণদ্বয়ের দৈর্ঘ্যের সমষ্টি চতুর্ভুজটির অর্ধ-পরিসীমার চেয়ে বড়ো।
সমাধানঃ-
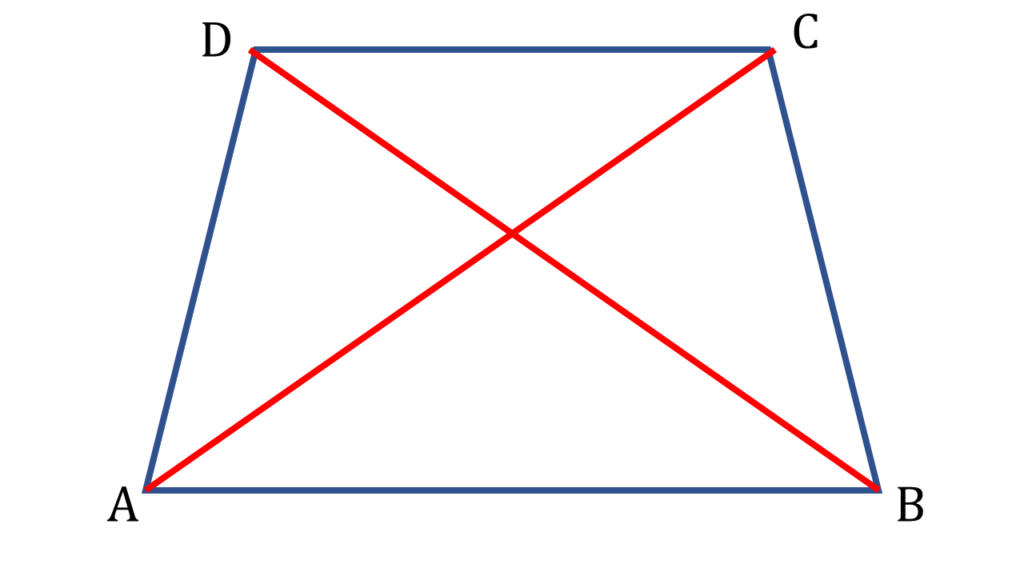
প্রদত্তঃ
ABCD একটি চতুর্ভুজ এবং AC ও BD দুটি কর্ণ।
প্রামাণ্যঃ
প্রমাণ করতে হবে
AC + BD > ½(AB + BC + CD + AD)
প্রমাণঃ
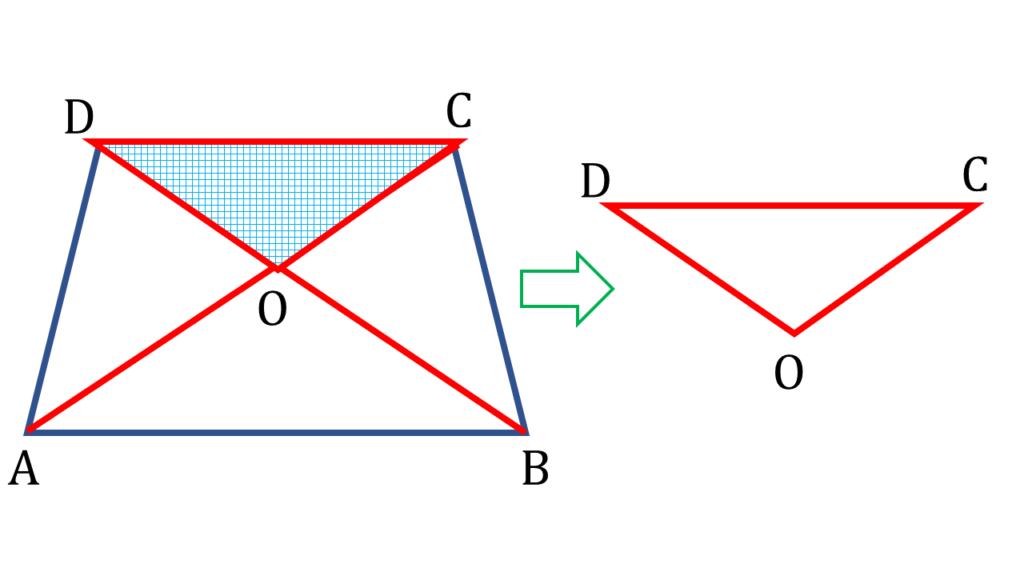
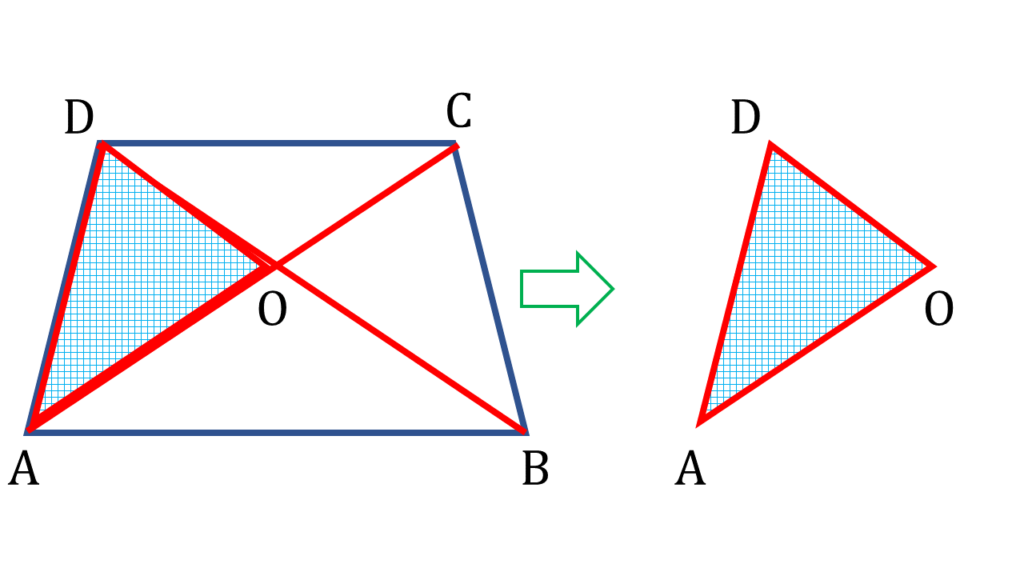
| ▲DOC থেকে পাই, |
|---|
| OD + OC > DC —(i) |
| ▲AOD থেকে পাই, |
|---|
| OD + OA > AD —(ii) |
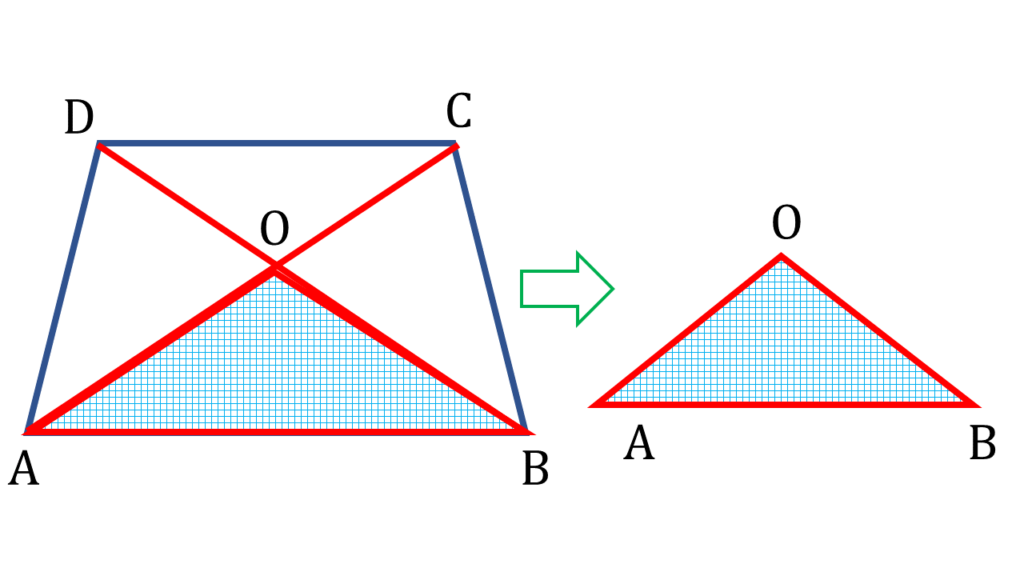
| ▲AOB থেকে পাই, |
|---|
| OA + OB > AB —(iii) |
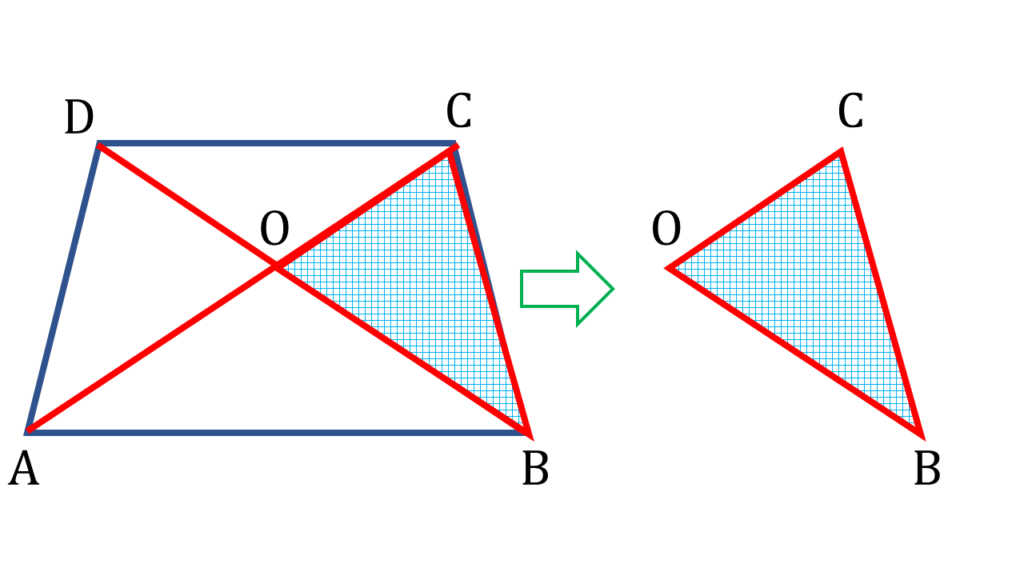
| ▲BOC থেকে পাই, |
|---|
| OB + OC > BC —(iv) |
(i), (ii), (iii) ও (iv) নং যোগ করে পাই,
| OD + OC + OD + OA + OA + OB + OB + OC > DC + AD + AB + BC |
| বা, OD + OB + OD + OB + OC + OA + OC + OA > AB + BC + CD + AD |
| বা, BD + BD + AC + AC > AB + BC + CD + AD |
| বা, 2 (AC + BD) > AB + BC + CD + AD |
| বা, AC + BD > ½(AB + BC + CD + AD) |
| ∴ চতুর্ভুজের কর্ণদ্বয়ের দৈর্ঘ্যের সমষ্টি চতুর্ভুজটির অর্ধ-পরিসীমার চেয়ে বড়ো প্রমাণিত । |
8. প্রমাণ করি যে, যেকোনো চতুর্ভুজের অন্তঃস্থ কোনো বিন্দু (কোনো কর্ণের উপর নয়) থেকে চতুভুজের শীর্ষবিন্দুগুলির সংযোজক সরলরেখাংশের দৈর্ঘ্যের সমষ্টি চতুভুজটির কর্ণদ্বয়ের দৈর্ঘ্যের সমষ্টির চেয়ে বড়ো। এবার দেখি যে চতুর্ভুজের ভিতর বিন্দুটির কোনো অবস্থানের জন্য চতুর্ভুজের শীর্ষবিন্দুগুলির সংযোজক সরলরেখাংশের দৈর্ঘ্যের সমষ্টি ক্ষুদ্রতম হবে।
সমাধানঃ-
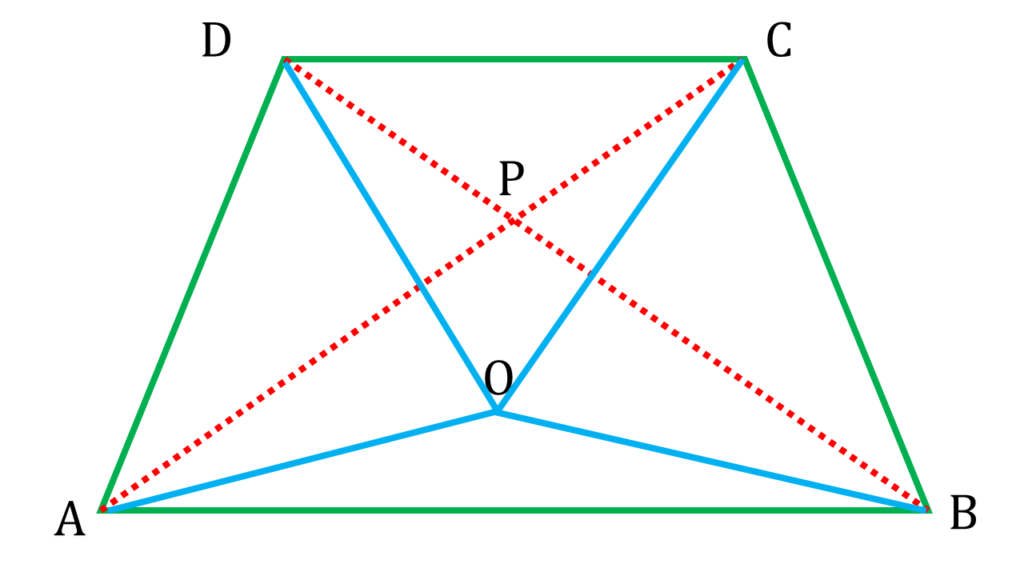
প্রদত্তঃ
ABCD একটি চতুর্ভুজ, চতুর্ভুজের মধ্যে O একটি বিন্দু যেটি কর্ণের উপর নেই এবং AC ও BD চতুর্ভুজের দুটি কর্ণ।
প্রামাণ্যঃ
প্রমাণ করতে হবে
OA + OB + OC + OD > AC + BD
প্রমাণঃ
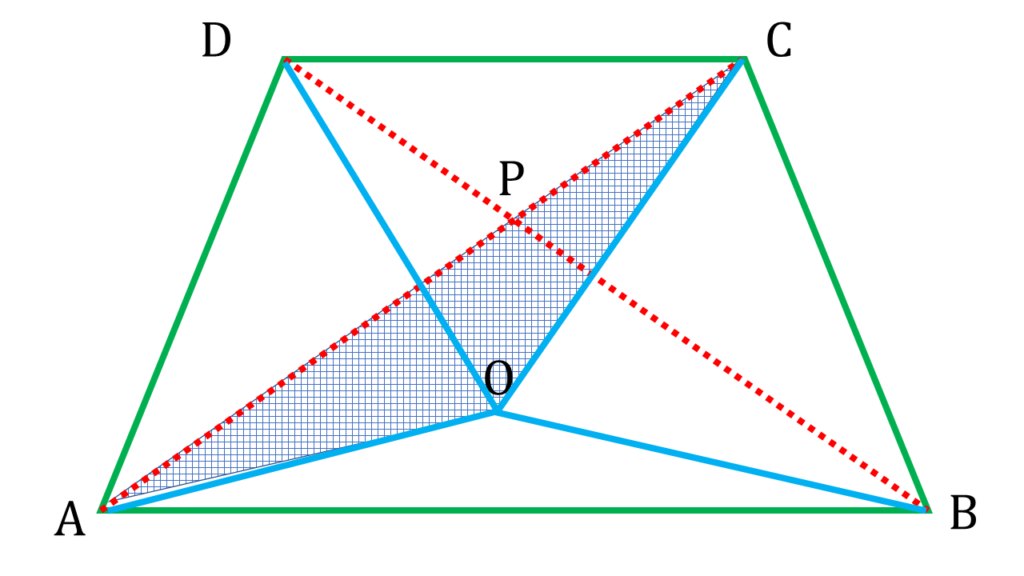
| ▲AOC থেকে পাই, |
|---|
| OA + OC > AC —(i) |
আবার,
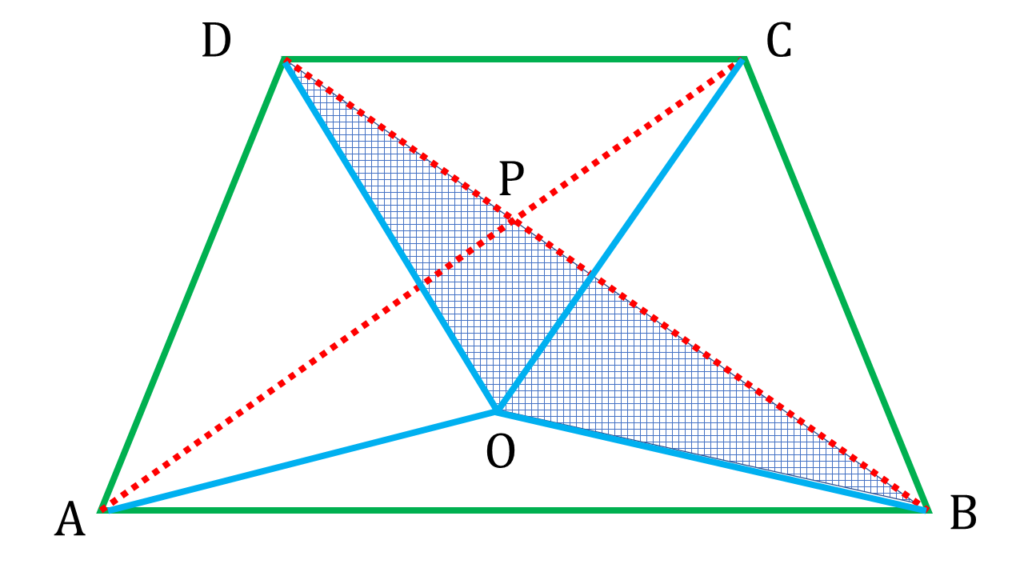
| ▲BOD থেকে পাই, |
|---|
| OB + OD > BD —(ii) |
(i) ও (ii) নং যোগ করে পাই,
| OA + OC + OB + OD > AC + BD |
| ∴ চতুর্ভুজের অন্তঃস্থ কোনো বিন্দু (কোনো কর্ণের উপর নয়) থেকে চতুভুজের শীর্ষবিন্দুগুলির সংযোজক সরলরেখাংশের দৈর্ঘ্যের সমষ্টি চতুভুজটির কর্ণদ্বয়ের দৈর্ঘ্যের সমষ্টির চেয়ে বড়ো প্রমাণিত। |
| জ্যামিতিক প্রমাণ অধ্যায়ের- | |
|---|---|
 | |
 | |
এই কষে দেখি 20.1 Class 8|Koshe Dekhi 20.1 Class 8 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।
| গনিতপ্রভা অষ্টম শ্রেণীর সমস্ত অধ্যায়ের সমাধান- | |
|---|---|
| অধ্যায় | সমাধান |
| 2. পাই চিত্র | কষে দেখি 2 |
| 3. মূলদ সংখ্যার ধারণা | অধ্যায়ের সারাংশ |
| কষে দেখি 3 | |
| 4. বীজগাণিতিক সংখ্যামালার গুণ ও ভাগ | অধ্যায়ের সারাংশ |
| কষে দেখি 4.1 | |
| কষে দেখি 4.2 | |
| 5. ঘনফল নির্ণয় | অধ্যায়ের সারাংশ |
| কষে দেখি 5.1 | |
| কষে দেখি 5.2 | |
| কষে দেখি 5.3 | |
| 6. পূরক কোণ, সম্পূরক কোণ ও সন্নিহিত কোণ | অধ্যায়ের সারাংশ |
| কষে দেখি 6 | |
| 7. বিপ্রতীপ কোণের ধারণা | অধ্যায়ের সারাংশ |
| কষে দেখি 7.1 | |
8. সমান্তরাল সরলরেখা ও ছেদকের ধর্ম | অধ্যায়ের সারাংশ |
| কষে দেখি 8 | |
9. ত্রিভুজের দুটি বাহু ও তাদের বিপরীত কোণের সম্পর্ক | অধ্যায়ের সারাংশ |
| কষে দেখি 9 | |
| 10. ত্রৈরাশিক | কষে দেখি 10.1 |
| কষে দেখি 10.2 | |
| 11. শতকরা | কষে দেখি 11 |
| 12. মিশ্রণ | কষে দেখি 12 |
13. বীজগাণিতিক সংখ্যামালার উৎপাদকে বিশ্লেষণ | কষে দেখি 13.1 |
| কষে দেখি 13.2 | |
14. বীজগাণিতিক সংখ্যামালার গ.সা.গু ও ল.সা.গু | কষে দেখি 14 |
15. বীজগাণিতিক সংখ্যামালার সরলীকরণ | কষে দেখি 15 |
16. ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই | কষে দেখি 16.1 |
| কষে দেখি 16.2 | |
17. সময় ও কার্য | কষে দেখি 17.1 |
| কষে দেখি 17.2 | |
18. লেখচিত্র | কষে দেখি 18 |
19. সমীকরণ গঠন ও সমাধান | কষে দেখি 19 |
| 20. জ্যামিতিক প্রমাণ | কষে দেখি 20.1 |
| কষে দেখি 20.2 | |
| কষে দেখি 20.3 | |

এখানে তোমরা তোমাদের অষ্টম শ্রেণীতে কি কি পড়ানো হয়, মানে তোমাদের অষ্টম শ্রেণীর সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

