শ্রেণী- অষ্টম ; অধ্যায়- ত্রৈরাশিক ; কষে দেখি 10.2
ত্রৈরাশিক কষে দেখি 10.2 এর অংক গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ
ত্রৈরাশিক, তোমাদের অষ্টম শ্রেণীর একটি অধ্যায় যাতে তোমাদের দুটি অনুশীলনী থেকে অংক করতে হবে, যথা- কষে দেখি 10.1 ও কষে দেখি 10.2।
এখানে কষে দেখি 10.2 এর সমস্ত অংকগুলি সমাধান করা হয়েছে। সমস্ত অংক গুলি যাতে তোমাদের কোনো বুঝতে অসুবিধা না হয় তার জন্যে কিছু উপদেশ থাকলো-
এই কষে দেখি 10.2 তে আমরা এর আগের অধ্যায়ের মতোই কিছু অংক করবো শুধু এর আগের অধ্যায়ে আমরা একসাথে দুটি রাশির মধ্যে সম্পর্ক কেমন হলে সরল না ব্যস্ত সমানুপাতী তা বুঝেছি কিন্তু এই অধ্যায়ে আমরা বুঝবো তিনটি রাশির মধ্যে সম্পর্ক ও তাদের সম্পর্ক অনুযায়ী অংক কেমন হবে।
আমরা কষে দেখি 10.2 এর অংক গুলি বোঝার আগে একটি উদাহরণের মাধ্যমে সম্পূর্ণ ব্যাপারটি বোঝার চেষ্টা করবো।
উদাহরণঃ বাপনদের বাড়ির ও পাচিলের দেয়াল গাঁথতে হবে। তাই রাজমিস্ত্রি দেয়াল গাঁথার কাজ করছে। যদি 5 জন রাজমিস্ত্রি 4 দিনে 128 বর্গমিটার দেয়াল গাঁথতে পারেন , তবে 10 জন রাজমিস্ত্রি 320 বর্গমিটার দেয়াল গাঁথতে কত দিন সময় নেবেন ত্রৈরাশিক পদ্ধতিতে হিসাব করে লিখি।
সমাধানঃ
গণিতের ভাষায় সমস্যা টি হলো-
প্রথম ধাপ-
| রাজমিস্ত্রি ( জন ) | সময় ( দিন ) |
|---|---|
| 5 | 4 |
| 10 | ? |
দ্বিতীয় ধাপ-
| দেয়াল গাঁথার পরিমাণ ( বর্গমিটার ) | সময় ( দিন ) |
|---|---|
| 128 | প্রথম ধাপের |
| 320 | ? |
এখানে তিনটি বিষয় আছে,
( i ) রাজমিস্ত্রি
( ii ) সময়
( iii ) কাজের পরিমাণ
এবার দুটি ধাপে আমরা সম্পর্ক খুজিঃ
প্রথম ধাপ- একই কাজ করতে রাজমিস্ত্রির সংখ্যা বাড়লে সময় কম লাগবে। এবং রাজমিস্ত্রির সংখ্যা কমলে সময় বেশী লাগবে। রাজমিস্ত্রির সংখ্যা এবং সময় ব্যস্ত সমানুপাতী ।
অতএব,
? : 4 :: 5 : 10
নির্ণেয় সময়
= 4 × 5/10
= 2 দিন
দ্বিতীয় ধাপ- রাজমিস্ত্রির সংখ্যা একই থাকলে বেশী পরিমাণ কাজ করার জন্য বেশী সময় লাগবে এবং কাজের পরিমাণ কম হলে কম সময় লাগবে। রাজমিস্ত্রির সংখ্যা ও কাজের পরিমাণ সরল সমানুপাতী ।
সুতরাং,
? : 2 : : 320 : 128
নির্ণেয় সময়
= 2×320/128
= 5 দিন
এবার দুটি ধাপ একসাথে করলে পাই,
অতএব,
নির্ণেয় সময়
= 4×5/10×320/128
= 5 দিন
অতএব,
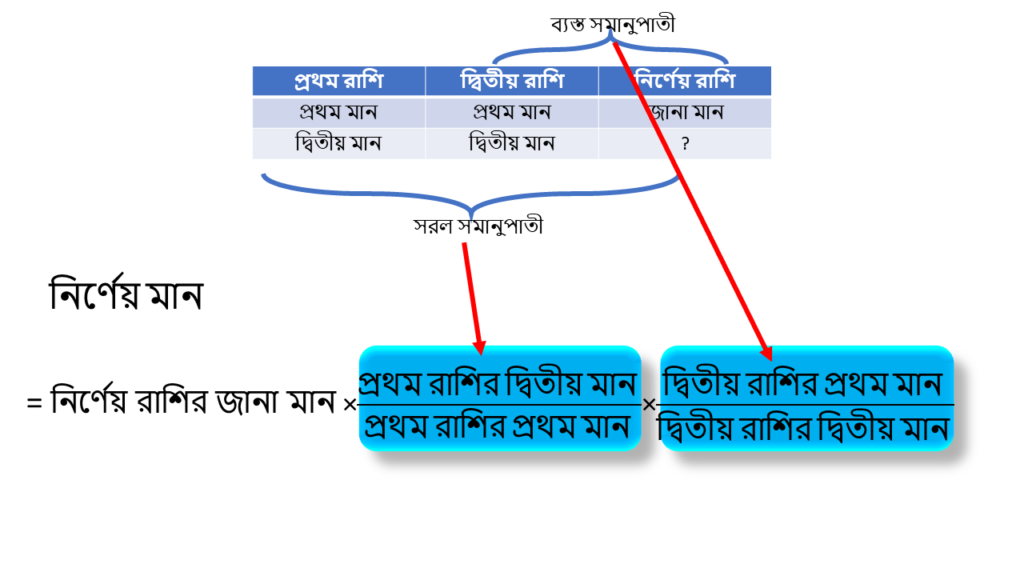
আমরা যখন নির্ণেয় মান বের করবো তখন আমাদের দুটি জিনিসের উপর খেয়াল রাখতে হবে যথা-
( i ) নির্ণেয় রাশির সাথে যে রাশিটি সরল সম্পর্কে থাকবে সেটি গুণ করার সময় উপরে দ্বিতীয় মান এবং নীচে প্রথম মান বসবে।
( ii ) নির্ণেয় রাশির সাথে যে রাশিটি ব্যস্ত সম্পর্কে থাকবে সেটি গুণ করার সময় উপরে প্রথম মান এবং নীচে দ্বিতীয় মান বসবে।
আগামিতে এই কষে দেখি 10.2 Class 8 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 10.2 Class 8 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 10.2 Class 8 তারপর 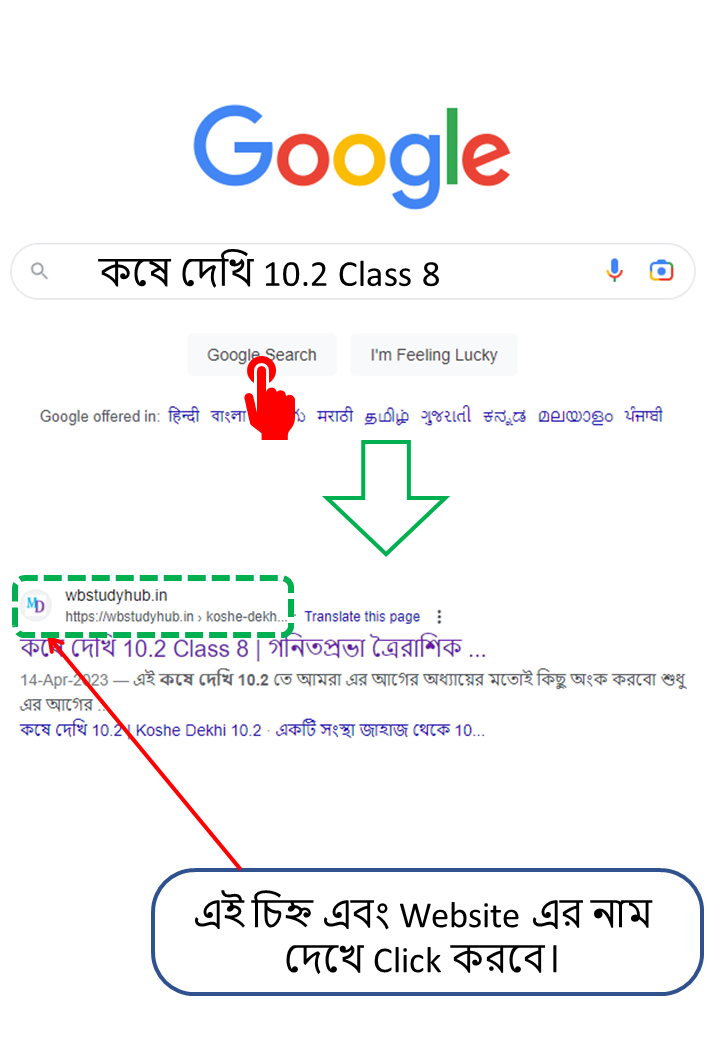 |

কষে দেখি 10.2 | Koshe Dekhi 10.2
1. গ্রামের রাস্তা বাধানোর কাজ শুরু হবে। ঠিক হয়েছে 14 জন লোক দৈনিক 4 ঘণ্টা কাজ করে 15 দিনে সম্পূর্ণ কাজটি করতে পারবেন। কিন্তু 24 জন লোক দৈনিক 7 ঘণ্টা কাজ শুরু করলে কতদিনে কাজটি করবেন ত্রৈরাশিক পদ্ধতিতে হিসাব করি।
সমাধানঃ-
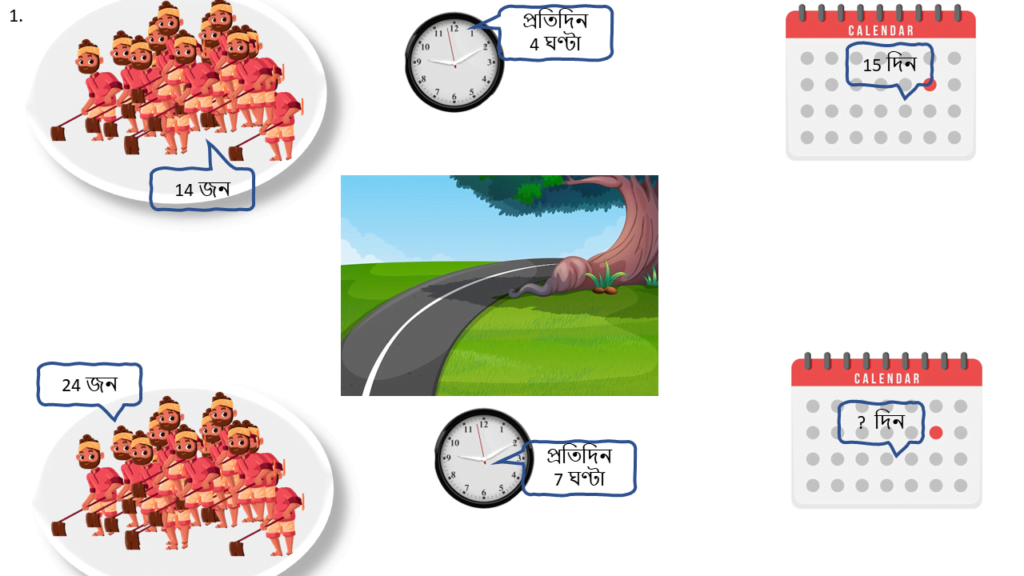
গণিতের ভাষায় সমস্যাটি হলো-
| লোক সংখ্যা ( জন ) | কাজ করার সময় ( ঘণ্টা ) | সময় (দিন ) |
|---|---|---|
| 14 | 4 | 15 |
| 24 | 7 | ? |
প্রথম ধাপঃ-
একই সময় ধরে কাজ করলে লোক সংখ্যা বাড়লে সময় কম লাগবে। লোকসংখ্যা ও সময় ব্যস্ত সমানুপাতী।
দ্বিতীয় ধাপঃ-
লোক সংখ্যা একই থাকলে কাজের সময় বাড়লে দিন সংখ্যা কমবে। কাজ করার সময় ও দিন সংখ্যা ব্যস্ত সমানুপাতী ।
অতএব নির্ণেয় দিন সংখ্যা
= 15 × ( 4/7 ) × ( 14/24 )
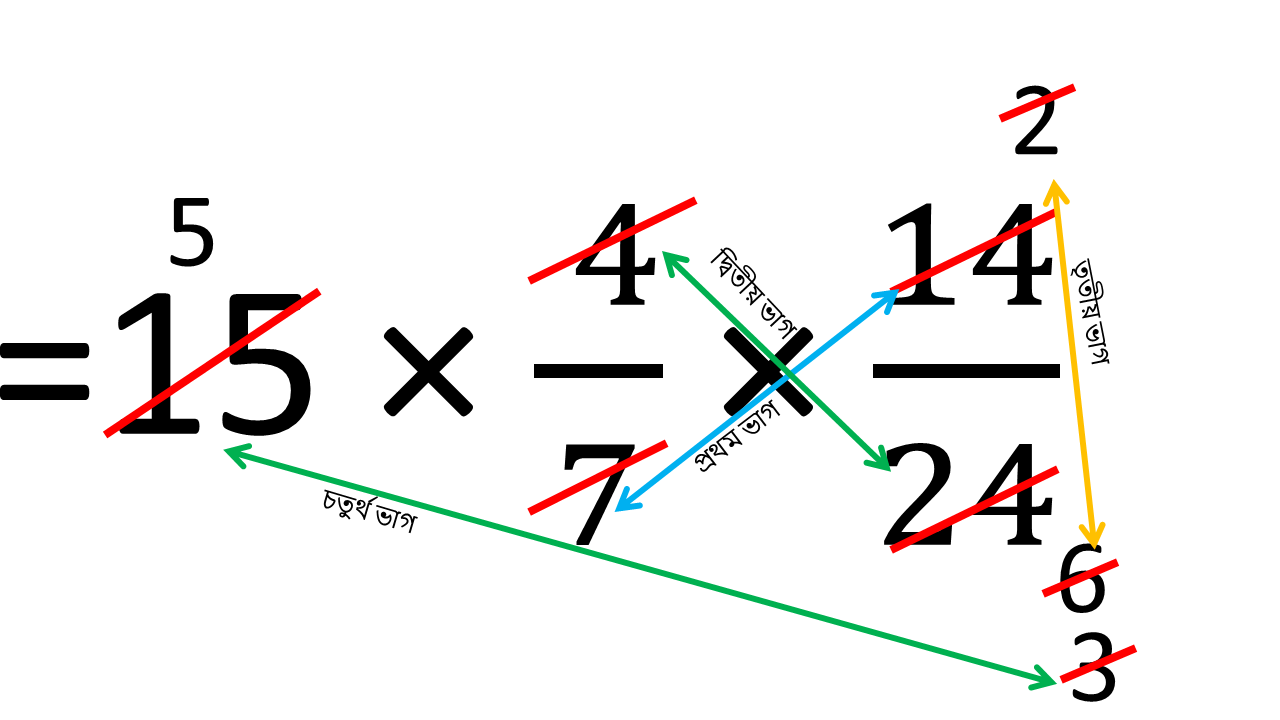
= 5 দিন
| 24 জন লোক দৈনিক 7 ঘণ্টা কাজ শুরু করলে 5 দিনে কাজটি করবেন । |
2. সুভাষকাকার হাটে লেখা একটি 105 পৃষ্ঠার বইয়ের প্রতি পৃষ্ঠায় গড়ে 25 টি করে লাইন আছে এবং প্রতি লাইনে গড়ে 8 টি করে শব্দ আছে। এই বইটি যদি এমনভাবে ছাপাই যাতে প্রতি পৃষ্ঠায় 30 টি করে লাইন থাকবে এবং প্রতি লাইন গড়ে 10 টি করে শব্দ থাকবে, তবে সেই ছাপা বইটি কত পৃষ্ঠার বই হবে ত্রৈরাশিক পদ্ধতিতে হিসাব করি।
সমাধানঃ-

গণিতের ভাষায় সমস্যাটি হলো-
| প্রতি পৃষ্ঠায় লাইনের সংখ্যা ( টি ) | প্রতি লাইনে শব্দের সংখ্যা ( টি ) | পৃষ্ঠার সংখ্যা ( টি ) |
|---|---|---|
| 25 | 8 | 105 |
| 30 | 10 | ? |
প্রথম ধাপঃ-
প্রতি পৃষ্ঠায় লাইনের সংখ্যা একই থাকলে প্রতি লাইনে শব্দের সংখ্যা বাড়ালে পৃষ্ঠার সংখ্যা কমবে। প্রতি লাইনে শব্দের সংখ্যা ও পৃষ্ঠার সংখ্যা ব্যস্ত সমানুপাতী।
দ্বিতীয় ধাপঃ-
প্রতি লাইনে শব্দের সংখ্যা একই থাকলে প্রতি পৃষ্ঠায় লাইনের সংখ্যা বাড়লে পৃষ্ঠার সংখ্যা কমবে। প্রতি পৃষ্ঠায় লাইনের সংখ্যা ও পৃষ্ঠার সংখ্যা ব্যস্ত সমানুপাতী।
অতএব নির্ণেয় পৃষ্ঠার সংখ্যা
= 105 × ( 8/10 ) × ( 25/30 )
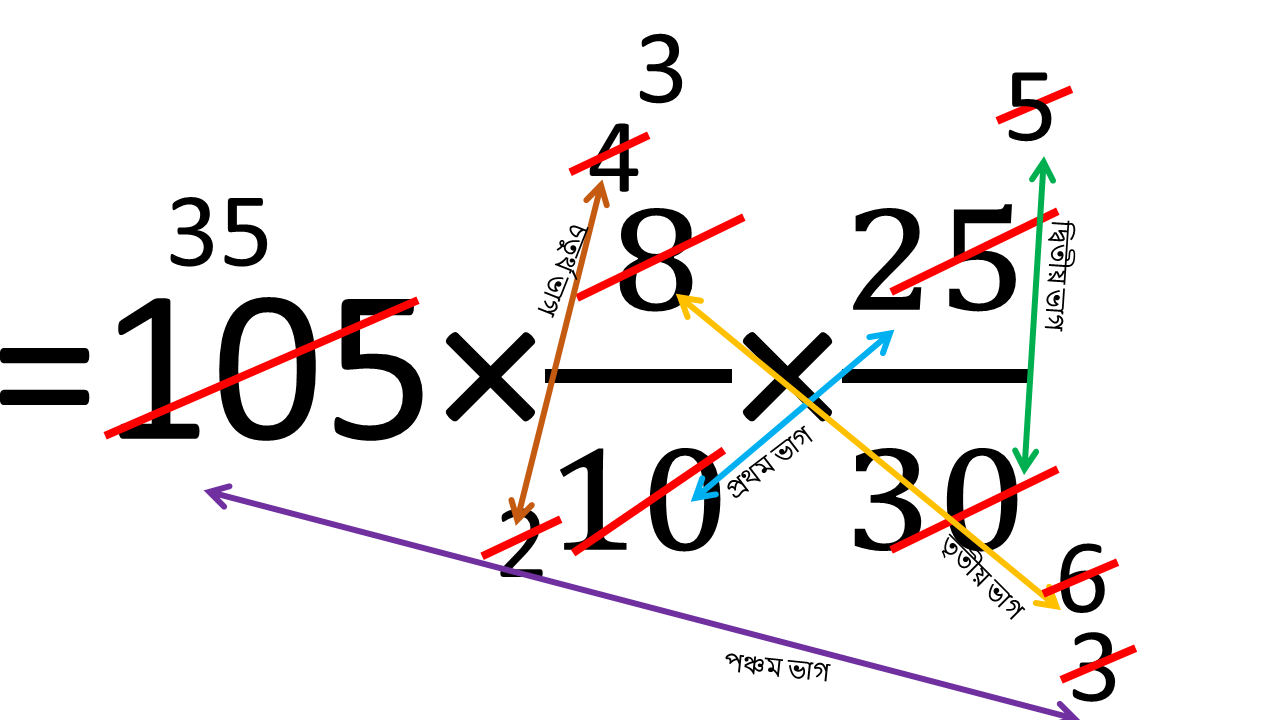
= 70 পৃষ্ঠা
| প্রতি পৃষ্ঠায় 30 টি করে লাইন থাকবে এবং প্রতি লাইন গড়ে 10 টি করে শব্দ থাকবে, তবে সেই ছাপা বইটি 70 পৃষ্ঠার বই হবে । |

| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
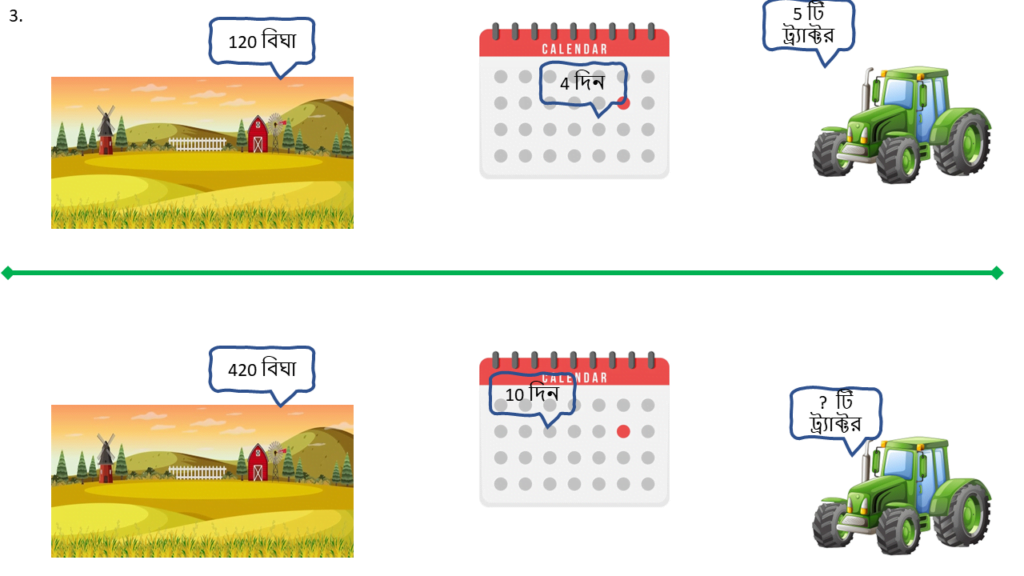
3. একটি কৃষি খামারের 540 বিঘা জমি 14 দিনে চাষ করতে হবে। প্রথম 4 দিনে সক্ষমতা সম্পন্ন 5 টি ট্রাক্টর 120 বিঘা জমি চাষ করল। সময় মতো চাষের কাজ শেষ করতে হলে আরকটি ট্রাক্টর লাগবে ত্রৈরাশিক পদ্ধতিতে হিসাব করি।
সমাধানঃ-
গণিতের ভাষায় সমস্যাটি হলো-
| সময় ( দিন ) | জমির পরিমাণ ( বিঘা ) | ট্রাক্টর সংখ্যা ( টি ) |
|---|---|---|
| 4 | 120 | 5 |
| 10 | 420 | ? |
প্রথম ধাপঃ-
সময় একই থাকলে জমির পরিমাণ বাড়লে ট্রাক্টর সংখ্যা বাড়বে। জমির পরিমাণ ও ট্রাক্টর সংখ্যা সরল সমানুপাতী।
দ্বিতীয় ধাপঃ-
জমির পরিমাণ একই থাকলে সময় বাড়লে ট্রাক্টর সংখ্যা কম লাগবে। জমির পরিমাণ ও ট্রাক্টর সংখ্যা ব্যস্ত সমানুপাতী।
অতএব নির্ণেয় ট্রাক্টর সংখ্যা
= 5 × ( 420/120 ) × ( 4/10 )
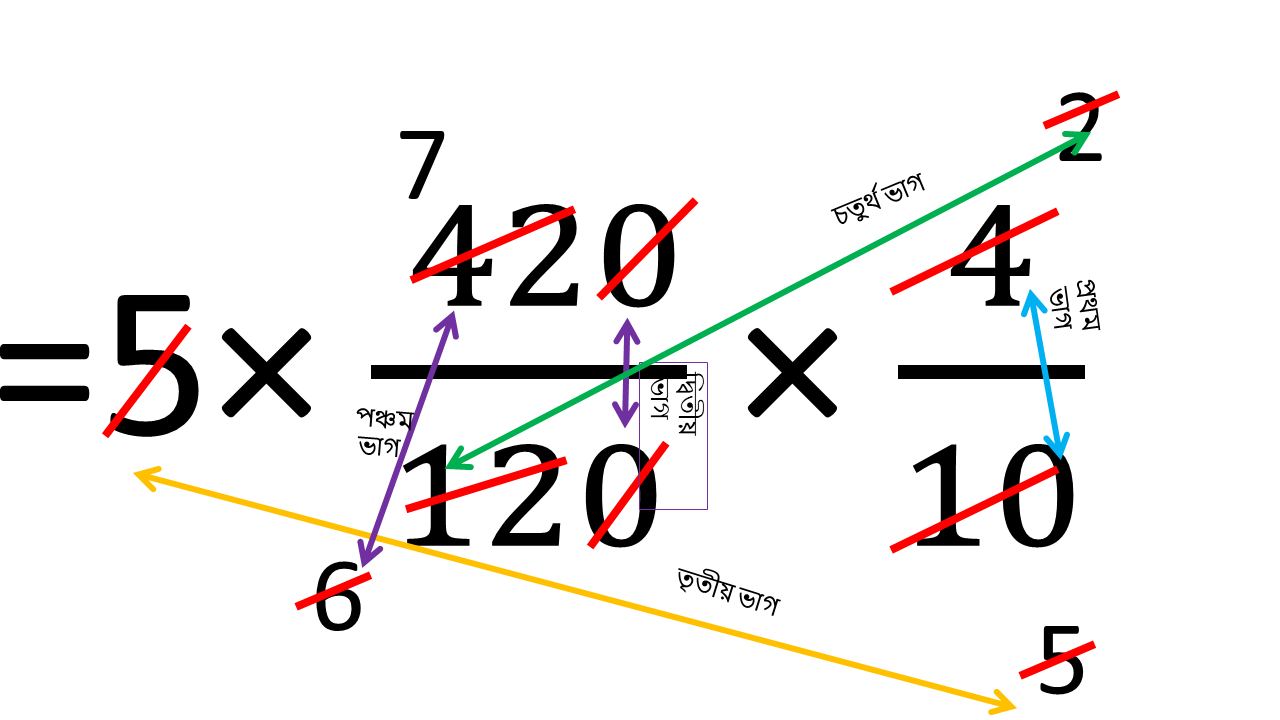
= 7 টি
আগে থেকেই 5 টি ট্রাক্টর আছে
অতএব আরও 2 টি ট্রাক্টর লাগবে।
| সময় মতো চাষের কাজ শেষ করতে হলে আর 2 টি ট্রাক্টর লাগবে । |
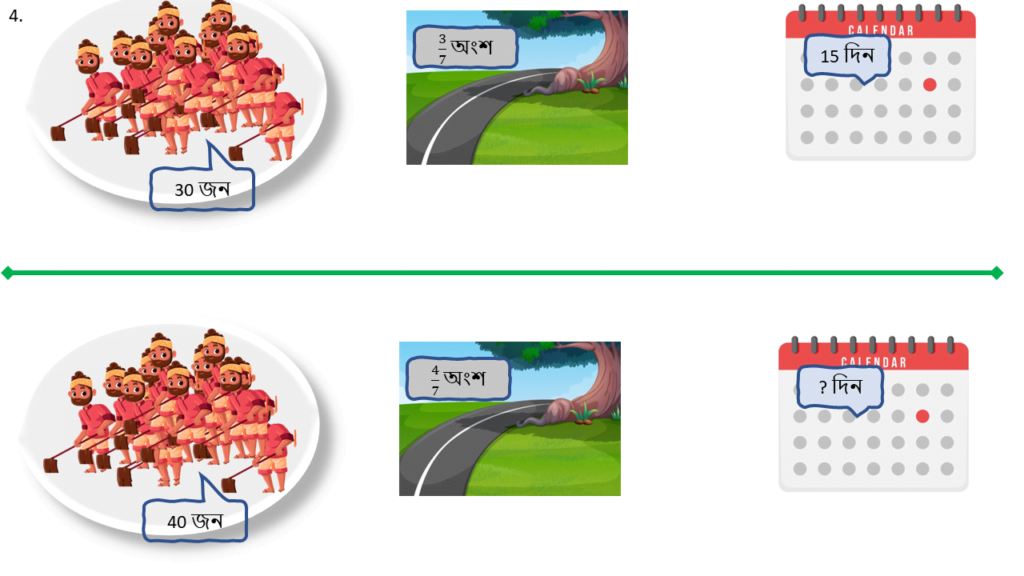
4. 30 জন লোক 15 দিনে একটি গ্রামের রাস্তার 3/7 অংশ সারান। যদি আরও 10 জন লোক কাজটি করতে আসেন তাহলে রাস্তাটির বাকি অংশ সারাতে কতদিন লাগবে ত্রৈরাশিক পদ্ধতিতে হিসাব করি।
সমাধানঃ-
গণিতের ভাষায় সমস্যাটি হলো-
| লোক সংখ্যা ( জন ) | রাস্তার পরিমাণ ( অংশ) | সময়( দিন ) |
|---|---|---|
| 30 | 3/7 | 15 |
| 40 | 4/7 | ? |
প্রথম ধাপঃ-
লোক সংখ্যা একই থাকলে রাস্তার পরিমাণ বাড়লে সময় বেশী লাগবে।রাস্তার পরিমাণ ও সময় সরল সমানুপাতী।
দ্বিতীয় ধাপঃ-
রাস্তার পরিমাণ একই থাকলে লোক সংখ্যা বাড়লে সময় কম লাগবে। লোক সংখ্যা ও সময় ব্যস্ত সমানুপাতী।
অতএব নির্ণেয় দিন সংখ্যা
= 15 × {(4/7)/( 3/7)} × 30/40
= 15 × 4/7×7/3×30/40
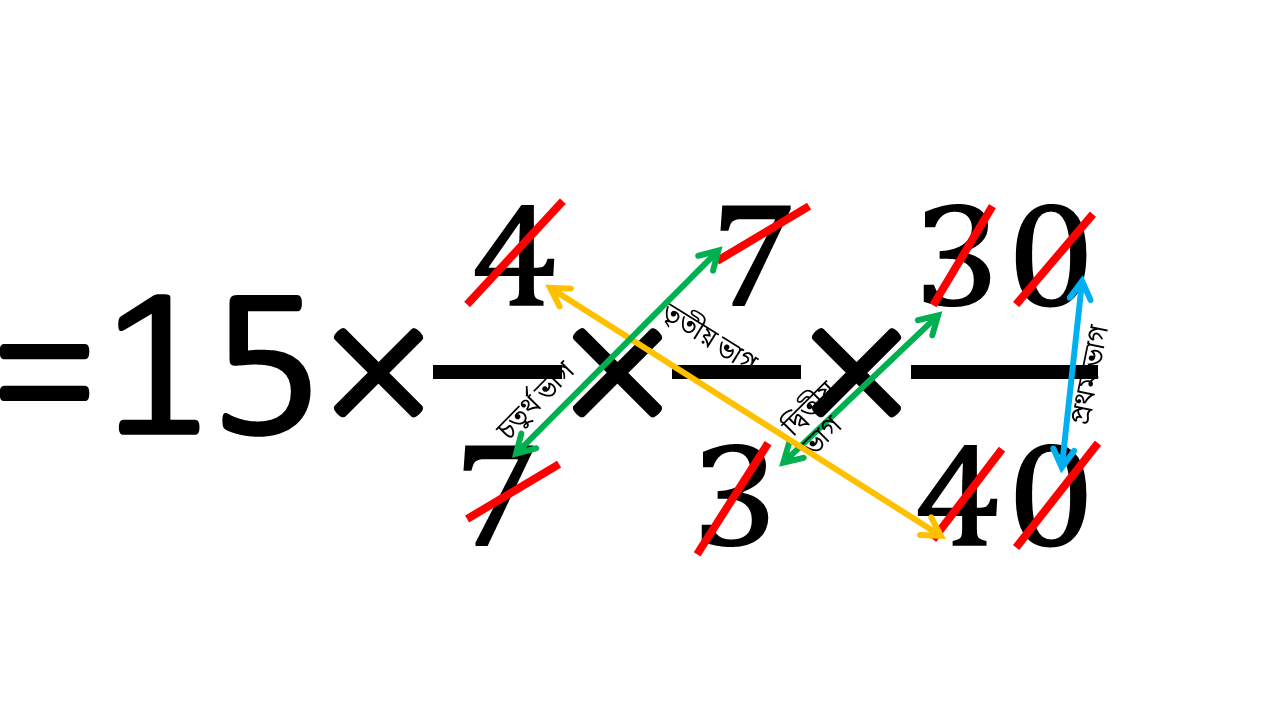
= 15 দিন
| যদি আরও 10 জন লোক কাজটি করতে আসেন তাহলে রাস্তাটির বাকি অংশ সারাতে 15 দিন লাগবে । |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
5. 5 অশ্বক্ষমতা সম্পন্ন একটি পাম্প 36000 লিটার জল 8 ঘণ্টায় উপরে তুলতে পারে। 7 অশ্বক্ষমতা সম্পন্ন পাম্পের 63000 লিটার জল তুলতে কত সময় লাগবে ত্রৈরাশিক পদ্ধতিতে হিসাব করি।
সমাধানঃ-

গণিতের ভাষায় সমস্যাটি হলো-
| পাম্পের ক্ষমতা ( অশ্বক্ষমতা ) | জলের পরিমাণ ( লিটার ) | সময় ( ঘন্টা ) |
|---|---|---|
| 5 | 36000 | 8 |
| 7 | 63000 | ? |
প্রথম ধাপঃ-
পাম্পের ক্ষমতা একই থাকলে জলের পরিমাণ বাড়লে সময় বেশী লাগবে।পাম্পের ক্ষমতা ও সময় সরল সমানুপাতী
দ্বিতীয় ধাপঃ-
জলের পরিমান একই থাকলে পাম্পের ক্ষমতা বাড়লে পানি তোলার সময় কম লাগবে। পাম্পের ক্ষমতা ও পানি তোলার সময় ব্যস্ত সমানুপাতী।
অতএব নির্ণেয় সময়
= 8 × 63000/36000×5/7
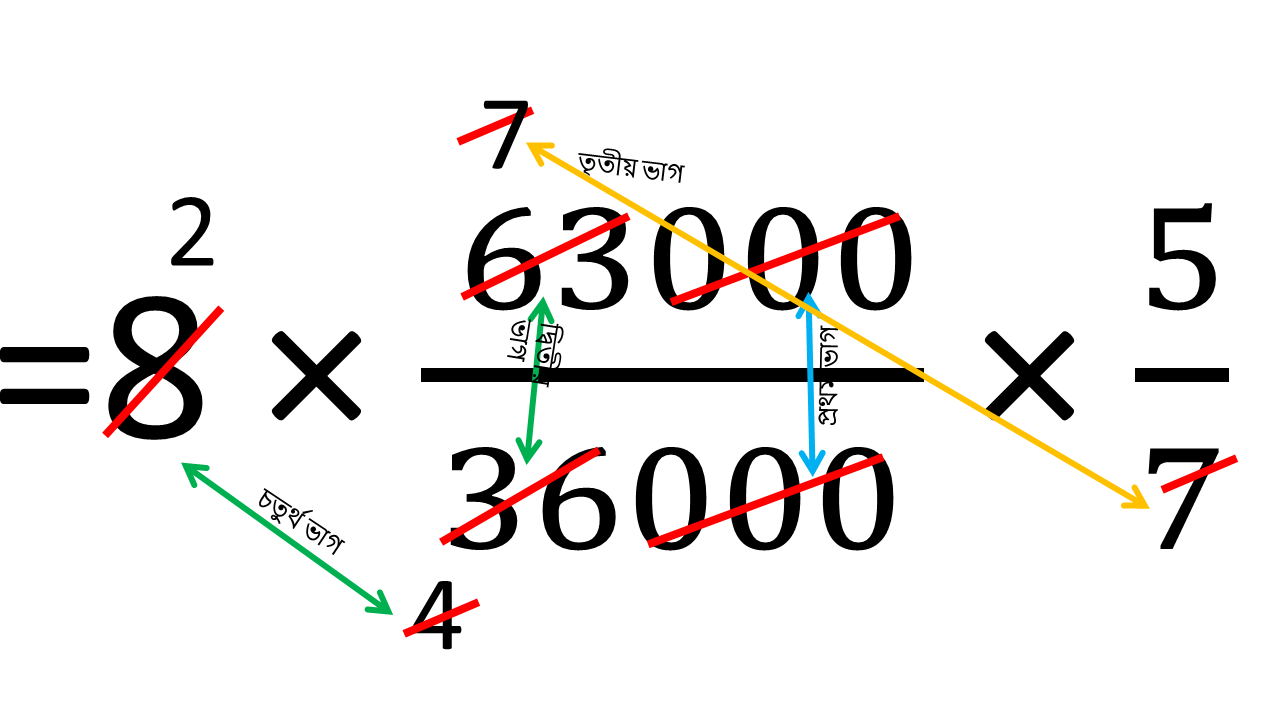
= 10 ঘন্টা
| 7 অশ্বক্ষমতা সম্পন্ন পাম্পের 63000 লিটার জল তুলতে 10 ঘন্টা সময় লাগবে। |
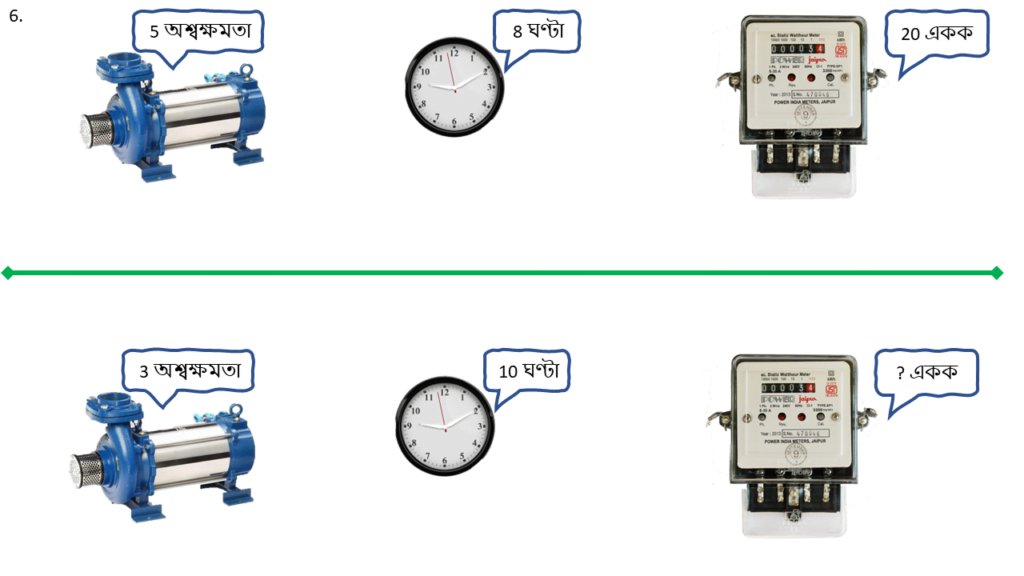
6. একটি কারখানায় 5 অশ্বক্ষমতা ও 3 অশ্বক্ষমতার দুটি মোটর আছে। 5 অশ্বক্ষমতার মোটর টি 8 ঘণ্টা চালালে 20 একক বিদ্যুৎ খরচ হয়। 3 অশ্বক্ষমতার মোটরটি 10 ঘণ্টা চালালে কত একক বিদ্যুৎ খরচ হবে ত্রৈরাশিক পদ্ধতিতে হিসাব করি।
সমাধানঃ-
গণিতের ভাষায় সমস্যাটি হলো-
| মোটরের ক্ষমতা ( অশ্বক্ষমতা ) | সময় ( ঘন্টা ) | বিদ্যুৎ খরচ ( একক ) |
|---|---|---|
| 5 | 8 | 20 |
| 3 | 10 | ? |
প্রথম ধাপঃ-
মোটরের ক্ষমতা একই থাকলে বেশী সময় মোটর চললে বেশী বিদ্যুৎ খরচ হবে। মোটর চলার সময় ও বিদ্যুৎ খরচ সরল সমানুপাতী।
দ্বিতীয় ধাপঃ-
মোটর চলার সময় একই থাকলে মোটরের ক্ষমতা বাড়লে বিদ্যুৎ খরচ বাড়বে। মোটরের ক্ষমতা ও বিদ্যুৎ খরচ সরল সমানুপাতী।
অতএব নির্ণেয় বিদ্যুৎ খরচ
= 20 × 10/8 × 3/5
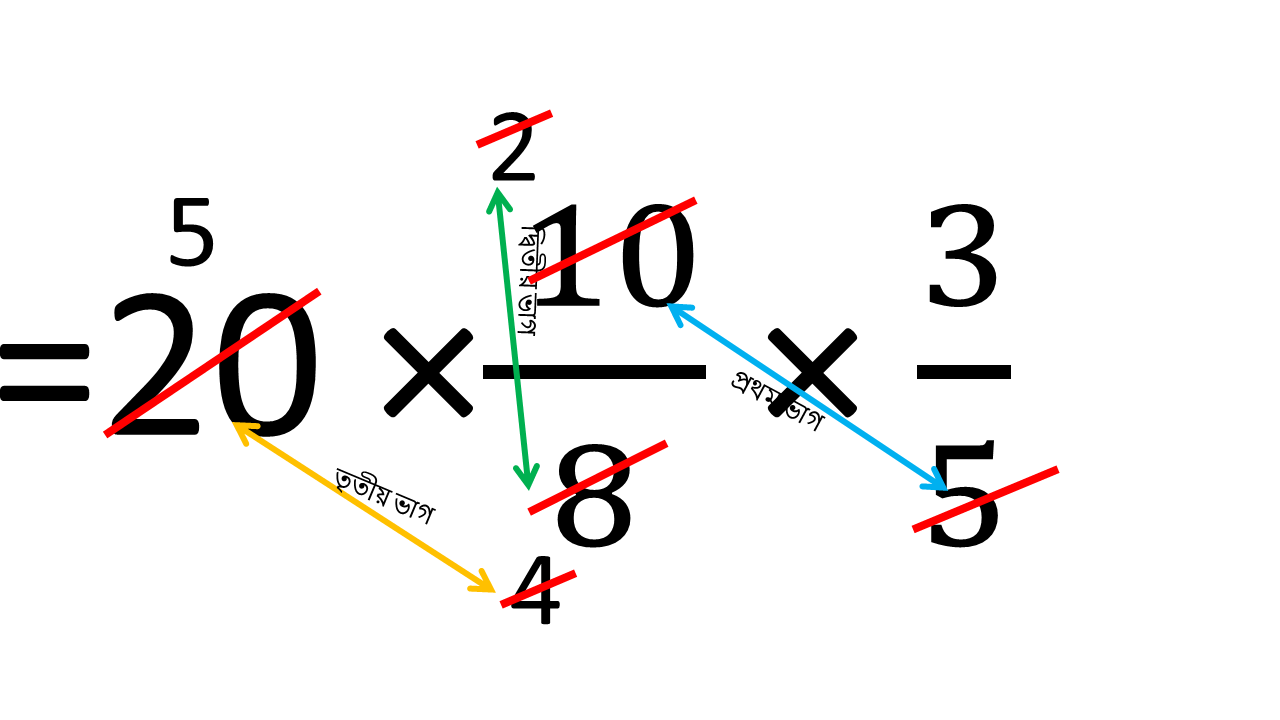
= 15 একক
| 3 অশ্বক্ষমতার মোটরটি 10 ঘণ্টা চালালে15 একক বিদ্যুৎ খরচ হবে। |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
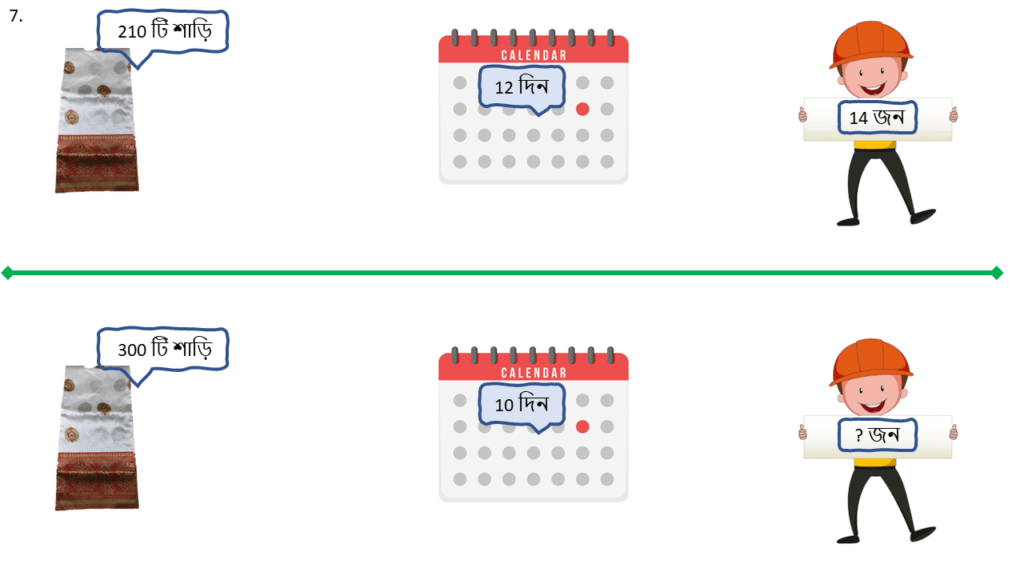
7. গোপালনগরের একটি তাঁত কারখানায় 14 জন তাঁতি 12 দিনে 210 টি শাড়ি বুন্তে পারেন। পুজোর সময়ে 10 দিনের মধ্যে 300 টি শাড়ি যোগান দেওয়ার অর্ডার এলো। সময়মতো সেই শাড়ি যোগান দিতে হলে আরও কতজন তাঁতি নিয়োগ করতে হবে ব্যাপকতর ত্রৈরাশিক পদ্ধতিতে হিসাব করি।
সমাধানঃ-
গণিতের ভাষায় সমস্যাটি হলো-
| শাড়ির সংখ্যা ( টি ) | সময় ( দিন ) | তাঁতির সংখ্যা ( জন ) |
|---|---|---|
| 210 | 12 | 14 |
| 300 | 10 | ? |
প্রথম ধাপঃ-
শাড়ির সংখ্যা একই থাকলে দিন সংখ্যা কমালে তাঁতির সংখ্যা বাড়াতে হবে।দিন সংখ্যা ও তাঁতির সংখ্যা ব্যস্ত সমানুপাতী।
দ্বিতীয় ধাপঃ-
সময় একই থাকলে শাড়ির সংখ্যা বাড়লে তাঁতির সংখ্যা বাড়াতে হবে। শাড়ির সংখ্যা ও তাঁতির সংখ্যা সরল সমানুপাতী।
অতএব নির্ণেয় তাঁতির সংখ্যা
= 14 × 12/10 × 300/210
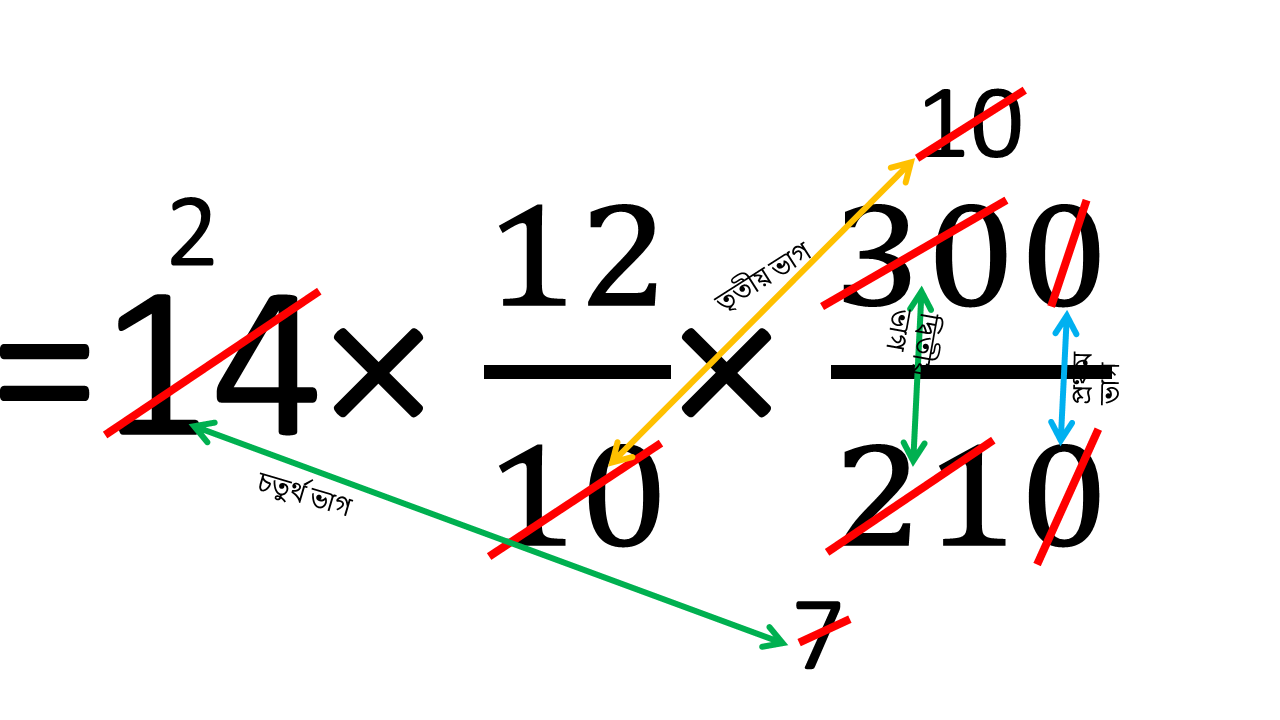
= 24 জন
অতএব 14 জন তাঁতি আছেন আরো 10 জন তাঁতি নিয়োগ করতে হবে।
| সময়মতো সেই শাড়ি যোগান দিতে হলে আরও 10 জন তাঁতি নিয়োগ করতে হবে। |
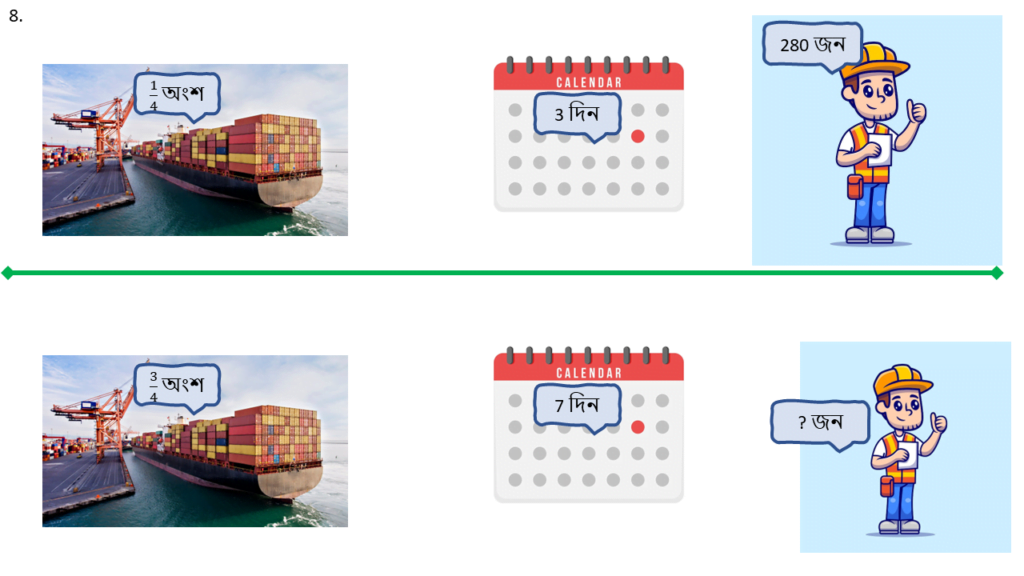
8. একটি সংস্থা জাহাজ থেকে 10 দিনে জাহাজের মাল নামানোর বরাত পেয়েছে। সংস্থাটি তার জন্য 280 জন লোক নিয়োগ করেছে। 3 দিন পরে দেখা গেলো কাজটির 1/4 অংশ সম্পূর্ণ হয়েছে। আর কতজন লোক নিয়োগ করলে কাজটি সময়মতো শেষ হবে তা ত্রৈরাশিক পদ্ধতিতে হিসাব করি।
সমাধানঃ-
গণিতের ভাষায় সমস্যাটি হলো-
| সময় ( দিন ) | কাজের পরিমাণ ( অংশ ) | লোক সংখ্যা ( জন ) |
|---|---|---|
| 3 | 1/4 | 280 |
| 7 | 3/4 | ? |
প্রথম ধাপঃ-
দিন সংখ্যা একই থাকলে কাজের পরিমাণ বাড়লে লোক সংখ্যা বাড়াতে হবে।কাজের পরিমাণ ও লোক সংখ্যা সরল সমানুপাতী।
দ্বিতীয় ধাপঃ-
কাজের পরিমাণ একই থাকলে দিন সংখ্যা বাড়লে লোক সংখ্যা কমবে।দিন সংখ্যা ও লোক সংখ্যা ব্যস্ত সমানুপাতী।
অতএব নির্ণেয় মোট লোক সংখ্যা
280 × ( 3/4 ) / ( 1/4 ) × 3/7
= 280×3/4×4/1×3/7
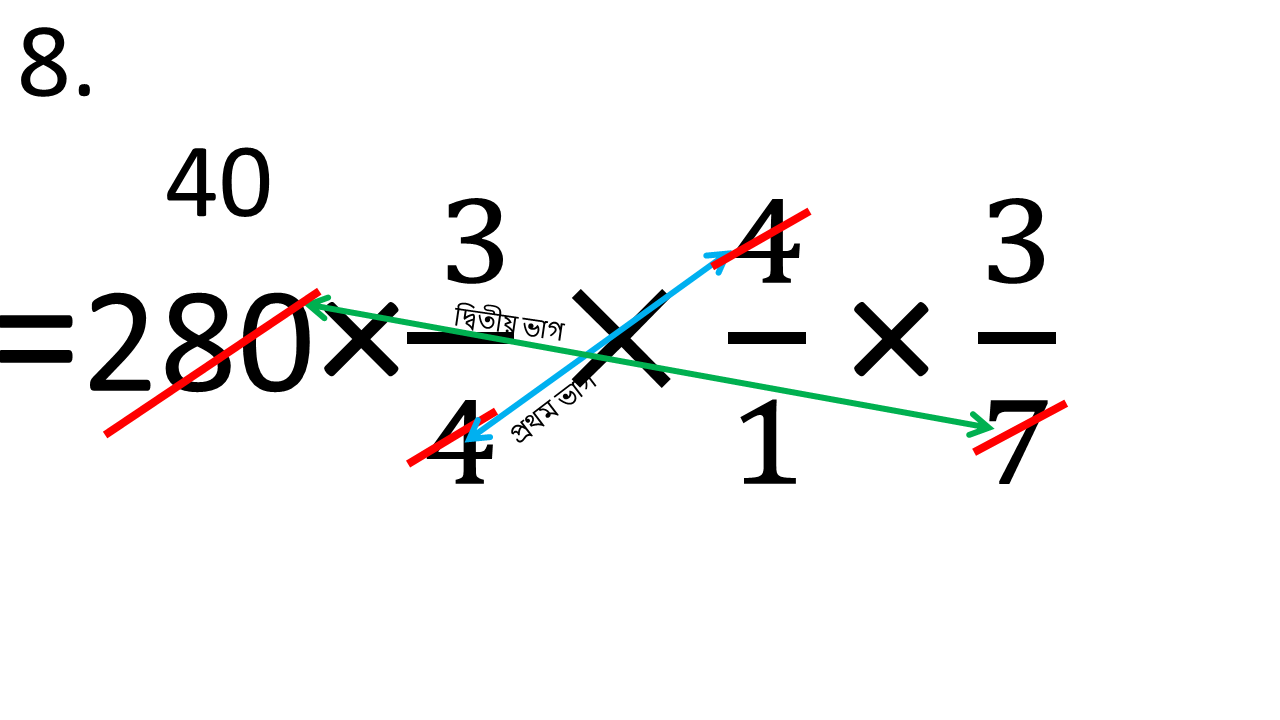
= 360 জন
280 জন লোক নিয়োগ করা হয়েছে।
অর্থাৎ এখনো (360-280)= 80 জন লোক নিয়োগ করতে হবে।
| আর 80 জন লোক নিয়োগ করলে কাজটি সময়মতো শেষ হবে। |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
9. একটি যন্ত্রচালিত তাঁতের ক্ষমতা একটি হস্তচালিত তাঁতের ক্ষমতার 2¼ গুণ। 12 টি হস্তচালিত তাঁত 1080 মিটার দৈর্ঘ্যের কাপড় 18 দিনে তৈরি করে। 2700 মিটার দৈর্ঘ্যের কাপড় 15 দিনে তৈরি করতে কতগুলি যন্ত্রচালিত তাঁত লাগবে তা ত্রৈরাশিক পদ্ধতিতে হিসাব করি।
সমাধানঃ-
গণিতের ভাষায় সমস্যাটি হলো-
| কাপড়ের দৈর্ঘ্য ( মিটার ) | সময় ( দিন ) | হস্তচালিত তাঁতের সংখ্যা ( টি ) |
|---|---|---|
| 1080 | 18 | 12 |
| 2700 | 15 | ? |
প্রথম ধাপঃ-
কাপড়ের পরিমাণ একই থাকলে দিন সংখ্যা কমলে হস্তচালিত তাঁতের সংখ্যা বাড়াতে হবে।দিন সংখ্যা ও হস্তচালিত তাঁতের সংখ্যা ব্যস্ত সমানুপাতী।
দ্বিতীয় ধাপঃ-
দিন সংখ্যা একই থাকলে কাপড়ের পরিমান বাড়লে হস্তচালিত তাঁতের সংখ্যা বাড়াতে হবে।কাপড়ের পরিমান ও হস্তচালিত তাঁতের সংখ্যা সরল সমানুপাতী।
অতএব নির্ণেয় হস্তচালিত তাঁতের সংখ্যা
= 12 × 18/15 × 2700/1080
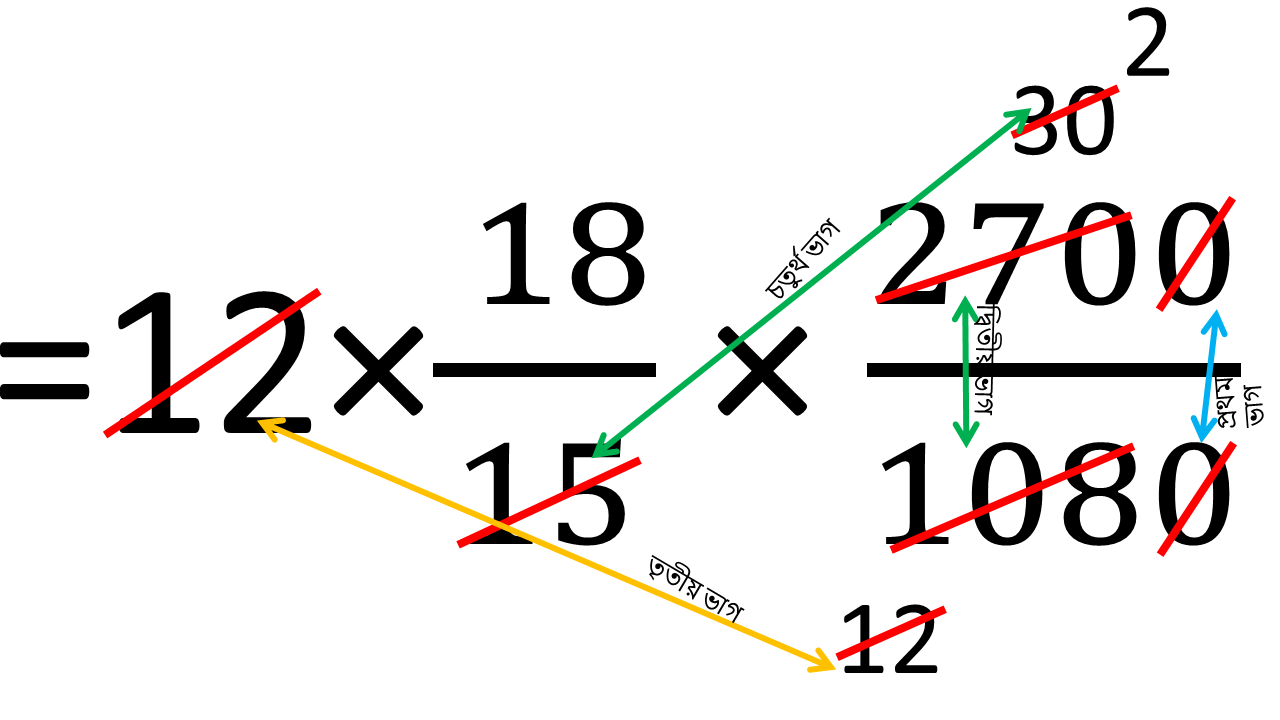
= 36 টি
দেওয়া আছে,
| 1 টি যন্ত্র চালিত তাঁতের ক্ষমতা = 9/4 × 1 টি হস্তচালিত যন্ত্রের ক্ষমতা |
| 1 টি হস্তচালিত যন্ত্রের ক্ষমতা=4/9 × 1 টি যন্ত্র চালিত তাঁতের ক্ষমতা |
| 36 টি হস্তচালিত যন্ত্রের ক্ষমতা=4/9×36 টি যন্ত্র চালিত তাঁতের ক্ষমতা=16 টি যন্ত্র চালিত তাঁতের ক্ষমতা |
| 2700 মিটার দৈর্ঘ্যের কাপড় 15 দিনে তৈরি করতে 16 টি যন্ত্রচালিত তাঁত লাগবে। |
10. 25 জন কৃষক একটি সমবায় সমিতির 2400 বিঘা জমি 36 দিনে চাষ করেন। সমিতি একটি ট্রাক্টর কেনায় দেখা যায় অর্ধেক জমি 30 দিনে চাষ করা যায়। একটি ট্রাক্টরের ক্ষমতা কতজন কৃষকের চাষ করার ক্ষমতার সমান তা ত্রৈরাশিক পদ্ধতিতে হিসাব করি।
সমাধানঃ-

গণিতের ভাষায় সমস্যাটি হলো-
| জমির পরিমাণ ( বিঘা ) | সময় ( দিন ) | কৃষক সংখ্যা ( জন ) |
|---|---|---|
| 2400 | 36 | 25 |
| 1200 | 30 | ? |
প্রথম ধাপঃ-
জমির পরিমাণ একই থাকলে দিন সংখ্যা বাড়লে কৃষক সংখ্যা কমাতে হবে। দিন সংখ্যা ও কৃষক সংখ্যা ব্যস্ত সমানুপাতী।
দ্বিতীয় ধাপঃ-
দিন সংখ্যা একই রেখে জমির পরিমাণ বাড়লে কৃষক সংখ্যা বাড়াতে হবে।জমির পরিমান ও কৃষক সংখ্যা সরল সমানুপাতী।
অতএব নির্ণেয় কৃষক সংখ্যা
= 25 ×36/30 × 12/24
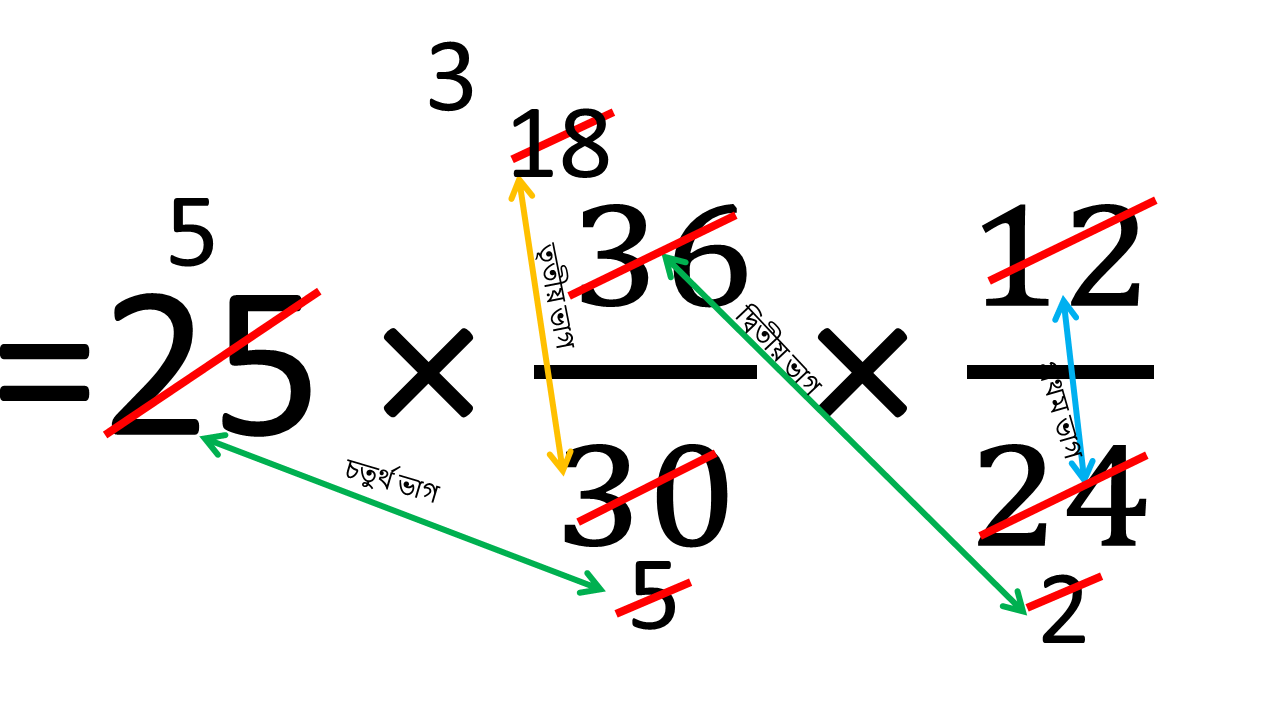
= 15
প্রশ্নে দেওয়া আছে এই কাজটি করতে ট্রাক্টর লাগে 1 টি।
অতএব,
| একটি ট্রাক্টরের ক্ষমতা 15 জন কৃষকের চাষ করার ক্ষমতার সমান |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
11. একটি জাহাজের কলকাতা থেকে কোচিন যেতে 25 দিন সময় লাগে। জাহাজটি 36 জন নাবিকসহ এবং প্রত্যেক নাবিকের জন্য প্রতিদিন 850 গ্রাম খাবারের ব্যবস্থা করে যাত্রা শুরু করল। কিন্তু 13 দিন পরে ওই জাহাজটি অপর একটি ডুবন্ত জাহাজ থেকে 15 জন নাবিককে উদ্ধার করল এবং জাহাজটির গতিবেগ বাড়িয়ে দিয়ে 10 দিনে কোচিন পৌঁছাল। এখন প্রত্যেক নাবিক প্রতিদিন কতটা পরিমাণ খাবার খেলে ওই মজুত খাবারে তারা কোচিন নিরাপদে পৌঁছাতে পারবে এবং সমস্ত খাবার ওই সময়ে শেষ হয়ে যাবে। ত্রৈরাশিক পদ্ধতিতে হিসাব করি।
সমাধানঃ-
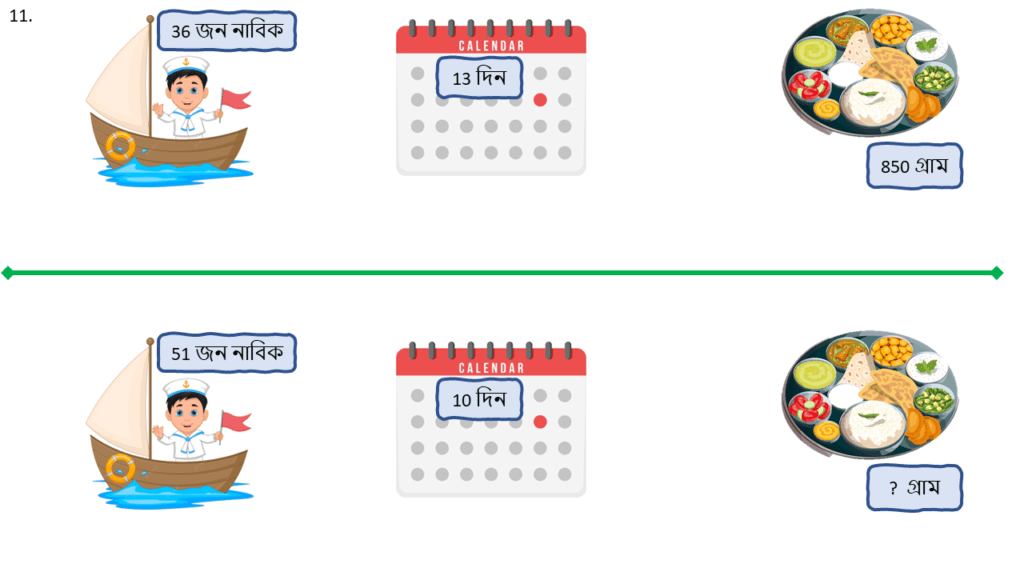
গণিতের ভাষায় সমস্যাটি হলো-
| নাবিকের সংখ্যা ( জন ) | সময় ( দিন ) | নাবিক পিছু খাবারের পরিমাণ ( গ্রাম ) |
|---|---|---|
| 36 | 12 | 850 |
| 51 | 10 | ? |
প্রথম ধাপঃ-
এখানে নাবিক সংখ্যা একই থাকলে দিন সংখ্যা কমলে নাবিক পিছু খাবারের পরিমাণ বাড়বে। দিন সংখ্যা ও নাবিক পিছু খাবারের পরিমাণ ব্যস্ত সমানুপাতী।
দ্বিতীয় ধাপঃ-
দিন সংখ্যা একই থাকলে নাবিকের সংখ্যা বাড়লে নাবিক পিছু খাবারের পরিমাণ কমবে। নাবিকের সংখ্যা ও নাবিক পিছু খাবারের পরিমাণ ব্যস্ত সমানুপাতী ।
অতএব নির্ণেয় খাবারের পরিমাণ
= 850 × 12/10 × 36/51
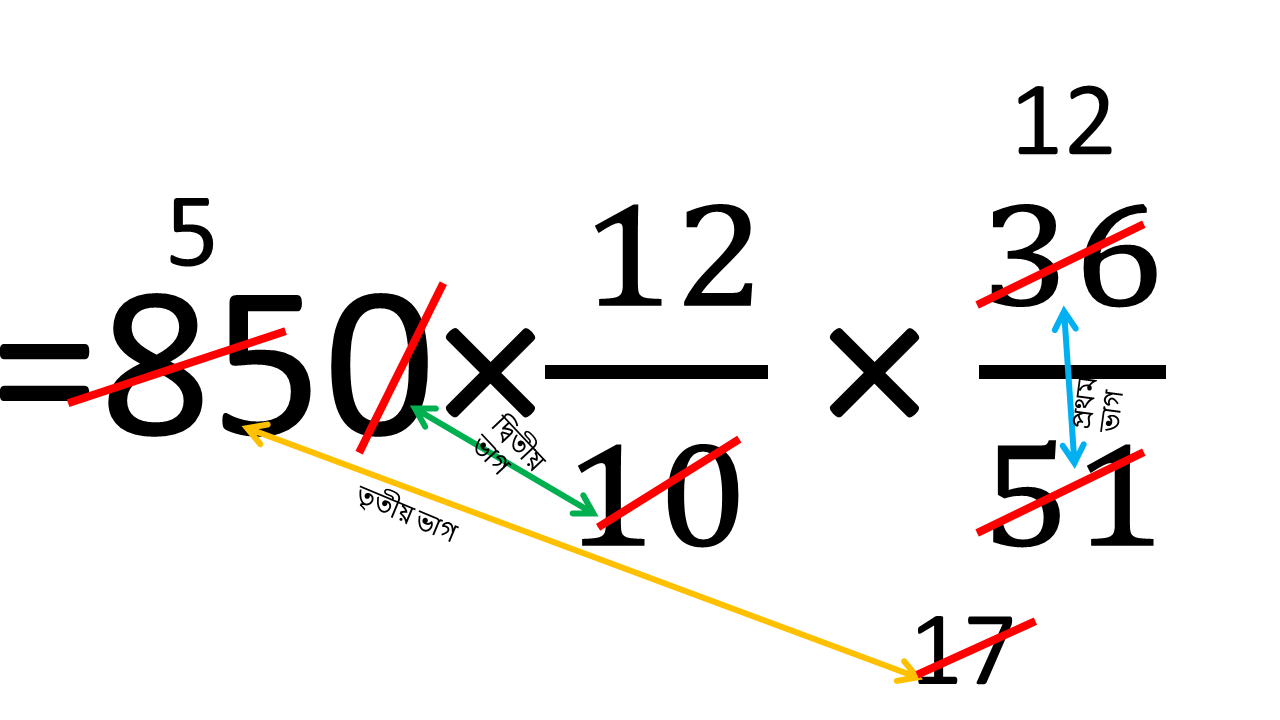
= 720 গ্রাম
| প্রত্যেক নাবিক প্রতিদিন 720 গ্রাম পরিমাণ খাবার খেলে ওই মজুত খাবারে তারা কোচিন নিরাপদে পৌঁছাতে পারবে এবং সমস্ত খাবার ওই সময়ে শেষ হয়ে যাবে। |
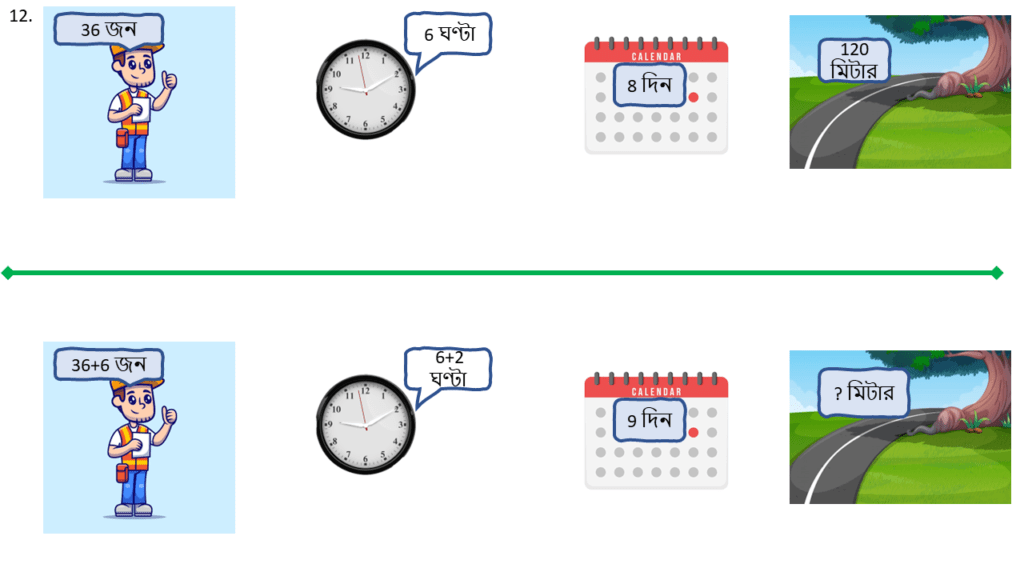
12. একটি গ্রামে 36 জন লোক প্রতিদিন 6 ঘণ্টা কাজ করে 8 দিনে 120 মিটার রাস্তা তৈরি করতে পারেন। আরও 6 জন লোক কাজটির সাথে যুক্ত হলো এবং দৈনিক কাজের পরিমাণ আরও 2 ঘণ্টা করে বাড়ানো হলো। এখন 9 দিনে কত দৈর্ঘ্যের রাস্তা তৈরি করা যাবে তা ত্রৈরাশিক পদ্ধতিতে হিসাব করি।
সমাধানঃ-
গণিতের ভাষায় সমস্যাটি হলো-
| লোক সংখ্যা ( জন ) | প্রতিদিন কাজের সময় ( ঘণ্টা ) | কাজ শেষ হওয়ার সময় ( দিন ) | রাস্তার পরিমাণ ( মিটার ) |
|---|---|---|---|
| 36 | 6 | 8 | 120 |
| 42 | 8 | 9 | ? |
প্রথম ধাপঃ-
লোক সংখ্যা ও প্রতিদিন কাজ করার সময় একই থাকলে কাজ শেষ হওয়ার সময় বাড়ালে রাস্তার পরিমাণ বাড়বে। কাজ শেষ হওয়ার সময় ও রাস্তার পরিমাণ সরল সমানুপাতী ।
দ্বিতীয় ধাপঃ-
লোক সংখ্যা ও কাজ শেষ হওয়ার সময় একই রেখে প্রতিদিন কাজের সময় বাড়ালে রাস্তার পরিমাণ বাড়বে। প্রতিদিন কাজের সময় ও রাস্তার পরিমাণ সরল সমানুপাতী।
তৃতীয় ধাপঃ- প্রতিদিন কাজের সময় ও কাজ শেষ হওয়ার সময় একই রেখে লোক সংখ্যা বাড়ালে রাস্তার পরিমাণ বাড়বে। লোক সংখ্যা ও রাস্তার পরিমাণ সরল সমানুপাতী।
অতএব নির্ণেয় রাস্তার পরিমাণ
= 120×9/8×8/6×42/36
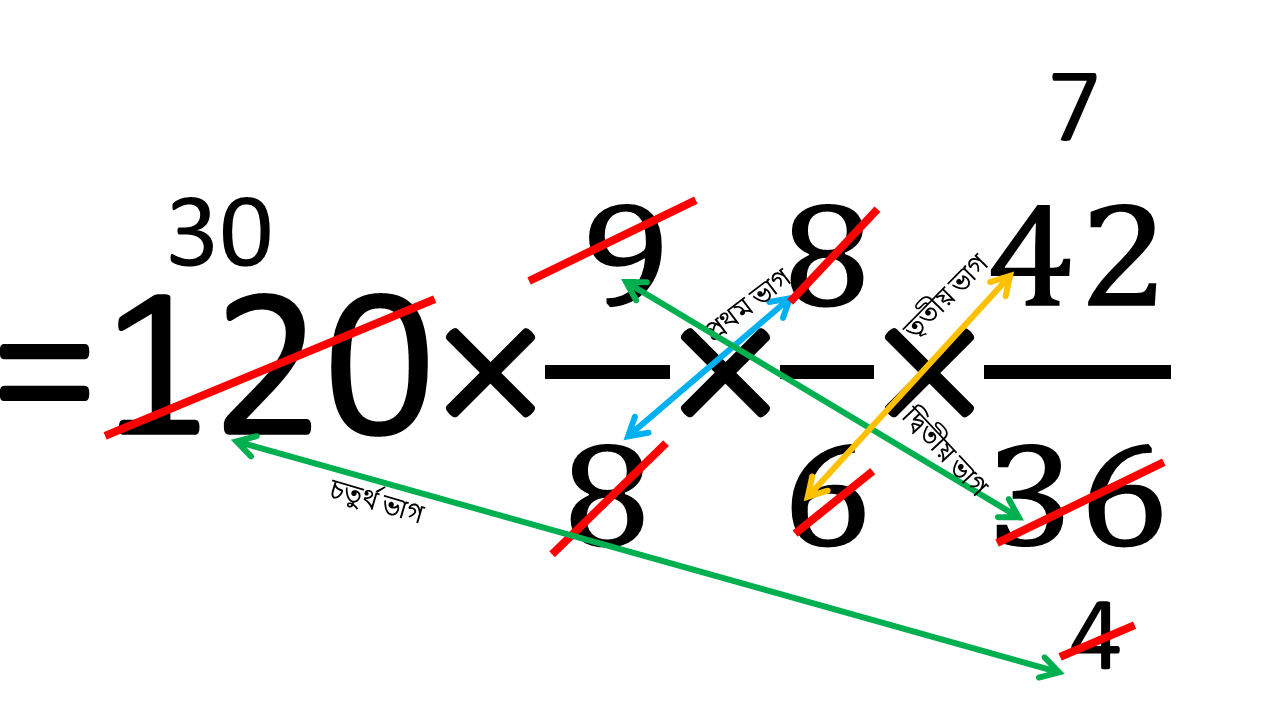
= 210 মিটার
| 9 দিনে 210 মিটার দৈর্ঘ্যের রাস্তা তৈরি করা যাবে । |

| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
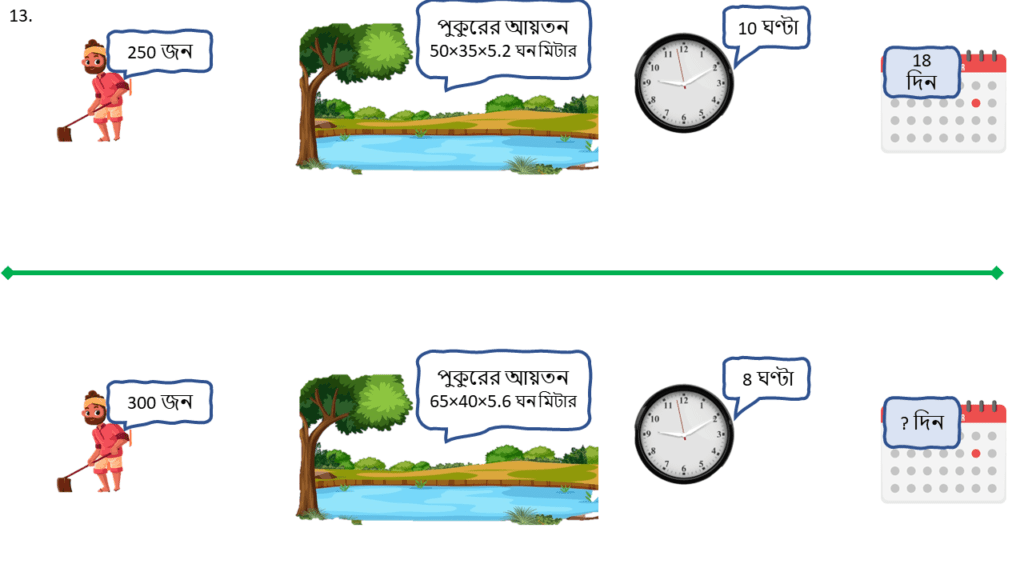
13. 250 জন লোক 50 মিটার দীর্ঘ, 35 মিটার প্রশস্থ এবং 5.2 মিটার গভীর একটি পুকুর প্রতিদিন 10 ঘণ্টা কাজ করে 18 দিনে কাটতে পারেন। 65 মিটার দীর্ঘ, 40 মিটার প্রশস্থ এবং 5.6 মিটার গভীর অপর একটি পুকুর 300 জন লোক প্রতিদিন 8 ঘণ্টা কাজ করে কতদিনে কাটতে পারবেন তা ত্রৈরাশিক পদ্ধতিতে হিসাব করি।
সমাধানঃ-
গণিতের ভাষায় সমস্যাটি হলো-
| লোক সংখ্যা ( জন ) | সময় ( ঘন্টা ) | কাজের জমির আয়তন ( ঘন মিটার ) | সময় ( দিন ) |
|---|---|---|---|
| 250 | 10 | 50×35×5.2 | 18 |
| 300 | 8 | 65×40×5.6 | ? |
প্রথম ধাপঃ- লোক সংখ্যা ও প্রতিদিন কাজ করার সময় একই রেখে কাজের জমির আয়তন বাড়ালে সময় বেশি লাগবে।কাজের জমির আয়তন ও সময় সরল সমানুপাতী।
দ্বিতীয় ধাপঃ- লোক সংখ্যা ও কাজের জমির আয়তন একই রেখে প্রতিদিন কাজ করার সময় কমালে মোট সময় বেশী লাগবে। প্রতিদিন কাজ করার সময় ও মোট সময় ব্যস্ত সমানুপাতী।
তৃতীয় ধাপ:- লোক সংখ্যা ও প্রতিদিন কাজ করার সময় একই রেখে কাজের জমির আয়তন বাড়লে মোট সময় বেশী লাগবে। কাজের জমির আয়তন ও মোট সময় সরল সমানুপাতী।
অতএব নির্ণেয় মোট সময় লাগবে,
= 18 × ( 65 × 40 × 5.6 )/( 50 × 35 × 5.2 ) × 10/8 × 250/300
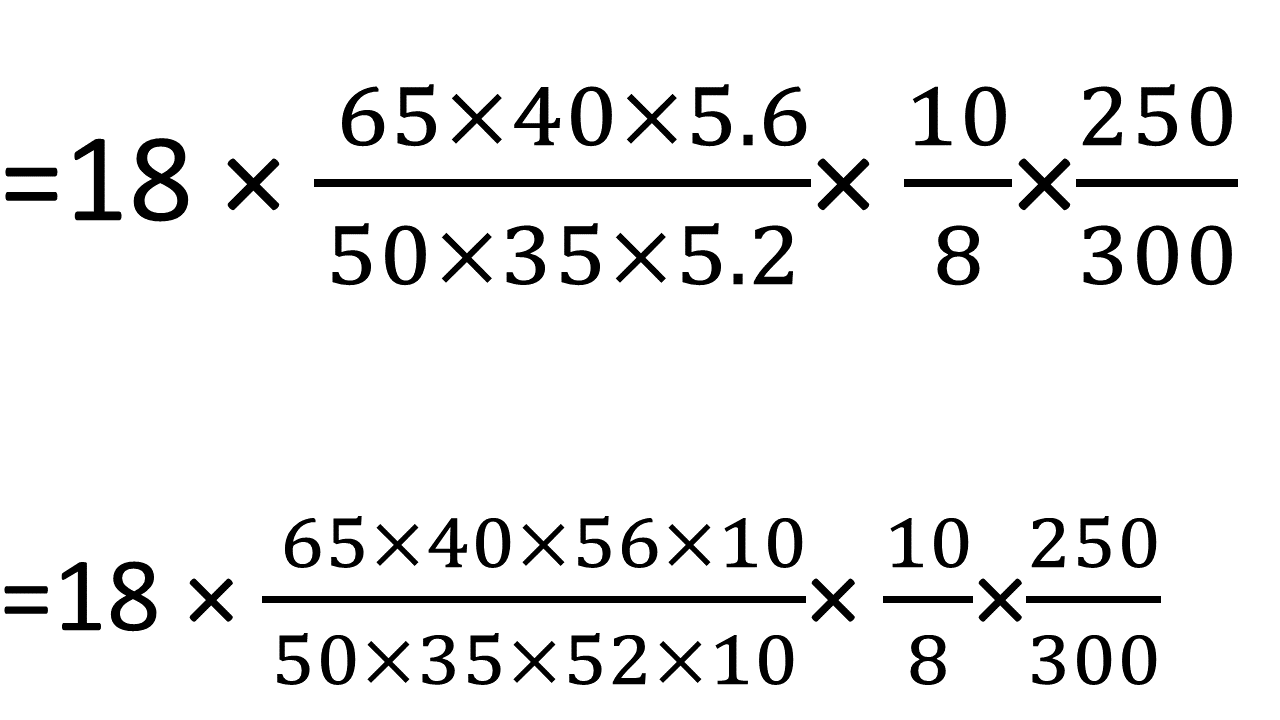
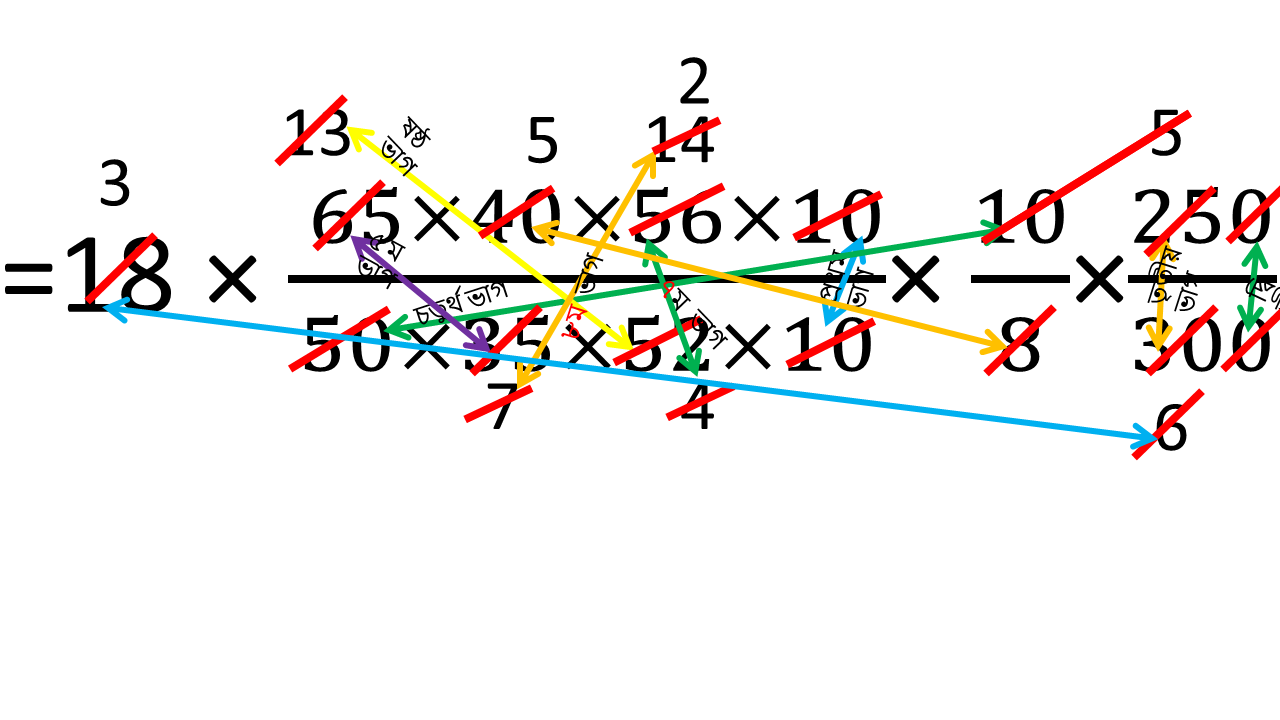
= 30 দিন
| 65 মিটার দীর্ঘ, 40 মিটার প্রশস্থ এবং 5.6 মিটার গভীর অপর একটি পুকুর 300 জন লোক প্রতিদিন 8 ঘণ্টা কাজ করে 30 দিনে কাটতে পারবেন |
14. নীচের পারস্পারিক সম্পর্কগুলি দেখে গণিতের গল্প তৈরি করি ও ত্রৈরাশিক পদ্ধতিতে উত্তর খুঁজি ।
( a )
| ক্ষমতা ( অশ্বশক্তি ) | সময় ( ঘণ্টা ) | বিদ্যুৎ খরচ ( ইউনিট ) |
|---|---|---|
| 5 | 8 | 20 |
| 3 | 10 | ? |
সমাধানঃ-
নির্ণেয় বিদ্যুৎ খরচ
= 20×10/8×3/5
= 15 ইউনিট
( b )
| ক্ষেতমজুরের সংখ্যা ( জন ) | সময় ( দিন ) | জমির পরিমাণ ( বিঘা ) |
|---|---|---|
| 5 | 15 | 18 |
| 10 | 10 | ? |
সমাধানঃ-
নির্ণেয় জমির পরিমাণ
= 18×10/15×10/5
= 24 বিঘা
এই কষে দেখি 10.2 Class 8|Koshe Dekhi 10.2 Class 8 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।
 কষে দেখি 10.1
কষে দেখি 10.1
তোমাদের এই ত্রৈরাশিক কষে দেখি 10.2 এর সমাধান গুলি কেমন লাগলো অবশ্যই কমেন্ট করে জানাবে এবং কোথাও বুঝতে অসুবিধা হলে সেটাও কমেন্ট এ জানাবে। তোমাদের জন্যে এই অধ্যায়ের আর একটি কষে দেখি 10.1 এর সমস্ত অংকের সমাধান আমি করে দিয়েছি। ওই কষে দেখি তে কোনো অংক বুঝতে না পারলে তোমরা এখান থেকে দেখে নিতে পারবে।   কষে দেখি 10.1 কষে দেখি 10.1 |
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 10.2 Class 8 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 10.2 Class 8 তারপর  |
| গনিতপ্রভা অষ্টম শ্রেণীর সমস্ত অধ্যায়ের সমাধান- | |
|---|---|
| অধ্যায় | সমাধান |
| 2. পাই চিত্র | কষে দেখি 2 |
| 3. মূলদ সংখ্যার ধারণা | অধ্যায়ের সারাংশ |
| কষে দেখি 3 | |
| 4. বীজগাণিতিক সংখ্যামালার গুণ ও ভাগ | অধ্যায়ের সারাংশ |
| কষে দেখি 4.1 | |
| কষে দেখি 4.2 | |
| 5. ঘনফল নির্ণয় | অধ্যায়ের সারাংশ |
| কষে দেখি 5.1 | |
| কষে দেখি 5.2 | |
| কষে দেখি 5.3 | |
| 6. পূরক কোণ, সম্পূরক কোণ ও সন্নিহিত কোণ | অধ্যায়ের সারাংশ |
| কষে দেখি 6 | |
| 7. বিপ্রতীপ কোণের ধারণা | অধ্যায়ের সারাংশ |
| কষে দেখি 7.1 | |
8. সমান্তরাল সরলরেখা ও ছেদকের ধর্ম | অধ্যায়ের সারাংশ |
| কষে দেখি 8 | |
9. ত্রিভুজের দুটি বাহু ও তাদের বিপরীত কোণের সম্পর্ক | অধ্যায়ের সারাংশ |
| কষে দেখি 9 | |
| 10. ত্রৈরাশিক | কষে দেখি 10.1 |
| কষে দেখি 10.2 | |
| 11. শতকরা | কষে দেখি 11 |
| 12. মিশ্রণ | কষে দেখি 12 |
13. বীজগাণিতিক সংখ্যামালার উৎপাদকে বিশ্লেষণ | কষে দেখি 13.1 |
| কষে দেখি 13.2 | |
14. বীজগাণিতিক সংখ্যামালার গ.সা.গু ও ল.সা.গু | কষে দেখি 14 |
15. বীজগাণিতিক সংখ্যামালার সরলীকরণ | কষে দেখি 15 |
16. ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই | কষে দেখি 16.1 |
| কষে দেখি 16.2 | |
17. সময় ও কার্য | কষে দেখি 17.1 |
| কষে দেখি 17.2 | |
18. লেখচিত্র | কষে দেখি 18 |
19. সমীকরণ গঠন ও সমাধান | কষে দেখি 19 |
| 20. জ্যামিতিক প্রমাণ | কষে দেখি 20.1 |
| কষে দেখি 20.2 | |
| কষে দেখি 20.3 | |

এখানে তোমরা তোমাদের অষ্টম শ্রেণীতে কি কি পড়ানো হয়, মানে তোমাদের অষ্টম শ্রেণীর সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

