শ্রেণী-অষ্টম ; অধ্যায় – ত্রিভুজের দুটি বাহু ও তাদের বিপরীত কোণের সম্পর্ক ; কষে দেখি 9
এই কষে দেখি 9 এ যে অংক আছে সেগুলি ভালো ভাবে বোঝার জন্যে যে যে বিষয় গুলি আমাদের অবশ্যই জানতে হবে সেগুলি হলো-
( i ) একটি ত্রিভুজের উচ্চতা কাকে বলে?
( ii ) একটি ত্রিভুজের মধ্যমা কাকে বলে?
( iii ) ত্রিভুজ কতোপ্রকার এর হতে পারে?
( iv ) দুটি ত্রিভুজ সর্বসম হওয়ার শর্তঃ
উপরোক্ত বিষয়গুলি তোমরা যদি না জেনে থাকো তাহলে চিন্তার কোন কারণ নেই । কারণ আমি উপরোক্ত বিষয় গুলি খুব সুন্দর এবং সহজ ভাষায় তোমাদের বোঝার জন্যে লিখেছি। যা তোমরা নীচে দেওয়া লিংক থেকে দেখতে পারবে। তোমাদেরকে বলবো আগে উপরোক্ত বিষয়গুলি ভালো করে জানো তারপর কষে দেখি 9 শুরু করো দেখবে কোথাও বুঝতে অসুবিধা হবেনা।
আগামিতে এই কষে দেখি 9 Class 8 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 9 Class 8 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 9 Class 8 তারপর  |
কিছু উপদেশঃ
এখানে কষে দেখি 9 থেকে যে সমস্ত অংক গুলি করে দেওয়া আছে সেগুলি ভালোভাবে বোঝার জন্যে তোমাদের কিছু উপদেশ দিতে চাই-
( i ) প্রথমেই বলি এই অধ্যায়ের যে সারাংশ আমি তৈরি করেছি তোমাদের বোঝার জন্যে সেটা অবশ্যই তোমরা দেখবে। অধ্যায়ের সারাংশ তে আমি বলেছি কিভাবে উপপাদ্য কে লিখে বুঝতে হবে এবং তার প্রমাণ খুব সহজেই কিভাবে করা যায়।
( ii ) একটি উপপাদ্য প্রমাণ করার সময় প্রতিটা step ফলো করতে হবে। যেমন প্রদত্ত, প্রামাণ্য, অঙ্কন, প্রমাণ । তুমি যদি একটি উপপাদ্য কিভাবে প্রমাণ করতে হবে সেটা নাও পারো তাহলে বাকি step গুলো অবশ্যই পরীক্ষায় লিখে আসবে। কারণ পরীক্ষায় যতগুলো dtep তুমি করবে ওই steps এর উপর পরীক্ষক নম্বর দিয়ে থাকেন।
( iii ) এই কষে দেখি 9 এর কিছু কিছু উপপাদ্য তে অঙ্কন করতে হয়। এবার একটা উপপাদ্য তে কিভাবে অঙ্কন করবে সেটা তোমরা practice করলে সেগুলো তোমরাও বুঝে যাবে কোথায় কি অঙ্কন করতে হবে।
( iv ) তোমরা উপপাদ্য অবশ্যই practice করবে কেননা উপপাদ্য করলে brain খুব সক্রিয় হয়ে কাজ করে যার ফলে বুদ্ধি খুলতে থাকে।

কষে দেখি 9 | Koshe Dekhi 9
1. নীচের সমদ্বিবাহু ত্রিভুজগুলি দেখি ও না মেপে প্রতিটি ত্রিভুজের কোন দুটি বাহু সমান হবে লিখিঃ
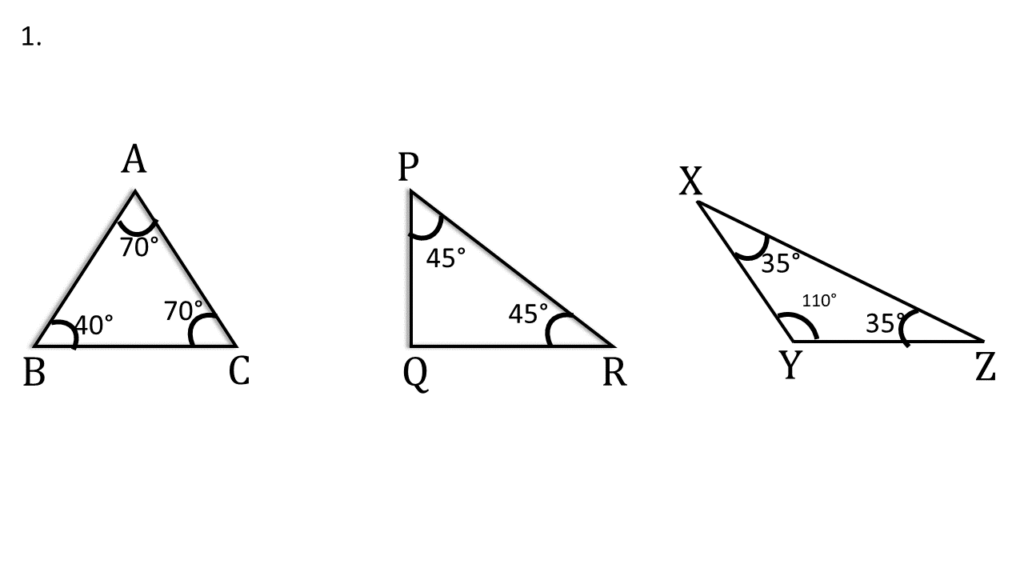
সমাধানঃ-
প্রথম ছবিঃ
এখানে ∠A = ∠C
অতএব,
∠A এর বিপরীত বাহু BC
এবং
∠C এর বিপরীত বাহু AB
এরা পরস্পর সমান হবে।
অর্থাৎ, AB = BC ।
| AB = BC |
দ্বিতীয় ছবিঃ
এখানে ∠P = ∠R
অতএব,
∠P এর বিপরীত বাহু QR
এবং
∠R এর বিপরীত বাহু PQ
এরা পরস্পর সমান হবে।
অর্থাৎ, PQ = QR ।
| PQ = QR |
তৃতীয় ছবিঃ
এখানে ∠X = ∠Z
অতএব,
∠X এর বিপরীত বাহু YZ
এবং
∠Z এর বিপরীত বাহু XY
এরা পরস্পর সমান হবে।
অর্থাৎ, XY = YZ ।
| XY = YZ |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
2. নীচের সমদ্বিবাহু ত্রিভুজগুলি দেখি ও না মেপে প্রতিটি ত্রিভুজের কোন কোণগুলি সমান হবে লিখিঃ
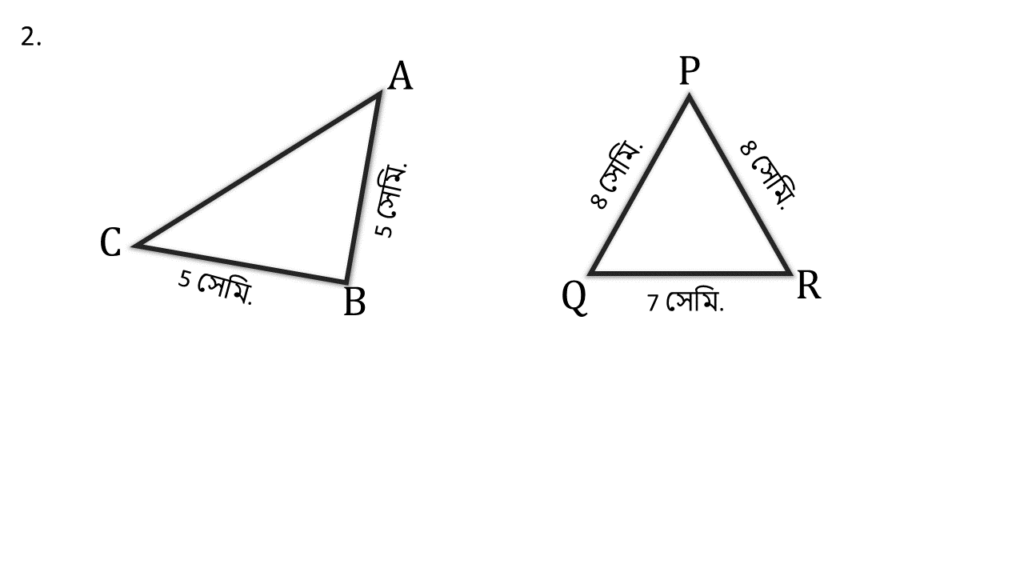
সমাধানঃ-
প্রথম ছবিঃ
এখানে AB = BC
অতএব,
AB বাহুর বিপরীত কোণ ∠C
এবং
BC বাহুর বিপরীত কোণ ∠A
এরা পরস্পর সমান হবে।
অর্থাৎ, ∠A = ∠C ।
| ∠A = ∠C |
দ্বিতীয় ছবিঃ
এখানে PQ = PR
অতএব,
PQ বাহুর বিপরীত কোণ ∠R
এবং
PR বাহুর বিপরীত কোণ ∠Q
এরা পরস্পর সমান হবে।
অর্থাৎ, ∠R = ∠Q ।
| ∠R = ∠Q |
3. AB এবং CD সরলরেখাংশ দুটি পরস্পরকে O বিন্দুতে সমদ্বিখণ্ডিত করে। প্রমাণ করি যে AC ও BD সরলরেখাংশ দুটি পরস্পর সমান্তরাল। ACBD চতুর্ভুজটি কি ধরনের চতুর্ভুজ তা লিখি।
সমাধানঃ-
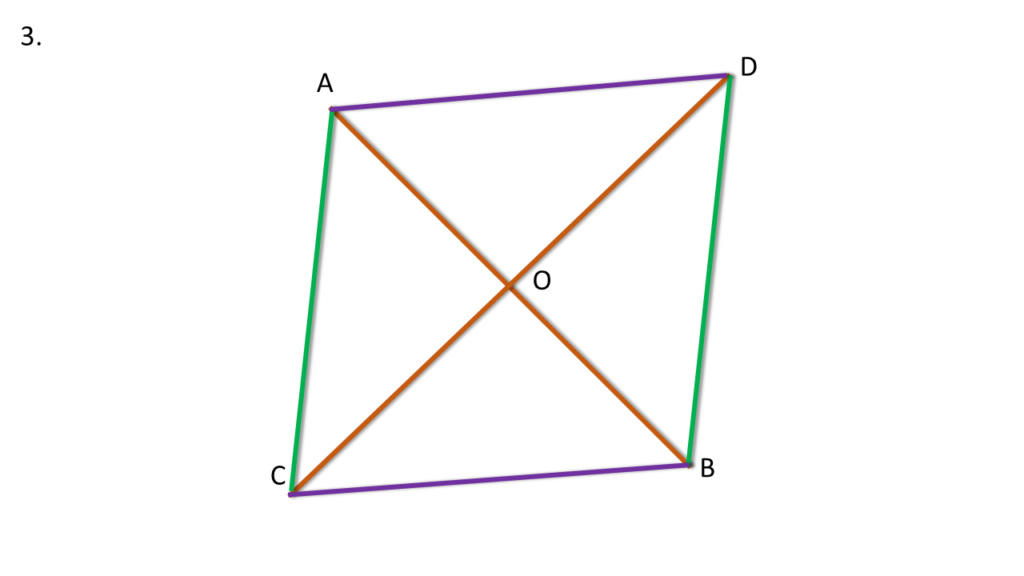
প্রদত্তঃ
AB এবং CD সরলরেখাংশ দুটি পরস্পরকে O বিন্দুতে সমদ্বিখণ্ডিত করে।
অর্থাৎ,
| CO = OD |
| AO = OB |
| ∠COA = বিপ্রতীপ∠BOC |
প্রামাণ্যঃ
AC||BD
প্রমাণঃ
▲AOC ও ▲BOC এর মধ্যে
| AO = OB |
| ∠COA = বিপ্রতীপ∠BOC |
| CO = OD |
| ∴ ▲AOC ≅ ▲BOC [ S-A-S শর্তানুযায়ী ] |
অতএব, ▲AOC ≅ ▲BOC থেকে পাই,
∠BCD =∠ADC
অতএব, AB ও CD দুটি সরলরেখা এবং CD একটি ছেদক যার ফলে একজোড়া একান্তর কোণ উৎপন্ন হয়েছে যা পরস্পর সমান। অর্থাৎ,
∠BCD = একান্তর∠ADC
অতএব, AC||BD । ( প্রমানিত )
| AC ও BD সরলরেখাংশ দুটি পরস্পর সমান্তরাল প্রমাণিত। |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
4. AB এবং CD দুটি সমান্তরাল সরলরেখার উপর E ও F দুটি বিন্দু। EF সরলরেখাংশের মধ্যবিন্দু O; O বিন্দু দিয়ে যেকোনো সরলরেখাংশ টানা হলো যা AB ও CD সরলরেখাকে যথাক্রমে P ও Q বিন্দুতে ছেদ করে। প্রমাণ করি যে, PQ সরলরেখাংশ O বিন্দুতে সমদ্বিখণ্ডিত হয়।
সমাধানঃ-
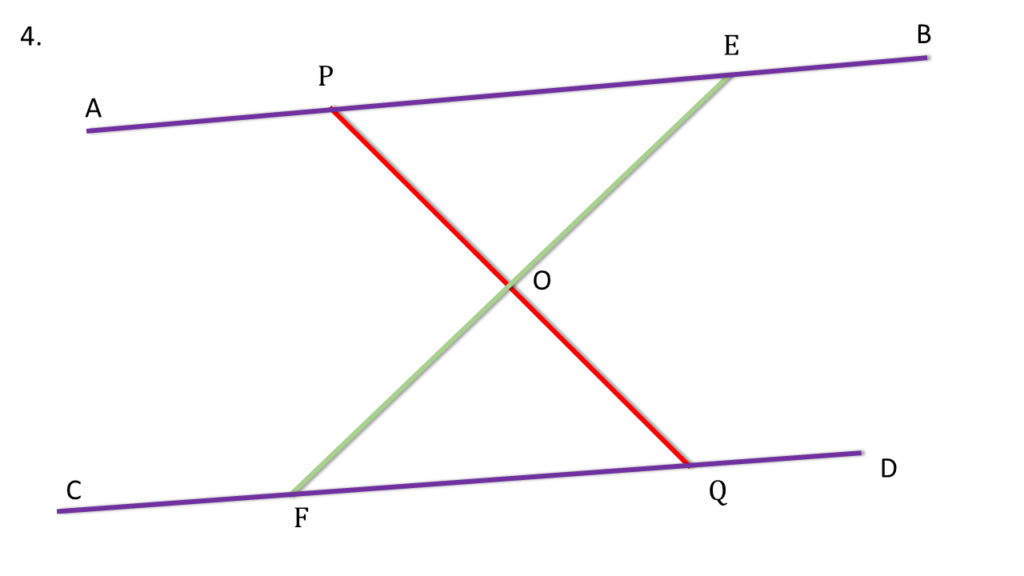
প্রদত্তঃ
AB এবং CD দুটি সমান্তরাল সরলরেখার উপর E ও F দুটি বিন্দু। EF সরলরেখাংশের মধ্যবিন্দু O । অর্থাৎ,
| AB||CD |
| EO = OF |
আবার AB||CD এবং EF একটি ছেদক,
অতএব,
∠PEF = একান্তর ∠EFQ
আবার, AB||CD এবং PQ একটি ছেদক,
অতএব,
∠PQF = একান্তর ∠QPE
প্রামাণ্যঃ
PQ সরলরেখাংশ O বিন্দুতে সমদ্বিখণ্ডিত হয়। অর্থাৎ,
PO = OQ
প্রমাণঃ
▲FOQ ও ▲POE এর মধ্যে,
| ∠PQF = একান্তর ∠QPE |
| ∠PEF = একান্তর ∠EFQ |
| EO = OF |
| ∴ ▲FOQ ≅ ▲POE [ A-A-S শর্তানুসারে ] |
∴ ▲FOQ ≅ ▲POE এর জন্যে পাই,
PO=OQ
অর্থাৎ,
| PQ সরলরেখাংশ O বিন্দুতে সমদ্বিখণ্ডিত হয় প্রমাণিত । |
5. প্রমাণ করি যে, একটি সমদ্বিবাহু ত্রিভুজের ভূমিকে উভয়দিকে বর্ধিত করলে যে দুটি বহিঃকোণ উৎপন্ন হয় তাদের পরিমাপ সমান।
সমাধানঃ-
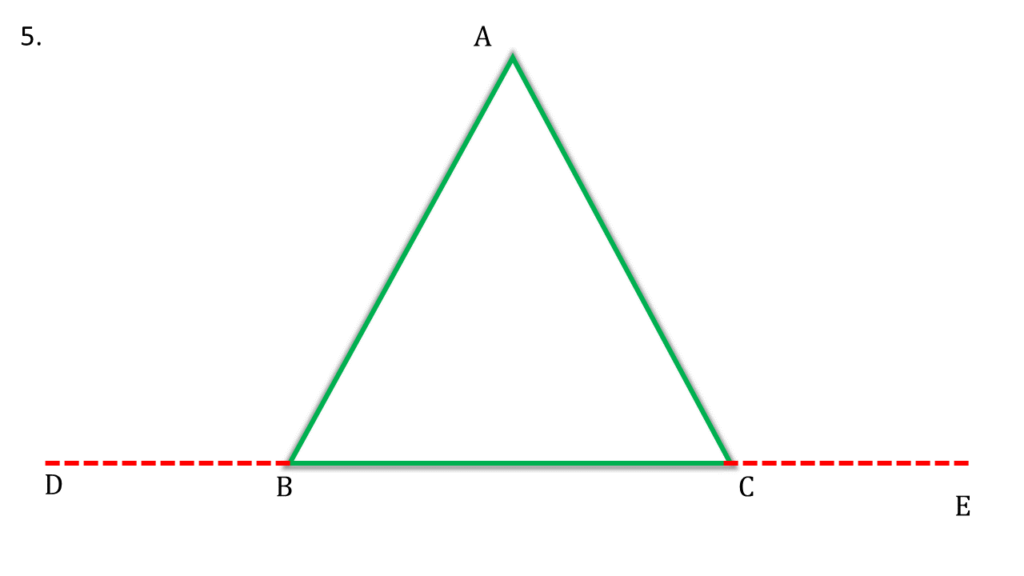
ABC একটি সমদ্বিবাহু ( AB = AC ) ত্রিভুজ যার ভূমি হলো BC । BC বাহুকে বামদিকে D এবং ডানদিকে E পর্যন্ত বর্ধিত করলাম।
প্রদত্তঃ
| AB = AC |
| ∠ABC = ∠ACB |
∠ACE = ∠ABD
প্রমাণঃ
BE সরলরেখা থেকে পাই,
| ∠ACB + ∠ACE = 180° |
| বা, ∠ACE = 180° – ∠ACB |
আবার CD সরলরেখা থেকে পাই,
| ∠ABC + ∠ABD = 180° |
| বা, ∠ABD = 180° – ∠ABC |
| বা, ∠ABD = 180° – ∠ACB [ যেহেতু ∠ABC = ∠ACB ] |
অতএব,
∠ABD = 180° – ∠ACB = ∠ACE
| প্রমানিত যে, একটি সমদ্বিবাহু ত্রিভুজের ভূমিকে উভয়দিকে বর্ধিত করলে যে দুটি বহিঃকোণ উৎপন্ন হয় তাদের পরিমাপ সমান । |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
6. প্রমাণ করি যে, সমবাহু ত্রিভুজের মধ্যমা তিনটির দৈর্ঘ্য সমান।
সমাধানঃ-
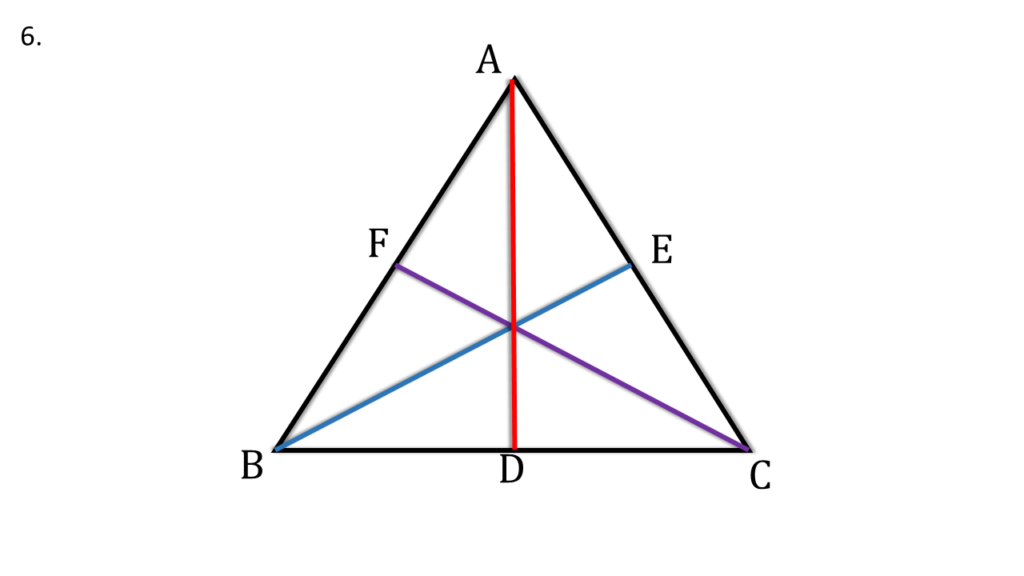
▲ABC একটি সমবাহু ত্রিভুজ এবং AD, BE, CF হলো তিনটি মধ্যমা।
প্রদত্তঃ
| AB = BC = CA |
| ∠ABC = ∠BCA = ∠CAB |
| AF = FB = BD = DC = CE = EA |
প্রামাণ্যঃ
AD = BE = CF
প্রমাণঃ
▲ABD ও ▲ABE এর মধ্যে

| AB সাধারণ বাহু |
| ∠ABD = ∠BAE |
| BD = EA |
| ∴ ▲ABD ≅ ▲ABE [ S-A-S শর্তে ] |
| সুতরাং, AD = BE |
একইরকম ভাবে ∴ ▲ADC ও ▲AFC এর মধ্যে থেকে পাবো,
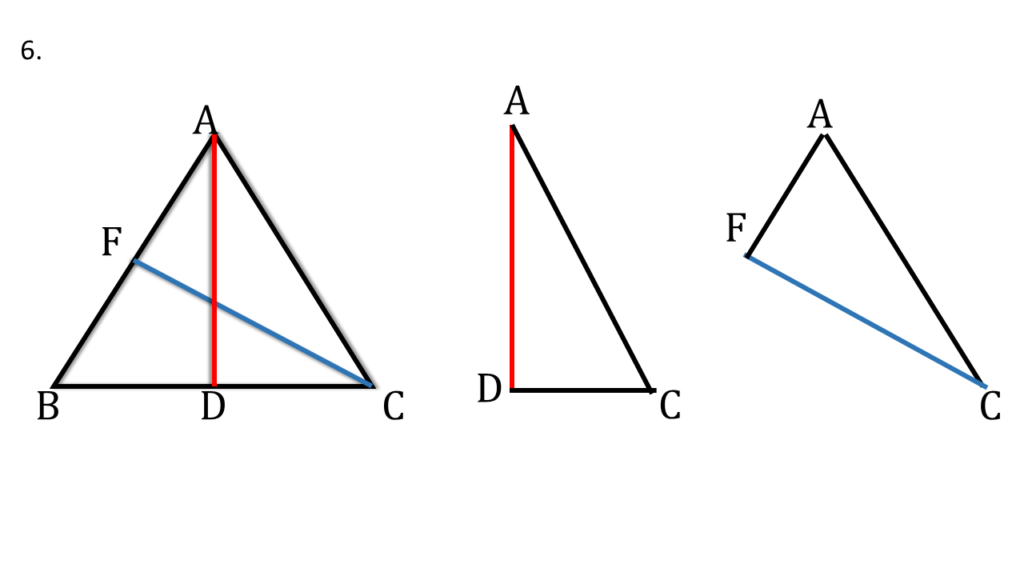
AD = CF
অতএব AD = BE = CF।
| সমবাহু ত্রিভুজের মধ্যমা তিনটির দৈর্ঘ্য সমান প্রমাণিত । |
7. ABCD ট্রাপিজিয়ামের AD||BC এবং ∠ABC= ∠BCD ; প্রমাণ করি যে, ABCD একটি সমদ্বিবাহু ট্রাপিজিয়াম।
সমাধানঃ-
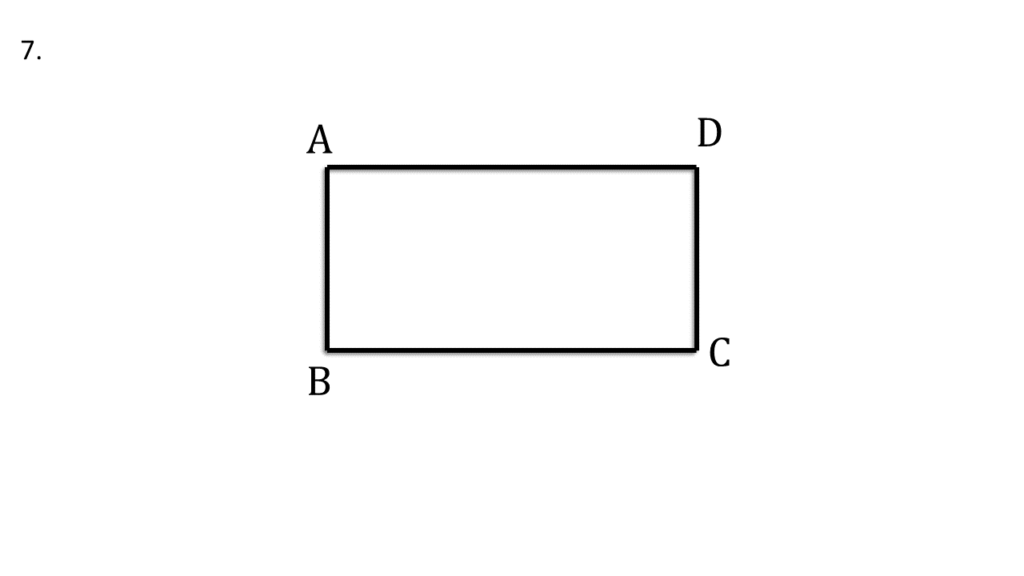
প্রদত্তঃ
ABCD ট্রাপিজিয়ামের AD||BC এবং ∠ABC= ∠BCD
প্রামাণ্যঃ
ABCD একটি সমদ্বিবাহু ট্রাপিজিয়াম
অঙ্কনঃ
B ও D বিন্দু যোগ করলাম।
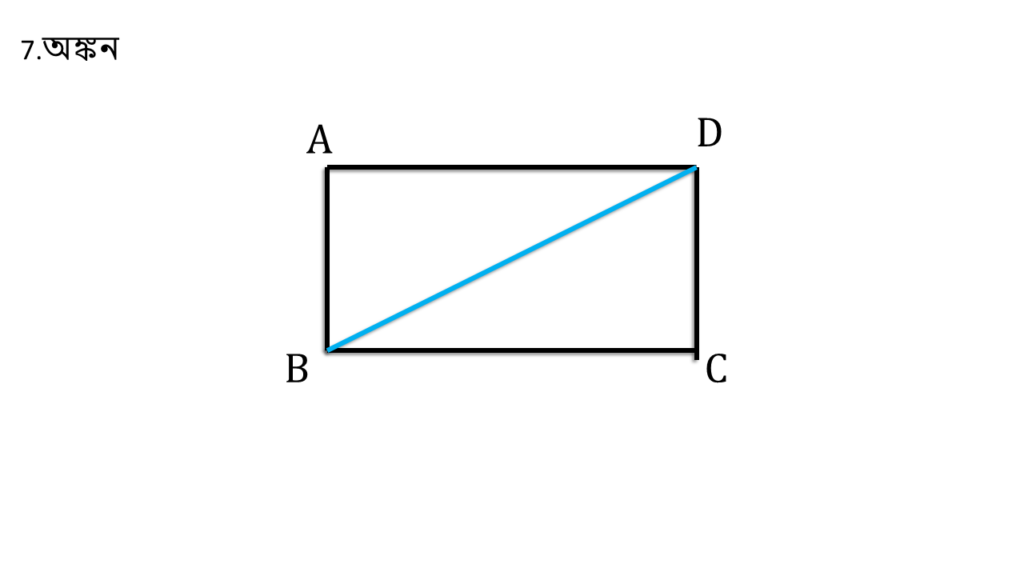
প্রমাণঃ
ABCD ট্রাপিজিয়ামের AD||BC এবং AB ও DC ছেদক,
অতএব,
∠ABC + ∠BAD = 180°—-( i )
এবং
∠BCD + ∠ADC = 180°—-( ii )
( i ) ও ( ii ) সমান করে পাই,
∠ABC + ∠BAC = ∠BCD + ∠ADC
বা, ∠BAD = ∠ADC—-( iii )
আবার,
( i ) ও ( ii ) যোগ করে পাই,
| ∠ABC + ∠BAD + ∠BCD + ∠ADC = 360° |
| বা, ∠ABC + ∠BCD + ∠BAD + ∠ADC = 360° |
| বা, ∠ABC + ∠ABC + ∠BAD + ∠BAD = 360° [ যেহেতু, ∠ABC= ∠BCD এবং ∠BAD = ∠ADC ] |
| বা, 2∠ABC + 2∠BAD = 360° |
| বা, ∠ABC + ∠BAD = 180° |
| অতএব, AB||DC [ AB ছেদকের একই পাশের কোণদ্বয়ের সমষ্টি 180° ] |
সুতরাং, AB||CD এবং BD একটি ছেদক।
অতএব, ∠ABD = একান্তর ∠BDC
▲ABD ও ▲BCD এর মধ্যে থেকে পাই,
| ∠ABD = একান্তর ∠BDC |
| BD সাধারণ বাহু |
| ∠DBC = একান্তর ∠BDA |
| ∴ ▲ABD ≅ ▲BCD |
| সুতরাং, AB = CD |
| ABCD একটি সমদ্বিবাহু ট্রাপিজিয়াম প্রমাণিত। |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
8. ABC সমকোণী সমদ্বিবাহু ত্রিভুজের AB অতিভুজ। ∠BAC -এর সমদ্বিখণ্ডক AD, BC বাহুকে D বিন্দুতে ছেদ করে। প্রমাণ করি যে, AC + CD = AB.
সমাধানঃ-
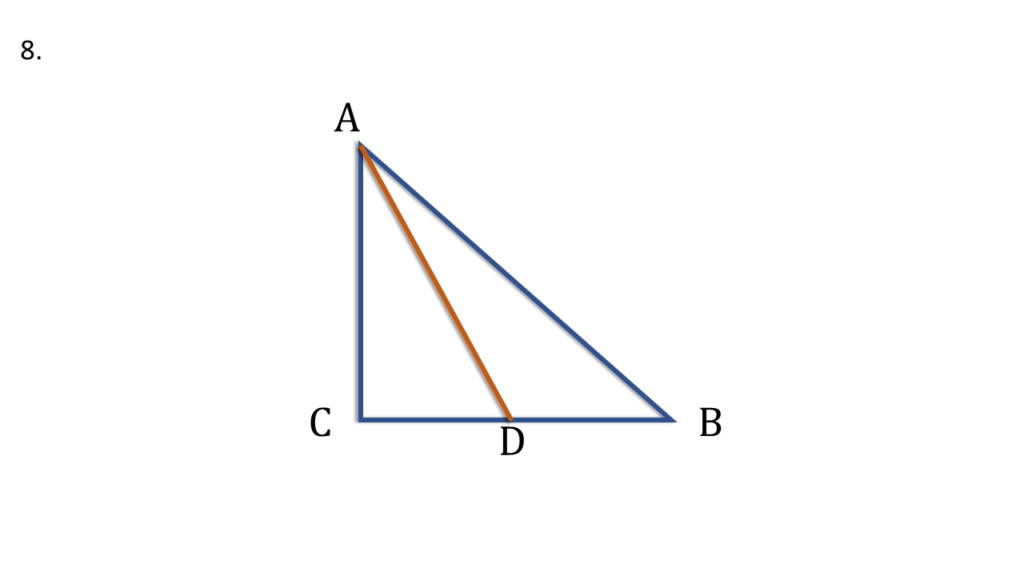
প্রদত্তঃ
ABC সমকোণী সমদ্বিবাহু ত্রিভুজের AB অতিভুজ। ∠BAC -এর সমদ্বিখণ্ডক AD, BC বাহুকে D বিন্দুতে ছেদ করে।
অতএব,
| AC = BC |
| ∠DAC=∠BAD |
প্রামাণ্যঃ
AC + CD = AB
অঙ্কনঃ
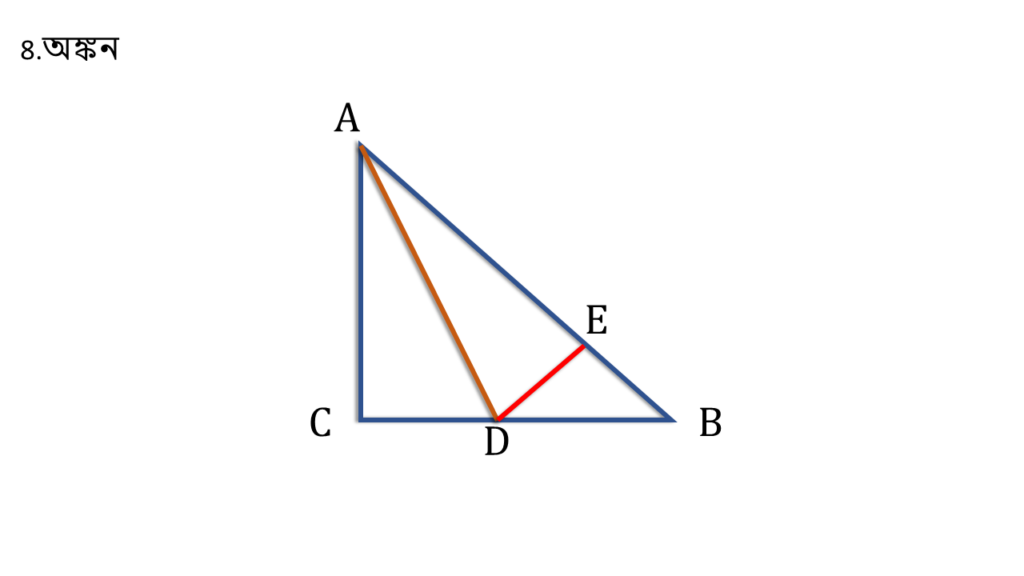
D বিন্দু থেকে AB বাহুর উপর লম্ব অঙ্কন করলাম যা AB বাহুকে E বিন্দুতে ছেদ করেছে।
প্রমাণঃ
▲ABC এর মধ্যে পাই,
| AC = AB এবং ∠ACD=90° |
| অতএব, ∠CAB = ∠ABC |
| এখন ▲ABC এর তিনটি কোণের সমষ্টি করে পাই, |
| ∠ACB + ∠CAB + ∠ABC = 180° |
| বা, ∠CAB + ∠ABC = 180° – 90° |
| বা, ∠ABC + ∠ABC = 90° |
| বা, ∠ABC = 45° —-( i ) |
এখন ▲ACD ও ▲ADE এর মধ্যে,
| ∠ACD = ∠AED |
| AD সাধারণ বাহু |
| ∠CAD = ∠DAE |
| ∴ ▲ACD ≅ ▲ADE [ A-S-A শর্তে ] |
অতএব, ▲ACD ≅ ▲ADE থেকে পাই,
| AC = AE |
| CD = DE |
অতএব,
AC + CD = AE + DE—-( ii )
এখন ▲DEB এর মধ্যে পাই,
| ∠DEB=90° এবং ∠DBE=45° [ ( i ) থেকে পাই ] |
| ▲DEB এর তিনটি কোণের সমষ্টি করে পাই, |
| ∠EDB + ∠DEB + EBD = 180° |
| বা, ∠EDB = 180° – 90° – 45° |
| বা, ∠EDB = 45° |
▲DEB এর মধ্যে পেলাম,
| ∠EDB = 45° = ∠DBE |
| অতএব, |
| DE = EB —-( iii ) |
( ii ) ও ( iii ) থেকে পাই,
| AC + CD = AE + DE |
| বা, AC + CD = AE + EB |
| বা, AC + CD = AB |
| AC + CD = AB প্রমাণিত । |
9. ABC এবং DBC দুটি সমদ্বিবাহু ত্রিভুজ যাদের AB = AC ও DB = DC এবং তারা BC বাহুর বিপরীত পাশে অবস্থিত । প্রমাণ করি যে, AD, BC বাহুকে সমদ্বিখণ্ডিত করে।
সমাধানঃ-
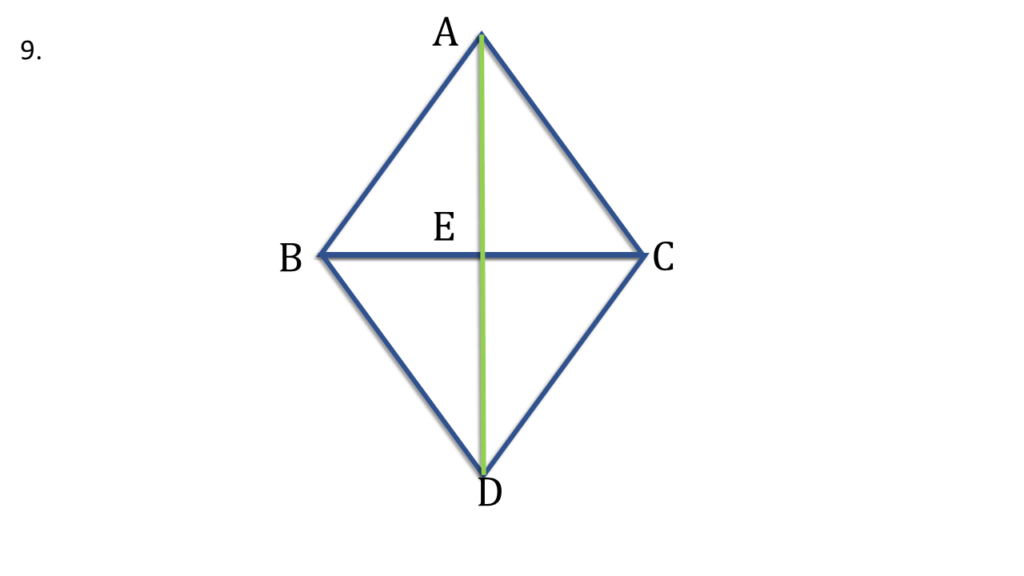
প্রদত্তঃ
ABC এবং DBC দুটি সমদ্বিবাহু ত্রিভুজ যাদের AB = AC ও DB = DC এবং তারা BC বাহুর বিপরীত পাশে অবস্থিত ।
প্রামাণ্যঃ
AD, BC বাহুকে সমদ্বিখণ্ডিত করে।
প্রমাণঃ
AD, BC বাহুকে E বিন্দুতে ছেদ করেছে।
▲ABE ও ▲ACE এর মধ্যে থেকে পাই,
| AB = AC |
| ∠ABC = ∠ACB |
| AE সাধারণ বাহু |
| ∴ ▲ABE ≅ ▲ACE [ S-A-S শর্তে ] |
| ∴ BE = EC |
▲BDE ও ▲CED এর মধ্যে থেকে পাই,
∴ ▲ABE ≅ ▲ACE
∴ BE = EC
সুতরাং, DE এবং AE উভয়েই BC সরলরেখাকে E বিন্দুতে সমদ্বিখণ্ডিত করছে।
অতএব,
| AD, BC বাহুকে সমদ্বিখণ্ডিত করে প্রমাণিত । |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
10. দুটি সরলরেখাংশ PQ এবং RS পরস্পরকে X বিন্দুতে এমনভাবে ছেদ করে যাতে XP = XR এবং ∠PSX = ∠RQX হয়। প্রমাণ করি যে, ▲PXS ≅ ▲RQX.
সমাধানঃ-
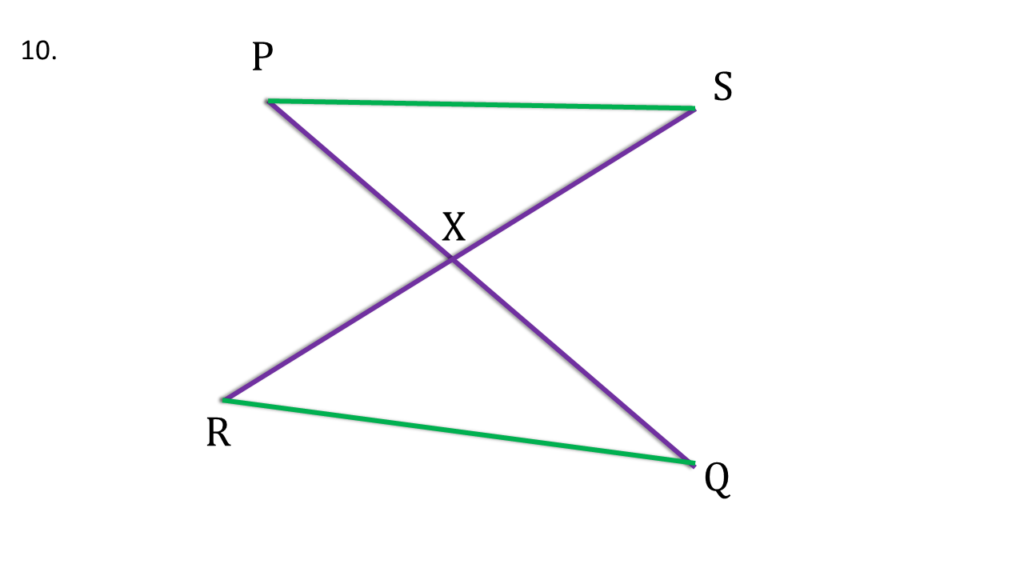
প্রদত্তঃ
| দুটি সরলরেখাংশ PQ এবং RS পরস্পরকে X বিন্দুতে ছেদ করেছে |
| XP = XR |
| ∠PSX = ∠RQX |
প্রামাণ্যঃ
▲PXS ≅ ▲RQX
প্রমাণঃ
▲PXS ও ▲RQX এর মধ্যে থেকে ,
| ∠PSX = ∠RQX |
| ∠PXS = বিপ্রতীপ ∠RXQ |
| XP = XR |
| ∴▲PXS ≅ ▲RQX [ A-A-S শর্তে ] |
| ▲PXS ≅ ▲RQX প্রমাণিত। |
এই কষে দেখি 9 Class 8|Koshe Dekhi 9 Class 8 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 9 Class 8 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 9 Class 8 তারপর  |
| জ্যামিতিক এই অধ্যায় টি অনেকে মনে করে খুবই কঠিন একটা বিষয় ! উপপাদ্য বোঝা, তা প্রমাণ করা এবং তা থেকে প্রয়োগ করা । কিন্তু তোমরা যদি সঠিক পদ্ধতি মেনে ত্রিভুজের দুটি বাহু ও তাদের বিপরীত কোণের সম্পর্ক কষে দেখি 9 তে যে সমস্ত অংক গুলি আছে সেগুলি করো তাহলে কোথাও বুঝতে অসুবিধে হবেনা । সেজন্যে তোমাদের বলবো তোমরা উপপাদ্য করার , কিভাবে উপপাদ্য লিখবে তার সঠিক পদ্ধতিটি নিচের লিংক থেকে জানো এবং তারপর কষে দেখি এর অংক গুলি করলে নিশ্চয় কিছু পার্থক্য বুঝতে পারবে । এই অধ্যায় এর কষে দেখি তে যে সমস্ত অংক গুলি করতে দেওয়া আছে তার জন্যে- একটি ত্রিভুজ কাকে বলে এবং ত্রিভুজ যে কতো রকম হতে পারে, একটি ত্রিভুজের মধ্যমা কাকে বলে?, একটি ত্রিভুজের উচ্চতা কাকে বলে? এবং দুটি ত্রিভুজকে আমরা কোন কোন শর্তে সর্বসম বলবো তা নীচের এই লিংকে আমি বিস্তারিত ভাবে তোমাদের বোঝার সুবিধার জন্যে খুব সুন্দর করে লিখেছি। তোমাদের বলবো এটা অবশ্যই একবার দেখে নেবে। |
| গনিতপ্রভা অষ্টম শ্রেণীর সমস্ত অধ্যায়ের সমাধান- | |
|---|---|
| অধ্যায় | সমাধান |
| 2. পাই চিত্র | কষে দেখি 2 |
| 3. মূলদ সংখ্যার ধারণা | অধ্যায়ের সারাংশ |
| কষে দেখি 3 | |
| 4. বীজগাণিতিক সংখ্যামালার গুণ ও ভাগ | অধ্যায়ের সারাংশ |
| কষে দেখি 4.1 | |
| কষে দেখি 4.2 | |
| 5. ঘনফল নির্ণয় | অধ্যায়ের সারাংশ |
| কষে দেখি 5.1 | |
| কষে দেখি 5.2 | |
| কষে দেখি 5.3 | |
| 6. পূরক কোণ, সম্পূরক কোণ ও সন্নিহিত কোণ | অধ্যায়ের সারাংশ |
| কষে দেখি 6 | |
| 7. বিপ্রতীপ কোণের ধারণা | অধ্যায়ের সারাংশ |
| কষে দেখি 7.1 | |
8. সমান্তরাল সরলরেখা ও ছেদকের ধর্ম | অধ্যায়ের সারাংশ |
| কষে দেখি 8 | |
9. ত্রিভুজের দুটি বাহু ও তাদের বিপরীত কোণের সম্পর্ক | অধ্যায়ের সারাংশ |
| কষে দেখি 9 | |
| 10. ত্রৈরাশিক | কষে দেখি 10.1 |
| কষে দেখি 10.2 | |
| 11. শতকরা | কষে দেখি 11 |
| 12. মিশ্রণ | কষে দেখি 12 |
13. বীজগাণিতিক সংখ্যামালার উৎপাদকে বিশ্লেষণ | কষে দেখি 13.1 |
| কষে দেখি 13.2 | |
14. বীজগাণিতিক সংখ্যামালার গ.সা.গু ও ল.সা.গু | কষে দেখি 14 |
15. বীজগাণিতিক সংখ্যামালার সরলীকরণ | কষে দেখি 15 |
16. ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই | কষে দেখি 16.1 |
| কষে দেখি 16.2 | |
17. সময় ও কার্য | কষে দেখি 17.1 |
| কষে দেখি 17.2 | |
18. লেখচিত্র | কষে দেখি 18 |
19. সমীকরণ গঠন ও সমাধান | কষে দেখি 19 |
| 20. জ্যামিতিক প্রমাণ | কষে দেখি 20.1 |
| কষে দেখি 20.2 | |
| কষে দেখি 20.3 | |

এখানে তোমরা তোমাদের অষ্টম শ্রেণীতে কি কি পড়ানো হয়, মানে তোমাদের অষ্টম শ্রেণীর সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।
