শ্রেণী-অষ্টম ; অধ্যায় – সমীকরণ গঠন ও সমাধান ; কষে দেখি 19
নিচের এই Telegram চ্যানেলটি তোমাদের সুবিধার জন্যে অর্থাৎ, তোমাদের
- কি সমস্যা?
- বিশেষ করে অংক বুঝতে কোথায় সমস্যা হয়!
- নিজেদের মধ্যে আলোচনা
- ক্যারিয়ার নিয়ে আলোচনা
ইত্যাদি বিষয়ের উপর ভিত্তি করে এই গ্রুপটি তৈরি করা হয়েছে-
কষে দেখি 19 Class 8 এর সূচিপত্রঃ
কষে দেখি 19 Class 8 এর অংকের সমাধান গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ
কষে দেখি 19 Class 8 | Koshe Dekhi 19 Class 8 হল তোমাদের অষ্টম শ্রেণীর একটি অধ্যায় সমীকরণ গঠন ও সমাধান এর অনুশীলনী। এই অধ্যায়টিতে সমিকরণের গঠন ও সমাধান নিয়ে আলোচনা করা হয়েছে।
সমীকরণ গঠন ও সমাধান অধ্যায়টি সমীকরণের সংক্ষিপ্ত ধারণা দিয়ে শুরু হয়েছে যাতে বোঝানো হয়েছে সমীকরণ হল একটি বিবৃতি যে দুটি অভিব্যক্তি সমান। যা একটি সমান চিহ্নের দুই দিকে লেখা হয়। সমান চিহ্নের উভয় পাশের অভিব্যক্তিগুলিকে সমীকরণের বামদিকের অভিব্যক্তিকে L.H.S এবং ডানদিকের অভিব্যক্তিকে R.H.S বলে।
এই কষে দেখি 19 Class 8 | Koshe Dekhi 19 Class 8 এ তোমরা যে অংকগুলি করবে তা হল একটি প্রদত্ত অবস্থা থেকে কিভাবে সমিকরনে গঠন করা যায় এবং সেখান থেকে কিভাবে একটি অজানা রাশির মান বের করা যায়।
সমীকরণ সমাধানের জন্য বিভিন্ন পদ্ধতি রয়েছে, তবে সবচেয়ে সাধারণ পদ্ধতি হল ট্রায়াল এবং ত্রুটি ব্যবহার করা। ট্রায়াল এবং ত্রুটি অজানা রাশির জন্য বিভিন্ন মান চেষ্টা খোঁজার চেষ্টা করা যতক্ষণ না তুমি সমীকরণকে সন্তুষ্ট করে এমন একটি মান খুঁজে পাও।
উদাহরণস্বরূপ,
যদি তোমাকে শর্ত দেওয়া হয় যে “দুটি সংখ্যার যোগফল 10”, তুমি “x + y = 10” সমীকরণ গঠন করতে পারবে ।
এবার তোমরা সমীকরণ গঠন ও সমাধান এর কষে দেখি 19 এর অংক গুলি করলে আরও সুন্দর ভাবে বুঝতে পারবে।
আগামিতে এই কষে দেখি 19 Class 8 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 19 Class 8 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 19 Class 8 তারপর  |

কষে দেখি 19 | Koshe Dekhi 19
প্রতিক্ষেত্রে সমীকরণ গঠন করি ও নিজে করি –
1. সীমা একটি সংখ্যা লিখেছে যার দ্বিগুণের সঙ্গে 2 যোগ করলে যা হয় তা সংখ্যাটির তিনগুণের চেয়ে 5 ছোটো। সীমার লেখা সংখ্যাটি লিখি।
সমাধানঃ-
ধরি সংখ্যাটি হল-x
সংখ্যাটির দ্বিগুণ = 2x
সংখ্যাটির তিনগুন = 3x
সংখ্যাটির দ্বিগুণের সঙ্গে 2 যোগ করলে যা হয় তা সংখ্যাটির তিনগুণের চেয়ে 5 ছোটো
শর্তানুসারে,
| 2x + 2 = 3x – 5 |
| বা, 3x – 5 = 2x + 2 |
| বা, 3x – 2x = 5 + 2 |
| বা, x = 7 |
| ∴ সংখ্যাটি হল- 7 |
2. তিনটি ক্রমিক সংখ্যা লিখি যাদের যোগফল থেকে 5 বিয়োগ করলে বিয়োগফলটি মাঝের সংখ্যার দ্বিগুণের চেয়ে 11 বেশি হয়। ক্রমিক সংখ্যা তিনটি লিখি।
সমাধানঃ-
ধরি, তিনটি ক্রমিক সংখ্যার প্রথম সংখ্যাটি হল-x
অতএব পরের দুটি সংখ্যা হল- x + 1, x + 2
তিনটি সংখ্যার যোগফল হল
= x + (x + 1) + (x + 2)
= 3x + 3
ক্রমিক সংখ্যা গুলির যোগফল থেকে 5 বিয়োগ করলে বিয়োগফলটি মাঝের সংখ্যার দ্বিগুণের চেয়ে 11 বেশি হয়
শর্তানুসারে,
| (3x + 3) – 5 = 2(x + 1) + 11 |
| বা, 3x + 3 – 5 = 2x + 2 + 11 |
| বা, 3x – 2 = 2x + 13 |
| বা, 3x – 2x = 13 + 2 |
| বা, x = 15 |
| ∴ প্রথম সংখ্যা- x=15 দ্বিতীয় সংখ্যা – x+1=16 তৃতীয় সংখ্যা – x+2=17 |
3. আমি এমন একটি সংখ্যা খুঁজি যার এক-তৃতীয়াংশ থেকে তার এক-চতুর্থাংশ 1 কম।
সমাধানঃ-
ধরি, সংখ্যাটি হল-x
সংখ্যাটির এক-তৃতীয়াংশ= x/3
সংখ্যাটির এক-চতুর্থাংশ = x/4
সংখ্যাটির এক-তৃতীয়াংশ থেকে তার এক-চতুর্থাংশ 1 কম
শর্তানুসারে,
| x/3 – 1 = x/4 |
| বা, x/3 – x/4 = 1 |
| বা, x (1/3 – 1/4) = 1 |
| বা, x (4 – 3)/12 = 1 |
| বা, x/12 = 1 |
| বা, x = 12 |
| ∴ সংখ্যাটি হল- 12 |
4. আমি এমন একটি ভগ্নাংশ খুঁজি যার হর তার লব থেকে 2 বড়ো এবং লবের সঙ্গে 3 যোগ ও হর থেকে 3 বিয়োগ করলে ভগ্নাংশটি 7/3-এর সমান হয়।
সমাধানঃ-
ধরি, ভগ্নাংশের লব = x
অতএব ভগ্নাংশের হর = x + 2
ভগ্নাংশের লবের সঙ্গে 3 যোগ ও হর থেকে 3 বিয়োগ করলে ভগ্নাংশটি 7/3-এর সমান হয়
শর্তানুসারে,
| (x + 3)/ (x + 2 – 3) = 7/3 |
| বা, 3(x + 3) = 7(x – 1) |
| বা, 3x + 9 = 7x – 7 |
| বা, 7x – 7 = 3x + 9 |
| বা, 7x – 3x = 9+7 |
| বা, 4x = 16 |
| বা, x = 16/4 |
| বা, x = 4 |

ভগ্নাংশের লব x = 4
অতএব ভগ্নাংশের হর x + 2 = 6
| ∴ ভগ্নাংশটি হল- 4/6 |
5. সুচেতা একটি ভগ্নাংশ লিখল যার হর তার লবের চেয়ে 3 বড়ো। আবার ভগ্নাংশটির লবের সঙ্গে 2 যোগ ও হর থেকে 1 বিয়োগ এবং লব থেকে 1 বিয়োগ ও হরের সঙ্গে 2 যোগ করলে যে দুটি নতুন ভগ্নাংশ পাব তাদের গুণফল 2/5 । সুচেতার লেখা ভগ্নাংশটি লিখি।
সমাধানঃ-
ধরি,
ভগ্নাংশের লব = x
অতএব ভগ্নাংশের হর = x + 3
ভগ্নাংশটির লবের সঙ্গে 2 যোগ ও হর থেকে 1 বিয়োগ করলে ভগ্নাংশ টি হয় – (x + 2)/(x + 3 – 1)
আবার,
ভগ্নাংশটির লব থেকে 1 বিয়োগ ও হরের সঙ্গে 2 যোগ করলে ভগ্নাংশটি হয়- (x – 1)/(x + 3 + 2)
নতুন ভগ্নাংশ দুটির গুণফল 2/5
শর্তানুসারে,

অতএব ভগ্নাংশের লব x=5 এবং ভগ্নাংশের হর x + 3=8
| ∴ভগ্নাংশটি হল- 5/8 |
6. রাজু দুই অঙ্ক বিশিষ্ট একটি সংখ্যা লিখল যার দশক স্থানীয় অঙ্ক একক স্থানীয় অঙ্কের তিনগুন এবং অঙ্ক দুটি স্থানবিনিময় করলে যে সংখ্যাটি তৈরি হবে তা মূল সংখ্যাটি থেকে 36 কম। রাজুর লেখা দুই অঙ্ক বিশিষ্ট সংখ্যাটি লিখি।
সমাধানঃ-
ধরি, সংখ্যাটির একক স্থানীয় অংক = x
অতএব দশক স্থানীয় অংক = 3x
| দশক | একক |
|---|---|
| 3x | x |
| ∴ সংখ্যাটি হল- 10×3x + x = 30x + x = 31x | |
আবার,
অংক দুটির স্থান বিনিময় করে পাই,
| দশক | একক |
|---|---|
| x | 3x |
| ∴ সংখ্যাটি হল- 10×x + 3x = 10x + 3x = 13x | |
সংখ্যাটির দশক স্থানীয় অঙ্ক একক স্থানীয় অঙ্কের তিনগুন এবং অঙ্ক দুটি স্থানবিনিময় করলে যে সংখ্যাটি তৈরি হবে তা মূল সংখ্যাটি থেকে 36 কম
শর্তানুসারে,
| 13x = 31x – 36 |
| বা, 31x – 36 = 13x |
| বা, 31x – 13x = 36 |
| বা, 18x = 36 |
| বা, x = 36/18 = 2 |
অতএব
সংখ্যাটির একক স্থানীয় অংক x= 2
দশক স্থানীয় অংক 3x = 6
সংখ্যাটি হল-
10×6 + 2= 60 + 2 = 62
| ∴সংখ্যাটি হল- 62 |
7. দুটি সংখ্যার যোগফল 89 এবং অন্তর 15 হলে সংখ্যা দুটির মান খুঁজি।
সমাধানঃ-
ধরি, একটি সংখ্যা- x
অপর সংখ্যাটি হল- 89 – x
শর্তানুসারে,
| x – (89 – x) = 15 |
| বা, x – 89 + x = 15 |
| বা, 2x = 15 + 89 |
| বা, 2x = 104 |
| বা, x = 104/2 = 52 |
অতএব একটি সংখ্যা x = 52
অপর সংখ্যা 89 – 52 = 37
| ∴সংখ্যাটি দুটি হল- 52 ও 37 |
8. 830-কে এমন দুটি অংশে ভাগ করি যেন একটি অংশের 30% অপর অংশের 40% অপেক্ষা 4 বেশি হয়।
সমাধানঃ-
ধরি, 830 এর একটি অংশ x
অপর অংশ 830 – x
শর্তানুসারে,

| ∴830 এর একটি অংশ x=480 অপর অংশ 830 – x=350 |
9. 56-কে এমন দুটি অংশে ভাগ করি যেন প্রথম অংশের তিনগুণ, দ্বিতীয় অংশের এক-তৃতীয়াংশ অপেক্ষা 48 বেশি হয়।
সমাধানঃ-
ধরি, 56 এর একটি অংশ x
অপর অংশ 56 – x
শর্তানুসারে,
| 3x = (56 – x)/3 + 48 |
| বা, 3x = (56 – x + 48×3)/3 |
| বা, 3×3x = 56 – x + 144 |
| বা, 9x + x = 200 |
| বা, 10x = 200 |
| বা, x = 200/10 = 20 |
| ∴56 এর একটি অংশ x=20 অপর অংশ 56 – x=36 |
10. একটি দণ্ডের 1/5 অংশ কাদায়, 3/5 অংশ জলে এবং অবশিষ্ট 5 মিটার জলের উপর আছে। দন্ডটির দৈর্ঘ্য হিসাব করে লিখি।
সমাধানঃ-
ধরি, দণ্ডটির দৈর্ঘ্য x মিটার
শর্তানুসারে,
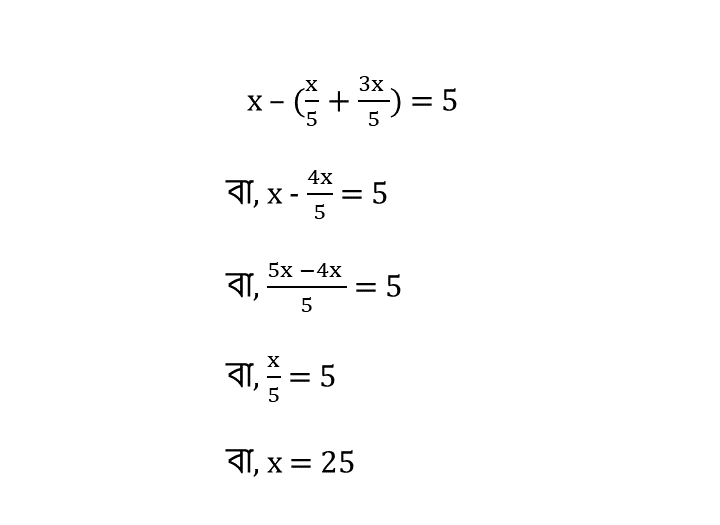
| ∴ দণ্ডটির দৈর্ঘ্য = 25 মিটার । |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
11. আমার বাবার বর্তমান বয়স আমার বর্তমান বয়সের 7 গুণ। 10 বছর পরে বাবার বয়স আমার বয়সের 3 গুণ হবে। আমার ও বাবার বর্তমান বয়স লিখি।
সমাধানঃ-
ধরি, আমার বর্তমান বয়স = x বছর
বাবার বর্তমান বয়স = 7x বছর
| 10 বছর পরে, | |
|---|---|
| বাবার বয়স = 7x + 10 বছর | আমার বয়স = 10 +x বছর |
শর্তানুসারে,
| 3(10 + x) = 7x + 10 |
| বা, 30 + 3x = 7x + 10 |
| বা, 7x + 10 = 3x + 30 |
| বা, 7x – 3x = 30 – 10 |
| বা, 4x = 20 |
| বা, x = 20/4 = 5 |
| ∴ আমার বর্তমান বয়স = 5 বছর এবং বাবার বর্তমান বয়স = 35 বছর |
12. আমার মামা 1000 টাকার একটি চেক ব্যাংক থেকে ভাঙালেন। তিনি কয়েকটি পাঁচ টাকার নোট ও কয়েকটি দশ টাকার নোট পেলেন। যদি মামা মোট 137 টি নোট পেয়ে থাকেন তাহলে কতগুলি 5 টাকার নোট পেলেন দেখি।
সমাধানঃ-
ধরি, মামা x টি 5 টাকার নোট পেলেন।
তাহলে 10 টাকার নোট পাবেন (137 – x) টি ।
শর্তানুসারে,
| 5x + 10(137 – x) = 1000 |
| বা, 5x + 1370 – 10x = 1000 |
| বা, 10x – 5x = 1370 – 1000 |
| বা, 5x = 370 |
| বা, x = 370/5 = 74 |
| ∴মামা 74 টি 5 টাকার নোট পেলেন। |
13. আমাদের গ্রামের সালেমচাচা সরকারি চাকুরি থেকে অবসর গ্রহণ করার পর তার সঞ্চয়ের ½ অংশ দিয়ে একটি বাড়ি কেনেন। হঠাৎ বিপদে পড়ে তিনি বাড়িটি বিক্রি করে কেনা দামের 5% বেশি পান। যদি তিনি বাড়িটি 3450 টাকা বেশি দামে বিক্রি করতেন তাহলে কেনা দামের উপর 8% বেশি পেতেন। সালেমচাচা কত টাকায় বাড়িটি কিনেছিলেন এবং তার সঞ্চয় কত ছিল দেখি।
সমাধানঃ-
ধরি, সালেম চাচার সঞ্চয় = x টাকা
সঞ্চয়ের ½ অংশ দিয়ে একটি বাড়ি কেনেন
তিনি বাড়িটি বিক্রি করে কেনা দামের 5% বেশি পান
অতএব বাড়িটি বিক্রি করেন
x/2 + x/2×5/100 টাকায়
= x/2 + x/40 টাকায়
আবার,
তিনি বাড়িটি 3450 টাকা বেশি দামে বিক্রি করতেন তাহলে কেনা দামের উপর 8% বেশি পেতেন
অতএব এক্ষেত্রে বাড়িটি বিক্রি করেন
x/2 + x/2×8/100 টাকায়
= x/2 + x/25 টাকায়
শর্তানুসারে,

| ∴ সালেমচাচা 115000 টাকায় বাড়িটি কিনেছিলেন এবং তার সঞ্চয় ছিল 230000 টাকা । |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
14. গোপালপুর গ্রামের আশ্রয় শিবিরে আশ্রয়প্রার্থীদের জন্য 20 দিনের খাবার মজুত ছিল। 7 দিন পরে আরও 100 জন আশ্রয়প্রার্থী সেই শিবিরে আশ্রয় নিলে 11 দিনের মাথায় সব খাবার শেষ হয়ে যায়। প্রথমে কতজন আশ্রয়প্রার্থী ছিল লিখি।
সমাধানঃ-
ধরি, আশ্রয়শিবিরে প্রথমে x জন আশ্রয়প্রার্থী ছিল ।
| এখানে আমরা সমানুপাতের মাধ্যমে অঙ্কটি বোঝার চেষ্টা করবো। |
গণিতের ভাষায় সমস্যাটি হল-
| লোক সংখ্যা ( টি ) | সময় (দিন) |
|---|---|
| x | 13 |
| 100 + x | ? |
সম্পর্কটি হল-
এখানে লোক সংখ্যা বাড়লে একই খাবার কম দিন যাবে। লোক সংখ্যা ও সময় ব্যস্ত সম্পর্কে আছে।
অতএব,
নির্ণেয় সময়
= 13x/(100 + x)
এখন 100 জন আশ্রয়প্রার্থী সেই শিবিরে আশ্রয় নিলে 11 দিনের মাথায় সব খাবার শেষ হয়ে যায়।
শর্তানুসারে,
| 13x/(100 + x) = 11 |
| বা, 13x = 11×100 + 11x |
| বা, 13x – 11x = 1100 |
| বা, 2x = 1100 |
| বা, x = \(\frac{1100}{2}\) = 550 |
| ∴আশ্রয়শিবিরে প্রথমে 550 জন আশ্রয়প্রার্থী ছিল । |
15. নীচের সমীকরণগুলির বীজ খুঁজি (সমাধান করি) :
(i) 3/ (x + 3) = 5/ (x + 2)
সমাধানঃ-
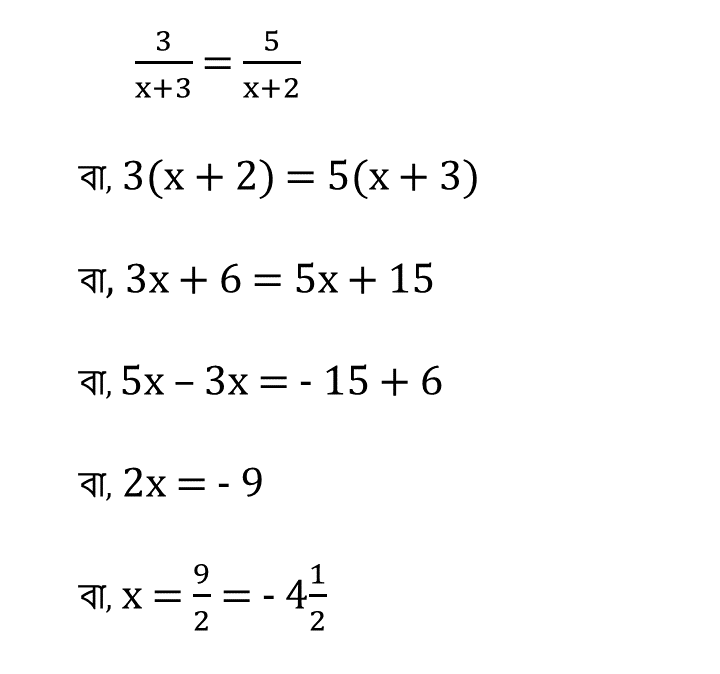
| ∴ x = – \(\frac{9}{2}\) |
(ii) 5/ (3x + 4) = 4/ {5(x – 3)}
সমাধানঃ-
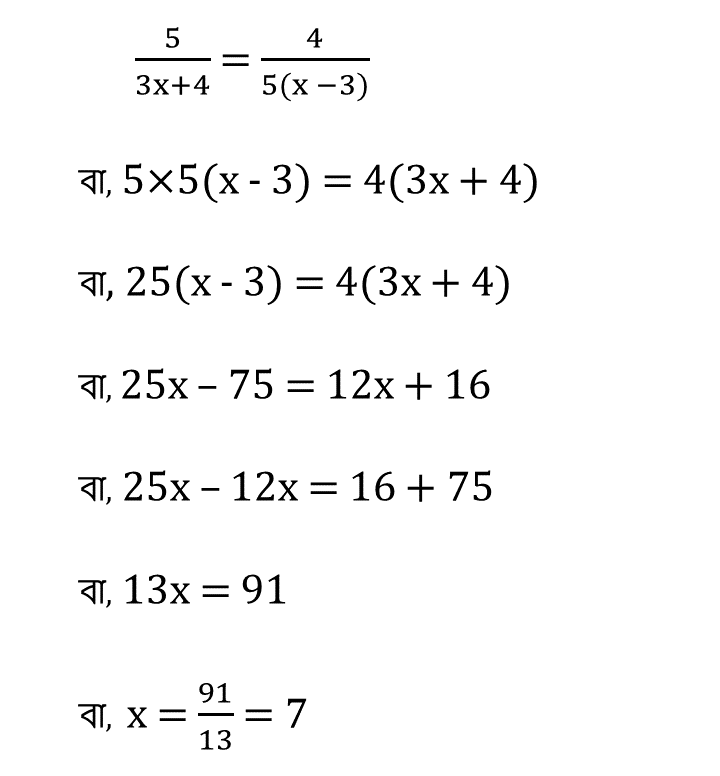
| ∴ x = 7 |
(iii) 14(x – 2) + 3(x + 5) = 3(x + 8) + 5
সমাধানঃ-
| 14(x – 2) + 3(x + 5) = 3(x + 8) + 5 |
| বা, 14x – 28 + 3x + 15 = 3x + 24 + 5 |
| বা, 14x + 3x – 3x = 24 + 28 – 15 + 5 |
| বা, 14x = 57 – 15 |
| বা, 14x = 42 |
| বা, x = \(\frac{42}{14}\) = 3 |
| ∴ x = 3 |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
(iv) x/2 + 5 = x/3 + 7
সমাধানঃ-
| x/2 + 5 = x/3 + 7 |
| বা, (x + 10)/2 = (x + 21)/3 |
| বা, 3(x + 10) = 2(x + 21) |
| বা, 3x + 30 = 2x + 42 |
| বা, 3x – 2x = 42 – 30 |
| বা, x = 12 |
| ∴ x = 12 |
(v) (x + 1)/8 + (x – 2)/5 = (x + 3)/10 + (3x – 1)/20
সমাধানঃ-

| ∴ x = 7 |
(vi) (x + 1)/4 + 3 = (2x + 4)/5 + 2
সমাধানঃ-

| ∴ x = 3 |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
(vii) (x + 1)/7 + x = (3x – 4)/14 + 6
সমাধানঃ-

| ∴ x = 6 |
(viii) 3/5(x – 4) – 1/3(2x – 9) = 1/4(x – 1) – 2
সমাধানঃ-

| ∴ x =9 |
(ix) (x + 5)/3 + (2x – 1)/7 = 4
সমাধানঃ-
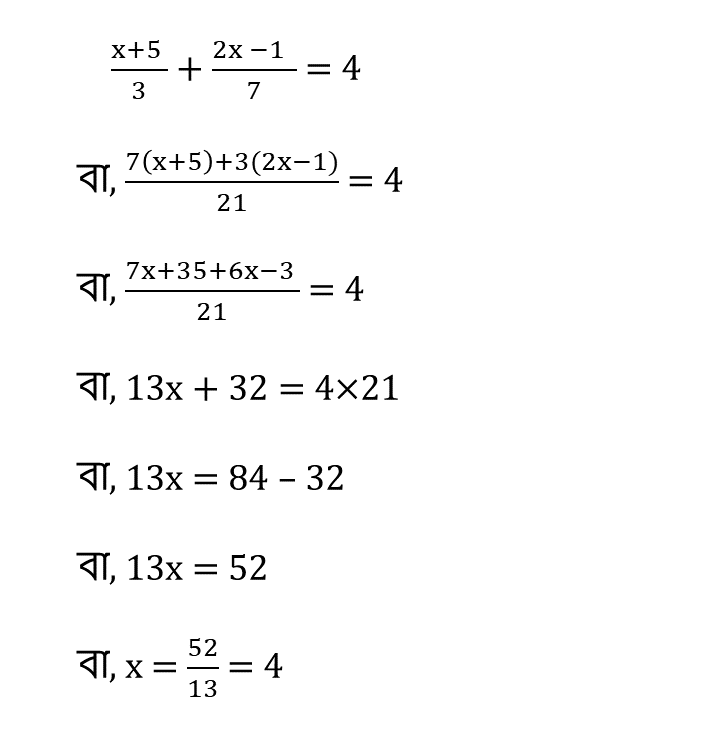
| ∴ x = 4 |
(x) 25 + 3(4x – 5) + 8(x + 2) = x + 3
সমাধানঃ-
| 25 + 3(4x – 5) + 8(x + 2) = x + 3 |
| বা, 25 + 12x – 15 + 8x + 16 = x + 3 |
| বা, 20x + 41 – 15 = x + 3 |
| বা, 20x + 26 = x + 3 |
| বা, 20x – x = 3 – 26 |
| বা, 19x = – 23 |
| বা, x = – \(\frac{23}{19}\) |
| ∴ x = – \(\frac{23}{19}\) |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
(xi) (x – 8)/3 + (2x + 2)/12 + (2x – 1)/18 = 3
সমাধানঃ-
| ∴ x = |
(xii)
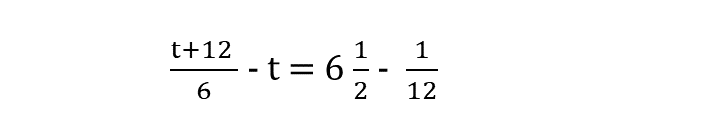
সমাধানঃ-

| ∴ t = – 53/10 |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
(xiii) (x + 1)/2 – (5x + 9)/28 = (x + 6)/21 + 5 – (x – 12)/3
সমাধানঃ-

| ∴ x = 15 |
(xiv) (9x + 5)/14 + (8x – 7)/7 = (18x + 11)/28 + 5/4
সমাধানঃ-

| ∴ x = 2 |
(xv) (3y + 1)/16 + (2y – 3)/7 = (y + 3)/8 + (3y – 1)/14
সমাধানঃ-

| ∴ y = 5 |
(xvi) 5x – (4x – 7) (3x – 5) = 6 – 3(4x – 9) (x – 1)
সমাধানঃ-
| 5x – (4x – 7) (3x – 5) = 6 – 3(4x – 9) (x – 1) |
| বা, 5x – {(4x)(3x) – 7(3x) – 5(4x) + 35} = 6 – 3{(4x)(x) – 9x – 4x + 9} |
| বা, 5x – (12x2 – 21x – 20x + 35) = 6 – 3(4x2 – 13x + 9) |
| বা, 5x – 12x2 + 41x – 35 = 6 – 12x2 + 39x – 27 |
| বা, – 12x2 + 46x – 35 = – 12x2 + 39x – 21 |
| বা, 46x – 35 = 39x – 21 |
| বা, 46x – 39x = 35 – 21 |
| বা, 7x = 14 |
| বা, x = 14/7 = 2 |
| ∴ x = 2 |
(xvii) 3(x – 4)2 + 5(x – 3)2 = (2x – 5) (4x – 1) – 40
সমাধানঃ-
| 3(x – 4)2 + 5(x – 3)2 = (2x – 5) (4x – 1) – 40 |
| বা, 3 (x2 – 8x + 16) + 5 (x2 – 6x + 9) = {(2x)(4x) – 5(4x) – 2x + 5} – 40 |
| বা, 3x2 – 24x + 48 + 5x2 – 30x + 45 = 8x2 – 20x – 2x + 5 – 40 |
| বা, 8x2 – 54x + 93 = 8x2 – 22x – 35 |
| বা, – 54x + 93 = – 22x – 35 |
| বা, 54x – 22x = 93 + 35 |
| বা, 32x = 128 |
| বা, x = 128/32 = 4 |
| ∴ x = 4 |
(xviii) 3(y – 5)2 + 5y = (2y- 3)2 – (y + 1)2 + 1
সমাধানঃ-
| 3(y – 5)2 + 5y = (2y- 3)2 – (y + 1)2 + 1 |
| বা, 3 (y2 – 10y + 25) + 5y = 4y2 – 12y + 9 – (y2 + 2y + 1) + 1 |
| বা, 3y2 – 30y + 75 + 5y = 4y2 – 12y + 9 – y2 – 2y – 1 + 1 |
| বা, 3y2 – 4y2 + y2 – 30y + 5y + 12y + 2y + 75 – 9 + 1 – 1 = 0 |
| বা, 4y2 – 4y2 -30y + 19y + 75 – 9 = 0 |
| বা, -11y + 66 = 0 |
| বা, 11y = 66 |
| বা, y = 66/11=6 |
| ∴ y = 6 |
সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।
| গনিতপ্রভা অষ্টম শ্রেণীর সমস্ত অধ্যায়ের সমাধান- | |
|---|---|
| অধ্যায় | সমাধান |
| 2. পাই চিত্র | কষে দেখি 2 |
| 3. মূলদ সংখ্যার ধারণা | অধ্যায়ের সারাংশ |
| কষে দেখি 3 | |
| 4. বীজগাণিতিক সংখ্যামালার গুণ ও ভাগ | অধ্যায়ের সারাংশ |
| কষে দেখি 4.1 | |
| কষে দেখি 4.2 | |
| 5. ঘনফল নির্ণয় | অধ্যায়ের সারাংশ |
| কষে দেখি 5.1 | |
| কষে দেখি 5.2 | |
| কষে দেখি 5.3 | |
| 6. পূরক কোণ, সম্পূরক কোণ ও সন্নিহিত কোণ | অধ্যায়ের সারাংশ |
| কষে দেখি 6 | |
| 7. বিপ্রতীপ কোণের ধারণা | অধ্যায়ের সারাংশ |
| কষে দেখি 7.1 | |
8. সমান্তরাল সরলরেখা ও ছেদকের ধর্ম | অধ্যায়ের সারাংশ |
| কষে দেখি 8 | |
9. ত্রিভুজের দুটি বাহু ও তাদের বিপরীত কোণের সম্পর্ক | অধ্যায়ের সারাংশ |
| কষে দেখি 9 | |
| 10. ত্রৈরাশিক | কষে দেখি 10.1 |
| কষে দেখি 10.2 | |
| 11. শতকরা | কষে দেখি 11 |
| 12. মিশ্রণ | কষে দেখি 12 |
13. বীজগাণিতিক সংখ্যামালার উৎপাদকে বিশ্লেষণ | কষে দেখি 13.1 |
| কষে দেখি 13.2 | |
14. বীজগাণিতিক সংখ্যামালার গ.সা.গু ও ল.সা.গু | কষে দেখি 14 |
15. বীজগাণিতিক সংখ্যামালার সরলীকরণ | কষে দেখি 15 |
16. ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই | কষে দেখি 16.1 |
| কষে দেখি 16.2 | |
17. সময় ও কার্য | কষে দেখি 17.1 |
| কষে দেখি 17.2 | |
18. লেখচিত্র | কষে দেখি 18 |
19. সমীকরণ গঠন ও সমাধান | কষে দেখি 19 |
| 20. জ্যামিতিক প্রমাণ | কষে দেখি 20.1 |
| কষে দেখি 20.2 | |
| কষে দেখি 20.3 | |

এখানে তোমরা তোমাদের অষ্টম শ্রেণীতে কি কি পড়ানো হয়, মানে তোমাদের অষ্টম শ্রেণীর সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

