শ্রেণী-অষ্টম ; অধ্যায় -সময় ও কার্য ; কষে দেখি 17.2
সময় ও কার্য কষে দেখি 17.2 এর অংকের সমাধান গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ
কষে দেখি 17.2|Koshe Dekhi 17.2 হল Class 8|অষ্টমশ্রেণীর গণিত প্রভা বইয়ের একটি সমস্যা সমাধানের অনুশীলন, যা পশ্চিমবঙ্গে গণিত শেখানোর জন্য ব্যবহৃত হয়। এই কষে দেখি 17.2|koshe dekhi 17.2 Class 8 এর সমস্ত অংক সময় ও কার্য এর উপর নির্ভরশীল।
সমস্যাটি পাঠককে তিনজন/দুইজন একসাথে কাজ করলে একটি কাজ সম্পূর্ণ করতে কতটা সময় লাগে তা খুঁজে বের করতে বলে।
একটি উদাহরণ দিয়ে কষে দেখি 17.2 Class 8|koshe dekhi 17.2 Class 8 এর অংক গুলি বোঝার চেষ্টা করি-
একটি কাজ হল জল দিয়ে একটি ট্যাঙ্ক পূরণ করা। প্রথম ব্যক্তি 6 ঘন্টার মধ্যে ট্যাঙ্কটি পূরণ করতে পারে, দ্বিতীয় ব্যক্তিটি 8 ঘন্টার মধ্যে এটি পূরণ করতে পারে এবং তৃতীয় ব্যক্তিটি 12 ঘন্টার মধ্যে এটি পূরণ করতে পারে।
এই কষে দেখি 17.2 Class 8 এর অংক গুলি সমাধানের জন্য, আমরা নিম্নলিখিত পদক্ষেপগুলি ব্যবহার করব:
- প্রথমে তিনটি মানুষের মিলিত হার নির্ণয় করতে হবে। এটি প্রতিটি ব্যক্তির হার যোগ করে করা হয়।
- প্রথম ব্যক্তির হার 1/6 ট্যাঙ্ক প্রতি ঘন্টা,
- দ্বিতীয় ব্যক্তির হার 1/8 ট্যাঙ্ক প্রতি ঘন্টা, এবং
- তৃতীয় ব্যক্তির হার 1/12 ট্যাঙ্ক প্রতি ঘন্টা।
- অতএব মিলিত হার হল 1/6 + 1/8 + 1/12 = 7/24 ট্যাঙ্ক প্রতি ঘন্টা।
- সম্মিলিত হার দ্বারা কাজের মোট পরিমাণ ভাগ কর।
- কাজের মোট পরিমাণ হল 1 ট্যাঙ্ক, এবং মিলিত হার হল 7/24 ট্যাঙ্ক প্রতি ঘন্টা। কাজটি সম্পূর্ণ করতে যে সময় লাগে তা হল 1/(7/24) = 24/7 ঘন্টা।
সমস্যার উত্তর হলো, তিনজনের ট্যাঙ্কে পানি ভরতে 24/7 ঘণ্টা সময় লাগে।
এখানে সমাধানের আরও বিশদ ব্যাখ্যা রয়েছে:
প্রথম ধাপ হল তিনটি মানুষের সম্মিলিত হার বের করা। এটি প্রতিটি ব্যক্তির হার যোগ করে করা হয়। প্রথম ব্যক্তির হার 1/6 ট্যাঙ্ক প্রতি ঘন্টা, দ্বিতীয় ব্যক্তির হার 1/8 ট্যাঙ্ক প্রতি ঘন্টা, এবং তৃতীয় ব্যক্তির হার 1/12 ট্যাঙ্ক প্রতি ঘন্টা। মিলিত হার হল 1/6 + 1/8 + 1/12 = 7/24 ট্যাঙ্ক প্রতি ঘন্টা।
পরবর্তী ধাপ হল কাজের মোট পরিমাণকে সম্মিলিত হার দিয়ে ভাগ করা। কাজের মোট পরিমাণ হল 1 ট্যাঙ্ক, এবং মিলিত হার হল 7/24 ট্যাঙ্ক প্রতি ঘন্টা। কাজটি সম্পূর্ণ করতে যে সময় লাগে তা হল 1/(7/24) = 24/7 ঘন্টা।
তাই তিনজনের ট্যাঙ্কে পানি ভরতে 24/7 ঘন্টা সময় লাগে।
আগামিতে এই কষে দেখি 17.2 Class 8 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 17.2 Class 8 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 17.2 Class 8 তারপর  |

কষে দেখি 17.2 | Koshe Dekhi 17.2
1. প্রিয়া ও দেবু প্রত্যেকে আলাদা ভাবে একটি কাজ যথাক্রমে 10 ঘণ্টায় ও 12 ঘণ্টায় করতে পারে। তারা যদি একসঙ্গে ওই কাজটি করে তবে কত ঘণ্টায় কাজটি শেষ করবে হিসাব করি।
সমাধানঃ-
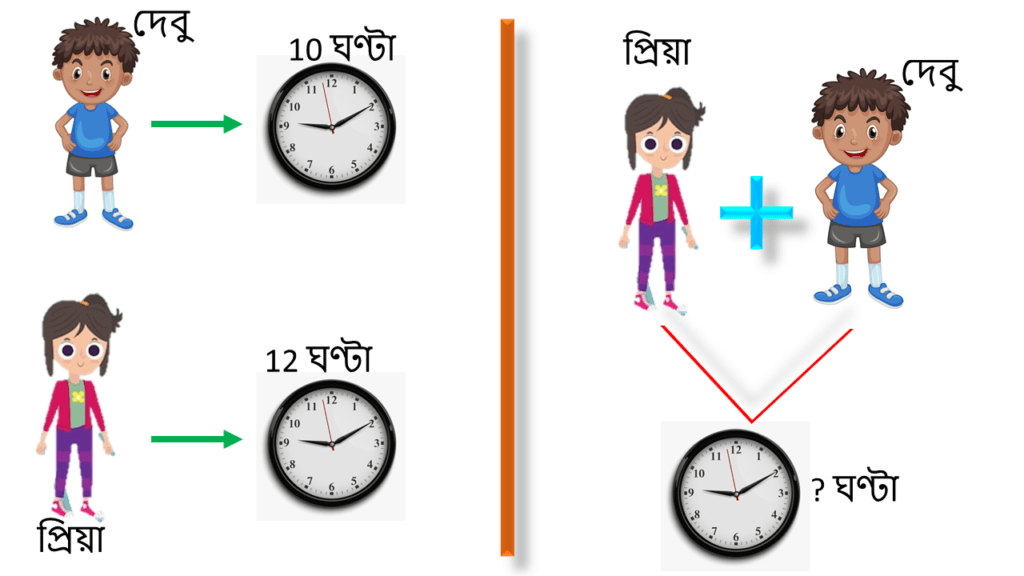
| প্রিয়া একা 1 ঘণ্টায় কাজ করে ওই কাজের 1/10 অংশ |
| দেবু একা 1 ঘণ্টায় কাজ করে ওই কাজের 1/12 অংশ |
∴ প্রিয়া ও দেবু একসঙ্গে 1 ঘণ্টায় করে মোট কাজের,
(1/10 + 1/12) অংশ
= (6 + 5)/60
= 11/60 অংশ
| প্রিয়া ও দেবু একসঙ্গে 11/60 অংশ কাজ করে 1 ঘণ্টায় |
| প্রিয়া ও দেবু একসঙ্গে 1 অংশ করে 1 ÷ 11/60 = 60/11 ঘণ্টায় |
| ∴ প্রিয়া ও দেবু একসঙ্গে ওই কাজটি করে তবে 60/11 ঘণ্টায় কাজটি শেষ করবে । |
2. আমি, আমার দাদা ও আমার দিদি তিনজনে মিলে বাড়ির জানালাগুলি রং করব। আমার দাদা, দিদি ও আমি আলাদাভাবে এই কাজটি যথাক্রমে 12, 4 ও 6 দিনে করতে পারি। আমরা তিনজন যদি একসাথে কাজটি করি তবে কতদিনে কাজটি শেষ করতে পারবো হিসাব করে লিখি।
সমাধানঃ-
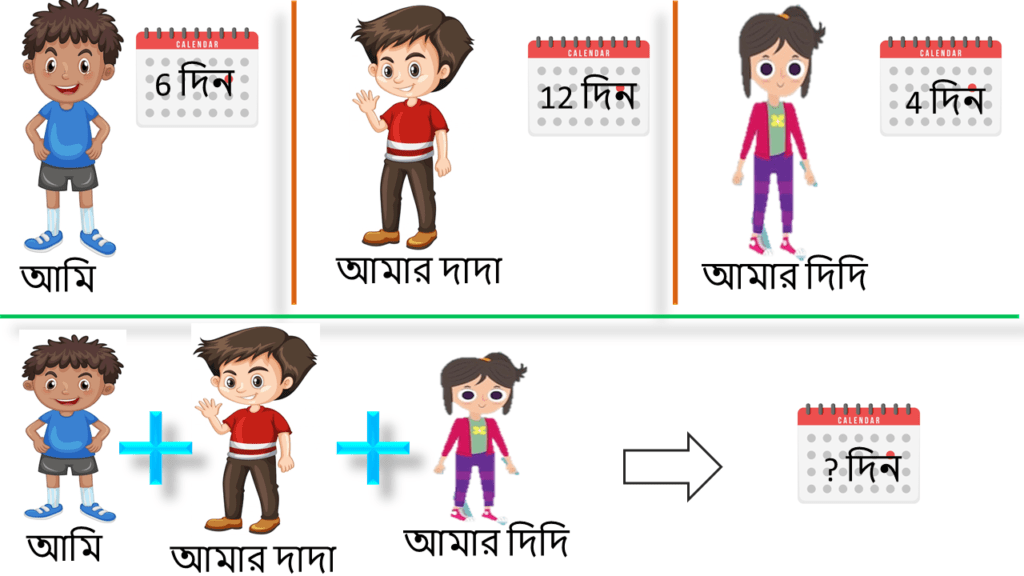
| আমার দাদা একা 1 দিনে করে মোট কাজের 1/12 অংশ |
| আমার দিদি একা 1 দিনে করে মোট কাজের 1/4 অংশ |
| আমি একা 1 দিনে করি মোট কাজের 1/6 অংশ |
∴ আমরা তিনজনে একসাথে 1 দিনে করি মোট কাজের,
(1/12 + 1/4 + 1/6) অংশ
= (1 + 3 + 2)/12
= 6/12
= 1/2 অংশ
| আমরা তিনজন একসাথে 1/2 অংশ করি 1 দিনে |
| আমরা তিনজন একসঙ্গে 1 অংশ করি 1 ÷ 1/2 = 2 দিনে |
| ∴ আমরা তিনজন যদি একসাথে কাজটি করি তবে 2 দিনে কাজটি শেষ করতে পারবো । |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |

3. কোনো একটি কাজ অবনী ও আনোয়ার আলাদাভাবে যথাক্রমে 20 এবং 25 দিনে করতে পারে। তারা একসঙ্গে কাজ শুরু করার 10 দিন পর দু-জনেই চলে গেল। সুখেন এসে বাকি কাজটি 3 দিনে শেষ করল। যদি সুখেন পুরো কাজটি একা করত তবে কতদিনে কাজটি শেষ করতে পারত হিসাব করে লিখি।
সমাধানঃ-
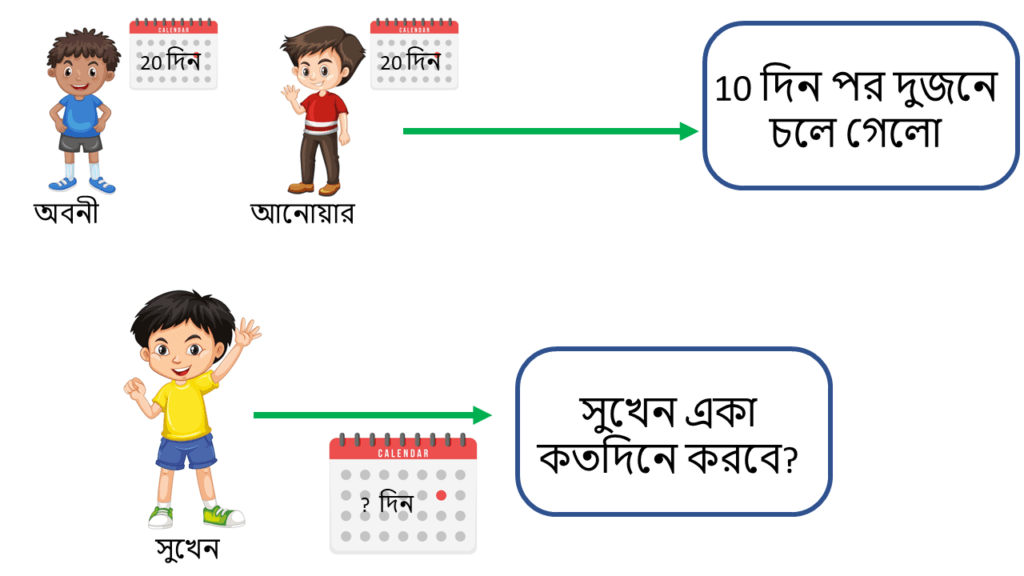
| অবনী একা 1 দিনে করে মোট কাজের 1/20 অংশ |
| আনোয়ার একা 1 দিনে করে মোট কাজের 1/25 অংশ |
অবনী ও আনোয়ার একসঙ্গে 1 দিনে করে মোট কাজের
(1/20 + 1/25) অংশ
= (5 + 4)/100
= 9/100 অংশ
| অবনী ও আনোয়ার একসঙ্গে 1 দিনে করে মোট কাজের 9/100 অংশ |
| অবনী ও আনোয়ার একসঙ্গে 10 দিনে করে মোট কাজের 9/100 × 10 = 9/10 অংশ |
∴ অবনী ও আনোয়ার একসঙ্গে 10 দিন কাজ করার পর কাজ বাকি থাকে মোট কাজের
(1 – 9/10) অংশ
= (10 – 9)/10
= 1/10 অংশ
এখন মোট কাজের এই 1/10 অংশ 3 দিনে শেষ করে।
∴ সুখেন 1 অংশ করে 3 ÷ 1/10 = 30 দিনে
| ∴ যদি সুখেন পুরো কাজটি একা করত তবে 30 দিনে কাজটি শেষ করতে পারত । |

4. পৌরসভার একটি জলের ট্যাঙ্ক থেকে জল নেওয়ার দুটি নল আছে। নলদুটি দিয়ে আলাদাভাবে 4 ঘণ্টায় ট্যাঙ্কটি খালি করা যায়। দুটি নলকে একই সঙ্গে খুলে রাখলে কতক্ষণে ট্যাঙ্কটি খালি হবে হিসাব করে লিখি।
সমাধানঃ-
| প্রথম নলটি 1 ঘণ্টায় খালি করে ট্যাঙ্ক এর 1/4 অংশ |
| দ্বিতীয় নলটি 1 ঘণ্টায় খালি করে ট্যাঙ্ক এর 1/4 অংশ |
দুটি নল একসঙ্গে 1 ঘণ্টায় খালি করে ট্যাঙ্ক এর
(1/4 + 1/4) অংশ
= 1/2 অংশ
| দুটি নল একসঙ্গে 1/2 অংশ খালি করে 1 ঘণ্টায় |
| দুটি নল একসঙ্গে 1 অংশ খালি করে 1÷1/2 = 2 ঘণ্টায় |
| ∴ দুটি নলকে একই সঙ্গে খুলে রাখলে 2 ঘণ্টায় ট্যাঙ্কটি খালি হবে । |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
5. আমাদের চৌবাচ্চায় 3 টি নল আছে। ওই তিনটি নল দিয়ে আলাদাভাবে যথাক্রমে 18, 21 ও 24 ঘণ্টায় চৌবাচ্চা পূর্ণ করা যায়।
( a ) একসাথে 3 টি নল খোলা থাকলে কতক্ষণে চৌবাচ্চাটি জলপূর্ণ হবে সমানুপাত তৈরি করি ও হিসাব করে লিখি।
সমাধানঃ-
| প্রথম নলটি 1 ঘণ্টায় পূর্ণ করে চৌবাচ্চার 1/18 অংশ |
| দ্বিতীয় নলটি 1 ঘণ্টায় পূর্ণ করে চৌবাচ্চার 1/21 অংশ |
| তৃতীয় নলটি 1 ঘণ্টায় পূর্ণ করে চৌবাচ্চার 1/24 অংশ |
তিনটি নল একসঙ্গে 1 ঘণ্টায় পূর্ণ করে চৌবাচ্চার
(1/18 + 1/21 + 1/24) অংশ
= (28 + 24 + 21)/504
= 73/504 অংশ
গণিতের ভাষায় সমস্যাটি হল-
| ভর্তির পরিমাণ (অংশ) | সময় (ঘণ্টা) |
|---|---|
| 73/504 | 1 |
| 1 | ? |
এখানে ভর্তির পরিমাণ বাড়লে ভর্তি হতে বেশী সময় লাগবে। সুতরাং, ভর্তির পরিমাণ ও সময় সরল সম্পর্কে আছে।
সরল সমানুপাত তৈরি করে পাই,
73/504 : 1 : : 1 : ?
∴ নির্ণেয় সময়
= 1 × 504/73
= 504/73 ঘণ্টা
| ∴ একসাথে 3 টি নল খোলা থাকলে 504/73 ঘণ্টায় চৌবাচ্চাটি জলপূর্ণ হবে । |
( b ) যদি প্রথম দুটি নল খোলা থাকত তাহলে চৌবাচ্চাটি পূর্ণ করতে কত সময় লাগত হিসাব করি।
সমাধানঃ-
| প্রথম নলটি 1 ঘণ্টায় পূর্ণ করে চৌবাচ্চার 1/18 অংশ |
| দ্বিতীয় নলটি 1 ঘণ্টায় পূর্ণ করে চৌবাচ্চার 1/21 অংশ |
দুটি নল একসঙ্গে 1 ঘণ্টায় পূর্ণ করে চৌবাচ্চার
(1/18 + 1/21) অংশ
= (7 + 6)/126
= 13/126 অংশ
| দুটি নল একসঙ্গে 13/126 অংশ পূর্ণ করে 1 ঘণ্টায় |
| দুটি নল একসঙ্গে 1 অংশ পূর্ণ করে 1÷13/126 = 126/13 ঘণ্টায় |
| ∴ যদি প্রথম দুটি নল খোলা থাকত তাহলে চৌবাচ্চাটি পূর্ণ করতে 126/13 ঘণ্টা সময় লাগত । |
( c ) যদি শেষের দুটি নল খোলা থাকত তাহলে চৌবাচ্চাটি পূর্ণ করতে কত সময় লাগত হিসাব করি।
সমাধানঃ-
| দ্বিতীয় নলটি 1 ঘণ্টায় পূর্ণ করে চৌবাচ্চার 1/21 অংশ |
| তৃতীয় নলটি 1 ঘণ্টায় পূর্ণ করে চৌবাচ্চার 1/24 অংশ |
দুটি নল একসঙ্গে 1 ঘণ্টায় পূর্ণ করে চৌবাচ্চার
(1/21 + 1/24) অংশ
= (8 + 7)/168
= 15/168
= 5/56 অংশ
| দুটি নল একসঙ্গে 5/56 অংশ পূর্ণ করে 1 ঘণ্টায় |
| দুটি নল একসঙ্গে 1 অংশ পূর্ণ করে 1÷5/56 = 56/5 ঘণ্টায় |
| ∴ যদি শেষের দুটি নল খোলা থাকত তাহলে চৌবাচ্চাটি পূর্ণ করতে 56/5 ঘণ্টা সময় লাগত । |


6. পৌরসভার জল সরবরাহের নলটি দিয়ে রেহানদের বাড়ির চৌবাচ্চাটি 30 মিনিটে পূর্ণ করা যায়। ওদের বাড়ির সব নলের কল খুলে ওরা 4 ঘণ্টায় ওই পূর্ণ চৌবাচ্চার সমস্ত জল দিয়ে কাজ করতে পারে। কোনো একদিন জল সরবরাহের নলটি মাত্র 25 মিনিট খোলা থাকে তাহলে ওই জল দিয়ে কতক্ষণ ওরা বাড়ির কাজ করতে পারবে হিসাব করে লিখি।
সমাধানঃ-
| 30 মিনিটে পূর্ণ হয় 1 অংশ |
| 1 মিনিটে পূর্ণ হয় 1/30 অংশ |
| 25 মিনিটে পূর্ণ হয় 1/30×25=5/6 অংশ |
∴ জল সরবরাহের নলটি মাত্র 25 মিনিটে চৌবাচ্চাটির 5/6 অংশ ভর্তি হবে।
| চৌবাচ্চার সমস্ত জল দিয়ে কাজ করতে পারে 4 ঘণ্টা |
| চৌবাচ্চার 5/6 অংশ জল দিয়ে কাজ করতে পারবে 4×5/6=10/3 ঘণ্টা |
10/3 ঘণ্টা = 3 ঘণ্টা 20 মিনিট
| ∴জল সরবরাহের নলটি 25 মিনিট খোলা থাকলে ওই জল দিয়ে ওরা 3 ঘণ্টা 20 মিনিট বাড়ির কাজ করতে পারবে । |
7. কোনো একটি কাজ রমা ও রোহিত 20 দিনে, রোহিত ও সাব্বা 15 দিনে এবং রমা ও সাব্বা 20 দিনে করতে পারে। হিসাব করে লিখি তিনজনে একত্রে কতদিনে কাজটি শেষ করবে। রমা, রোহিত ও সাব্বা প্রত্যেকে আলাদা আলাদা কাজ করলে কে কতদিনে কাজটি করতে পারবে হিসাব করি।
সমাধানঃ-
| রমা ও রোহিত 1 দিনে করে 1/20 অংশ —- (i) |
| রোহিত ও সাব্বা 1 দিনে করে 1/15 অংশ —– (ii) |
| রমা ও সাব্বা 1 দিনে করে 1/20 অংশ —- (iii) |
| রমা ও রোহিত, রোহিত ও সাব্বা, রমা ও সাব্বা একত্রে 1 দিনে করে = (1/20 + 1/15 + 1/20) = 1/6 অংশ |
| ∴ 2(রমা, রোহিত, সাব্বা) একত্রে 1 দিনে করে = 1/6 অংশ |
| বা, রমা, রোহিত, সাব্বা একত্রে 1 দিনে করে = 1/6×1/2=1/12 অংশ ———-(iv) |
| রমা, রোহিত, সাব্বা একত্রে 1/12 অংশ করে 1 দিনে |
| রমা, রোহিত, সাব্বা একত্রে 1 অংশ করে 1÷1/12 = 12 দিনে |
এখন,
| (iv) নং থেকে (i) নং বিয়োগ করে পাই, |
|---|
| সাব্বা একা 1 দিনে করে = (1/12 – 1/20) অংশ = (5 – 3)/60 = 2/60 = 1/30 অংশ |
∴ সাব্বা 1/30 অংশ করে 1 দিনে
সাব্বা 1 অংশ করে 1÷1/30 = 30 দিনে
আবার,
| (iv) নং থেকে (ii) নং বিয়োগ করে পাই, |
|---|
| রমা একা 1 দিনে করে = (1/12 – 1/15) অংশ = (5 – 4)/60 = 1/60 = 1/60 অংশ |
∴ রমা 1/60 অংশ করে 1 দিনে
রমা 1 অংশ করে 1÷1/60 = 60 দিনে
আবার,
| (iv) নং থেকে (iii) নং বিয়োগ করে পাই, |
|---|
| রোহিত একা 1 দিনে করে = (1/12 – 1/20) অংশ = (5 – 3)/60 = 2/60 = 1/30 অংশ |
∴ রোহিত 1/30 অংশ করে 1 দিনে
রোহিত 1 অংশ করে 1÷1/30 = 30 দিনে
| ∴ তিনজনে একত্রে 12 দিনে কাজটি শেষ করবে । রমা একা করে 60 দিনে রোহিত একা করে 30 দিনে সাব্বা একা করে 30 দিনে |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
8. অলোক, কালাম ও জোসেফ প্রত্যেকে কোনো একটি কাজ যথাক্রমে 10,12 ও 15 দিনে করতে পারে। তারা একসাথে কাজটি শুরু করল। 3 দিন পরে কালামকে চলে যেতে হলো। বাকি কাজটি অলোক ও জোসেফ কতদিনে শেষ করতে পারবে সমানুপাত তৈরি করে হিসাব করি।
সমাধানঃ-
| অলোক 1 দিনে করে 1/10 অংশ |
| কালাম 1 দিনে করে 1/12 অংশ |
| জোসেফ 1 দিনে করে 1/15 অংশ |
তিনজনে একত্রে 1 দিনে করে
= (1/10 + 1/12 + 1/15)
= (6 + 4 + 5)/60
= 15/60
= 1/4 অংশ
∴ তিনজনে একত্রে 3 দিনে করে
= 3×1/4
= 3/4 অংশ
∴ মোট কাজের বাকি থাকে
= 1 – 3/4
= (4 – 3)/4
= 1/4 অংশ
এখন,
| অলোক ও জোসেফ একত্রে 1 দিনে করে |
| = 1/10 + 1/15 |
| = (3 + 2)/30 |
| = 5/30 |
| = 1/6 অংশ |
গণিতের ভাষায় সমস্যাটি হল-
| কাজের পরিমাণ (অংশ) | সময় (দিন) |
|---|---|
| 1/6 | 1 |
| 1/4 | ? |
এখানে কাজের পরিমাণ বাড়লে সময় বেশী লাগবে। সুতরাং কাজের পরিমাণ ও সময় সরল সম্পর্কে আছে।
সরল সমানুপাত তৈরি করে পাই,
1/6 : 1/4 : : 1 : ?
∴ নির্ণেয় সময়,
= 1 × 1/4 × 6
= 3/2
| ∴বাকি কাজটি অলোক ও জোসেফ 3/2 দিনে শেষ করতে পারবে । |

9. একটি কাজ মেরি ও ডেভিড একা একা যথাক্রমে 10 দিনে ও 15 দিনে করতে পারে। প্রথমে মেরি একা 4 দিন ও পরে ডেভিড একা 5 দিন কাজ করে চলে গেল। মারিয়া এসে একা বাকি কাজটি 4 দিনে শেষ করল। যদি মেরি, ডেভিড ও মারিয়া একসাথে কাজটি করত তবে কতদিনে কাজটি শেষ করত হিসাব করে লিখি।
সমাধানঃ-
| মেরি, |
|---|
| একা 1 দিনে করে 1/10 অংশ |
| ∴ 4 দিনে করে 4/10=2/5 অংশ |
| ডেভিড, |
|---|
| একা 1 দিনে করে 1/15 অংশ |
| ∴ 5 দিনে করে 5/15=1/3 অংশ |
মেরি ও ডেভিডের কাজ করা হয়েছে,
(2/5 + 1/3) অংশ
= (6 + 5)/15
= 11/15 অংশ
এখন কাজ বাকি আছে
(1 – 11/15) অংশ
= 4/15 অংশ
এই বাকি 4/15 অংশ কাজ মারিয়া এসে 4 দিনে শেষ করে ।
∴ মারিয়া 1 দিনে করে 1/15 অংশ ।
মেরি, ডেভিড ও মারিয়া একসাথে 1 দিনে করে
(1/10 + 1/15 + 1/15) অংশ
= (1/10 + 2/15)
= (3 + 4)/30
= 7/30 অংশ
মেরি, ডেভিড ও মারিয়া একসাথে,
7/30 অংশ কাজ করে 1 দিনে
1 অংশ কাজ করে 30/7 দিনে
| ∴ যদি মেরি, ডেভিড ও মারিয়া একসাথে কাজটি করত তবে 30/7 দিনে কাজটি শেষ করত। |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |

10. একটি পৌরসভা পানীয় জল সংরক্ষণের জন্য একটি জলাধার নিরমান করে তাতে পাম্প যুক্ত করেছে। পাম্পগুলি আলাদা ভাবে যথাক্রমে 16, 20, 30 ঘণ্টায় খালি জলাধারটি পূর্ণ করতে পারে। আজ সকাল 7 টায় তিনটি পাম্প যখন একসঙ্গে চালু করা হলো, তখন জলাধারটি 1/3 অংশ জলপূর্ণ ছিল। 1 ঘণ্টা 36 মিনিট পর প্রথম পাম্পটি এবং তারও 2 ঘণ্টা পর তৃতীয় পাম্পটি বন্ধ হয়ে যায়।
সমাধানঃ-
জলাধারটি 1/3 অংশ জলপূর্ণ ছিল
∴ জলাধারটি খালি ছিল (1-1/3)=2/3 অংশ —–(i)
| প্রথম পাম্পটি 1 ঘণ্টায় পূর্ণ করে 1/16 অংশ |
| দ্বিতীয় পাম্পটি 1 ঘণ্টায় পূর্ণ করে 1/20 অংশ |
| তৃতীয় পাম্পটি 1 ঘণ্টায় পূর্ণ করে 1/30 অংশ |
তিনটি পাম্প একসঙ্গে 1 ঘণ্টায় পূর্ণ করে
= (1/16 + 1/20 + 1/30) অংশ
= (15 + 12 + 18)/240
= 35/240
= 7/48 অংশ —–(ii)
এখন,
1 ঘণ্টা 36 মিনিট=96 মিনিট পর প্রথম পাম্পটি বন্ধ হয়ে যায়।
| (ii) নং থেকে পাই, |
|---|
| 60 মিনিটে তিনটি পাম্প একসঙ্গে পূর্ণ করে 7/48 অংশ |
| 1 মিনিটে তিনটি পাম্প একসঙ্গে পূর্ণ করে 7/48×1/60 অংশ |
| 96 মিনিটে তিনটি পাম্প একসঙ্গে পূর্ণ করে (7×1×96)/(48×60)=7/30 অংশ |
∴ 96 মিনিট পর তিনটি পাম্প জলাধারটির খালি অংশের 7/30 অংশ পূর্ণ করে।
96 মিনিট পর জলাধারটি খালি থাকে,
(2/3 – 7/30) অংশ
= (20 – 7)/30
= 13/30 অংশ —- ( iii )
প্রথম পাম্পটি খারাপ হওয়ার আরও 2 ঘণ্টা=120 মিনিট পর তৃতীয় পাম্পটি বন্ধ হয়ে যায়।
অর্থাৎ, 120 মিনিট একসঙ্গে দ্বিতীয় ও তৃতীয় পাম্পটি চলেছে।
দ্বিতীয় ও তৃতীয় পাম্প দুটি একসঙ্গে 1 ঘণ্টা=60 মিনিটে পূর্ণ করে
(1/20 + 1/30) অংশ
= (3 + 2)/60
= 5/60
= 1/12 অংশ
দ্বিতীয় ও তৃতীয় পাম্প দুটি একসঙ্গে,
| 60 মিনিটে পূর্ণ করে 1/12 অংশ |
| 1 মিনিটে পূর্ণ করে 1/12×1/60 অংশ |
| 120 মিনিটে পূর্ণ করে 1/12×1/60×120=1/6 অংশ —- (iv) |
এরপরে জলাধারটি খালি থাকে
(13/30 – 1/6) অংশ
= (13 – 5)/30
= 8/30
= 4/15 অংশ
এখন দ্বিতীয় পাম্পটি,
| 1/20 অংশ পূর্ণ করে 1 ঘণ্টায় |
| 1 অংশ পূর্ণ করে 1÷1/20=20 ঘণ্টায় |
| 4/15 অংশ পূর্ণ করে 4/15×20=16/3 ঘণ্টা=5 ঘণ্টা 20 মিনিটে |
( a ) হিসাব করে দেখি জলাধারটি কখন সম্পূর্ণ জলপূর্ণ হয়েছিল।
অতএব,
জলাধারটি পূর্ণ হতে মোট সময় লাগলো
= 1 ঘণ্টা 36 মিনিট + 2 ঘণ্টা + 5 ঘণ্টা 20 মিনিট
= 8 ঘণ্টা 56 মিনিট
অর্থাৎ, সকাল 7 টা থেকে 8 ঘণ্টা 56 মিনিট সময় লেগেছে।
| ∴ জলাধারটি বিকাল 3 টা 56 মিনিটে সম্পূর্ণ জলপূর্ণ হয়েছিল। |

( b ) হিসাব করে দেখি দ্বিতীয় পাম্পটি জলাধারের কত অংশ পূর্ণ হয়েছিল।
সমাধানঃ-
8 ঘণ্টা 56 মিনিট = 536 মিনিট
দ্বিতীয় পাম্পটি,
60 মিনিটে পূর্ণ করে 1/20 অংশ
536 মিনিটে পূর্ণ করে 536/(20×60) =67/150 অংশ
| ∴দ্বিতীয় পাম্পটি জলাধারের 67/150 অংশ পূর্ণ হয়েছিল । |
( c ) তৃতীয় পাম্পটি যখন বন্ধ হয়, তখন জলাধারটির কত অংশ জলপূর্ণ ছিল হিসাব করে লিখি।
সমাধানঃ-
তৃতীয় পাম্পটি যখন বন্ধ হয় তখন জলাধারটি জলপূর্ণ ছিল
(1/3 + 7/30 + 1/6) অংশ
= (20 + 14 + 10)/60
= 44/60
= 11/15 অংশ
| ∴তৃতীয় পাম্পটি যখন বন্ধ হয়, তখন জলাধারটির 11/15 অংশ জলপূর্ণ ছিল । |
11. আমার বন্ধু রিণা বাগানের কাজ একা 4 ঘণ্টায় করতে পারে। আমি ওই কাজ একা ……… ঘণ্টায় করতে পারি। কিন্ত দু-জনে একসাথে বাগানের ওই কাজ করলে কত সময় লাগবে হিসাব করে লিখি। ( ফাঁকা ঘরে নিজে সংখ্যা বসাই )
সমাধানঃ- নিজে করো।

 কষে দেখি 17.1
কষে দেখি 17.1
এই কষে দেখি 17.2 Class 8|Koshe Dekhi 17.2 Class 8 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 17.2 Class 8 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 17.2 Class 8 তারপর  |
| গনিতপ্রভা অষ্টম শ্রেণীর সমস্ত অধ্যায়ের সমাধান- | |
|---|---|
| অধ্যায় | সমাধান |
| 2. পাই চিত্র | কষে দেখি 2 |
| 3. মূলদ সংখ্যার ধারণা | অধ্যায়ের সারাংশ |
| কষে দেখি 3 | |
| 4. বীজগাণিতিক সংখ্যামালার গুণ ও ভাগ | অধ্যায়ের সারাংশ |
| কষে দেখি 4.1 | |
| কষে দেখি 4.2 | |
| 5. ঘনফল নির্ণয় | অধ্যায়ের সারাংশ |
| কষে দেখি 5.1 | |
| কষে দেখি 5.2 | |
| কষে দেখি 5.3 | |
| 6. পূরক কোণ, সম্পূরক কোণ ও সন্নিহিত কোণ | অধ্যায়ের সারাংশ |
| কষে দেখি 6 | |
| 7. বিপ্রতীপ কোণের ধারণা | অধ্যায়ের সারাংশ |
| কষে দেখি 7.1 | |
8. সমান্তরাল সরলরেখা ও ছেদকের ধর্ম | অধ্যায়ের সারাংশ |
| কষে দেখি 8 | |
9. ত্রিভুজের দুটি বাহু ও তাদের বিপরীত কোণের সম্পর্ক | অধ্যায়ের সারাংশ |
| কষে দেখি 9 | |
| 10. ত্রৈরাশিক | কষে দেখি 10.1 |
| কষে দেখি 10.2 | |
| 11. শতকরা | কষে দেখি 11 |
| 12. মিশ্রণ | কষে দেখি 12 |
13. বীজগাণিতিক সংখ্যামালার উৎপাদকে বিশ্লেষণ | কষে দেখি 13.1 |
| কষে দেখি 13.2 | |
14. বীজগাণিতিক সংখ্যামালার গ.সা.গু ও ল.সা.গু | কষে দেখি 14 |
15. বীজগাণিতিক সংখ্যামালার সরলীকরণ | কষে দেখি 15 |
16. ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই | কষে দেখি 16.1 |
| কষে দেখি 16.2 | |
17. সময় ও কার্য | কষে দেখি 17.1 |
| কষে দেখি 17.2 | |
18. লেখচিত্র | কষে দেখি 18 |
19. সমীকরণ গঠন ও সমাধান | কষে দেখি 19 |
| 20. জ্যামিতিক প্রমাণ | কষে দেখি 20.1 |
| কষে দেখি 20.2 | |
| কষে দেখি 20.3 | |

এখানে তোমরা তোমাদের অষ্টম শ্রেণীতে কি কি পড়ানো হয়, মানে তোমাদের অষ্টম শ্রেণীর সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।


THANKS SIR….