শ্রেণী-অষ্টম ; অধ্যায় – ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই ; কষে দেখি 16.1
ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই এর কষে দেখি 16.1 এর অংকের সমাধান গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ
ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই, তোমাদের অষ্টম শ্রেণীর একটি অধ্যায়। এখানে এই অধ্যায়ের কষে দেখি 16.1 এর সমস্ত অংক এর সমাধান করে দেওয়া হয়েছে। অংকের সমাধান গুলি দেখার আগে তোমাদের জন্যে কিছু দরকারি উপদেশ দিতে চাই। কেননা এই কষে দেখি 16.1 এ যে সমস্ত অংক গুলি আছে সেগুলি করার জন্যে কিছু পদ্ধতি তোমাদের খেয়াল রাখতে হবে।
এই ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই অধ্যায় টির আগেও তোমাদের অষ্টম শ্রেণীর বইতে আরও তিনটি অধ্যায় আছে যথা-
( i ) বিপ্রতীপ কোণের ধারণা
( ii ) সমান্তরাল সরলরেখা ও ছেদকের ধর্ম
( iii ) ত্রিভুজের দুটি বাহু ও তাদের বিপরীত কোণের সম্পর্ক
এই কষে দেখি 16.1 এর বেশির ভাগ অংক করতে গেলে ওই আগের অধ্যায় গুলির জ্ঞান থাকা জরুরি, নাহলে কিছু কিছু প্রমাণ করার পদ্ধতি তোমরা বুঝতে পারবেনা। আগের অধ্যায় গুলি আগে ভালো করে বুঝতে হবে।যদি না বুঝে থাকো তাহলে তোমরা Google এ গিয়ে Search করবে –
( i ) কষে দেখি 7.1 Class 8 wbstudyhub.in
( ii ) কষে দেখি 8 Class 8 wbstudyhub.in
( iii ) কষে দেখি 9 Class 8 wbstudyhub.in
এই কষে দেখি 16.1 এর অংকগুলি বোঝার জন্যে কিছু উপদেশঃ
( i )
| উপদেশ 1 |
|---|
| প্রথমেই তোমাদের বলবো এই কষে দেখি 16.1 এর অংক গুলি বোঝার আগে উপরে উল্লিখিত তিনটি অধ্যায় থেকে বিষয় গুলি ভালো করে বুঝে নেবে। |
( ii )
| উপদেশ 2 |
|---|
| এই কষে দেখি 16.1 এর বেশিরভাগ অংক জ্যামিতিক প্রমাণের অংক। সুতরাং একটি উপপাদ্য কিভাবে প্রমাণ করতে হবে সেটা তোমাদের জানতে হবে। |
( iii )
| উপদেশ 3 |
|---|
| এই কষে দেখি 16.1 এর অংক গুলিতে কিছু কিছু অংকে খুব সাবধানে step গুলো খেয়াল করতে হবে। নাহলে পরবর্তী step বুঝতে অসুবিধা হবে। |
( iv )
| উপদেশ 4 |
|---|
| প্রতিটা অংক তোমাদের বোঝার জন্যে প্রতি step এ ছবি দিয়ে বোঝানোর চেষ্টা করা হয়েছে। তারপরেও যদি বুঝতে অসুবিধা হয় তাহলে কমেন্ট করে অবশ্যই জানাবে। |
( v )
| উপদেশ 5 |
|---|
| অংকের লেখা যদি ছোটো মনে হয় তাহলে একটু zoom করে নেব। |
আগামিতে এই কষে দেখি 16.1 Class 8 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 16.1 Class 8 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 16.1 Class 8 তারপর  |

কষে দেখি 16.1 | Koshe Dekhi 16.1
1. নীচের প্রতিক্ষেত্রে ( x ) এর মান লিখিঃ
( i )
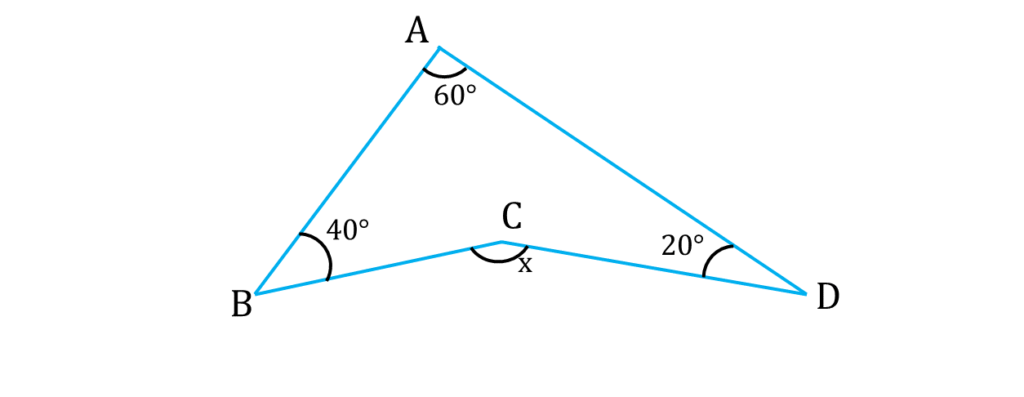
সমাধানঃ-
অঙ্কনঃ
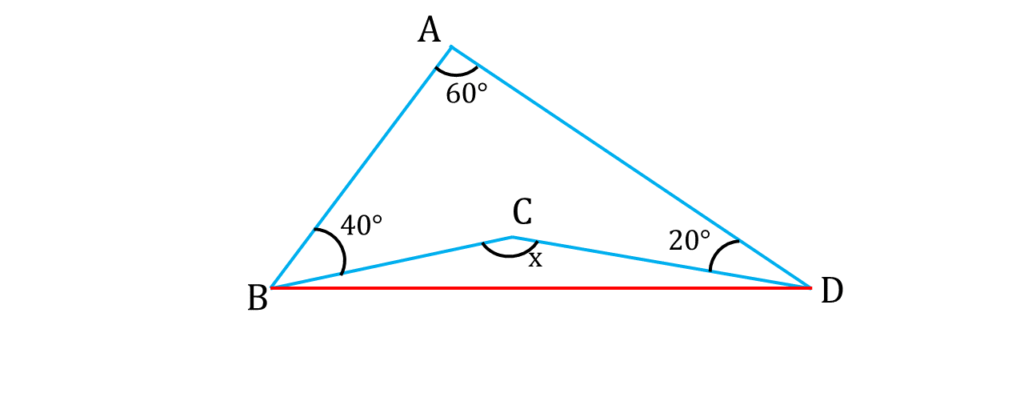
B ও D বিন্দু যোগ করলাম।
এখন,
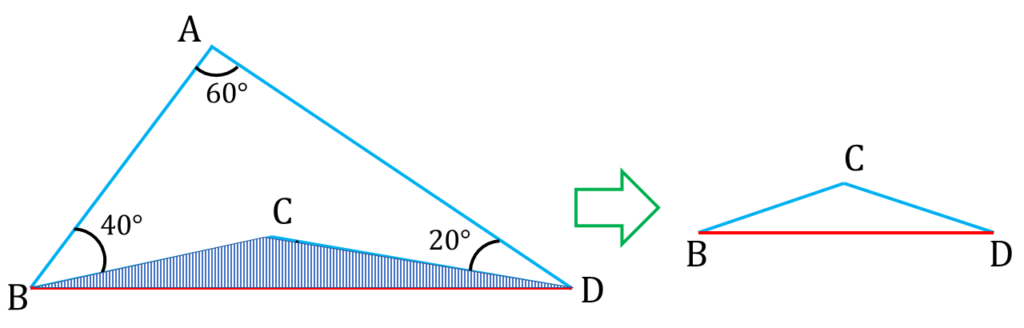
| ▲BCD থেকে পাই, |
|---|
| ∠CBD + ∠BCD + ∠BDC = 180° ——-( i ) |
আবার,
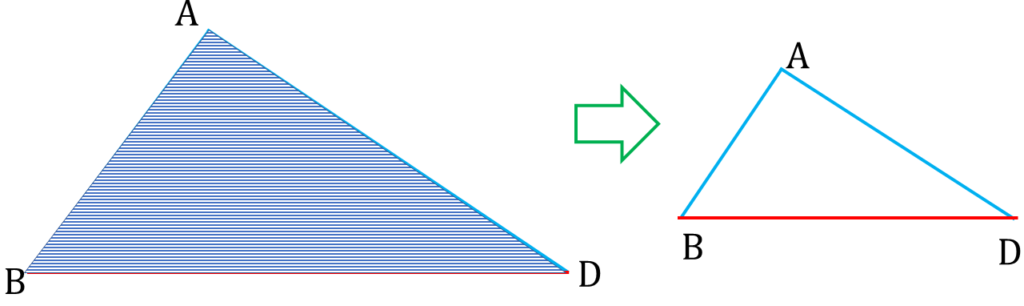
| ▲ABD থেকে পাই, |
|---|
| ∠ABD + ∠BAD + ∠ADB = 180° |
| বা, ∠ABC + ∠CBD + ∠BAD + ∠ADC + ∠CDB = 180° [ ∵ ∠ABD = ∠ABC + ∠CBD, ∠ADB = ∠ADC + ∠CDB ] |
| বা, 40° + ∠CBD + 60° + 20° + ∠CDB = 180° |
| বা, ∠CBD + ∠CDB = 180° – 40° – 60° – 20° |
| বা, ∠CBD + ∠CDB = 60° —-( ii ) |
| ( i ) ও ( ii ) থেকে পাই, |
|---|
| ∠CBD + ∠BCD + ∠BDC = 180° |
| বা, ∠BCD + ∠CBD + ∠CDB =180° |
| বা, ∠BCD + 60° = 180° |
| বা, ∠BCD = 180° – 60° |
| বা, ∠BCD = 120° |
| অতএব x = 120° |


( ii )
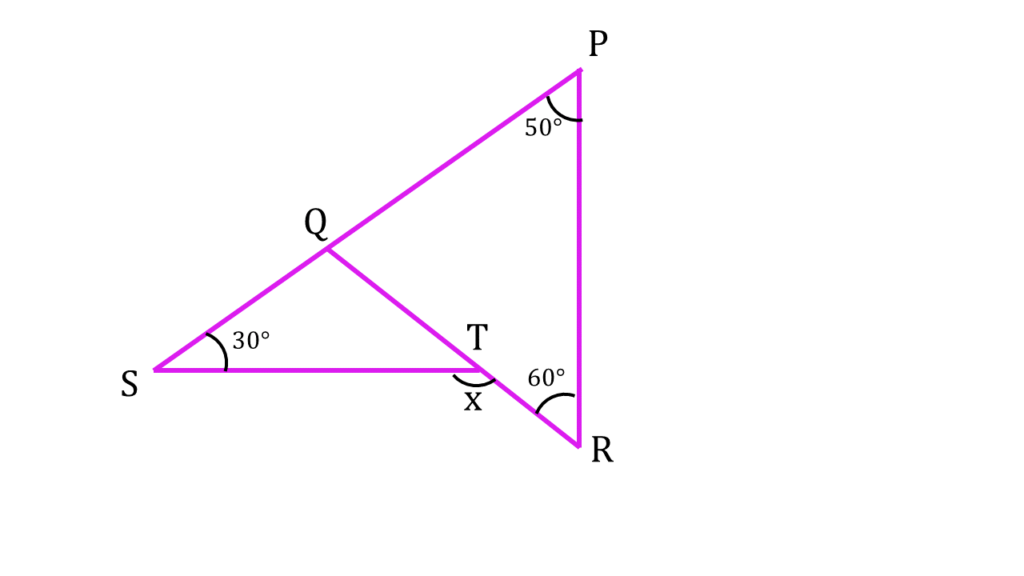
সমাধানঃ-
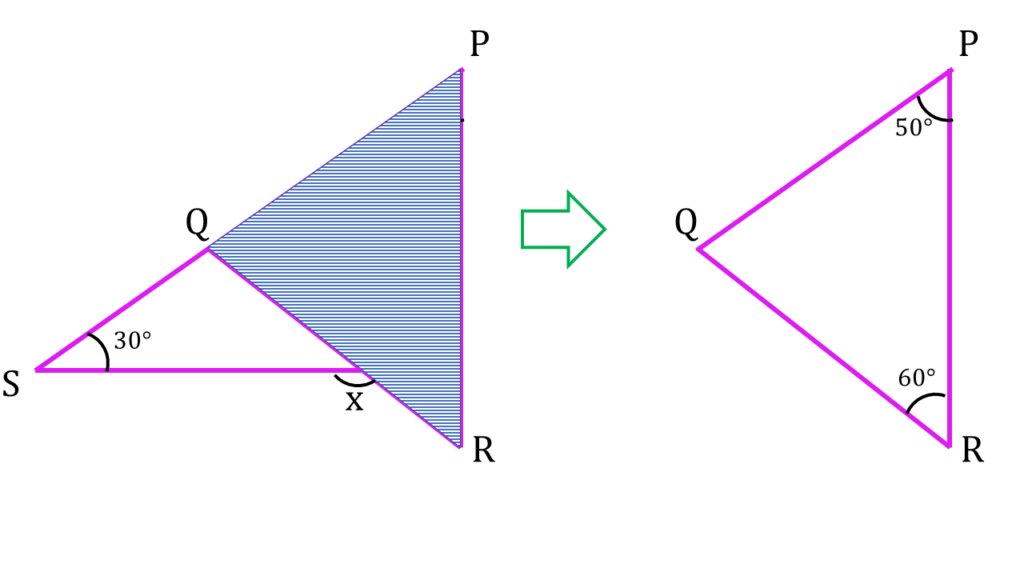
| ▲PQR থেকে পাই, |
|---|
| ∠QPR + ∠PRQ + ∠PQR = 180° |
| বা, 50° + 60° + ∠PQR = 180° |
| বা, ∠PQR = 180° – 60° – 50° |
| বা, ∠PQR = 180° – 110° |
| বা, ∠PQR = 70° —-( i ) |
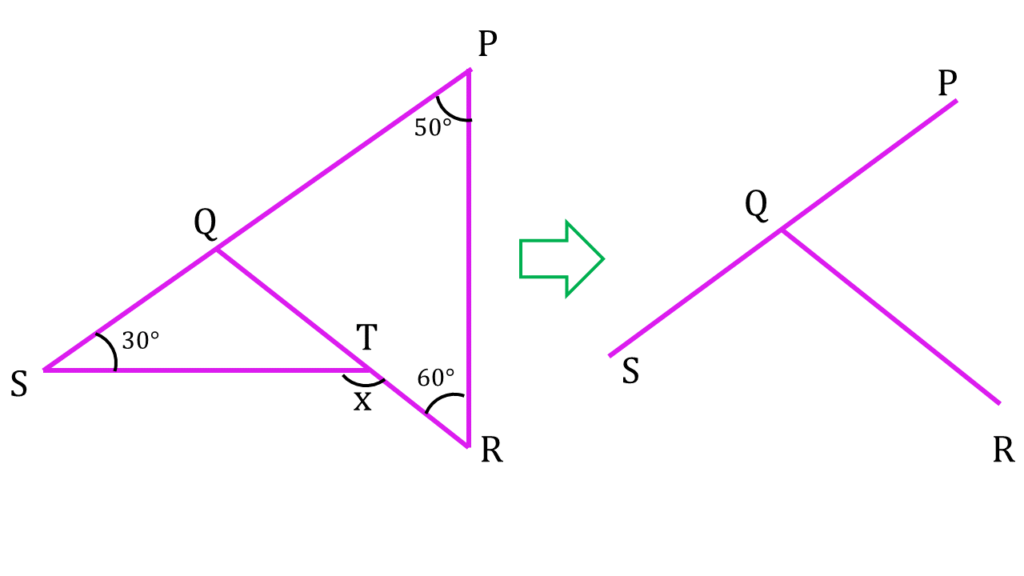
| সরলরেখা PS থেকে পাই, |
|---|
| ∠PQR + ∠SQR = 180° |
| ( i ) নম্বর থেকে ∠PQR এর মান বসিয়ে পাই, |
| ∠PQR + ∠SQR = 180° |
| বা, 70° + ∠SQR = 180° |
| বা, ∠SQR = 180° – 70° |
| বা, ∠SQR = 110° |
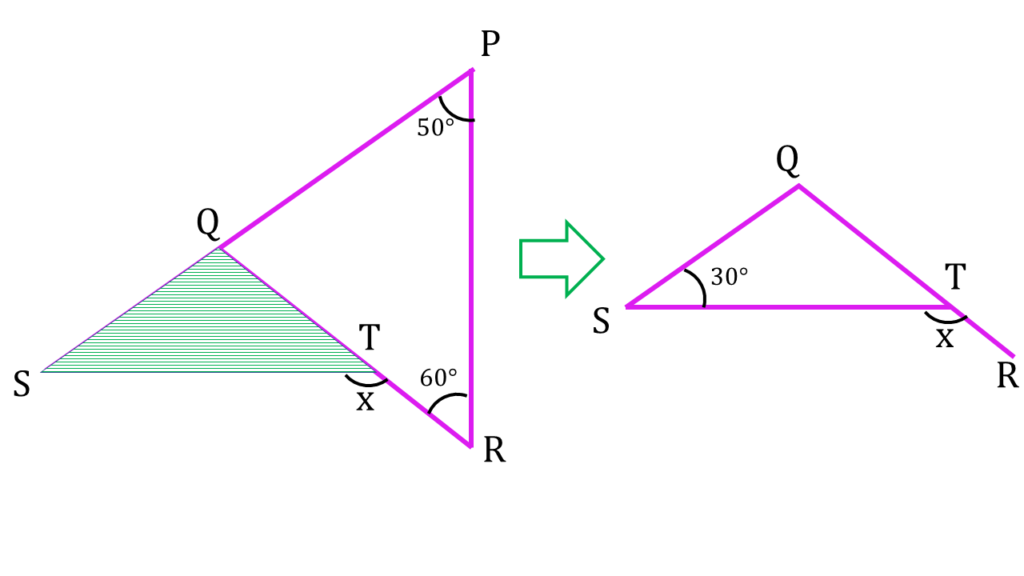
চিত্রে আমরা দেখতে পাচ্ছি,
▲SQT তে ∠QTS এর বহিঃস্থ ∠STR=x°
অতএব,
x°=∠STR = ∠QST + ∠SQT
বা, ∠STR = 30° + 110°
বা, ∠STR = 140°
| অতএব x = 140° |
( iii )
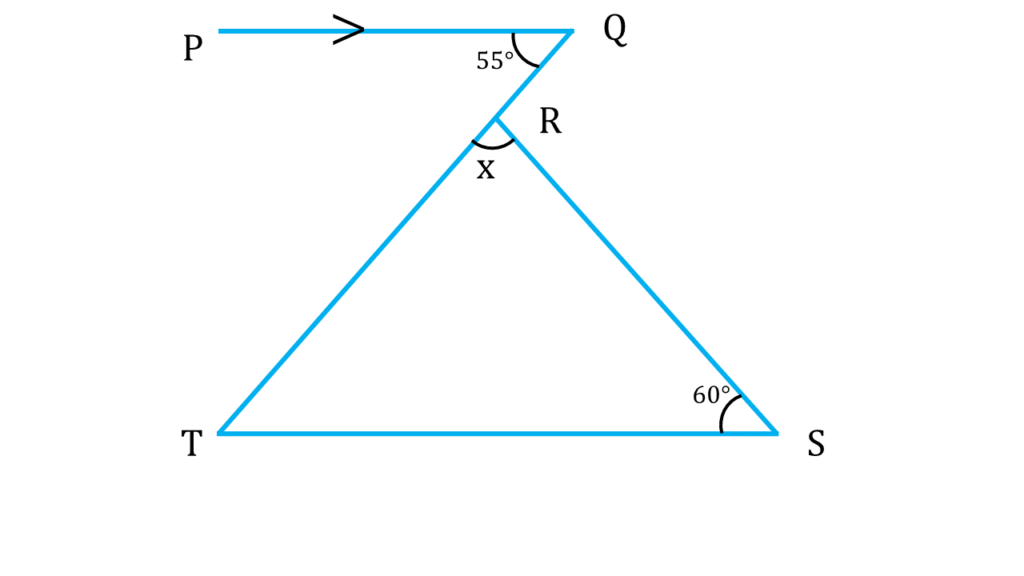
সমাধানঃ-
চিত্রে PQ||TS এবং TQ ছেদক
অতএব,
∠PQT = একান্তর ∠QTS
বা, ∠QTS = 55°
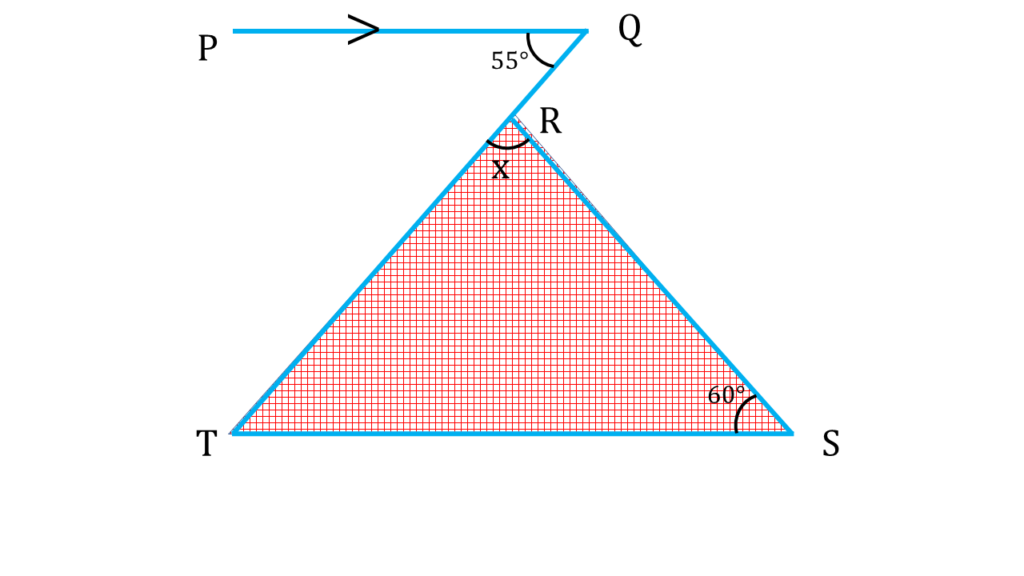
| ▲TRS থেকে পাই, |
|---|
| ∠TRS + ∠RTS + ∠RST = 180° |
| বা, ∠TRS + 55° + 60° = 180° |
| বা, ∠TRS = 180° – 60° – 55° |
| বা, ∠TRS = 180° – 115° |
| বা, ∠TRS = 65° |
| অতএব x = 65° |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |

2. পাশের চিত্রে ▲EHG এর কোণগুলির পরিমাপ লিখি।
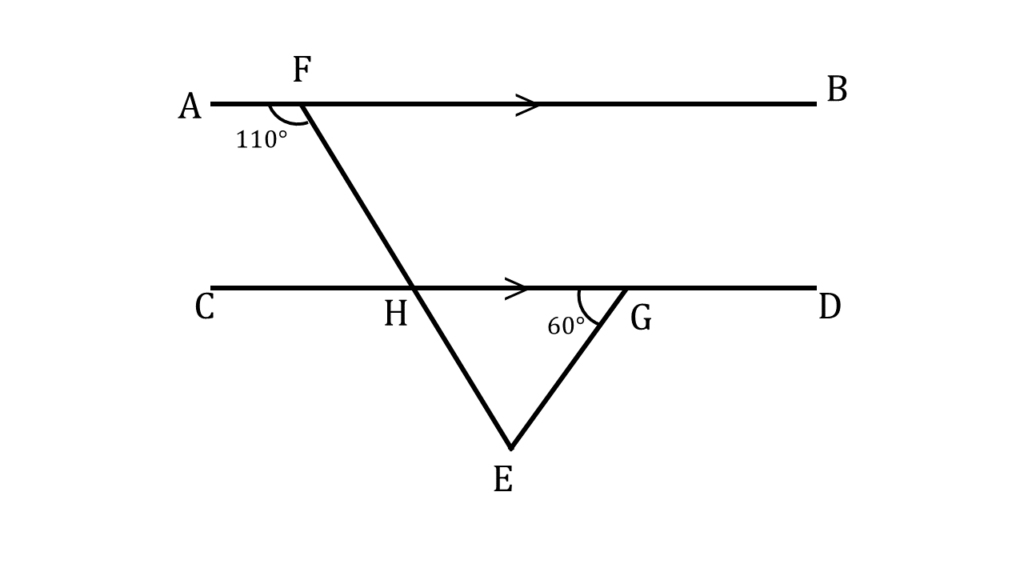
সমাধানঃ-
চিত্রে আমরা দেখতে পাচ্ছি,
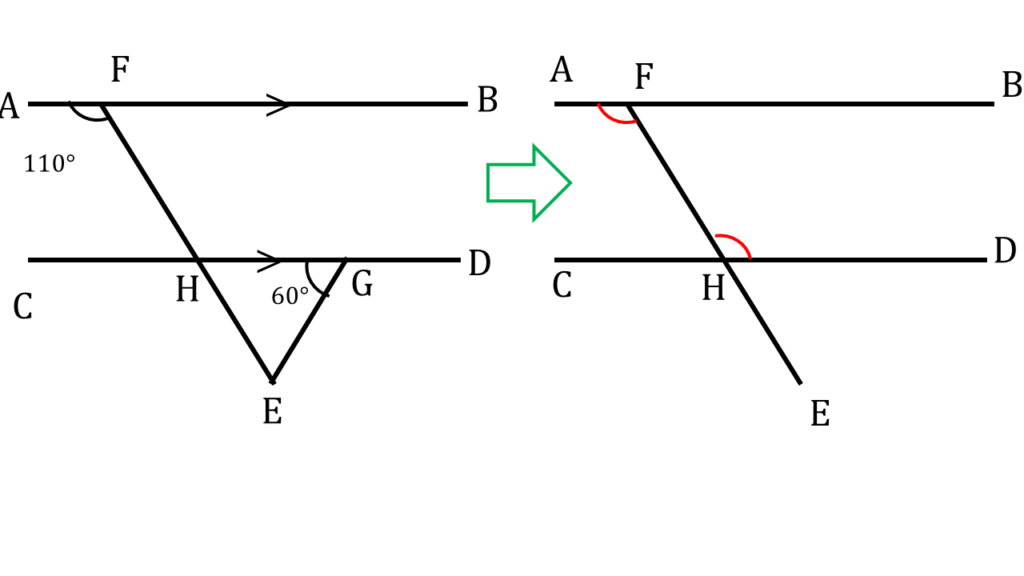
AB||CD এবং FH ছেদক
অতএব,
∠AFH = একান্তর ∠FHD
বা, ∠FHD = 110° —( i )
আবার,
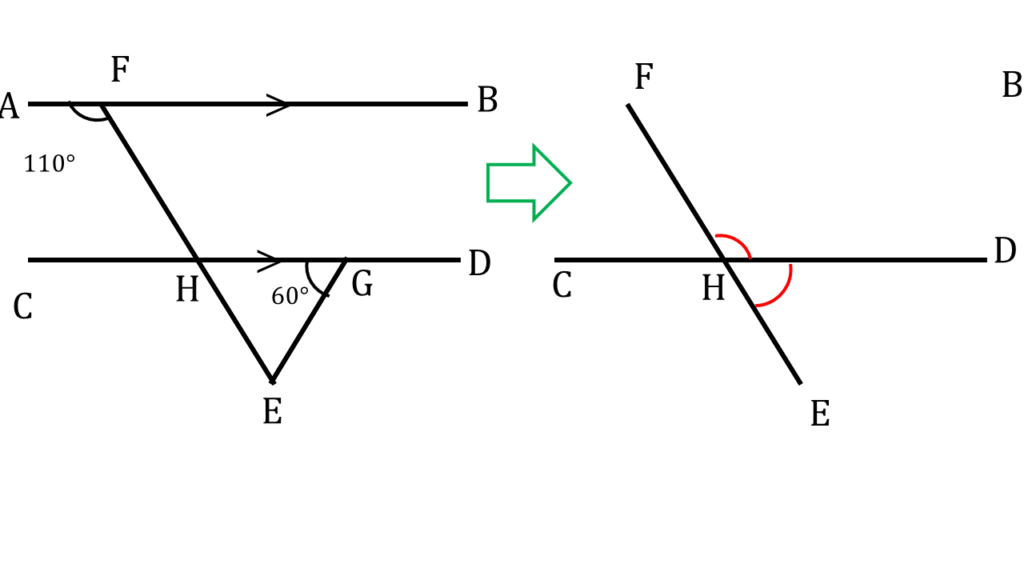
| সরলরেখা FE থেকে পাই, |
|---|
| ∠FHD + ∠EHD = 180° |
| ( i ) নম্বর থেকে ∠FHD এর মান বসিয়ে পাই, |
| ∠FHD + ∠EHD = 180° |
| বা, 110° + ∠EHD = 180° |
| বা, ∠EHD = 180° – 110° |
| বা, ∠EHD= 70° |
আবার,
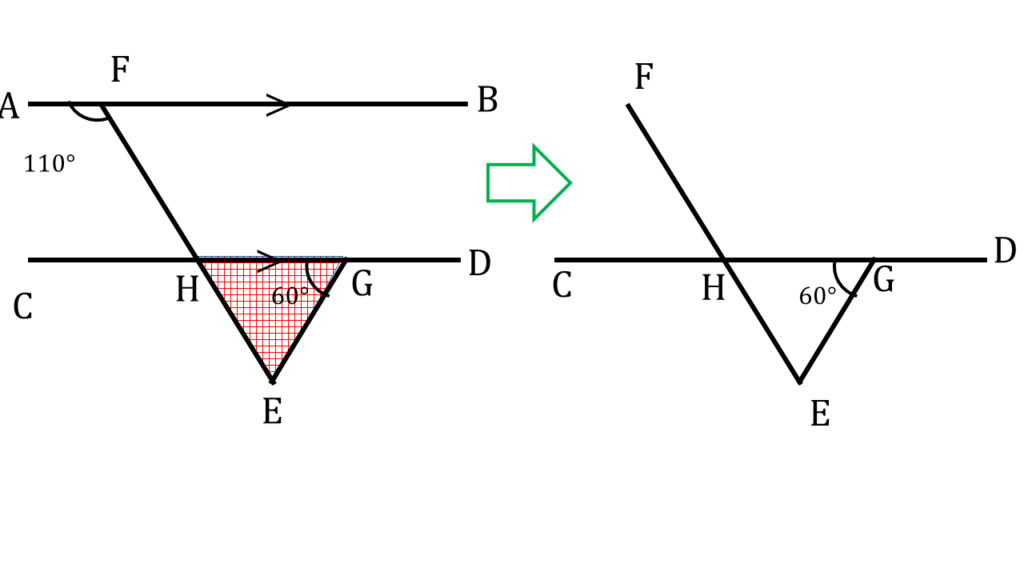
| ▲EHG থেকে পাই, |
|---|
| ∠HEG + ∠EGH + ∠GHE = 180° |
| বা, ∠HEG + 60° + 70° = 180° |
| বা, ∠HEG = 180° – 60° – 70° |
| বা, ∠HEG = 180° – 130° |
| বা, ∠HEG = 50° |
| ∠EHG= 70° ∠HEG = 50° |
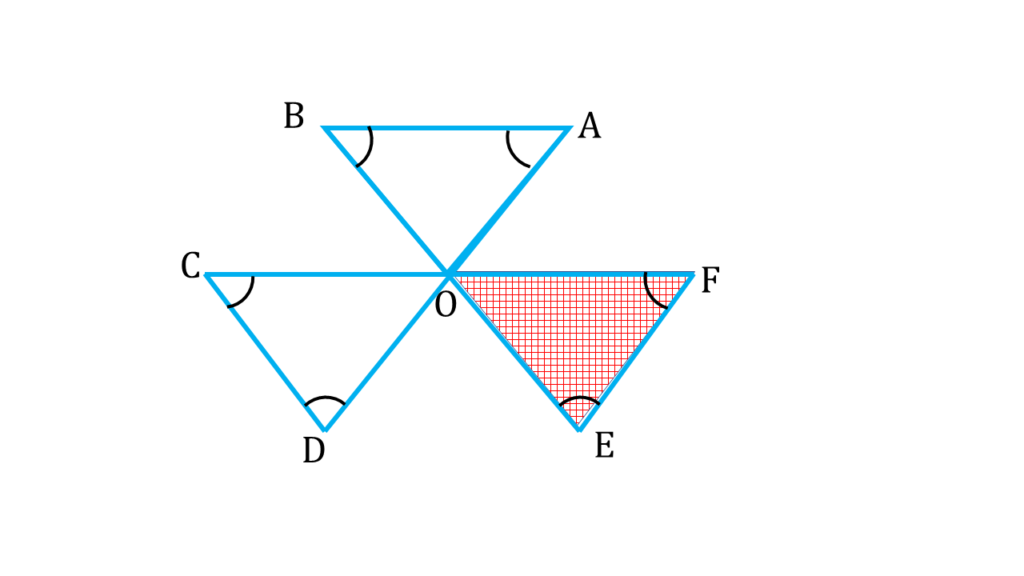
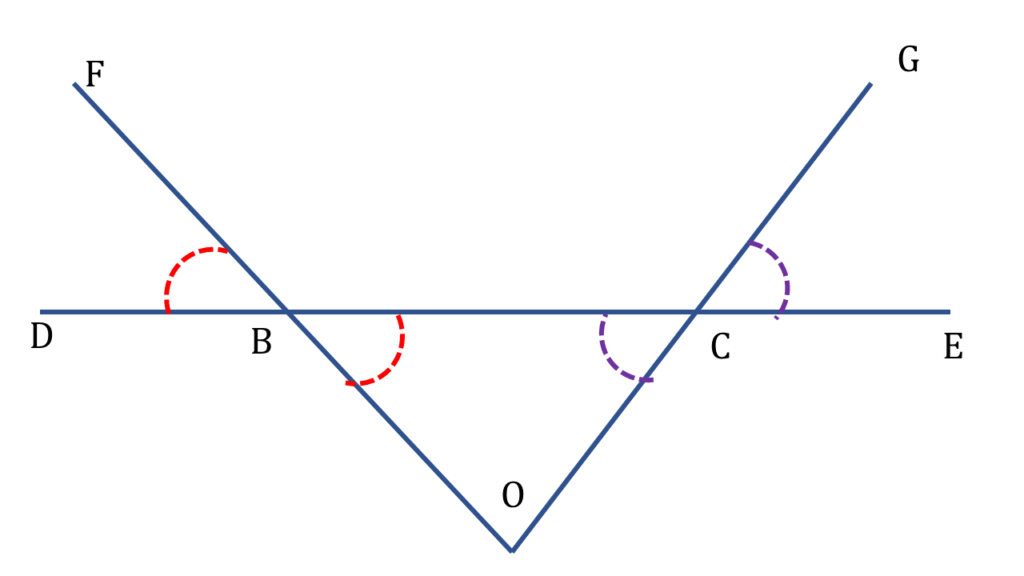
3. পাশের চিত্রে ∠A + ∠B + ∠C + ∠D + ∠E + ∠F এর পরিমাপ লিখি।
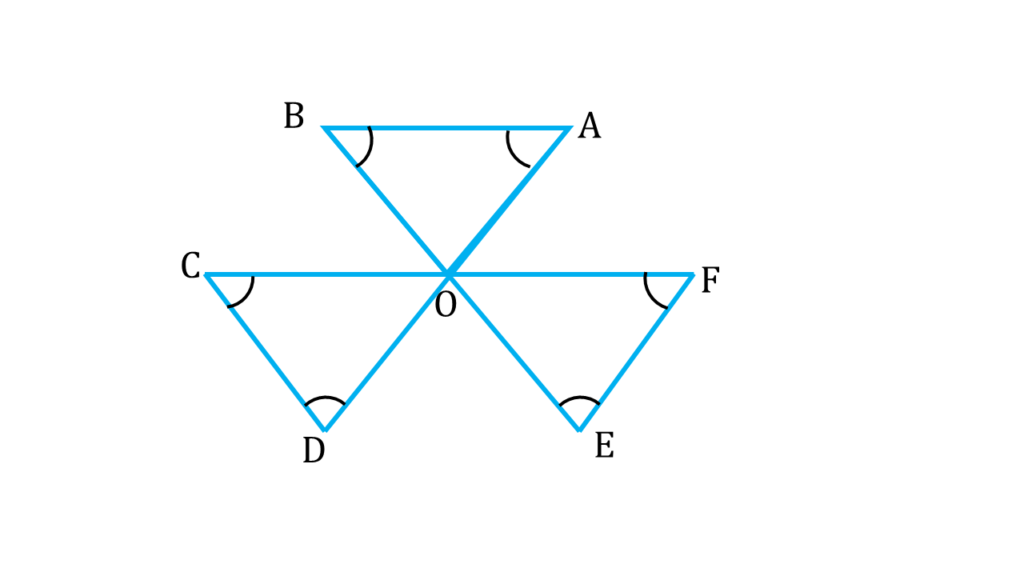
সমাধানঃ-
চিত্রে আমরা দেখতে পাচ্ছি
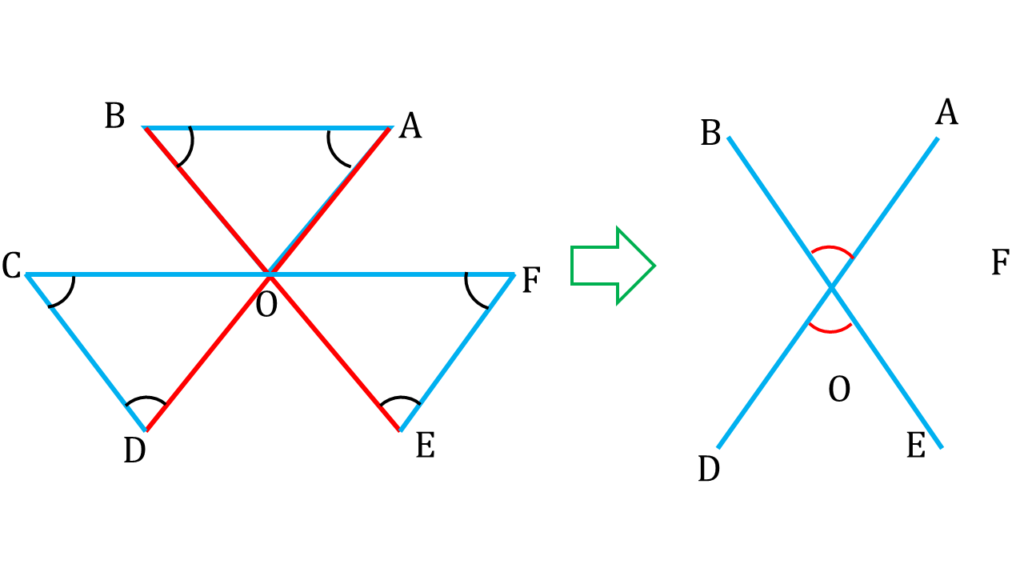
AD ও BE সরলরেখা পরস্পরকে O বিন্দুতে ছেদ করেছে।
অতএব,
∠AOB = বিপ্রতীপ ∠DOE
আবার,
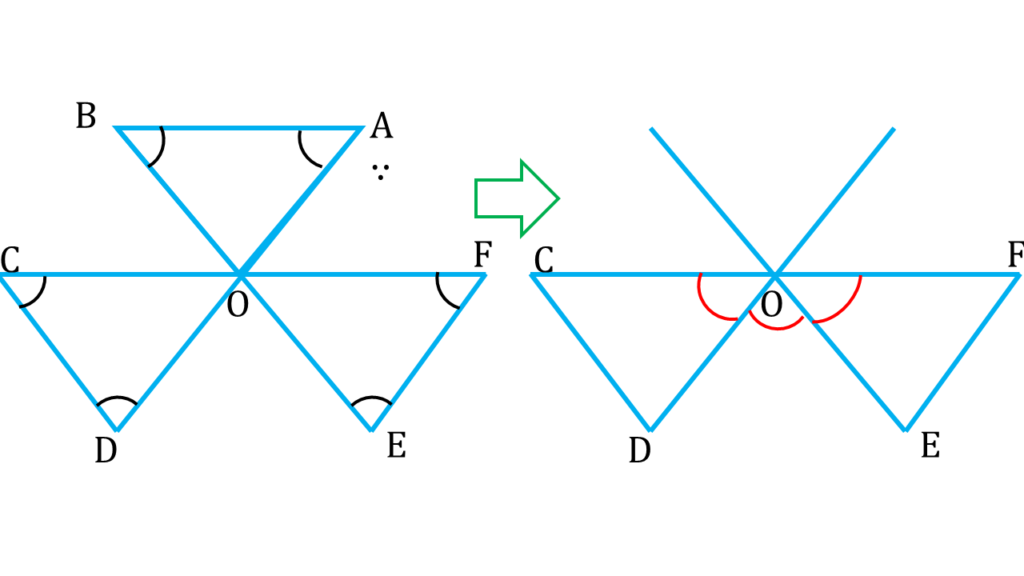
| সরলরেখা CF থেকে পাই, |
|---|
| ∠COD + ∠DOE + ∠EOF = 180° |
| বা, ∠COD + ∠AOB + ∠EOF = 180° –( i ) [ ∵ ∠AOB = বিপ্রতীপ ∠DOE ] |
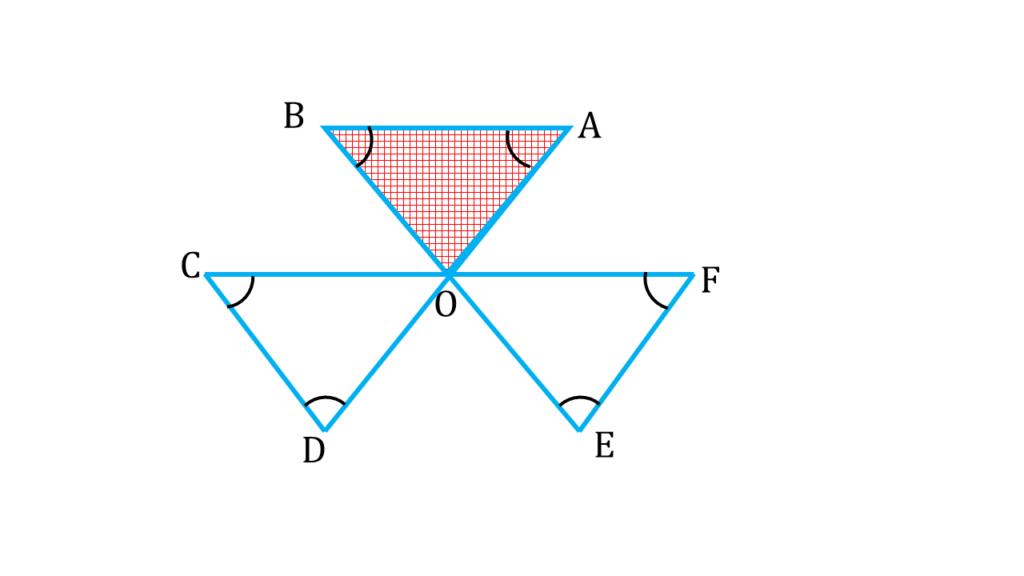
| ▲AOB থেকে পাই, |
|---|
| ∠OBA+ ∠BAO + ∠AOB = 180° ——-( ii ) |
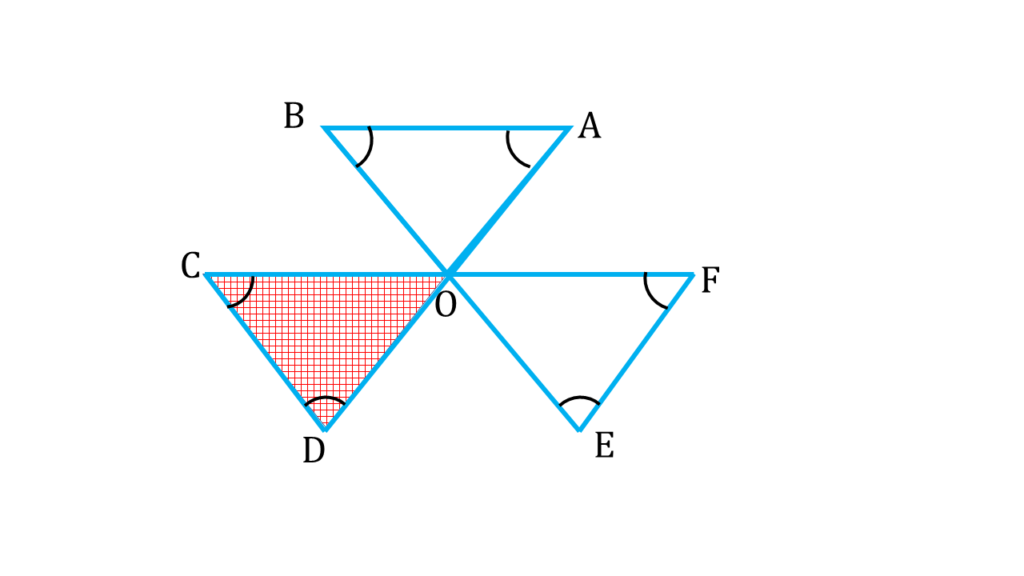
| ▲COD থেকে পাই, |
|---|
| ∠OCD+ ∠CDO + ∠DOC = 180° ——-( iii ) |
| ▲EOF থেকে পাই, |
|---|
| ∠OEF+ ∠EFO + ∠FOE = 180° ——-( iv ) |
( ii ), ( iii ) ও ( iv ) যোগ করে পাই,
| ∠OBA+ ∠BAO + ∠AOB + ∠OCD+ ∠CDO + ∠DOC + ∠OEF+ ∠EFO + ∠FOE = 180° + 180° + 180° |
| বা, ∠OBA+ ∠BAO + ∠OCD+ ∠CDO + ∠OEF+ ∠EFO + ∠COD + ∠AOB + ∠EOF = 540° |
| বা, ∠OBA+ ∠BAO + ∠OCD+ ∠CDO + ∠OEF+ ∠EFO + ∠COD + ∠AOB + ∠EOF = 540° |
| ( i ) নং থেকে ∠COD + ∠AOB + ∠EOF এর মান বসিয়ে পাই, |
| ∠OBA+ ∠BAO + ∠OCD+ ∠CDO + ∠OEF+ ∠EFO + ∠COD + ∠AOB + ∠EOF = 540° |
| বা, ∠OBA+ ∠BAO + ∠OCD+ ∠CDO + ∠OEF+ ∠EFO + 180° = 540° |
| বা, ∠OBA+ ∠BAO + ∠OCD+ ∠CDO + ∠OEF+ ∠EFO = 540° – 180° |
| বা, ∠B + ∠A + ∠C + ∠D + ∠E + ∠F = 360° |
| বা, ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 360° |
| ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 360° |

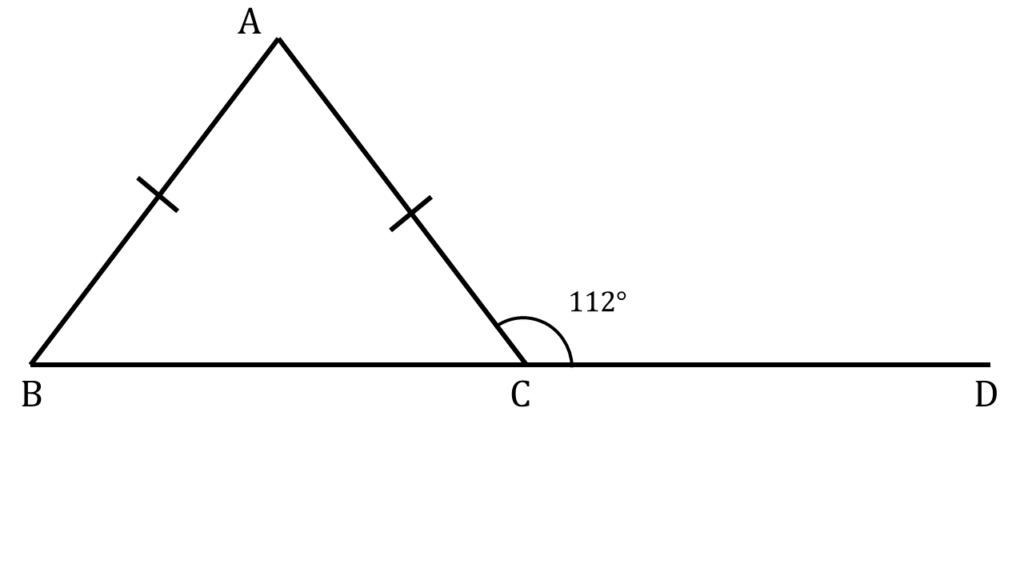
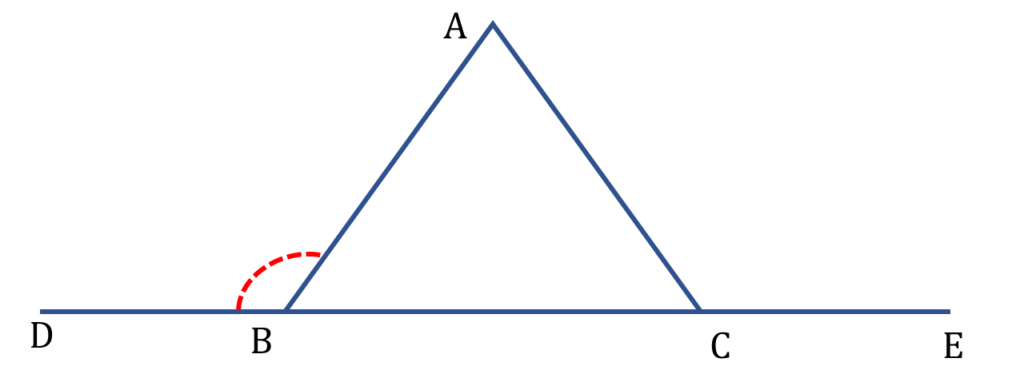
4. AB = AC হলে ∠ABC, ∠ACB, ∠BAC -এর পরিমাপ লিখি।
সমাধানঃ-
দেওয়া আছে,
AB = AC
অতএব,
∠ABC = ∠ACB — ( i )
আবার,
| সরলরেখা BD থেকে পাই, |
|---|
| ∠BCA + ∠ACD = 180° |
| বা, ∠ACB + 112° = 180° |
| বা, ∠ACB = 180° – 112° |
| বা, ∠ACB = 68° |
( i ) নং থেকে পাই,
∠ABC = ∠ACB
বা, ∠ABC = 68°
আবার,
| ▲ABC থেকে পাই, |
|---|
| ∠ABC + ∠ACB + ∠BAC = 180° |
| বা, 68° + 68° + ∠BAC = 180° |
| বা, ∠BAC = 180° – 68° – 68° |
| বা, ∠BAC = 180° – 136° |
| বা, ∠BAC = 44° |
| ∠ACB = 68° ∠ABC = 68° ∠BAC = 44° |

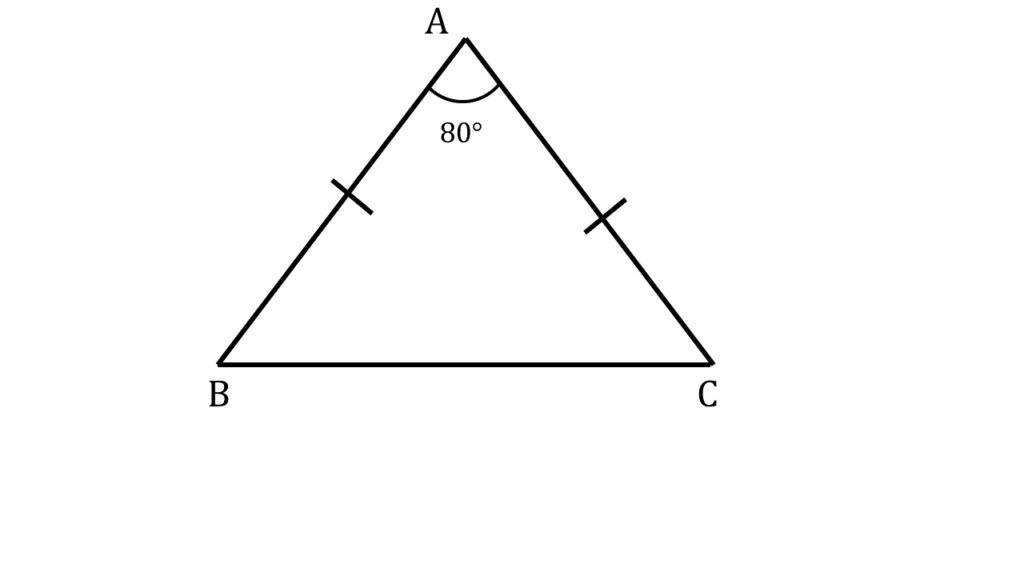
5. AB = AC হলে ∠ABC ও ∠ACB -এর পরিমাপ লিখি।
সমাধানঃ-
| দেওয়া আছে, |
|---|
| AB = AC |
| এবং |
| ∠BAC = 80° |
অতএব,
∠ABC = ∠ACB [ ∵ AB = AC ]
আবার,
| ▲ABC থেকে পাই, |
|---|
| ∠ABC + ∠ACB + ∠BAC = 180° |
| বা, ∠ABC + ∠ABC + 80° = 180° |
| বা, 2∠ABC= 180° – 80° |
| বা, 2∠ABC = 100° |
| বা, ∠ABC = 100°/2 |
| বা, ∠ABC = 50° |
| বা, ∠ABC = 50° |
| অতএব , ∠ABC = ∠ACB = 50° |
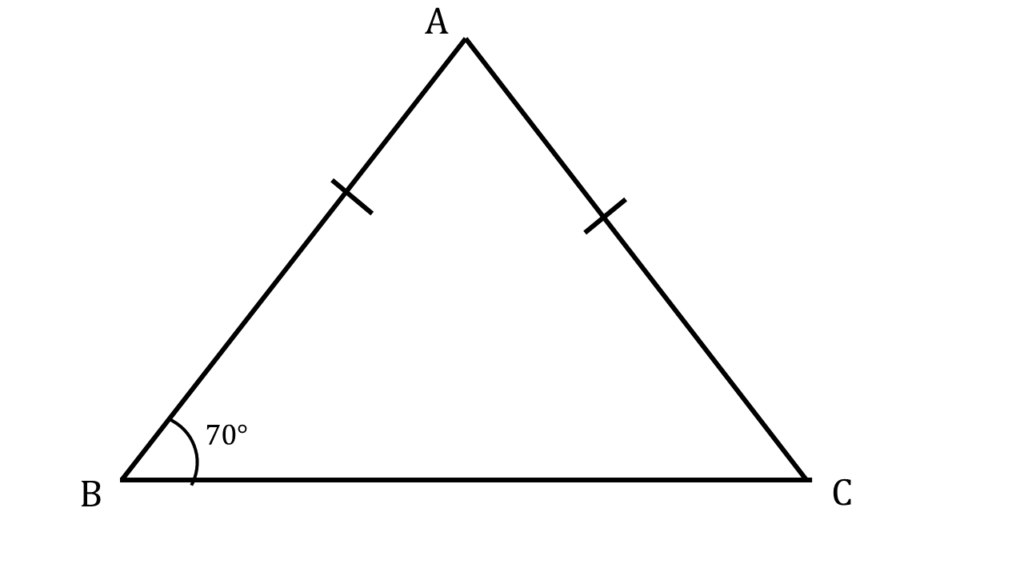
6. AB = AC হলে ∠ACB ও ∠BAC -এর পরিমাপ লিখি।
সমাধানঃ-
| দেওয়া আছে, |
|---|
| AB = AC |
| এবং |
| ∠ABC = 70° |
অতএব,
∠ABC = ∠ACB [ ∵ AB = AC ]
বা, ∠ABC = ∠ACB = 70°
আবার,
| ▲ABC থেকে পাই, |
|---|
| ∠ABC + ∠ACB + ∠BAC = 180° |
| বা, ∠ABC + ∠ABC + ∠BAC = 180° |
| বা, 2∠ABC + ∠BAC = 180° |
| বা, 2×70° + ∠BAC = 180° |
| বা, ∠BAC = 180° – 140° |
| বা, ∠BAC = 40° |
| বা, ∠BAC = 40° |
| ∠ACB= 70° ∠BAC = 40° |

7. AB = AC এবং ∠BAC + ∠ACB = 50° ; ▲ABC -এর কোণগুলির পরিমাপ লিখি।
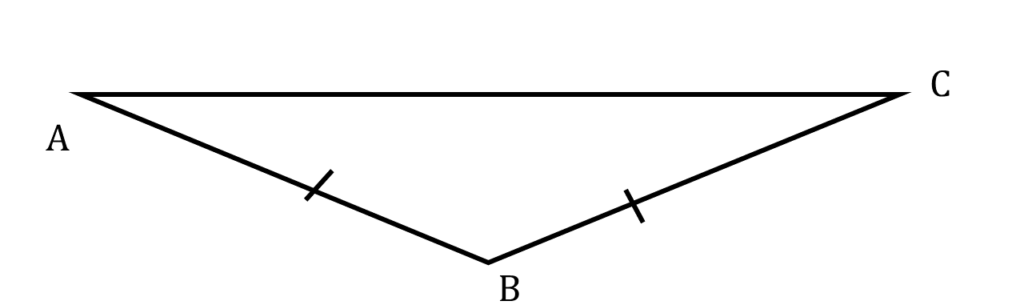
সমাধানঃ-
| দেওয়া আছে, | |
|---|---|
| AB = AC অতএব, ∠BAC = ∠ACB | |
| এবং | |
| ∠BAC + ∠ACB = 50° বা, ∠ACB + ∠ACB = 50° বা, 2∠ACB = 50° বা, ∠ACB = 25° |
অতএব,
আমরা পেলাম ∠BAC = ∠ACB = 25°
আবার,
| ▲ABC থেকে পাই, |
|---|
| ∠ABC + ∠ACB + ∠BAC = 180° |
| বা, ∠ABC + ∠ACB + ∠ACB = 180° [ ∵ ∠BAC = ∠ACB ] |
| বা, ∠ABC + 2∠ACB = 180° |
| বা, ∠ABC + 2×25° = 180° |
| বা, ∠ABC= 180° – 50° |
| বা, ∠ABC= 130° |
| বা, ∠ABC= 130° |
| ∠ABC= 130° ∠BAC = ∠ACB = 25° |
8. ▲ABC এর অন্তঃস্থ একটি বিন্দু O; প্রমাণ করি যে ∠BOC > ∠BAC
সমাধানঃ-
প্রদত্তঃ
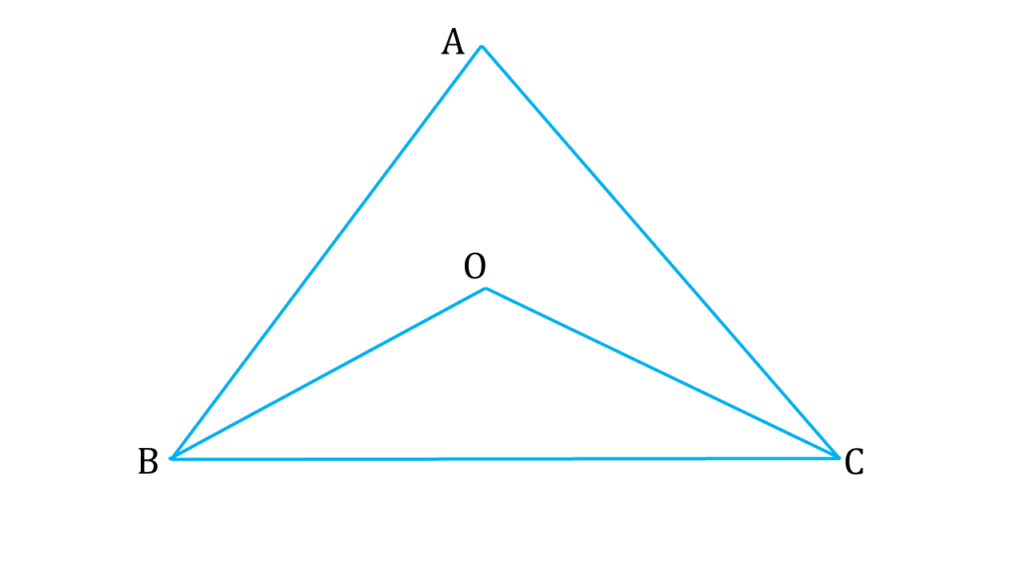
| ▲ABC এর |
|---|
| ∠ABC = ∠ABO + ∠OBC —— ( i ) |
| এবং |
| ∠ACB = ∠ACO + ∠OCB ——- ( ii ) |
প্রামাণ্যঃ প্রমান করতে হবে ∠BOC > ∠BAC ।
প্রমাণঃ
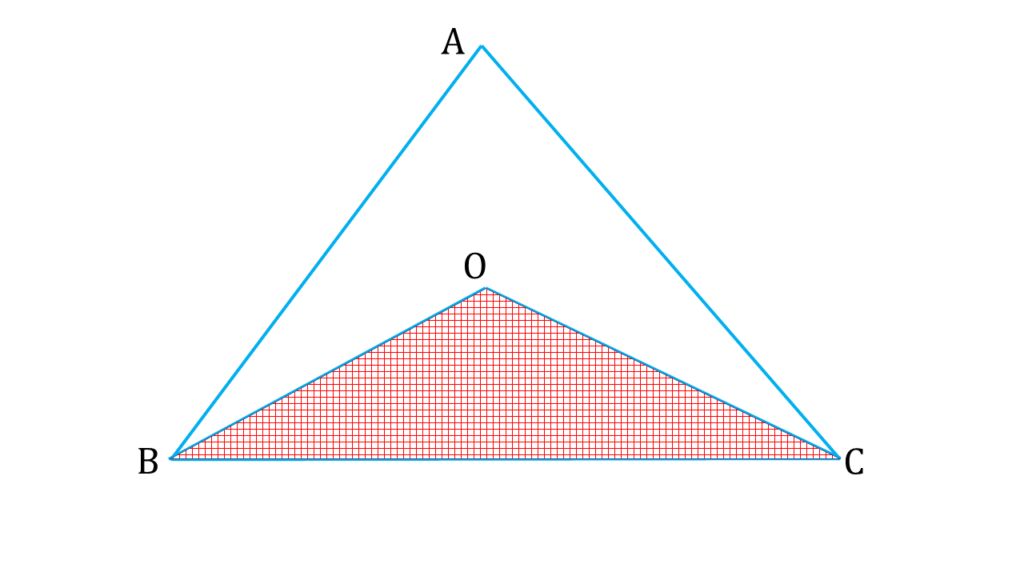
| ▲BOC থেকে পাই, |
|---|
| ∠OBC + ∠BCO + ∠BOC = 180° |
| বা, ∠BOC = 180° – (∠OBC + ∠BCO) —- ( iii ) |
আবার,
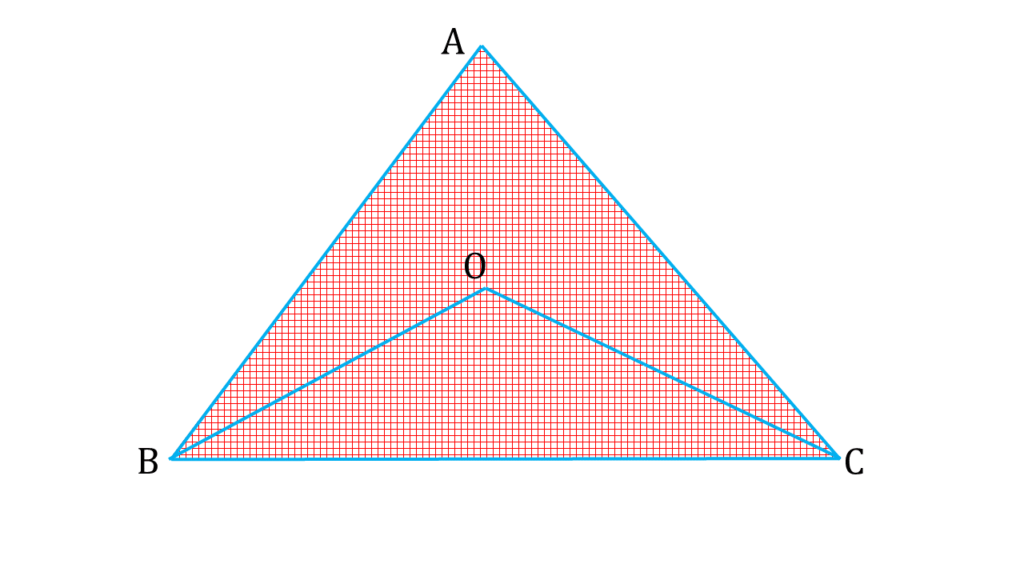
| ▲ABC থেকে পাই, |
|---|
| ∠ABC + ∠ACB + ∠BAC = 180° |
| ( i ) ও ( ii ) নং থেকে ∠ABC ও ∠ACB এর মান বসিয়ে পাই, |
| ∠ABO + ∠OBC + ∠ACO + ∠OCB + ∠BAC = 180° |
| বা, ∠ABO + ∠ACO + ∠BAC = 180° – (∠OBC + ∠BCO) |
| বা, ∠BAC + ∠ABO + ∠ACO = ∠BOC [ ∵∠BOC = 180° – (∠OBC + ∠BCO) ] |
| অতএব, ∠BOC > ∠BAC [ ∵ ∠ABO + ∠ACO ≠ 0 ] |
| অতএব ∠BOC > ∠BAC প্রমানিত। |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
9. প্রমাণ করি যে ▲ABC -এর BC বাহুকে উভয়দিকে বাড়ালে যে দুটি বহিঃকোণ উৎপন্ন হয় তাদের সমষ্টি 2 সমকোণের বেশি।
সমাধানঃ-
▲ABC এর BC বাহুকে উভয় দিকে যথাক্রমে D ও E বিন্দু পর্যন্ত বাড়ালাম।
এর ফলে ∠ABD ও ∠ACE দুটি বহিঃকোন উৎপন্ন হয়েছে।
প্রমাণ করতে হবে,
∠ABD + ∠ACE > 180°
| ▲ABC এর ∠ACB এর বহিঃকোণ ∠ACE |
|---|
| অতএব, |
| ∠ACE = ∠BAC + ∠ABC —– ( i ) |
আবার,
| ▲ABC এর ∠ABC এর বহিঃকোণ ∠ABD |
|---|
| অতএব, |
| ∠ABD = ∠BAC + ∠BCA —– ( ii ) |
( i ) ও ( ii ) নং যোগ করে পাই,
| ∠ACE + ∠ABD = ∠BAC + ∠ABC + ∠BAC + ∠BCA |
| বা, ∠ACE + ∠ABD = ∠BAC + ∠ABC + ∠BCA + ∠BAC |
| বা, ∠ACE + ∠ABD = ∠BAC + 180° [ ∵ ▲ ABC এর তিনটি কোণ ∠BAC, ∠ABC ও ∠BCA এর সমষ্টি 180° ] |
| বা, ∠ACE + ∠ABD > 180° [ ∵ ∠BAC ≠ 0 ] |
| অতএব ▲ABC -এর BC বাহুকে উভয়দিকে বাড়ালে যে দুটি বহিঃকোণ উৎপন্ন হয় তাদের সমষ্টি 2 সমকোণের বেশি প্রমানিত। |

10. ▲ABC এর কৌনিক বিন্দু A ও C দিয়ে যথাক্রমে BC ও BA বাহুর সমান্তরাল সরলরেখাংশ D বিন্দুতে মিলিত হয়। প্রমাণ করি যে, ∠ABC = ∠ADC
সমাধানঃ-
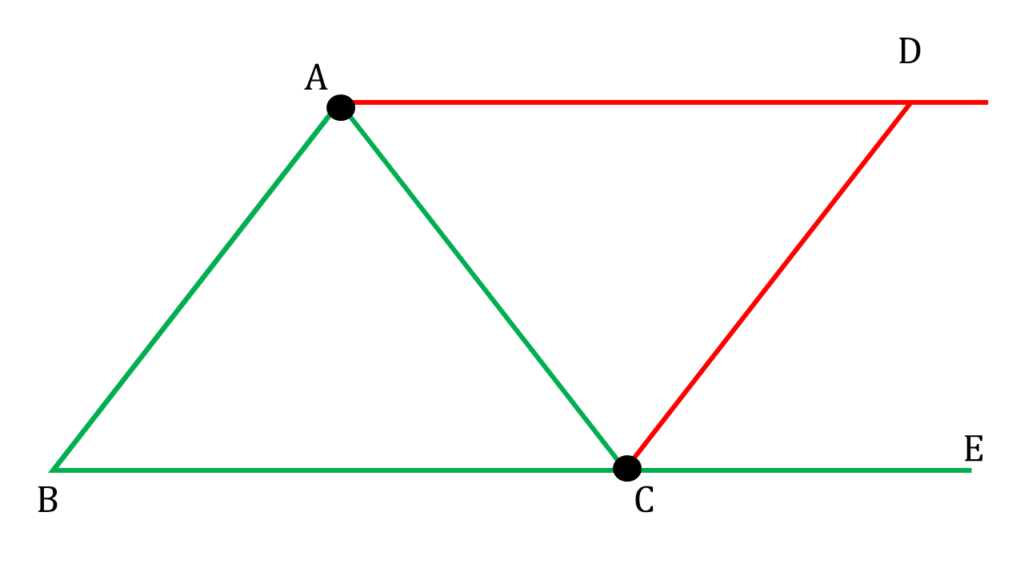
▲ABC এর কৌনিক বিন্দু A ও C দিয়ে যথাক্রমে BC ও BA বাহুর সমান্তরাল সরলরেখাংশ D বিন্দুতে মিলিত হয়েছে এবং BC বাহুকে E পর্যন্ত বর্ধিত করা হয়েছে।
সুতরাং,
| AD||BE এবং DC ছেদক |
|---|
| অতএব, |
| ∠ADC = একান্তর ∠DCE ——( i ) |
এবং
| AB||CD এবং ছেদক AC |
|---|
| অতএব, |
| ∠BAC = একান্তর ∠ACD —– ( ii ) |
প্রমাণ করতে হবে,
∠ABC = ∠ADC
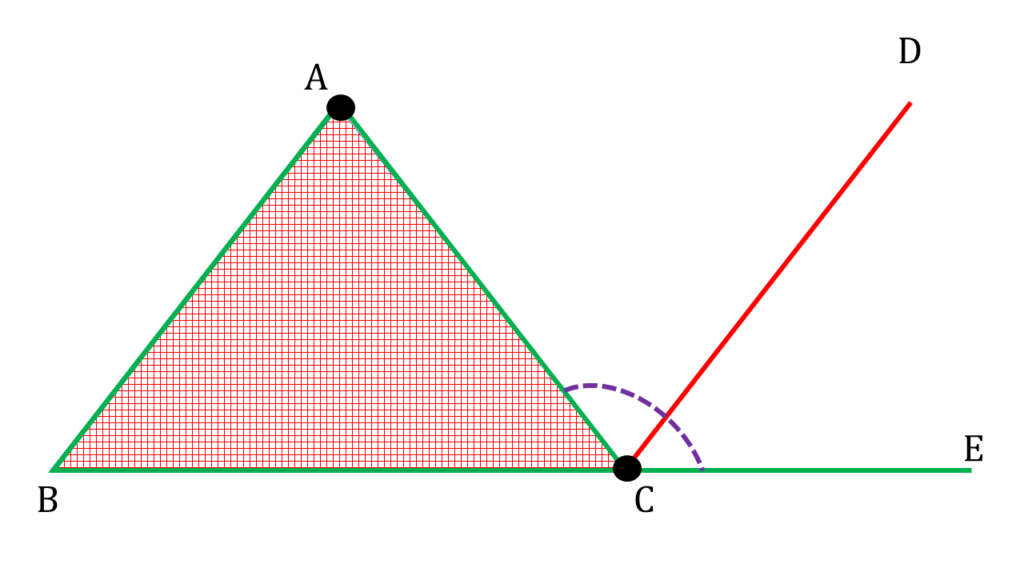
| ▲ABC এর ∠ACB এর বহিঃকোণ ∠ACE |
|---|
| অতএব, |
| ∠ACE = ∠BAC + ∠ABC |
| বা, ∠ACD + ∠DCE = ∠BAC + ∠ABC |
| বা, ∠BAC + ∠ADC = ∠BAC + ∠ABC [ ∵ ∠BAC = একান্তর ∠ACD এবং ∠ADC = একান্তর ∠DCE ] |
| বা, ∠ABC = ∠ADC |
| অতএব ∠ABC = ∠ADC প্রমানিত । |
11. ▲ABC এর ∠ABC ও ∠ACB এর অন্তঃসমদ্বিখণ্ডকদ্বয় O বিন্দুতে মিলিত হয়। প্রমাণ করি যে, ∠BOC = 90° + ½∠BAC
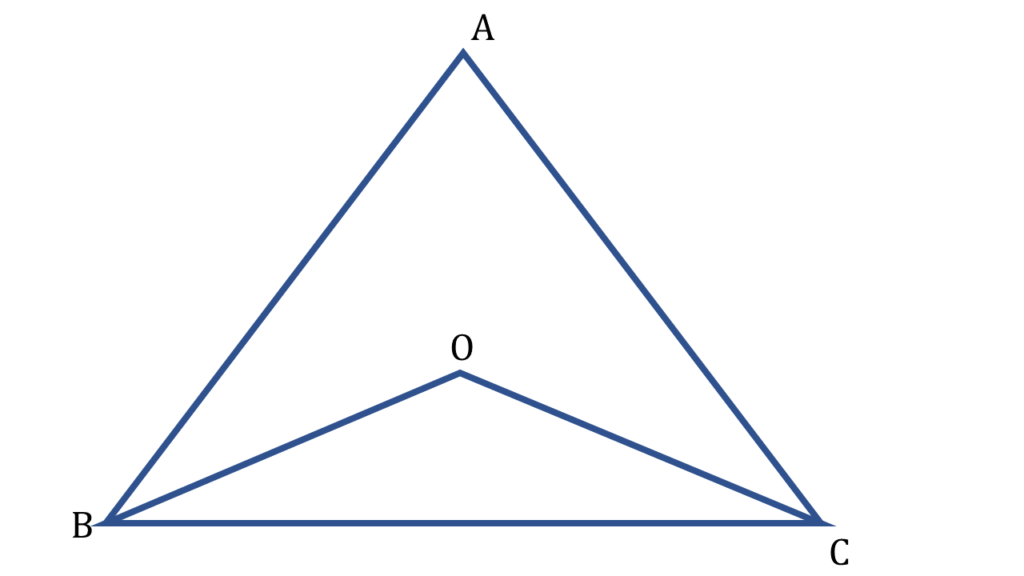
সমাধানঃ-
▲ABC এর ∠ABC ও ∠ACB এর অন্তঃসমদ্বিখণ্ডকদ্বয় O বিন্দুতে মিলিত হয়।
অতএব,
∠ACB = 2∠OCB — ( i )
এবং
∠ABC = 2∠OBC — ( ii )
| ▲ABC থেকে পাই, |
|---|
| ∠ABC + ∠ACB + ∠BAC = 180° |
| ( i ) ও ( ii ) নং থেকে ∠ABC ও ∠ACB এর মান বসিয়ে পাই, |
| 2∠OBC + 2∠OCB + ∠BAC = 180° |
| বা, ∠BAC = 180° – 2 (∠OBC + ∠OCB ) |
| বা, ∠BAC = 2 { 90° – (∠OBC + ∠OCB)} |
| বা, ½∠BAC = 90° – (∠OBC + ∠OCB) ——( iii ) |
আবার,
| ▲BOC থেকে পাই, |
|---|
| ∠OBC + ∠OCB + ∠BOC = 180° |
| বা, ∠BOC = 180° – (∠OBC + ∠OCB) |
| বা, ∠BOC = 90° + 90° – (∠OBC + ∠OCB) |
| ( iii ) নং থেকে 90° – (∠OBC + ∠OCB) এর মান বসিয়ে পাই, |
| ∠BOC = 90° + ½∠BAC |
| অতএব ∠BOC = 90° + ½∠BAC প্রমাণিত। |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |

12. ▲ABC এর ∠ABC ও ∠ACB এর বহিঃসমদ্বিখণ্ডকদ্বয় O বিন্দুতে মিলিত হয়। প্রমাণ করি যে, ∠BOC = 90° – ½ ∠BAC
সমাধানঃ-
প্রদত্তঃ
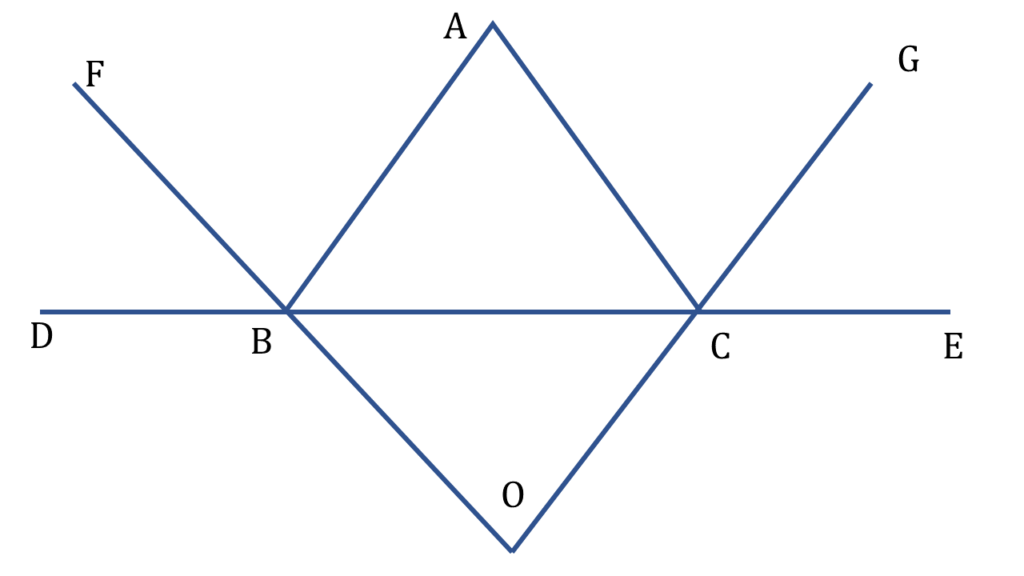
▲ABC এর ABC ও ACB এর বহিঃসমদ্বিখণ্ডকদ্বয় যথাক্রমে OF ও OG, O বিন্দুতে মিলিত হয়েছে এবং BC বাহুকে উভয়দিকে D এবং E বিন্দু পর্যন্ত বর্ধিত করা হয়েছে।
অতএব,
| ∠ACG = ∠GCE |
| ∠FBD = ∠ABF |
প্রামাণ্যঃ
প্রমাণ করতে হবে,
∠BOC = 90° – ½ ∠BAC
প্রমাণঃ
দেওয়া আছে,
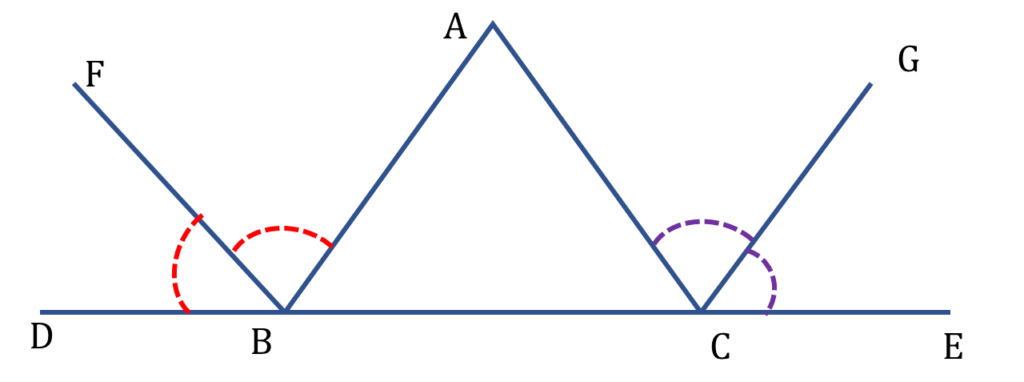
∠ACG = ∠GCE
এবং
∠FBD = ∠ABF
অতএব,
∠ACE = 2∠GCE —( i )
এবং
∠ABD = 2∠FBD — ( ii )
আবার,
| ▲ABC এর ∠ACB এর বহিঃ কোণ ∠ACE |
|---|
| অতএব, |
| ∠ACE = ∠ABC + ∠BAC |
| ( i ) নং থেকে ∠ACE = 2∠GCE বসিয়ে পাই, |
| 2∠GCE = ∠ABC + ∠BAC —– ( iii ) |
এবং
| ▲ABC এর ∠ABC এর বহিঃ কোণ ∠ABD |
|---|
| অতএব, |
| ∠ABD = ∠ACB + ∠BAC |
| ( ii ) নং থেকে ∠ABD = 2∠FBD বসিয়ে পাই, |
| 2∠FBD = ∠ACB + ∠BAC —– ( iv ) |
| OF ও OG সরলরেখা DE সরলরেখাকে যথাক্রমে B ও C বিন্দুতে ছেদ করেছে |
|---|
| সুতরাং |
| ∠GCE = বিপ্রতীপ ∠BCO |
| এবং |
| ∠FBD = বিপ্রতীপ ∠OBC |
| উপরের ∠GCE ও ∠FBD এর মান ( iii ) ও ( iv ) নং এ বসিয়ে পাই, |
|---|
| 2∠BCO = ∠ABC + ∠BAC বা, ∠BCO = ½(∠ABC + ∠BAC) —– ( v ) |
| এবং |
| 2∠OBC = ∠ACB + ∠BAC বা, ∠OBC = ½(∠ACB + ∠BAC) —-( vi ) |
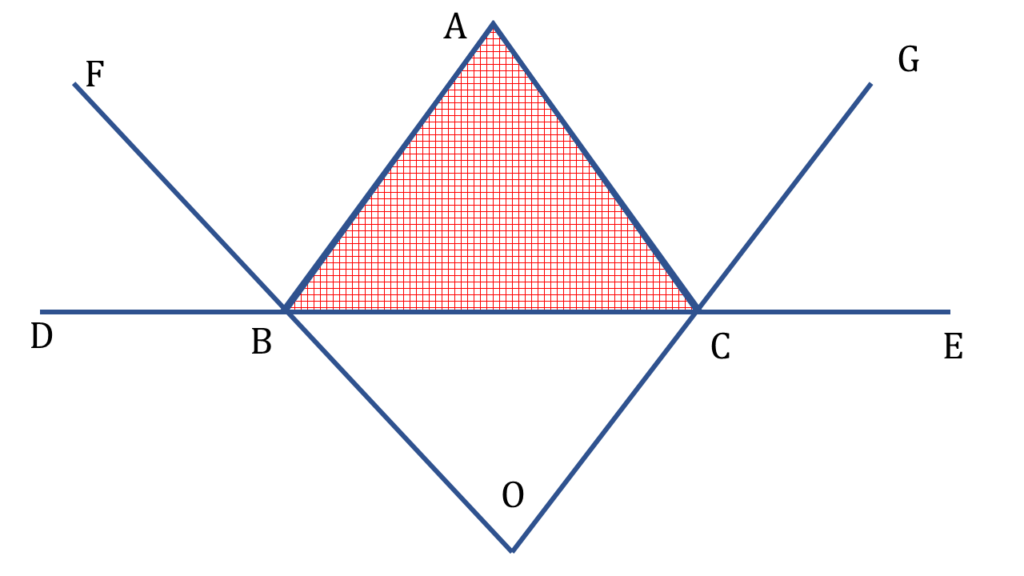
| ▲ABC থেকে পাই, |
|---|
| ∠BAC + ∠ABC + ∠ACB = 180° —- ( vii ) |
আবার,
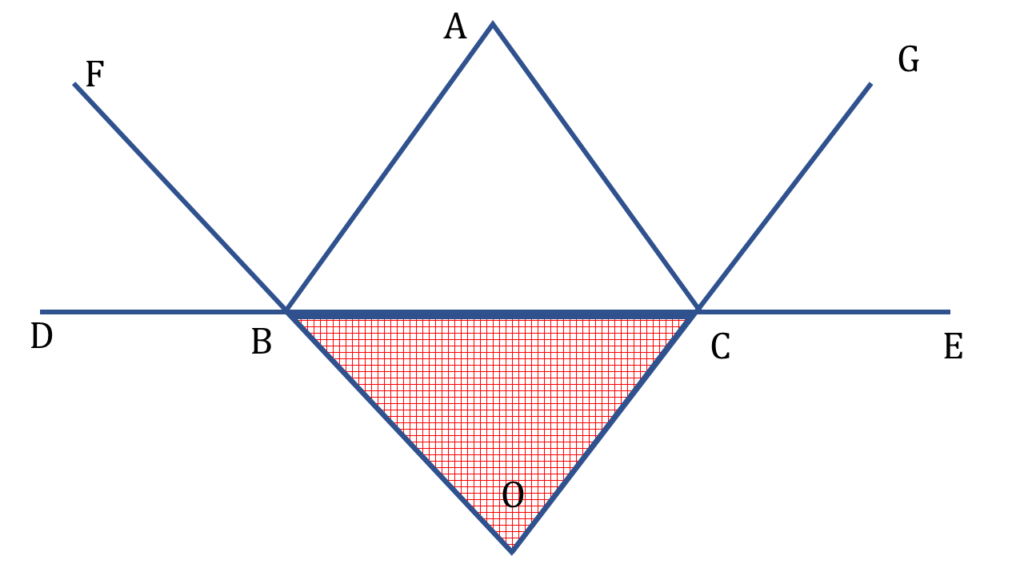
| ▲BOC থেকে পাই, |
|---|
| ∠BOC + ∠OBC + ∠OCB = 180° |
| বা, ∠BOC = 180° – (∠OBC + ∠OCB) |
| ( v ) ও ( vi ) নং থেকে ∠OBC ও ∠OCB মান বসিয়ে পাই, |
| ∠BOC = 180° – ½ (∠ABC + ∠BAC + ∠ACB + ∠BAC) |
| বা, ∠BOC = 180° – ½ (180° + ∠BAC) [ ( vii ) নং থেকে ∠BAC + ∠ABC + ∠ACB = 180° বসিয়ে পাই ] |
| বা, ∠BOC = 180° – 90° – ½∠BAC |
| বা, ∠BOC = 90° – ½∠BAC |
| অতএব ∠BOC = 90° – ½∠BAC প্রমাণিত । |
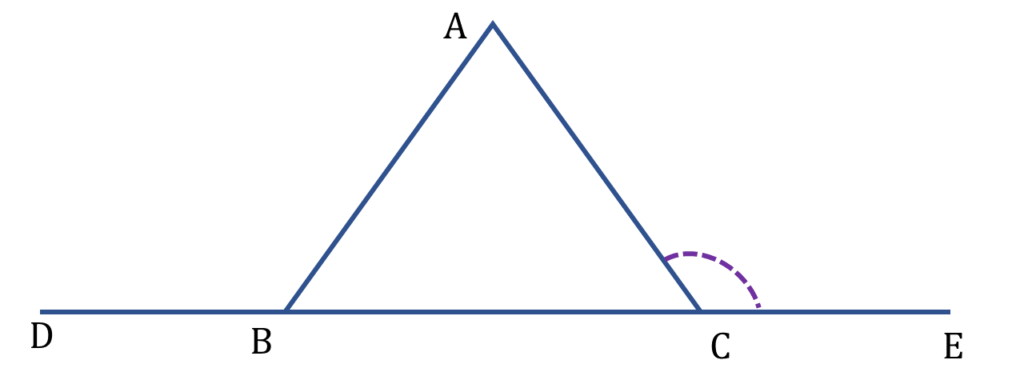
13. ▲ABC -এর ∠ACB -এর বহিঃ সমদ্বিখণ্ডক A বিন্দুদিয়ে BC বাহুর সমান্তরাল সরলরেখাকে D বিন্দুতে ছেদ করে। প্রমাণ করি যে,
∠ADC = 90° – ½∠ACB
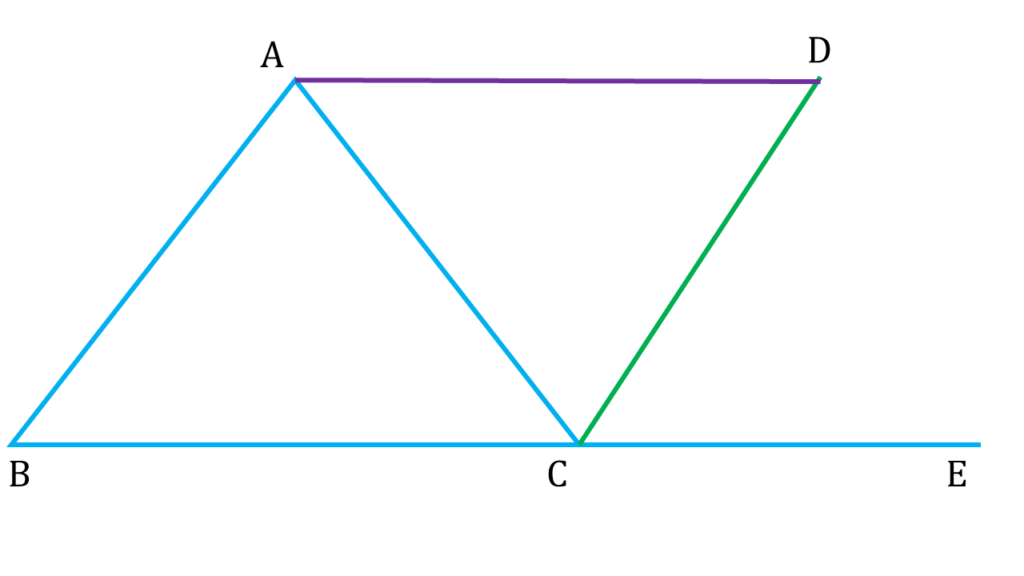
সমাধানঃ-
▲ABC -এর ∠ACB -এর বহিঃ সমদ্বিখণ্ডক A বিন্দুদিয়ে BC বাহুর সমান্তরাল সরলরেখাকে D বিন্দুতে ছেদ করেছে এবং BC বাহুকে E পর্যন্ত বর্ধিত করা হয়েছে।
| AD||BE এবং DC ছেদক |
|---|
| অতএব, |
| ∠ADC = একান্তর ∠DCE ——( i ) |
এবং
| ∠ACE এর সমদ্বিখণ্ডক CD |
|---|
| অতএব, |
| ∠ACD = ∠DCE —–( ii ) |
প্রমাণ করতে হবে,
∠ADC = 90° – ½∠ACB
∠ACE = ∠ACD + ∠DCE
বা, ∠ACE = ∠DCE + ∠DCE
বা, ∠ACE = 2∠DCE
বা,∠ACE = 2∠ADC —–( iii )
| সরলরেখা BE থেকে পাই, |
|---|
| ∠BCA + ∠ACE = 180° |
| বা, ∠ACB +2∠ADC = 180° [ ( iii ) নং থেকে ∠ACE এর মান বসিয়ে পাই, ] |
| বা, 2∠ADC + ∠ACB = 180° |
| বা, ∠ADC = 90° – ½∠ACB |
| অতএব ∠ADC = 90° – ½∠ACB প্রমাণিত। |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |

14. প্রমাণ করি যে, একটি ত্রিভুজের শীর্ষকোণের সমদ্বিখণ্ডক এবং শীর্ষকোণ থেকে ভূমির উপর অঙ্কিত লম্বের অন্তর্ভুক্ত কোণ ত্রিভুজের ভুমিস্থ কোণদ্বয়ের অন্তরের অর্ধেক।
সমাধানঃ-
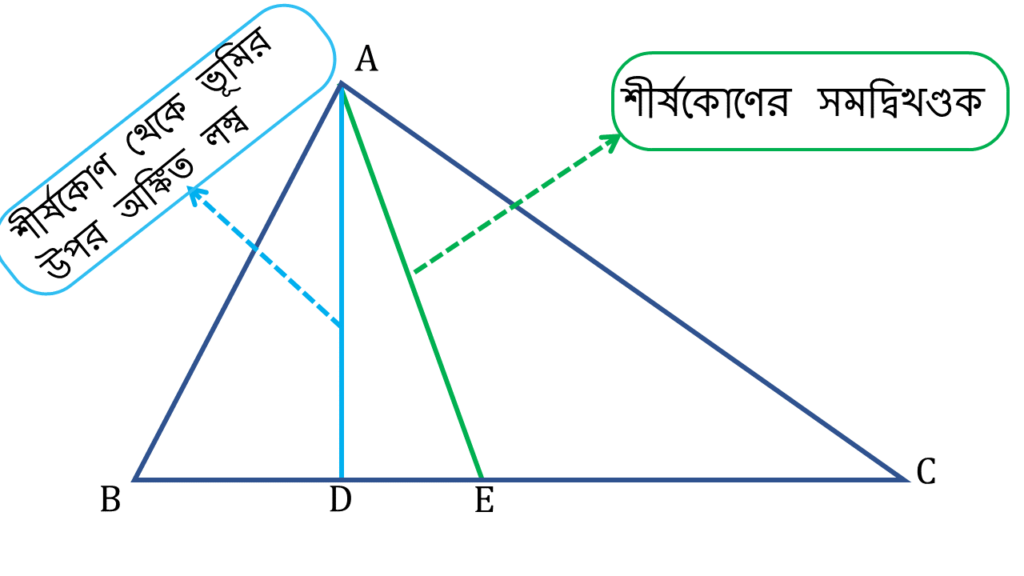
প্রদত্তঃ
▲ABC এর শীর্ষকোণ ∠BAC এর সমদ্বিখণ্ডক যা BC বাহুকে E বিন্দুতে ছেদ করেছে এবং শীর্ষকোণ থেকে ভূমির উপর অঙ্কিত লম্ব যা BC বাহুকে D বিন্দুতে ছেদ করেছে।
অতএব
| আমরা পেলাম, |
|---|
| ∠BAE = ∠EAC |
| এবং |
| ∠ADB = 90° = ∠ADC |
প্রামাণ্যঃ
প্রমাণ করতে হবে,
∠DAE = ½ (∠ABD – ∠ACB)
প্রমাণঃ
▲ABC এর AD⊥BC
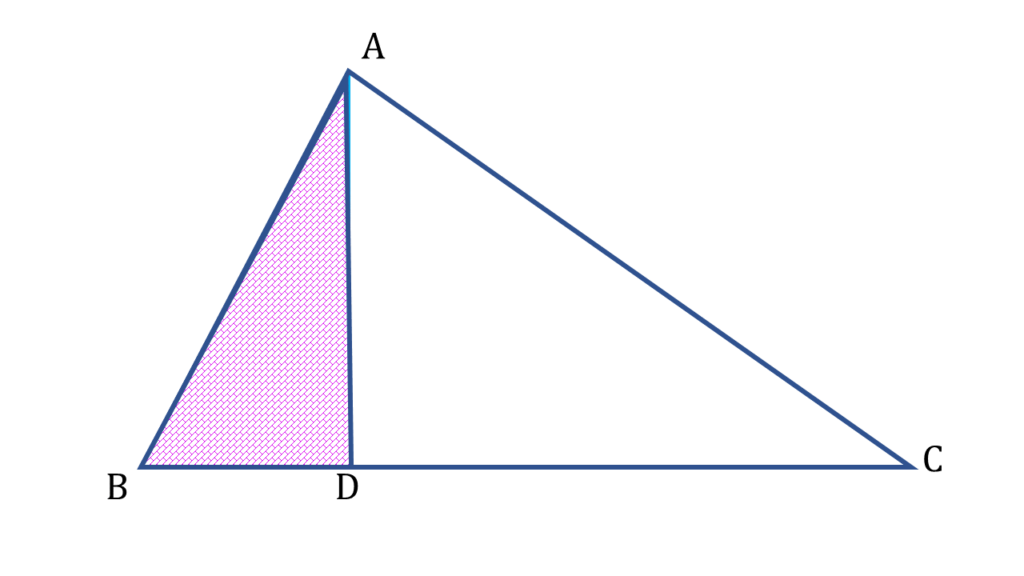
| সমকোণী ত্রিভুজ ▲ADB থেকে পাই, |
|---|
| ∠BAD + ∠ABD + ∠ADB = 180° |
| বা, ∠BAD + ∠ABD + 90° = 180° |
| বা, ∠ABD = 180° – 90° – ∠BAD |
| বা, ∠ABD = 90° – ∠BAD —— ( i ) |
আবার,
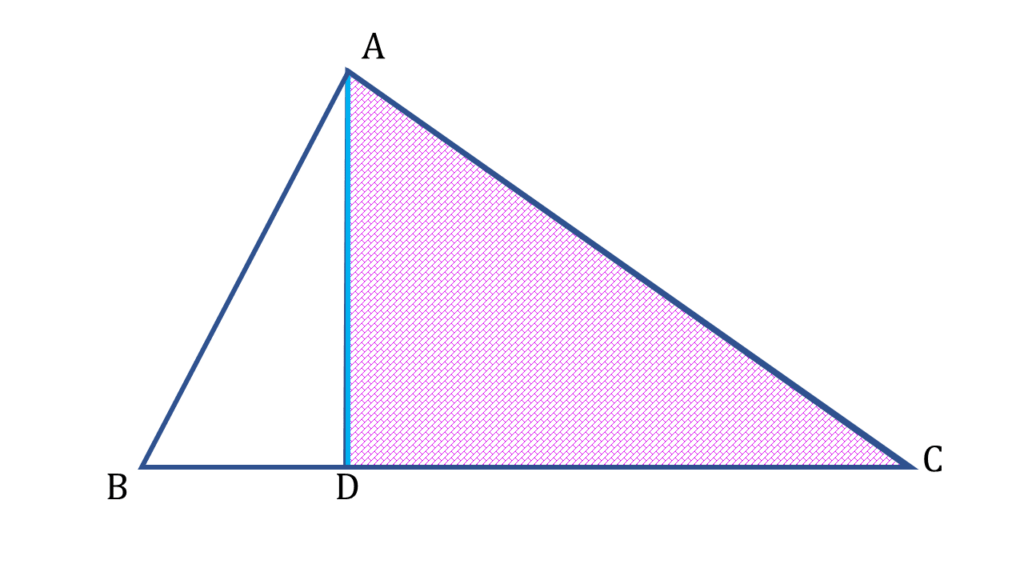
| সমকোণী ত্রিভুজ ▲ADC থেকে পাই, |
|---|
| ∠DAC + ∠ACD + ∠ADC = 180° |
| বা, ∠DAC + ∠ACD + 90° = 180° |
| বা, ∠ACD = 180° – 90° – ∠DAC |
| বা, ∠ACD = 90° – ∠DAC ——-( ii ) |
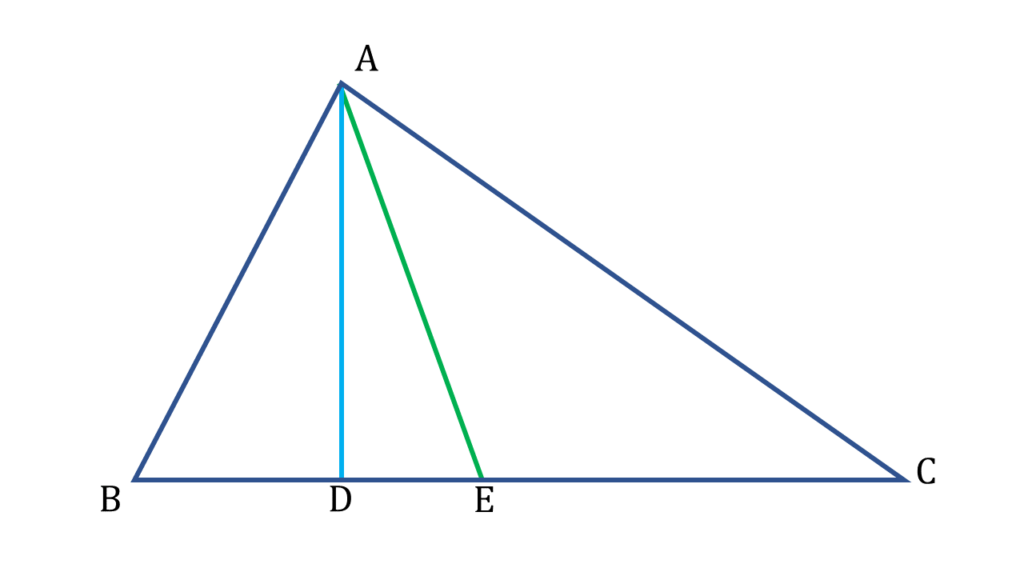
| ( i ) নং থেকে ( ii ) নং বিয়োগ করে পাই, |
|---|
| ∠ABD – ∠ACD = 90° – ∠BAD – (90° – ∠DAC) |
| বা, ∠ABD – ∠ACD = 90° – ∠BAD – 90° + ∠DAC |
| বা, ∠ABD – ∠ACD = ∠DAC – ∠BAD |
| বা, ∠ABD – ∠ACD = ∠DAE + ∠EAC – ∠BAD |
| বা, ∠ABD – ∠ACD = ∠DAE + ∠BAE – ∠BAD [ ∵ ∠BAE = ∠EAC ] |
| বা, ∠ABD – ∠ACD = ∠DAE + ∠BAD + ∠DAE – ∠BAD |
| বা, ∠ABD – ∠ACD = 2∠DAE |
| বা, ∠DAE = ½ (∠ABD – ∠ACD ) |
| অতএব ∠DAE = ½ (∠ABD – ∠ACD ) প্রমাণিত । |
15. ABC সমদ্বিবাহু ত্রিভুজের ভূমির একটি কোণ শীর্ষকোণের দ্বিগুণ । ত্রিভুজটির কোণগুলির পরিমাপ লিখি।
সমাধানঃ-
▲ABC এর
AB = AC
এবং
∠ABC = ∠ACB
মনে করি ▲ABC এর শীর্ষকোণ ∠BAC = x°
প্রশ্নানুসারে,
∠ABC = ∠ACB = 2x°
| ▲ABC থেকে পাই, |
| ∠ABC + ∠ACB + ∠BAC = 180° |
| বা, 2x° + 2x° + x° = 180° |
| বা, 5x° = 180° |
| বা, x° = 180°/5 |
| বা, x° = 36° |
| ∠BAC = 36° ∠ABC = ∠ACB = 72° |
16. ▲ABC -এর ∠BAC = 90° এবং ∠BCA = 30°; প্রমাণ করি যে, AB = ½BC
সমাধানঃ-
প্রদত্তঃ
▲ABC -এর,
∠BAC = 90°
এবং
∠BCA = 30°
প্রামাণ্যঃ
প্রমান করতে হবে,
AB = ½BC
অঙ্কনঃ
A বিন্দু থেকে একটি সরলরেখা অঙ্কন করলাম যা BC বাহুকে D বিন্দুতে ছেদ করেছে
এবং
AD = DC
প্রমাণঃ
▲ADC থেকে পাই,
∠DAC = ∠DCA [ ∵AD = DC]
অতএব,
∠DAC = ∠DCA = 30°
আবার,
▲ABC এর
∠BAD + ∠DAC = 90°
বা, ∠BAD = 90° – ∠DAC
বা, ∠BAD = 90° – 30°
বা, ∠BAD = 60°
আবার,
| ▲ABD থেকে পাই, |
| ∠ABD + ∠ADB + ∠BAD = 180° |
| বা, 60° + ∠ADB + 60° = 180° |
| বা, ∠ADB = 180° – 60° – 60° |
| বা, ∠ADB = 60° |
সুতরাং ∠ABD একটি সমবাহু ত্রিভুজ।
অতএব,
AB = AD = BD = DC
| AB + AB = BD + DC |
| বা, 2AB = BC |
| বা, AB = ½BC |
| অতএব AB = ½BC প্রমাণিত । |
17. ▲XYZ -এর ∠XYZ = 90° এবং XY = ½XZ; প্রমাণ করি যে, ∠YXZ = 60°
সমাধানঃ-
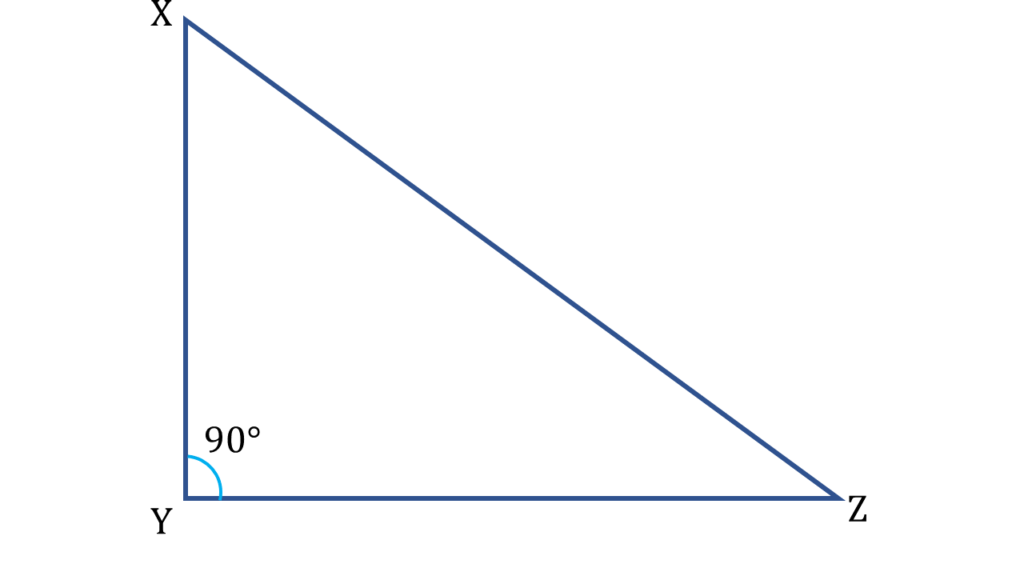
প্রদত্তঃ
▲XYZ -এর ∠XYZ = 90° এবং XY = ½XZ
প্রামাণ্যঃ
প্রমাণ করতে হবে,
∠YXZ = 60°
অঙ্কনঃ
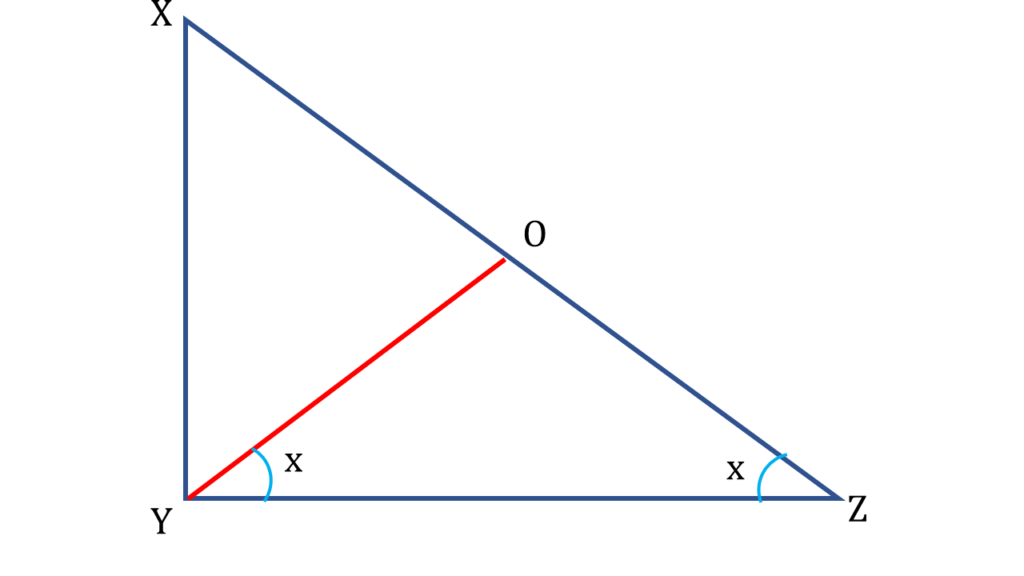
YO অঙ্কন করলাম যাতে করে,
∠OYZ = ∠OZY = x°
প্রমাণঃ
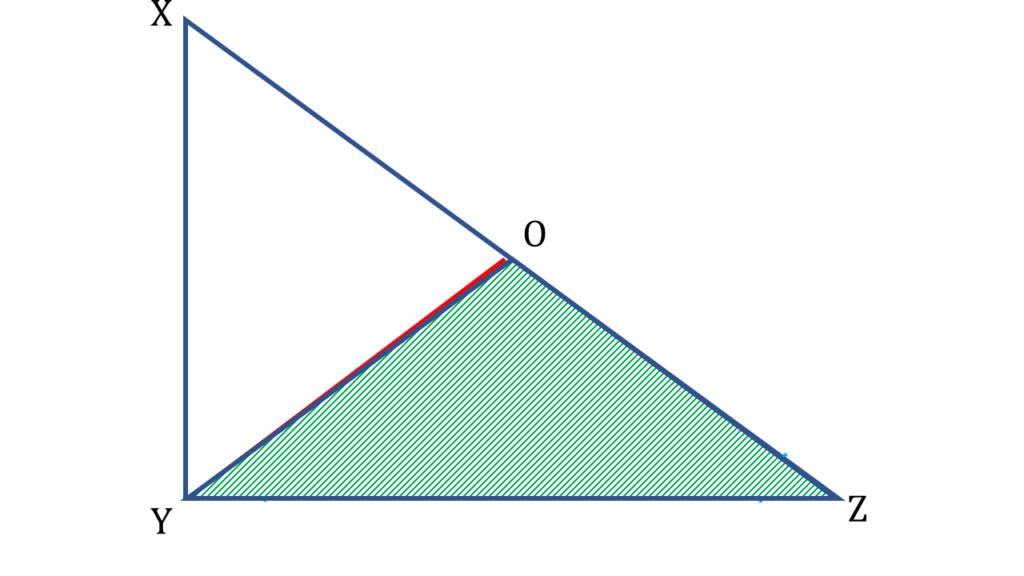
| ▲YOZ থেকে পাই, |
| ∠OYZ = ∠OZY = x° |
| অতএব, |
| OY = OZ —–( i ) |
| ▲XYO এর, |
| ∠XYO = 90° – x° —–( ii ) |
এবং
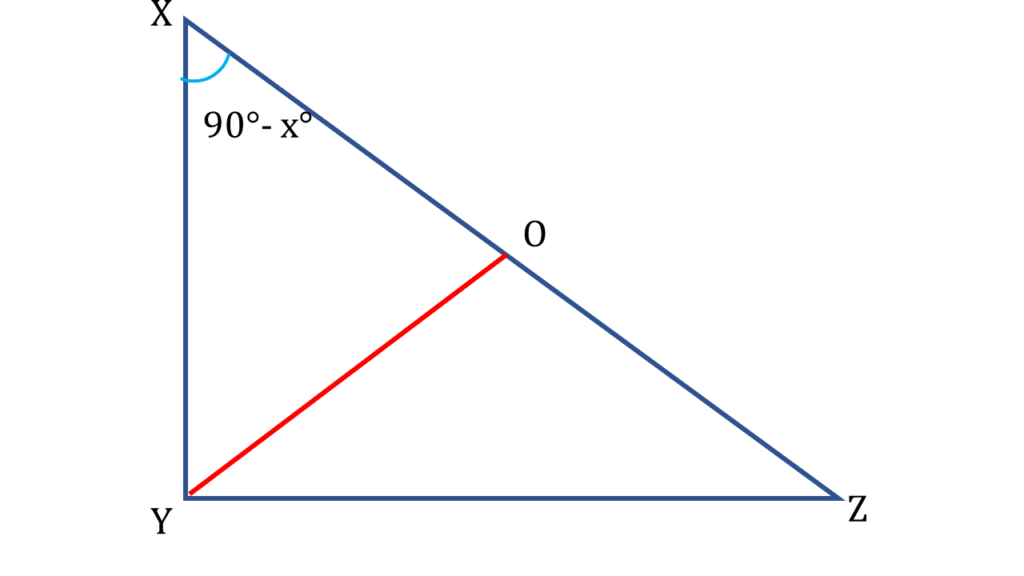
| ▲XYZ এর, |
| ∠YXZ + ∠XZY + ∠XYZ = 180° |
| বা, ∠YXZ + x° + 90° = 180° |
| বা, ∠YXZ = 180° – 90° – x° |
| বা, ∠YXZ = 90° – x° —–( iii ) |
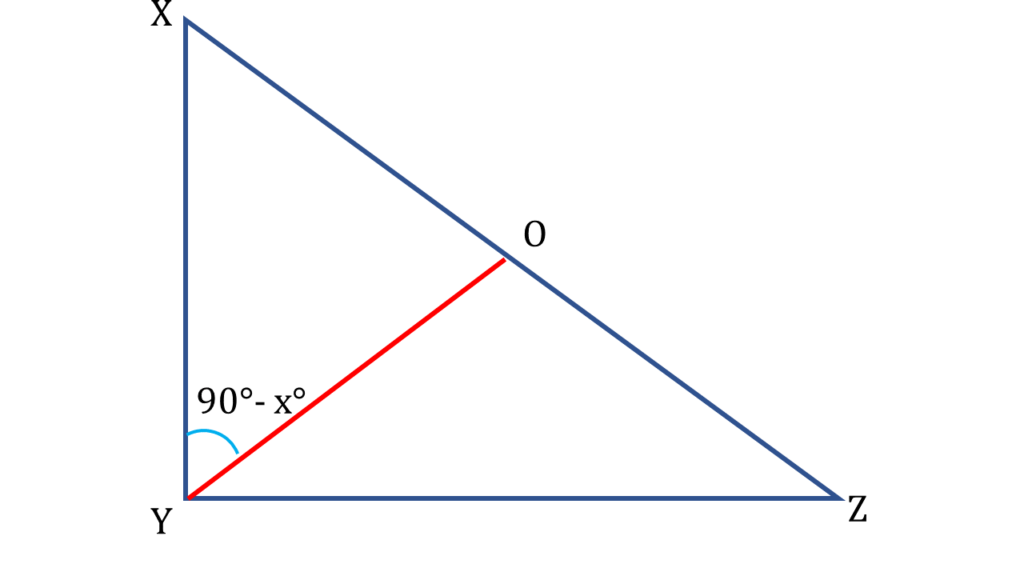
| ( ii ) ও ( iii ) নং থেকে পাই, |
| ∠XYO = 90° – x° = ∠YXZ |
অতএব,
▲XOY এর
OY = OX —( iv )
( i ) ও ( iv ) নং থেকে পাই,
OY = OX = OZ = ½XZ
আবার দেওয়া আছে XY = ½XZ
অতএব,
XY = OY = OX = OZ —( v )
( v ) নং থেকে পেলাম,
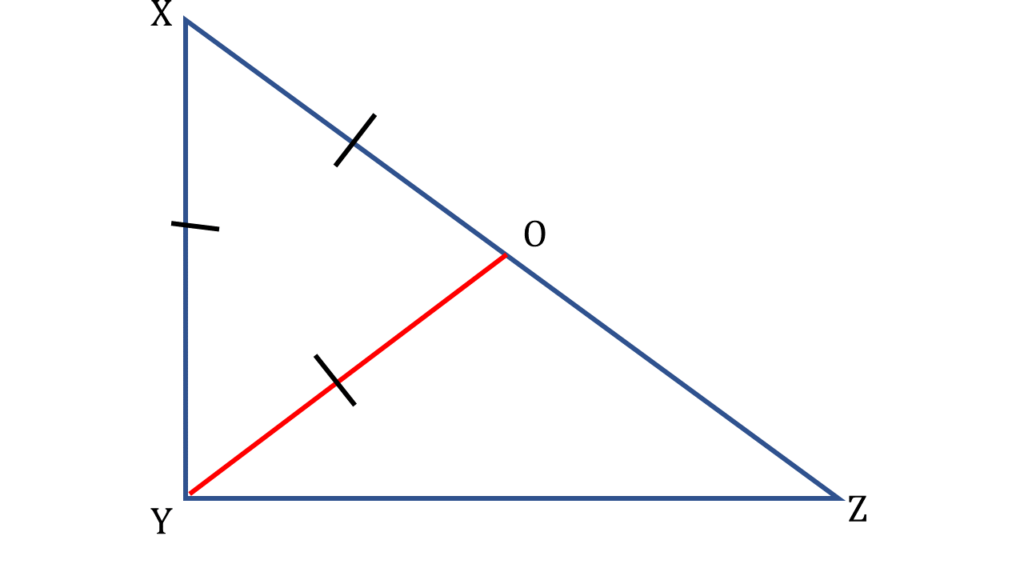
▲XOY একটি সর্বসম ত্রিভুজ।
অতএব,
∠XYO = ∠YXO = ∠XOY = 90° – x°
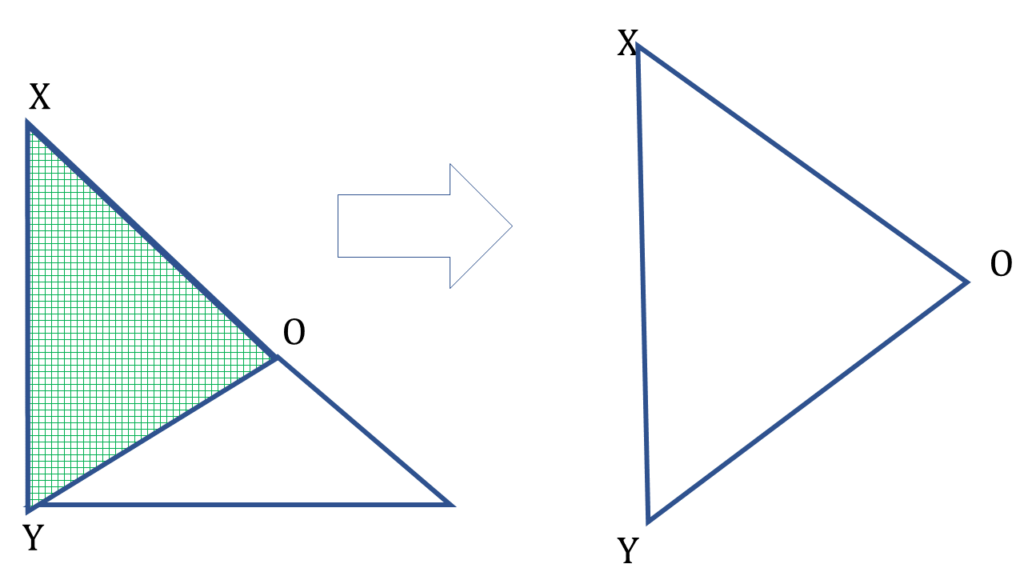
| সর্বসম ত্রিভুজ ▲XOY থেকে পাই, |
| ∠XYO + ∠YXO + ∠XOY = 180° |
| বা, 90° – x° + 90° – x° + 90° – x° = 180° |
| বা, 3(90° – x°) = 180° |
| বা, 90° – x° = 60° |
অতএব,
∠XYO = ∠YXO = ∠XOY = 90° – x° = 60°
| অতএব ∠YXZ = 60° প্রমাণিত । |

| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |

18. প্রমাণ করি যে, সমবাহু ত্রিভুজের প্রতিটি কোণের পরিমাপ 60°
সমাধানঃ-
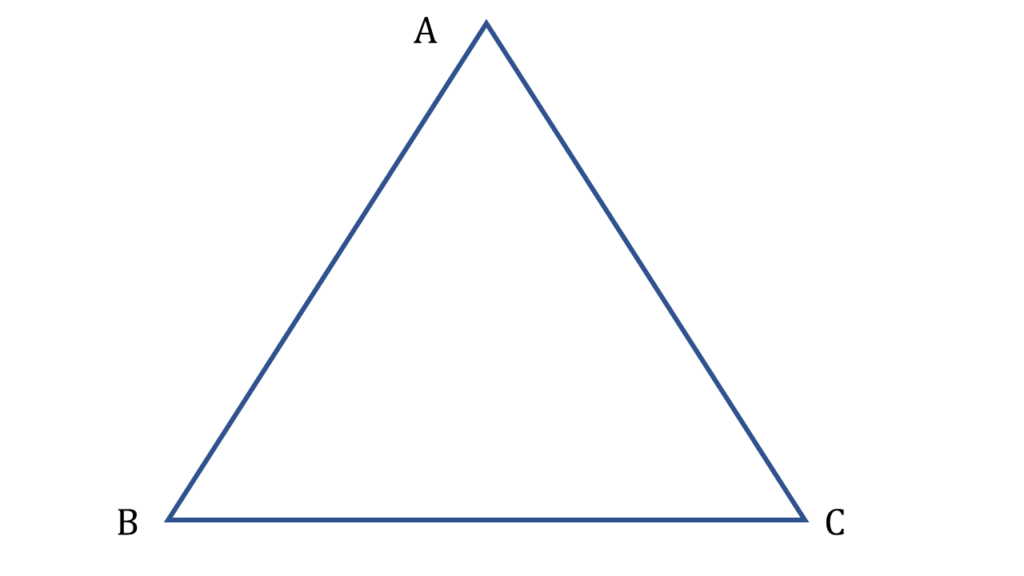
প্রদত্তঃ
▲ABC একটি সম্বাহু ত্রিভুজ।
∴ AB = BC = CA
∴ ∠ABC = ∠BCA = ∠CAB
প্রামাণ্যঃ
প্রমাণ করতে হবে ,
∠ABC = ∠BCA = ∠CAB = 60°
প্রমাণঃ
| ▲ABC থেকে পাই, |
| ∠ABC + ∠ACB + ∠BAC = 180° |
| বা, ∠ABC + ∠ABC + ∠ABC= 180° |
| বা, 3∠ABC = 180° |
| বা, ∠ABC = 180°/3 |
| বা, ∠ABC = 60° |
| অতএব ∠ABC = ∠BCA = ∠CAB = 60° প্রমাণিত। |
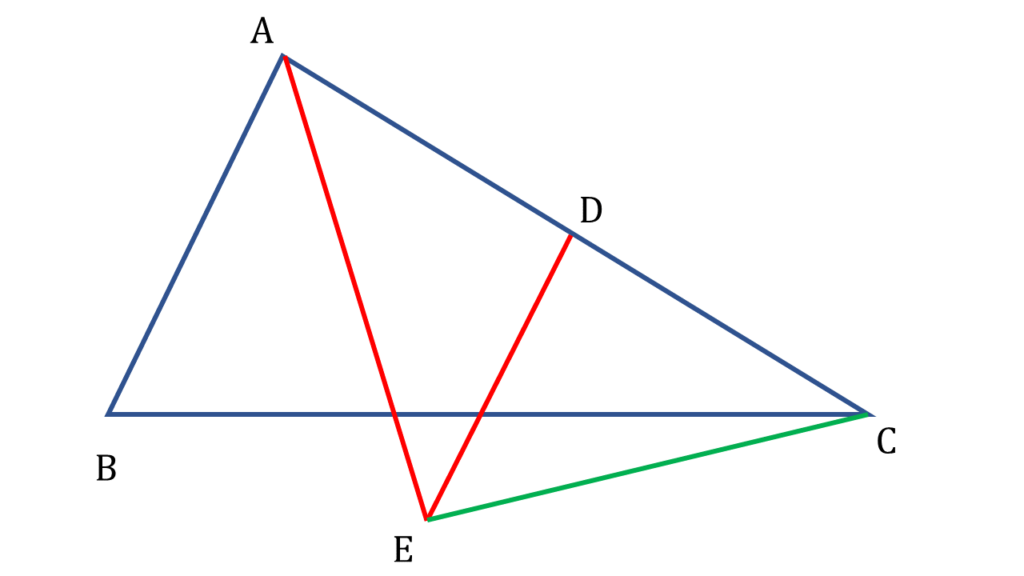
19. ABC ত্রিভুজের ∠BAC -এর সমদ্বিখণ্ডক এবং AC বাহুর মধ্যবিন্দু D দিয়ে AB বাহুর সমান্তরাল সরলরেখা পরস্পর BC বাইরে E বিন্দুতে মিলিত হয়। প্রমান করি যে, ∠AEC = 1 সমকোণ।
সমাধানঃ-
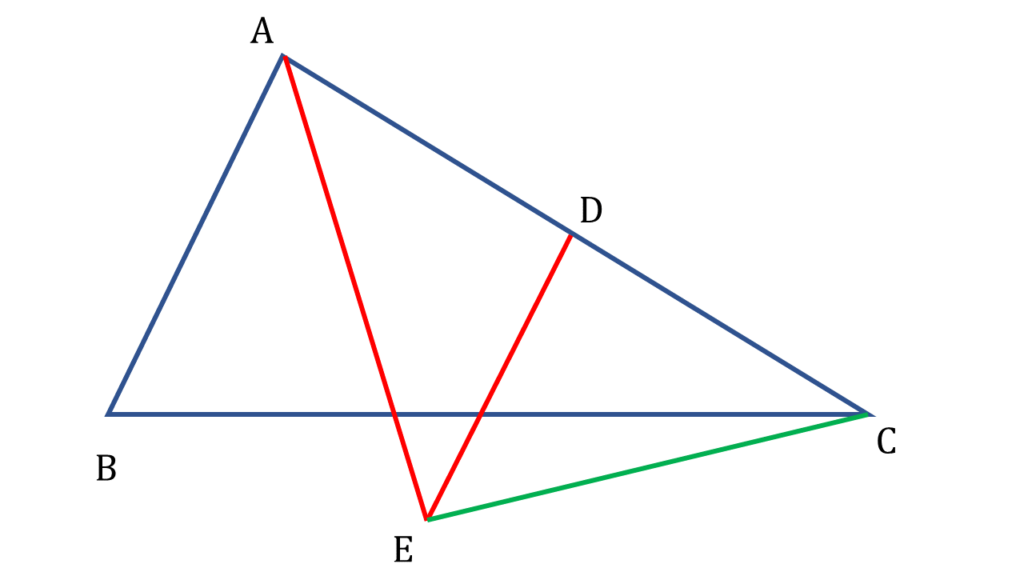
প্রদত্তঃ
ABC ত্রিভুজের ∠BAC -এর সমদ্বিখণ্ডক এবং AC বাহুর মধ্যবিন্দু D দিয়ে AB বাহুর সমান্তরাল সরলরেখা পরস্পর BC বাইরে E বিন্দুতে মিলিত হয়েছে।
| অতএব আমরা পেলাম, |
|---|
| ∠BAE = ∠EAC |
| এবং |
| AB||DE |
প্রামাণ্যঃ
প্রমাণ করতে হবে,
∠AEC = 1 সমকোণ
প্রমাণঃ
AB||DE এবং AE ছেদক
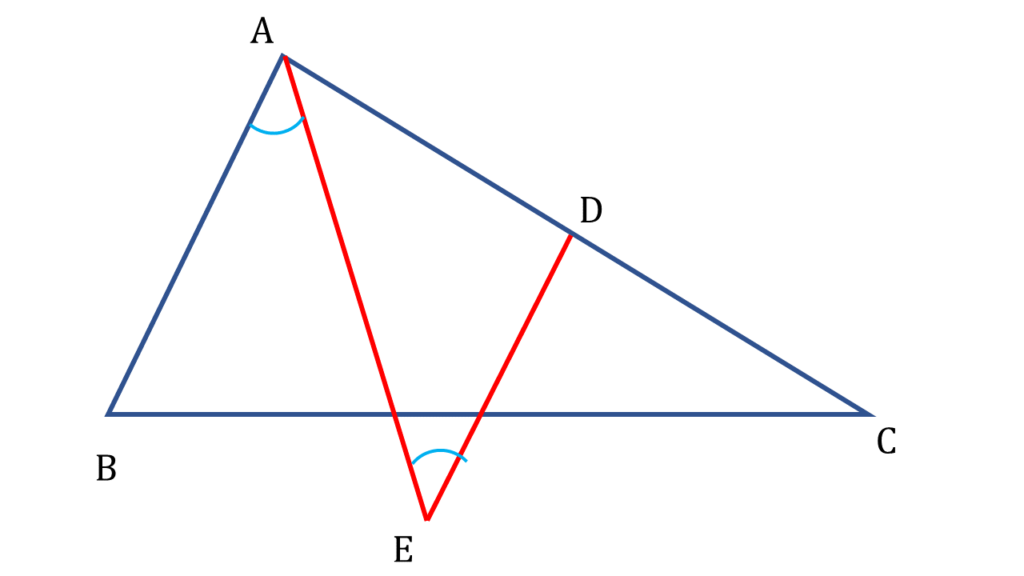
∠BAE = একান্তর ∠AED
আবার,
∠BAE = ∠EAC
∴ ∠BAE = ∠EAC = ∠AED
∴ AD = DE = DC
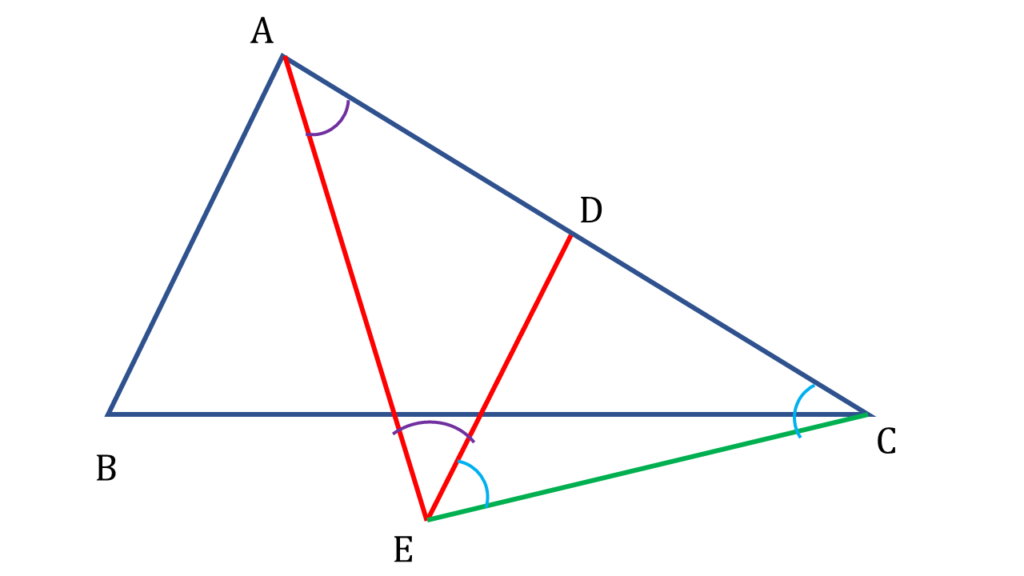
▲DEC এর
DE = DC
∴ ∠DEC = ∠DCE
| ▲AEC থেকে পাই, |
|---|
| ∠AEC + ∠ACE + ∠EAC = 180° |
| বা, ∠AEC + ∠DEC + ∠AED = 180° [ ∵∠EAC = ∠AED এবং ∠DEC = ∠DCE ] |
| বা, ∠AEC + ∠AEC = 180° |
| বা, 2∠AEC = 180° |
| বা, ∠AEC = 180°/2 |
| বা, ∠AEC = 90° = 1 সমকোণ |
| অতএব ∠AEC = 1 সমকোণ প্রমাণিত । |
এই কষে দেখি 16.1 Class 8|Koshe Dekhi 16.1 Class 8 সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।
তোমাদের এই ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই কষে দেখি 16.1 এর সমাধান গুলি কেমন লাগলো অবশ্যই কমেন্ট করে জানাবে এবং কোথাও বুঝতে অসুবিধা হলে সেটাও কমেন্ট এ জানাবে। তোমাদের জন্যে এই অধ্যায়ের আর একটি কষে দেখি 16.2 এর সমস্ত অংকের সমাধান আমি করে দিয়েছি। ওই কষে দেখি তে কোনো অংক বুঝতে না পারলে তোমরা এখান থেকে দেখে নিতে পারবে।   কষে দেখি 16.2 Class 8 কষে দেখি 16.2 Class 8 |
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 16.1 Class 8 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 16.1 Class 8 তারপর  |
| গনিতপ্রভা অষ্টম শ্রেণীর সমস্ত অধ্যায়ের সমাধান- | |
|---|---|
| অধ্যায় | সমাধান |
| 2. পাই চিত্র | কষে দেখি 2 |
| 3. মূলদ সংখ্যার ধারণা | অধ্যায়ের সারাংশ |
| কষে দেখি 3 | |
| 4. বীজগাণিতিক সংখ্যামালার গুণ ও ভাগ | অধ্যায়ের সারাংশ |
| কষে দেখি 4.1 | |
| কষে দেখি 4.2 | |
| 5. ঘনফল নির্ণয় | অধ্যায়ের সারাংশ |
| কষে দেখি 5.1 | |
| কষে দেখি 5.2 | |
| কষে দেখি 5.3 | |
| 6. পূরক কোণ, সম্পূরক কোণ ও সন্নিহিত কোণ | অধ্যায়ের সারাংশ |
| কষে দেখি 6 | |
| 7. বিপ্রতীপ কোণের ধারণা | অধ্যায়ের সারাংশ |
| কষে দেখি 7.1 | |
8. সমান্তরাল সরলরেখা ও ছেদকের ধর্ম | অধ্যায়ের সারাংশ |
| কষে দেখি 8 | |
9. ত্রিভুজের দুটি বাহু ও তাদের বিপরীত কোণের সম্পর্ক | অধ্যায়ের সারাংশ |
| কষে দেখি 9 | |
| 10. ত্রৈরাশিক | কষে দেখি 10.1 |
| কষে দেখি 10.2 | |
| 11. শতকরা | কষে দেখি 11 |
| 12. মিশ্রণ | কষে দেখি 12 |
13. বীজগাণিতিক সংখ্যামালার উৎপাদকে বিশ্লেষণ | কষে দেখি 13.1 |
| কষে দেখি 13.2 | |
14. বীজগাণিতিক সংখ্যামালার গ.সা.গু ও ল.সা.গু | কষে দেখি 14 |
15. বীজগাণিতিক সংখ্যামালার সরলীকরণ | কষে দেখি 15 |
16. ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই | কষে দেখি 16.1 |
| কষে দেখি 16.2 | |
17. সময় ও কার্য | কষে দেখি 17.1 |
| কষে দেখি 17.2 | |
18. লেখচিত্র | কষে দেখি 18 |
19. সমীকরণ গঠন ও সমাধান | কষে দেখি 19 |
| 20. জ্যামিতিক প্রমাণ | কষে দেখি 20.1 |
| কষে দেখি 20.2 | |
| কষে দেখি 20.3 | |

এখানে তোমরা তোমাদের অষ্টম শ্রেণীতে কি কি পড়ানো হয়, মানে তোমাদের অষ্টম শ্রেণীর সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

