শ্রেণী-নবম ; অধ্যায় -সূচকের নিয়মাবলি ; কষে দেখি 2
| সূচিপত্রে সংখ্যার সূচক গুলো বোঝা যাবেনা। তোমরা বই এর দাগ নম্বর দেখে সুচিপত্রের দাগ মিলিয়ে অংক দেখবে। |
কষে দেখি 2 Class 9 এর সুচিপত্রঃ-
কষে দেখি 2 Class 9 এর অংকের সমাধান গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ
কষে দেখি 2|Koshe Dekhi 2 পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদ | WBBSE বোর্ডের অন্তর্গত তোমাদের নবম|Class 9 এর একটি অধ্যায় সূচকের নিয়মাবলি । এই সূচকের নিয়মাবলি তে আমরা শিখবো এক বা একাধিক সংখ্যা কে বহুবার গুণ করা ও ভাগ করে তা দিয়ে কিভাবে বিভিন্ন অংক সমাধান করা যায়!
এই কষে দেখি তে যে সমস্ত অংক গুলি আছে সেগুলি সমাধান করার জন্যে তোমাদের এই সূচকের কিছু নিয়ম সম্পর্কে অবগত হতে হবে।
সূচক কাকে বলে? |What is Index?
x যেকোনো বাস্তব সংখ্যা এবং n যেকোনো ধনাত্মক পূর্ণসংখ্যা হলে
x.x.x.x.x.x…..x(n সংখ্যক)
= xn
এক্ষেত্রে n-কে সূচক বলে।
নিধান কাকে বলে?|What is Base?
x যেকোনো বাস্তব সংখ্যা এবং n যেকোনো ধনাত্মক পূর্ণসংখ্যা হলে
x.x.x.x.x.x…..x(n সংখ্যক)
= xn
এক্ষেত্রে x-কে নিধান বলে।
xn কে x-এর n ঘাত বলা হয় ।
সূচকের নিয়মাবলিঃ
| সূচকের যে নিয়মাবলি তোমাদের এই কষে দেখি 2 এর অংকগুলি সমাধান করার জন্যে লাগবে সেগুলি হল- | ||
|---|---|---|
| x ও y যেকোনো বাস্তব সংখ্যা এবং m ও n দুটি ধনাত্মক পূর্ণসংখ্যা হলে- | ||
| (i) | xm × xn = xm+n | |
| (ii) | \(\frac{x^m}{x^n}\) = | xm-n ( m>n ) |
| \(\frac{1}{x^{n-m}}\) (n>m) | ||
| (iii) | (xm)n = xmn | |
| (iv) | (xy)m = xm . ym | |
| (v) | (\(\frac{x}{y}\))m = \(\frac{x^m}{y^m}\) | |
| (vi) | a একটি বাস্তব সংখ্যা ও a≠0, 1, -1 এবং x, y মূলদ সংখ্যা। যদি ax = ay হয়, তখন x = y হবে। | |
| (vii) | a, b ধনাত্মক বাস্তবসংখ্যা এবং x শূন্য ছাড়া যে কোনো বাস্তব সংখ্যা হলে যদি ax = bx হয়, তখন a = b অথবা x = 0 হবে। | |
| (viii) | x শূন্য ছাড়া যে কোনো বাস্তব সংখ্যা হলে x0 = 1 হবে। | |
আগামিতে এই কষে দেখি 2 Class 9 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 2 Class 9 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 2 Class 9 তারপর  |
কষে দেখি 2 Class 9 এর  YouTube Video:
YouTube Video:
কষে দেখি 2 | Koshe Dekhi 2
1. মান নির্ণয় করি :
(i) \((\sqrt[5]{8})^{\frac{5}{2}} \times (16)^{\frac{-3}{2}}\)
সমাধানঃ-
| \((\sqrt[5]{8})^{\frac{5}{2}} \times (16)^{\frac{-3}{2}}\) |
| \(= (8^{\frac{1}{5}})^{\frac{5}{2}} \times (2^4)^{\frac{-3}{2}}\) |
| \(= 8^{\frac{1}{5} \times \frac{5}{2}} \times 2^{-4 \times \frac{3}{2}}\) |
| \(= 8^{\frac{1}{2}} × 2^{-6}\) |
| \(= (2^3)^{\frac{1}{2}} \times 2^{-6}\) |
| \(= 2^{\frac{3}{2}} \times 2^{-6}\) |
| \(= 2^{\frac{3}{2} – 6}\) |
| \(= 2^{\frac{3 – 12}{2}}\) |
| \(= 2^{-\frac{9}{2}}\) |
(ii) \([(125)^{-2} \times (16)^{\frac{-3}{2}}]^{\frac{-1}{6}}\)
সমাধানঃ-
| \([(125)^{-2} \times (16)^{\frac{-3}{2}}]^{\frac{-1}{6}}\) |
| = { ( 53 )-2 × ( 24 )-\(\frac{3}{2}\) }-\(\frac{1}{6}\) |
| = { 5-6 × 2\(4×(-\frac{3}{2}\)) }-\(\frac{1}{6}\) |
| = { 5-6 × 2-6 }-\(\frac{1}{6}\) |
| = (5-6 )-\(\frac{1}{6}\) ×( 2-6 )-\(\frac{1}{6}\) |
| = 5-6×(-\(\frac{1}{6}\)) × 2-6×(\(-\frac{1}{6}\)) |
| = 5 × 2 |
| = 10 |
(iii) \(4^{\frac{1}{3}} \times [2^{\frac{1}{3}} \times 3^{\frac{1}{2}}] ÷ 9^{\frac{1}{4}}\)
সমাধানঃ-
| \(4^{\frac{1}{3}} \times [2^{\frac{1}{3}} \times 3^{\frac{1}{2}}] ÷ 9^{\frac{1}{4}}\) |
| \(= (2^2)^{\frac{1}{3}} \times [2^{\frac{1}{3}} \times 3^{\frac{1}{2}}] ÷ (3^2)^{\frac{1}{4}}\) |
| \(= 2^{\frac{2}{3}} \times [2^{\frac{1}{3}} \times 3^{\frac{1}{2}}] ÷ 3^{\frac{1}{2}}\) |
| \(= 2^{\frac{2}{3}} \times [2^{\frac{1}{3}} \times 3^{\frac{1}{2}}] \times (\frac{1}{3})^{\frac{1}{2}}\) |
| \(= 2^{\frac{2}{3}} \times 2^{\frac{1}{3}} \times 3^{\frac{1}{2}} \times 3^{-\frac{1}{2}}\) |
| \(= 2^{\frac{2}{3} + \frac{1}{3}} \times 3^{\frac{1}{2}-\frac{1}{2}}\) |
| \(= 2^{\frac{3}{3}} \times 3^0\) |
| \(= 2 × 1\) |
| \(= 2\) |
2. সরল করি :
(i) \((8a^3 ÷ 27x^{-3})^{\frac{2}{3}} \times (64a^3 ÷ 27x^{-3})^{-\frac{2}{3}}\)
সমাধানঃ-
| \((8a^3 ÷ 27x^{-3})^{\frac{2}{3}} \times (64a^3 ÷ 27x^{-3})^{-\frac{2}{3}}\) |
| \(= [\frac{(2a)^3}{3^3x^{-3}}]^{\frac{2}{3}} \times [\frac{(4a)^3}{3^3x^{-3}}]^{-\frac{2}{3}}\) |
| \(= [(2a)^3 \times (3^{-3}x^3)]^{\frac{2}{3}} \times [(4a)^3 \times (3^{-3}x^3)]^{-\frac{2}{3}}\) |
| \(= (2a)^{3\times \frac{2}{3}} \times (3^{-3}x^3)^{\frac{2}{3}} \times (4a)^{3 \times (-\frac{2}{3})} \times (3^{-3}x^3)^{-\frac{2}{3}}\) |
| \(= (2a)^{3\times \frac{2}{3}} \times 3^{-3 \times \frac{2}{3}} \times x^{3 \times \frac{2}{3}} \times (4a)^{3 \times (-\frac{2}{3})} \times 3^{-3 \times (-\frac{2}{3})} \times x^{3 \times (-\frac{2}{3})}\) |
| \(= (2a)^2 \times 3^{-2} \times x^2 \times (4a)^{-2} \times 3^2 \times x^{-2}\) |
| \(= (2a)^2 \times 3^{-2} \times x^2 \times (2\times2a)^{-2} \times 3^2 \times x^{-2}\) |
| \(= (2a)^2 \times 3^{-2} \times x^2 \times 2^{-2} \times (2a)^{-2} \times 3^2 \times x^{-2}\) |
| \(= (2a)^{2-2} \times 3^{-2+2} \times x^{2-2} \times 2^{-2} \) |
| \(= (2a)^0 \times 3^0 \times x^0 \times 2^{-2}\) |
| \(= 1 \times 1 \times 1 \times \frac{1}{4}\) |
| \(= \frac{1}{4}\) |
(ii) \([(x^{-5})^{\frac{2}{3}}]^{\frac{-3}{10}}\)
সমাধানঃ-
| \([(x^{-5})^{\frac{2}{3}}]^{\frac{-3}{10}}\) |
| \(= (x^{-5})^{\frac{2}{3} \times (\frac{-3}{10})}\) |
| \(= (x^{-5})^{\frac{-1}{5}}\) |
| \(= (x^{-5 \times (\frac{-1}{5})}\) |
| \(= x\) |
(iii) [ { ( 2-1 )-1 }-1 ]-1
সমাধানঃ-
| [ { ( 2-1 )-1 }-1 ]-1 |
| = [ { ( 2-1 )-1 }-1×(-1) |
| = {( 2-1 )-1 }1 |
| = ( 2-1 )-1 |
| = 2-1×(-1) |
| = 2 |
(iv)
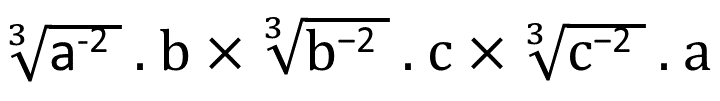
সমাধানঃ-
| = (a)-2/3 . b × (b)-2/3 . c × (c)-2/3 . a |
| \(= a^{\frac{-2}{3}} . b \times b^{\frac{-2}{3}} . c \times c^{\frac{-2}{3}} . a\) |
| \(= a^{1 – \frac{2}{3}} . b^{1 – \frac{2}{3}} . c^{1 – \frac{2}{3}} \) |
| \(= a^{\frac{1}{3}} . b^{\frac{1}{3}} . c^{\frac{1}{3}}\) |
| \(= (abc)^{\frac{1}{3}}\) |
| = |
(v)
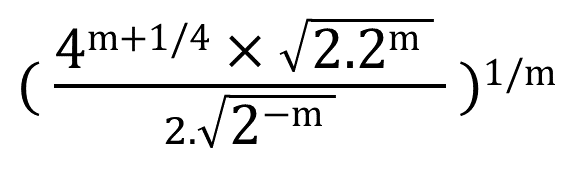
সমাধানঃ-
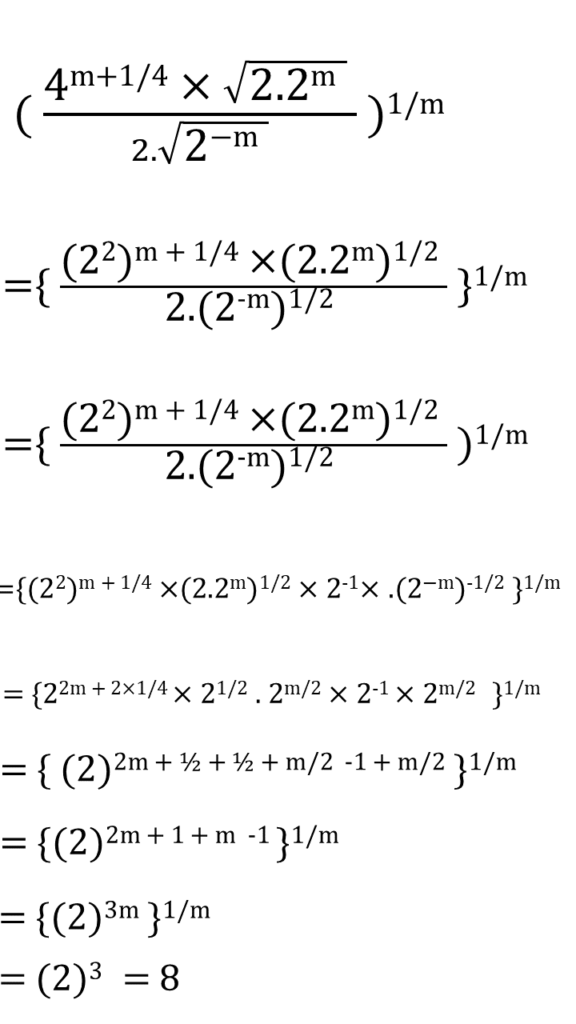
(vi) \(9^{-3} \times \frac{16^{\frac{1}{4}}}{6^{-2}} \times (\frac{1}{27})^{-\frac{4}{3}}\)
সমাধানঃ-
| \(9^{-3} \times \frac{16^{\frac{1}{4}}}{6^{-2}} \times (\frac{1}{27})^{-\frac{4}{3}}\) |
| \(= (3^2)^{-3} \times \frac{(2^4)^{\frac{1}{4}}}{(2 \times 3)^{-2}} \times (\frac{1}{3^3})^{-\frac{4}{3}}\) |
| \(= 3^{2 \times (-3)} \times \frac{2^{\frac{4}{4}}}{2^{-2} \times 3^{-2}} \times (3^{-3})^{-\frac{4}{3}}\) |
| \(= 3^{-6} \times 2 \times 2^2 \times 3^2 \times (3^{-3 \times (-\frac{4}{3})}\) |
| \(= 3^{-6} \times 2 \times 2^2 \times 3^2 \times 3^4\) |
| = 3-6+2+4 × 22+1 |
| = 30 × 23 |
| = 1 × 8 |
| = 8 |
(vii) (\(\frac{x^a}{x^b}\) )a2 + ab +b2 × (\(\frac{x^b}{x^c}\) )b2+bc+c2 × (\(\frac{x^c}{x^a}\))c2+ca+a2
সমাধানঃ-
| (\(\frac{x^a}{x^b}\) )a2 + ab +b2 × (\(\frac{x^b}{x^c}\) )b2+bc+c2 × (\(\frac{x^c}{x^a}\))c2+ca+a2 |
| = (xa-b )a2 + ab +b2 × (xb-c )b2+bc+c2 × (xc-a )c2+ca+a2 |
| = x(a-b)(a2 + ab +b2) × x(b-c)(b2+bc+c2) × x(c-a)(c2+ca+a2) |
| = xa3-b3 × xb3-c3 × xc3-a3 |
| = xa3-b3+b3-c3+c3-a3 |
| = x0 |
| = 1 |
3. মানের ঊর্ধ্বক্রমানুসারে সাজাই :
(i) \(5^{\frac{1}{2}}, 10^{\frac{1}{4}}, 6^{\frac{1}{3}}\)
সমাধানঃ-
| \(5^{\frac{1}{2}}\) | \(10^{\frac{1}{4}}\) | \(6^{\frac{1}{3}}\) |
|---|---|---|
| \(= [(5^{\frac{1}{2}})^{12}] ^{\frac{1}{12}}\) | \(= [(10^{\frac{1}{4}})^{12}] ^{\frac{1}{12}}\) | \(= [(6^{\frac{1}{3}})^{12}] ^{\frac{1}{12}}\) |
| \(= (5^6)^{\frac{1}{12}}\) | \(= (10^3)^{\frac{1}{12}}\) | \(= (6^4)^{\frac{1}{12}}\) |
যেহেতু
103<64<56
সুতরাং, \(10^{\frac{1}{4}}< 6^{\frac{1}{3}} < 5^{\frac{1}{2}}\)
(ii) \(3^{\frac{1}{3}}, 2^{\frac{1}{2}}, 8^{\frac{1}{4}}\)
সমাধানঃ-
| \(3^{\frac{1}{3}}\) | \(2^{\frac{1}{2}}\) | \(8^{\frac{1}{4}}\) |
|---|---|---|
| \(= [(3^{\frac{1}{3}})^{12}] ^{\frac{1}{12}}\) | \(= [(2^{\frac{1}{2}})^{12}] ^{\frac{1}{12}}\) | \(= [(8^{\frac{1}{4}})^{12}] ^{\frac{1}{12}}\) |
| \(= (3^4)^{\frac{1}{12}}\) | \(= (2^6)^{\frac{1}{12}}\) | \(= (8^3)^{\frac{1}{12}}\) |
| \(= (81)^{\frac{1}{12}}\) | \(= (64)^{\frac{1}{12}}\) | \(= (512)^{\frac{1}{12}}\) |
মানের ঊর্ধ্বক্রমে সাজিয়ে পাই,
\(2^{\frac{1}{2}} < 3^{\frac{1}{3}} < 8^{\frac{1}{4}}\)
(iii) 260, 348, 436, 524
সমাধানঃ-
| 260 | 348 | 436 | 524 |
|---|---|---|---|
| = (25)12 | = (34)12 | = (43)12 | = (52)12 |
| = (32)12 | = (81)12 | = (64)12 | = (25)12 |
মানের ঊর্ধ্বক্রমে সাজিয়ে পাই,
524 <260 <436 <348
4. প্রমাণ করি :
(i) ( \(\frac{a^q}{a^r}\))p × ( \(\frac{a^r}{a^p}\))q × ( \(\frac{a^p}{a^q}\) )r = 1
সমাধানঃ-
| ( \(\frac{a^q}{a^r}\))p × ( \(\frac{a^r}{a^p}\))q × ( \(\frac{a^p}{a^q}\) )r |
| = ( aq-r )p × ( ar-p )q × ( ap-q )r |
| = ap(q-r) × aq(r-p) × ar(p-q) |
| = apq-pr × aqr-pq × apr-qr |
| = apq-pr+qr-pq+pr-qr |
| = a0 |
| = 1 |
(ii) (\(\frac{x^m}{x^n}\))m+n (\(\frac{x^n}{x^l}\))n+\(l\) (\(\frac{x^l}{x^m}\))\(l\)+m = 1
সমাধানঃ-
| (\(\frac{x^m}{x^n}\))m+n (\(\frac{x^n}{x^l}\))n+\(l\) (\(\frac{x^l}{x^m}\))\(l\)+m |
| = (xm-n)m+n (xn-l)n+l (xl-m)l+m |
| = x(m-n)(m+n) . x(n-l)(n+l) . x(l-m)(l+m) |
| =xm2-n2 . xn2-l2 . xl2-m2 |
| = xm2-n2+n2-l2+l2-m2 |
| = x0 |
| = 1 |
(iii)(\(\frac{x^m}{x^n}\))m+n-\(l\) (\(\frac{x^n}{x^l}\))n+\(l\)-m (\(\frac{x^l}{x^m}\))\(l\)+m-n = 1
সমাধানঃ-
| (\(\frac{x^m}{x^n}\))m+n-\(l\) (\(\frac{x^n}{x^l}\))n+\(l\)-m (\(\frac{x^l}{x^m}\))\(l\)+m-n |
| = (xm-n)m+n-l (xn-l)n+l-m (xl-m)l+m-n |
| = x(m-n)(m+n-l) . x(n-l)(n+l-m) . x(l-m)(l+m-n) |
| =xm2-n2-l(m-n) . xn2-l2-m(n-l) . xl2-m2-n(l-m) |
| =xm2-n2-lm+ln . xn2-l2-mn+lm . xl2-m2-nl+mn |
| =xm2-n2-lm+ln+n2-l2-mn+lm+l2-m2-nl+mn |
| = x0 |
| = 1 |
(iv) \((a^{\frac{1}{x-y}})^{\frac{1}{x-z}} \times (a^{\frac{1}{y-z}})^{\frac{1}{y-x}} \times (a^{\frac{1}{z-x}})^{\frac{1}{z-y}}\)
সমাধানঃ-
| \((a^{\frac{1}{x-y}})^{\frac{1}{x-z}} \times (a^{\frac{1}{y-z}})^{\frac{1}{y-x}} \times (a^{\frac{1}{z-x}})^{\frac{1}{z-y}}\) |
| \(= a^{\frac{1}{(x-y)(x-z)}} \times a^{\frac{1}{(y-z)(y-x)}} \times a^{\frac{1}{(z-x)(z-y)}}\) |
| \(= a^{\frac{1}{(x-y)(x-z)} + \frac{1}{(y-z)(y-x)} + \frac{1}{(z-x)(z-y)}}\) |
এখন
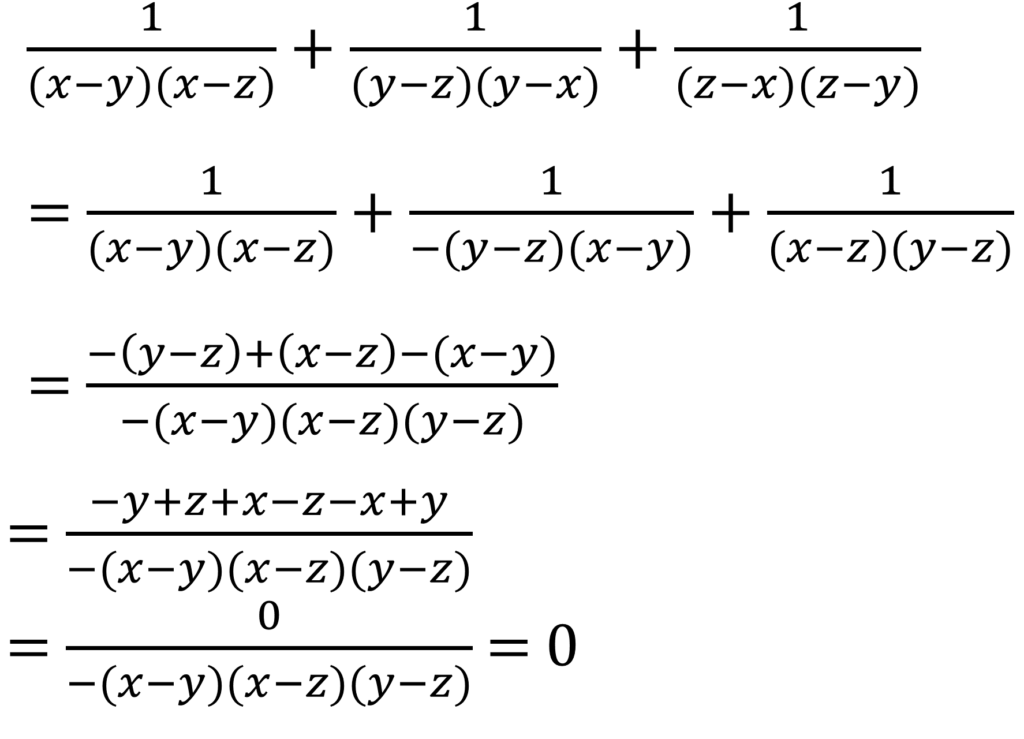
অতএব
| \( a^{\frac{1}{(x-y)(x-z)} + \frac{1}{(y-z)(y-x)} + \frac{1}{(z-x)(z-y)}}\) |
| = a0 |
| = 1 |
5. x + z =2y এবং b²=ac হলে দেখাই যে ay-z bz-xcx-y=1
সমাধানঃ-
| দেওয়া আছে, |
|---|
| x + z = 2y |
| বা, z = 2y – x —(i) |
| ay-z bz-xcx-y |
| (i) নং থেকে z -এর মান বসিয়ে পাই, |
| = ay-z b2y-x-xcx-y |
| = ay-z b2y-2xcx-y |
| = ay-z b2(y-x)cx-y |
| = ay-z (b2)(y-x) cx-y |
| = ay-z (ac)(y-x) cx-y [ দেওয়া আছে b2=ac] |
| = ay-z ay-xcy-x cx-y |
| = ay-z+y-xcy-x+x-y |
| = a0c0 |
| = 1×1 |
| = 1 |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  |
6. a=xyp-1 , b=xyq-1 এবং c=xyr-1 হলে দেখাই যে, aq-rbr-pcp-q = 1
সমাধানঃ-
| aq-rbr-pcp-q |
| = (xyp-1)q-r (xyq-1)r-p (xyr-1)p-q |
| = xq-ry(p-1)(q-r) xr-py(q-1)(r-p) xp-qy(r-1)(p-q) |
| = xq-r+r-p+p-q y(p-1)(q-r)+(q-1)(r-p)+(r-1)(p-q) |
| = x0 yp(q-r)-(q-r)+q(r-p)-(r-p)+r(p-q)-(p-q) |
| = ypq-pr-q+r+qr-pq-r+p+pr-qr-p+q |
| = y0 |
| = 1 |
7. \(x^{\frac{1}{a}} = y^{\frac{1}{b}} = z^{\frac{1}{c}}\) এবং xyz = 1 হলে দেখাই যে , a + b + c = 0
সমাধানঃ-
ধরি, \(x^{\frac{1}{a}} = y^{\frac{1}{b}} = z^{\frac{1}{c}} = k\)(ধ্রুবক)
অতএব
| \(x^{\frac{1}{a}} = k\) | \(y^{\frac{1}{b}} = k\) | \(z^{\frac{1}{c}} = k\) |
| বা,\((x^{\frac{1}{a}})^a = k^a\) | বা,\((y^{\frac{1}{b}})^b = k^b\) | বা,\((z^{\frac{1}{c}})^c = k^c\) |
| বা, x = ka | বা, y = kb | বা, z = kc |
আবার,
xyz = 1
অতএব
ka . kb . kc = 1
বা, ka+b+c = k0
বা, a + b + c = 0
8. ax = by = cz এবং abc = 1 হলে দেখাই যে, xy + yz + zx = 0
সমাধানঃ-
ধরি, ax = by = cz = k(ধ্রুবক)
অতএব
| ax = k | by = k | cz = k |
| বা, a = k\(\frac{1}{x}\) | বা, b = k\(\frac{1}{y}\) | বা, c = k\(\frac{1}{z}\) |
আবার,
| abc = 1 |
| বা, \(k^{\frac{1}{x}}.k^{\frac{1}{y}}.k^{\frac{1}{z}}\) = 1 |
| বা, \(k^{(\frac{1}{x} + \frac{1}{y} + \frac{1}{z})} = k^0\) |
| বা, \(\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = 0\) |
| বা, \(\frac{xy+yz+zx}{xyz} = 0\) |
| বা, xy + yz + zx = 0 |
9. সমাধান করি:
(i) 49x= 73
সমাধানঃ-
| 49x= 73 |
| বা, (72)x = 73 |
| বা, 72x = 73 |
| বা, 2x = 3 |
| বা, x = \(\frac{3}{2}\) |
(ii) 2x+2 + 2x – 1 = 9
সমাধানঃ-
| 2x+2 + 2x – 1 = 9 |
| বা, 22.2x + \(\frac{2^x}{2}\) = 9 |
| বা, 2x (4 + \(\frac{1}{2}\)) = 9 |
| বা, 2x . \(\frac{9}{2}\) = 9 |
| বা, 2x = 9 ×\(\frac{2}{9}\) |
| বা, 2x = 21 |
| বা, x = 1 |
(iii) 2x+1 + 2x +2 = 48
সমাধানঃ-
| 2x+1 + 2x +2 = 48 |
| বা, 2x . 2 + 2x . 22 = 48 |
| বা, 2x (2 + 4) = 48 |
| বা, 2x . 6 = 48 |
| বা, 2x = \(\frac{48}{6}\) = 8 |
| বা, 2x = 23 |
| বা, x = 3 |
(iv) 24x . 43x – 1 = \(\frac{4^{2x}}{2^{3x}}\)
সমাধানঃ-
| 24x . 43x – 1 = \(\frac{4^{2x}}{2^{3x}}\) |
| বা, 24x . 22(3x – 1) = \(\frac{2^{2.2x}}{2^{3x}}\) |
| বা, 24x . 26x – 2 = 24x-3x |
| বা, \(\frac{2^{6x}}{2^2} = \frac{1}{2^{3x}}\) |
| বা, 26x .23x = 22 |
| বা, 26x+3x = 22 |
| বা, 29x = 22 |
| বা, 9x = 2 |
| বা, \(x = \frac{9}{2}\) |
(v) 9 × 81x = 272-x
সমাধানঃ-
| 9 × 81x = 272-x |
| বা, 32 × (34)x = (33)2-x |
| বা, 32 × 34x = 36-3x |
| বা, 32 × 34x = \(\frac{3^6}{3^{3x}}\) |
| বা, 34x . 33x= \(\frac{3^6}{3^{2}}\) |
| বা, 34x+3x= 36-2 |
| বা, 37x= 34 |
| বা, 7x = 4 |
| বা, \(x = \frac{4}{7}\) |
(vi) 25x+4 + 29 = 210
সমাধানঃ-
| 25x+4 + 29 = 210 |
| বা, 25x+4 = 210 – 29 |
| বা, 25x . 24 = 29 (2 – 1) |
| বা, 25x = \(\frac{2^9}{2^4}\) |
| বা, 25x = 29-4 |
| বা, 25x = 25 |
| বা, 5x = 5 |
| বা, x = 1 |
(vii) 62x+4 = 33x . 2x+8
সমাধানঃ-
| 62x+4 = 33x . 2x+8 |
| বা, (2.3)2x+4 = 33x . 2x . 28 |
| বা, (2.3)2x (2.3)4 = 33x . 2x . 28 |
| বা, 22x.32x.24.34 = 33x . 2x . 28 |
| বা, \(\frac{2^{2x}.3^{2x}}{3^{3x}.2^x} = \frac{2^8}{2^4 . 2^4}\) |
| বা, \(\frac{2^{2x-x}}{3^{3x-2x}} = \frac{2^4}{3^4}\) |
| বা, \((\frac{2}{3})^x = (\frac{2}{3})^4\) |
| বা, \(x = 4\) |
(viii) \(2^{x^2-4} = 3^{x^2-4}\)
সমাধানঃ-
| \(2^{x^2 – 4} = 3^{x^2 – 4}\) |
| বা, \(\frac{2^{x^2 – 4}}{3^{x^2 – 4}} = 1\) |
| বা,\((\frac{2}{3})^{x^2 – 4} = (\frac{2}{3})^0\) |
| বা, \(x^2 – 4 = 0\) |
| বা, \(x^2 = 4\) |
| বা, \(x = \pm2\) |
10. বহু বিকল্পীয় প্রশ্ন (M.C.Q.):
(i) (0.243)0.2 x (10)0.6 -এর মান
উত্তরঃ-
(b) 3
| (0.243)0.2 x (10)0.6 |
| \(= (\frac{243}{1000})^{\frac{2}{10}} \times 10^{\frac{6}{10}}\) |
| \(= (\frac{(3)^5}{10^3})^{\frac{1}{5}} \times 10^{\frac{3}{5}}\) |
| \(= 3 \times 10^{-\frac{3}{5}} \times 10^{\frac{3}{5}}\) |
| \(= 3\) |
(ii) 2½ × 2-½ × (16)½ এর মান
উত্তরঃ-
(c) 4
[ কারণ-
2½ × 2-½ × (16)½
=2½-½ × (24)½
= 1 × 24×½
= 22
= 4 ]
(iii) 4x = 83 হলে, x এর মান
উত্তরঃ-
(b) \(\frac{9}{2}\)
[ কারণ-
4x = 83
বা, (22)x = (23)3
বা, 22x = 29
বা, 2x = 9
বা, \(x = \frac{9}{2}\) ]
(iv) 20-x = \(\frac{1}{7}\) হলে, (20)2x -এর মান
উত্তরঃ-
(c) 49
[ কারণ-
20-x = \(\frac{1}{7}\)
বা, 20x = 7
বা, (20x )2= 72
বা, 202x = 49 ]
(v) 4 × 5x = 500 হলে, xx এর মান
উত্তরঃ-
(d) 27
[ কারণ-
4 × 5x = 500
বা, 5x = 125
বা, 5x = 53
বা, x = 3
33 = 27 ]
11. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ
(i) (27)x = (81)y হলে, x : y কত হয় লিখি ।
সমাধানঃ-
| (27)x = (81)y |
| বা, (33 )x = (34 )y |
| বা, 33x = 34y |
| বা, 3x = 4y |
| বা, \(\frac{x}{y} = \frac{4}{3}\) |
| বা, x : y = 4 : 3 |
| ∴ (27)x = (81)y হলে, x : y = 4 : 3 । |
(ii) (55 + 0.01)2 – (55 – 0.01)2 = 5x হলে, x এর মান কত হিসাব করে লিখি ।
সমাধানঃ-
| ধরি 55 = a এবং 0.01 = b |
| (55 + 0.01)2 – (55 – 0.01)2 |
| = (a+b)2 – (a-b)2 |
| = 4ab |
| a ও b এর মান বসিয়ে পাই, |
| 4× 55 × 0.01 |
| = 4 × 55 × \(\frac{1}{100}\) |
| = 55 × \(\frac{1}{25}\) |
| = 55 × \(\frac{1}{5^2}\) |
| = 55 × 5-2 |
| = 55-2 = 53 |
অতএব
(55 + 0.01)2 – (55 – 0.01)2 = 5x
বা, 53 = 5x
বা, x = 3
| ∴ (55 + 0.01)2 – (55 – 0.01)2 = 5x হলে, x এর মান 3 । |
(iii) 3 × 27x = 9x+4 হলে, x এর মান কত হিসাব করে লিখি।
সমাধানঃ-
| 3 × 27x = 9x+4 |
| বা, 3 × (33 )x = (32 )x + 4 |
| বা, 3 × 33x = 32x+8 |
| বা, 33x-2x = 38-1 |
| বা, 3x = 37 |
| বা, x = 7 |
| ∴ 3 × 27x = 9x+4 হলে, x এর মান 7 । |
(iv) ((64)½)\(\frac{1}{3}\) -এর মান কত হিসাব করে লিখি।
সমাধানঃ-
| ((64)½)\(\frac{1}{3}\) |
| = (26 )\(\frac{1}{6}\) |
| = 2 |
| ∴((64)½)\(\frac{1}{3}\) = 2 |
(v) 333 এবং (33 )3 এর মধ্যে কোনটি বৃহত্তর যুক্তিসহ লিখি।
সমাধানঃ-
33 = 27
অতএব
| 333 | (33 )3 |
|---|---|
| = 327 | = 39 |
| ∴333 এবং (33 )3 এর মধ্যে 333 বৃহত্তর |
| WB Class 9 এর গণিত প্রকাশের সমস্ত অধ্যায়ের সমাধান- | |
|---|---|
| অধ্যায় | সমাধান |
| 1. বাস্তব সংখ্যা (Real Numbers) | কষে দেখি 1.1 |
| কষে দেখি 1.2 | |
| কষে দেখি 1.3 | |
| 2. সূচকের নিয়মাবলি (Laws of Indices) | কষে দেখি 2 |
| 3. লেখচিত্র (Graph) | কষে দেখি 3.1 |
| কষে দেখি 3.2 | |
| 4. স্থানাঙ্ক জ্যামিতি : দূরত্ব নির্ণয় (Co-ordinate Geometry: Distance Formula) | কষে দেখি 4 |
| 5. রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) (Linear Simultaneous Equations) | কষে দেখি 5.1 |
| কষে দেখি 5.2 | |
| কষে দেখি 5.3 | |
| কষে দেখি 5.4 | |
| কষে দেখি 5.5 | |
| কষে দেখি 5.6 | |
| কষে দেখি 5.7 | |
| 6. সামান্তরিকের ধর্ম (Properties of Parallelogram) | কষে দেখি 6 |
| 7. বহুপদী সংখ্যামালা (Polynomial) | কষে দেখি 7.1 |
| কষে দেখি 7.2 | |
| কষে দেখি 7.3 | |
| কষে দেখি 7.4 | |
| 8. উৎপাদকে বিশ্লেষণ (Factorisation) | কষে দেখি 8.1 |
| কষে দেখি 8.2 | |
| কষে দেখি 8.3 | |
| কষে দেখি 8.4 | |
| কষে দেখি 8.5 | |
| 9. ভেদক ও মধ্যবিন্দু সংক্রান্ত উপপাদ্য (Transversal & Mid-Point Theorem). | কষে দেখি 9 |
| 10. লাভ ও ক্ষতি (Profit and Loss) | কষে দেখি 10.1 |
| কষে দেখি 10.2 | |
| 11. রাশিবিজ্ঞান (Statistics) | কষে দেখি 11.1 |
| কষে দেখি 11.2 | |
| 12. ক্ষেত্রফল সংক্রান্ত উপপাদ্য (Theorems on Area) | কষে দেখি 12 |
| 13. সম্পাদ্য : ত্রিভুজের সমান ক্ষেত্রফল বিশিষ্ট সামান্তরিক অঙ্কন | কষে দেখি 13 |
| 14. সম্পাদ্য : চতুর্ভুজের সমান ক্ষেত্রফল বিশিষ্ট ত্রিভুজ অঙ্কন | কষে দেখি 14 |
| 15. ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল (Area & Perimeter of Triangle & Quadrilateral) | কষে দেখি 15.1 |
| কষে দেখি 15.2 | |
| কষে দেখি 15.3 | |
| 16. বৃত্তের পরিধি (Circumference of Circle) | কষে দেখি 16 |
| 17. সমবিন্দু সংক্রান্ত উপপাদ্য (Theorems on concurrence) | কষে দেখি 17 |
| 18. বৃত্তের ক্ষেত্রফল (Area of Circle) | কষে দেখি 18 |
| 19. স্থানাঙ্ক জ্যামিতি: সরলরেখাংশের অন্তর্বিভক্ত ও বহিঃবিভক্ত (Co-ordinate Geometry: Internal and External Division of Straight-Line Segment) | কষে দেখি 19 |
| 20. স্থানাঙ্ক জ্যামিতি: ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল (Co-ordinate Geometry: Area of Triangular Region) | কষে দেখি 20 |
| 21. লগারিদম (Logarithm) | কষে দেখি 21 |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
এই কষে দেখি 2 Class 9|Koshe Dekhi 2 Class 9 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।

এখানে তোমরা তোমাদের নবম শ্রেণীতে| Class 9 এ কি কি পড়ানো হয়, মানে তোমাদের নবম শ্রেণী| Class 9 সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

