শ্রেণী-নবম ; অধ্যায় – বহুপদী সংখ্যামালা ; কষে দেখি 7.4
কষে দেখি 7.4 Class 9 এর সুচিপত্রঃ-
কষে দেখি 7.4 Class 9 এর অংকের সমাধান গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ
কষে দেখি 7.4 Class 9 WBBSE বোর্ডের অন্তর্গত তোমাদের বহুপদী সংখ্যামালা অধ্যায়ের চার নম্বর অনুশীলনী। এই Koshe Dekhi 7.4 Class 9 এর অংক গুলিতে বহুপদী সংখ্যামালার উৎপাদক কিভাবে হবে তার পদ্ধতি কাজে লাগিয়ে সমাধান করতে হবে।
কষে দেখি 7.4 Class 9|Koshe Dekhi 7.4 Class 9 এর অংক গুলি সমাধানের জন্যে নিম্নের গুণনীয়ক উপপাদ্যটি আমাদের জানতে হবে।
গুণনীয়ক উপপাদ্য | Factor Theorem :
যদি f(x) কোনো একটি বহুপদী সংখ্যামালা যার মাত্রা n(n ≥ 1) এবং a যেকোনো একটি বাস্তব সংখ্যা হয়, তাহলে
(i) (x – a), f(x) -এর একটি উৎপাদক হবে যদি f(a) = 0 হয়,
এবং
(ii) f(a)=0 হবে যদি (x – a), f(x) -এর একটি উৎপাদক হয়।
আগামিতে এই কষে দেখি 7.4 Class 9 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 7.4 Class 9 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 7.4 Class 9 তারপর 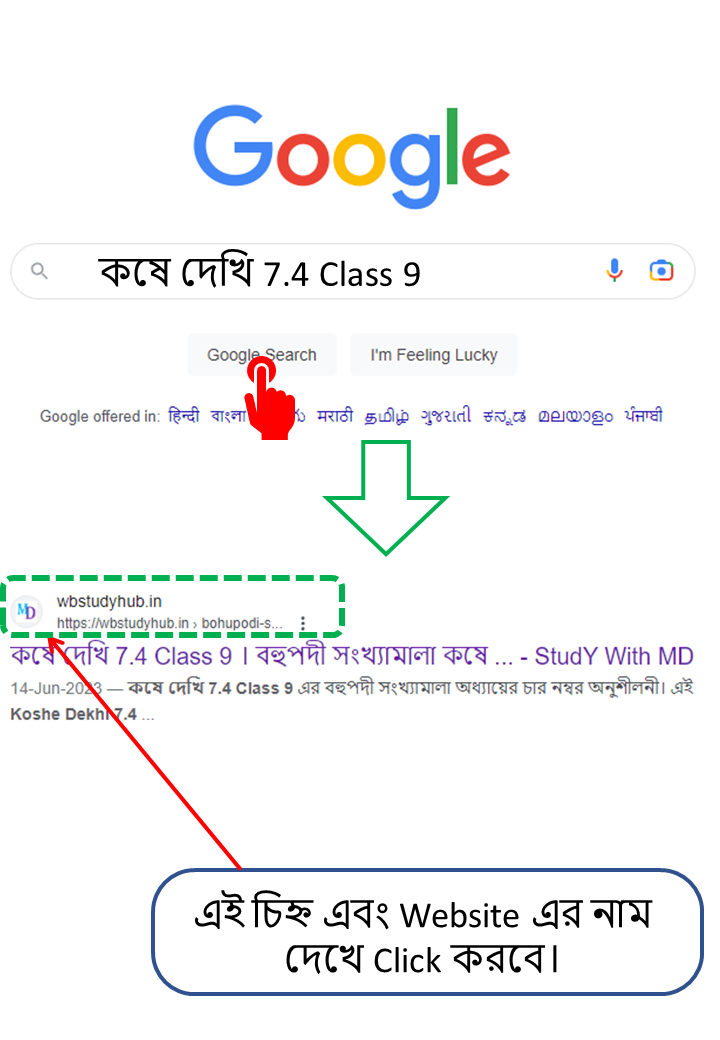 |
কষে দেখি 7.4 Class 9 এর অংক ভিডিওতে দেখার জন্যে-
কষে দেখি 7.4 | Koshe Dekhi 7.4
সমাধানঃ-
1. নীচের বহুপদী সংখ্যামালাগুলির মধ্যে কোনগুলির একটি উৎপাদক (x + 1) হিসাব করে লিখি।
(i) 2x3 + 3x2 – 1
সমাধানঃ-
x + 1 = x – (-1)
ধরি, f(x) = 2x3 + 3x2 – 1
অতএব,
| f(-1) |
| = 2(-1)3 + 3(-1)2 – 1 |
| = -2 + 3 – 1 |
| = 0 |
| ∴ (x + 1) , f(x) = 2x3 + 3x2 – 1 এর একটি উৎপাদক । |
(ii) x4 + x3 – x2 + 4x + 5
সমাধানঃ-
x + 1 = x – (-1)
ধরি, f(x) = x4 + x3 – x2 + 4x + 5
অতএব,
| f(-1) |
| = (-1)4 + (-1)3 – (-1)2 + 4(-1) + 5 |
| = 1 – 1 – 1 -4 + 5 |
| = 0 |
| ∴ (x + 1) , f(x) = x4 + x3 – x2 + 4x + 5 এর একটি উৎপাদক । |
(iii) 7x3 + x2 + 7x + 1
সমাধানঃ-
x + 1 = x – (-1)
ধরি, f(x) = 7x3 + x2 + 7x + 1
অতএব,
| f(-1) |
| = 7(-1)3 + (-1)2 + 7(-1) + 1 |
| = -7 + 1 – 7 + 1 |
| = -12 ≠ 0 |
| ∴ (x + 1) , f(x) = 7x3 + x2 + 7x + 1 এর একটি উৎপাদক নয় । |
(iv) 3 + 3x – 5x3 – 5x4
সমাধানঃ-
x + 1 = x – (-1)
ধরি, f(x) = 3 + 3x – 5x3 – 5x4
অতএব,
| f(-1) |
| = 3 + 3(-1) – 5(-1)3 – 5(-1)4 |
| = 3 – 3 + 5 – 5 |
| = 0 |
| ∴ (x + 1) , f(x) = 3 + 3x – 5x3 – 5x4 এর একটি উৎপাদক । |
(v) x4 + x2 + x + 1
সমাধানঃ-
x + 1 = x – (-1)
ধরি, f(x) = x4 + x2 + x + 1
অতএব,
| f(-1) |
| = (-1)4 + (-1)2 + (-1) + 1 |
| = 1 + 1 – 1 + 1 |
| = 2 ≠ 0 |
| ∴ (x + 1) , f(x) = x4 + x2 + x + 1 এর একটি উৎপাদক নয় । |
(vi) x3 + x2 + x + 1
সমাধানঃ-
x + 1 = x – (-1)
ধরি, f(x) = x3 + x2 + x + 1
অতএব,
| f(-1) |
| = (-1)3 + (-1)2 + (-1) + 1 |
| = -1 + 1 – 1 + 1 |
| = 0 |
| ∴ (x + 1) , f(x) = x3 + x2 + x + 1এর একটি উৎপাদক । |
2. গুণনীয়ক উপপাদ্য ব্যবহার করে নীচের বহুপদী সংখ্যামালাগুলি f(x)-এর একটি উৎপাদক g(x) কিনা লিখি।
(i) f(x) = x4 – x2 – 12 এবং g (x) = x + 2
সমাধানঃ-
g (x) = x + 2 = x – (-2)
অতএব,
| f(-2) |
| = (-2)4 – (-2)2 – 12 |
| = 16 – 4 – 12 |
| = 0 |
| ∴ g(x)= x + 2 , f(x) = x4 – x2 – 12 এর একটি উৎপাদক । |
(ii) f(x) = 2x3 + 9x2 – 11x – 30 এবং g (x) = x + 5
সমাধানঃ-
g (x) = x + 5 = x – (-5)
অতএব,
| f(-5) |
| = 2(-5)3 + 9(-5)2 – 11(-5) – 30 |
| = – 250 + 225 + 55 – 30 |
| = 0 |
| ∴ g(x)= x + 5 , f(x) = 2x3 + 9x2 – 11x – 30 এর একটি উৎপাদক । |
(iii) f(x) = 2x3 + 7x2 – 24x – 45 এবং g (x) = x – 3
সমাধানঃ-
g (x) = x – 3
অতএব,
| f(3) |
| = 2.33 + 7.32 – 24.3 – 45 |
| = 54 + 63 – 72 – 45 |
| = 0 |
| ∴ g(x)= x – 3 , f(x) = 2x3 + 7x2 – 24x – 45 এর একটি উৎপাদক । |
(iv) f(x) = 3x3 + x2 – 20x + 12, এবং g (x) = 3x – 2
সমাধানঃ-
g (x) = 3x – 2 = 3(x – \(\frac{2}{3}\))
অতএব,
| f(\(\frac{2}{3}\)) |
| = 3(\(\frac{2}{3}\))3 + (\(\frac{2}{3}\))2 – 20(\(\frac{2}{3}\)) + 12 |
| = \(\frac{8}{9} + \frac{4}{9} – \frac{40}{3} + 12\) |
| = \(\frac{8 + 4 – 120 + 108}{9}\) |
| = \(\frac{120-120}{9} = 0\) |
| ∴ g(x)= 3x – 2 , f(x) = 3x3 + x2 – 20x + 12 এর একটি উৎপাদক । |
3. k- এর মান কত হলে x + 2 দ্বারা 2x4 + 3x3 + 2kx2 + 3x + 6 বহুপদী সংখ্যামালাটি বিভাজ্য হবে হিসাব করে লিখি।
সমাধানঃ-
x + 2 = x – (-2)
ধরি, f(x) = 2x4 + 3x3 + 2kx2 + 3x + 6
f(x) কে {x – (-2)} দ্বারা বিভাজ্য হবে যখন {x – (-2)} দ্বারা f(x) -কে ভাগ করলে ভাগশেষ শূন্য হবে।
অতএব,
| f(-2) = 0 |
| বা, 2(-2)4 + 3(-2)3 + 2k(-2)2 + 3(-2) + 6 = 0 |
| বা, 32 – 24 + 8k – 6 + 6 = 0 |
| বা, 8k = – 8 |
| বা, k = -1 |
| ∴ k- এর মান -1 হলে x + 2 দ্বারা 2x4 + 3x3 + 2kx2 + 3x + 6 বহুপদী সংখ্যামালাটি বিভাজ্য হবে। |
4. k এর মান কত হলে, নীচের বহুপদী সংখ্যামালাগুলি f(x) – এর একটি উৎপাদক g (x) হবে হিসাব করি:
(i) f(x) = 2x3 + 9x2 + x + k এবং g (x) = x – 1
সমাধানঃ-
g(x) = x – 1
f(x) = 2x3 + 9x2 + x + k
f(x) এর একটি উৎপাদক g(x) = x – 1 হবে , যখন f(1) = 0 হবে ।
অতএব,
| f(1) = 0 |
| বা, 2.13 + 9.12 + 1 + k = 0 |
| বা, 2 + 9 + 1 + k = 0 |
| বা, k = – 12 |
| ∴ k- এর মান -12 হলে g(x), f(x) এর একটি উৎপাদক হবে। |
(ii) f(x) = kx2 -3x + k এবং g (x) = x – 1
সমাধানঃ-
g(x) = x – 1
f(x) = kx2 -3x + k
f(x) এর একটি উৎপাদক g(x) = x – 1 হবে যখন f(1) = 0 হবে ।
অতএব,
| f(1) = 0 |
| বা, k.12 -3.1 + k = 0 |
| বা, k – 3 + k = 0 |
| বা, 2k = 3 |
| বা, k = \(\frac{3}{2}\) |
| ∴ k- এর মান \(\frac{3}{2}\) হলে g(x), f(x) এর একটি উৎপাদক হবে। |
(iii) f(x) = 2x4 + x3 – kx2 – x + 6 এবং g (x) = 2x – 3
সমাধানঃ-
g(x) = 2x – 3 = 2(x – \(\frac{3}{2}\))
f(x) = 2x4 + x3 – kx2 – x + 6
f(x) এর একটি উৎপাদক g(x) = 2(x – \(\frac{3}{2}\)) হবে যখন f(\(\frac{3}{2}\)) = 0 হবে ।
অতএব,
| f(\(\frac{3}{2}\)) = 0 |
| বা, 2(\(\frac{3}{2}\))4 + (\(\frac{3}{2}\))3 – k(\(\frac{3}{2}\))2 – \(\frac{3}{2}\) + 6 = 0 |
| বা, \(\frac{81}{8} + \frac{27}{8} – \frac{9k}{4} – \frac{3}{2} + 6 = 0\) |
| বা, \(\frac{81 + 27 – 18k – 12 + 48}{8} = 0\) |
| বা, 144 – 18k = 0 |
| বা, k = \(\frac{144}{18}\) |
| বা, k = 8 |
| ∴ k- এর মান 8 হলে g(x), f(x) এর একটি উৎপাদক হবে। |
(iv) f(x) = 2x3 + kx2 + 11x + k + 3 এবং g (x) = 2x – 1
সমাধানঃ-
g(x) = 2x – 1 = 2(x – ½)
ধরি, f(x) = 2x3 + kx2 + 11x + k + 3
f(x) এর একটি উৎপাদক g(x) = 2(x – ½) হবে যখন f(½) = 0 হবে ।
অতএব,
| f(½) = 0 |
| বা, 2(½)3 + k(½)2 + 11(½) + k + 3 = 0 |
| বা, \(\frac{1}{4} + \frac{k}{4} + \frac{11}{2} + k + 3 = 0\) |
| বা, (1 + k + 22 + 4k + 12) = 0 |
| বা, 5k + 35 = 0 |
| বা, k = -7 |
| ∴ k- এর মান -7 হলে g(x), f(x) এর একটি উৎপাদক হবে। |
5. ax4 + 2x3 – 3x2 + bx – 4 বহুপদী সংখ্যামালার উৎপাদক x2 – 4 হলে, a ও b এর মান কত হবে হিসাব করে লিখি।
সমাধানঃ-
x2 – 4 = (x + 2)(x – 2)
(x2 – 4) যদি উৎপাদক হয় তাহলে (x + 2) এবং (x – 2) উভয়েই উৎপাদক হবে।
ধরি, f(x) = ax4 + 2x3 – 3x2 + bx – 4
এখন (x + 2) = {x – (-2)}, f(x) -এর একটি উৎপাদক হবে যখন f(-2) = 0 হবে এবং (x – 2), f(x) -এর একটি উৎপাদক হবে যখন f(2) = 0
অতএব,
| f(-2) | = a(-2)4 + 2(-2)3 – 3(-2)2 + b(-2) – 4 |
| = 16a – 16 – 12 – 2b – 4 | |
| = 16a – 2b – 32 | |
| ∴ f(-2) = 16a – 2b – 32 = 0 ⇒ 8a – b = 16 ——–(i) | |
| f(2) | = a(2)4 + 2(2)3 – 3(2)2 + b(2) – 4 |
| = 16a + 16 – 12 + 2b – 4 | |
| = 16a + 2b | |
| ∴ f(2) = 16a + 2b = 0 বা, 8a + b = 0 ——(ii) | |
(i) নং ও (ii) নং যোগ করে পাই,
8a – b + 8a + b = 16
বা, 16a = 16
বা, a = 1
(ii) নং এ a=1বসিয়ে পাই,
b = -8
| ∴ a = 1 b = -8 |
6. x3 + 3x2 + 2ax + b বহুপদী সংখ্যামালার দুটি উৎপাদক (x + 1) এবং (x + 2) হলে, a ও b এর মান কত হবে হিসাব করে লিখি।
সমাধানঃ-
ধরি, f(x) = x3 + 3x2 + 2ax + b
f(x) = x3 + 3x2 + 2ax + b বহুপদী সংখ্যামালার দুটি উৎপাদক (x + 1) এবং (x + 2) হলে f(-1)=0 এবং f(-2)=0 হবে।
| f(-1) | =(-1)3 + 3(-1)2 + 2a(-1) + b |
| = -1 + 3 – 2a + b | |
| = -2a + b + 2 | |
| ∴ f(-1) = -2a + b + 2 = 0 ⇒ – 2a + b = -2 ——–(i) | |
| f(-2) | = (-2)3 + 3(-2)2 + 2a(-2) + b |
| = -8 + 12 – 4a + b | |
| = -4a + b + 4 | |
| ∴ f(-2) = – 4a + b + 4= 0 বা, – 4a + b = -4 ——(ii) | |
(i) নং থেকে (ii) নং বিয়োগ করে পাই,
-2a + b – (-4a + b) = -2 – (-4)
বা, -2a + b + 4a – b = -2 + 4
বা, 2a = 2
বা, a = 1
(i) নং এ a = 1 বসিয়ে পাই,
b = 0
| ∴ a = 1 b = 0 |
7. ax3 + bx2 + x – 6 বহুপদী সংখ্যামালাকে (x – 2) দ্বারা ভাগ করলে ভাগশেষ 4 হয় এবং এই বহুপদী সংখ্যামালার একটি উৎপাদক x + 2 হলে, a ও b এর মান কত হবে হিসাব করি।
সমাধানঃ-
ধরি, f(x) = ax3 + bx2 + x – 6
ax3 + bx2 + x – 6 বহুপদী সংখ্যামালাকে (x – 2) দ্বারা ভাগ করলে ভাগশেষ 4 হয় অর্থাৎ, f(2)=4 এবং এই বহুপদী সংখ্যামালার একটি উৎপাদক x + 2, অতএব f(-2)=0
| f(2) | = a(2)3 + b(2)2 + 2 – 6 |
| = 8a + 4b – 4 | |
| ∴ f(2) = 8a + 4b – 4 = 0 ⇒ 2a + b = 2 ——–(i) | |
| f(-2) | = a(-2)3 + b(-2)2 – 2 – 6 |
| = -8a + 4b – 8 | |
| ∴ f(-2) = – 8a + 4b – 8 = 0 বা, – 2a + b = 2 ——(ii) | |
(i) নং ও (ii) নং যোগ করে পাই,
2a + b – 2a + b = 2 + 2
বা, 2b = 4
বা, b = 2
(i) নং এ b = 2 বসিয়ে পাই,
a = 0
| ∴ a = 0 b = 2 |
8. n যেকোনো ধনাত্মক পূর্ণসংখ্যা (যুগ্ম বা অযুগ্মা) হলে, দেখাই যে, xn – yn বহুপদী সংখ্যামালাটির একটি উৎপাদক x – y.
সমাধানঃ-
ধরি, f(x) = xn – yn
| f(y) = yn – yn |
| বা, f(y) = 0 |
| ∴ n যেকোনো ধনাত্মক পূর্ণ সংখ্যার জন্যে f(y) = 0 হবে। |
| সুতরাং , xn – yn বহুপদী সংখ্যামালাটির একটি উৎপাদক x – y |
9. n যেকোনো অযুগ্ম ধনাত্মক পূর্ণসংখ্যা হলে, দেখাই যে xn + yn বহুপদী সংখ্যামালাটির একটি উৎপাদক x + y
সমাধানঃ-
ধরি, f(x) = xn + yn
| f(-y) = (-y)n – yn |
| অতএব, f(-y) = 0 যখন n একটি অযুগ্ম ধনাত্মক পূর্ণ সংখ্যা হবে অর্থাৎ, n=2m |
| f(-y) = (-y)2m – y2m |
| বা, f(-y) = (-1)2my2m – y2m |
| বা, f(-y) = y2m – y2m = 0 |
10. n যেকোনো ধনাত্মক পূর্ণসংখ্যা (যুগ্ম বা অযুগ্ম) হলে, দেখাই যে xn + yn বহুপদী সংখ্যামালাটির একটি উৎপাদক কখনই x – y হবে না।
সমাধানঃ-
ধরি, f(x) = xn + yn
f(y) = yn + yn
বা, f(y) = 2yn
এখন f(y) = 0 অর্থাৎ, 2yn = 0 হবে শুধুমাত্র y=0 এর জন্যে। y এর অন্য কোনো মানের জন্যে f(y) = 0 হবেনা।
11. বহু বিকল্পীয় প্রশ্ন (M. C. Q.):
(i) x3 + 6x2 + 4x + k বহুপদী সংখ্যামালাটি (x + 2) দ্বারা বিভাজ্য হলে, k-এর মান
উত্তরঃ- (c) – 8
সমাধানঃ-
ধরি, f(x) = x3 + 6x2 + 4x + k
f(-2)
= (-2)3 + 6(-2)2 + 4(-2) + k
= – 8 + 24 – 8 + k
= k + 8
অতএব f(-2) = 0
বা, k + 8 = 0
বা, k = -8
(ii) f(x) বহুপদী সংখ্যামালার f (-½)=0 হলে, f(x) এর একটি উৎপাদক হবে
উত্তরঃ- (b) 2x + 1
(iii) f(x) বহুপদী সংখ্যামালার (x – 1 ) একটি উৎপাদক, কিন্তু g (x) বহুপদী সংখ্যামালার উৎপাদক নয়। সুতরাং (x – 1 ) একটি উৎপাদক হবে
উত্তরঃ- (a)
(iv) xn + 1 বহুপদী সংখ্যামালার (x + 1) একটি উৎপাদক হবে যখন
উত্তরঃ- (a) n একটি অযুগ্ম ধনাত্মক পূর্ণসংখ্যা
(v) an4 + bn3 + cn2 + dn + e বহুপদী সংখ্যামালার n2 – 1 উৎপাদক হলে
উত্তরঃ- (a) a+c+e=b+d
সমাধানঃ-
ধরি, f(n) = an4 + bn3 + cn2 + dn + e
n2 – 1 উৎপাদক
অতএব f(-1) = 0 এবং f(1) = 0
f(-1)
= a(-1)4 + b(-1)3 + c(-1)2 + d(-1) + e
= a – b + c – d + e
এখন f(-1) = 0
বা, a – b + c – d + e = 0
বা, a + c + e = b + d
12. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ
(i) x3 + ax2 – 2x + a – 12 বহুপদী সংখ্যামালার x + a একটি উৎপাদক হলে, a-এর মান কত হিসাব করে লিখি।
সমাধানঃ-
ধরি, f(x) = x3 + ax2 – 2x + a – 12
f(x)=x3 + ax2 – 2x + a – 12 বহুপদী সংখ্যামালার x + a একটি উৎপাদক হলে f(-a) = 0 হবে।
f(-a) = 0
বা, (-a)3 + a(-a)2 – 2(-a) + a – 12 = 0
বা, -a3 + a3 + 2a + a – 12 = 0
বা, a = 4
(ii) k2x3 – kx2 + 3kx – k বহুপদী সংখ্যামালার x – 3 একটি উৎপাদক হলে, k-এর মান কত হিসাব করে লিখি।
সমাধানঃ-
ধরি, f(x) = k2x3 – kx2 + 3kx – k
f(x)=x3 + ax2 – 2x + a – 12 বহুপদী সংখ্যামালার x – 3 একটি উৎপাদক হলে f(3) = 0 হবে।
f(3) = 0
বা, k2.33 – k.32 + 3k.3 – k = 0
বা, 27k2 – 9k + 9k – k = 0
বা, 27k2 – k = 0
বা, k(27k – 1) = 0
বা, k = 0 অথবা, k = \(\frac{1}{27}\)
(iii) f(x) = 2x + 5 হলে, f(x) + f(-x) এর মান কত হবে লিখি।
সমাধানঃ-
f(x) = 2x + 5
f(x) + f(-x)
= 2x + 5 + 2(-x) + 5
= 2x – 2x + 10
= 10
(iv) px2 + 5x + r বহুপদী সংখ্যামালার (x – 2 ) এবং (x – ½) উভয়েই উৎপাদক হলে, p ও r -এর মধ্যে সম্পর্ক হিসাব করে লিখি।
সমাধানঃ-
ধরি, f(x) = px2 + 5x + r
f(x) = px2 + 5x + r বহুপদী সংখ্যামালার (x – 2 ) এবং (x – ½) উভয়েই উৎপাদক ।
অতএব , f(2)=0 এবং f(½)=0 ।
f(2) = 0
বা, p(2)2 + 5.2 + r = 0
বা, 4p + r = – 10 ——–(i)
আবার,
f(½) = 0
বা, p(½)2 + 5.½ + r = 0
বা, \(\frac{p}{4} + \frac{5}{2} + r\) = 0
বা, p + 10 + 4r = 0
বা, p + 4r = -10 ——(ii)
(ii) নং কে 4 দিয়ে গুণ করে (i) নং থেকে বিয়োগ করে পাই,
4p + r – 4p – 16r = -10 + 40
বা, -15r = 30
বা, r = -2
r = -2 , (i) নং এ বসিয়ে পাই,
p = -2
অতএব p = r = -2
(v) f(x) = 2x + 3 রৈখিক বহুপদী সংখ্যামালার শূন্য কত হবে লিখি।
সমাধানঃ-
2x + 3 = 0
বা, x = -\(\frac{3}{2}\)
f(x) = 2x + 3 রৈখিক বহুপদী সংখ্যামালার শূন্য -\(\frac{3}{2}\)
| বহুপদী সংখ্যামালা অধ্যায়ের- | |
|---|---|
 | কষে দেখি 7.1 |
| কষে দেখি 7.2 | |
| কষে দেখি 7.3 | |
| WB Class 9 এর গণিত প্রকাশের সমস্ত অধ্যায়ের সমাধান- | |
|---|---|
| অধ্যায় | সমাধান |
| 1. বাস্তব সংখ্যা (Real Numbers) | কষে দেখি 1.1 |
| কষে দেখি 1.2 | |
| কষে দেখি 1.3 | |
| 2. সূচকের নিয়মাবলি (Laws of Indices) | কষে দেখি 2 |
| 3. লেখচিত্র (Graph) | কষে দেখি 3.1 |
| কষে দেখি 3.2 | |
| 4. স্থানাঙ্ক জ্যামিতি : দূরত্ব নির্ণয় (Co-ordinate Geometry: Distance Formula) | কষে দেখি 4 |
| 5. রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) (Linear Simultaneous Equations) | কষে দেখি 5.1 |
| কষে দেখি 5.2 | |
| কষে দেখি 5.3 | |
| কষে দেখি 5.4 | |
| কষে দেখি 5.5 | |
| কষে দেখি 5.6 | |
| কষে দেখি 5.7 | |
| 6. সামান্তরিকের ধর্ম (Properties of Parallelogram) | কষে দেখি 6 |
| 7. বহুপদী সংখ্যামালা (Polynomial) | কষে দেখি 7.1 |
| কষে দেখি 7.2 | |
| কষে দেখি 7.3 | |
| কষে দেখি 7.4 | |
| 8. উৎপাদকে বিশ্লেষণ (Factorisation) | কষে দেখি 8.1 |
| কষে দেখি 8.2 | |
| কষে দেখি 8.3 | |
| কষে দেখি 8.4 | |
| কষে দেখি 8.5 | |
| 9. ভেদক ও মধ্যবিন্দু সংক্রান্ত উপপাদ্য (Transversal & Mid-Point Theorem). | কষে দেখি 9 |
| 10. লাভ ও ক্ষতি (Profit and Loss) | কষে দেখি 10.1 |
| কষে দেখি 10.2 | |
| 11. রাশিবিজ্ঞান (Statistics) | কষে দেখি 11.1 |
| কষে দেখি 11.2 | |
| 12. ক্ষেত্রফল সংক্রান্ত উপপাদ্য (Theorems on Area) | কষে দেখি 12 |
| 13. সম্পাদ্য : ত্রিভুজের সমান ক্ষেত্রফল বিশিষ্ট সামান্তরিক অঙ্কন | কষে দেখি 13 |
| 14. সম্পাদ্য : চতুর্ভুজের সমান ক্ষেত্রফল বিশিষ্ট ত্রিভুজ অঙ্কন | কষে দেখি 14 |
| 15. ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল (Area & Perimeter of Triangle & Quadrilateral) | কষে দেখি 15.1 |
| কষে দেখি 15.2 | |
| কষে দেখি 15.3 | |
| 16. বৃত্তের পরিধি (Circumference of Circle) | কষে দেখি 16 |
| 17. সমবিন্দু সংক্রান্ত উপপাদ্য (Theorems on concurrence) | কষে দেখি 17 |
| 18. বৃত্তের ক্ষেত্রফল (Area of Circle) | কষে দেখি 18 |
| 19. স্থানাঙ্ক জ্যামিতি: সরলরেখাংশের অন্তর্বিভক্ত ও বহিঃবিভক্ত (Co-ordinate Geometry: Internal and External Division of Straight-Line Segment) | কষে দেখি 19 |
| 20. স্থানাঙ্ক জ্যামিতি: ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল (Co-ordinate Geometry: Area of Triangular Region) | কষে দেখি 20 |
| 21. লগারিদম (Logarithm) | কষে দেখি 21 |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
এই কষে দেখি 7.4 Class 9|Koshe Dekhi 7.4 Class 9 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।

এখানে তোমরা তোমাদের নবম শ্রেণীতে| Class 9 এ কি কি পড়ানো হয়, মানে তোমাদের নবম শ্রেণী| Class 9 সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

