শ্রেণী-নবম ; অধ্যায় – লাভ ও ক্ষতি ; কষে দেখি 10.1
কষে দেখি 10.1 Class 9 এর সুচিপত্রঃ-
কষে দেখি 10.1 Class 9 এর অংকের সমাধান গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ
এই কষে দেখি 10.1 পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদ | WBBSE বোর্ডের অন্তর্গত তোমাদের নবম|Class 9 এর দশ নম্বর অধ্যায় লাভ ও ক্ষতি এর প্রথম অনুশীলনী। এই Koshe Dekhi 10.1 Class 9 এর অংকগুলি খুবই বাস্তব সমস্যা যেমন কোনো কিছু বিক্রয় করে তার উপর কতোটা লাভ বা ক্ষতি হলো।
লাভ কাকে বলে?
কোনো জিনিস বিক্রি করে কেনার দামের থেকে বেশি টাকা পাওয়াকে লাভ বলা হয়।
ক্ষতি কাকে বলে?
কোনো জিনিস বিক্রি করে কেনা দামের থেকে কম টাকা পাওয়াকে ক্ষতি বলে।
আগামিতে এই কষে দেখি 10.1 Class 9 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 10.1 Class 9 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 10.1 Class 9 তারপর  |
কষে দেখি 10.1 Class 9 এর Video:
এখানে তোমরা video এর মাধ্যমে অংক গুলো বুঝে নিতে পারবে-
Part 1
Part 2

কষে দেখি 10.1 | Koshe Dekhi 10.1
1. নীচের ছক পূরণ করঃ
| ক্রয় মূল্য | বিক্রয়মূল্য | লাভ/ক্ষতি | শতকরা লাভ/ক্ষতি |
|---|---|---|---|
| 500 টাকা | 25 লাভ | ||
| 300 টাকা | 7 ক্ষতি | ||
| 1250 টাকা | 8 ক্ষতি | ||
| 23000 টাকা | 15 লাভ |
সমাধানঃ-
(i) ক্রয়মূল্য=500 টাকা ; লাভ=25%
এখানে শতকরা লাভ = 25%
| 100 টাকায় লাভ = 25 টাকা |
| 1 টাকায় লাভ = \(\frac{25}{100}\) টাকা |
| 500 টাকায় লাভ = ¼×500 = 125 টাকা |
অতএব,
| বিক্রয়মূল্য | লাভ |
|---|---|
| ক্রয়মুল্য+লাভ = 500+125 = 625 টাকা | 125 টাকা |
(ii) ক্রয়মূল্য=300 টাকা ; ক্ষতি=7%
এখানে শতকরা ক্ষতি = 7%
| 100 টাকায় ক্ষতি = 7 টাকা |
| 1 টাকায় ক্ষতি = \(\frac{7}{100}\) টাকা |
| 300 টাকায় ক্ষতি = \(\frac{7}{100} \times 300\) = 21 টাকা |
অতএব,
| বিক্রয়মূল্য | ক্ষতি |
|---|---|
| ক্রয়মুল্য-ক্ষতি = 300-21 = 279 টাকা | 21 টাকা |
(iii) ক্রয়মূল্য=1250 টাকা ; ক্ষতি=8%
এখানে শতকরা ক্ষতি = 8%
| 100 টাকায় ক্ষতি = 8 টাকা |
| 1 টাকায় ক্ষতি = \(\frac{8}{100}\) টাকা |
| 1250 টাকায় ক্ষতি = \(\frac{8}{100}\)×1250 =100 টাকা |
অতএব,
| বিক্রয়মূল্য | ক্ষতি |
|---|---|
| ক্রয়মুল্য-ক্ষতি = 1250-100 = 1150 টাকা | 100 টাকা |
(iv) বিক্রয়মূল্য=23000 টাকা ; লাভ=15%
এখানে শতকরা লাভ = 15 টাকা
| 115 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হয় 100 টাকা |
| 1 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হয় \(\frac{100}{115}\) টাকা |
| 23000 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হয় =\(\frac{100}{115}\)×23000 টাকা = 20000 টাকা |
অতএব
| ক্রয়মূল্য | লাভ |
|---|---|
| 20000 টাকা | বিক্রয়মূল্য-ক্রয়মূল্য =23000-20000 = 3000 টাকা |
সম্পূর্ণ ছকটি পূরণ করলে হয়,
| ক্রয় মূল্য | বিক্রয়মূল্য | লাভ/ক্ষতি | শতকরা লাভ/ক্ষতি |
|---|---|---|---|
| 500 টাকা | 625 টাকা | 125 টাকা | 25 লাভ |
| 300 টাকা | 279 টাকা | 21 টাকা | 7 ক্ষতি |
| 1250 টাকা | 1150 টাকা | 100 টাকা | 8 ক্ষতি |
| 20000 টাকা | 23000 টাকা | 3000 টাকা | 15 লাভ |
2. লেখচিত্রটি থেকে নীচের প্রশ্নের উত্তর খুঁজি :
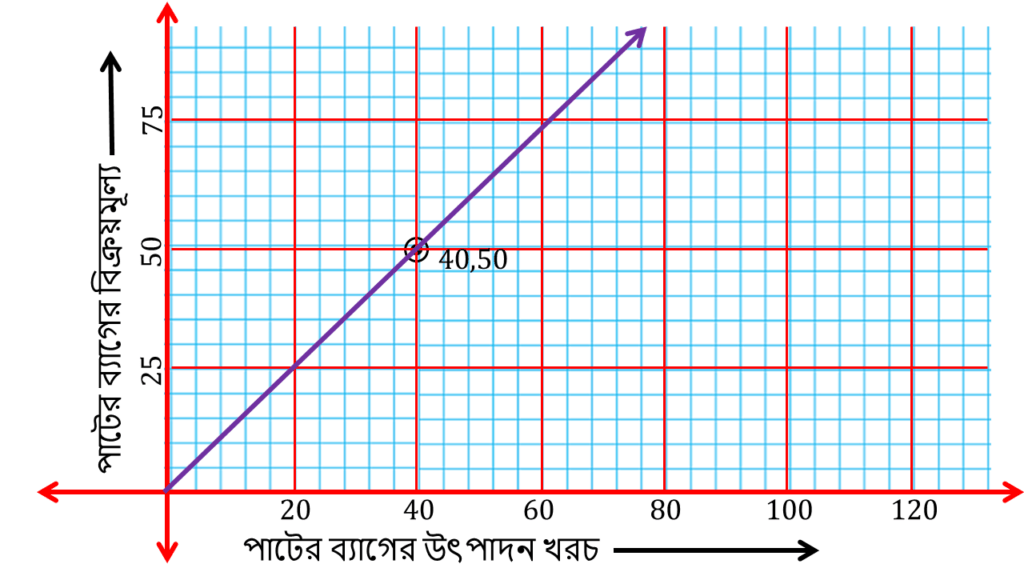
(a) লেখচিত্র দেখে ক্রয়মূল্য ও বিক্রয়মূল্যের সম্পর্ক লিখি।
সমাধানঃ-
লেখচিত্র থেকে দেখতে পাচ্ছি যে পাটের ব্যগের উৎপাদন খরচ বাড়লে পাটের ব্যাগের বিক্রয়মুল্য বাড়ছে।
অতএব ক্রয়মূল্য ও বিক্রয়মূল্যে সরল সম্পর্কে আছে।
(b) যে পাটের ব্যাগের উৎপাদন খরচ 60 টাকা তার বিক্রয়মূল্য কত হবে লিখি।
সমাধানঃ-
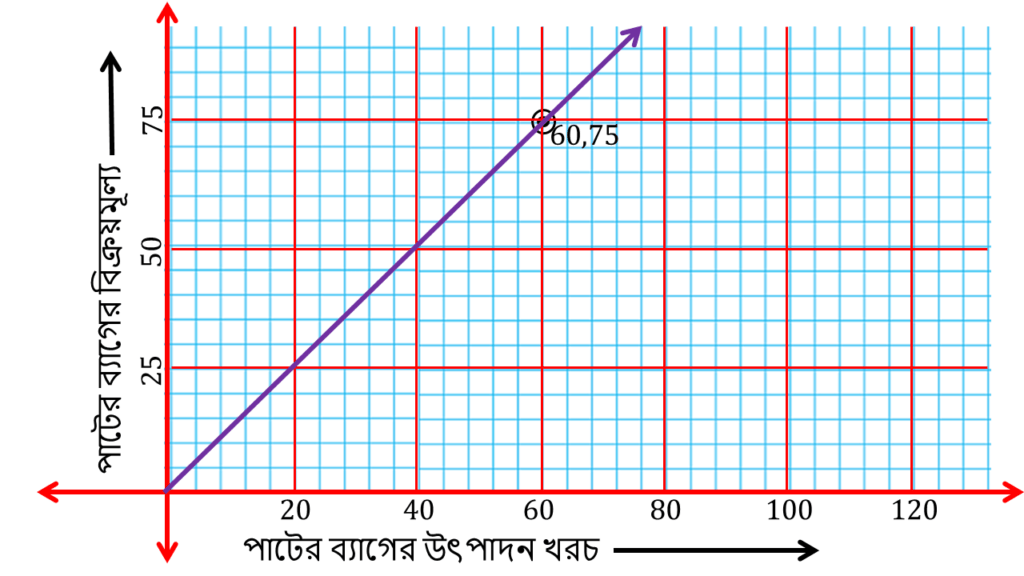
লেখচিত্র থেকে দেখতে পাচ্ছি যে পাটের ব্যগেরুতপাদন খরচ 60 টাকা তার বিক্রয়মূল্য=75 টাকা ।
(c) যে পাটের ব্যাগের বিক্রয়মূল্য 125 টাকা তার উৎপাদন খরচ কী হাবে লেখচিত্র দেখে লিখি।
সমাধানঃ-
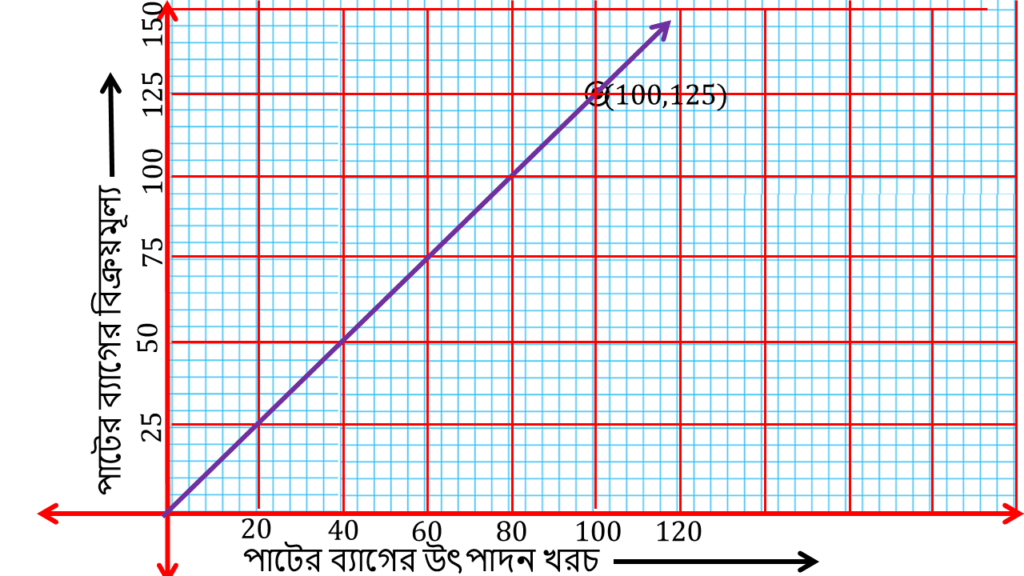
লেখচিত্র থেকে দেখতে পাচ্ছি যে পাটের ব্যাগের বিক্রয়মূল্য 125 টাকা হলে ক্রয়মুল্য=100 টাকা হবে।
(d) লেখচিত্র থেকে শতকরা লাভ বা ক্ষতি হিসাব করে লিখি।
সমাধানঃ-
| ক্রয়মূল্য= 100 টাকা | বিক্রয়মূল্য= 125 টাকা |
| লাভ = 125-100 = 25 টাকা | |
| অতএব শতকরা লাভ = 25% | |
(e) লেখচিত্র থেকে বিক্রয়মূল্যের উপর শতকরা লাভ বা ক্ষতি লিখি
সমাধানঃ-
| 125 টাকায় বিক্রি করে লাভ হয় 25 টাকা | |
| 1 টাকায় বিক্রি করে লাভ হয় \(\frac{25}{125}\) টাকা | |
| 100 টাকায় বিক্রি করে লাভ হয় \(\frac{1}{5}\)×100 টাকা = 20 টাকা | |
| অতএব বিক্রয়মূল্যের উপর শতকরা লাভ হয় 20 টাকা । |
3. সুবীরকাকা 176 টাকা মূল্যে একটি ঘড়ি বিক্রি করেছেন। যদি ঘড়ি বিক্রি করে সুবীরকাকার 12% ক্ষতি হয়, তাহলে হিসাব করে দেখি তিনি কত টাকায় ঘড়িটি কিনেছিলেন।
সমাধানঃ-
সুবীরকাকার 12% ক্ষতি হয়
| 88 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হয় 100 টাকা |
| 1 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হয় \(\frac{100}{88}\) টাকা |
| 176 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হয় \(\frac{25}{22}\)×176 টাকা = 200 টাকা |
| ∴ তিনি 200 টাকায় ঘড়িটি কিনেছিলেন। |
4. আনোয়ারাবিবি 10টি লেবু 30 টাকায় কিনে প্রতি ডজন 42 টাকায় বিক্রি করলেন। হিসাব করে দেখি, আনোয়ারাবিবির শতকরা কত লাভ বা ক্ষতি হলো।
সমাধানঃ-
10টি লেবুর ক্রয়মূল্য 30 টাকা
12 টি লেবুর ক্রয়মূল্য = \(\frac{30}{10}\)×12=36 টাকা
12 টি লেবুর,
| বিক্রয়মূল্য = 42 টাকা | ক্রয়মূল্য = 36 টাকা |
| ∴ তিনি লাভ করেছেন 42-36=6 টাকা। | |
∴ আনোয়ারা বিবির শতকরা লাভ
= \(\frac{6}{36}\)×100
= \(\frac{50}{3}\) টাকা
| ∴ আনোয়ারাবিবির শতকরা \(\frac{50}{3}\) টাকা লাভ হলো |
5. অমলবাবু একটি ছবি 20% ক্ষতিতে বিক্রয় করলেন। কিন্তু আরও 200 টাকা বেশি মূল্যে বিক্রয় করলে 5% লাভ করতেন। তিনি ছবিটি কত মূল্যে কিনেছিলেন হিসাব করে লিখি।
সমাধানঃ-
ধরি, অমলবাবু ছবিটি x টাকায় কিনেছিলেন।
অমলবাবু ছবিটি 20% ক্ষতিতে বিক্রয় করলেন।
তাহলে,
| 100 টাকা ক্রয়মূল্য হলে বিক্রয়মূল্য হয় 80 টাকা |
| 1 টাকা ক্রয়মূল্য হলে বিক্রয়মূল্য হয় \(\frac{80}{100}\) টাকা |
| x টাকা ক্রয়মূল্য হলে বিক্রয়মূল্য হয় \(\frac{80x}{100}\)=\(\frac{8x}{10}\) টাকা |
আরও 200 টাকা বেশী মূল্যে বিক্রি করলে বিক্রয়মূল্য হয় = \(\frac{8x}{10}\) + 200 টাকা।
∴ আরও 200 টাকা বেশী মূল্যে বিক্রি করে লাভ হয়
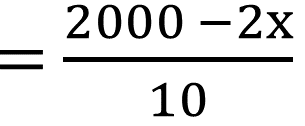 টাকা টাকা |
এখন 200 টাকা বেশী দামে বিক্রি করে
লাভ হয় 5%
অতএব,
| 100 টাকায় লাভ হয় 5 টাকা |
| 1 টাকায় লাভ হয় \(\frac{5}{100}\) টাকা |
| x টাকায় লাভ হয় \(\frac{x}{20}\) টাকা |
প্রশ্নানুসারে,
| বা, 2(2000 – 2x) = x |
| বা, 4000 – 4x = x |
| বা, 4x + x = 2000 |
| বা, 5x = 2000 |
| বা, x = \(\frac{2000}{5}\) = 800 |
| ∴অমলবাবু ছবিটি 800 টাকায় কিনেছিলেন। |
6. সুপ্রিয়া একটি ঘড়ি কিনেছে। যদি সে ঘড়িটি 370 টাকায় বিক্রি করে তখন তার যত টাকা লাভ হবে, 210 টাকায় বিক্রি করলে তত টাকা ক্ষতি হবে। হিসাব করে ঘড়িটির ক্রয়মূল্য লিখি।
সমাধানঃ-
ধরি, ঘড়িটির ক্রয়মূল্য = x টাকা
এখন 370 টাকায় বিক্রি করে লাভ হয়
= (370 – x) টাকা
আবার, 210 টাকায় বিক্রি করলে ক্ষতি হয়
= (x – 210) টাকা
প্রশ্নানুসারে,
| 370 – x = x – 210 |
| বা, x + x = 370 + 210 |
| বা, 2x = 560 |
| বা, x = \(\frac{560}{2}\) = 290 |
| ∴ ঘড়িটির ক্রয়মূল্য = 290 টাকা |
7. আমার দিদি অরুণমামার দোকান থেকে 255 টাকায় একটি ছাতা কিনল। অরুণমামা যদি ছাতার ধার্যমূল্যের উপর 15% ছাড় দিয়ে থাকেন, তবে ওই ছাতার ধার্যমূল্য কত ছিল হিসাব করে লিখি।
সমাধানঃ-
ধরি, ছাতার ধার্যমূল্য = \(x\) টাকা।
এখন অরুনমামা ধার্যমূল্যের উপর 15% ছাড় দিয়ে থাকেন।
তাহলে,
| 100 টাকায় ছাড় দেন 15 টাকা |
| 1 টাকায় ছাড় দেন \(\frac{15}{100}\) টাকা |
| \(x\) টাকায় ছাড় দেন \(\frac{15x}{100}\) টাকা |
ধার্যমূল্যের উপর 15% ছাড় দেওয়ার পর ছাতাটির দাম
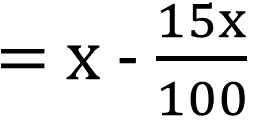 |
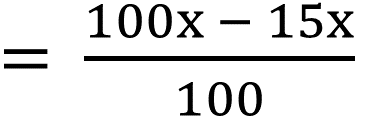 |
প্রশ্নানুসারে,
| বা, \(85x = 255 \times 100\) |
| বা, x = \(\frac{255×100}{85}\) |
| বা, x = 300 |
| ∴ ছাতার ধার্যমূল্য = 300 টাকা। |
8. আমার বন্ধু একটি গল্পের বই লিখিত মূল্যের উপর 25% ছাড়ে কিনল। সে যদি ওই বইটি লিখিত মূল্যেই বিক্রি করে, তবে সে শতকরা কত লাভ করবে হিসাব করে লিখি।
সমাধানঃ-
ধরি, গল্পের বই এর লিখিত মূল্য = 100 টাকা।
বন্ধু বইটি কেনে 75 টাকায়
আবার বন্ধু বইটি লিখিত মূল্যেই বিক্রি করে।
অতএব,
বন্ধুর লাভ হয় = (100 – 75) = 25 টাকা
এখন,
| 75 টাকায় লাভ হয় 25 টাকা |
| 1 টাকায় লাভ হয় \(\frac{25}{75}\) টাকা |
| 100 টাকায় লাভ হয় \(\frac{100}{3}\) টাকা |
| ∴ বন্ধুর শতকরা লাভ হয় \(\frac{100}{3}\) টাকা। |
9. নিয়ামতচাচা প্রতিটি 5 টাকা দরে 150টি ডিম কিনেছেন। কিন্তু দোকানে এনে দেখলেন 8 টি ডিম ফেটে গেছে এবং 7 টি ডিম পচা। প্রতিটি ডিম 6 টাকা দরে বিক্রি করলে, নিয়ামতচাচার শতকরা কত লাভ বা ক্ষতি হবে হিসাব করে লিখি।
সমাধানঃ-
নিয়ামতচাচা প্রতিটি 5 টাকা দরে 150টি ডিম কিনেছেন।
তাহলে 150টি ডিমের ক্রয়মূল্য
= 5×150 = 750 টাকা
এখন 8 টি ডিম ফেটে গেছে এবং 7 টি ডিম পচা।
অতএব, 8+7 = 15 টি ডিম তিনি বিক্রি করতে পারবেন না।
∴ এখন ডিম বিক্রি করতে পারবেন
= 150 – 15 = 135 টি
প্রতিটি ডিম 6 টাকা করে বিক্রি করলে 135 টি ডিমের বিক্রয়মূল্য = 135×6 = 810 টাকা ।
সুতরাং লাভ হয় = 810-750 = 60 টাকা
অতএব শতকরা লাভ হয়
= \(\frac{60}{750}\)×100
![]()
= 8 টাকা
| ∴ নিয়ামতচাচার শতকরা 8 টাকা লাভ হবে । |
10. আসিফচাচা একটি খেলনা 5% লাভে বিক্রি করলেন। যদি খেলনাটির ক্রয়মূল্য 20% কম এবং বিক্রয়মূল্য 34 টাকা কম হতো, তাহলে আসিফচাচার 10% লাভ হতো। খেলনাটির ক্রয়মূল্য কত হিসাব করি।
সমাধানঃ-
ধরি, খেলনাটির ক্রয়মূল্য = \(x\) টাকা ।
খেলনাটি 5% লাভে বিক্রি করলেন
অতএব
| 100 টাকা ক্রয়মূল্য হলে বিক্রয়মূল্য হবে 105 টাকা |
| \(x\) টাকা ক্রয়মূল্য হলে বিক্রয়মূল্য হবে \(\frac{105x}{100}\) টাকা । |
ক্রয়মূল্য 20% কম
অতএব
| 100 টাকা ক্রয়মূল্য হলে কমে হয় 80 টাকা |
| \(x\) টাকা ক্রয়মূল্য হলে কমে হয় \(\frac{80x}{100}\) টাকা । |
আবার,
বিক্রয়মূল্য 34 টাকা কম হলে নতুন বিক্রয়মূল্য হয় = (\(\frac{105x}{100} – 34\)) টাকা
নতুন দামের ক্ষেত্রে লাভ হয়,
নতুন দামের ক্ষেত্রে লাভ হয় 10%.
অতএব,
| 100 টাকায় লাভ হয় 10 টাকা |
| \(\frac{80x}{100}\) টাকায় লাভ হয় = \(\frac{10}{100}\)×\(\frac{80x}{100}\) = \(\frac{8x}{100}\) টাকা |
প্রশ্নানুসারে,
| বা, 25x – 3400 = 8x |
| বা, 25x – 8x = 3400 |
| বা, 17x = 3400 |
| বা, x = \(\frac{3400}{17}\) = 200 |
| ∴ খেলনাটির ক্রয়মূল্য = 200 টাকা । |
11. টাকায় 12টি জিনিস বিক্রি করে 4% ক্ষতি হয়। টাকায় কটি জিনিস বিক্রি করলে 44% লাভ হবে ?
সমাধানঃ-
ধরি, টাকায় \(x\) টি জিনিস বিক্রি করলে 44% লাভ হবে।
সেক্ষেত্রে,
\(x\) টি জিনিসের,
| 144 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হবে 100 টাকা |
| 1 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হবে \(\frac{100}{144}\) টাকা |
অতএব,
\(x\) টি জিনিসের ক্রয়মূল্য = \(\frac{100}{144}\) টাকা
1 টি জিনিসের ক্রয়মূল্য = \(\frac{100}{144x}\) টাকা
আবার,
টাকায় 12টি জিনিস বিক্রি করে 4% ক্ষতি হয়
সেক্ষেত্রে,
12 টি জিনিসের,
| 96 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হবে 100 টাকা |
| 1 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হবে \(\frac{100}{96}\) টাকা |
সুতরাং,
12 টি জিনিসের ক্রয়মূল্য = \(\frac{100}{96}\) টাকা
1 টি জিনিসের ক্রয়মূল্য = \(\frac{100}{96 \times 12}\) টাকা
শর্তানুসারে,
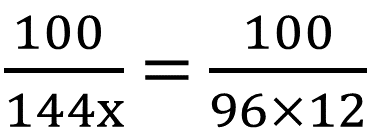 |
| বা, 144x = 96×12 |
| বা, x = \(\frac{96 \times 12}{144}\) |
| বা, x = 8 |
| ∴ টাকায় 8 টি জিনিস বিক্রি করলে 44% লাভ হবে |
12. রমা পিসি দুটি শাড়ি তৈরি করে একটি 15% এবং অপরটি 20% লাভে বিক্রি করলেন। তাঁর মোট লাভ হলো 262.50 টাকা । শাড়ি দুটির উৎপাদন ব্যয় 1:3 হলে, শাড়ি দুটির প্রত্যেকটির উৎপাদন ব্যয় কত?
সমাধানঃ-
ধরি, শাড়ি দুটির উৎপাদন ব্যয় যথাক্রমে \(x\) ও \(3x\) টাকা ।
| প্রথম শাড়ির ক্ষেত্রে লাভ = | \(\frac{15x}{100}\) |
| দ্বিতীয় শাড়ির ক্ষেত্রে লাভ = | \(\frac{60x}{100}\) |
প্রশ্নানুসারে,
| বা, 15x + 60x = 262.50×100 |
| বা, 75x = 26250 |
| বা, x = \(\frac{26250}{75}\) = 350 |
| ∴শাড়ি দুটির উৎপাদন ব্যয় যথাক্রমে 350 ও 3×350=1050 টাকা । |
13. এক ব্যক্তি 2 টাকায় 15টি হিসাবে কিছু লজেন্স কিনলেন। তিনি অর্ধেক টাকায় 5টি দরে এবং বাকি অর্ধেক টাকায় 10টি দরে বিক্রি করলেন। তার শতকরা কত লাভ বা ক্ষতি হলো?
সমাধানঃ-
ধরি, এক ব্যক্তি 2 টাকায় 15টি হিসাবে \(2x\) টি লজেন্স কিনলেন।
15 টি লজেন্সের দাম = 2 টাকা
\(2x\) টি লজেন্সের দাম = \(\frac{2 \times 2x}{15} = \frac{4x}{15}\) টাকা
তাহলে \(2x\) টি লজেন্সের ক্রয়মূল্য = \(\frac{4x}{15}\) টাকা।
প্রথম ক্ষেত্রে,
| অর্ধেক লজেন্স টাকায় 5টি দরে বিক্রি করলেন। | |
| 5 টি লজেন্সের বিক্রয়মূল্য = | 1 টাকা |
| \(x\) টি লজেন্সের বিক্রয়মূল্য = | \(\frac{x}{5}\) টাকা |
দ্বিতীয় ক্ষেত্রে,
| অর্ধেক লজেন্স টাকায় 10টি দরে বিক্রি করলেন। | |
| 10টি লজেন্সের বিক্রয় মূল্য = | 1 টাকা |
| \(x\) টি লজেন্সের বিক্রয়মূল্য = | \(\frac{x}{10}\) টাকা |
অতএব,
\(2x\) টি লজেন্সের বিক্রয়মূল্য
= \(\frac{x}{5} + \frac{x}{10}\)
= \(\frac{2x + x}{10}\)
= \(\frac{3x}{10}\) টাকা
তাহলে,
\(2x\) টি লজেন্সের লাভ হয়
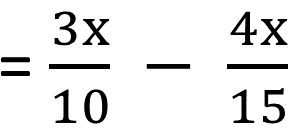 |
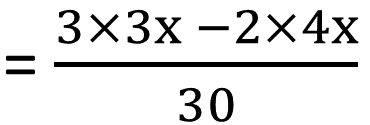 |
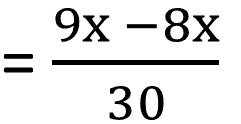 |
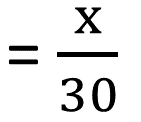 টাকা টাকা |
শতকরা লাভ হয় ,
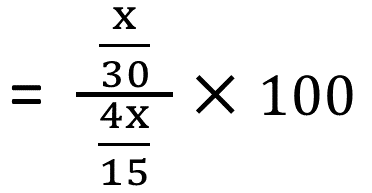 |
| ∴ শতকরা লাভ হলো টাকা |
14. আফসারচাচা দুটি কাঠের চেয়ার একই দামে তৈরি করলেন এবং চেয়ার দুটির প্রত্যেকটির ধার্যমূল্য ঠিক করলেন 1250 টাকা। তিনি একটি চেয়ার 8% ছাড়ে বিক্রি করে 15% লাভ করলেন। যদি তিনি দ্বিতীয় চেয়ারটি 1120 টাকায় বিক্রি করেন, তাহলে তাঁর মোটের উপর শতকরা লাভ কত হলো হিসাব করি।
সমাধানঃ-
চেয়ার দুটির প্রত্যেকটির ধার্যমূল্য 1250 টাকা।
একটি চেয়ার 8% ছাড়ে বিক্রি করলেন ।
সেক্ষেত্রে,
| 100 টাকায় ছাড় দিয়ে দাম হয় 92 টাকা |
| 1250 টাকায় ছাড় দিয়ে দাম হয় \(\frac{92 \times 1250}{100}\) টাকা = 1150 টাকা |
আবার, একটি চেয়ার 8% ছাড়ে বিক্রি করে 15% লাভ করলেন।
সেক্ষেত্রে,
| 115 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হয় 100 টাকা |
| 1150 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হয় \(\frac{100 \times 1150}{115} = 1000\) টাকা |
অতএব দুটি চেয়ার তৈরির দাম
= 1000 + 1000
= 2000 টাকা
এখন,
| প্রথম চেয়ারে লাভ হয় = 1150 – 1000 = 150 | দ্বিতীয় চেয়ারে লাভ হয় = 1120 – 1000 = 120 |
| ∴ দুটি চেয়ারে মোট লাভ = 150 + 120 = 270 টাকা | |
অতএব,
দুটি চেয়ারে শতকরা লাভ
= \(\frac{270}{200}×100\)
![]()
= \(\frac{27}{2}\) টাকা
| ∴ তাঁর মোটের উপর শতকরা লাভ হলো 27/2 টাকা। |
15. একটি বিশেষ ধরনের কলমের ধার্যমূল্য 36.50 টাকা। রফিকচাচা শুভমকে একটি পেনে 2.90 টাকা ছাড় দিয়ে বিক্রি করে, 12% লাভ করলেন। যদি তিনি ওই ধরনের আর একটি কলম মিতাকে 34.50 টাকায় বিক্রি করেন, তাহলে দ্বিতীয় কলমটিতে তাঁর শতকরা লাভ কত হলো নির্ণয় করি।
সমাধানঃ-
একটি বিশেষ ধরনের কলমের ধার্যমূল্য 36.50 টাকা।
রফিকচাচা শুভমকে একটি পেনে 2.90 টাকা ছাড় দিয়ে বিক্রি করলে বিক্রয়মূল্য
= 36.50-2.90 = 33.60 টাকা
এই দামে বিক্রি করে চাচা 12% লাভ করলেন।
সেক্ষেত্রে,
| 112 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হয় =100 টাকা |
| 33.60 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হয় \(\frac{100×33.60}{112}\) = 30 টাকা |
আবার চাচা ওই ধরনের আর একটি কলম মিতাকে 34.50 টাকায় বিক্রি করেন।
সেক্ষেত্রে,
চাচার লাভ হয় (34.50-30) = 4.50 টাকা
চাচার শতকরা লাভ হয়
= \(\frac{4.50}{30} ×100\)
![]()
= 15 টাকা
| ∴ দ্বিতীয় কলমটিতে তাঁর শতকরা 8 টাকা লাভ হলো |
16. এক পুস্তক প্রকাশক 2000 কপি বই ছাপার জন্য 3,875 টাকার কাগজ কিনতে. 3,315 টাকা ছাপতে এবং 810 টাকা বাঁধানোর জন্য খরচ করেন। তিনি পুস্তক বিক্রেতাদের 20% ছাড় দিয়ে 20% লাভে বিক্রি করেন। প্রতিটি বইয়ের ধার্যমূল্য কত নির্ণয় করি?
সমাধানঃ-
পুস্তক প্রকাশকের 2000 কপি বই ছাপতে উৎপাদন খরছ হয়েছে
= (3875+3315+810)
= 8000 টাকা ।
ধরি, প্রতিটি বইয়ের ধার্যমূল্য = \(x\) টাকা ।
তাহলে 2000 কপি বই এর ধার্যমূল্য
= \(2000x\) টাকা ।
এই ধার্যমূল্য এর উপর তিনি 20% ছাড় দেন।
সেক্ষেত্রে,
| 100 টাকায় ছাড় দিয়ে দাম হয় 80 টাকা |
| \(2000x\) টাকায় ছাড় দিয়ে দাম হয় = \(\frac{80×2000x}{100}\) = \(80×20x\) = \(1600x\) টাকা |
ধার্যমূল্য এর উপর 20% ছাড় দেওয়ার পর তিনার 20% লাভ হয়।
সেক্ষেত্রে,
| 120 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হয় =100 টাকা |
| \(1600x\) টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হয় = \(\frac{100×1600x}{120}\) = \(\frac{4000x}{3}\) টাকা |
সুতরাং, পুস্তক প্রকাশকের 2000 কপি বই এর উৎপাদন খরছ হয়েছে = \(\frac{4000x}{3}\) টাকা ।
শর্তে,
| \(\frac{4000x}{3} = 8000\) |
| বা, \(x = \frac{8000×3}{4000}\) |
| বা, x = 6 |
| ∴ প্রতিটি বইয়ের ধার্যমূল্য = 6 টাকা । |
17. হাসিমাবিবি দুটি হস্তশিল্পের প্রত্যেকটি 1248 টাকায় বিক্রি করেন। তিনি প্রথমটিতে 4% লাভ করেন, কিন্তু দ্বিতীয়টিতে তার 4% ক্ষতি হয়। তার মোট লাভ বা ক্ষতি কত হলো?
সমাধানঃ-
তিনি প্রথমটিতে 4% লাভ করেন
সেক্ষেত্রে,
| 104 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হয় =100 টাকা |
| 1248 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হয় = \(\frac{100×1248}{104}\) = 1200 টাকা |
∴ তিনি প্রথম টিতে লাভ করেন
= 1248 – 1200 = 48 টাকা
আবার, দ্বিতীয়টিতে তার 4% ক্ষতি হয়
সেক্ষেত্রে,
| 96 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হয় =100 টাকা |
| 1248 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হয় = \(\frac{100×1248}{96}\) = 1300 টাকা |
∴ তার দ্বিতীয়টিতে ক্ষতি হয়
= 1300 – 1248 = 52 টাকা ।
সুতরাং,
তার মোট ক্ষতি হয়েছে = 52-48=4 টাকা
| ∴ তার মোট ক্ষতি হয়েছে 4 টাকা |
18. করিম, মোহনকে 4860 টাকায় একটি মোবাইল ফোন বিক্রি করায় 19% ক্ষতি হয়। মোহন, রহিমকে যে দামে বিক্রি করে সেই দামে করিম মোহনকে বিক্রি করলে করিমের 17% লাভ হয়। মোহনের শতকরা লাভ কত ?
সমাধানঃ-
করিম, মোহনকে 4860 টাকায় একটি মোবাইল ফোন বিক্রি করায় 19% ক্ষতি হয়।
∴ মোহনের ক্রয়মূল্য = 4860 টাকা
এবং
| 81 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হয় =100 টাকা |
| 4860 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হয় =\(\frac{100×4860}{81}\) = 6000 টাকা |
আবার,
মোহন, রহিমকে যে দামে বিক্রি করে সেই দামে করিম মোহনকে বিক্রি করলে করিমের 17% লাভ হয়।
সেক্ষেত্রে,
| 100 টাকা ক্রয়মূল্য হলে বিক্রয়মূল্য হয় =117 টাকা |
| 6000 টাকা ক্রয়মূল্য হলে বিক্রয়মূল্য হয় = \(\frac{117×6000}{100 }\)= 7020 টাকা |
∴ মোহনের বিক্রয়মূল্য = 7020 টাকা।
মোহনের লাভ হয়
= 7020-4860 = 2160 টাকা
∴ মোহনের শতকরা লাভ হয়
= \(\frac{2160×100}{4860}\)
![]()
= \(\frac{400}{9}\) টাকা
| ∴ ∴ মোহনের শতকরা লাভ হয় \(\frac{400}{9}\) টাকা । |
19. ফিরোজচাচা একটি প্যান্ট 20% লাভে এবং একটি জামা 15% লাভে বিক্রি করে মোট 719.50 টাকা পেলেন। তিনি যদি প্যান্টটি 25% এবং জামাটি 20% লাভে বিক্রি করতেন, তাহলে তিনি আরও 30.50 টাকা বেশি পেতেন। প্যান্ট ও জামার ক্রয়মূল্য নির্ণয় করি।
সমাধানঃ-
ধরি,
| প্যান্ট এর ক্রয়মূল্য = | \(x\) টাকা |
| জামার ক্রয়মূল্য = | \(y\) টাকা |
প্যান্ট 20% লাভে এবং জামা 15% লাভে বিক্রি করেন।
সুতরাং,
| প্যান্ট এর বিক্রয়মূল্য = | \(\frac{120x}{100}\) টাকা |
| জামার বিক্রয়মূল্য = | \(\frac{115y}{100}\) টাকা |
শর্তে,
| বা, 120x + 115y = 719.50×100 |
| বা, 120x + 115y = 71950 |
| বা, 24x + 23y = 14390 ——-(i) |
আবার,
তিনি যদি প্যান্টটি 25% এবং জামাটি 20% লাভে বিক্রি করতেন, তাহলে তিনি আরও 30.50 টাকা বেশি পেতেন।
সেক্ষেত্রে,
| প্যান্ট এর বিক্রয়মূল্য = | \(\frac{125x}{100}\) টাকা |
| জামার বিক্রয়মূল্য = | \(\frac{120y}{100}\) টাকা |
শর্তে,
| বা, 125x + 120y = 750×100 |
| বা, 25x + 24y = 15000 ——–(ii) |
x চলকে অপনয়ন করার জন্যে (i) নং সমীকরণকে 25 এবং (ii) নং সমীকরণকে 24 দিয়ে গুণ করে পাই,
| 600x + 575y = 359750 |
| 600x + 576y = 360000 |
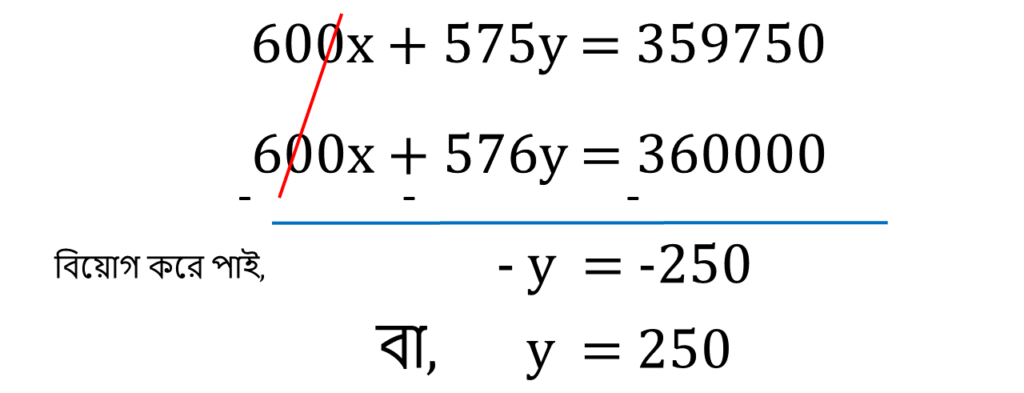
y এর মান (i) নং সমীকরণে বসিয়ে পাই,
| 24x + 23×250 = 14390 |
| বা, 24x = 14390 – 5750 |
| বা, x = \(\frac{8640}{24}\) = 360 |
অতএব,
| প্যান্ট এর ক্রয়মূল্য = | 360 টাকা |
| জামার ক্রয়মূল্য = | 250 টাকা |
20. রবীনকাকু 3000 টাকার চাল কিনলেন । তিনি \(\frac{1}{3}\) অংশ 20% ক্ষতিতে এবং \(\frac{2}{5}\) অংশ 25% লাভে বিক্রি করলেন। শতকরা কত লাভে তিনি বাকি অংশ বিক্রি করলে তাঁর মোটের উপর 10% লাভ হবে?
সমাধানঃ-
\(\frac{1}{3}\) অংশের ক্রয়মূল্য
= 3000×\(\frac{1}{3}\) = 1000 টাকা
তিনি \(\frac{1}{3}\) অংশ 20% ক্ষতিতে বিক্রি করেন,
| 100 টাকা ক্রয়মূল্য হলে বিক্রয় মূল্য হয় =80 টাকা |
| 1000 টাকা ক্রয়মূল্য হলে বিক্রয় মূল্য হয় = \(\frac{80×1000}{100}\) = 800 টাকা |
∴ \(\frac{1}{3}\) অংশের বিক্রয়মূল্য = 800 টাকা
\(\frac{2}{5}\) অংশের ক্রয়মূল্য
= \(\frac{2×3000}{5}\) = 1200 টাকা
আবার, তিনি \(\frac{2}{5}\) অংশ 25% লাভে বিক্রি করেন,
| 100 টাকা ক্রয়মূল্য হলে বিক্রয় মূল্য হয় =125 টাকা |
| 1200 টাকা ক্রয়মূল্য হলে বিক্রয় মূল্য হয় = \(\frac{125×1200}{100}\) = 1500 টাকা |
∴ \(\frac{2}{5}\) অংশের বিক্রয়মূল্য = 1500 টাকা
বাকি অংশ = \(1-(\frac{1}{3}+\frac{2}{5}) = \frac{4}{15}\)
বাকি অংশের ক্রয়মূল্য
= \(\frac{4×3000}{15}\) = 800 টাকা
এখন তিনার মোটের উপর 10% লাভ হওয়ার ক্ষেত্রে,
| 100 টাকা ক্রয়মূল্য হলে বিক্রয় মূল্য হয় =110 টাকা |
| 3000 টাকা ক্রয়মূল্য হলে বিক্রয় মূল্য হয় = \(\frac{110×3000}{100}\) = 3300 টাকা |
অতএব সমস্ত অংশের বিক্রয়মূল্য
= 3300 টাকা
তাহলে বাকি অংশের বিক্রয়মূল্য
= 3300 – (1500 + 800)
= 3300 – 2300
= 1000 টাকা
বাকি অংশে লাভ হয় = 1000-800 = 200 টাকা
অতএব,
বাকি অংশে শতকরা লাভ হয়
= \(\frac{200}{800}×100\)
![]()
= 25 টাকা
| ∴ শতকরা 25 টাকা লাভে তিনি বাকি অংশ বিক্রি করলে তাঁর মোটের উপর 10% লাভ হবে। |
21. এক ব্যবসায়ী এক ধরনের চা 80 টাকা প্রতি কিগ্রা দরে বিক্রি করে 20% ক্ষতি এবং অপর এক ধরনের চা 200 টাকা প্রতি কিগ্রা দরে বিক্রি করে 25% লাভ করেন। তিনি দু-ধরনের চা কি অনুপাতে মিশিয়ে প্রতি কিগ্রা 150 টাকা দরে বিক্রি করলে 25% লাভ হবে?
সমাধানঃ-
ধরি, প্রথম প্রকারের \(x\) কেজি চা -এর সঙ্গে দ্বিতীয় প্রকারের \(y\) কেজি চা মেশাতে হবে।
মোট মিশ্রিত চা এর পরিমাণ = \((x + y)\) কেজি
প্রথম প্রকার চা 80 টাকা প্রতি কিগ্রা দরে বিক্রি করে 20% ক্ষতি হয়
সেক্ষেত্রে,
1 কেজি চা এর,
| 80 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হয় =100 টাকা |
অতএব \(x\) কেজি চা এর ক্রয়মূল্য = \(100x\) টাকা।
আবার,
দ্বিতীয় প্রকার চা 200 টাকা প্রতি কিগ্রা দরে বিক্রি করে 25% লাভ হয়
সেক্ষেত্রে,
1 কেজি চা এর,
| 125 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হয় =100 টাকা |
| 200 টাকা বিক্রয়মূল্য হলে ক্রয়মূল্য হয় = \(\frac{200×100}{125}\) = 160 টাকা |
অতএব \(y\) কেজি চা এর ক্রয়মূল্য = \(160y\) টাকা।
এখন \((x + y)\) কেজি চা এর ক্রয়মূল্য
= \((100x + 160y)\) টাকা
এখন মিশ্রিত চা প্রতি কিগ্রা 150 টাকা দরে বিক্রি করলে 25% লাভ হবে সেক্ষেত্রে,
\((x+y)\) কেজি চা এর বিক্রয়মূল্য
= \(150(x+y)\) টাকা
অতএব \((x+y)\) কেজি চা বিক্রি করে লাভ হয়
| = \(150(x + y) – (100x + 160y)\) |
| = \(150x + 150x – 150y – 160y\) |
| = \(50x – 10y\) টাকা |
অতএব \((x+y)\) কেজি চা বিক্রি করে শতকরা লাভ হয়
শর্তানুসারে,
| বা, (50x – 10y)×100 = 25×(100x + 160y) |
| বা, 5000x – 1000y = 2500x + 4000y |
| বা, 5000x – 2500x = 4000y + 1000y |
| বা, 2500x = 5000y |
| বা, \(\frac{x}{y}\ = \frac{5000}{2500}\) |
| বা, \(x : y = 2 : 1\) |
| ∴ নির্ণেয় অনুপাত = 2 : 1 । |
| WB Class 9 এর গণিত প্রকাশের সমস্ত অধ্যায়ের সমাধান- | |
|---|---|
| অধ্যায় | সমাধান |
| 1. বাস্তব সংখ্যা (Real Numbers) | কষে দেখি 1.1 |
| কষে দেখি 1.2 | |
| কষে দেখি 1.3 | |
| 2. সূচকের নিয়মাবলি (Laws of Indices) | কষে দেখি 2 |
| 3. লেখচিত্র (Graph) | কষে দেখি 3.1 |
| কষে দেখি 3.2 | |
| 4. স্থানাঙ্ক জ্যামিতি : দূরত্ব নির্ণয় (Co-ordinate Geometry: Distance Formula) | কষে দেখি 4 |
| 5. রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) (Linear Simultaneous Equations) | কষে দেখি 5.1 |
| কষে দেখি 5.2 | |
| কষে দেখি 5.3 | |
| কষে দেখি 5.4 | |
| কষে দেখি 5.5 | |
| কষে দেখি 5.6 | |
| কষে দেখি 5.7 | |
| 6. সামান্তরিকের ধর্ম (Properties of Parallelogram) | কষে দেখি 6 |
| 7. বহুপদী সংখ্যামালা (Polynomial) | কষে দেখি 7.1 |
| কষে দেখি 7.2 | |
| কষে দেখি 7.3 | |
| কষে দেখি 7.4 | |
| 8. উৎপাদকে বিশ্লেষণ (Factorisation) | কষে দেখি 8.1 |
| কষে দেখি 8.2 | |
| কষে দেখি 8.3 | |
| কষে দেখি 8.4 | |
| কষে দেখি 8.5 | |
| 9. ভেদক ও মধ্যবিন্দু সংক্রান্ত উপপাদ্য (Transversal & Mid-Point Theorem). | কষে দেখি 9 |
| 10. লাভ ও ক্ষতি (Profit and Loss) | কষে দেখি 10.1 |
| কষে দেখি 10.2 | |
| 11. রাশিবিজ্ঞান (Statistics) | কষে দেখি 11.1 |
| কষে দেখি 11.2 | |
| 12. ক্ষেত্রফল সংক্রান্ত উপপাদ্য (Theorems on Area) | কষে দেখি 12 |
| 13. সম্পাদ্য : ত্রিভুজের সমান ক্ষেত্রফল বিশিষ্ট সামান্তরিক অঙ্কন | কষে দেখি 13 |
| 14. সম্পাদ্য : চতুর্ভুজের সমান ক্ষেত্রফল বিশিষ্ট ত্রিভুজ অঙ্কন | কষে দেখি 14 |
| 15. ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল (Area & Perimeter of Triangle & Quadrilateral) | কষে দেখি 15.1 |
| কষে দেখি 15.2 | |
| কষে দেখি 15.3 | |
| 16. বৃত্তের পরিধি (Circumference of Circle) | কষে দেখি 16 |
| 17. সমবিন্দু সংক্রান্ত উপপাদ্য (Theorems on concurrence) | কষে দেখি 17 |
| 18. বৃত্তের ক্ষেত্রফল (Area of Circle) | কষে দেখি 18 |
| 19. স্থানাঙ্ক জ্যামিতি: সরলরেখাংশের অন্তর্বিভক্ত ও বহিঃবিভক্ত (Co-ordinate Geometry: Internal and External Division of Straight-Line Segment) | কষে দেখি 19 |
| 20. স্থানাঙ্ক জ্যামিতি: ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল (Co-ordinate Geometry: Area of Triangular Region) | কষে দেখি 20 |
| 21. লগারিদম (Logarithm) | কষে দেখি 21 |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
এই কষে দেখি 10.1 Class 9|Koshe Dekhi 10.1 Class 9 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।

এখানে তোমরা তোমাদের নবম শ্রেণীতে| Class 9 এ কি কি পড়ানো হয়, মানে তোমাদের নবম শ্রেণী| Class 9 সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

