শ্রেণী-নবম ; অধ্যায় -ত্রিভুজ ও চতুরভুজের পরিসীমা ও ক্ষেত্রফল ; কষে দেখি 15.1
কষে দেখি 15.1 Class 9 এর সূচিপত্র:-
কষে দেখি 15.1 Class 9 এর অংকের সমাধান গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ
এই কষে দেখি 15.1 পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদ | WBBSE এর অন্তর্গত Class 9|নবম শ্রেণীর গণিত বই এর 15 নম্বর অধ্যায় ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল এর প্রথম অনুশীলনী।
এই কষে দেখি 15.1 Class 9 এর অংক গুলি করার জন্যে যে যে বিষয়গুলি জানতে হবে সেগুলি হলো একটি আয়তক্ষেত্রের কর্ণ ও একটি বর্গক্ষেত্রের কর্ণ কিভাবে বের করতে হয়!
আয়তক্ষেত্রের কর্ণের সূত্রঃ
একটি আয়তক্ষেত্রের দৈর্ঘ্য ও প্রস্থ যথাক্রমে x ও y হয় তাহলে আয়তক্ষেত্রের কর্ণ
= \(\sqrt{x^2+y^2}\)
বর্গক্ষেত্রের কর্ণের সূত্রঃ
একটি বর্গক্ষেত্রের কর্ণের সুত্র হলো –
বর্গক্ষেত্রের কর্ণ
= √2 × (বর্গক্ষেত্রের একটি বাহুর দৈর্ঘ্য)
আগামিতে এই কষে দেখি 15.1 Class 9 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 15.1 Class 9 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 15.1 Class 9 তারপর  |
কষে দেখি 15.1| Koshe Dekhi 15.1
1. আমি কামালদের বাড়ির ছবি দেখি ও উত্তর খুঁজি।
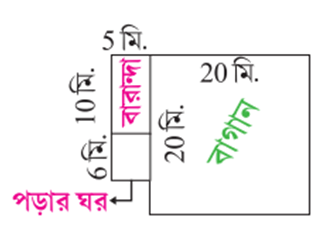
(i) কামালদের বাগানের ক্ষেত্রফল হিসাব করে লিখি।
সমাধানঃ-
কামালদের বাগানের,
| দৈর্ঘ্য = | 20 মি. |
| প্রস্থ = | 20 মি. |
| ∴ ক্ষেত্রফল | 20 × 20 = 400 বর্গ মিটার |
(ii) প্রতি বর্গমিটারে 30 টাকা হিসাবে কামালদের বারান্দার মেঝে মেরামত করতে কত খরচ হবে হিসাব করে লিখি।
সমাধানঃ-
কামালদের বারান্দার,
| দৈর্ঘ্য = | 10 মি. |
| প্রস্থ = | 5 মি. |
| ∴ ক্ষেত্রফল | 10 × 5 = 50 বর্গ মিটার |
∴ প্রতি বর্গমিটারে 30 টাকা হিসাবে কামালদের বারান্দার মেঝে মেরামত করতে খরচ হবে
= 50 × 30
= 1500 টাকা
(iii) কামাল তার পড়ার ঘরের মেঝেতে টালি বসাতে চায়। যদি প্রতিটি টালি 25সেমি. × 25 সেমি হয়, তবে তার পড়ার ঘরের মেঝেতে টালি বসাতে কতগুলি টালি লাগবে হিসাব করে লিখি।
সমাধানঃ-
কামালদের পড়ার ঘরের,
| দৈর্ঘ্য = | 6 মি. |
| প্রস্থ = | 5 মি. |
| ∴ ক্ষেত্রফল | 6 × 5 = 30 বর্গ মিটার = 30×100×100 = 300000 বর্গ সেমি. |
যদি প্রতিটি টালি 25সেমি. × 25 সেমি হয়, তবে তার পড়ার ঘরের মেঝেতে টালি বসাতে টালি লাগবে
= \(\frac{300000}{25 \times 25}\)
= 480 টি
2. নীচের ছবি দেখি ও রঙিন অংশের ক্ষেত্রফল হিসাব করে লিখি
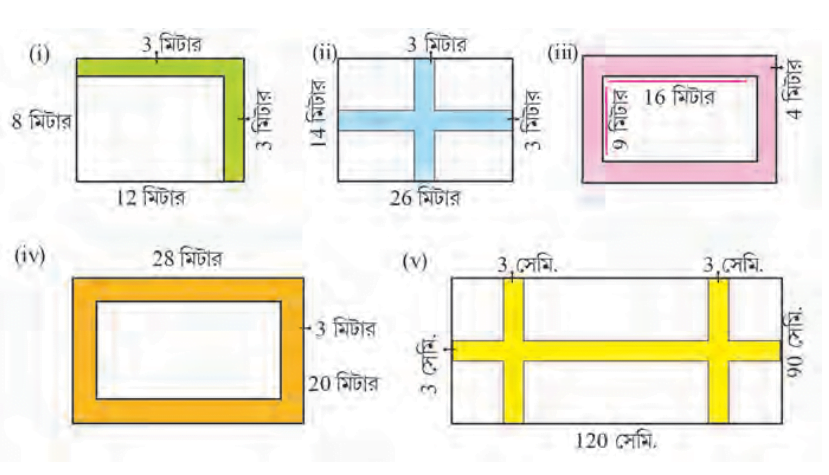
(i)
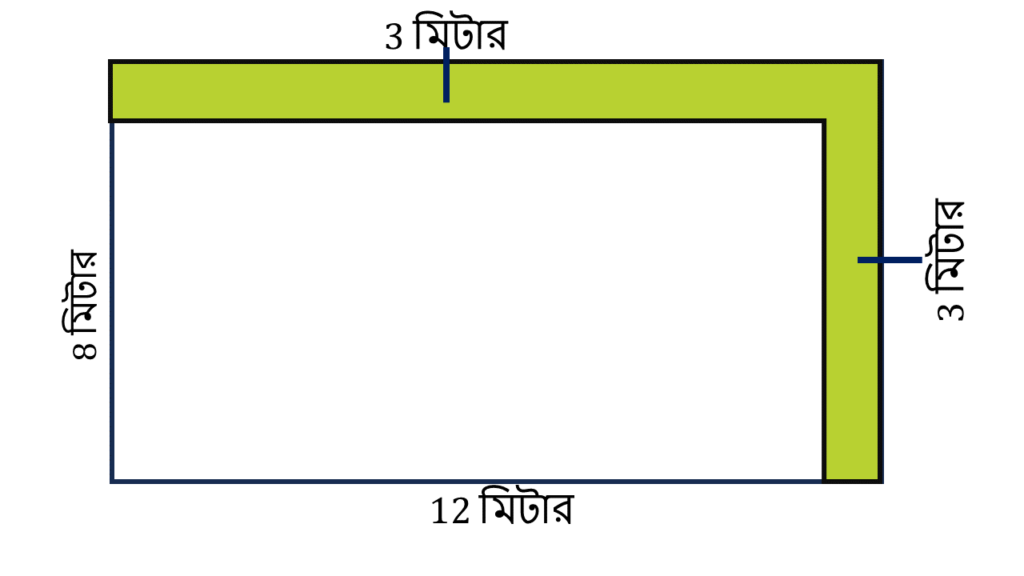
[ ছবির রঙিন অংশ টিকে আমাদের বোঝার সুবিধার্থে দুটি অংশে ভাগ করে নেবো। ]

রঙিন অংশের ক্ষেত্রফল
= (আয়তখেত্র ABDE + আয়তখেত্র CDGF) এর ক্ষেত্রফল
আয়তক্ষেত্র ABDE এর,
| দৈর্ঘ্য = | 12 মি. |
| প্রস্থ = | 3 মি. |
| ∴ ক্ষেত্রফল | 12 × 3 = 36 বর্গ মিটার |
আয়তক্ষেত্র CDGF এর,
| দৈর্ঘ্য = | (8-3)=5 মি. |
| প্রস্থ = | 3 মি. |
| ∴ ক্ষেত্রফল | 5 × 3 = 15 বর্গ মিটার |
রঙিন অংশের ক্ষেত্রফল
= 36 + 15
= 51 বর্গ মি.
(ii)
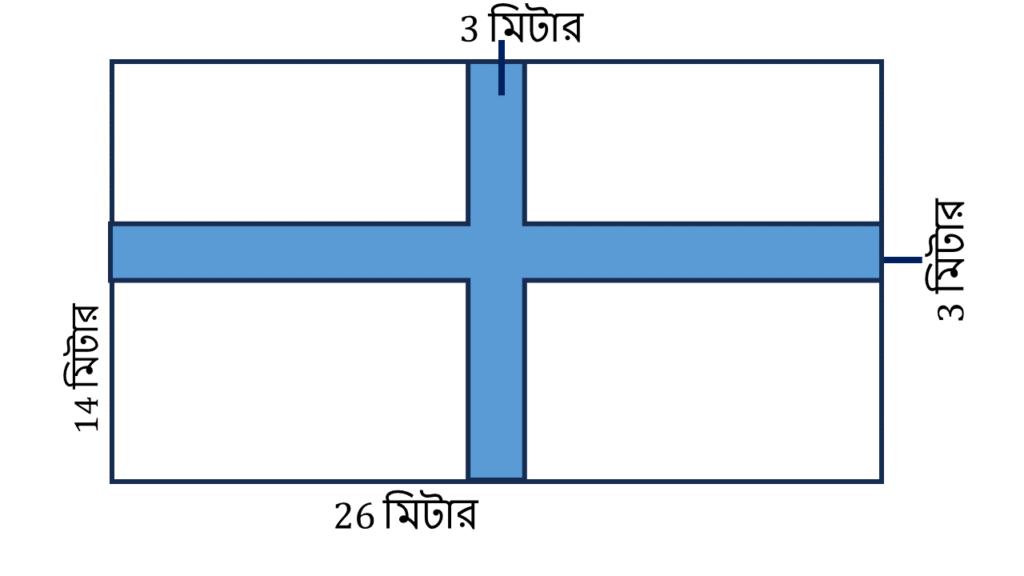
[ ছবির রঙিন অংশ টিকে আমাদের বোঝার সুবিধার্থে তিনটি অংশে ভাগ করে নেবো।]
রঙিন অংশের ক্ষেত্রফল
= (আয়তক্ষেত্র ABCD + আয়তক্ষেত্র FEHG + আয়তক্ষেত্র IJKL) এর ক্ষেত্রফল
আয়তক্ষেত্র ABCD এর,
| দৈর্ঘ্য = | 26 মি. |
| প্রস্থ = | 3 মি. |
| ∴ ক্ষেত্রফল | 26 × 3 = 78 বর্গ মিটার |
আয়তক্ষেত্র FEHG এর + আয়তক্ষেত্র IJKL এর,
| দৈর্ঘ্য = | 14-3=11 মি. |
| প্রস্থ = | 3 মি. |
| ∴ ক্ষেত্রফল | 11 × 3 = 33 বর্গ মিটার |
রঙিন অংশের ক্ষেত্রফল
= 78 + 33
= 111 বর্গ মিটার.
(iii)

রঙিন অংশের ক্ষেত্রফল
= 2(আয়তক্ষেত্র ABDE + আয়তক্ষেত্র CDGF) এর ক্ষেত্রফল
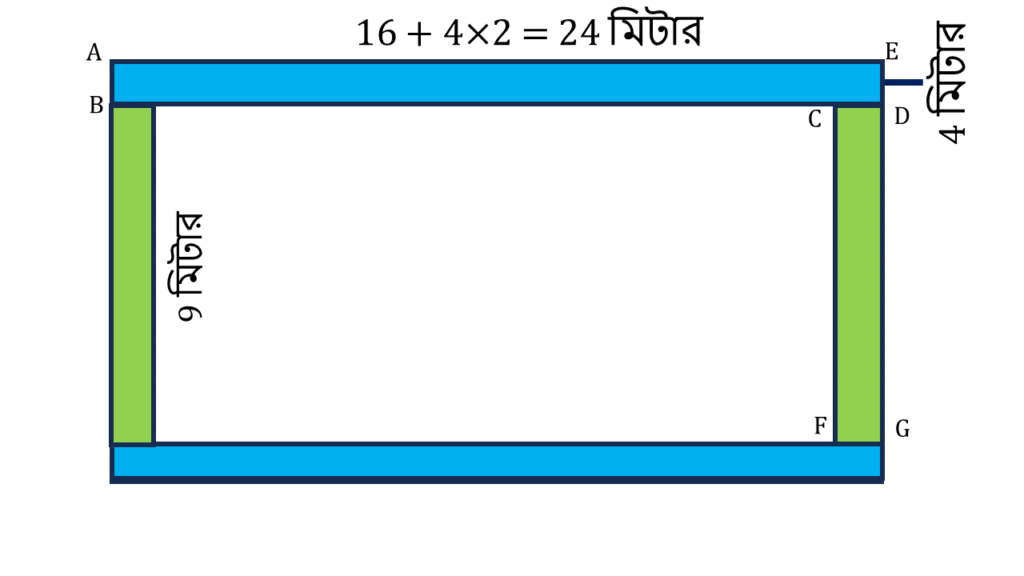
আয়তক্ষেত্র ABDE এর,
| দৈর্ঘ্য = | 16+4×2=24 মি. |
| প্রস্থ = | 4 মি. |
| ∴ ক্ষেত্রফল | 24 × 4 = 96 বর্গ মিটার |
আয়তক্ষেত্র CDGF এর,
| দৈর্ঘ্য = | 9 মি. |
| প্রস্থ = | 4 মি. |
| ∴ ক্ষেত্রফল | 9 × 4 = 36 বর্গ মিটার |
রঙিন অংশের ক্ষেত্রফল
= 2(96 + 36)
= 2 × 132
= 264 বর্গমিটার.
(iv)
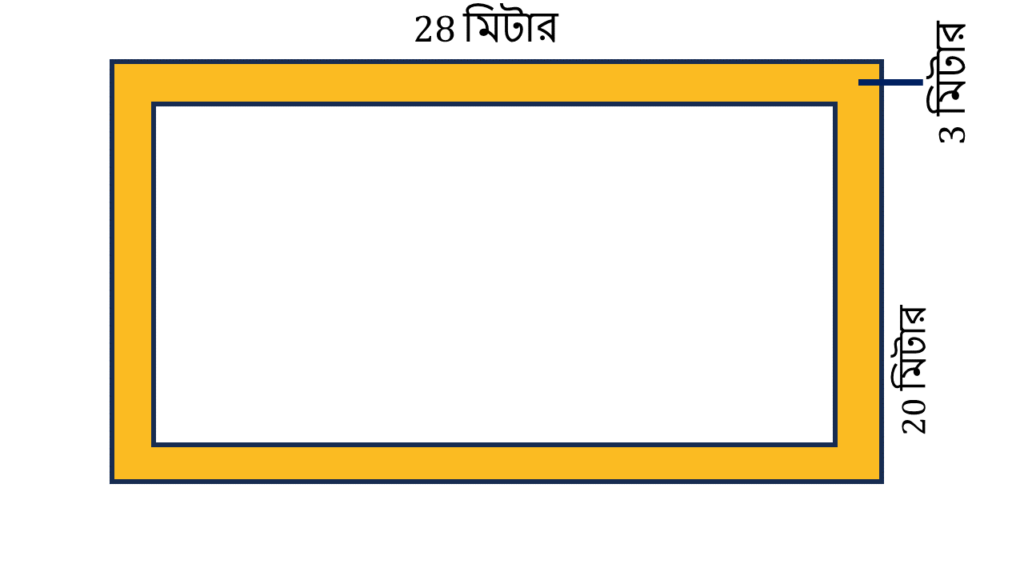
রঙিন অংশের ক্ষেত্রফল
= 2(আয়তক্ষেত্র ABDE + আয়তক্ষেত্র CDGF) এর ক্ষেত্রফল
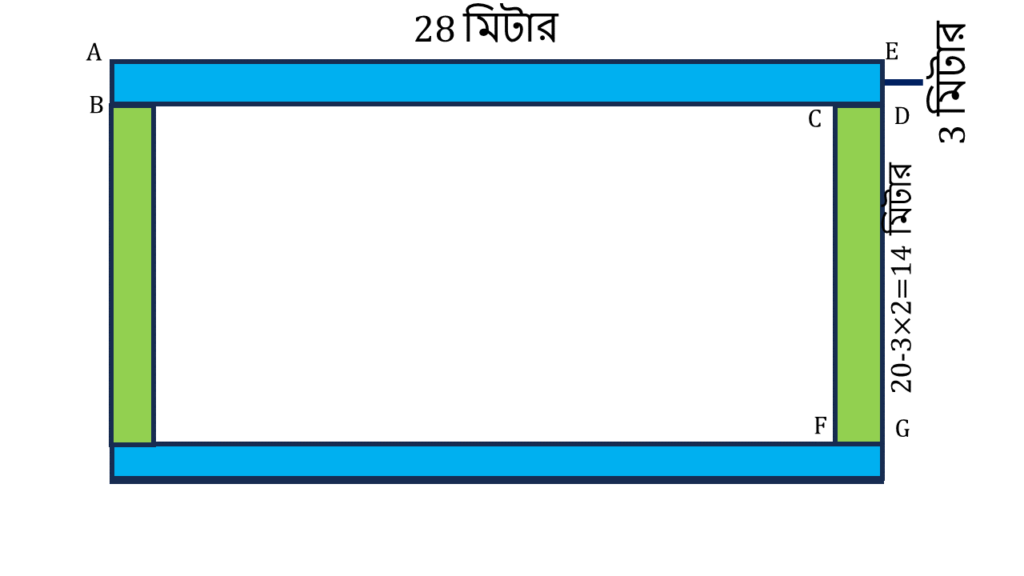
আয়তক্ষেত্র ABDE এর,
| দৈর্ঘ্য = | 28 মি. |
| প্রস্থ = | 3 মি. |
| ∴ ক্ষেত্রফল | 28 × 3 = 84 বর্গ মিটার |
আয়তক্ষেত্র CDGF এর,
| দৈর্ঘ্য = | 20 – 3×2=14 মি. |
| প্রস্থ = | 3 মি. |
| ∴ ক্ষেত্রফল | 14 × 3 = 42 বর্গ মিটার |
রঙিন অংশের ক্ষেত্রফল
= 2(84 + 42)
= 2 × 126
= 252 বর্গমিটার.
(v)
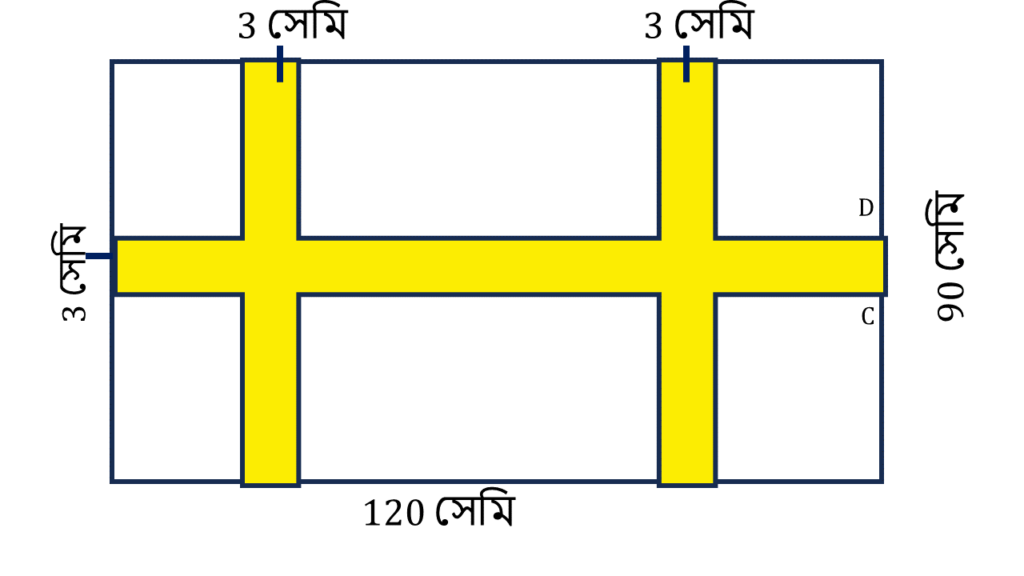
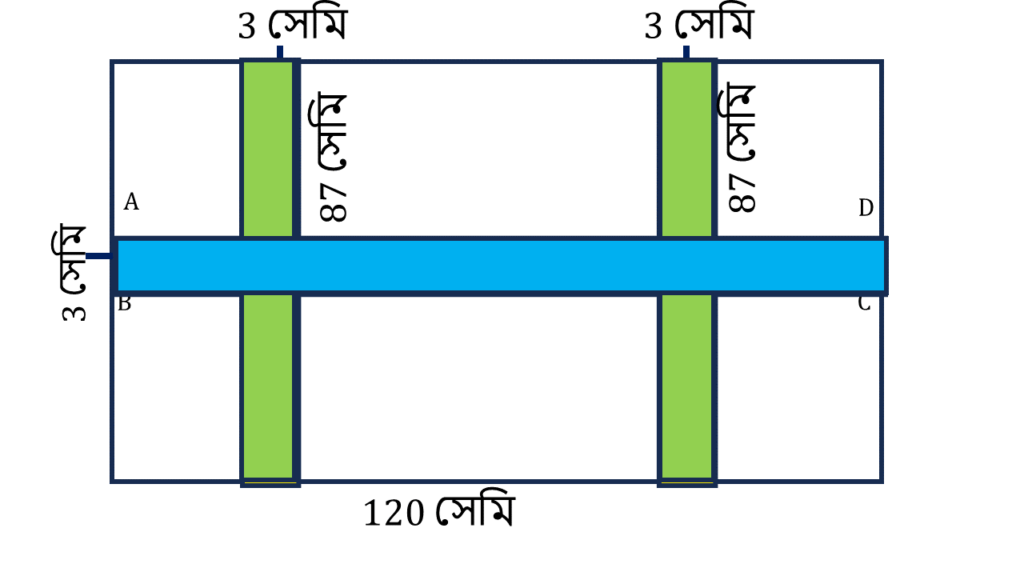
রঙিন অংশের ক্ষেত্রফল
= আয়তক্ষেত্র ABCD এর ক্ষেত্রফল + বাকি অংশের ক্ষেত্রফল
আয়তক্ষেত্র ABCD এর,
| দৈর্ঘ্য = | 120 সেমি. |
| প্রস্থ = | 3 সেমি. |
| ∴ ক্ষেত্রফল | 120 × 3 = 360 বর্গ সেমি |
বাকি অংশের,
| দৈর্ঘ্য = | 90 – 3 = 87 সেমি. |
| প্রস্থ = | 3 সেমি. |
| ∴ ক্ষেত্রফল | 87 × 3 = 261 বর্গ সেমি |
| মোট ক্ষেত্রফল = | 2×261 = 522 বর্গ সেমি |
রঙিন অংশের ক্ষেত্রফল
= 360 + 522
= 882 বর্গ সেমি
3. বিরাটি মহাজাতি সঙ্ঘের আয়তাকার মাঠের দৈর্ঘ্য ও প্রস্থের অনুপাত 4 : 3; মাঠটির চারদিকে একবার হেঁটে এলে 336 মিটার পথ অতিক্রম করা যায়। মাঠের ক্ষেত্রফল হিসাব করে লিখি।
সমাধানঃ-

বিরাটি মহাজাতি সঙ্ঘের আয়তাকার মাঠের দৈর্ঘ্য ও প্রস্থের অনুপাত 4 : 3
ধরি, মাঠের
| দৈর্ঘ্য = | 4x মিটার |
| প্রস্থ = | 3x মিটার |
| ∴ মাঠের পরিসীমা = 2(4x + 3x) = 2×7x = 14x মিটার | |
অতএব,
| 14x = 336 |
| বা, x = \(\frac{336}{14}\) |
| বা, x = 24 |
সুতরাং, মাঠের
| দৈর্ঘ্য = | 4×24=96 মিটার |
| প্রস্থ = | 3×24=72 মিটার |
| ∴ মাঠের ক্ষেত্রফল = 96×72 = 6912 বর্গ মিটার | |
4. প্রতি বর্গ মিটারে 3.50 টাকা হিসাবে সমরদের একটি বর্গাকার জমি চাষ করতে খরচ হয় 1400 টাকা। প্রতি মিটারে 8.50 টাকা হিসাবে সমরদের জমিটির চারধারে একই উচ্চতার তারের বেড়া দিতে কত খরচ হবে হিসাব করি।
সমাধানঃ-
| 3.50 টাকা খরচ হয় 1 বর্গমিটারে |
| 1400 টাকা খরচ হয় \(\frac{1400}{3.5}\) = 400 বর্গমিটারে |
∴ জমিটির ক্ষেত্রফল = 400 বর্গমিটার
ধরি, জমিটির বাহুর দৈর্ঘ্য = a মিটার ।
∴ a2 = 400
বা, a = 20
সুতরাং জমিটির পরিসীমা
= 4a = 4×20 = 80 মিটার
প্রতি মিটারে 8.50 টাকা হিসাবে সমরদের জমিটির চারধারে একই উচ্চতার তারের বেড়া খরচ হবে
= 8.50 × 80
= 680 টাকা ।
5. সুহাসদের আয়তাকার জমির ক্ষেত্রফল 500 বর্গ মিটার। জমিটির দৈর্ঘ্য 3 মিটার কমালে এবং প্রস্থ 2 মিটার বাড়ালে জমিটি বর্গাকার হয়। সুহাসদের জমির দৈর্ঘ্য ও প্রস্থ হিসাব করে লিখি।
সমাধানঃ-
ধরি, সুহাসদের আয়তাকার জমির
| দৈর্ঘ্য = | x মি. |
| প্রস্থ = | y মি. |
সুহাসদের আয়তাকার জমির ক্ষেত্রফল
= xy বর্গ মিটার
শর্তে, xy = 500 ——-(i)
জমিটির দৈর্ঘ্য 3 মিটার কমালে এবং প্রস্থ 2 মিটার বাড়ালে জমিটি বর্গাকার হয়।
জমিটির দৈর্ঘ্য 3 মিটার কমালে এবং প্রস্থ 2 মিটার বাড়ালে জমিটির নতুন দৈর্ঘ্য ও প্রস্থ হয়,
| দৈর্ঘ্য = | x – 3 মি. |
| প্রস্থ = | y + 2 মি. |
শর্তে,
| x – 3 = y + 2 |
| বা, x – y = 5 ——-(ii) |
এখন,
| (x + y)2 |
| = (x – y)2 + 4xy |
| = 52 + 4×500 |
| = 25 + 2000 |
| = 2025 |
| ∴ (x + y)2 = 2025 |
| বা, x + y = 45 ——(iii) |
(ii) ও (iii) নং যোগ করে পাই,
2x = 50
বা, x = 25
এখন x = 25 (ii) নং সমীকরণে বসিয়ে পাই,
y = 20
∴ সুহাসদের আয়তাকার জমির
| দৈর্ঘ্য = | 25 মি. |
| প্রস্থ = | 20 মি. |
6. আমাদের গ্রামে একটি বর্গাকার জমির প্রতিটি বাহুর দৈর্ঘ্য 300 মিটার। এই বর্গাকার জমির চারধার একই উচ্চতার 3 ডেসিমিটার চওড়া দেয়াল দিয়ে ঘিরব। হিসাব করে দেখি প্রতি 100 বর্গ মিটার জমিতে 5000 টাকা হিসাবে দেয়ালের জন্য কত খরচ পড়বে।
সমাধানঃ-
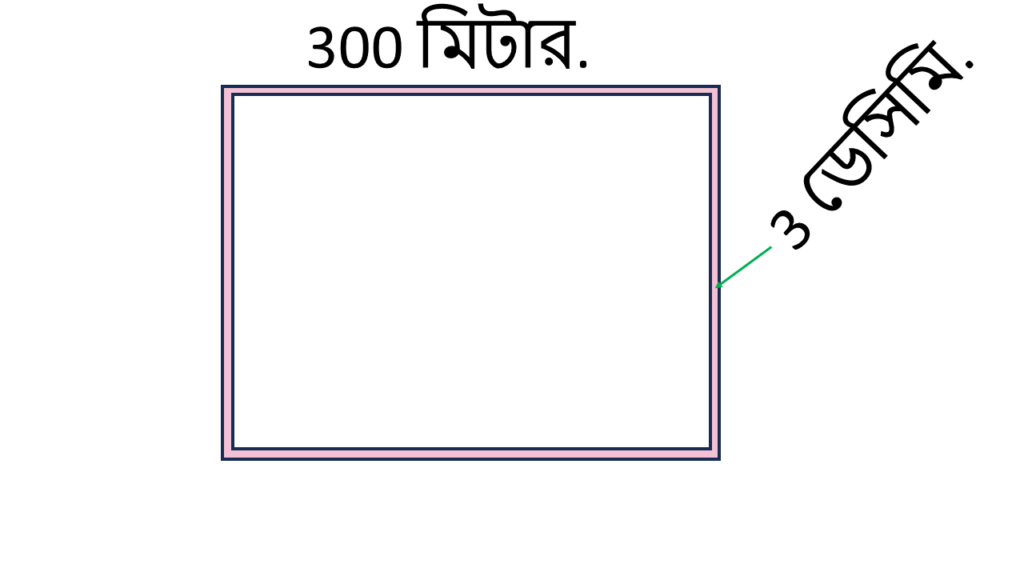
বর্গাকার জমির প্রতিটি বাহুর দৈর্ঘ্য 300 মিটার
বর্গাকার জমির ক্ষেত্রফল
= 300 × 300
= 90000 বর্গ মিটার
বর্গাকার জমির চারধার একই উচ্চতার 3 ডেসিমিটার চওড়া দেয়াল দেওয়ার পর বর্গাকার জমিটির একটি বাহুর দৈর্ঘ্য
= 300 – .3×2
= 299.4 মিটার
দেওয়াল বাদে বর্গাকার জমিটির ক্ষেত্রফল
= 299.4 × 299.4
= 89640.36 বর্গ মিটার
∴ শুধু দেওয়ালের ক্ষেত্রফল
= 90000 – 89640.36
= 359.64 বর্গ মিটার
| প্রতি 100 বর্গ মিটার জমিতে দেওয়াল দিতে খরচ = 5000 টাকা |
| 359.64 বর্গ মিটার জমিতে দেওয়াল দিতে খরচ = \(\frac{5000 \times 359.64}{100}\) = 17982 টাকা |
7. রেহানাদের আয়তাকার বাগানের দৈর্ঘ্য 14 মিটার এবং প্রস্থ 12 মিটার। বাগানটির ভিতরে চারদিকে সমান চওড়া একটি রাস্তা তৈরি করতে প্রতি বর্গ মিটারে 20 টাকা হিসাবে মোট 1380 টাকা খরচ হলে, রাস্তাটি কত চওড়া হিসাব করে লিখি।
সমাধানঃ-

| 20 টাকা খরচ হয় 1 বর্গ মিটারে |
| 1380 টাকা খরচ হয় = \(\frac{1380}{20}\) = 69 বর্গ মিটারে |
সমান চওড়া রাস্তাটির ক্ষেত্রফল=69 বর্গ মিটার
ধরি, সমান রাস্তাটি x মিটার চওড়া ।
রাস্তা বাদে বাগানের,
| দৈর্ঘ্য = | 14 – 2×x = 14 – 2x মি. |
| প্রস্থ = | 12 – 2×x = 12 – 2x মি. |
রাস্তা বাদে বাগানের ক্ষেত্রফল
= (14 – 2x) (12 – 2x)
= 14×12 – 24x – 28x + 4x2 বর্গ মিটার
এখন বাগানের ক্ষেত্রফল
= 14 × 12 বর্গ মিটার
∴ রাস্তার ক্ষেত্রফল
= 14 × 12 – 14×12 + 24x + 28x – 4x2
= 52x – 4x2
শর্তে,
| 52x – 4x2 = 69 |
| বা, 4x2 – 52x + 69 = 0 |
| বা, 4x2 – 46x – 6x + 69 = 0 |
| বা, 2x (2x – 23) – 3(2x – 23) = 0 |
| বা, (2x – 3) (2x – 23) = 0 |
| 2x – 3 = 0 | 2x -23 = 0 |
| বা, x = 1.5 | বা, x = \(\frac{23}{2}\) |
∴ রাস্তাটি 1.5 মিটার চওড়া ।
8. 1200 বর্গ সেমি. ক্ষেত্রফল বিশিষ্ট একটি আয়তক্ষেত্রাকার জমির দৈর্ঘ্য 40 সেমি. হলে, তার কর্ণের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল হিসাব করে লিখি।
সমাধানঃ-
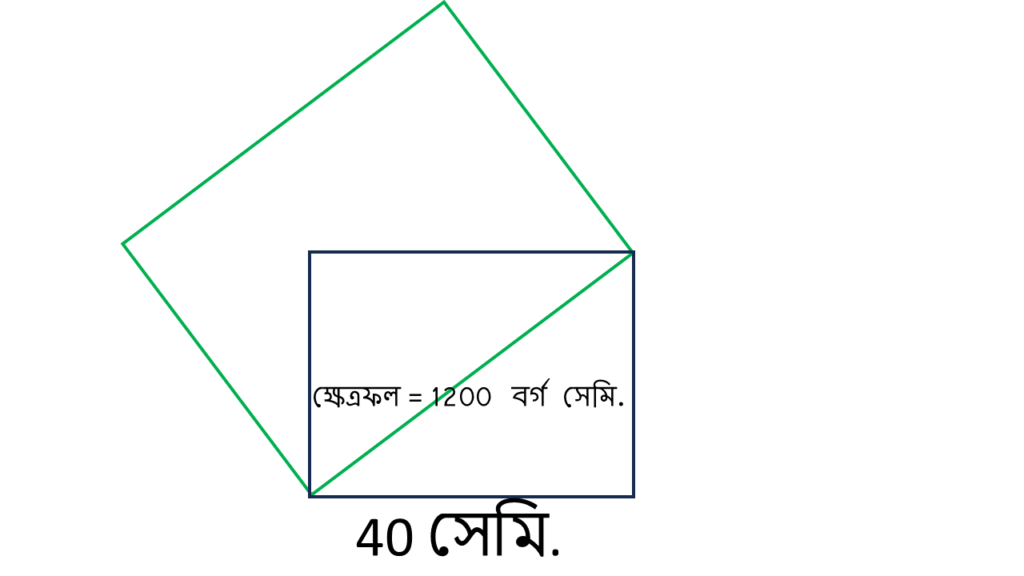
আয়তক্ষেত্রাকার জমির প্রস্থ
= ক্ষেত্রফল /দৈর্ঘ্য
= \(\frac{1200}{40}\)
= 30 সেমি.
আয়তক্ষেত্রাকার জমির কর্ণ
= \(\sqrt{40^2 + 30^2}\)
= \(\sqrt{1600 + 900}\)
= \(\sqrt{2500}\)
= 50 সেমি.
কর্ণের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল
= 50 × 50
= 2500 বর্গ সেমি.
9. একটি হলঘরের দৈর্ঘ্য 4 মিটার, প্রস্থ 6 মিটার এবং উচ্চতা 4 মিটার। ঘরটিতে তিনটি দরজা আছে যাদের প্রত্যেকটি 1.5মি. × 1 মি. এবং চারটি জানালা আছে যাদের প্রত্যেকটি 1.2 মি. × 1 মি.। ঘরটির চার দেয়াল প্রতি বর্গ মিটারে 70 টাকা হিসাবে রঙিন কাগজ দিয়ে ঢাকতে কত খরচ হবে।
সমাধানঃ-
হলঘরের চার দেওয়ালের ক্ষেত্রফল
= 2(6×4 + 4×4)
= 80 বর্গ মিটার .
তিনটি দরজার ক্ষেত্রফল
= 3×1.5×1
= 4.5 বর্গ মিটার.
চারটি জানালার ক্ষেত্রফল
= 4×1.2×1
= 4.8 বর্গ মিটার.
দরজা জানালা বাদে চার দেওয়ালের ক্ষেত্রফল
= 80 – (4.5 + 4.8)
= 80 – 9.3
= 70.7 বর্গ মিটার.
অতএব , চার দেয়াল প্রতি বর্গ মিটারে 70 টাকা হিসাবে রঙিন কাগজ দিয়ে ঢাকতে খরচ হবে
= 70×70.7
= 4949 টাকা
10. একটি ঘরের চার দেয়ালের ক্ষেত্রফল 42 বর্গ মিটার এবং মেঝের ক্ষেত্রফল 12 বর্গ মিটার। ঘরটির দৈর্ঘ্য 4 মিটার হলে, ঘরটির উচ্চতা হিসাব করে লিখি।
সমাধানঃ-
ঘরটির মেঝের প্রস্থ
= \(\frac{মেঝের খেত্রফল}{মেঝের দৈর্ঘ্য}\)
= \(\frac{12}{4}\)
= 3 মিটার.
ধরি, ঘরটির উচ্চতা = x মিটার
অতএব, ঘরটির চার দেওয়ালের ক্ষেত্রফল হবে
= 2(4 + 3)x
= 14x বর্গ মিটার.
শর্তে, 14x = 42
বা, x = 3
অতএব, ঘরটির উচ্চতা = 3 মিটার
11. সুজাতা 84 বর্গ সেমি. ক্ষেত্রফলবিশিষ্ট একটি আয়তাকার কাগজে ছবি আঁকবে। কাগজটির দৈর্ঘ্য ও প্রস্থের অন্তর 5 সেমি । সুজাতার কাগজটির পরিসীমা হিসাব করি।
সমাধানঃ-
ধরি, আয়তকার কাগজ টির,
| দৈর্ঘ্য = | x সেমি. |
| প্রস্থ = | y সেমি. |
| ক্ষেত্রফল xy = 84 বর্গ সেমি. ——- (i) |
| দৈর্ঘ্য ও প্রস্থের অন্তর 5 সেমি অর্থাৎ, x – y = 5 ———-(ii) |
এখন,
| (x + y)2 |
| = (x – y)2 + 4xy |
| = 52 + 4×84 [(i) ও (ii) নং থেকে মান বসিয়ে পেলাম] |
| = 25 + 336 |
| = 361 |
| ∴ x + y = \(\sqrt{361}\) |
| বা, x + y = 19 ——–(iii) |
আয়তকার কাগজ টির পরিসীমা,
| 2(x + y) |
| = 2 × 19 [(iii) নং থেকে পেলাম] |
| = 38 সেমি. |
12. সিরাজদের বর্গাকার বাগানের বাইরের চারদিকে 2.5 মিটার চওড়া একটি রাস্তা আছে। রাস্তাটির ক্ষেত্রফল 165 বর্গ মিটার। বাগানটির ক্ষেত্রফল এবং কর্ণের দৈর্ঘ্য হিসাব করি। (√2 = 1.414)
সমাধানঃ-
ধরি, বর্গাকার বাগানের দৈর্ঘ্য = x মিটার.
∴ বর্গাকার বাগানের ক্ষেত্রফল = x2 বর্গমি.
রাস্তা সমেত বাগানের,
| দৈর্ঘ্য = | x + 2×2.5 = x + 5 মি. |
রাস্তা সমেত বাগানের ক্ষেত্রফল,
= (x + 5)2 বর্গ মিটার.
∴ রাস্তার ক্ষেত্রফল
= (x + 5)2 – x2 বর্গমি.
শর্তে,
| (x + 5)2 – x2 = 165 |
| বা, x2 + 10x + 25 – x2 = 165 |
| বা, 10x = 165 – 25 |
| বা, 10x = 140 |
| বা, x = 14 |
∴ বাগানের ক্ষেত্রফল = 14×14=196 বর্গ মিটার.
এবং বাগানের কর্ণের দৈর্ঘ্য
= \(\sqrt{14^2 + 14^2}\)
= \(\sqrt{196 + 196}\)
= \(\sqrt{392}\)
= 14√2
= 14×1.414
= 19.796 মিটার.
13. যে বর্গাকার জমির কর্ণের দৈর্ঘ্য 20√2 মিটার তার চারধার পাঁচিল দিয়ে ঘিরতে কত মিটার দৈর্ঘ্যের পাঁচিল দিতে হবে হিসাব করে লিখি। প্রতি বর্গমিটারে 20 টাকা হিসাবে ঘাস বসাতে কত খরচ হবে হিসাব করে লিখি।
সমাধানঃ-
ধরি, বর্গাকার বাগানের দৈর্ঘ্য = a মিটার.
বর্গাকার বাগানের কর্ণের দৈর্ঘ্য = a√2 মিটার.
অতএব,
a√2 = 20√2
বা, a = 20
∴ বর্গাকার বাগানের পরিসীমা
= 4×20 = 80 মিটার.
এবং বর্গাকার বাগানের ক্ষেত্রফল
= 20×20
= 400 বর্গ মি.
প্রতি বর্গমিটারে 20 টাকা হিসাবে ঘাস বসাতে খরচ হবে
= 20×400
= 8000 বর্গ মিটার.
14. আমাদের আয়তাকার বাগানের একটি কর্ণ বরাবর একটি বেড়া দেব। আয়তাকার বাগানের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 12 মিটার ও 7 মিটার হলে, বেড়ার দৈর্ঘ্য হিসাব করে দেখি। বেড়াটি আয়তাকার বাগানকে যে দুটি ত্রিভুজে ভাগ করবে তার পরিসীমা লিখ
সমাধানঃ-
আয়তাকার বাগানের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 12 মিটার ও 7 মিটার
আয়তাকার বাগানের কর্ণ
= \(\sqrt{(দৈর্ঘ্য)^2 + (প্রস্থ)^2}\)
= \(\sqrt{12^2 + 7^2}\)
= \(\sqrt{144 + 49}\)
= \(\sqrt{193}\) মিটার
বেড়াটি আয়তাকার বাগানকে যে দুটি ত্রিভুজে ভাগ করবে তার পরিসীমা
= 12 + 7 + \(\sqrt{193}\)
= 19 + \(\sqrt{193}\) মিটার.
15. মৌসুমীদের বাড়ির আয়তাকার বড় হলঘরের দৈর্ঘ্য ও প্রস্থের অনুপাত 9:5 এবং পরিসীমা 140 মিটার।মৌসুমীরা হলঘরের মেঝেতে 25 সেমি x 20 সেমি. আকারের আয়তাকার টালি বসাতে চায়। প্রতি 100 টালির দাম 500 টাকা হলে, মৌসুমীদের হলঘরের মেঝেতে টালি বসাতে কত খরচ হবে হিসাব করি।
সমাধানঃ-
আয়তাকার বড় হলঘরের দৈর্ঘ্য ও প্রস্থের অনুপাত 9:5
ধরি, আয়তাকার বড় হলঘরের
| দৈর্ঘ্য = | 9x মি. |
| প্রস্থ = | 5x মি. |
∴ আয়তাকার বড় হলঘরের পরিসীমা
= 2(9x + 5x)
= 28x মি.
শর্তে,
28x = 140
বা, x = \(\frac{140}{28}\) = 5
অতএব, আয়তাকার বড় হলঘরের
| দৈর্ঘ্য = | 45 মি. |
| প্রস্থ = | 25 মি. |
∴ আয়তাকার বড় হলঘরের ক্ষেত্রফল
= 45×25
= 1125 বর্গ মিটার.
এখন একটি টালির ক্ষেত্রফল
= 25×20
= 500 বর্গ সেমি.
= 0.05 বর্গ মিটার.
আয়তাকার বড় হলঘরে টালি লাগবে
= \(\frac{1125}{0.05}\)
= 22500 টি
| 100 টি টালির মূল্য 500 টাকা |
| 22500 টি টালির মূল্য =\(\frac{500 \times 22500}{100}\) = 112500 টাকা |
∴ মৌসুমীদের হলঘরের মেঝেতে টালি বসাতে খরচ হবে 112500 টাকা।
16. 18 মিটার দৈর্ঘ্যবিশিষ্ট একটি বড়ো হলঘরে কার্পেট দিয়ে মুড়তে 2160 টাকা খরচ হয়। যদি হলঘরের প্রস্থ 4 মিটার কম হতো তাহলে 1620 টাকা খরচ হতো। হলঘরের ক্ষেত্রফল হিসাব করি।
সমাধানঃ-
ধরি, হলঘরের প্রস্থ = x মিটার.
হলঘরের ক্ষেত্রফল = 18x বর্গ মিটার.
অতএব, প্রতি বর্গ মিটার মুড়তে খরচ হয়
= \(\frac{2160}{18x}\) টাকা
হলঘরের প্রস্থ 4 মিটার কম হতো তাহলে হলঘরের ক্ষেত্রফল = 18(x – 4) বর্গ মিটার.
সেক্ষেত্রে প্রতি বর্গ মিটার মুড়তে খরচ হয়
= \(\frac{1620}{18(x – 4)}\)
শর্তে,
| \(\frac{2160}{18x} = \frac{1620}{18(x – 4)}\) |
| বা, \(\frac{216}{x} = \frac{162}{x – 4}\) |
| বা, \(\frac{108}{x} = \frac{81}{x – 4}\) |
| বা, 108x – 4×108 = 81x |
| বা, 108x – 81x = 4×108 |
| বা, 27x = 4×108 |
| বা, x = \(\frac{4 \times 108}{27}\) |
| বা, x = 16 |
হলঘরের ক্ষেত্রফল
= 18 × 16
= 288 বর্গ মিটার.
17. একটি আয়তাকার জমির কর্ণের দৈর্ঘ্য 15 মিটার এবং দৈর্ঘ্য ও প্রস্থের অন্তর 3 মিটার। জমিটির পরিসীমা ও ক্ষেত্রফল নির্ণয় করি।
সমাধানঃ-
ধরি, আয়তাকার জমির
| দৈর্ঘ্য = | x মি. |
| প্রস্থ = | y মি. |
দৈর্ঘ্য ও প্রস্থের অন্তর 3 মিটার
অর্থাৎ, x – y = 3 ——-(i)
প্রশ্নানুসারে,
| 152 = x2 + y2 |
| বা, x2 + y2 = 225 |
| বা, (x – y)2 + 2xy = 225 |
| বা, 32 + 2xy = 225 [ (i) নং থেকে মান বসিয়ে পেলাম] |
| বা, 2xy = 225 – 9 |
| বা, 2xy = 216 |
| বা, xy = 108 ——-(ii) |
অতএব, জমিটির ক্ষেত্রফল = 108 বর্গ মিটার.
আবার,
| x2 + y2 = 225 |
| বা, (x + y)2 – 2xy = 225 |
| বা, (x + y)2 = 225 + 216 |
| বা, (x + y)2 = 441 |
| বা, x + y = 21 |
| ∴ 2(x + y) = 42 |
অতএব, জমিটির পরিসীমা = 42 মিটার.
18. 385 মিটার × 60 মিটার পরিমাপের একটি আয়তাকার চাতাল পাকা করতে সর্ববৃহৎ কত মাপের বর্গাকার টাইলস ব্যবহার করা যাবে এবং সেক্ষেত্রে টাইলসের সংখ্যা কত হবে হিসাব করি।
সমাধানঃ-
আয়তাকার চাতাল এর,
| দৈর্ঘ্য = | 385 = 5×7×11 মি. |
| প্রস্থ = | 60 = 5×3×4 মি. |
দৈর্ঘ্য ও প্রস্থের গ.সা.গু = 5
অতএব, সর্ববৃহৎ 5 মিটার×5 মিটার মাপের বর্গাকার টাইলস ব্যবহার করা যাবে.
এবং টাইলস এর সংখ্যা
= \(\frac{385\times 60}{5 \times 5}\)
= 924 টি।
বহু বিকল্পীয় প্রশ্ন (M.C.Q):
(i) একটি বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য 12√2 সেমি। বর্গক্ষেত্রটির ক্ষেত্রফল
উত্তরঃ- (b) 144 বর্গ সেমি.
সমাধানঃ-
ধরি, বর্গক্ষেত্রের বাহু = a সেমি.
∴ a√2 = 12√2
⇒ a = 12
বর্গক্ষেত্রের ক্ষেত্রফল = a2 = 12×12 = 144 বর্গ সেমি.
(ii) যদি একটি বর্গক্ষেত্রের ক্ষেত্রফল A1 বর্গ একক এবং ওই বর্গক্ষেত্রের কর্ণের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল A2 বর্গ একক হয়, তাহলে A1:A2 হবে
উত্তরঃ- (a) 1:2
সমাধানঃ-
ধরি বর্গক্ষেত্রের বাহুর দৈর্ঘ্য = a একক।
A1 = a2
এবং
A2 = (a√2)2
A1:A2 = a2 : 2a2 = 1 : 2
(iii) 6 মিটার লম্বা ও 4 মিটার চওড়া একটি আয়তাকার জায়গা 2 ডেসিমি, বর্গ টালি দিয়ে বাঁধাতে হলে টালি লাগবে
উত্তরঃ- (c) 600
সমাধানঃ-
ক্ষেত্রফল = 60×40 = 2400 বর্গ ডেসিমি.
টালি লাগবে = \(\frac{2400}{2\times 2}\) = 600 টি ।
(iv) সমান পরিসীমাবিশিষ্ট একটি বর্গক্ষেত্র এবং একটি আয়তক্ষেত্রের ক্ষেত্রফল যথাক্রমে S এবং R হলে,
উত্তরঃ- (b) S>R
সমাধানঃ-
ধরি, বর্গক্ষেত্রের পরিসীমা = 4a একক যেখানে a বর্গক্ষেত্রের বাহুর দৈর্ঘ্য।
এবং ধরি, 2(x + y) = আয়তক্ষেত্রের পরিসীমা যেখানে x ও y যথাক্রমে আয়তক্ষেত্রের দৈর্ঘ্য ও প্রস্থ।
শর্তে,
| 4a = 2(x+y) |
| [ উভয়পক্ষ বর্গ করে পাই, ] |
| 16a2 = 4(x+y)2 |
| বা, 4a2 = (x – y)2 + 4xy |
| বা, a2 = (x – y)2/4 + xy |
| বা, a2 > xy [ ∵ (x – y)2 > 0 ] |
| ⇒ S > R |
(v) একটি আয়তক্ষেত্রের কর্ণের দৈর্ঘ্য 10 সেমি. এবং ক্ষেত্রফল 62.5 বর্গ সেমি. হলে, আয়তক্ষেত্রটির দৈর্ঘ্য ও প্রস্থের সমষ্টি
উত্তরঃ- (b) 15 সেমি
সমাধানঃ-
ধরি, আয়তক্ষেত্রের দৈর্ঘ্য ও প্রস্থ যথাক্রমে x ও y একক।
অতএব,
xy = 62.5
এবং
| \(\sqrt{x^2 + y^2}\) = 10 |
| বা, x2 + y2 = 100 |
এখন,
| (x + y)2 |
| = x2 + y2 + 2xy |
| = 100 + 2×62.5 |
| = 100 + 125 |
| = 225 |
| ∴ (x + y)2 = 225 |
| বা, x + y = 15 |
20. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ
(i) একটি বর্গক্ষেত্রের বাহুর দৈর্ঘ্য 10% বৃদ্ধি করলে, বর্গক্ষেত্রটির ক্ষেত্রফল শতকরা কত বৃদ্ধি পাবে?
সমাধানঃ-
ধরি, বর্গক্ষেত্রের বাহুর দৈর্ঘ্য = 100 একক
ক্ষেত্রফল = 10000 বর্গ একক
বর্গক্ষেত্রের বাহুর দৈর্ঘ্য 10% বৃদ্ধি করলে বাহুর দৈর্ঘ্য হয় = 110 একক
সেক্ষেত্রে ক্ষেত্রফল = 12100 বর্গ একক
ক্ষেত্রফল বৃদ্ধি
= 12100 – 10000 = 2100 বর্গএকক
শতকরা বৃদ্ধি
= \(\frac{2100 \times 100}{10000}\) = 21 বর্গ একক
(ii) একটি আয়তক্ষেত্রের দৈর্ঘ্য 10% বৃদ্ধি এবং প্রস্থ 10% হ্রাস করা হলে, ক্ষেত্রফল শতকরা কত বৃদ্ধি বা হ্রাস পাবে?
সমাধানঃ-
ধরি , আয়তক্ষেত্রের দৈর্ঘ্য ও প্রস্থ যথাক্রমে x ও y একক।
ক্ষেত্রফল = xy বর্গ একক
দৈর্ঘ্য 10% বৃদ্ধি এবং প্রস্থ 10% হ্রাস করা হলে
| দৈর্ঘ্য = | \(\frac{110x}{100}\) একক |
| প্রস্থ = | \(\frac{90y}{100}\) একক |
ক্ষেত্রফল
= \(\frac{110x \times 90y}{10000}\) বর্গ একক
ক্ষেত্রফলের হ্রাস
= \(xy – \frac{110x \times 90y}{10000}\)
= \(\frac{(10000 – 9900)xy}{10000}\)
= \(\frac{100xy}{10000}\)
শতকরা হ্রাস
= \(\frac{100xy \times 100}{xy×10000}\)
= 1 বর্গ একক
(iii) একটি আয়তক্ষেত্রের কর্ণের দৈর্ঘ্য 5 সেমি । কর্ণদ্বয়ের ছেদবিন্দু থেকে আয়তক্ষেত্রের একটি প্রস্থের উপর লম্বের দৈর্ঘ্য 2 সেমি.। আয়তক্ষেত্রের প্রস্থের দৈর্ঘ্য কত?
সমাধানঃ-
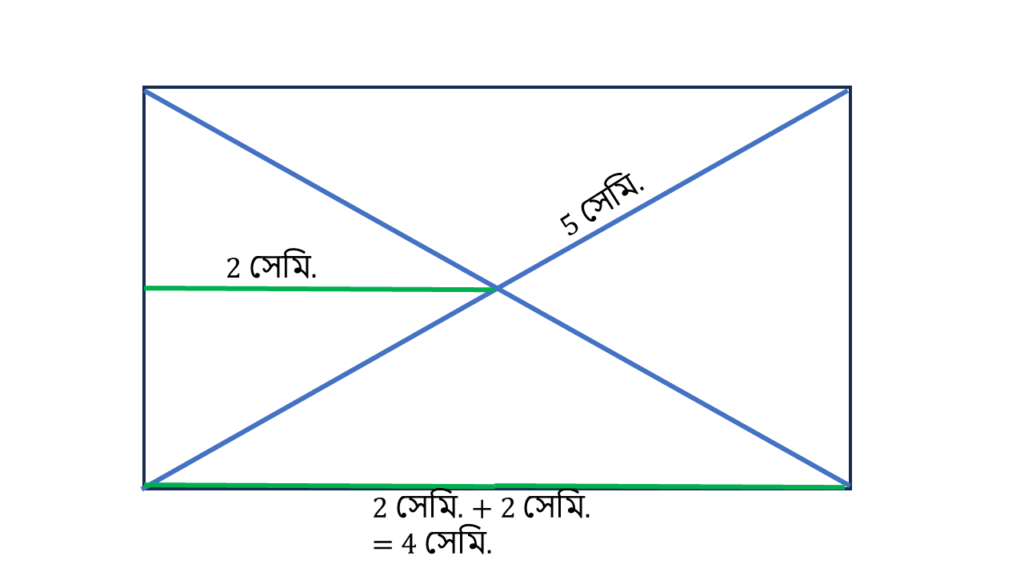
অতএব, আয়তক্ষেত্রের প্রস্থের দৈর্ঘ্য
= \(\sqrt{5^2 – 4^2}\)
= \(\sqrt{25 – 16}\)
= √9 = 3 সেমি.
(iv) একটি বর্গক্ষেত্রের কর্ণদ্বয়ের ছেদবিন্দু থেকে তার যে-কোনো বাহুর উপর অঙ্কিত লম্বের দৈর্ঘ্য 2√2 সেমি. হলে, বর্গক্ষেত্রটির প্রতিটি কর্ণের দৈর্ঘ্য কত?
সমাধানঃ-
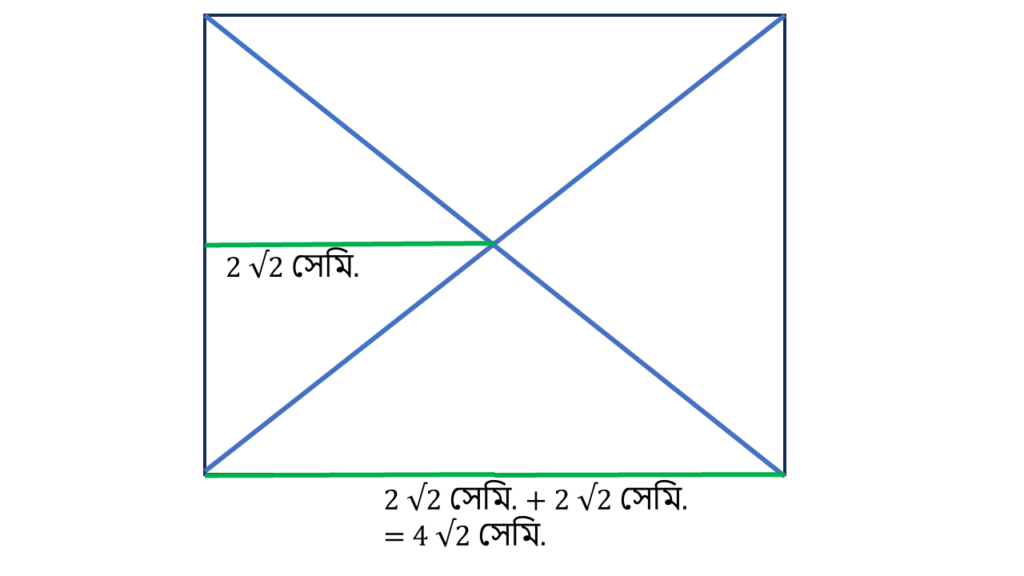
অতএব কর্ণের দৈর্ঘ্য
= 4√2×√2
= 4×2 = 8 সেমি.
(v) একটি আয়তক্ষেত্রের পরিসীমা 34 সেমি, এবং ক্ষেত্রফল 60 বর্গ সেমি.। আয়তক্ষেত্রের প্রতিটি কর্ণের দৈর্ঘ্য কত?
সমাধানঃ-
ধরি, আয়তক্ষেত্রের দৈর্ঘ্য ও প্রস্থ যথাক্রমে x ও y সেমি.
অতএব,
2(x+y) = 34 বা, x + y = 17 —–(i)
এবং xy = 60 —–(ii)
এখন,
| x2 + y2 |
| = (x + y)2 – 2xy |
| = 17×17 – 2×60 |
| = 289 – 120 |
| = 169 |
| ∴ x2 + y2 = 169 |
| বা, \(\sqrt{x^2 + y^2}\) = 13 |
প্রতিটি কর্ণের দৈর্ঘ্য = 13 সেমি.
ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল অধ্যায়ের বাকি কষে দেখিঃ-
| WB Class 9 এর গণিত প্রকাশের সমস্ত অধ্যায়ের সমাধান- | |
|---|---|
| অধ্যায় | সমাধান |
| 1. বাস্তব সংখ্যা (Real Numbers) | কষে দেখি 1.1 |
| কষে দেখি 1.2 | |
| কষে দেখি 1.3 | |
| 2. সূচকের নিয়মাবলি (Laws of Indices) | কষে দেখি 2 |
| 3. লেখচিত্র (Graph) | কষে দেখি 3.1 |
| কষে দেখি 3.2 | |
| 4. স্থানাঙ্ক জ্যামিতি : দূরত্ব নির্ণয় (Co-ordinate Geometry: Distance Formula) | কষে দেখি 4 |
| 5. রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) (Linear Simultaneous Equations) | কষে দেখি 5.1 |
| কষে দেখি 5.2 | |
| কষে দেখি 5.3 | |
| কষে দেখি 5.4 | |
| কষে দেখি 5.5 | |
| কষে দেখি 5.6 | |
| কষে দেখি 5.7 | |
| 6. সামান্তরিকের ধর্ম (Properties of Parallelogram) | কষে দেখি 6 |
| 7. বহুপদী সংখ্যামালা (Polynomial) | কষে দেখি 7.1 |
| কষে দেখি 7.2 | |
| কষে দেখি 7.3 | |
| কষে দেখি 7.4 | |
| 8. উৎপাদকে বিশ্লেষণ (Factorisation) | কষে দেখি 8.1 |
| কষে দেখি 8.2 | |
| কষে দেখি 8.3 | |
| কষে দেখি 8.4 | |
| কষে দেখি 8.5 | |
| 9. ভেদক ও মধ্যবিন্দু সংক্রান্ত উপপাদ্য (Transversal & Mid-Point Theorem). | কষে দেখি 9 |
| 10. লাভ ও ক্ষতি (Profit and Loss) | কষে দেখি 10.1 |
| কষে দেখি 10.2 | |
| 11. রাশিবিজ্ঞান (Statistics) | কষে দেখি 11.1 |
| কষে দেখি 11.2 | |
| 12. ক্ষেত্রফল সংক্রান্ত উপপাদ্য (Theorems on Area) | কষে দেখি 12 |
| 13. সম্পাদ্য : ত্রিভুজের সমান ক্ষেত্রফল বিশিষ্ট সামান্তরিক অঙ্কন | কষে দেখি 13 |
| 14. সম্পাদ্য : চতুর্ভুজের সমান ক্ষেত্রফল বিশিষ্ট ত্রিভুজ অঙ্কন | কষে দেখি 14 |
| 15. ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল (Area & Perimeter of Triangle & Quadrilateral) | কষে দেখি 15.1 |
| কষে দেখি 15.2 | |
| কষে দেখি 15.3 | |
| 16. বৃত্তের পরিধি (Circumference of Circle) | কষে দেখি 16 |
| 17. সমবিন্দু সংক্রান্ত উপপাদ্য (Theorems on concurrence) | কষে দেখি 17 |
| 18. বৃত্তের ক্ষেত্রফল (Area of Circle) | কষে দেখি 18 |
| 19. স্থানাঙ্ক জ্যামিতি: সরলরেখাংশের অন্তর্বিভক্ত ও বহিঃবিভক্ত (Co-ordinate Geometry: Internal and External Division of Straight-Line Segment) | কষে দেখি 19 |
| 20. স্থানাঙ্ক জ্যামিতি: ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল (Co-ordinate Geometry: Area of Triangular Region) | কষে দেখি 20 |
| 21. লগারিদম (Logarithm) | কষে দেখি 21 |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
এই কষে দেখি 15.1 Class 9|Koshe Dekhi 15.1 Class 9 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।

এখানে তোমরা তোমাদের নবম শ্রেণীতে| Class 9 এ কি কি পড়ানো হয়, মানে তোমাদের নবম শ্রেণী| Class 9 সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

