শ্রেণী-নবম ; অধ্যায় – বাস্তব সংখ্যা ; কষে দেখি 1.2
কষে দেখি 1.2 Class 9 এর অংকের সমাধান গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ
বাস্তব সংখ্যা এর পরিসর অনেক বড়ো হলেও পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদ | WBBSE বোর্ডের অন্তর্গত তোমাদের নবম শ্রেণী | Class 9 এর প্রথম অধ্যায়ে এই বাস্তব সংখ্যা সম্পর্কে কিছু ধারণা দেওয়া হয়েছে যা তোমাদের বাস্তব সংখ্যা সম্পর্কে একটু অবগত করাবে।
এই বাস্তব সংখ্যা থেকে তোমাদের নবম শ্রেণী | Class 9 এ কষে দেখি 1.2|Koshe Dekhi 1.2 এ যে সমস্ত অংক গুলি আছে সেগুলি সমাধান করার জন্যে যে নিয়ম বা theory আছে তা একটু তোমাদের জানতে হবে, নাহলে এই কষে দেখি 1.2|Koshe Dekhi 1.2 এর অংকগুলি সমাধান করতে অসুবিধা হবে।
আগামিতে এই কষে দেখি 1.2 Class 9 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 1.2 Class 9 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 1.2 Class 9 তারপর  |
কষে দেখি 1.2 Class 9 এর  Youtube ভিডিও-
Youtube ভিডিও-
কষে দেখি 1.2 | Koshe Dekhi 1.2
1. নীচের বক্তব্যের কোনটি সত্য ও কোনটি মিথ্যা লিখি:
(i) দুটি মূলদ সংখ্যার সমষ্টি সর্বদা মূলদ সংখ্যা হবে।
=> সত্য
(ii) দুটি অমূলদ সংখ্যার সমষ্টি সর্বদা অমূলদ সংখ্যা হবে।
=> মিথ্যা
কারণ- √5 + (-√5) = 0
(iii) দুটি মূলদ সংখ্যার গুণফল সর্বদা মূলদ সংখ্যা হবে।
=> সত্য
(iv) দুটি অমূলদ সংখ্যার গুণফল সর্বদা মূলদ সংখ্যা হবে ।
=> মিথ্যা
কারণ-
√5×√5 = 5
(v) প্রতিটি মূলদ সংখ্যাই বাস্তব সংখ্যা।
=> সত্য
(vi) প্রতিটি বাস্তব সংখ্যাই অমূলদ সংখ্যা।
=> মিথ্যা
কারণ- 2 একটি বাস্তব সংখ্যা কিন্তু অমূলদ সংখ্যা নয়।
2. অমূলদ সংখ্যা বলতে কী বুঝি? 4 টি অমূলদ সংখ্যা লিখি ।
উত্তরঃ-
যে সকল সংখ্যাকে \(\frac{p}{q}\) আকারে প্রকাশ করা যাবেনা( যেখানে p ও q পূর্ণসংখ্যা এবং q≠0) তাদের অমূলদ সংখ্যা বলে।
যেমন- √5, √6, √7, -√8, –\(\sqrt{11}\)
3. নীচের সংখ্যাগুলির মধ্যে কোনটি মূলদ সংখ্যা এবং কোনটি অমূলদ সংখ্যা লিখি :
(i) √9
সমাধানঃ-
√9= 3
একটি মূলদ সংখ্যা
(ii) \(\sqrt{225}\)
সমাধানঃ-
\(\sqrt{225}\) = 15
একটি মূলদ সংখ্যা
(iii) √7
সমাধানঃ-
একটি অমূলদ সংখ্যা
(iv) \(\sqrt{50}\)
সমাধানঃ-
একটি অমূলদ সংখ্যা
(v) \(\sqrt{100}\)
সমাধানঃ-
\(\sqrt{100}\) = 10
একটি মূলদ সংখ্যা
(vi) -\(\sqrt{81}\)
সমাধানঃ-
একটি মূলদ সংখ্যা
(vii) \(\sqrt{42}\)
সমাধানঃ-
একটি অমূলদ সংখ্যা
(viii) \(\sqrt{29}\)
সমাধানঃ-
একটি অমূলদ সংখ্যা
(ix) -\(\sqrt{1000}\)
সমাধানঃ-
একটি অমূলদ সংখ্যা
4. সংখ্যারেখায় √5 স্থাপন করি।
সমাধানঃ-
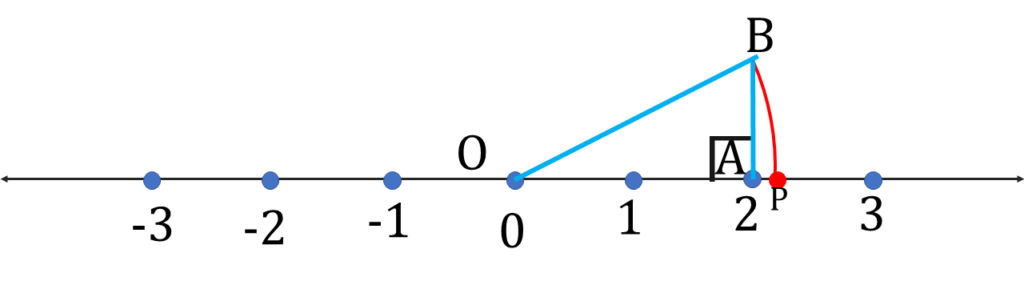
প্রথমে সংখ্যারেখার O বিন্দুতে শূন্য স্থাপন করলাম। সংখ্যারেখার উপর এমনভাবে A বিন্দু নিলাম যাতে OA = 2 একক হয়।
A বিন্দুতে OA ⊥ AB আঁকলাম এবং AB = 1 একক নিলাম।
পিথাগোরাসের উপপাদ্য থেকে পেলাম OB = \(\sqrt{2^2 + 1^2}\) একক = √5 একক
O বিন্দুকে কেন্দ্র করে OB-এর সমান দৈর্ঘ্যের ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ অঙ্কন করলাম যা সংখ্যারেখাকে
P বিন্দুতে ছেদ করল,
অতএব OP = √5 একক
√5 সংখ্যারেখায় স্থাপন করে P বিন্দু পেলাম।
5. সংখ্যারেখায় √3 স্থাপন করি।
সমাধানঃ-
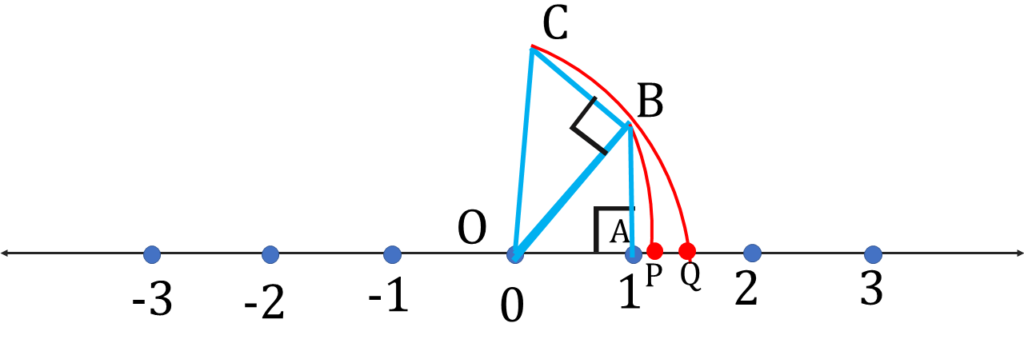
প্রথমে সংখ্যারেখার O বিন্দুতে শূন্য স্থাপন করলাম। সংখ্যারেখার উপর এমনভাবে A বিন্দু নিলাম যাতে OA = 1 একক হয়।
A বিন্দুতে OA ⊥ AB আঁকলাম এবং AB = 1 একক নিলাম।
পিথাগোরাসের উপপাদ্য থেকে পেলাম OB = \(\sqrt{1^2 + 1^2}\) একক = √2 একক
O বিন্দুকে কেন্দ্র করে OB-এর সমান দৈর্ঘ্যের ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ অঙ্কন করলাম যা সংখ্যারেখাকে
P বিন্দুতে ছেদ করল,
অতএব OP = √2 একক
√2 সংখ্যারেখায় স্থাপন করে P বিন্দু পেলাম।
এবার OB-এর উপর BC লম্ব টানলাম এবং BC = 1 একক নিলাম ।
পিথাগোরাসের উপপাদ্য থেকে পেলাম,
OC2
= OB2 + BC2
= {(√2)2 + (1)2} বর্গ একক
= (2 + 1) বর্গ একক
= 3 বর্গএকক
অতএব OC = √3 একক
O বিন্দুকে কেন্দ্র করে OC-এর সমান দৈর্ঘ্যের ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ অঙ্কন করলাম যা সংখ্যারেখাকে
Q বিন্দুতে ছেদ করল,
অতএব OQ = √3 একক
6. একই সংখ্যারেখায় √5, √6, √7, -√6, -√8, –\(\sqrt{11}\) স্থাপন করি।
সমাধানঃ-
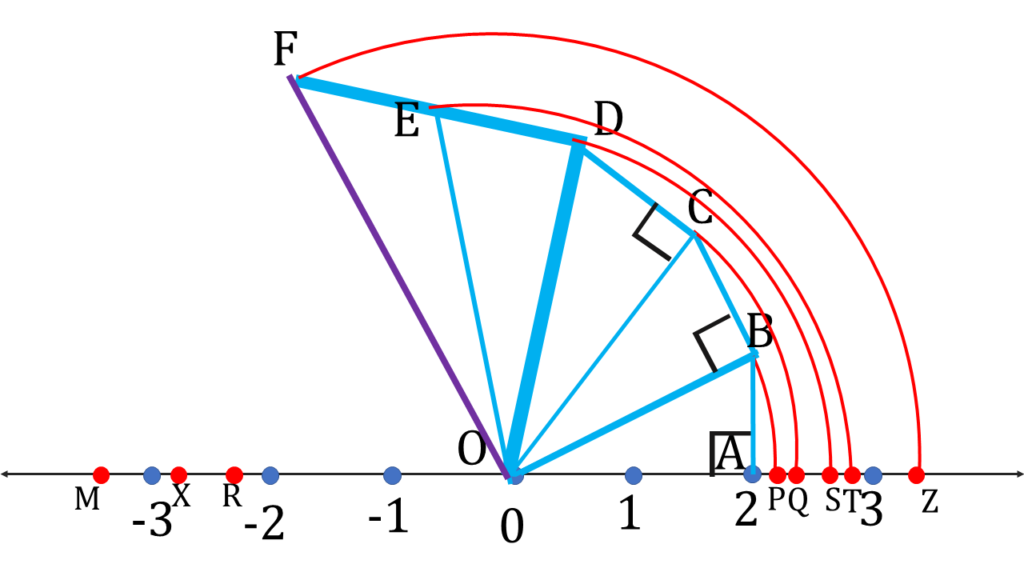
(i) প্রথমে সংখ্যারেখার O বিন্দুতে শূন্য স্থাপন করলাম। সংখ্যারেখার উপর এমনভাবে A বিন্দু নিলাম যাতে OA = 2 একক হয়।
A বিন্দুতে OA ⊥ AB আঁকলাম এবং AB = 1 একক নিলাম।
পিথাগোরাসের উপপাদ্য থেকে পেলাম OB = \(\sqrt{2^2 + 1^2}\) একক = √5 একক
O বিন্দুকে কেন্দ্র করে OB-এর সমান দৈর্ঘ্যের ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ অঙ্কন করলাম যা সংখ্যারেখাকে
P বিন্দুতে ছেদ করল,
অতএব OP = √5 একক
√5 সংখ্যারেখায় স্থাপন করে P বিন্দু পেলাম।
(ii)
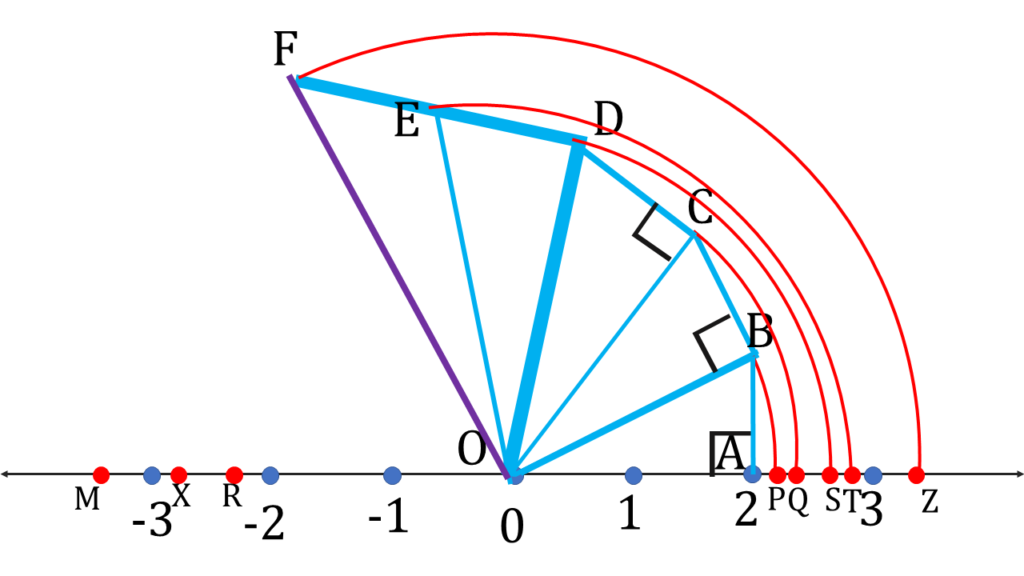
এবার OB-এর উপর BC লম্ব টানলাম এবং BC = 1 একক নিলাম ।
পিথাগোরাসের উপপাদ্য থেকে পেলাম,
OC2
= OB2 + BC2
= {(√5)2 + (1)2} বর্গ একক
= (5 + 1) বর্গ একক
= 6 বর্গএকক
অতএব OC = √6 একক
O বিন্দুকে কেন্দ্র করে OC- এর সমান দৈর্ঘ্যের ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ অঙ্কন করলাম যা সংখ্যারেখাকে Q বিন্দুতে ছেদ করল।
OQ =√6 একক
সংখ্যারেখায় √6 অমূলদ সংখ্যাটি স্থাপন করে Q বিন্দু পেলাম।
(iii) & (iv)
একইরকমভাবে পেলাম
OD = OS =√7
এবং
OE = OT = √8
OQ সমান করে শূন্য এর বামদিকে OR নিলাম
অতএব OR = – √6
আবার
OT সমান করে শূন্য এর বামদিকে OX নিলাম
অতএব OX = – √8
(v)
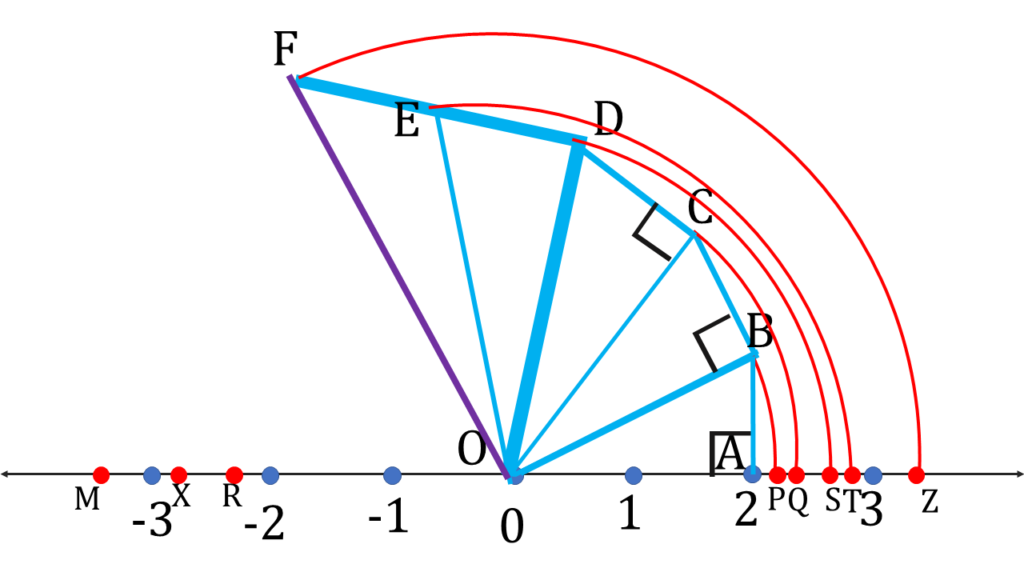
এখন OD এর উপর DE লম্বকে বাড়িয়ে DF টানলাম যেখানে DF=2 একক।
OF যুক্ত করলাম।
পিথাগোরাসের উপপাদ্য থেকে পেলাম,
OF2
= OD2 + DF2
= {(√7)2 + (2)2} বর্গ একক
= (7 + 4) বর্গ একক
= 11 বর্গএকক
অতএব OF = √11 একক
O বিন্দুকে কেন্দ্র করে OF- এর সমান দৈর্ঘ্যের ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ অঙ্কন করলাম যা সংখ্যারেখাকে Z বিন্দুতে ছেদ করল।
OZ =√11 একক
OZ সমান করে শূন্য এর বামদিকে OM নিলাম
অতএব OM = – √11
| বাস্তব সংখ্যা অধ্যায়ের- | |
|---|---|
 | |
 | |
| WB Class 9 এর গণিত প্রকাশের সমস্ত অধ্যায়ের সমাধান- | |
|---|---|
| অধ্যায় | সমাধান |
| 1. বাস্তব সংখ্যা (Real Numbers) | কষে দেখি 1.1 |
| কষে দেখি 1.2 | |
| কষে দেখি 1.3 | |
| 2. সূচকের নিয়মাবলি (Laws of Indices) | কষে দেখি 2 |
| 3. লেখচিত্র (Graph) | কষে দেখি 3.1 |
| কষে দেখি 3.2 | |
| 4. স্থানাঙ্ক জ্যামিতি : দূরত্ব নির্ণয় (Co-ordinate Geometry: Distance Formula) | কষে দেখি 4 |
| 5. রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) (Linear Simultaneous Equations) | কষে দেখি 5.1 |
| কষে দেখি 5.2 | |
| কষে দেখি 5.3 | |
| কষে দেখি 5.4 | |
| কষে দেখি 5.5 | |
| কষে দেখি 5.6 | |
| কষে দেখি 5.7 | |
| 6. সামান্তরিকের ধর্ম (Properties of Parallelogram) | কষে দেখি 6 |
| 7. বহুপদী সংখ্যামালা (Polynomial) | কষে দেখি 7.1 |
| কষে দেখি 7.2 | |
| কষে দেখি 7.3 | |
| কষে দেখি 7.4 | |
| 8. উৎপাদকে বিশ্লেষণ (Factorisation) | কষে দেখি 8.1 |
| কষে দেখি 8.2 | |
| কষে দেখি 8.3 | |
| কষে দেখি 8.4 | |
| কষে দেখি 8.5 | |
| 9. ভেদক ও মধ্যবিন্দু সংক্রান্ত উপপাদ্য (Transversal & Mid-Point Theorem). | কষে দেখি 9 |
| 10. লাভ ও ক্ষতি (Profit and Loss) | কষে দেখি 10.1 |
| কষে দেখি 10.2 | |
| 11. রাশিবিজ্ঞান (Statistics) | কষে দেখি 11.1 |
| কষে দেখি 11.2 | |
| 12. ক্ষেত্রফল সংক্রান্ত উপপাদ্য (Theorems on Area) | কষে দেখি 12 |
| 13. সম্পাদ্য : ত্রিভুজের সমান ক্ষেত্রফল বিশিষ্ট সামান্তরিক অঙ্কন | কষে দেখি 13 |
| 14. সম্পাদ্য : চতুর্ভুজের সমান ক্ষেত্রফল বিশিষ্ট ত্রিভুজ অঙ্কন | কষে দেখি 14 |
| 15. ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল (Area & Perimeter of Triangle & Quadrilateral) | কষে দেখি 15.1 |
| কষে দেখি 15.2 | |
| কষে দেখি 15.3 | |
| 16. বৃত্তের পরিধি (Circumference of Circle) | কষে দেখি 16 |
| 17. সমবিন্দু সংক্রান্ত উপপাদ্য (Theorems on concurrence) | কষে দেখি 17 |
| 18. বৃত্তের ক্ষেত্রফল (Area of Circle) | কষে দেখি 18 |
| 19. স্থানাঙ্ক জ্যামিতি: সরলরেখাংশের অন্তর্বিভক্ত ও বহিঃবিভক্ত (Co-ordinate Geometry: Internal and External Division of Straight-Line Segment) | কষে দেখি 19 |
| 20. স্থানাঙ্ক জ্যামিতি: ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল (Co-ordinate Geometry: Area of Triangular Region) | কষে দেখি 20 |
| 21. লগারিদম (Logarithm) | কষে দেখি 21 |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
এই কষে দেখি 1.2 Class 9|Koshe Dekhi 1.2 Class 9 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।

এখানে তোমরা তোমাদের নবম শ্রেণীতে| Class 9 এ কি কি পড়ানো হয়, মানে তোমাদের নবম শ্রেণী| Class 9 সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

