শ্রেনিঃ- অষ্টম ; অধ্যায়ঃ- পূরক কোণ, সম্পূরক কোণ ও সন্নিহিত কোণ ; কষে দেখি 6
আমরা পূরক কোণ , সম্পূরক কোণ ও সন্নিহিত কোণ এর অধ্যায়ের সারাংশ তে জেনেছি –
( i ) পূরক কোণ
( ii ) সম্পূরক কোণ
( iii ) সন্নিহিত কোণ
কি এবং কাকে বলে!
যদি তোমরা অধ্যায়ের সারাংশ না দেখে থাকো তাহলে একবার দেখে নিও ।
আমাদের শুধু অধ্যায়ের সারাংশ বুঝলেই হবেনা , তারসাথে আমি কতোটা শিখলাম , নিজে কতোটা বুঝলাম এবং নিজে নিজে কারোর সাহাজ্য ছাড়ায় কতোটা অংক সমাধান করতে পারবো তা আমাদের অষ্টম শ্রেণী-এর পূরক কোণ , সম্পূরক কোণ ও সন্নিহিত কোণ এর কষে দেখি 6 Class 8 | Koshe Dekhi 6 Class 8 থেকে অংক করলে তবেই আমরা বুঝতে পারবো।
শুধু তায় নয়, অংক যতো সমাধান করা যাবে ( নিজে নিজে ) ততো নিজের প্রতি বিশ্বাস টা শক্ত হবে। এমনকি এই বিষয়ে নতুন অংক সামনে পেলে সেটা করতে সাহস পাবে ।
এবার আমরা অষ্টম শ্রেণী-এর পূরক কোণ , সম্পূরক কোণ ও সন্নিহিত কোণ এর কষে দেখি 6|Koshe Dekhi 6 Class 8 আমরা শুরু করবো। । এখানে প্রতিটি অঙ্ক সুন্দর করে STEP BY STEP গুছিয়ে লেখা হয়েছে এবং সহজ ভাষায় উপস্থাপন করা হয়েছে যাতে তোমরা সহজেই এই কষে দেখি 6 এর প্রতিটি অঙ্ক বুঝতে পারো তারসাথে ভবিষ্যতে এরকম অংক পরীক্ষায় আসলে তা যেনো সহজেই করে উঠতে পারো।
আগে তোমরা নিজেরা অংক গুলি করবে, তারপর যেখানে আটকে যাবে এখান থেকে দেখে নেবে ।
এখানে করে দেওয়া অংক গুলি ভালো ভাবে বোঝার জন্যে নিম্নে কিছু নির্দেশিকা তোমাদের জন্যে থাকলোঃ
কিছু উপদেশঃ-
( i ) প্রথমত এই অধ্যায়ের যে সারাংশ আমি তৈরি করেছি তোমাদের বোঝার জন্যে আগে অবশ্যই তোমরা সেটা দেখবে। তাহলে পূরক কোণ, সম্পূরক কোণ সম্পরকে ধারণা সহজ হবে বুঝতা।
( ii ) কষে দেখিতে যে অংকগুলো আছে সেগুলো করার সময় কোণের সংজ্ঞা গুলো মাথায় রাখবে তাহলে দেখবে কোথাও অসুবিধে হবেনা।
( iii ) সন্নিহিত কোণ সম্পর্কে খুব সুন্দর করে লেখা হয়েছে। তোমরা ওই বৈশিষ্ট্য গুলো সবসময় মাথায় রেখে অংকের সমাধান করবে।
আগামিতে এই কষে দেখি 6 Class 8 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 6 Class 8 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 6 Class 8 তারপর  এই চিহ্ন দেখে Click করলে আবার তোমরা এখানে এসে যাবে।  |
কষে দেখি 6 | Koshe Dekhi 6
1. মনে মনে ভাবি ও লিখিঃ
( a ) দুটি সূক্ষ্মকোণ পরস্পর পূরক হতে পারে কিনা লিখি ।
সমাধানঃ-
দুটি সূক্ষ্মকোণ পরস্পর পূরক হতে পারে কিনা দেখার জন্যে আমরা দুটি সূক্ষ্মকোণ নেবো ।
একটি 60° এবং অপরটি 30°
60° + 30° = 90°
অতএব 60° এবং 30° একে অপরের পূরক কোণ ।
| অতএব দুটি সূক্ষ্মকোণ পরস্পর পূরক হতে পারে । |
( b ) দুটি সূক্ষ্মকোণ পরস্পর সম্পূরক হতে পারে কিনা লিখি ।
সমাধানঃ-
সূক্ষ্মকোণ যেহেতু 90° অপেক্ষা ছোটো , সেহেতু দুটি সূক্ষ্মকোণ এর যোগফল ও 180° অপেক্ষা ছোটো হবে।
কারণ,
| সূক্ষ্মকোণ < 90° |
| সূক্ষ্মকোণ + সূক্ষ্মকোণ < 90° + 90° |
| সূক্ষ্মকোণ + সূক্ষ্মকোণ < 180° |
আমরা এখানে দেখতে পাচ্ছি যে, দুটি সূক্ষ্মকোণ এর সমষ্টি কখনই 180° হতে পারে না। দুটি সূক্ষ্মকোণ এর সমষ্টি সবসময় 180° অপেক্ষা ছোটো হবে। অতএব কোনো দুটি সূক্ষ্মকোণ একে অপরের সম্পূরক হতে পারে না ।
| অতএব দুটি সূক্ষ্মকোণ পরস্পর সম্পূরক হতে পারে না । |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
( c ) একটি সূক্ষ্মকোণ ও একটি স্থুলকোণ পরস্পর পূরক হতে পারে কিনা লিখি । দুটি সমকোণ পরস্পর পূরক হতে পারে কিনা লিখি ।
সমাধানঃ-
স্থুলকোণ হলো 90° অপেক্ষা বড়ো কোণ । সুতরাং, একটি স্থুলকোণ এর সঙ্গে কোনো কোণই পূরক হতে পারেনা ।
কারণ,
| স্থুলকোণ > 90° |
| স্থুলকোণ + সূক্ষ্মকোণ > 90° |
আমরা দেখতে পাচ্ছি যে, একটি সূক্ষ্মকোণ ও একটি স্থুলকোণ এর যোগফল সবসময় 90° অপেক্ষা বড়ো হবে ।
| অতএব একটি সূক্ষ্মকোণ ও একটি স্থুলকোণ পরস্পর পূরক হতে পারে না । |
আবার একটি সমকোণ হলো 90°। সুতরাং, দুটি সমকোণ পরস্পর পূরক হতে পারে না ।
কারণ,
| 1 সমকোণ = 90° |
| 1 সমকোণ + 1 সমকোণ = 90° + 90° |
| 1 সমকোণ + 1 সমকোণ = 180° |
অতএব আমরা দেখতে পাচ্ছি যে, দুটি সমকোণের যোগফল = 180° অর্থাৎ দুটি সমকোণের যোগ ফল সবসময় 90° অপেক্ষা বড়ো হবে ।
| অতএব দুটি সমকোণ পরস্পর পূরক হতে পারে না । |
( d ) দুটি স্থুলকোণ পরস্পর সম্পূরক হতে পারে কিনা লিখি ।
সমাধানঃ-
স্থুলকোণ হলো 90° অপেক্ষা বড়ো এবং 180° অপেক্ষা ছোটো । সুতরাং, দুটি স্থুলকোণ এর যোগফল সবসময় 180° অপেক্ষা বড়ো হবে ।
| 90° < স্থুলকোণ < 180° |
| 90° + 90° < স্থুলকোণ + স্থুলকোণ < 180° + 180° |
| 180° < স্থুলকোণ + স্থুলকোণ < 360° |
আমরা এখানে দেখতে পাচ্ছি যে, দুটি স্থুলকোণ এর যোগফল সবসময় 180° অপেক্ষা বড়ো হবে ।
| অতএব দুটি স্থুলকোণ পরস্পর সম্পূরক হতে পারে না । |
( e ) দুটি সমকোণ পরস্পর সম্পূরক হতে পারে কিনা লিখি ।
সমাধানঃ-
1 সমকোণ = 90°
| 1 সমকোণ = 90° |
| 1 সমকোণ + 1 সমকোণ = 180° |
আমরা দেখতে পাচ্ছি যে, দুটি সমকোণের যোগফল = 180°
| অতএব দুটি সমকোণ পরস্পর সম্পূরক হতে পারে / হবে । |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share] |
( f ) একটি সূক্ষ্মকোণ ও একটি স্থুলকোণ পরস্পর সম্পূরক হতে পারে কিনা লিখি ।
সমাধানঃ-
একটি সূক্ষ্মকোণ ও একটি স্থুলকোণ পরস্পর সম্পূরক হতে পারে কিনা দেখার জন্যে আমরা একটি সূক্ষ্মকোণ = 60° এবং একটি স্থুলকোণ=120° নিলাম।
| 60° + 120° = 180° |
এখানে আমরা একটি সূক্ষ্মকোণ ও একটি স্থুলকোণ নিয়েছি যাদের যোগফল = 180° ।
| অতএব একটি সূক্ষ্মকোণ ও একটি স্থুলকোণ পরস্পর সম্পূরক হতে পারে । |
( g ) দুটি সন্নিহিত কোণ পরস্পর পূরক কোণ হতে পারে কিনা লিখি ।
সমাধানঃ-
আমরা দুটি সন্নিহিত কোণ আঁকলাম এবং দেখলাম দুটি কোণের সমষ্টি 90° হচ্ছে ।
| অতএব দুটি সন্নিহিত কোণ পরস্পর পূরক কোণ হতে পারে । |
( h ) দুটি সন্নিহিত কোণ পরস্পর সম্পূরক কোণ হতে পারে কিনা লিখি ।
সমাধানঃ-
আমরা দুটি সন্নিহিত কোণ আঁকলাম এবং দেখলাম দুটি কোণের সমষ্টি 180° হচ্ছে ।
| অতএব দুটি সন্নিহিত কোণ পরস্পর সম্পূরক কোণ হতে পারে । |
2. নীচের সন্নিহিত কোণ গুলি আঁকি ও কোন কোণগুলি পরস্পর পূরক অথবা সম্পূরক লিখিঃ
45° , 45° ;
সমাধানঃ-
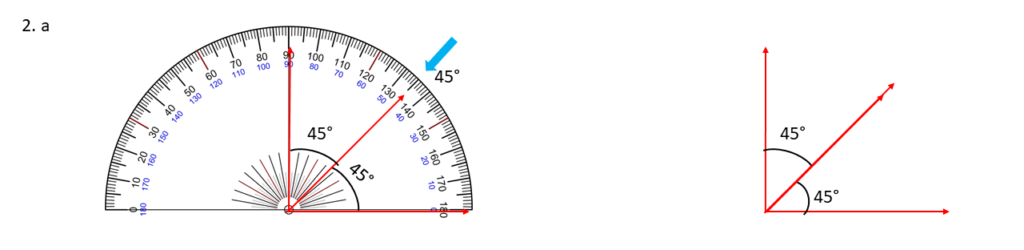
উপরের সন্নিহিত কোণগুলি আঁকলাম এবং দেখলাম কোণগুলি পরস্পর পূরক অর্থাৎ একে অপরের পূরক কোণ ।
আবার,
45° + 45° = 90°
| 45° , 45° কোণ দুটি একে অপরের পূরক কোণ । |
120° , 30° ;
সমাধানঃ-
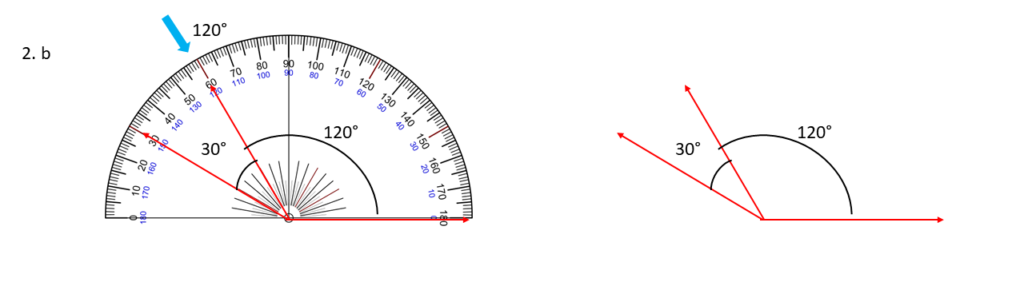
উপরের সন্নিহিত কোণগুলি আঁকলাম এবং দেখলাম কোণগুলি পরস্পর পূরক / সমপূরক কোনো টাই নয় ।
আবার,
| 120° + 30° = 150° |
| 120° + 30° ≠ 90° |
| 120° + 30° ≠ 180° |
| 120° , 30° কোণ দুটি একে অপরের পূরক/সমপূরক কোনোটাই নয় । |
70° , 110° ;
সমাধানঃ-
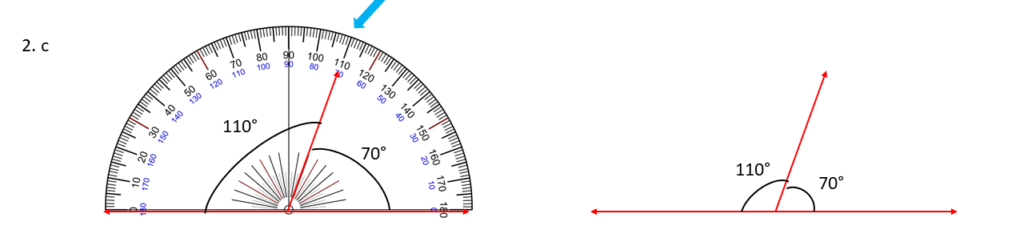
উপরের সন্নিহিত কোণগুলি আঁকলাম এবং দেখলাম কোণগুলি পরস্পর সম্পূরক , অর্থাৎ একে অপরের সম্পূরক কোণ ।
আবার,
70° + 110° = 180°
| 70° , 110° কোণ দুটি একে অপরের সম্পূরক । |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share] |
42° , 48° ;
সমাধানঃ-
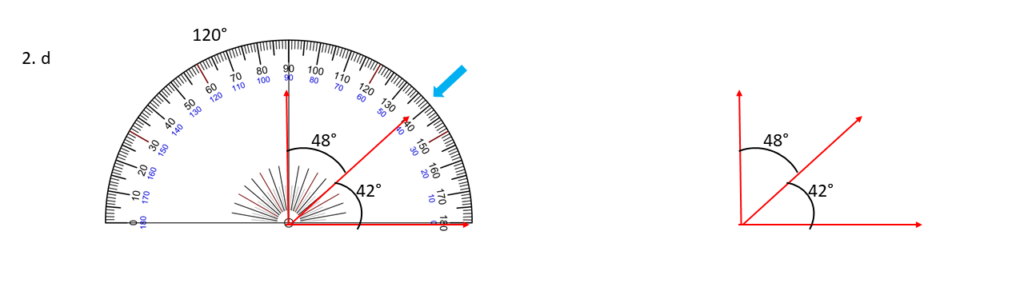
উপরের সন্নিহিত কোণগুলি আঁকলাম এবং দেখলাম কোণগুলি পরস্পর পূরক অর্থাৎ, একে অপরের পূরক কোণ ।
আবার ,
42° + 48° = 90°
| 42° , 48° কোণ দুটি একে অপরের পূরক কোণ । |
37° , 43° ;
সমাধানঃ-
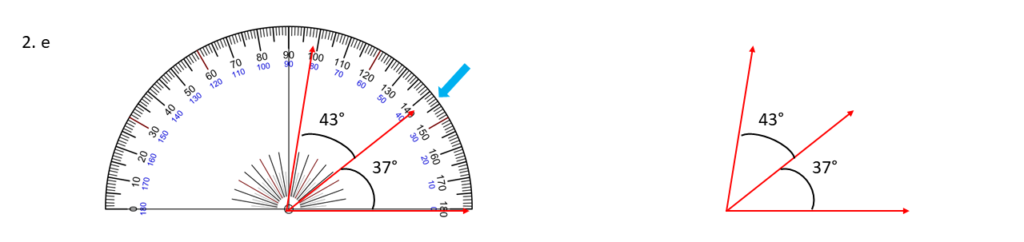
উপরের সন্নিহিত কোণগুলি আঁকলাম এবং দেখলাম কোণগুলি পরস্পর পূরক / সমপূরক কোনো টাই নয় ।
| 37° + 43° = 80° |
| 37° + 43° ≠ 90° |
| 37° + 43° ≠ 90° |
| 37° , 43° কোণ দুটি একে অপরের পূরক/সমপূরক কোনোটাই নয় । |
85° , 95° ;
সমাধানঃ-
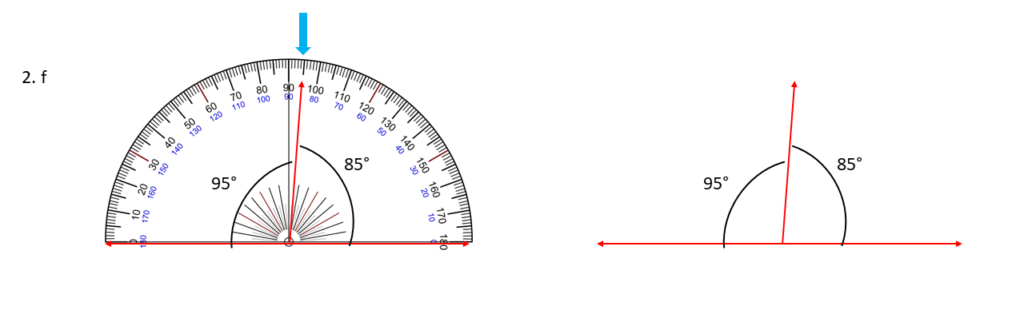
উপরের সন্নিহিত কোণগুলি আঁকলাম এবং দেখলাম কোণগুলি পরস্পর সম্পূরক অর্থাৎ, একে অপরের সম্পূরক কোণ ।
আবার,
85° + 95° = 180°
| 85° , 95° কোণ দুটি একে অপরের সম্পূরক । |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share] |
3. নীচের কোণগুলি দেখি ও কোন কোন কোণদুটি পরস্পর পূরক কোণ লিখিঃ
31° , 47° , 64° , 29° , 43° , 59° , 17° , 26°
সমাধানঃ-
31° এর পূরক কোণ
= 90° – 31°
=59°
| অতএব 31° এবং 59° একে অপরের পূরক কোণ । |
47° এর পূরক কোণ
= 90° – 47°
= 43°
| অতএব 47° এবং 43° একে অপরের পূরক কোণ । |
64° এর পূরক কোণ
= 90° – 64°
= 26°
| অতএব 64° এবং 26° একে অপরের পূরক কোণ । |
| উপরের কোণ গুলির মধ্যে 29° এবং 17° কোণ এর কোনো পূরক কোণ নেই । |
4. নীচের কোণগুলি দেখি ও কোন কোন কোণগুলি পরস্পর সম্পূরক কোণ লিখিঃ
47° , 58° , 69° , 75° , 133° , 105° , 122° , 125°
সমাধানঃ-
47° এর সম্পূরক কোণ
= 180° – 47°
= 133°
| অতএব 47° এবং 133° একে অপরের সম্পূরক কোণ । |
58° এর সম্পূরক কোণ
= 180° – 58°
= 122°
| অতএব 58° এবং 122° একে অপরের সম্পূরক কোণ । |
75° এর সম্পূরক কোণ
= 180° – 75°
= 105°
| অতএব 75° এবং 105° একে অপরের সম্পূরক কোণ । |
| উপরের কোণ গুলির মধ্যে 69° এবং 125° কোণ এর কোনো সম্পূরক কোণ নেই । |
5. সন্নিহিত কোণ কাকে বলে লিখি ও নীচের কোন কোণগুলি সন্নিহিত কোণ বুঝে লিখিঃ
সমাধানঃ-
সন্নিহিত কোণঃ
| একই শীর্ষ বিন্দু ও একই সাধারণ বাহুর দুপাশে অবস্থিত কোণদুটিকে একটি অপরটির সন্নিহিত কোণ বলা হয় । |
প্রথম কোণজোড়া :-
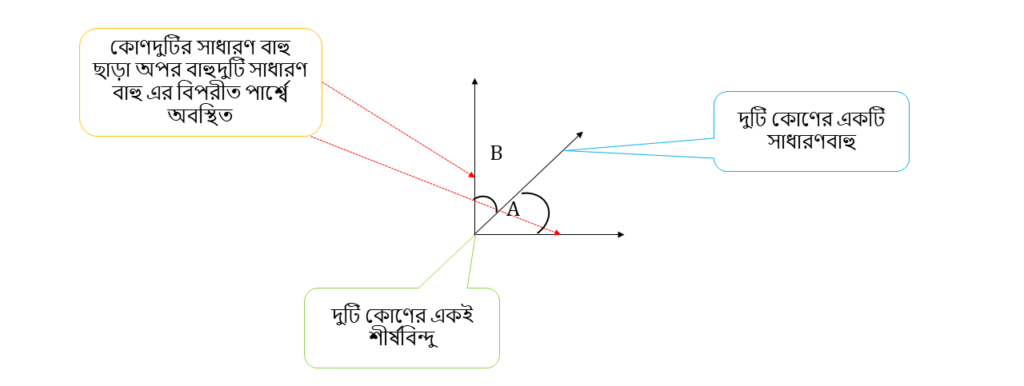
এই কোণ দুটি সন্নিহিত কোণ , কারণ –
( i ) দুটি কোণের একই শীর্ষবিন্দু
( ii ) দুটি কোণের একটি সাধারণ বাহু
( iii )কোণদুটির সাধারণ বাহু ছাড়া অপর বাহুদুটি সাধারণ বাহু এর বিপরীত পার্শ্বে অবস্থিত ।
দ্বিতীয় কোণজোড়া:-
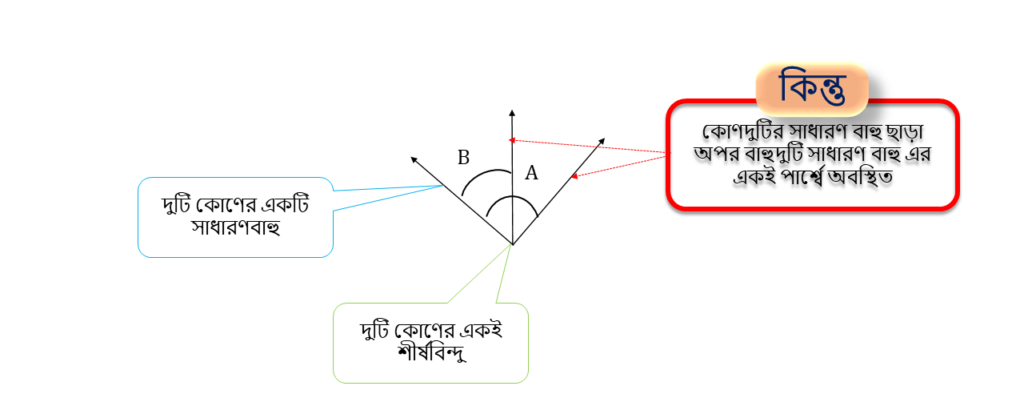
এই কোণ দুটি সন্নিহিত কোণ নয় , কারণ –
দুটি কোণের একই শীর্ষবিন্দু ও একটি সাধারণ বাহু থাকলেও কোণ দুটির সাধারণ বাহু ছাড়া অপর বাহুদুটি সাধারণ বাহু এর একই পার্শ্বে অবস্থিত ।
তৃতীয় কোণজোড়া:-
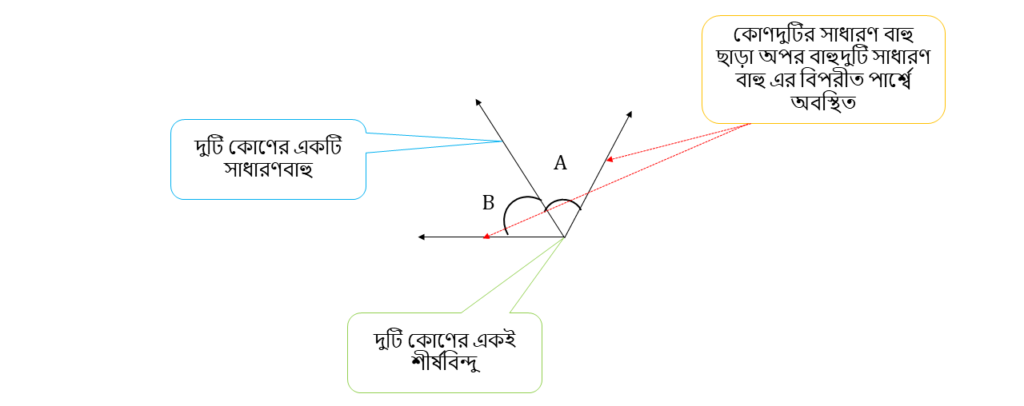
এই কোণ দুটি সন্নিহিত কোণ , কারণ –
( i ) দুটি কোণের একই শীর্ষবিন্দু
( ii ) দুটি কোণের একটি সাধারণ বাহু
( iii )কোণদুটির সাধারণ বাহু ছাড়া অপর বাহুদুটি সাধারণ বাহু এর বিপরীত পার্শ্বে অবস্থিত ।
চতুর্থ কোণজোড়া:-
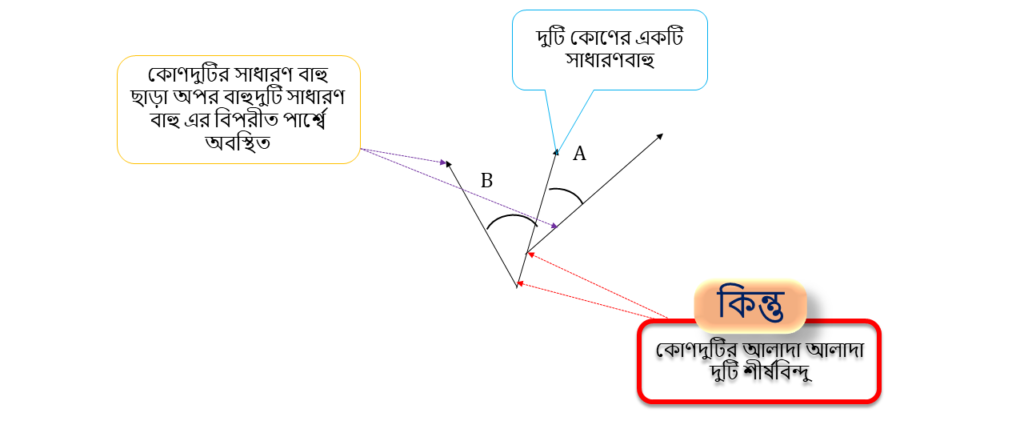
এই কোণ দুটি সন্নিহিত কোণ নয় , কারণ –
কোণদুটির একটি সাধারণ বাহু ও কোণদুটির সাধারণ বাহু ছাড়া অপর বাহুদুটি সাধারণ বাহু এর বিপরীত পার্শ্বে অবস্থিত হলেও কোণদুটির আলাদা আলাদা দুটি শীর্ষ বিন্দু ।
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share] |
6. নিজে চাঁদার সাহায্যে সন্নিহিত কোণ আঁকি যার কোণদুটির মান হলো-
35° , 45° ;
সমাধানঃ-
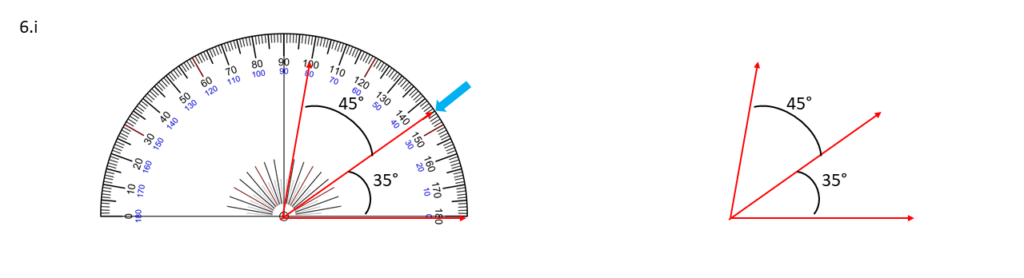
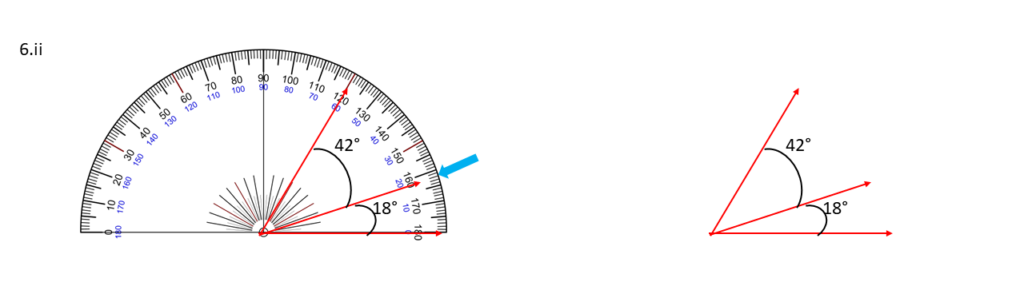
18° , 42° ;
সমাধানঃ-
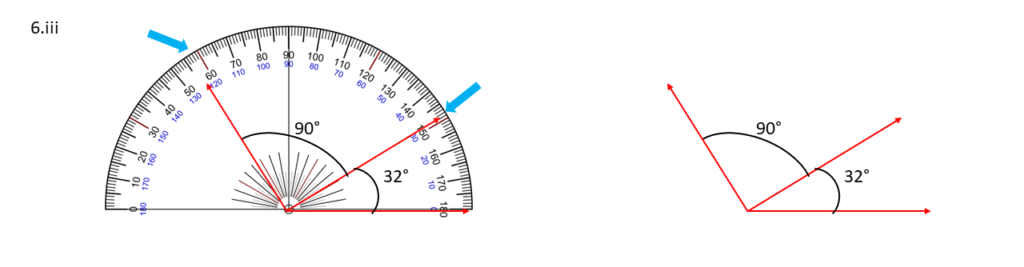
32° , 90° ;
সমাধানঃ-
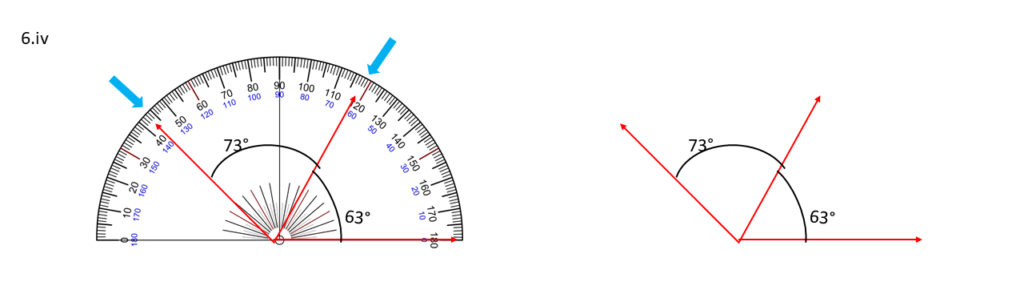
73° , 63°
সমাধানঃ-
7. সায়ন্তনী একটি সরলরেখা AB আঁকল । আমি সেই সরল রেখার উপর কোনো বিন্দু P -তে অপর একটি রশ্মি PQ আঁকলাম । এর ফলে দুটি সন্নিহিত কোণ ∠BPQ ও ∠APQ তৈরি হলো । চাঁদার সাহায্যে মেপে ∠BPQ ও ∠APQ এর পরিমাপ লিখি ও ∠PQB + ∠PQA = কত লিখি ।
সমাধানঃ-
সায়ন্তনী একটি সরলরেখা AB আঁকল
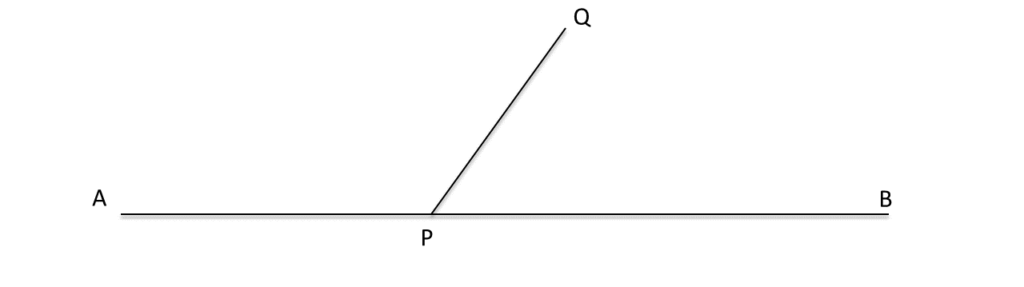
আমি সেই সরল রেখার উপর কোনো বিন্দু P -তে অপর একটি রশ্মি PQ আঁকলাম
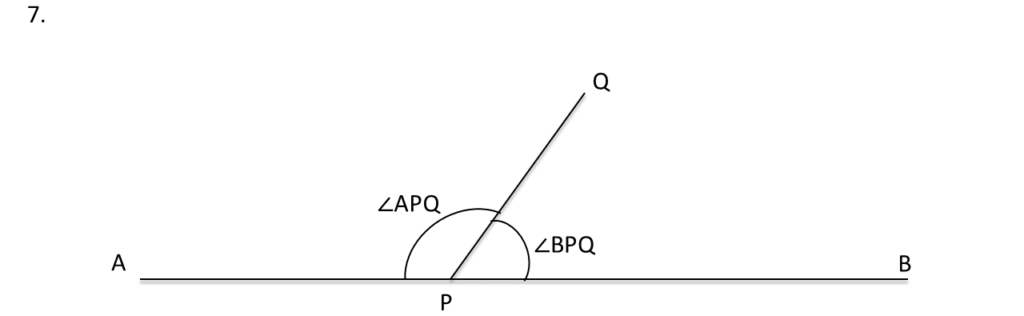
এর ফলে দুটি সন্নিহিত কোণ ∠BPQ ও ∠APQ তৈরি হলো
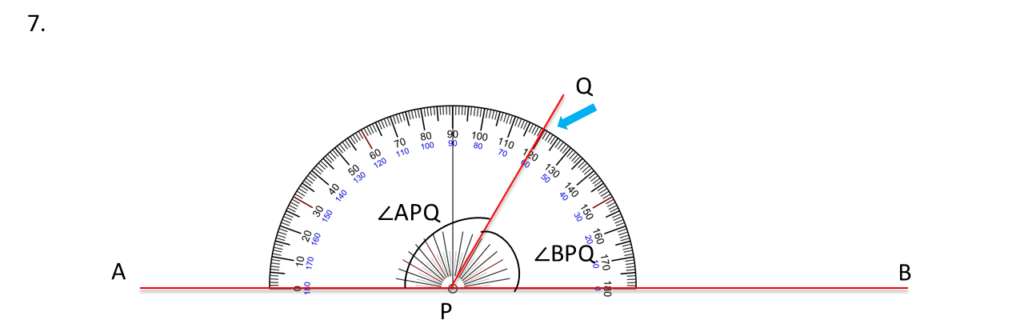
চাঁদার সাহায্যে মেপে ∠BPQ ও ∠APQ এর পরিমাপ পেলাম,
∠BPQ =60°
∠APQ = 120°
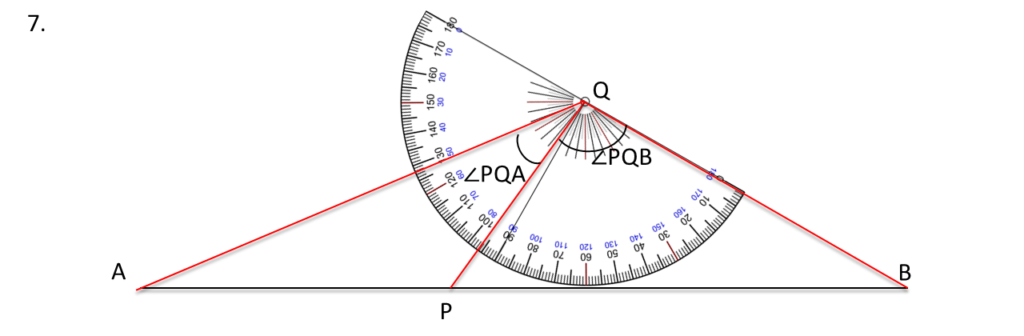
∠PQB + ∠PQA = 128°
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share] |
8. শাকিল দুটি সন্নিহিত কোণ ∠ABC ও ∠ABD আঁকল যাদের সমষ্টি 180°; আমিও শাকিলের মতো ∠ABC ও ∠ABD এঁকে দেখি D, B ও C বিন্দু তিনটি একই সরলরেখায় আছে কিনা ।
সমাধানঃ-
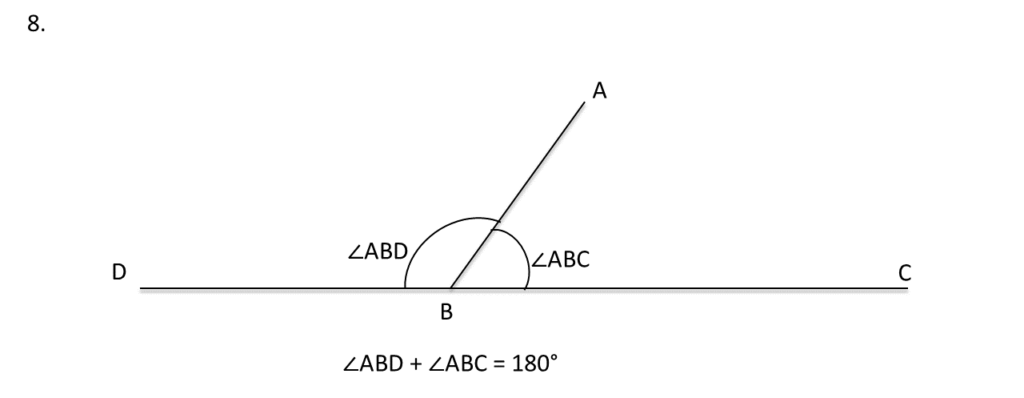
| আমিও শাকিলের মতো ∠ABC ও ∠ABD এঁকে দেখলাম D, B ও C বিন্দু তিনটি একই সরলরেখায় আছে। |
9. পাশের ছবি থেকে x-এর মান নির্ণয় করি।
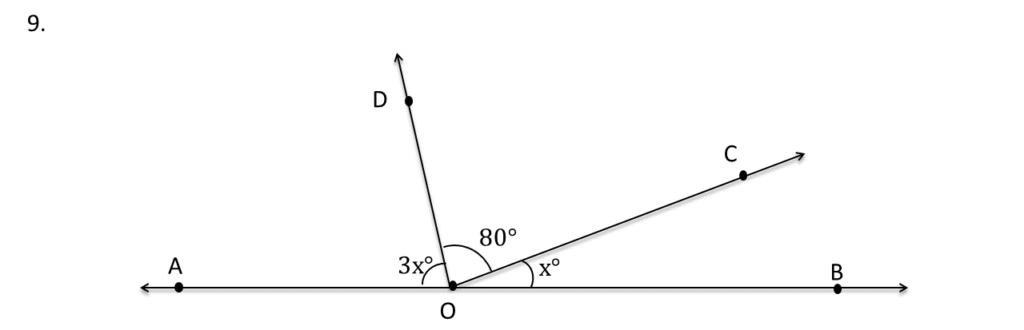
সমাধানঃ-
x° + 80° + 3x° = 180°
বা, 4x° = 180° – 80°
বা, x° = 100°/4°
বা, x° = 25°
| x-এর মান = 25 |
10. পাশের ছবিতে ∠AOP, ∠BOP এর চেয়ে 140° বেশি । ∠AOP ও ∠BOP – এর মান নির্ণয় করি ।
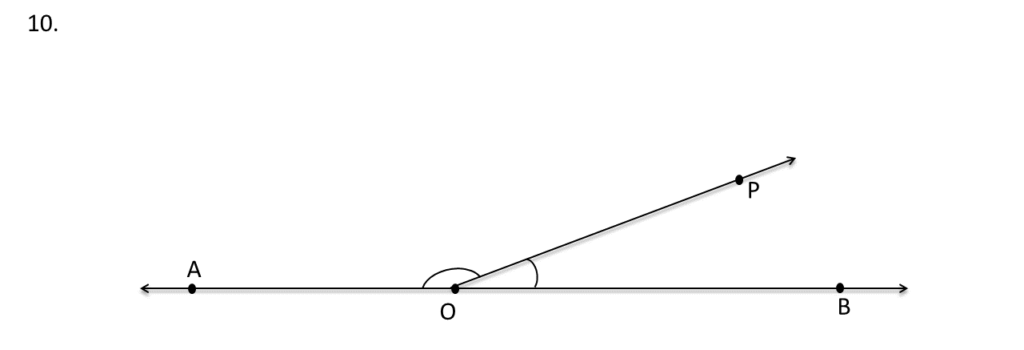
সমাধানঃ-
যেহেতু ∠AOP, ∠BOP এর চেয়ে 140° বেশি, ∠AOP = ∠BOP + 140°
উপরের ছবি থেকে আমরা পায়,
| ∠AOP + ∠BOP = 180° |
| বা, ∠BOP + 140° + ∠BOP = 180° |
| বা, 2∠BOP = 180° – 140° |
| বা, ∠BOP = 40°/2 |
| বা, ∠BOP = 20° |
অতএব
| ∠AOP = ∠BOP + 140° |
| বা, ∠AOP = 20° + 140° |
| বা, ∠AOP = 160° |
11. দুটি সন্নিহিত কোণের মান 35° ও 145° ; সন্নিহিত কোণের বহিঃস্থ বাহু দুটি কিভাবে অবস্থিত লিখি ।
সমাধানঃ-
| দুটি সন্নিহিত কোণের মান 35° ও 145° ; সন্নিহিত কোণের বহিঃস্থ বাহু দুটি একই সরলরেখায় অবস্থিত । |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share] |
12. পাশের ছবিতে OA ও OE কিভাবে অবস্থিত লিখি ।
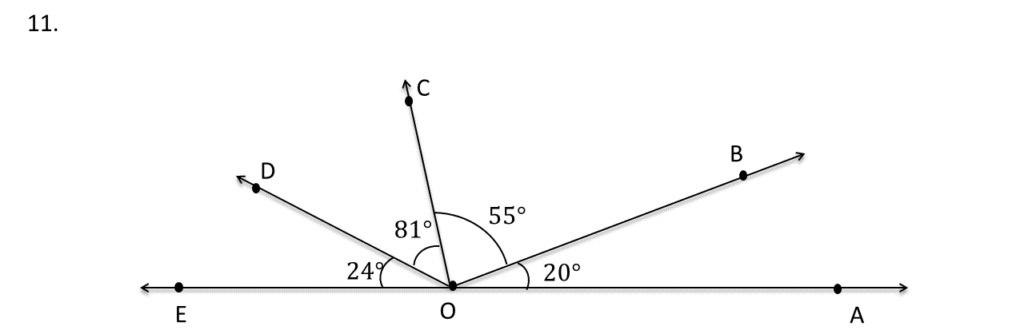
সমাধানঃ-
| পাশের ছবিতে OA ও OE একই সরলরেখায় অবস্থিত । |
এই কষে দেখি 6 Class 8|Koshe Dekhi 6 Class 8 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 6 Class 8 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 6 Class 8 তারপর এই চিহ্ন দেখে Click করলে আবার তোমরা এখানে এসে যাবে। |
তোমরা যদি সঠিক পদ্ধতি মেনে পূরক কোণ, সম্পূরক কোণ ও সন্নিহিত কোণ কষে দেখি 6 তে যে সমস্ত অংক গুলি আছে সেগুলি করো তাহলে কোথাও বুঝতে অসুবিধে হবেনা । সেজন্যে তোমাদের বলবো তোমরা পূরক কোণ, সম্পূরক কোণ ও সন্নিহিত কোণ এর বিষয়ে নিচের লিংক থেকে ভালভাবে জানো এবং তারপর কষে দেখি এর অংক গুলি করলে নিশ্চয় কিছু পার্থক্য বুঝতে পারবে ।   |
| গনিতপ্রভা অষ্টম শ্রেণীর সমস্ত অধ্যায়ের সমাধান- | |
|---|---|
| অধ্যায় | সমাধান |
| 2. পাই চিত্র | কষে দেখি 2 |
| 3. মূলদ সংখ্যার ধারণা | অধ্যায়ের সারাংশ |
| কষে দেখি 3 | |
| 4. বীজগাণিতিক সংখ্যামালার গুণ ও ভাগ | অধ্যায়ের সারাংশ |
| কষে দেখি 4.1 | |
| কষে দেখি 4.2 | |
| 5. ঘনফল নির্ণয় | অধ্যায়ের সারাংশ |
| কষে দেখি 5.1 | |
| কষে দেখি 5.2 | |
| কষে দেখি 5.3 | |
| 6. পূরক কোণ, সম্পূরক কোণ ও সন্নিহিত কোণ | অধ্যায়ের সারাংশ |
| কষে দেখি 6 | |
| 7. বিপ্রতীপ কোণের ধারণা | অধ্যায়ের সারাংশ |
| কষে দেখি 7.1 | |
8. সমান্তরাল সরলরেখা ও ছেদকের ধর্ম | অধ্যায়ের সারাংশ |
| কষে দেখি 8 | |
9. ত্রিভুজের দুটি বাহু ও তাদের বিপরীত কোণের সম্পর্ক | অধ্যায়ের সারাংশ |
| কষে দেখি 9 | |
| 10. ত্রৈরাশিক | কষে দেখি 10.1 |
| কষে দেখি 10.2 | |
| 11. শতকরা | কষে দেখি 11 |
| 12. মিশ্রণ | কষে দেখি 12 |
13. বীজগাণিতিক সংখ্যামালার উৎপাদকে বিশ্লেষণ | কষে দেখি 13.1 |
| কষে দেখি 13.2 | |
14. বীজগাণিতিক সংখ্যামালার গ.সা.গু ও ল.সা.গু | কষে দেখি 14 |
15. বীজগাণিতিক সংখ্যামালার সরলীকরণ | কষে দেখি 15 |
16. ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই | কষে দেখি 16.1 |
| কষে দেখি 16.2 | |
17. সময় ও কার্য | কষে দেখি 17.1 |
| কষে দেখি 17.2 | |
18. লেখচিত্র | কষে দেখি 18 |
19. সমীকরণ গঠন ও সমাধান | কষে দেখি 19 |
| 20. জ্যামিতিক প্রমাণ | কষে দেখি 20.1 |
| কষে দেখি 20.2 | |
| কষে দেখি 20.3 | |
এখানে তোমরা তোমাদের অষ্টম শ্রেণীতে কি কি পড়ানো হয়, মানে তোমাদের অষ্টম শ্রেণীর সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।