শ্রেনিঃ- অষ্টম ; অধ্যায়ঃ-বিপ্রতীপ কোণের ধারণা ; কষে দেখি 7.1
আমরা বিপ্রতীপ কোণের অধ্যায়ের সারাংশ তে দেখেছি-বিপ্রতীপ কোণ কাকে বলে?, উপপাদ্য কি?, উপপাদ্য প্রমাণের নিয়ম ।
যদি তোমরা অধ্যায়ের সারাংশ না দেখো তাহলে তোমরা উপপাদ্য কিভাবে প্রমাণ করতে হয় বুঝতে পারবেনা।
আমাদের শুধু অধ্যায়ের সারাংশ বুঝলেই হবেনা , তারসাথে আমি কতোটা শিখলাম , নিজে কতোটা বুঝলাম এবং নিজে নিজে কারোর সাহাজ্য ছাড়ায় কতোটা অংক সমাধান করতে পারবো তা আমাদের অষ্টম শ্রেণী-এর বিপ্রতীপ কোণের ধারণা এর কষে দেখি 7.1 | Koshe Dekhi 7.1 Class 8 থেকে অংক করলে তবেই আমরা বুঝতে পারবো।
শুধু তায় নয়, অংক যতো সমাধান করা যাবে ( নিজে নিজে ) ততো নিজের প্রতি বিশ্বাস টা শক্ত হবে। এমনকি এই বিষয়ে নতুন অংক সামনে পেলে সেটা করতে সাহস পাবে ।

এবার আমরা অষ্টম শ্রেণী-এর বিপ্রতীপ কোণের ধারণা এর কষে দেখি 7.1 | Koshe Dekhi 7.1 Class 8 আমরা শুরু করবো। । এখানে প্রতিটি অঙ্ক সুন্দর করে STEP BY STEP গুছিয়ে লেখা হয়েছে এবং সহজ ভাষায় উপস্থাপন করা হয়েছে যাতে তোমরা সহজেই এই কষে দেখি 7.1 এর প্রতিটি অঙ্ক বুঝতে পারো তারসাথে ভবিষ্যতে এরকম অংক পরীক্ষায় আসলে তা যেনো সহজেই করে উঠতে পারো।
আগামিতে এই কষে দেখি 7.1 Class 8 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 7.1 Class 8 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 7.1 Class 8 তারপর  |
আগে তোমরা নিজেরা অংক গুলি করবে, তারপর যেখানে আটকে যাবে এখান থেকে দেখে নেবে ।
এখানে করে দেওয়া অংক গুলি ভালো ভাবে বোঝার জন্যে নিম্নে কিছু নির্দেশিকা তোমাদের জন্যে থাকলোঃ
কিছু উপদেশঃ-
- প্রথমত প্রতিটি অংক খুবই সহজ ভাবে করা হয়েছে
- প্রতিটি অঙ্কে এক লাইন থেকে আর এক লাইন কি কারনে হলো সেটা বলা হয়েছে এবং সেটা আলাদা box এর মধ্যে লিখে দেখানো হয়েছে।
- তারসাথে arrow চিহ্ন প্রয়োগ করেও দেখানো হয়েছে
- প্রতিটি লাইনে কি সুত্র প্রয়োগ করে অঙ্কটি সমাধান করা হয়েছে সেটা আলাদা করে পাশে উল্লেখ করা হয়েছে।
- প্রতিটি প্রশ্নের উত্তর কিভাবে লিখতে হবে তা সমাধানের শেষে আলাদা ভাবে box এর মধ্যে লিখে দেওয়া হয়েছে

কষে দেখি 7.1|Koshe Deekhi 7.1
1. দুটি সরলরেখা PQ ও RS পরস্পরকে O বিন্দুতে ছেদ করলে যে বিপ্রতীপ কোণগুলি তৈরি হয় তাদের আঁকি ও নাম লিখি ।
সমাধানঃ-
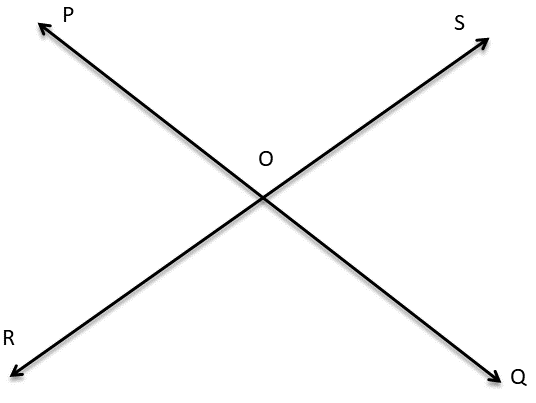
দুটি সরলরেখা PQ ও RS পরস্পরকে O বিন্দুতে ছেদ করলে যে বিপ্রতীপ কোণগুলি তৈরি হয় তাদের আঁকলাম এবং পেলাম,
∠POS এর বিপ্রতীপ ∠ROQ
এবং
∠POR এর বিপ্রতীপ ∠QOS
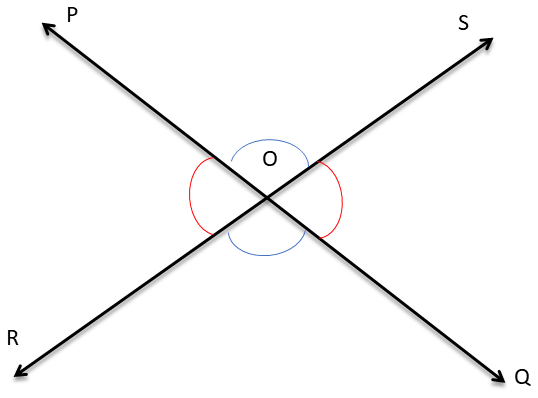
2. ছবি দেখি ও কোণগুলির মান লেখার চেষ্টা করিঃ
( a ) ∠1=35°, ∠2=?, ∠3=?, ∠4=? লিখি।
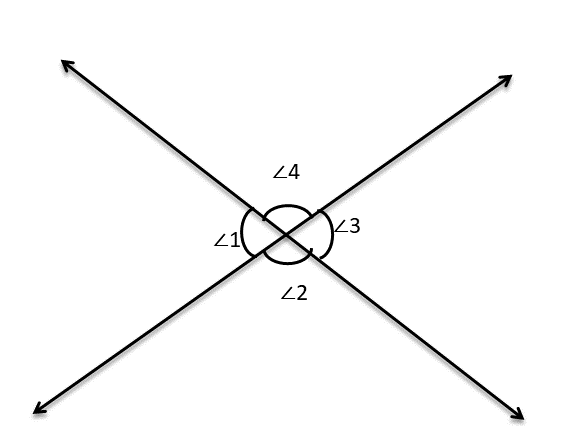
সমাধানঃ-
ছবিতে আমরা দেখতে পাচ্ছি
∠1 এর বিপ্রতীপ ∠3
এবং
∠2 এর বিপ্রতীপ ∠4
অতএব,
∠1 = ∠3
এবং
∠2 = ∠4
অতএব, ∠3=∠1=35°
আবার,
| ∠4 + ∠3 =180° |
| বা, ∠4 = 180°-∠3 |
| বা, ∠4 =180°-35° |
| বা, ∠4 = 145° |
অতএব, ∠2=∠4=145°
| ∠2=145° ∠3=35° ∠4=145° |
( b ) ∠TOS=20°, ∠ROQ=60°, ∠POT=?, ∠ROP=?, ∠QOS=?
সমাধানঃ-
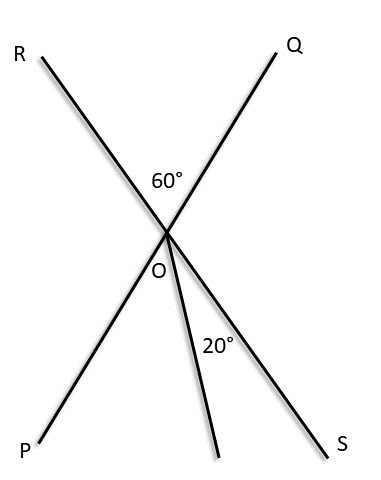
| দেওয়া আছে ∠TOS=20° এবং ∠ROQ=60° |
| ছবিতে আমরা দেখতে পাচ্ছি , |
| ∠ROQ এর বিপ্রতীপ ∠POS অতএব, ∠ROQ=∠POS |
| ∠ROP এর বিপ্রতীপ ∠QOS অতএব, ∠ROP = ∠QOS |
আবার,
| ∠ROQ = ∠POS=60° এবং ∠POS= ∠POT + ∠TOS |
| অতএব, ∠POT + ∠TOS = ∠POS |
| বা, ∠POT = ∠POS – ∠TOS |
| বা, ∠POT = 60° – 20° [ যেহেতু ∠POS=60° এবং ∠TOS= 20°] |
| বা, ∠POT = 40° |
আবার,
| ∠ROQ + ∠QOS = 180° |
| বা, ∠QOS= 180° – ∠ROQ |
| বা, ∠QOS= 180° – 60° [ ∠ROQ = 60°] |
| বা, ∠QOS = 120° |
যেহেতু,
∠ROP এর বিপ্রতীপ ∠QOS
সুতরাং, ∠ROP =120°
| ∠POT = 40° ∠ROP =120° ∠QOS = 120° |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
3. তীর্থ PQ ও XY দুটি সরলরেখা আঁকল যারা পরস্পরকে O বিন্দুতে ছেদ করেছে । আমি চাঁদার সাহায্যে বিপ্রতীপ কোণগুলি মেপে দেখি ।
সমাধানঃ-
তীর্থ PQ ও XY দুটি সরলরেখা আঁকল যারা পরস্পরকে O বিন্দুতে ছেদ করেছে।
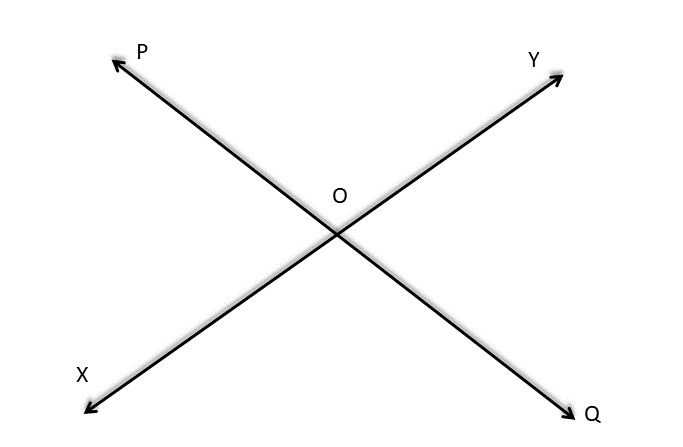
আমি চাঁদার সাহায্যে বিপ্রতীপ কোণগুলি মেপে পেলাম ,
∠POY= ∠XOY=107°
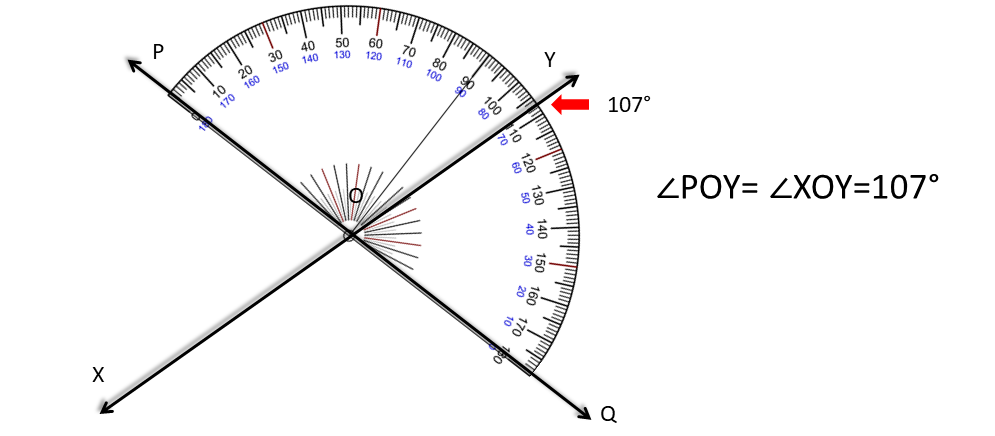
এবং
∠POX= ∠QOY=73°
4. পাশের ছবি দেখি ও নীচের প্রশ্নের উত্তর খোঁজার চেষ্টা করিঃ
( i ) দুটি কোণের নাম যারা পরস্পর পূরক কোণ ।
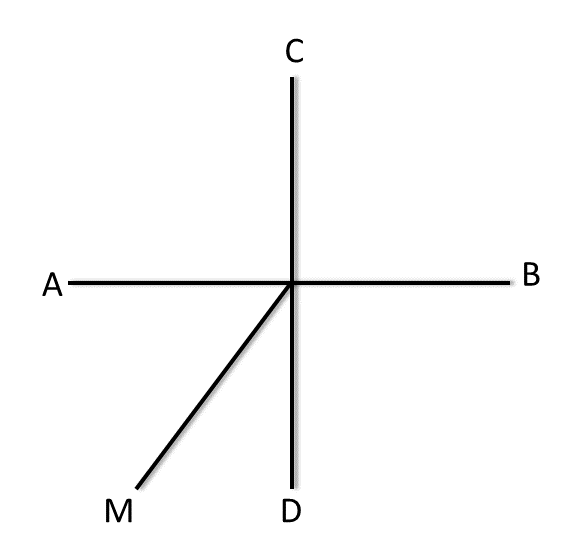
সমাধানঃ-
| ∠AOM ও ∠MOD কোণ দুটি পরস্পর পূরক কোণ। কারণ, |
| ∠AOM + ∠MOD=90° |
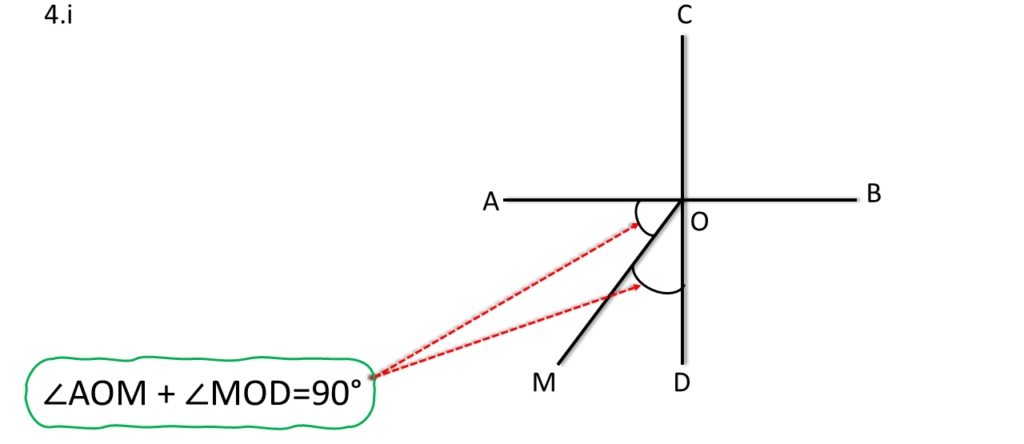
( ii ) দুটি কোণের নাম লিখি যারা পরস্পর সম্পূরক কোণ ।
সমাধানঃ-
| ∠AOM ও ∠MOB কোণ দুটি পরস্পর সম্পূরক কোণ। কারণ, |
| ∠AOM + ∠MOB=180° |
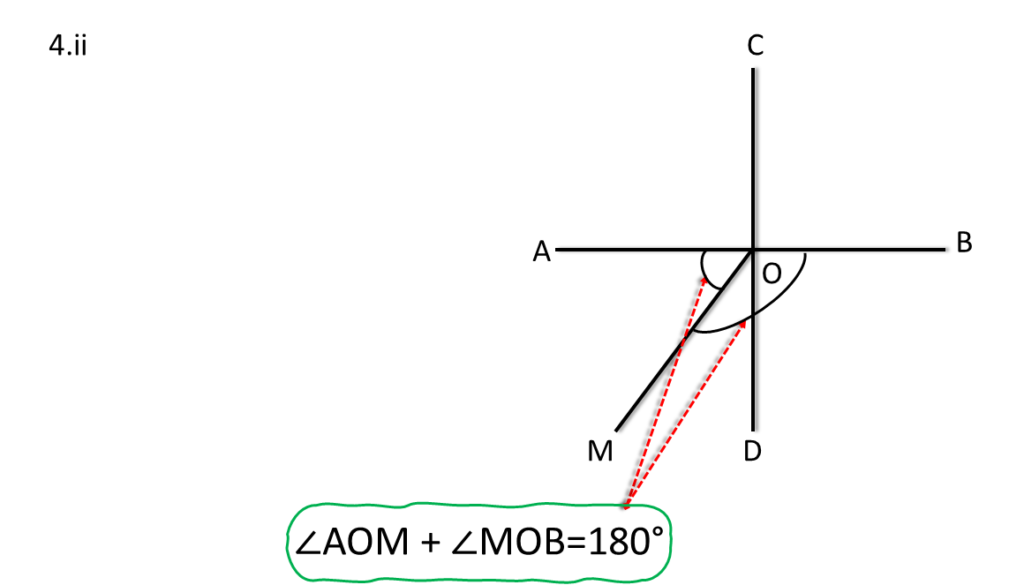
( iii ) দুটি কোণের নাম লিখি যারা পরস্পর বিপ্রতীপ কোণ ।
সমাধানঃ-
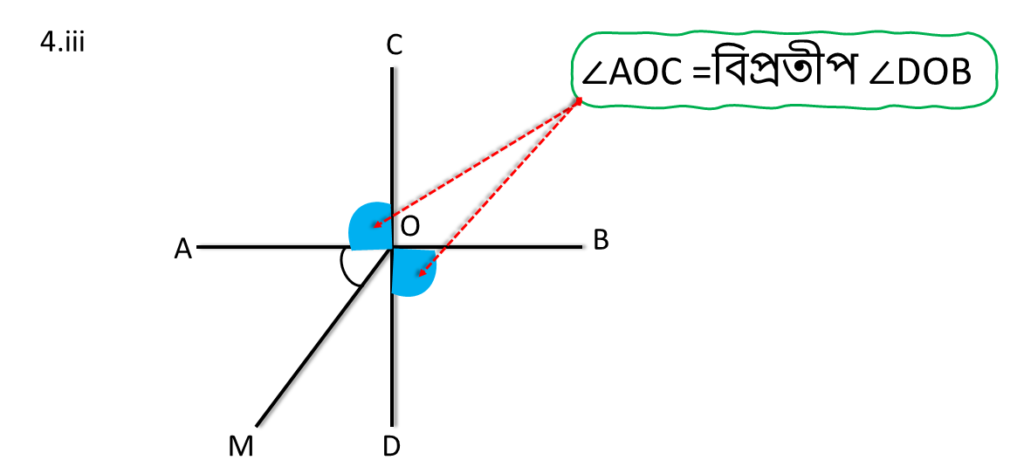
∠AOC এবং ∠DOB কোণ দুটি পরস্পরের বিপ্রতীপ কোণ ।
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
5. দুটি সরলরেখা কোনো বিন্দুতে ছেদ করলে বিপ্রতীপকোণগুলির পরিমাপ সমান হবে – যুক্তি দিয়ে প্রমাণ করি ।
সমাধানঃ-
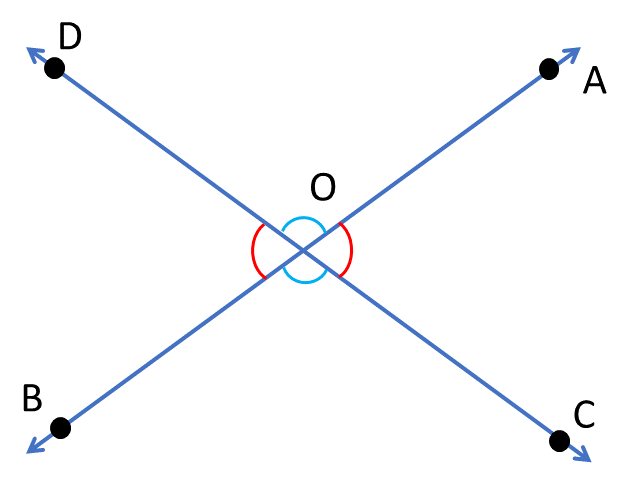
প্রদত্তঃ
AB ও CD দুটি সরলরেখা পরস্পরকে O বিন্দুতে ছেদ করেছে । এর ফলে দু-জোড়া বিপ্রতীপ কোণ ∠AOD, ∠BOC ও ∠AOC, ∠BOD তৈরি হয়েছে ।
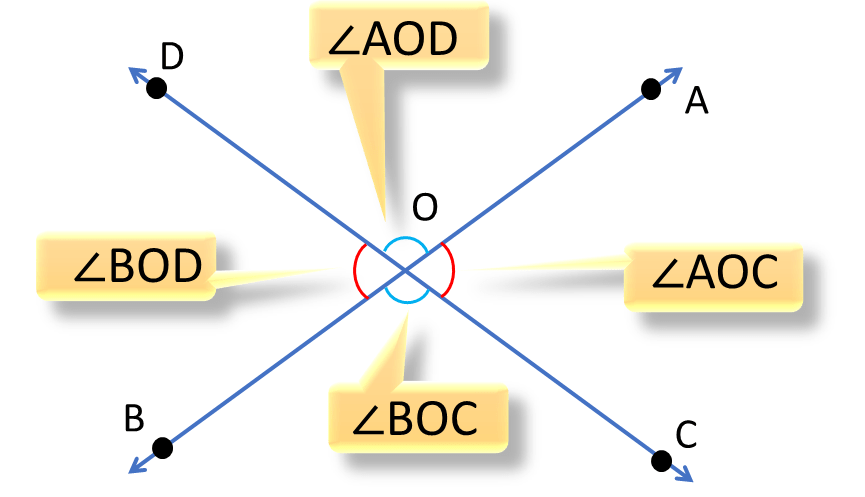
প্রামান্যঃ
প্রমাণ করতে হবে যে, প্রতিজোড়া বিপ্রতীপ কোণগুলির পরিমাপ সমান অর্থাৎ ∠AOD=∠BOC এবং ∠AOC=∠BOD
প্রমানঃ
∠AOD +∠AOC = 180° [ কারণ CD সরলরেখার উপরে OA রশ্মি দণ্ডায়মান হওয়ায় সন্নিহিত কোণদ্বয়ের সমষ্টি দুই সমকোণ – স্বতঃসিদ্ধ 1 ]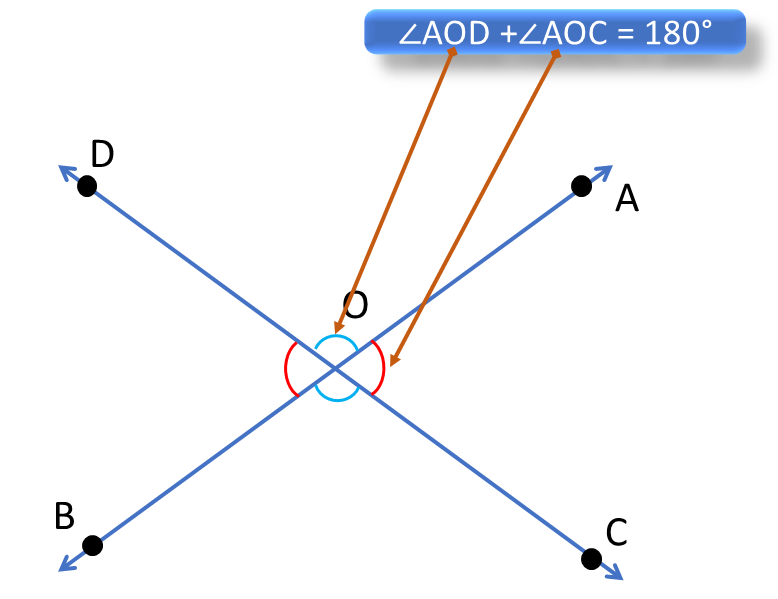 |
∠AOC + ∠BOC = 180° [ কারণ AB সরলরেখার উপরে OC রশ্মি দণ্ডায়মান হওয়ায় সন্নিহিত কোণদ্বয়ের সমষ্টি দুই সমকোণ – স্বতঃসিদ্ধ 1 ]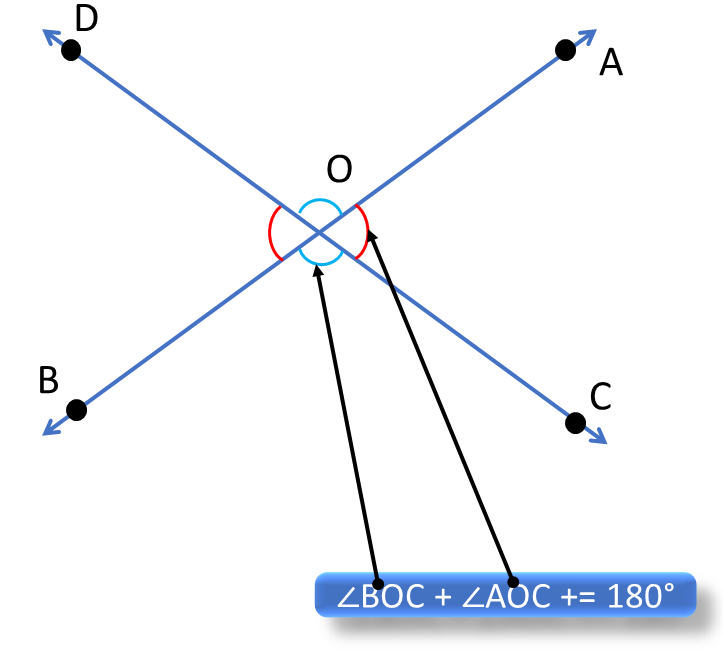 |
| ∠AOD +∠AOC =∠AOC + ∠BOC |
| সুতরাং ∠AOD = ∠BOC ( উভয়দিক থেকে ∠AOC বিয়োগ করে পাই ) |
| আবার একইভাবে লিখতে পারি- |
∠BOC + ∠BOD = 180° [ কারণ CD সরলরেখার উপরে OB রশ্মি দণ্ডায়মান হওয়ায় সন্নিহিত কোণদ্বয়ের সমষ্টি দুই সমকোণ – স্বতঃসিদ্ধ 1 ]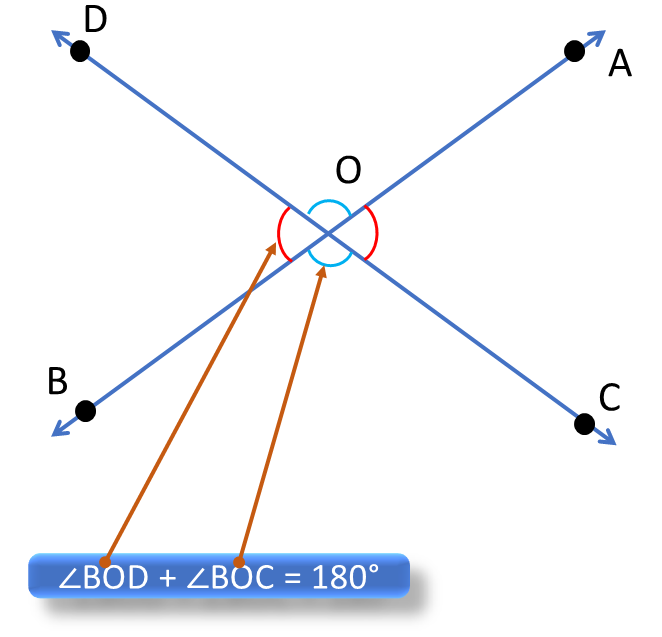 |
∠BOC + ∠AOC = 180° [ কারণ AB সরলরেখার উপরে OC রশ্মি দণ্ডায়মান হওয়ায় সন্নিহিত কোণদ্বয়ের সমষ্টি দুই সমকোণ – স্বতঃসিদ্ধ 1 ]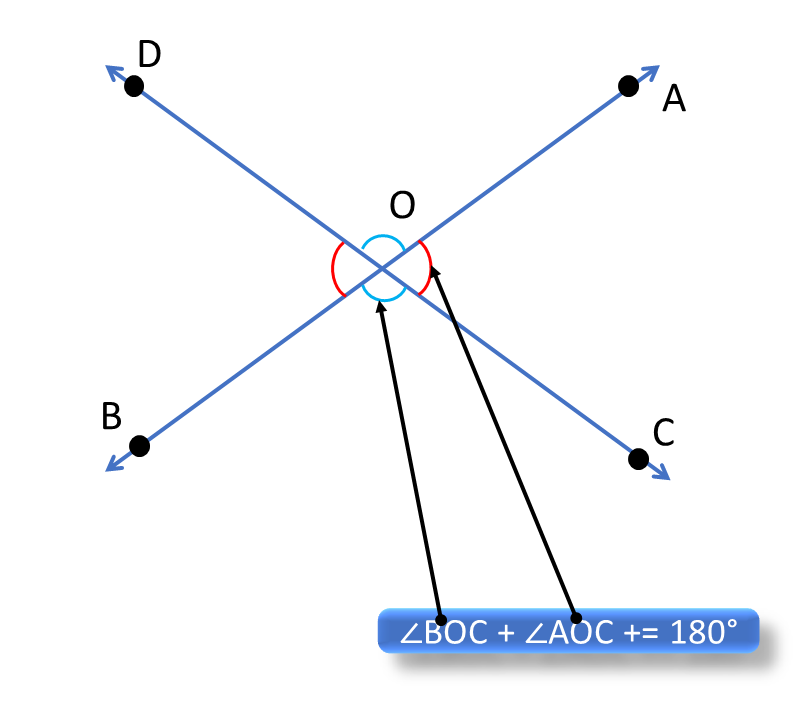 |
| ∠BOC + ∠BOD =∠BOC + ∠AOC |
| সুতরাং ∠BOD = ∠AOC ( উভয়দিক থেকে ∠BOC বিয়োগ করে পাই ) |
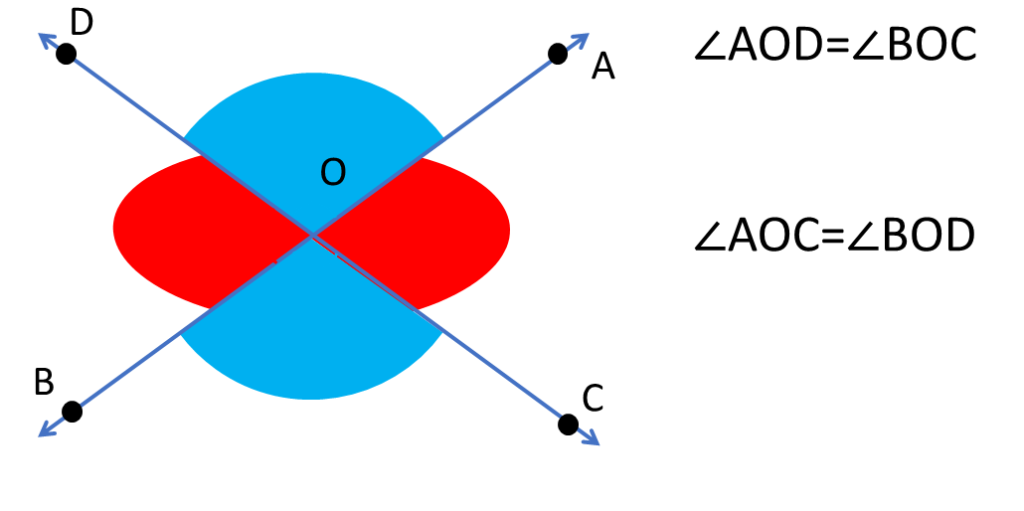
পেলাম AB ও CD দুটি সরলরেখা পরস্পরকে O বিন্দুতে ছেদ করায় বিপ্রতীপ কোণগুলি সমান অর্থাৎ-
∠AOD=∠BOC
এবং ∠AOC=∠BOD
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
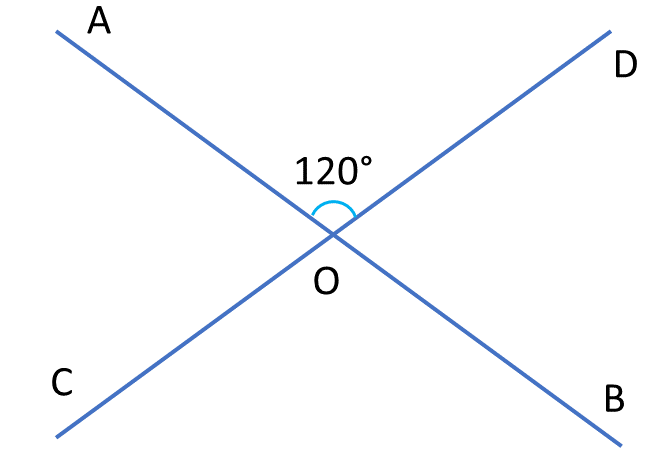
6.∠BOD , ∠BOC , ∠AOC এর পরিমাপ লিখি ।
সমাধানঃ-
| দেওয়া আছে, ∠DOA=120° |
| ছবিতে আমরা দেখতে পাচ্ছি, ∠DOA এর বিপ্রতীপ ∠BOC |
| অতএব, ∠DOA=∠BOC |
| ∠BOC=120° |
আবার,
| ∠BOD + ∠DOA = 180° |
| বা, ∠BOD = 180° – ∠DOA |
| বা, ∠BOD = 180° – 120° |
| বা, ∠BOD = 60° |
ছবিতে আমরা দেখতে পাচ্ছি,
| ∠BOD এর বিপ্রতীপ ∠AOC |
| অতএব, ∠BOD= ∠AOC |
| ∠AOC=∠BOD=60° |
| ∠BOD = 60° ∠BOC=120° ∠AOC=60° |
7. ∠PQR ও ∠QOS – এর সমষ্টি 110° ; ∠POS , ∠QOS, ∠QOR, ∠POR – এর পরিমাপ লিখি ।
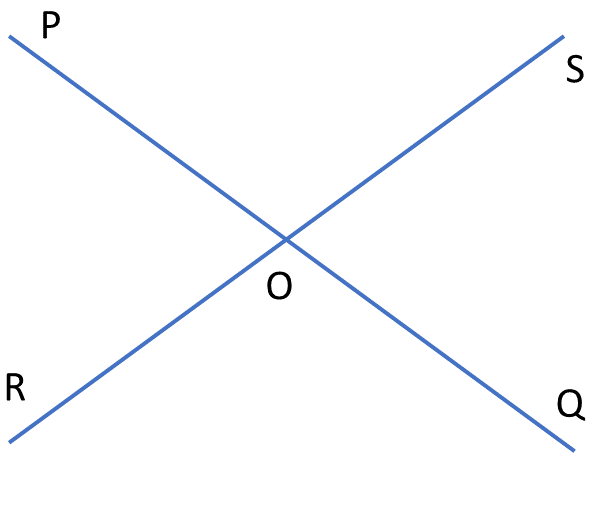
সমাধানঃ-
| ছবিতে আমরা দেখতে পাচ্ছি, |
| ∠POR এর বিপ্রতীপ ∠QOS অতএব, ∠POR=∠QOS |
| ∠POS এর বিপ্রতীপ ∠QOR অতএব, ∠POS=∠QOR |
| দেওয়া আছে, |
| ∠POR + ∠QOS=110° |
| বা, ∠POR + ∠POR =110° [ ∠POR=∠QOS ] |
| বা, 2∠POR = 110° |
| বা, ∠POR = 110°/2=55° |
| অতএব, ∠QOS=55° |
আবার,
| ∠POS + ∠QOS = 180° |
| বা, ∠POS = 180° – ∠QOS |
| বা, ∠POS= 180° – 55° |
| বা, ∠POS = 125° |
| আবার, ∠POS=∠QOR |
| অতএব, ∠QOR= 125° |
| ∠POS = 125° ∠QOS=55° ∠QOR= 125° ∠POR =55° |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
8. OP, OQ, OR এবং OS সমবিন্দু। OP এবং OR একই সরলরেখায় অবস্থিত। P ও R বিন্দু O বিন্দুর বিপরীত পাশে অবস্থিত । ∠POQ=∠ROS এবং ∠POS=∠QOR । যদি ∠POQ=50° হয় তবে ∠QOR, ∠ROS এবং ∠POS এর পরিমাপ লিখি ।
সমাধানঃ-
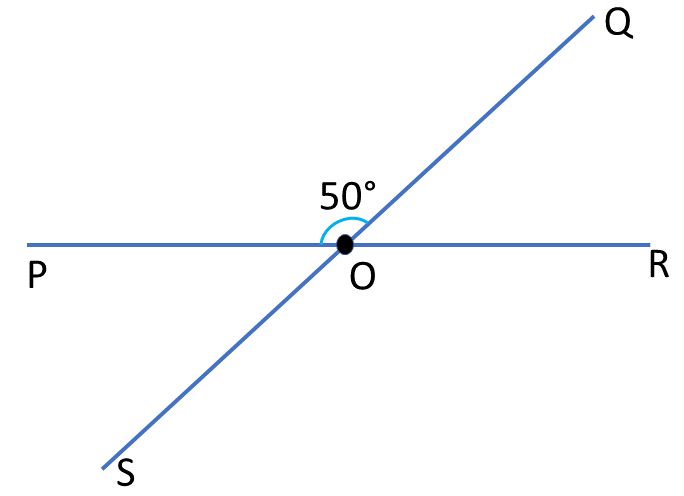
ছবিতে আমরা দেখতে পাচ্ছি,
OP, OQ, OR এবং OS সমবিন্দু। OP এবং OR একই সরলরেখায় অবস্থিত। P ও R বিন্দু O বিন্দুর বিপরীত পাশে অবস্থিত এবং ∠POQ=∠ROS এবং ∠POS=∠QOR ।
দেওয়া আছে,
∠POQ=50°
অতএব,
∠ROS=∠POQ=50°
যেহেতু OP এবং OR একই সরলরেখায় আছে তারসাথে OQ দণ্ডায়মান হয়েছে PR সরলরেখার উপর ।
সেহেতু,
| ∠POQ + ∠QOR = 180° |
| বা, ∠QOR = 180° – ∠POQ |
| বা, ∠QOR = 180° – 50° |
| বা, ∠QOR = 30° |
যেহেতু ∠POS=∠QOR
অতএব,
∠POS=30°
| ∠QOR = 30° ∠ROS= 50° ∠POS=30° |
9. চারটি রশ্মি একটি বিন্দুতে এমনভাবে মিলিত হয় যে বিপরীত দিকের কোণগুলি সমান । প্রমাণ করি যে ওই চারটি রশ্মি দ্বারা দুটি সরলরেখা তৈরি হয় ।
সমাধানঃ-
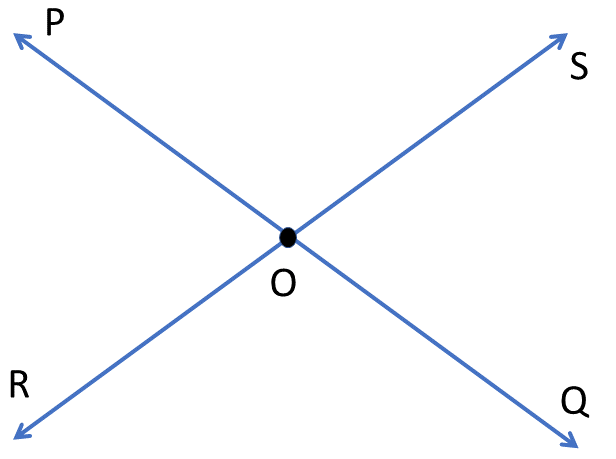
ছবিতে আমরা দেখতে পাচ্ছি চারটি রশ্মি যথা OP, OQ, OR এবং OS একটি বিন্দু O তে মিলিত হয়েছে ।
প্রদত্তঃ
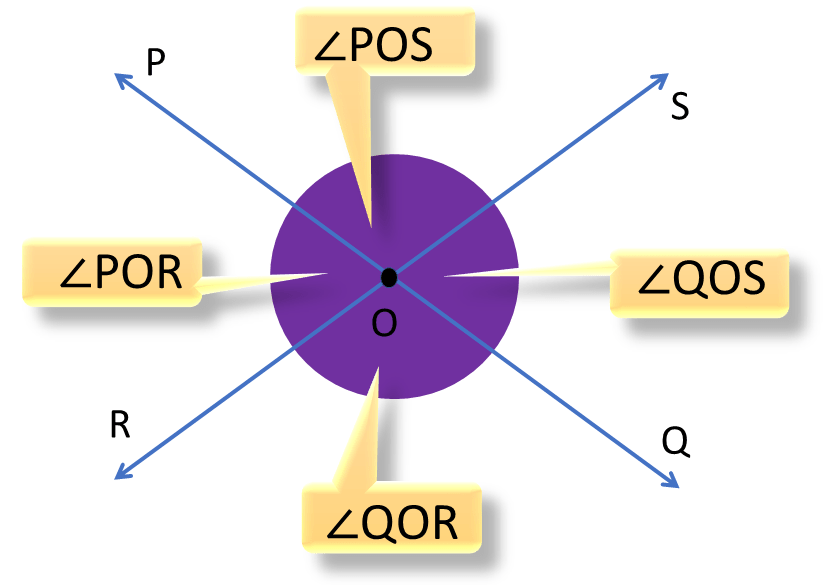
| ∠POS= ∠QOR |
| এবং |
| ∠POR = ∠QOS |
প্রামান্যঃ
চারটি রশ্মি যথা OP, OQ, OR এবং OS দ্বারা দুটি সরলরেখা তৈরি হয়েছে ।
প্রমানঃ
| ∠POS + ∠QOS + ∠QOR + ∠POR = 360° |
| বা,∠POS + ∠QOS + ∠POS +∠QOS = 360° |
| বা,2∠POS + 2∠QOS = 360° |
| বা,2(∠POS + ∠QOS)=360° |
| বা,∠POS + ∠QOS= 360°/2 |
| বা,∠POS + ∠QOS=180° |
তাহলে আমরা পেলাম ∠POS ও ∠QOS এমন দুটি সন্নিহিত কোণ যাদের সমষ্টি 180°.
অতএব, ∠POS ও ∠QOS দুটি সন্নিহিত কোণের সাধারণ বাহু ছাড়া অপর দুই বাহু একই সরলরেখায় থাকবে।
সুতরাং, PQ একটি সরলরেখা ।
এখানে যদি তোমরা বুঝতা না পারো যে কেন PQ সরলরেখা হলো ! তাহলে তোমরা অবশ্যই সন্নিহিত কোণের বৈশিষ্ট্য গুলি একবার দেখে নিও- 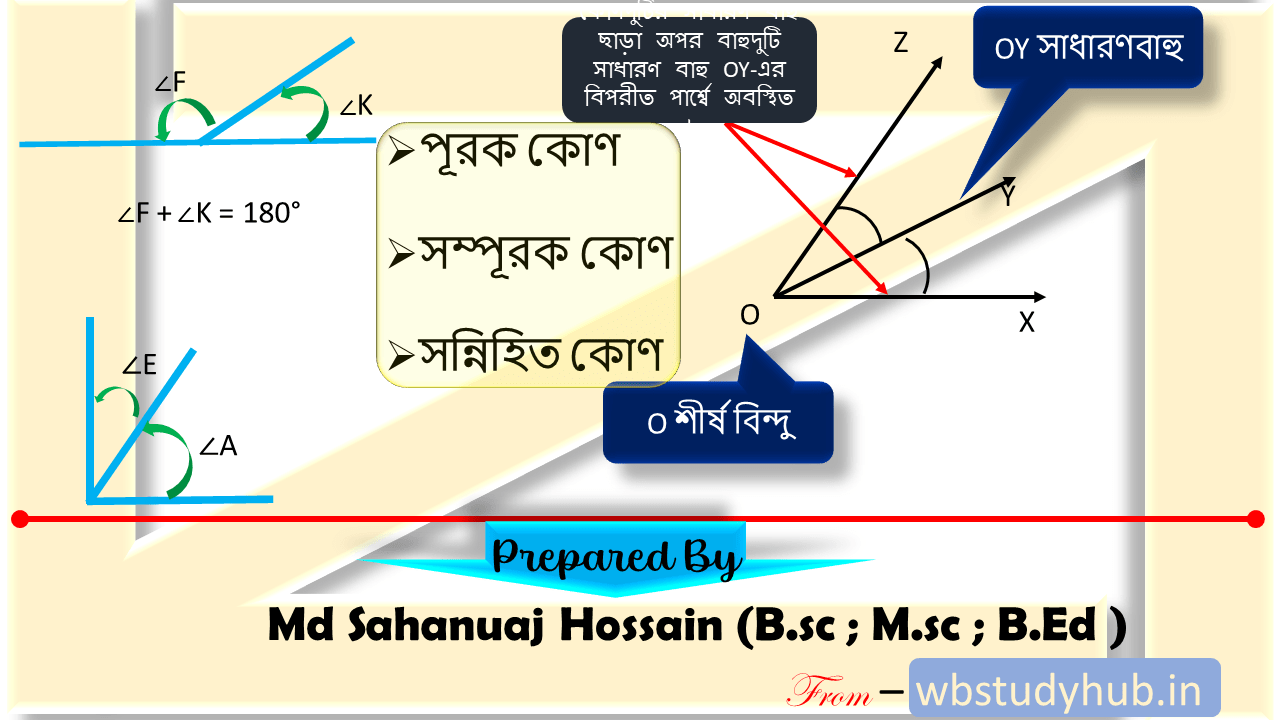  সন্নিহিত কোণের বৈশিষ্ট্য সন্নিহিত কোণের বৈশিষ্ট্য |
একইরকম ভাবে ∠QOS ও ∠QOR সন্নিহিত কোণের ক্ষেত্রে RS একটি সরলরেখা হবে।
অতএব প্রমানিত যে, চারটি রশ্মি একটি বিন্দুতে মিলিত হয়ে যদি বিপরীত দিকের কোণগুলি সমান হয় তাহলে ওই চারটি রশ্মি দ্বারা দুটি সরলরেখা তৈরি হয় ।
10. একটি কোণের অন্তঃসমদ্বিখণ্ডক ও বহিঃসমদ্বিখণ্ডক পরস্পর লম্বভাবে অবস্থিত – প্রমাণ করি ।
সমাধানঃ-
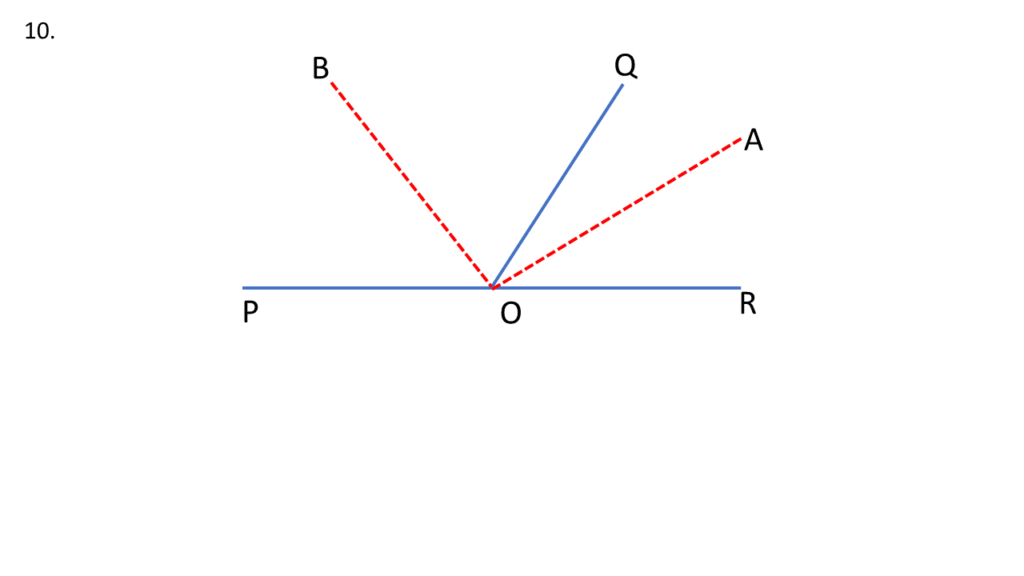
PR সরলরেখার উপর ∠QOR এর বহিঃকোণ হলো ∠POQ ।
| ∠QOR এর অন্তঃসমদ্বিখণ্ডক হলো OA |
| অতএব, |
| ∠QOA = ∠ROA |
আবার,
| ∠QOR এর বহিঃসমদ্বিখণ্ডক হলো OB |
| অতএব, |
| ∠POB = ∠QOB |
প্রদত্তঃ
PR সরলরেখার উপর ∠QOR এর বহিঃকোণ= ∠POQ । OA এবং OB হলো ∠QOR এর অন্তঃসমদ্বিখণ্ডক এবং বহিঃসমদ্বিখণ্ডক ।
∠QOA = ∠ROA
এবং
∠POB = ∠QOB
প্রামান্যঃ
প্রমাণ করতে হবে OA এবং OB পরস্পর লম্ব ।
প্রমানঃ
| ∠POQ + ∠QOR = 180° [ যেহেতু, PR সরলরেখার উপর ∠POQ ও ∠QOR দুটি সন্নিহিত কোণ ] |
| বা,∠POB + ∠QOB + ∠QOA + ∠AOR = 180° [ ∵ ∠POQ = ∠POB + ∠QOB এবং ∠QOR = ∠QOA + ∠AOR ] |
| বা,2∠QOB + 2∠QOA = 180° |
| বা,2(∠QOB + ∠QOA) = 180° |
| বা,(∠QOB + ∠QOA) = 180°/2 |
| বা,∠QOB + ∠QOA= 90° |
আমরা পেলাম ∠QOB + ∠QOA= 90°।
অতএব, OA এবং OB পরস্পর লম্ব প্রমানিত ।
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
11. দুটি সরলরেখা পরস্পর ছেদ করলে যে চারটি কোণ উৎপন্ন হয় তাদের সমষ্টি চার সমকোণ – প্রমাণ করি ।
সমাধানঃ-
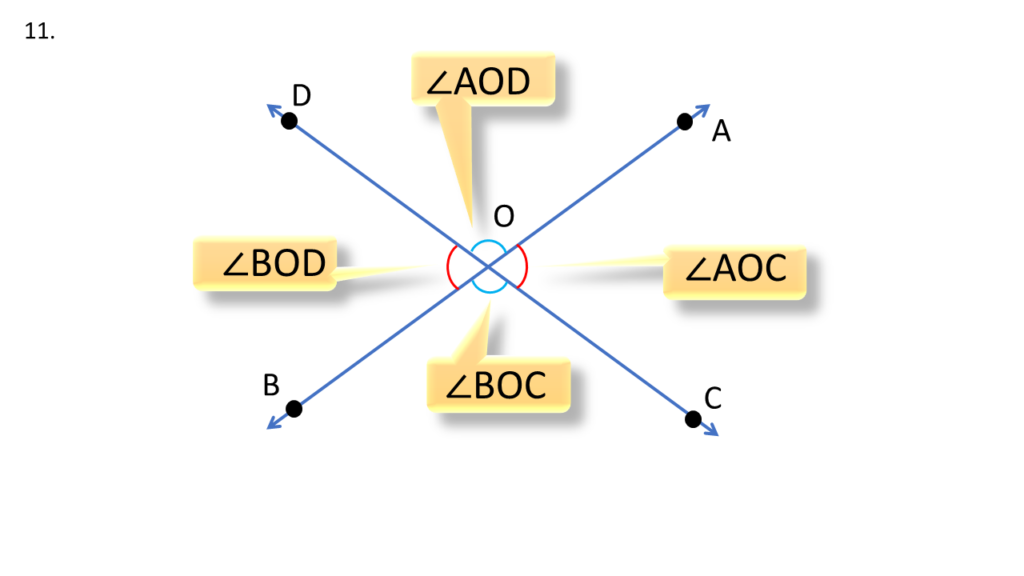
AB ও CD দুটি সরলরেখা পরস্পরকে O বিন্দুতে ছেদ করেছে ।
প্রদত্তঃ
AB ও CD দুটি সরলরেখা পরস্পরকে O বিন্দুতে ছেদ করার ফলে চারটি কোণ উৎপন্ন হয়েছে । যথা- ∠AOD, ∠AOC, ∠BOC, ∠BOD
প্রামান্যঃ
প্রমাণ করতে হবে ∠AOD, ∠AOC, ∠BOC, ∠BOD এই চারটি কোণের সমষ্টি চার সমকোণ ।
প্রমানঃ
| DC সরলরেখার উপর ∠AOD ও ∠AOC দুটি সন্নিহিত কোণ |
| অতএব, ∠AOD + ∠AOC = 180°——( i ) |
| আবার AB সরলরেখার উপর ∠BOC ও ∠BOD দুটি সন্নিহিত কোণ। |
| অতএব, ∠BOC + ∠BOD = 180° ——( ii ) |
| ( i ) ও ( ii ) যোগ করে পাই, |
| ∠AOD + ∠AOC + ∠BOC + ∠BOD = 180° + 180° |
| বা, ∠AOD + ∠AOC + ∠BOC + ∠BOD = 360° |
আমরা পেলাম
∠AOD + ∠AOC + ∠BOC + ∠BOD = 360°
অতএব প্রমানিত যে , দুটি সরলরেখা পরস্পর ছেদ করলে যে চারটি কোণ উৎপন্ন হয় তাদের সমষ্টি চার সমকোণ ।
12. ▲PQR ত্রিভুজের ∠PQR=∠PRQ; QR বাহুকে উভয়দিকে বর্ধিত করলে যে দুটি বহিঃকোণ উৎপন্ন হয় তাদের মান সমান – প্রমাণ করি ।
সমাধানঃ-
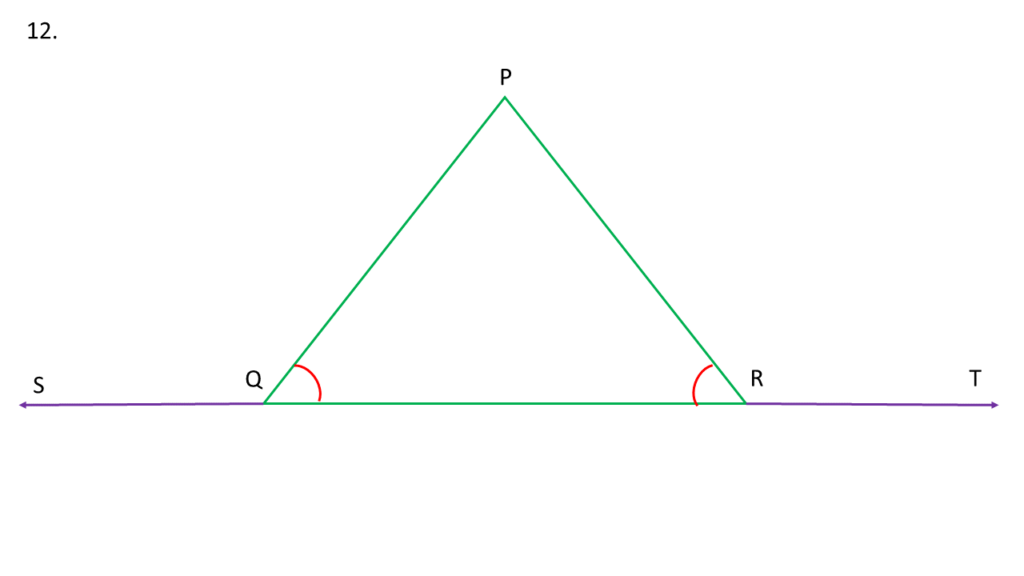
প্রদত্তঃ
▲PQR ত্রিভুজের ∠PQR=∠PRQ; QR বাহুকে উভয়দিকে বর্ধিত করে ∠PRT এবং ∠PQS দুটি বহিঃকোণ উৎপন্ন হয়েছে ।
প্রামান্যঃ
∠PRT = ∠PQS
প্রমানঃ
| QT সরলরেখার উপর ∠PRQ এবং ∠PRT দুটি সন্নিহিত কোণ । |
| অতএব, ∠PRQ + ∠PRT = 180°—–( i ) |
| আবার, SR সরলরেখার উপর ∠PQS এবং ∠PQR দুটি সন্নিহিত কোণ । |
| অতএব, ∠PQS + ∠PQR = 180°—–( ii ) |
| ( i ) ও ( ii ) সমান করে পাই, |
| ∠PRQ + ∠PRT = ∠PQS + ∠PQR |
| বা,∠PRQ + ∠PRT = ∠PQS + ∠PRQ [ ∵ ∠PQR=∠PRQ ] |
| বা, ∠PRT = ∠PQS [ উভয় দিক থেক ∠PRQ বিয়োগ করে পাই ] |
অতএব প্রমানিত যে, ▲PQR ত্রিভুজের ∠PQR=∠PRQ; QR বাহুকে উভয়দিকে বর্ধিত করলে যে দুটি বহিঃকোণ উৎপন্ন হয় তাদের মান সমান।
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
13. দুটি সরলরেখা পরস্পরকে একটি বিন্দুতে ছেদ করায় যে চারটি কোণ উৎপন্ন হয় তাদের সমদ্বিখণ্ডকগুলি পরস্পর দুটি লম্ব সরলরেখা – প্রমাণ করি ।
সমাধানঃ-
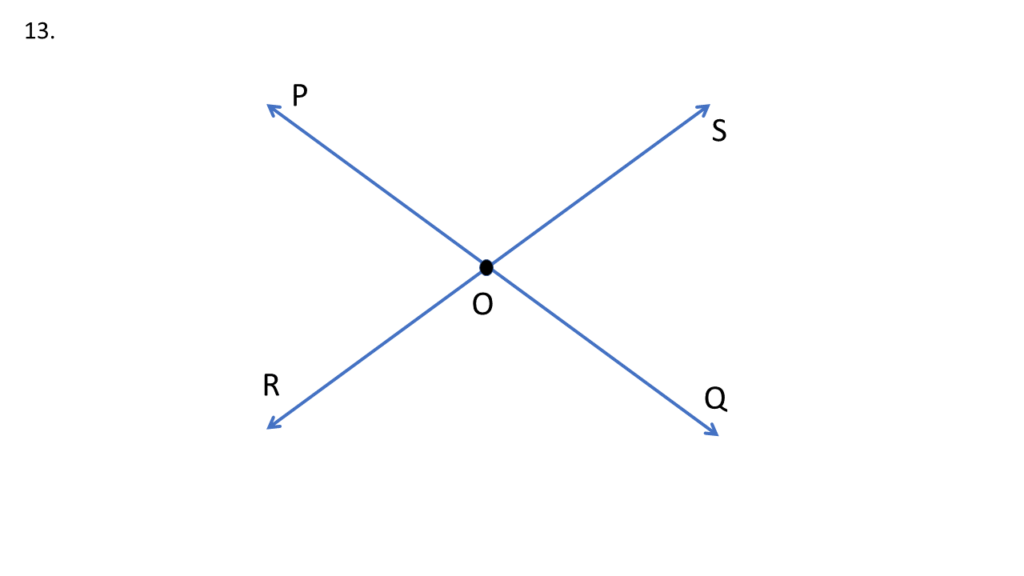
দুটি সরলরেখা PQ ও RS একটি বিন্দু O তে ছেদ করায় চারটি কোণ উৎপন্ন হয়েছে যথা-
∠POS, ∠QOS, ∠QOR এবং ∠POR
উপরের কোণগুলির সমদ্বিখণ্ডক যথাক্রমে OA, OC, OB এবং OD
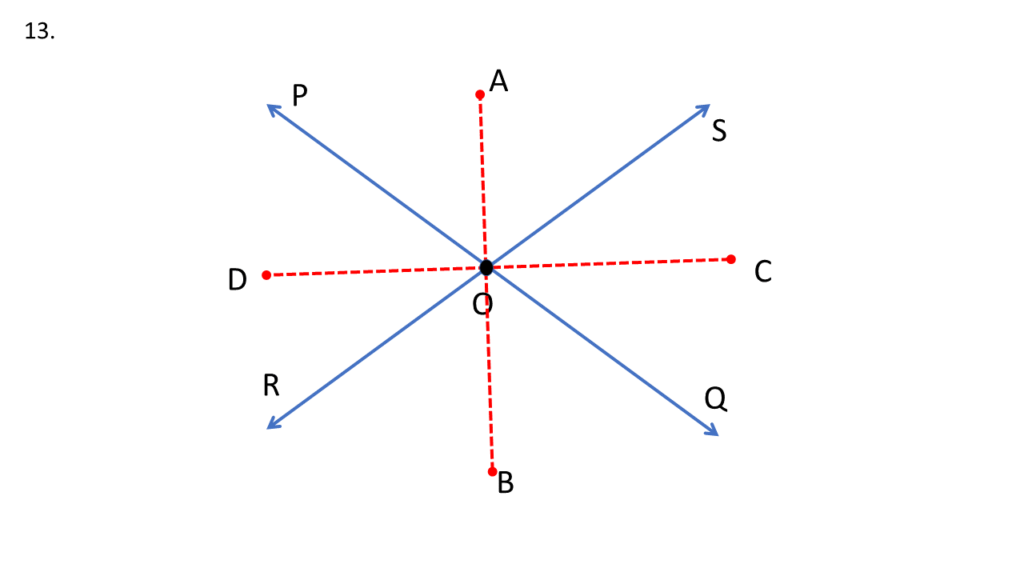
অতএব,
| ∠POA = ∠AOS—-( i ) |
| ∠SOC = ∠QOC—–( ii ) |
| ∠QOB = ∠ROB—–( iii ) |
| ∠ROD = ∠POD—–( iv ) |
প্রদত্তঃ
∠POS, ∠QOS, ∠QOR এবং ∠POR চারটি কোণের সমদ্বিখণ্ডক যথাক্রমে OA, OC, OB এবং OD ।
| ∠POA = ∠AOS—-( i ) |
| ∠SOC = ∠QOC—–( ii ) |
| ∠QOB = ∠ROB—–( iii ) |
| ∠ROD = ∠POD—–( iv ) |
প্রামান্যঃ
DC এবং AB সরলরেখা পরস্পর লম্ব ।
প্রমানঃ
| PQ সরলরেখার উপর ∠POS এবং ∠QOS দুটি সন্নিহিত কোণ। |
| অতএব, ∠POS + ∠QOS = 180°—-( v ) |
| বা, ∠POA + ∠AOS + ∠QOC +∠SOC = 180° [ ∠POS = ∠POA + ∠AOS এবং ∠QOS = ∠QOC + ∠SOC ] |
| বা, ∠AOS + ∠AOS + ∠SOC + ∠SOC = 180° |
| বা, 2( ∠AOS + ∠SOC ) = 180° |
| বা, ∠AOS + ∠SOC = 180°/2=90° |
একইরকম ভাবে আমরা পাবো ,
∠QOC + ∠QOB = 90°
অতএব ,
∠BOC = 90° এবং ∠ AOC = 90°
আমরা পেলাম ∠BOC এবং ∠AOC দুটি সন্নিহিত কোণ যাদের সমষ্টি 180°( ∠BOC + ∠AOC = 180° )
অতএব, AB একটি সরলরেখা ।
একইভাবে আমরা পাবো DC একটি সরলরেখা ।
অতএব AB ও DC পরস্পর দুটি লম্ব সরলরেখা , প্রমানিত ।
এখানে যদি তোমরা বুঝতা না পারো যে কেন AB সরলরেখা হলো ! তাহলে তোমরা অবশ্যই সন্নিহিত কোণের বৈশিষ্ট্য গুলি একবার দেখে নিও-   সন্নিহিত কোণের বৈশিষ্ট্য সন্নিহিত কোণের বৈশিষ্ট্য |
এই কষে দেখি 7.1 Class 8|Koshe Dekhi 7.1 Class 8 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 7.1 Class 8 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 7.1 Class 8 তারপর  |
| গনিতপ্রভা অষ্টম শ্রেণীর সমস্ত অধ্যায়ের সমাধান- | |
|---|---|
| অধ্যায় | সমাধান |
| 2. পাই চিত্র | কষে দেখি 2 |
| 3. মূলদ সংখ্যার ধারণা | অধ্যায়ের সারাংশ |
| কষে দেখি 3 | |
| 4. বীজগাণিতিক সংখ্যামালার গুণ ও ভাগ | অধ্যায়ের সারাংশ |
| কষে দেখি 4.1 | |
| কষে দেখি 4.2 | |
| 5. ঘনফল নির্ণয় | অধ্যায়ের সারাংশ |
| কষে দেখি 5.1 | |
| কষে দেখি 5.2 | |
| কষে দেখি 5.3 | |
| 6. পূরক কোণ, সম্পূরক কোণ ও সন্নিহিত কোণ | অধ্যায়ের সারাংশ |
| কষে দেখি 6 | |
| 7. বিপ্রতীপ কোণের ধারণা | অধ্যায়ের সারাংশ |
| কষে দেখি 7.1 | |
8. সমান্তরাল সরলরেখা ও ছেদকের ধর্ম | অধ্যায়ের সারাংশ |
| কষে দেখি 8 | |
9. ত্রিভুজের দুটি বাহু ও তাদের বিপরীত কোণের সম্পর্ক | অধ্যায়ের সারাংশ |
| কষে দেখি 9 | |
| 10. ত্রৈরাশিক | কষে দেখি 10.1 |
| কষে দেখি 10.2 | |
| 11. শতকরা | কষে দেখি 11 |
| 12. মিশ্রণ | কষে দেখি 12 |
13. বীজগাণিতিক সংখ্যামালার উৎপাদকে বিশ্লেষণ | কষে দেখি 13.1 |
| কষে দেখি 13.2 | |
14. বীজগাণিতিক সংখ্যামালার গ.সা.গু ও ল.সা.গু | কষে দেখি 14 |
15. বীজগাণিতিক সংখ্যামালার সরলীকরণ | কষে দেখি 15 |
16. ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই | কষে দেখি 16.1 |
| কষে দেখি 16.2 | |
17. সময় ও কার্য | কষে দেখি 17.1 |
| কষে দেখি 17.2 | |
18. লেখচিত্র | কষে দেখি 18 |
19. সমীকরণ গঠন ও সমাধান | কষে দেখি 19 |
| 20. জ্যামিতিক প্রমাণ | কষে দেখি 20.1 |
| কষে দেখি 20.2 | |
| কষে দেখি 20.3 | |

এখানে তোমরা তোমাদের অষ্টম শ্রেণীতে কি কি পড়ানো হয়, মানে তোমাদের অষ্টম শ্রেণীর সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।



