শ্রেনিঃ- অষ্টম ; অধ্যায়ঃ-সমান্তরাল সরলরেখা ও ছেদকের ধর্ম ; কষে দেখি 8
আমরা অধ্যায়ের সারাংশ তে শিখেছি অনুরূপ ও একান্তর কোণ কি । তোমরা যারা এই সারাংশ দেখনি তারা অবশ্যই দেখে নেবে।
আমাদের শুধু অধ্যায়ের সারাংশ বুঝলেই হবেনা , তারসাথে আমি কতোটা শিখলাম , নিজে কতোটা বুঝলাম এবং নিজে নিজে কারোর সাহাজ্য ছাড়ায় কতোটা অংক সমাধান করতে পারবো তা আমাদের অষ্টম শ্রেণী-এর সমান্তরাল সরলরেখা ও ছেদকের ধর্ম কষে দেখি 8 | Koshe Dekhi 8 Class VIII/8 থেকে অংক করলে তবেই আমরা বুঝতে পারবো।
শুধু তায় নয়, অংক যতো সমাধান করা যাবে ( নিজে নিজে ) ততো নিজের প্রতি বিশ্বাস টা শক্ত হবে। এমনকি এই বিষয়ে নতুন অংক সামনে পেলে সেটা করতে সাহস পাবে ।

এবার আমরা অষ্টম শ্রেণী-এর সমান্তরাল সরলরেখা ও ছেদকের ধর্ম এর কষে দেখি 8 | Koshe Dekhi 8 Class VIII/8 আমরা শুরু করবো। । এখানে প্রতিটি অঙ্ক সুন্দর করে STEP BY STEP গুছিয়ে লেখা হয়েছে এবং সহজ ভাষায় উপস্থাপন করা হয়েছে যাতে তোমরা সহজেই এই কষে দেখি 8 এর প্রতিটি অঙ্ক বুঝতে পারো তারসাথে ভবিষ্যতে এরকম অংক পরীক্ষায় আসলে তা যেনো সহজেই করে উঠতে পারো।
আগে তোমরা নিজেরা অংক গুলি করবে, তারপর যেখানে আটকে যাবে এখান থেকে দেখে নেবে ।
আগামিতে এই কষে দেখি 8 Class 8 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 8 Class 8 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 8 Class 8 তারপর  |
এখানে করে দেওয়া অংক গুলি ভালো ভাবে বোঝার জন্যে নিম্নে কিছু নির্দেশিকা তোমাদের জন্যে থাকলোঃ
কিছু উপদেশঃ-
( i ) আগে তোমরা অনুরূপ ও একান্তর কোণ কি সেটা ভালো করে বুঝে নিবে।
( ii ) কষে দেখি 8 এ যে সমস্ত অংক গুলি আছে সেগুলো করার সময় কোণের সংজ্ঞা গুলো মাথায় রেখে করবে তাহলে কোথাও অসুবিধে হবে না।
( iii ) দুটি সমান্তরাল সরলরেখা ও একটি ছেদকের ফলে কতোগুলি কোণ উৎপন্ন হয় সেটা তোমরা অবশ্যই একবার বুঝে মুখস্থ করে নেবে।
( iv ) একটি উপপাদ্য প্রমাণ করার সময় প্রতিটা step ফলো করতে হবে। যেমন প্রদত্ত, প্রামাণ্য, অঙ্কন, প্রমাণ । তুমি যদি একটি উপপাদ্য কিভাবে প্রমাণ করতে হবে সেটা নাও পারো তাহলে বাকি step গুলো অবশ্যই পরীক্ষায় লিখে আসবে।
কারণ পরীক্ষায় যতগুলো dtep তুমি করবে ওই steps এর উপর পরীক্ষক নম্বর দিয়ে থাকেন।

কষে দেখি 8 | Koshe Dekhi 8
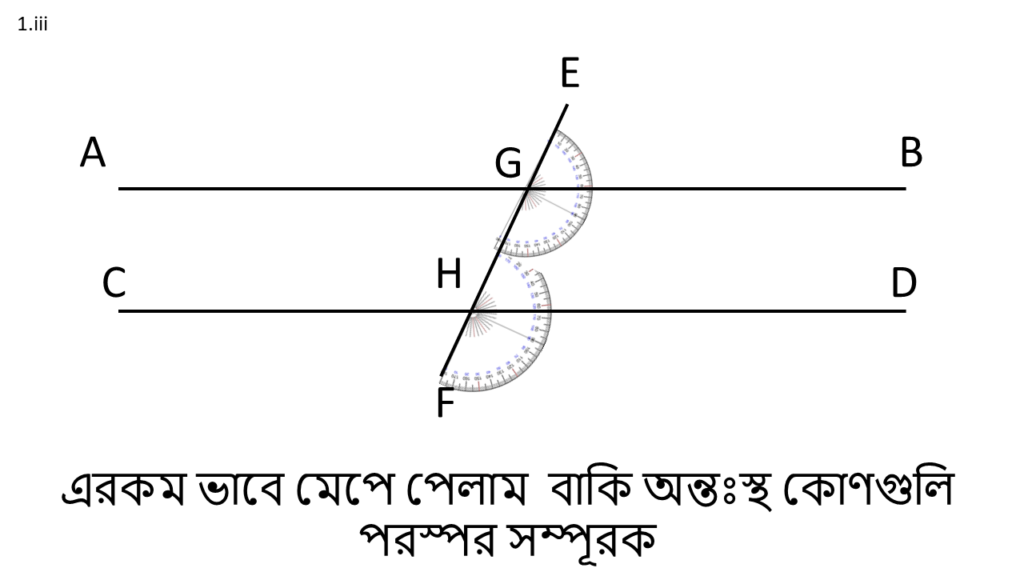
1. চন্দ্রা লাইন টানা খাতার পাতা নিল। দুটি লাইনের মাঝে একটি ছেদক টানল। এর ফলে 4 জোড়া অনুরূপ কোণ, 2 জোড়া একান্তর কোণ তৈরি হলো। তাদের খুঁজি নাম দিই ও লিখি। চাঁদার সাহায্যে মেপে যাচাই করি যে ( i ) অনুরূপ কোণগুলি পরস্পর সমান, ( ii ) একান্তর কোণগুলি পরস্পর সমান ও ( iii ) একই পাশের অন্তঃস্থ কোণগুলি পরস্পর সম্পূরক ।
সমাধানঃ-
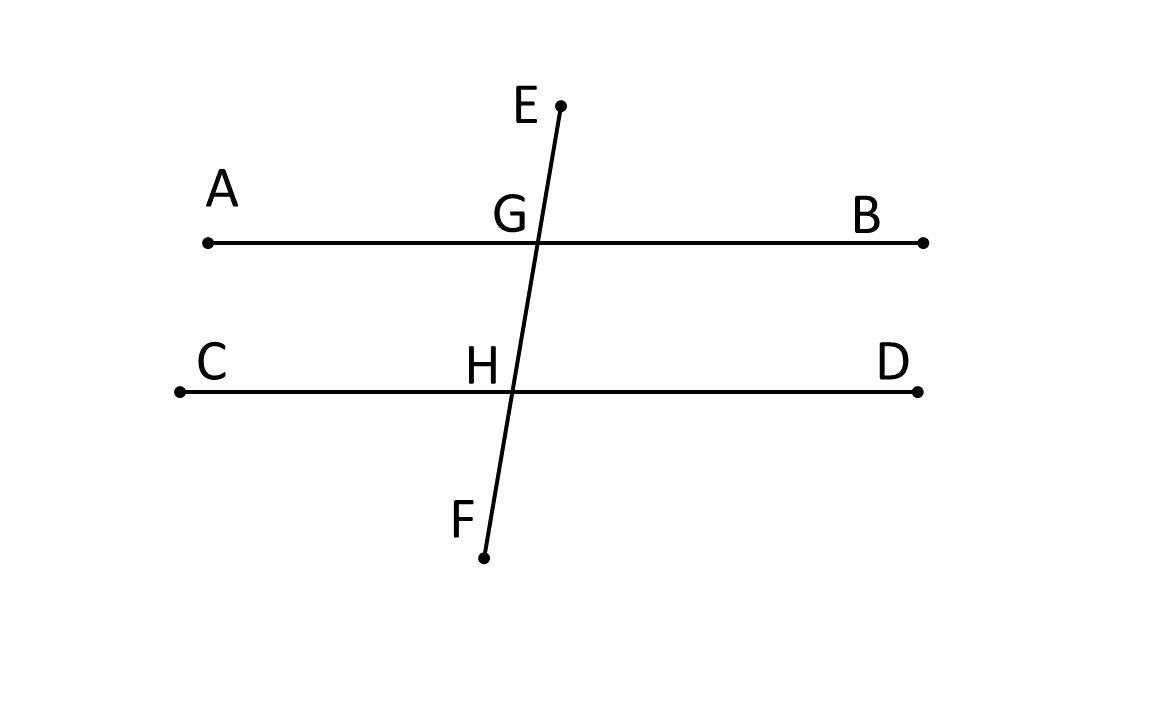
চন্দ্রা লাইন টানা খাতার পাতা নিল। দুটি লাইনের মাঝে একটি ছেদক টানল। এর ফলে-
চার জোড়া অনুরূপ কোণ যথা-
| ∠BGE এর অনুরূপ কোণ ∠DHG |
| ∠BGF এর অনুরূপ কোণ ∠DHF |
| ∠AGE এর অনুরূপ কোণ ∠CHE |
| ∠AGF এর অনুরূপ কোণ ∠CHF |
2 জোড়া একান্তর কোণ যথা-
| ∠BGE এর একান্তর কোণ ∠CHE |
| ∠AGE এর একান্তর কোণ ∠DHE |
2 জোড়া একই পাশের অন্তঃস্থ কোণ যথা-
| ছেদকের বাম পাশে | ছেদকের ডান পাশে |
|---|---|
| ∠BGF ও ∠DHE | ∠AGF ও ∠CHE |
যাচাই করি-
( i ) অনুরূপ কোণগুলি সমানঃ
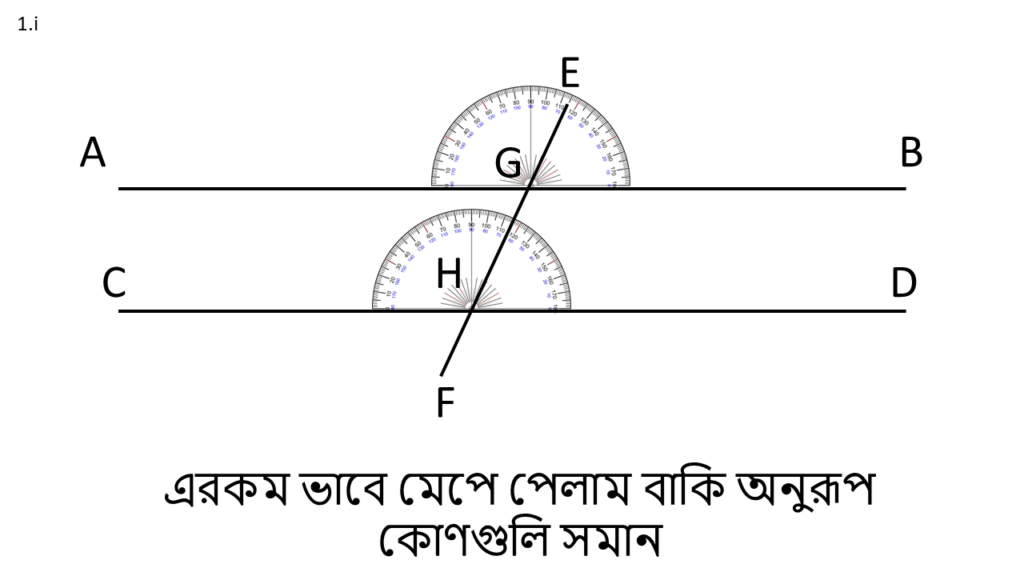
( ii ) একান্তর কোণগুলি পরস্পর স্মানঃ
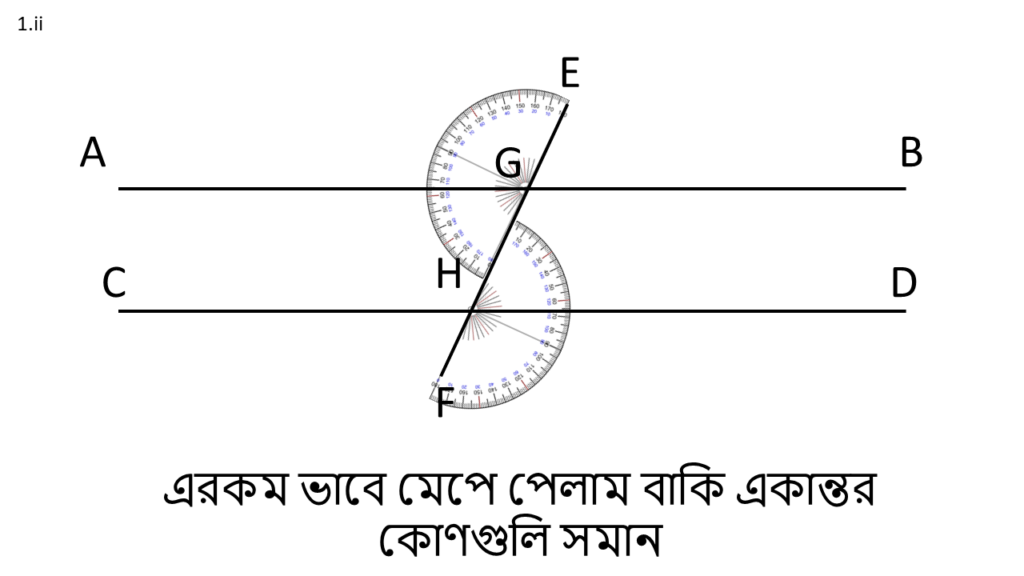
( iii ) একই পাশের অন্তঃস্থ কোণগুলি পরস্পর সম্পূরকঃ
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
2. পাশের ছবির কোণগুলি অনুরূপ কোণ, কোনগুলি একান্তর কোণ ও কোনগুলি একই পাশের অন্তঃস্থ কোণ লিখি ।
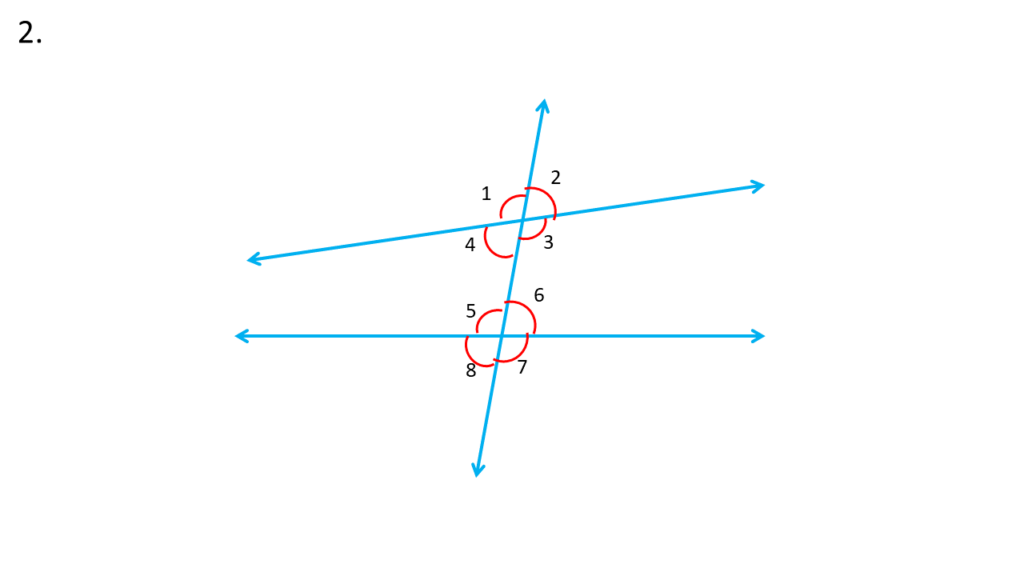
সমাধানঃ-
অনুরূপ কোণগুলি হলো-
| ∠2 এর অনুরূপ ∠6 |
| ∠3 এর অনুরূপ ∠7 |
| ∠1 এর অনুরূপ ∠5 |
| ∠4 এর অনুরূপ ∠8 |
একান্তর কোণগুলি হলো-
| ∠2 এর একান্তর ∠5 |
| ∠1 এর একান্তর ∠6 |
একই পাশের অন্তঃস্থ কোণগুলি হলো –
| ছেদকের বাম পাশে | ছেদকের ডান পাশে |
|---|---|
| ∠4 ও ∠5 | ∠3 ও ∠6 |
3. AB||CD হলে নীচের কোণগুলির মান লিখি-
( a )
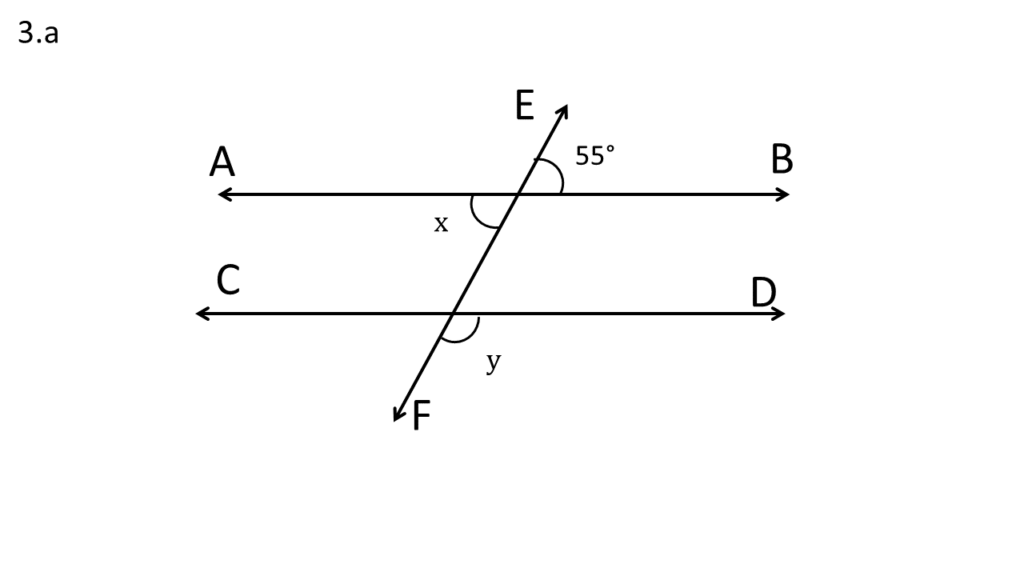
সমাধানঃ-
দেওয়া আছে AB||CD
ধরি EF ছেদকটি AB ও CD সরলরেখাকে যথাক্রমে G ও H বিন্দুতে ছেদ করেছে।
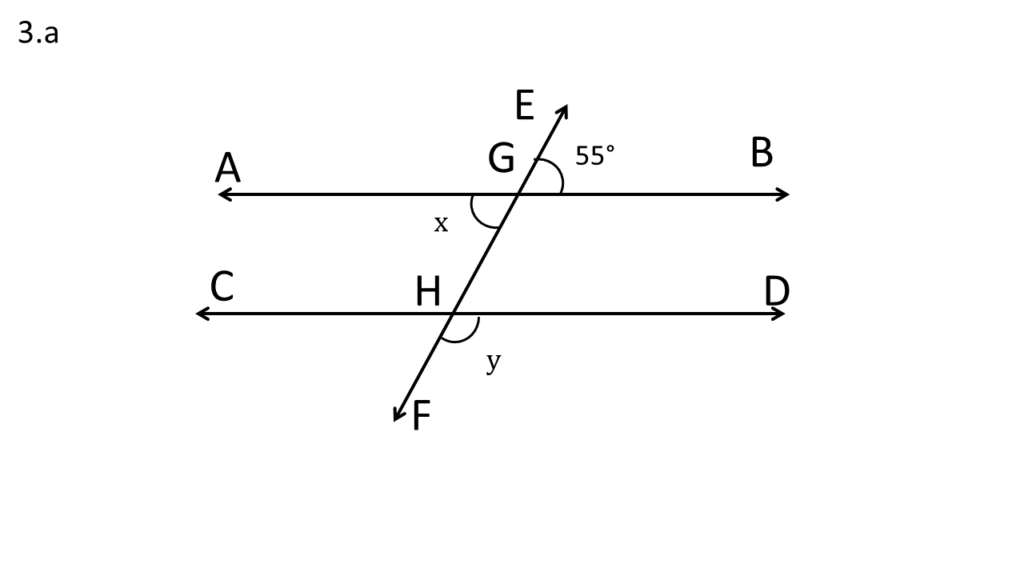
অতএব,
∠EGB = বিপ্রতীপ∠AGF
সুতরাং,
∠AGF= 55°= x
আবার,
| EF ছেদকের বাম পাশে অন্তঃস্থ কোণগুলি হলো – |
| ∠AGF এবং ∠CHE |
| অতএব, |
| ∠AGF + ∠CHE = 180° |
| বা,∠CHE = 180° – ∠AGF |
| বা,∠CHE = 180° – 55° |
| বা, ∠CHE = 125° |
আবার ∠CHE = বিপ্রতীপ কোণ ∠FHD
অতএব,
∠FHD = 125°= y
| x = 55° y = 125° |
( b )
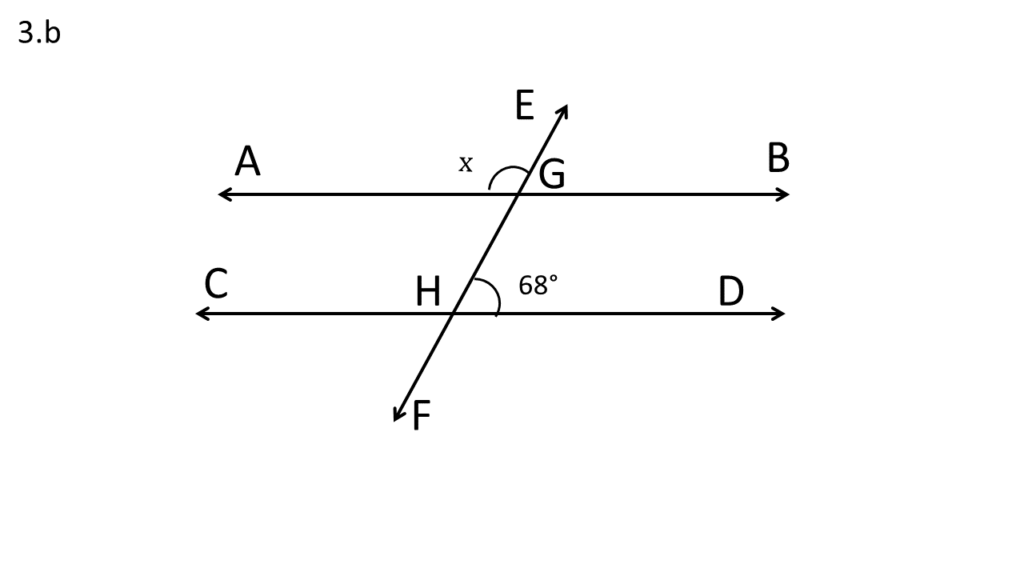
সমাধানঃ-
| ∠DHE = অনুরূপ ∠EGB |
| অতএব, |
| ∠EGB = 68° |
| আবার, |
| ∠AGE + ∠EGB = 180° |
| বা, ∠AGE = 180° – ∠EGB |
| বা, ∠AGE = 180° – 68° |
| বা, ∠AGE = 112°=x |
| x= 112° |
( c )
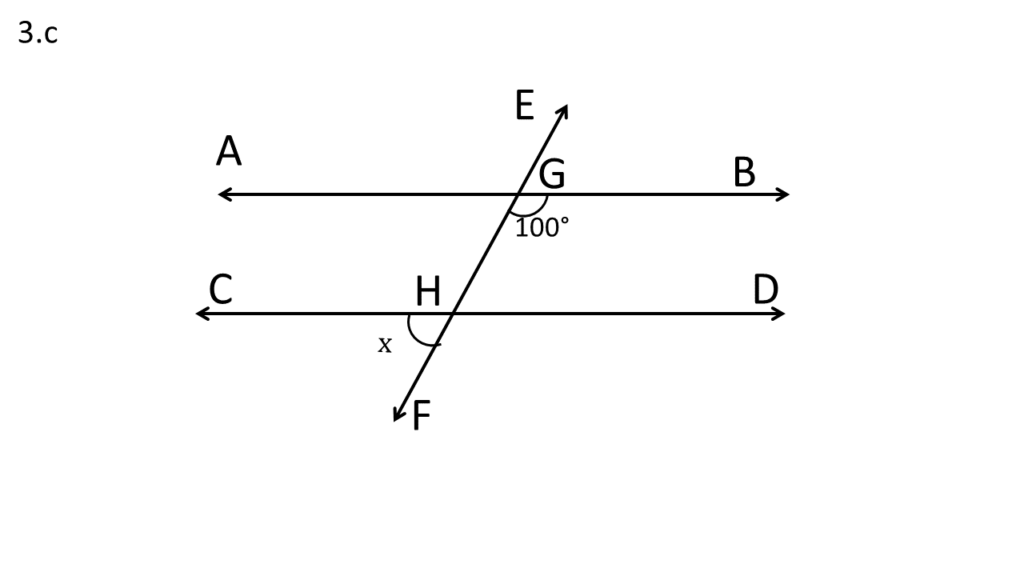
সমাধানঃ-
| EF ছেদকের ডান পাশে অবস্থিত দুটি অন্তঃস্থ কোণ হলো – |
| ∠BGF ও ∠DHE |
| অতএব, |
| ∠BGF + ∠DHE = 180° |
| বা, ∠DHE = 180° – ∠BGF |
| বা, ∠DHE = 180° – 100° |
| বা, ∠DHE = 80° |
আবার,
∠BGF = বিপ্রতীপ ∠CHF
অতএব,
∠CHF = 80° = x
| x = 80° |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
4. পাশের ছবির XY||PQ হলে 7 টি কোণের মান লিখি।
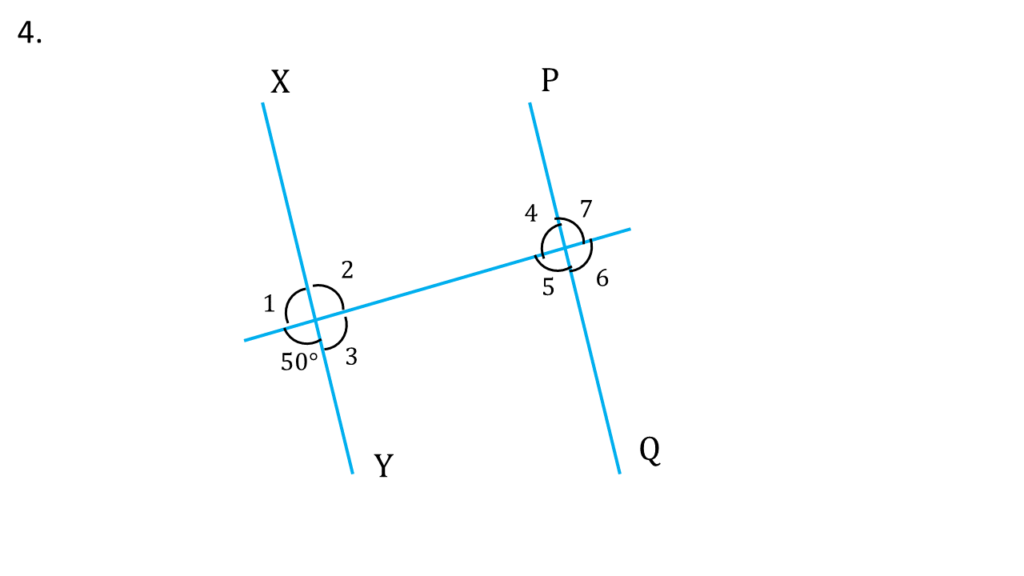
সমাধানঃ-
ছবি তে যে কোণের মান দেওয়া আছে সেই কোণটাকে ধরি 8. ∠8=50°
ছবি থেকে আমরা পাই,
চার জোড়া অনুরূপ কোণ যথা-
| ∠1 = অনুরূপ ∠4 —- ( i ) |
| ∠2 = অনুরূপ ∠7 —-( ii ) |
| ∠5 = অনুরূপ ∠8 —( iii ) |
| ∠3 = অনুরূপ ∠6 —- ( iv ) |
| ∠4 = একান্তর ∠3 — ( v ) |
| ∠5 = একান্তর ∠2 —- ( vi ) |
2 জোড়া অন্তঃস্থ কোণ যথা-
| ছেদকের উপরে | ছেদকের নীচে |
|---|---|
| ∠2 + ∠4 = 180° —( vii ) | ∠3 + ∠5 = 180° — ( viii ) |
দেওয়া আছে ∠8 = 50°
অতএব,
| ( iii ) নম্বর থেকে পাই- | ∠5 = অনুরূপ ∠8 বা, ∠5 = 50° |
| আবার, ( vi ) নম্বর থেকে পাই- | ∠5 = একান্তর ∠2 বা, ∠2 = 50° |
| আবার, ( ii ) এবং ( vii ) নম্বর থেকে পাই- | ∠2 = অনুরূপ ∠7 বা, ∠7 = 50° এবং ∠2 + ∠4 = 180° বা, ∠4 = 180° – ∠2 বা, ∠4 = 180° – 50° বা, ∠4 = 130° |
| আবার, ( v ) নম্বর থেকে পাই- | ∠4 = একান্তর ∠3 বা, ∠3 = 130° |
| আবার, ( i ) নম্বর থেকে পাই- | ∠1 = অনুরূপ ∠4 অতএব, ∠1 = 130° |
| আবার, ( iv ) নম্বর থেকে পাই- | ∠3 = অনুরূপ ∠6 অতএব, ∠6 = ∠3 = 130° |
| ∠1 = 130° ∠2 = 50° ∠3 = 130° ∠4 = 130° ∠5 = 50° ∠6= 130° ∠7 = 50° |
5. নীচের AB ও CD সরলরেখা দুটি সমান্তরাল কিনা কোণের মান দেখে যুক্তি দিয়ে লিখি-
( i )
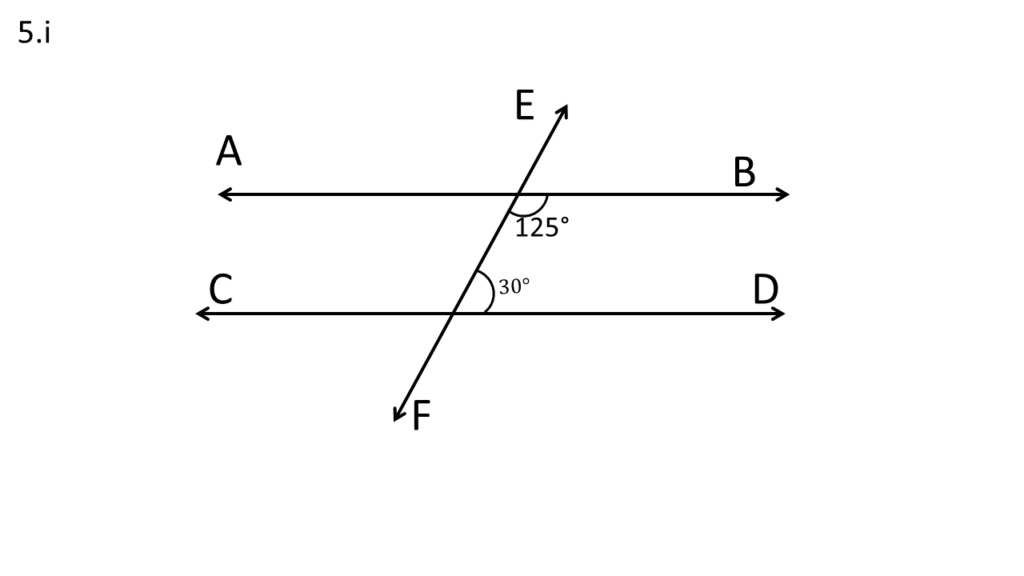
সমাধানঃ-
EF ছেদকের ডান পাশের অন্তঃস্থ কোণদ্বয়ের সমষ্টি-
125° + 30°
= 155°
সুতরাং, EF ছেদকের এক পাশের অন্তঃস্থ কোণদ্বয়ের সমষ্টি 180° নয় ।
অতএব,
| AB ও CD সরলরেখা দুটি সমান্তরাল নয় । |
( ii )
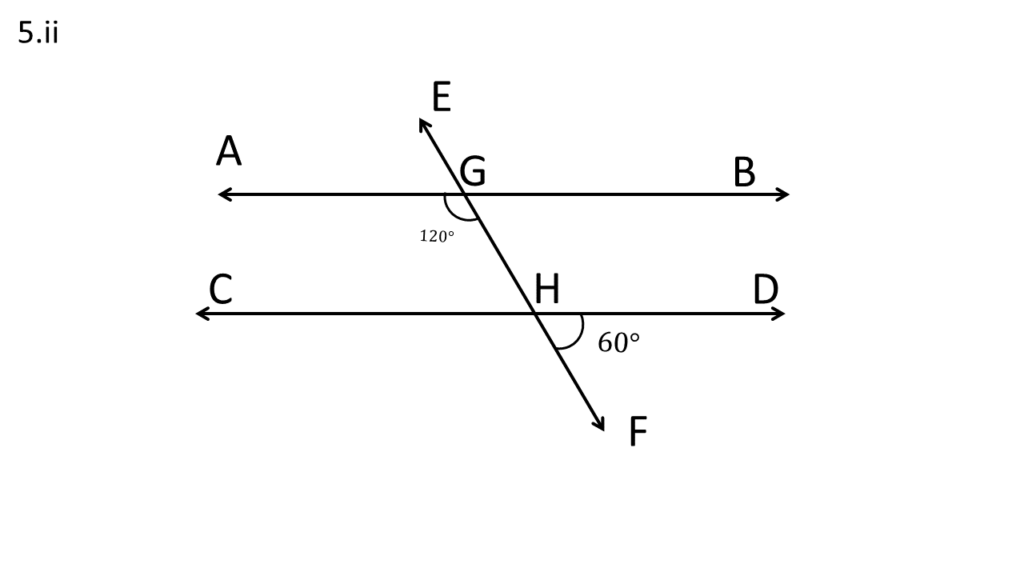
সমাধানঃ-
সরলরেখা AB ও CD কে EF ছেদক যথাক্রমে G ও H বিন্দুতে ছেদ করেছে ( ধরি ) ।
| ∠DHF = বিপ্রতীপ ∠CHG |
| অতএব, ∠CHG =60° |
EF ছেদকের বাম পাশের অন্তঃস্থ কোণদ্বয়ের সমষ্টি,
∠CHG + ∠AGE = 120° + 60°
বা, ∠CHG + ∠AGE = 180°
অতএব ,
| AB ও CD সরলরেখা দুটি সমান্তরাল । |
( iii )
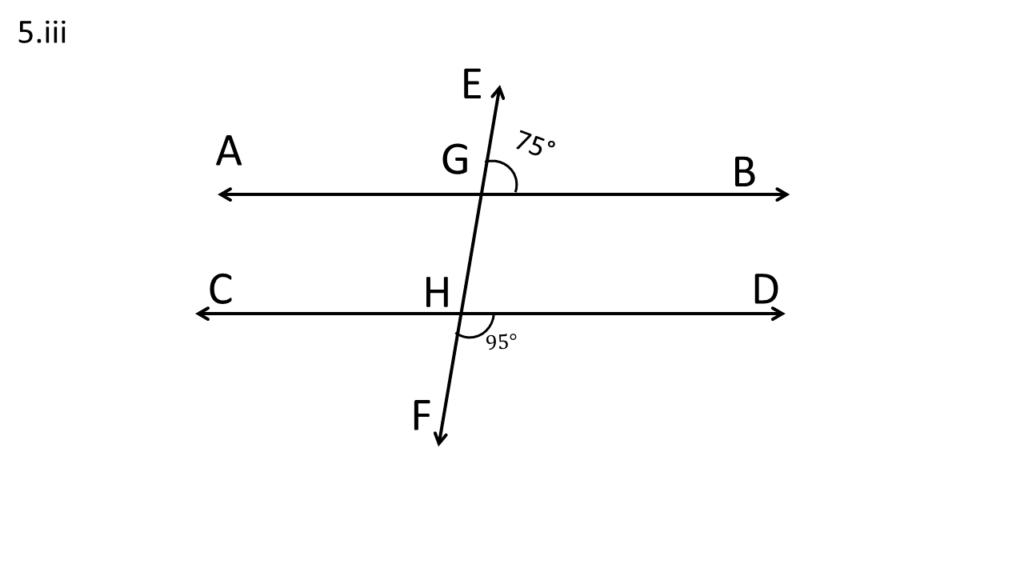
সরলরেখা AB ও CD কে EF ছেদক যথাক্রমে G ও H বিন্দুতে ছেদ করেছে ( ধরি ) ।
| ∠DHF + ∠DHG = 180° |
| বা, ∠DHG = 180° – ∠DHF |
| বা, ∠DHG = 180° – 95° |
| বা, ∠DHG = 85° |
EF ছেদকের ডান পাশের অনুরূপ কোণ যথা-
∠BGE ও ∠DHG পরস্পর সমান নয় ।
অতএব,
| AB ও CD সরলরেখা দুটি সমান্তরাল নয় । |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
6. চিত্রে AB||CD এবং ∠EGB=50°; ∠AGE, ∠AGH, ∠BGH, ∠GHC, ∠GHD, ∠CHF এবং ∠DHF -এর পরিমাপ লিখি।
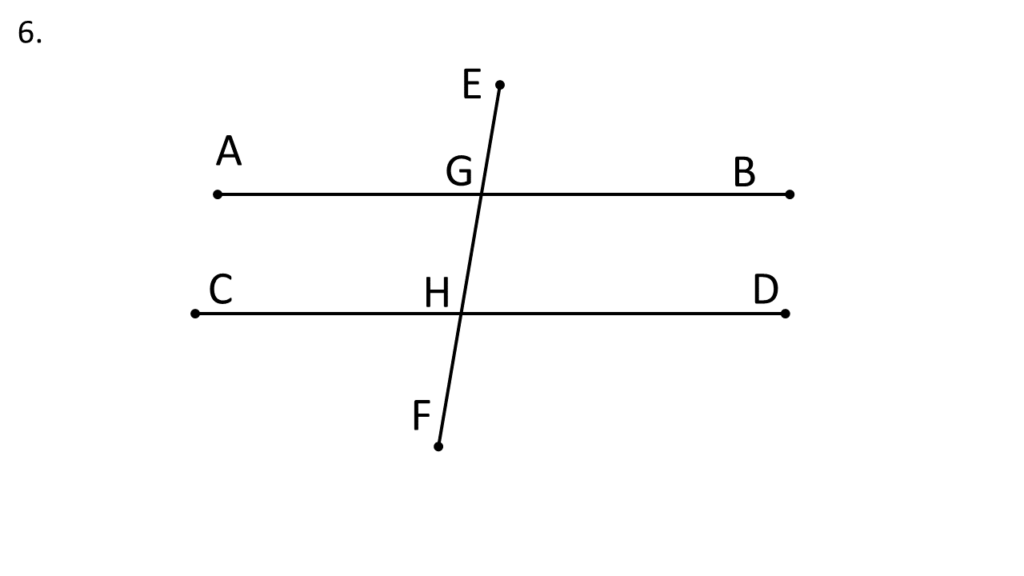
সমাধানঃ-
ছবি থেকে আমরা পাই,
চার জোড়া অনুরূপ কোণ যথা-
| ∠BGE =অনুরূপ ∠DHG—-( i ) |
| ∠BGH = অনুরূপ ∠DHF—–( ii ) |
| ∠CHG =অনুরূপ ∠AGE—–( iii ) |
| ∠AGH =অনুরূপ ∠CHF—–( iv ) |
দুই জোড়া একান্তর কোণ যথা-
| ∠AGH = একান্তর ∠GHD—-( v ) |
| ∠BGH = একান্তর ∠CHG—–( vi ) |
ছেদকের একপাশের অন্তঃস্থ কোণ যথা-
| ছেদকের বাম পাশে | ছেদকের ডান পাশে |
|---|---|
| ∠AGH + ∠CHG = 180°—( vii ) | ∠BGH + ∠GHD = 180°—-( viii ) |
দেওয়া আছে, ∠BGE = 50°
অতএব,
| ( i ) নম্বর থেকে পাই- | ∠BGE =অনুরূপ ∠DHG বা, ∠DHG= 50° |
| আবার, ( v ) নম্বর থেকে পাই- | ∠AGH = একান্তর ∠GHD বা, ∠AGH = 50° |
| আবার, ( iv ) এবং ( vii ) নম্বর থেকে পাই- | ∠AGH =অনুরূপ ∠CHF বা, ∠CHF= 50° এবং ∠AGH + ∠CHG= 180° বা, ∠CHG = 180° – ∠AGH বা, ∠CHG = 180° – 50° বা, ∠CHG = 130° |
| আবার, ( vi ) নম্বর থেকে পাই- | ∠BGH = একান্তর ∠CHG বা, ∠BGH = 130° |
| আবার, ( iii ) নম্বর থেকে পাই- | ∠CHG =অনুরূপ ∠AGE বা, ∠AGE = 130° |
| আবার, ( ii ) নম্বর থেকে পাই- | ∠BGH = অনুরূপ ∠DHF অতএব, ∠DHF = 130° |
| ∠AGE = 130° ∠AGH = 50° ∠BGH = 130° ∠CHG = 130° ∠DHG= 50° ∠CHF= 50° ∠DHF = 130° |
7. চিত্রে AB||CD; ∠PQR -এর পরিমাপ লিখি ।
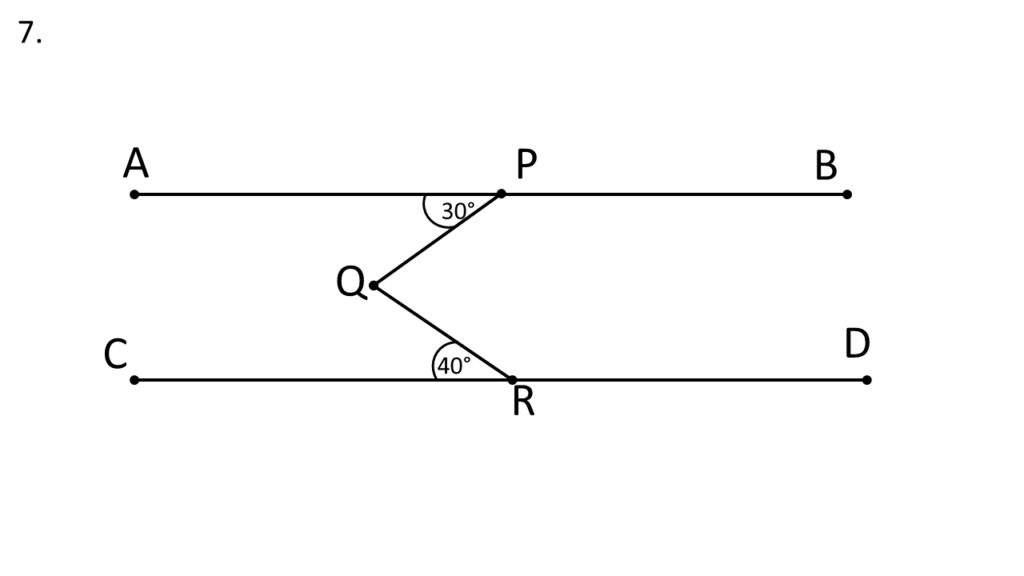
সমাধানঃ-
PQ সরলরেখাকে বর্ধিত করলাম যা CD সরলরেখা কে S( ধরি ) বিন্দুতে ছেদ করেছে ।
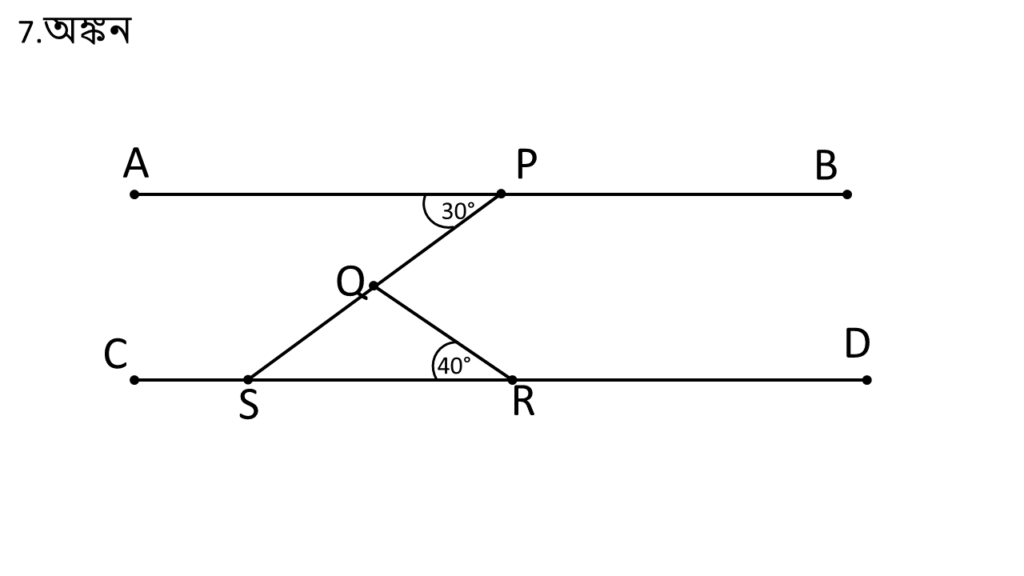
অতএব,
| ∠BPS = একান্তর ∠PSR |
| অতএব, |
| ∠PSR = 30° |
| আবার, দেওয়া আছে ∠QRS = 40° |
| অতএব, |
| ত্রিভুজ ▲QRS থেকে পাই, |
| ∠PSR + ∠QRS + ∠SQR = 180° ——( i ) |
| আবার, PS সরলরেখা থেকে পাই, |
| ∠PQR + ∠SQR = 180° —- ( ii ) |
| ( i ) ও ( ii ) সমান করে পাই, |
| ∠PQR + ∠SQR = ∠PSR +∠QRS +∠SQR |
| বা, ∠PQR = ∠PSR +∠QRS |
| বা, ∠PQR = 30° + 40° |
| বা, ∠PQR = 70° |
| ∠PQR = 70° |
8. চিত্রে PQ||RS, ∠BPQ=40°, ∠BPR=155° এবং ∠CRS=70°; ▲APR -এর কোণগুলির পরিমাপ লিখি।
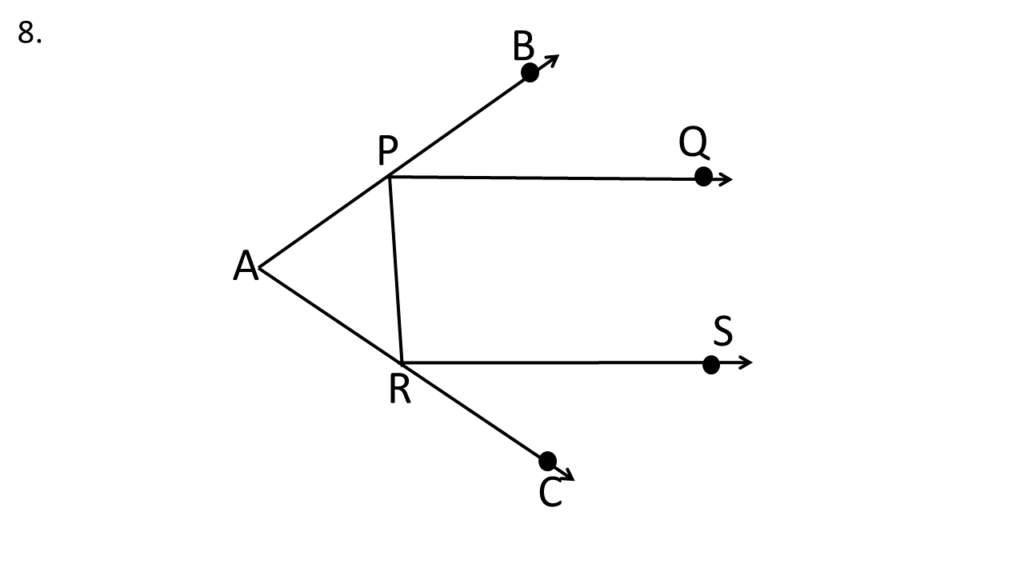
সমাধানঃ-
দেওয়া আছে,
| PQ||RS |
| ∠BPQ = 40° |
| ∠BPR = 155° |
| ∠CRS = 70° |
আবার,
| ∠BPR = ∠BPQ + ∠RPQ |
| বা, ∠RPQ = ∠BPR – ∠BPQ |
| বা, ∠RPQ = 155° – 40° |
| বা, ∠RPQ = 115° |
আবার, AB সরলরেখা থেকে পাই,
| ∠BPR + ∠APR = 180° |
| বা, ∠APR = 180° – ∠BPR |
| বা, ∠APR = 180° – 155° |
| বা, ∠APR = 25° |
আবার, PQ||RS এবং PR ছেদক।
অতএব,
| ∠RPQ + ∠PRS = 180° |
| বা, ∠PRS = 180° – ∠RPQ |
| বা, ∠PRS = 180° – 115° |
| বা, ∠PRS = 65° |
AC সরলরেখা থেকে পাই,
| ∠CRS +∠PRS +∠ARP =180° |
| বা, ∠ARP = 180° – ∠PRS -∠CRS |
| বা, ∠ARP = 180° – 65° -70° |
| বা, ∠ARP = 45° |
▲APR থেকে পাই,
| ∠APR + ∠ARP +∠PAR = 180° |
| বা, ∠PAR = 180° -∠APR – ∠ARP |
| বা, ∠PAR = 180° – 25° -45° |
| বা, ∠PAR = 110° |
▲APR এর
| ∠APR=25° ∠ARP=45° ∠PAR=110° |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
9. AB ও CD দুটি সমান্তরাল সরলরেখার ভিতর O যেকোনো একটি বিন্দু। OP ও OQ যথাক্রমে AB ও CD সরলরেখার উপর লম্ব । প্রমাণ করি যে P, O, Q বিন্দু তিনটি সমরেখ।
সমাধানঃ-
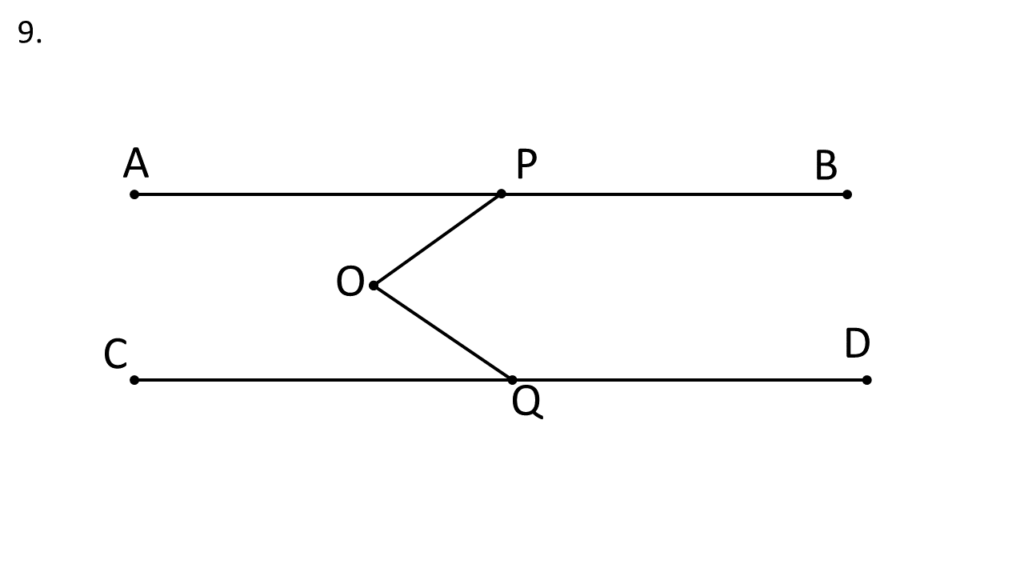
প্রদত্তঃ
AB ও CD দুটি সমান্তরাল সরলরেখার ভিতর O যেকোনো একটি বিন্দু। OP ও OQ যথাক্রমে AB ও CD সরলরেখার উপর লম্ব।
প্রামান্যঃ
P, O, Q বিন্দু তিনটি সমরেখ।
অতএব, ∠POQ=180°
অঙ্কনঃ
PO সরলরেখাকে বর্ধিত করলাম যা CD সরলরেখা কে R বিন্দুতে ছেদ করেছে।
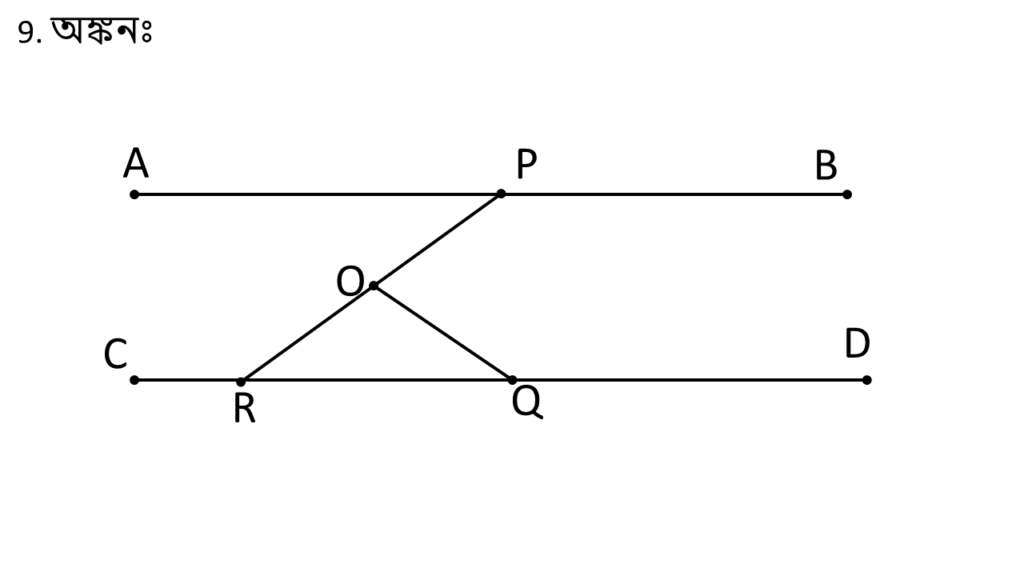
প্রমানঃ
| ∠RPB = একান্তর ∠CRP |
| অতএব, ∠CRP=90° |
| আবার, CD সরলরেখা ত্রহেকে পাই, |
| ∠CRP + ∠PRQ=180° |
| বা,∠PRQ = 180°-∠CRP |
| বা, ∠PRQ = 180° – 90° |
| বা, ∠PRQ = 90° |
▲ROQ থেকে পাই,
∠ROQ + ∠ORQ + ∠OQR = 180°—–( i )
আবার, PR সরলরেখা থেকে পাই,
∠POQ + ∠ROQ = 180°—( ii )
( i ) ও ( ii ) সমান করে পাই,
| ∠POQ + ∠ROQ = ∠ROQ + ∠ORQ + ∠OQR |
| বা, ∠POQ = ∠ROQ + ∠ORQ + ∠OQR – ∠ROQ |
| বা, ∠POQ = ∠ROQ + ∠ORQ |
| বা, ∠POQ = 90° + 90° |
| বা, ∠POQ =180° |
অতএব প্রমাণিত যে P, O, Q বিন্দু তিনটি সমরেখ।
10. দুটি কোণের প্রতিজোড়া বাহু পরস্পর সমান্তরাল। প্রমাণ করি যে, কোণদুটি সমান অথবা পরস্পর সম্পূরক।
সমাধানঃ-
প্রথম ধাপঃ
∠ABC ও ∠DEF দুটি কোণ ।
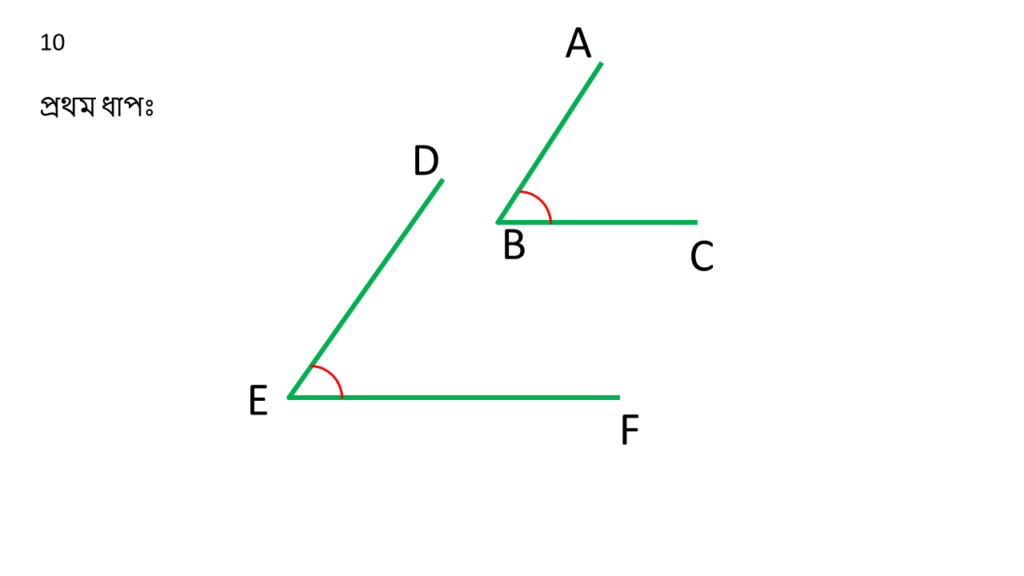
প্রদত্তঃ
| AB||ED |
| BC||EF |
প্রামান্যঃ
প্রমাণ করতে হবে,
| ∠ABC = ∠DEF |
অঙ্কনঃ
( i ) ∠ABC এর AB বাহুকে বর্ধিত করলাম যা ∠DEF এর EF বাহুকে G বিন্দুতে ছেদ করেছে।
( ii ) ∠ABC এর BC বাহুকে বর্ধিত করলাম যা ∠DEF এর ED বাহুকে H বিন্দুতে ছেদ করেছে।
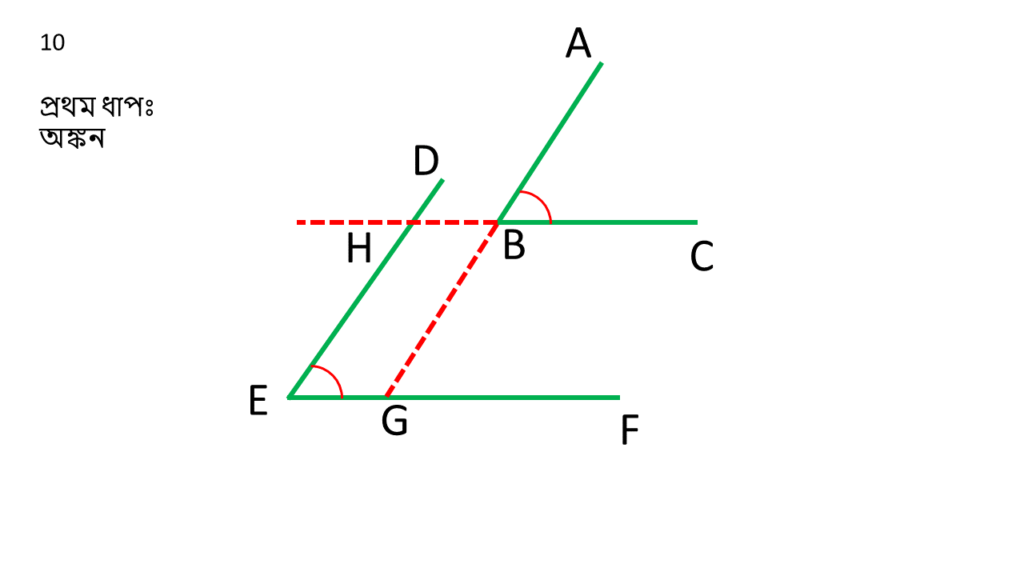
প্রমানঃ
| AG||DE এবং BH ছেদক |
| অতএব, |
| ∠ABC = অনুরূপ ∠DHB |
| আবার, |
| CH||EF এবং DE ছেদক |
| অতএব, |
| ∠DHB = অনুরূপ ∠DEF |
সুতরাং,
∠ABC = ∠DEF প্রমাণিত ।
দ্বিতীয় ধাপঃ
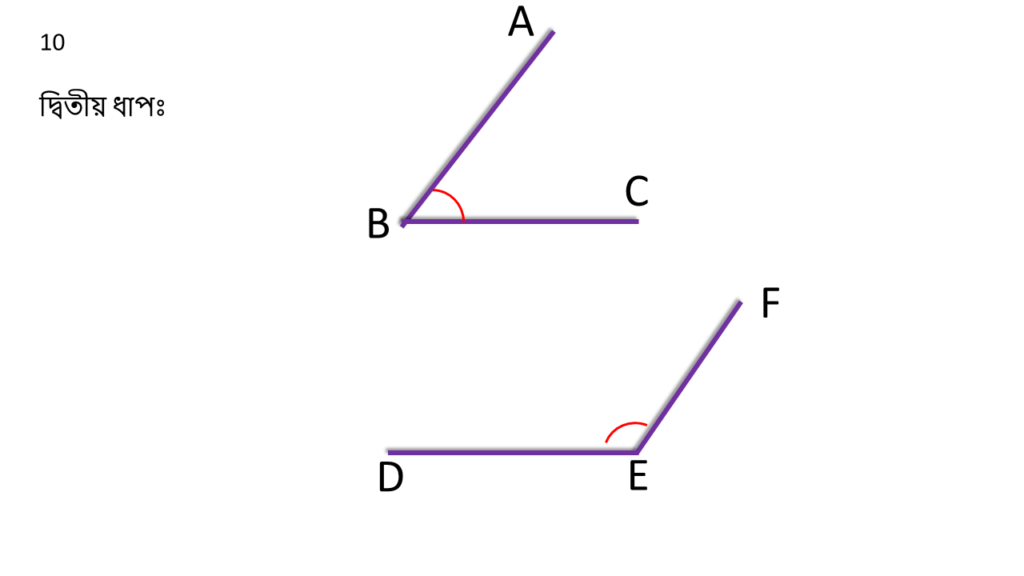
প্রামান্যঃ
| ∠ABC + ∠DEF = 180° |
অঙ্কনঃ
∠ABC এর AB বাহুকে বর্ধিত করলাম যা ∠DEF এর বর্ধিত বাহু EF কে G বিন্দুতে ছেদ করেছে।
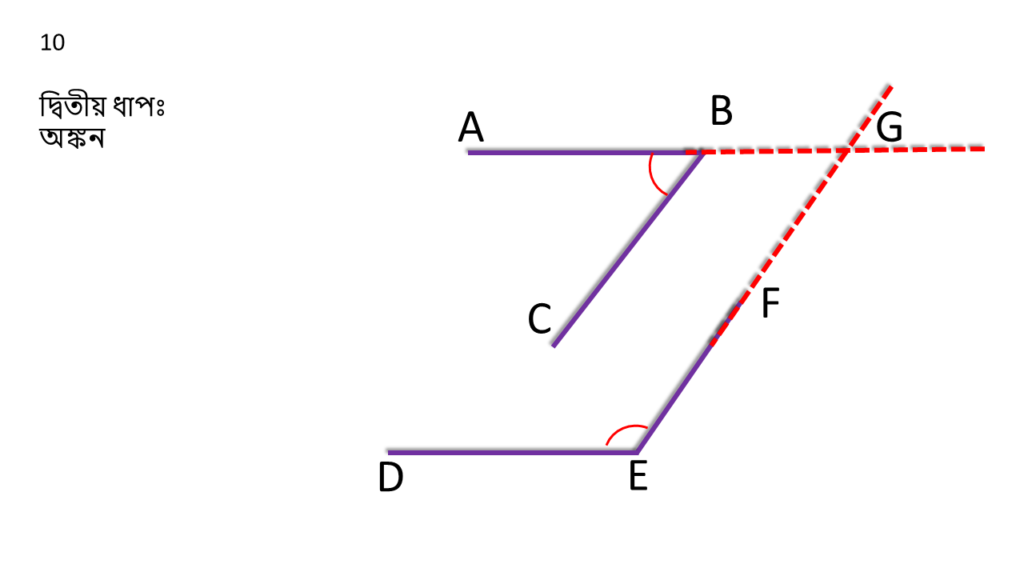
প্রমানঃ
| CB||EG এবং BG ছেদক |
| অতএব, |
| ∠ABC = অনুরূপ কোণ ∠BGE |
| আবার, |
| AG||DE এবং EG ছেদক |
| অতএব, |
| EG ছেদকের একই পাশে অবস্থিত কোণজোড়ার সমষ্টি হবে 180° |
| সুতরাং, |
| ∠AGE + ∠DEG = 180° |
| বা, ∠ABC + ∠DEF = 180° |
অতএব প্রমাণিত যে, কোণদুটি পরস্পর সম্পূরক।
প্রমাণিত যে,দুটি কোণের প্রতিজোড়া বাহু পরস্পর সমান্তরাল এবং কোণদুটি সমান অথবা পরস্পর সম্পূরক।
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
11. ABCD সামন্তরিকের AC কর্ণ ∠BAD -কে সমদ্বিখণ্ডিত করে। প্রমাণ করি যে AC কর্ণ ∠BCD -কেও সমদ্বিখণ্ডিত করে।
সমাধানঃ-
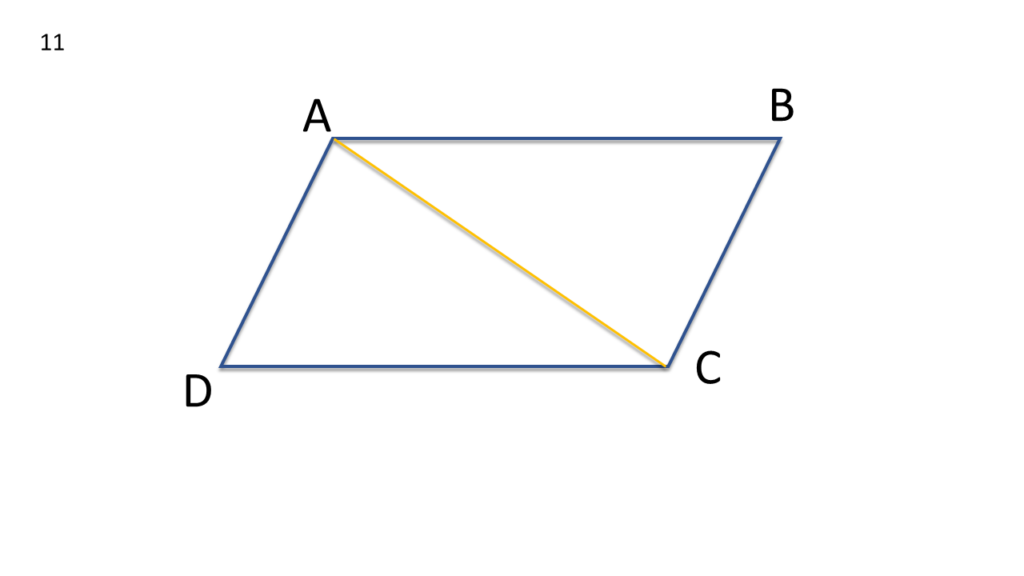
ABCD সামন্তরিকের AC কর্ণ ∠BAD -কে সমদ্বিখণ্ডিত করে।
প্রদত্তঃ
| AB||CD |
| AD||BC |
| AC কর্ণ |
| ∠DAC = ∠BAC —- ( i ) |
প্রামান্যঃ
AC কর্ণ ∠BCD কে সমদ্বিখণ্ডিত করে।
অর্থাৎ ∠DCA = ∠BCA
প্রমানঃ
| AB||CD এবং AC একটি ছেদক |
| অতএব, |
| ∠DAC = একান্তর ∠BCA —- ( ii ) |
| এবং |
| ∠BAC = একান্তর ∠DCA —- ( iii ) |
( i ) ও ( ii ) থেকে পাই,
∠BCA = ∠BAC
আবার ( iii ) থেকে পাই,
∠DCA = ∠BAC
অতএব,
∠BCA = ∠DCA = ∠BAC
প্রমাণিত যে AC কর্ণ ∠BCD -কেও সমদ্বিখণ্ডিত করে।
12. প্রমাণ করি যে, সামন্তরিকের একটি কোণ সমকোণ হলে, প্রতিটি কোণই সমকোণ ।
সমাধানঃ-
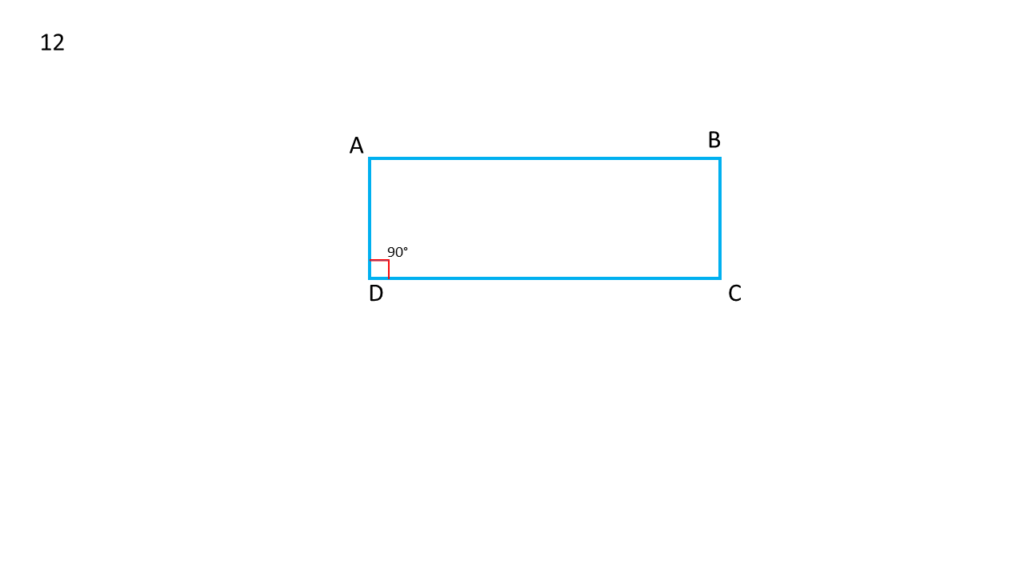
ABCD একটি সামন্তরিক।
প্রদত্তঃ
| AB||CD |
| AD||BC |
| একটি কোণ ∠ADC=90° |
প্রামান্যঃ
∠DAB, ∠ABC, ∠BCD প্রতিটি কোণ =90°.
প্রমানঃ
AB||CD এবং AD হলো একটি ছেদক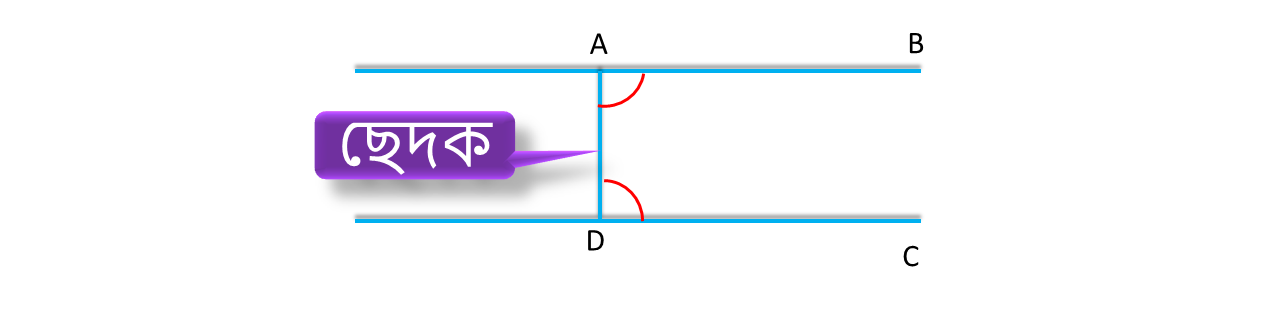 |
| সুতরাং, ছেদকের একই পার্শ্বে অবস্থিত অন্তঃস্থ কোণ এর সমষ্টি হবে 180° |
| অতএব, |
| ∠ADC +∠DAB = 180° |
| বা, ∠DAB = 180° – ∠ADC |
| বা, ∠DAB = 180° – 90° |
| বা, ∠DAB = 90° |
আবার,
AD||BC এবং DC হলো ছেদক ।
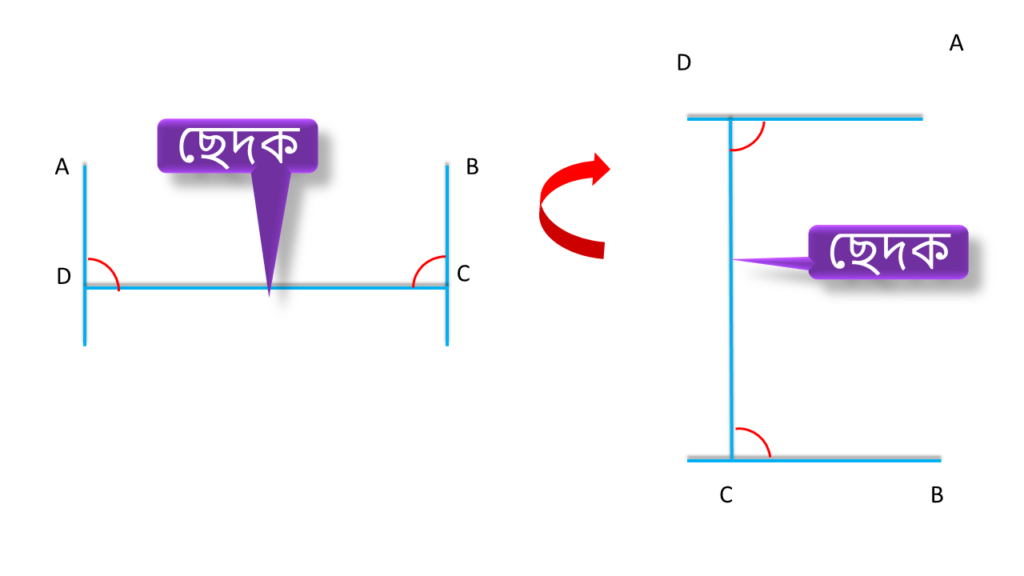
এক্ষেত্রে একইরকম ভাবে ছেদকের একই পাশে অবস্থিত কোণজোড়া যথা-
∠ADC ও ∠BCD থেকে পাই,
∠BCD=90°
AD||BC এবং AB কে ছেদক ধরে একইরকম ভাবে আমরা পাবো,
∠ABC = 90°
অতএব প্রমাণিত ∠DAB, ∠ABC, ∠BCD প্রতিটি কোণ =90°.
এই কষে দেখি 8 Class 8|Koshe Dekhi 8 Class 8 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 8 Class 8 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 8 Class 8 তারপর  |
| জ্যামিতিক এই অধ্যায় টি অনেকে মনে করে খুবই কঠিন একটা বিষয় ! উপপাদ্য বোঝা, তা প্রমাণ করা এবং তা থেকে প্রয়োগ করা । কিন্তু তোমরা যদি সঠিক পদ্ধতি মেনে সমান্তরাল সরলরেখা ও ছেদকের ধর্ম কষে দেখি 8তে যে সমস্ত অংক গুলি আছে সেগুলি করো তাহলে কোথাও বুঝতে অসুবিধে হবেনা । সেজন্যে তোমাদের বলবো তোমরা উপপাদ্য করার , কিভাবে উপপাদ্য লিখবে তার সঠিক পদ্ধতিটি নিচের লিংক থেকে জানো এবং তারপর কষে দেখি এর অংক গুলি করলে নিশ্চয় কিছু পার্থক্য বুঝতে পারবে । দুটি সমান্তরাল সরলরেখা ও একটি ছেদকের ফলে যে সমস্ত কোণ উৎপন্ন হয় এবং দুটি সরলরেখা ও একটি ছেদকের মধ্যে কোণ কোণ বৈশিষ্ট্যের জন্যে সরলরেখা দুটি সমান্তরাল হবে তা তোমাদের সঠিক ভাবে জানা প্রয়োজন।তার জন্যে তোমরা নীচে দেওয়া লিংক থেকে সমান্তরাল সরলরেখা ও ছেদকের সমস্ত ধর্ম গুলি জেনে নেবে( অবশ্যই )- |
| গনিতপ্রভা অষ্টম শ্রেণীর সমস্ত অধ্যায়ের সমাধান- | |
|---|---|
| অধ্যায় | সমাধান |
| 2. পাই চিত্র | কষে দেখি 2 |
| 3. মূলদ সংখ্যার ধারণা | অধ্যায়ের সারাংশ |
| কষে দেখি 3 | |
| 4. বীজগাণিতিক সংখ্যামালার গুণ ও ভাগ | অধ্যায়ের সারাংশ |
| কষে দেখি 4.1 | |
| কষে দেখি 4.2 | |
| 5. ঘনফল নির্ণয় | অধ্যায়ের সারাংশ |
| কষে দেখি 5.1 | |
| কষে দেখি 5.2 | |
| কষে দেখি 5.3 | |
| 6. পূরক কোণ, সম্পূরক কোণ ও সন্নিহিত কোণ | অধ্যায়ের সারাংশ |
| কষে দেখি 6 | |
| 7. বিপ্রতীপ কোণের ধারণা | অধ্যায়ের সারাংশ |
| কষে দেখি 7.1 | |
8. সমান্তরাল সরলরেখা ও ছেদকের ধর্ম | অধ্যায়ের সারাংশ |
| কষে দেখি 8 | |
9. ত্রিভুজের দুটি বাহু ও তাদের বিপরীত কোণের সম্পর্ক | অধ্যায়ের সারাংশ |
| কষে দেখি 9 | |
| 10. ত্রৈরাশিক | কষে দেখি 10.1 |
| কষে দেখি 10.2 | |
| 11. শতকরা | কষে দেখি 11 |
| 12. মিশ্রণ | কষে দেখি 12 |
13. বীজগাণিতিক সংখ্যামালার উৎপাদকে বিশ্লেষণ | কষে দেখি 13.1 |
| কষে দেখি 13.2 | |
14. বীজগাণিতিক সংখ্যামালার গ.সা.গু ও ল.সা.গু | কষে দেখি 14 |
15. বীজগাণিতিক সংখ্যামালার সরলীকরণ | কষে দেখি 15 |
16. ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই | কষে দেখি 16.1 |
| কষে দেখি 16.2 | |
17. সময় ও কার্য | কষে দেখি 17.1 |
| কষে দেখি 17.2 | |
18. লেখচিত্র | কষে দেখি 18 |
19. সমীকরণ গঠন ও সমাধান | কষে দেখি 19 |
| 20. জ্যামিতিক প্রমাণ | কষে দেখি 20.1 |
| কষে দেখি 20.2 | |
| কষে দেখি 20.3 | |

এখানে তোমরা তোমাদের অষ্টম শ্রেণীতে কি কি পড়ানো হয়, মানে তোমাদের অষ্টম শ্রেণীর সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

