feature 12

কষে দেখি 3.2 Class 9 । লেখচিত্র কষে দেখি 3.2 | Koshe Dekhi 3.2 Class 9 WBBSE.

by

শ্রেণী-নবম|Class 9 ; অধ্যায় -লেখচিত্র ; কষে দেখি – 3.2

telegram logo 2

কষে দেখি 3.2 Class 9 এর সুচিপত্রঃ-

Table of Contents

কষে দেখি 3.2 Class 9 এর অংকের সমাধান গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ

কষে দেখি 3.2|Koshe Dekhi 3.2 পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদ | WBBSE বোর্ডের অন্তর্গত তোমাদের নবম শ্রেণী|Class 9 এর একটি অধ্যায় লেখচিত্র এর দ্বিতীয় অনুশীলনী। লেখচিত্র এর আগের কষে দেখি তে আমরা লেখচিত্র সম্পর্কে সাধারণ ধারণা পড়েছি। এবার এই কষে দেখি 3.2|Koshe Dekhi 3.2 তে যে অংক গুলি আমরা করবো তা হল- প্রদত্ত অবস্থা থেকে একটি সমীকরণ গঠন এবং সেই সমীকরণ কে লেখচিত্র এর মাধ্যমে প্রকাশ করে তার সমাধান কি করে করবো!

এই Class 9 এর কষে দেখি 3.2|Koshe Dekhi 3.2 এর অংক গুলি সমাধানের জন্যে আমাদের যেগুলো জানতে হবে তা নিম্নে আলোচনা করা হল-

দুই চল বিশিষ্ট একঘাত বা রৈখিক সমীকরণ কাকে বলে?

এখানে প্রশ্নের মধ্যেই আমরা দেখতে পাচ্ছি দুই চল বিশিষ্ট মানে দুটি চলরাশি থাকবে আর একঘাত বা রৈখিক বলতে চলরাশির ঘাত/নিধান 1 হবে এবং এই সমীকরণ কে লেখচিত্র এর মাধ্যমে প্রকাশ করলে একটি সরলরেখা পাওয়া যাবে। এই জন্যে এই সমীকরণ কে রৈখিক বলা হয়েছে।
দুইচল বিশিষ্ট রৈখিক সমীকরণের সাধারণ রূপ হল-
ax + by + c = 0
(যেখানে – a, b, c বাস্তব সংখ্যা এবং x ও y চলরাশি ।

লেখচিত্র হলো একটি জ্যামিতিক চিত্র যার বীজগাণিতিক প্রকাশ হলো প্রদত্ত সমীকরণটি। অর্থাৎ লেখচিত্র হলো সমীকরণ দ্বারা প্রকাশিত চলরাশির মধ্যেকার সম্পর্কের চিত্ররূপ । এক বা দুই চলবিশিষ্ট কোনো সমীকরণের লেখচিত্র (দ্বিমাত্রিক) একটি সরলরেখা হবে। রৈখিক সমীকরণের লেখচিত্র সর্বদা একটি সমতলে থাকে। এই সমতলটিকে কার্তেজীয় তল বলে।

একটি এক বা দুই চলবিশিষ্ট একঘাত বা রৈখিক সমীকরণের লেখচিত্র অঙ্কনে কী কী করতে হবে—

(i) প্রথমে এক বা দুই চলবিশিষ্ট একঘাত সমীকরণের কয়েকটি সমাধান বিন্দু (অন্তত পক্ষে তিনটি) বের করতে হবে।

(ii) তারপর ছক কাগজের উভয়অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের কটি বাহু একক ধরে ঠিক করে বিন্দুগুলি স্থাপন করতে হবে এবং স্কেল দিয়ে তাদের যোগ করে যে সরলরেখা পাবো সেটিই প্রদত্ত এক বা দুই চল বিশিষ্ট একঘাত সমীকরণের লেখচিত্র।
[দুটি সমাধান বিন্দু যোগ করে সরলরেখা পাওয়া যায়। কিন্তু সতর্কতার জন্য তিনটি বিন্দু স্থাপন করে লেখচিত্র অঙ্কন করা হয়]

(iii) y -অক্ষ হলো x=0 সমীকরণের লেখচিত্র এবং y=0 সমীকরণের লেখচিত্র x-অক্ষ ।

(iv) y=b(ধ্রুবক) সমীকরণ টির লেখচিত্রটি x-অক্ষের সমান্তরাল এবং x=b সমীকরণটির লেখচিত্রটি y-অক্ষের সমান্তরাল।

আগামিতে এই কষে দেখি 3.2 Class 9 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?

আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে?
কষে দেখি 3.2 Class 9 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে-
কষে দেখি 3.2 Class 9
তারপর icon এই চিহ্ন দেখে Click করলে আবার তোমরা এখানে এসে যাবে।
Request For Search 15

কষে দেখি 3.2 Class 9 এর Youtube logo Youtube Video –

কষে দেখি 3.2

কষে দেখি 3.2|Koshe Dekhi 3.2

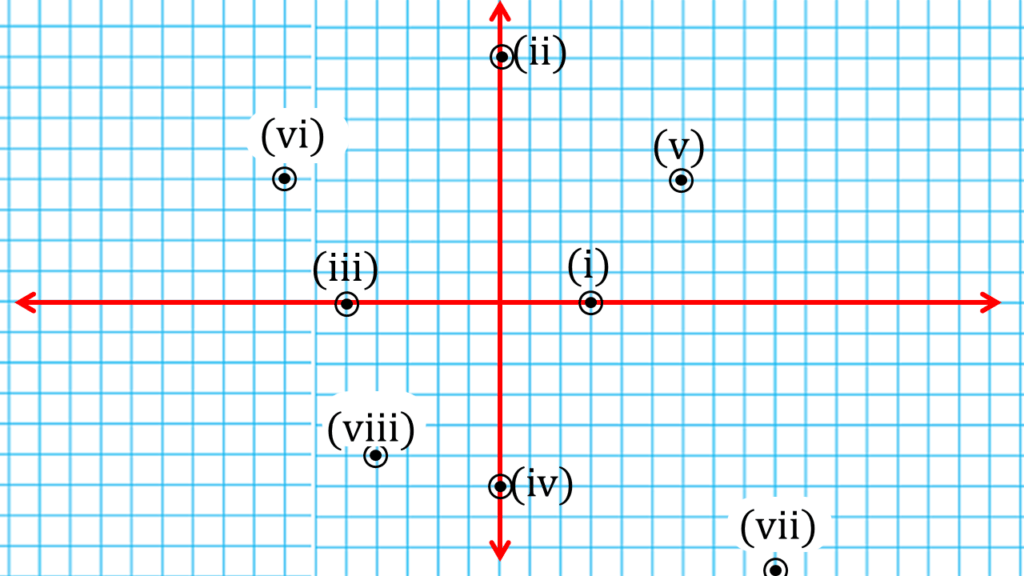
1. নিম্নলিখিত বিন্দুগুলি ছক কাগজে স্থাপন করি ও কোথায় (অক্ষের উপর অথবা কোন পাদে) অবস্থিত লিখি ।

(i) (3,0), (ii) (0,8), (iii) (-5,0), (iv) (0, -6), (v) (6,4), (vi) (-7, 4), (vii) (9,-9), (viii) (- 4,-5)

সমাধানঃ-

1 5
বিন্দুর স্থানাঙ্ক পাদ / অক্ষ
(i) (3 , 0)x-অক্ষ
(ii) (0 , 8)y-অক্ষ
(iii) (-5 , 0)x-অক্ষ
(iv) (0 , -6)y-অক্ষ
(v) (6 , 4)প্রথম
(vi) (-7 , 4)দ্বিতীয়
(vii) (9 , -9)চতুর্থ
(viii) (-4 , -5)তৃতীয়

2. ছক কাগজে XOX/ এবং YOY/ পরম্পর লম্ব অক্ষ টেনে যে কোনো 5 টি বিন্দু স্থাপন করি যারা তৃতীয় পাদে অবস্থিত।

সমাধানঃ-

(i) (-4 , -1)
(ii) (-1 , -1)
(iii) (-7 , -2)
(iv) (-10 , -4)
(v) (-4 , -5)

3. নীচের বক্তব্যগুলি রৈখিক সহসমীকরণ আকারে প্রকাশ করি :

(i) 3টি খাতা ও 2টি পেনের মোট দাম 55 টাকা এবং 4টি খাতা ও 3টি পেনের মোট দাম 75 টাকা।

সমাধানঃ-

ধরি একটি খাতার দাম x টাকা

এবং

একটি পেনের দাম y টাকা

বক্ত্যব্য রৈখিক সমীকরণ
3টি খাতা ও 2টি পেনের মোট দাম 55 টাকা3x + 2y = 55
4টি খাতা ও 3টি পেনের মোট দাম 754x + 3y = 75

(ii) দুটি সংখ্যার যোগফল 80 এবং ওই সংখ্যা দুটির বিয়োগফলের 3 গুণ বড়ো সংখ্যাটির থেকে 20 বেশি।

সমাধানঃ-

ধরি x ও y দুটি সংখ্যা যেখানে x>y ।

বক্ত্যব্য রৈখিক সমীকরণ
দুটি সংখ্যার যোগফল 80x + y = 80
সংখ্যা দুটির বিয়োগফলের 3 গুণ বড়ো সংখ্যাটির থেকে 203(x-y) = x + 20
বা, 3(x-y) – x = 20

(iii) কোনো ভগ্নাংশের লব ও হরের প্রত্যেকটির সঙ্গে 2 যোগ করলে ভগ্নাংশটির মান হয় \(\frac{7}{9}\) এবং ভগ্নাংশটির লব ও হরের প্রত্যেকটি থেকে 3 বিয়োগ করলে ভগ্নাংশটির মান হয় \(\frac{1}{2}\)

সমাধানঃ-

ধরি ভগ্নাংশটির লব =x এবং হর = y

বক্ত্যব্য রৈখিক সমীকরণ
লব ও হরের প্রত্যেকটির সঙ্গে 2 যোগ করলে ভগ্নাংশটির মান হয় \(\frac{7}{9}\)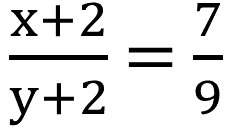3.iii .i
ভগ্নাংশটির লব ও হরের প্রত্যেকটি থেকে 3 বিয়োগ করলে ভগ্নাংশটির মান হয় \(\frac{1}{2}\)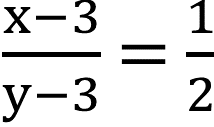3.iii .2

(iv) দুই অঙ্কবিশিষ্ট কোনো সংখ্যার দশকের অঙ্কটি এককের অঙ্কের দ্বিগুণ। অংকদ্বয়কে উলটে লিখলে যে সংখ্যাটি পাওয়া যায় তা মূল সংখ্যাটি অপেক্ষা 27 কম।

সমাধানঃ-

ধরি সংখ্যাটির এককের অংক = x

এবং

দশকের অংক = y

অতএব সংখ্যাটি হবে 10y + x

বক্ত্যব্য রৈখিক সমীকরণ
সংখ্যার দশকের অঙ্কটি এককের অঙ্কের দ্বিগুণy = 2x
অংকদ্বয়কে উলটে লিখলে যে সংখ্যাটি পাওয়া যায় তা মূল সংখ্যাটি অপেক্ষা 27 কম 10x + y = 10y + x – 27
বা, (10y+x) -(10x+y) = 27

4. নীচের বক্তব্যগুলি দুইচলবিশিষ্ট একঘাত সমীকরণ আকারে প্রকাশ করি ও সমীকরণগুলির লেখচিত্র অঙ্কন করি।

(i) বর্তমানে সুজাতার পিতার বয়স সুজাতার বয়স অপেক্ষা 26 বছর বেশি।

[ধরি, সুজাতার পিতার বয়স x বছর এবং সুজাতার বয়স y বছর]

সমাধানঃ-

ধরি, সুজাতার পিতার বয়স x বছর এবং সুজাতার বয়স y বছর

বক্ত্যব্য রৈখিক সমীকরণ
বর্তমানে সুজাতার পিতার বয়স সুজাতার বয়স অপেক্ষা 26 বছর বেশিx = y + 26
বা, x – y = 26
x – y = 26
x = y = x – 26স্থানাঙ্ক
16-10(i) (16, -10)
10-16(ii) (10, -16)
8-18(iii) (8, -18)

[ এখানে লেখচিত্রে যথেষ্ট ঘর না থাকায় আমরা একটি ঘরকে 2 একক ধরবো ]

4.i 5

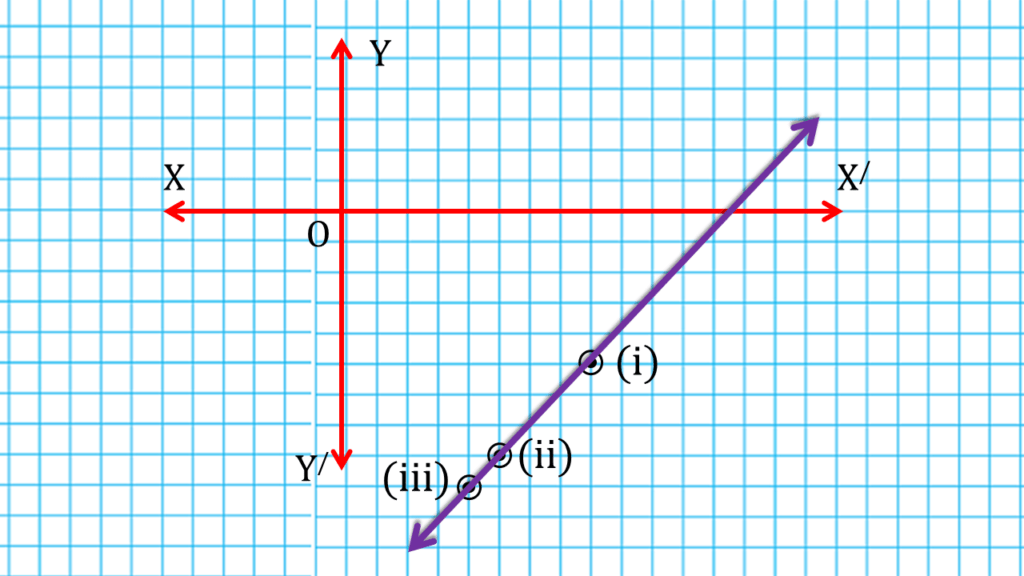
(ii) দুটি সংখ্যার সমষ্টি 15

সমাধানঃ-

ধরি সংখ্যা দুটি x ও y ।

বক্ত্যব্য রৈখিক সমীকরণ
দুটি সংখ্যার সমষ্টি 15x + y = 15
x + y = 15
x = y = 15-xস্থানাঙ্ক
69(i) (6, 9)
87(ii) (8, 7)
105(iii) (10, 5)
4.ii 3

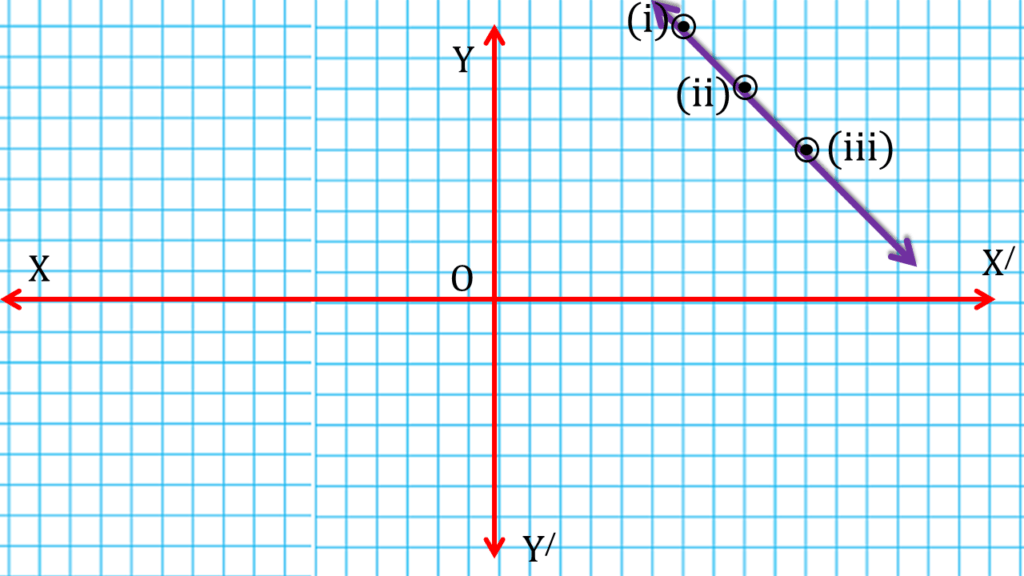
(iii) কোনো ভগ্নাংশের লব ও হরের প্রত্যেকটির সঙ্গে 2 যোগ করলে ভগ্নাংশটির মান \(\frac{7}{9}\) হয়।

সমাধানঃ-

ধরি, ভগ্নাংশটির লব= x এবং হর = y

বক্ত্যব্য রৈখিক সমীকরণ
ভগ্নাংশের লব ও হরের প্রত্যেকটির সঙ্গে 2 যোগ করলে ভগ্নাংশটির মান \(\frac{7}{9}\) হয়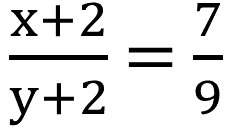3.iii .i
বা, 9(x+2) = 7(y+2)
বা, 9x + 18 = 7y + 14
বা, 9x – 7y = -4
বা, y = \(\frac{9x +4}{7}\)
9x – 7y = -4
x = y = \(\frac{9x +4}{7}\)স্থানাঙ্ক
57(i) (5,7)
-2-2(ii) (-2,-2)
-9-11(iii) (-9,-11)
4.iii 4

(iv) আমাদের আয়তাকার উঠানের পরিসীমা 80 মিটার।

সমাধানঃ-

ধরি উঠানের দৈর্ঘ্য = x মিটার এবং প্রস্থ = y মিটার

বক্ত্যব্য রৈখিক সমীকরণ
আয়তাকার উঠানের পরিসীমা 80 মিটারx + y = 80
x + y = 80
x = y = 80 – xস্থানাঙ্ক
4040(i) (40,40)
6020(ii) (60,20)
3050(iii) (30,50)

[ এখানে লেখচিত্রে যথেষ্ট ঘর না থাকায় আমরা একটি ঘরকে 10 একক ধরবো ]

4.iv 4

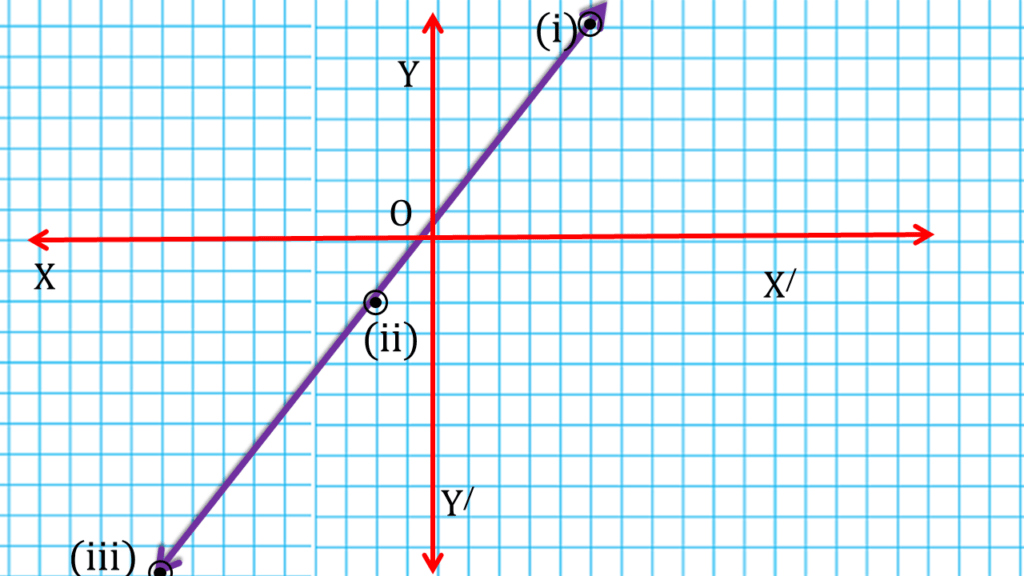
(v) দুটি সংখ্যার বড়োটির 5 গুণ ছোটোটির 8 গুণের সমান।

সমাধানঃ-

ধরি x ও y দুটি সংখ্যা যেখানে x>y

বক্ত্যব্য রৈখিক সমীকরণ
দুটি সংখ্যার বড়োটির 5 গুণ ছোটোটির 8 গুণের সমান5x = 8y
5x = 8y
x = y = \(\frac{5x}{8}\)স্থানাঙ্ক
00(i) (0,0)
85(ii) (8,5)
-8-5(iii) (-8,-5)
4.v 1

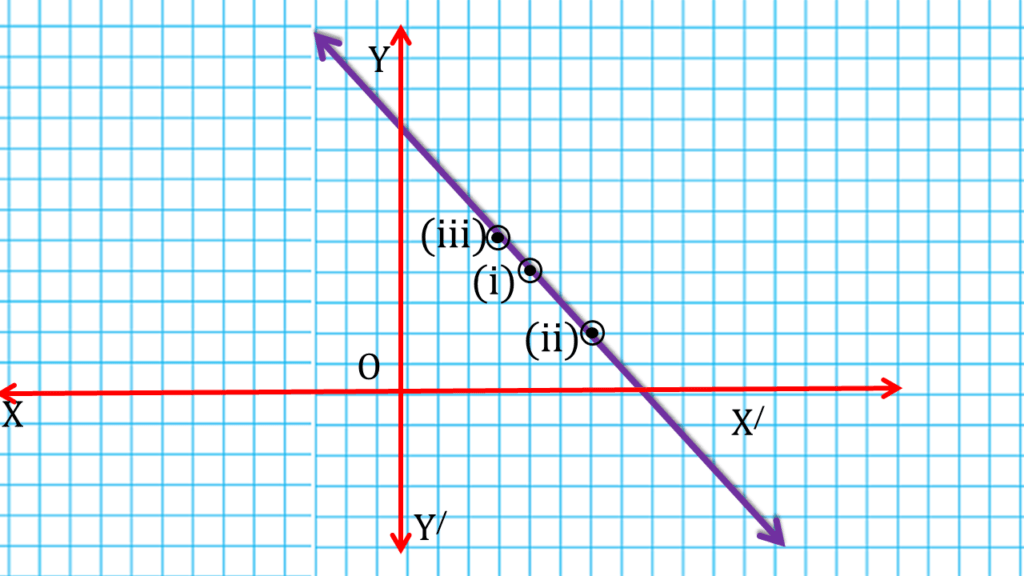
5. নীচের সমীকরণগুলির লেখচিত্র অঙ্কন করি।

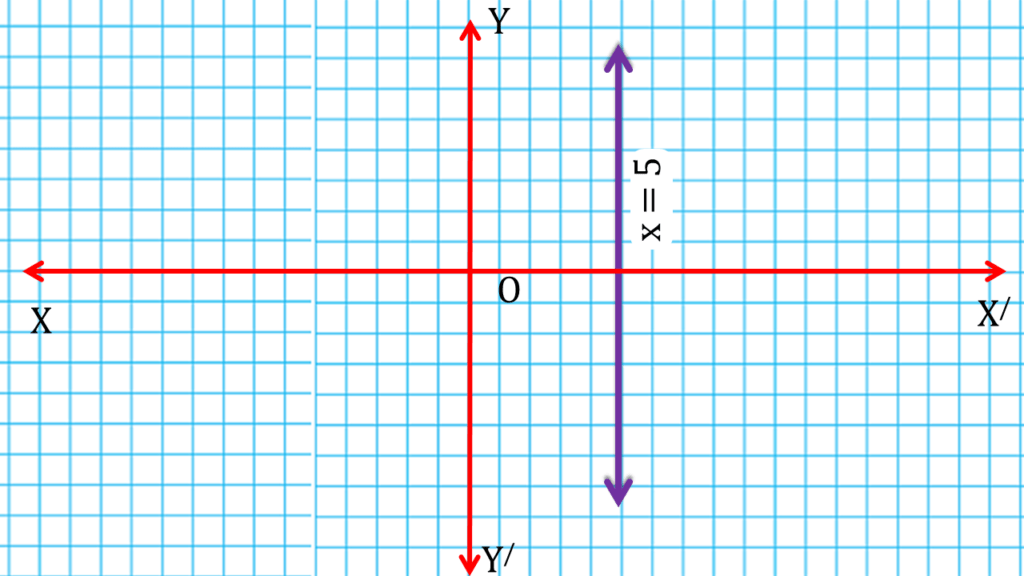
(i) x = 5

সমাধানঃ-

5.i 3

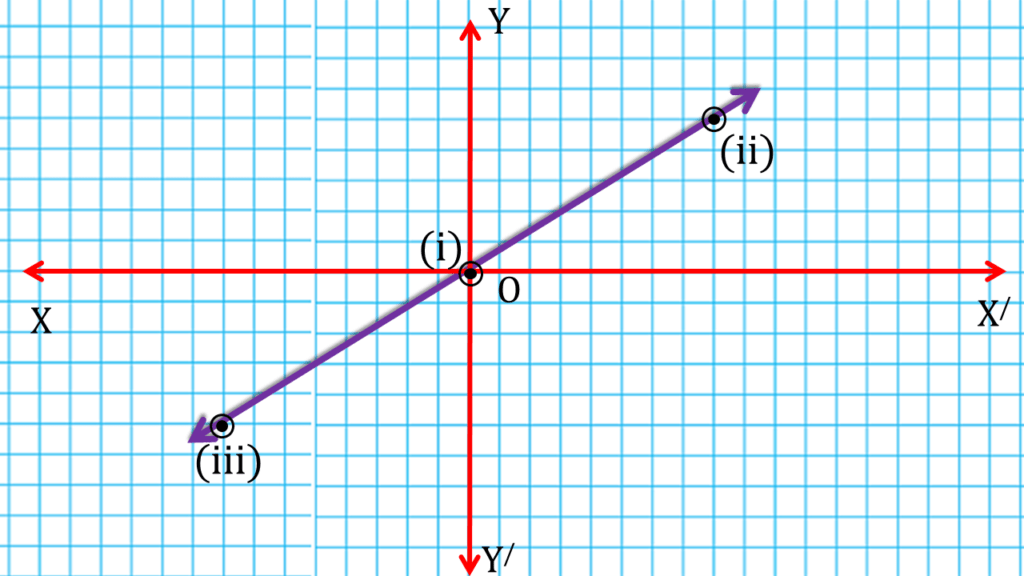
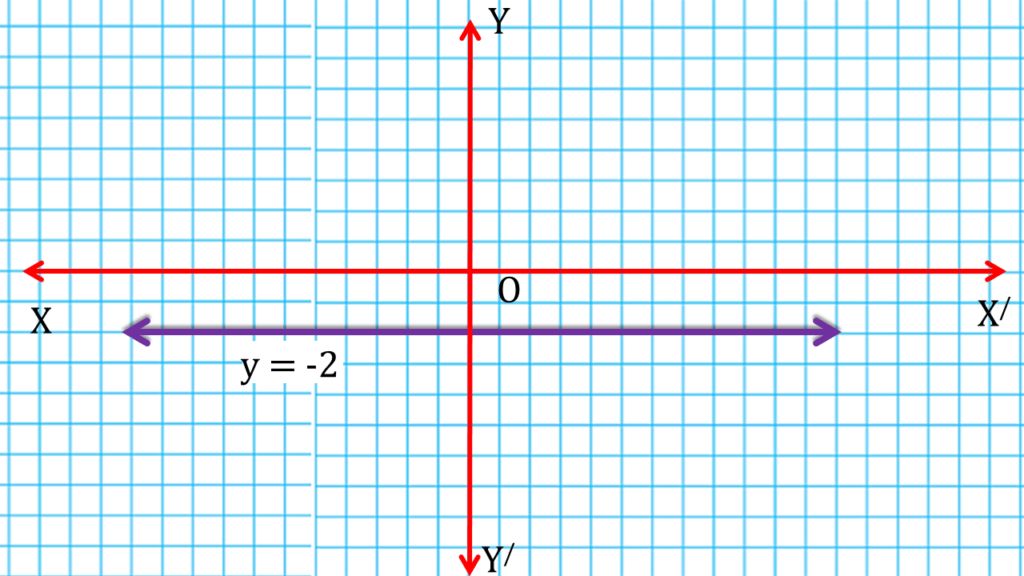
(ii) y + 2 = 0

সমাধানঃ-

y + 2 = 0

বা, y = -2

5.ii

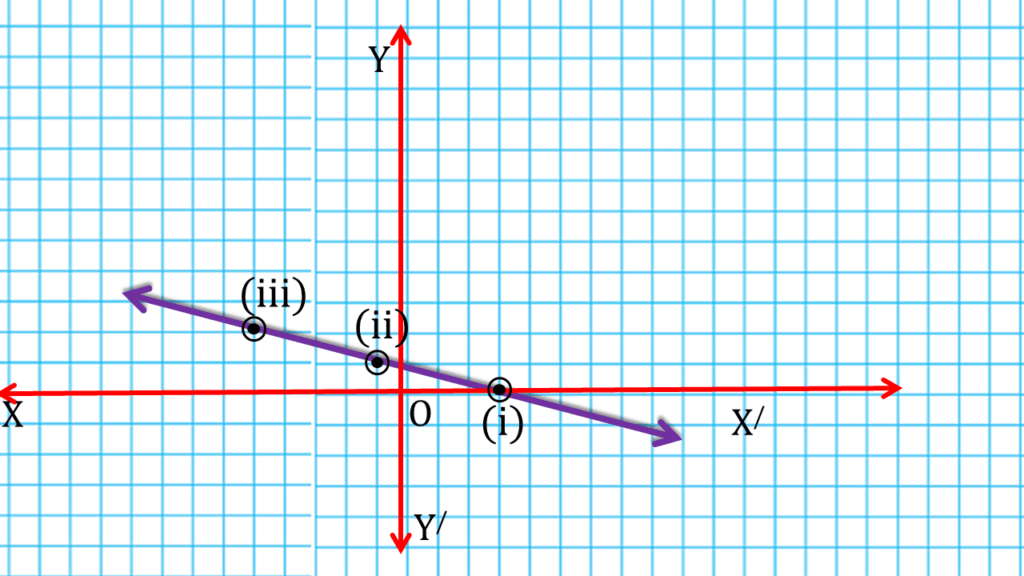
(iii) x = 3 – 4y

সমাধানঃ-

x = 3 – 4y
x = 3 – 4y y = স্থানাঙ্ক
30(i) (3,0)
-11(ii) (-1,1)
-52(iii) (-5,2)
5.iii

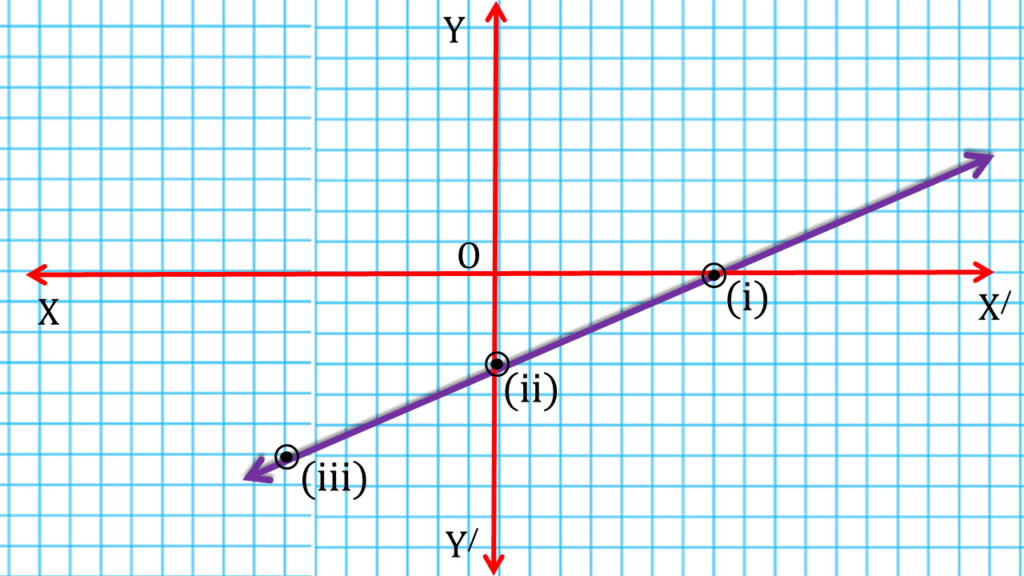
(iv) 3x – 7y = 21

সমাধানঃ-

3x – 7y = 21
x = y = \(\frac{3x-21}{7}\)স্থানাঙ্ক
70(i) (7,0)
0-3(ii) (0,-3)
-7-6(iii) (-7,-6)
5.iv

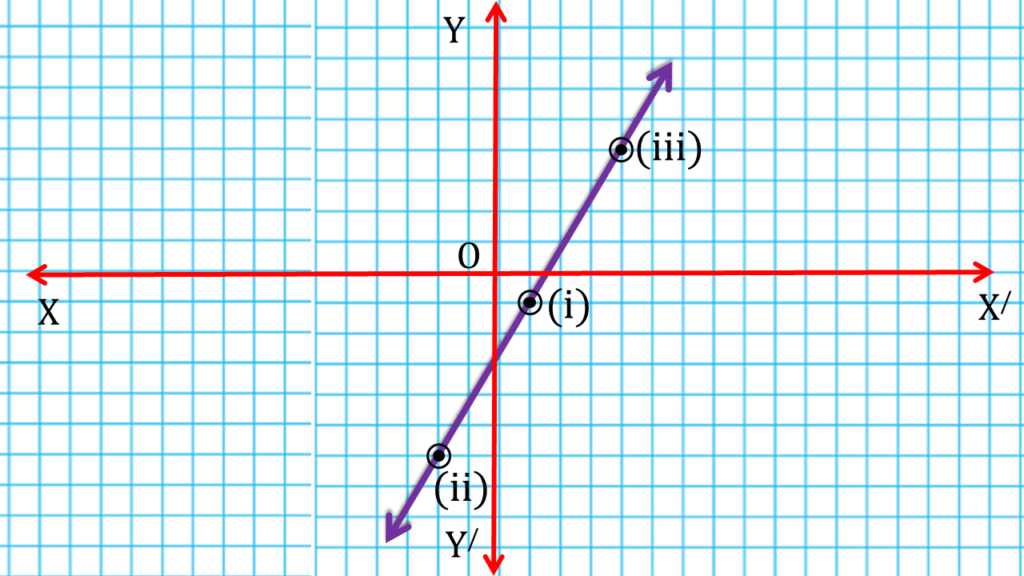
(v) 5x – 3y=8

সমাধানঃ-

5x – 3y=8
x = y = \(\frac{5x – 8}{3}\)স্থানাঙ্ক
1-1(i) (1,-1)
-2-6(ii) (-2,-6)
44(iii) (4,4)
5.v

(vi) 2x + 3y = 11

সমাধানঃ-

2x + 3y = 11
x = y = \(\frac{2x – 11}{3}\)স্থানাঙ্ক
1-3(i) (1,-3)
-2-5(ii) (-2,-5)
4-1(iii) (4,-1)
5.vi

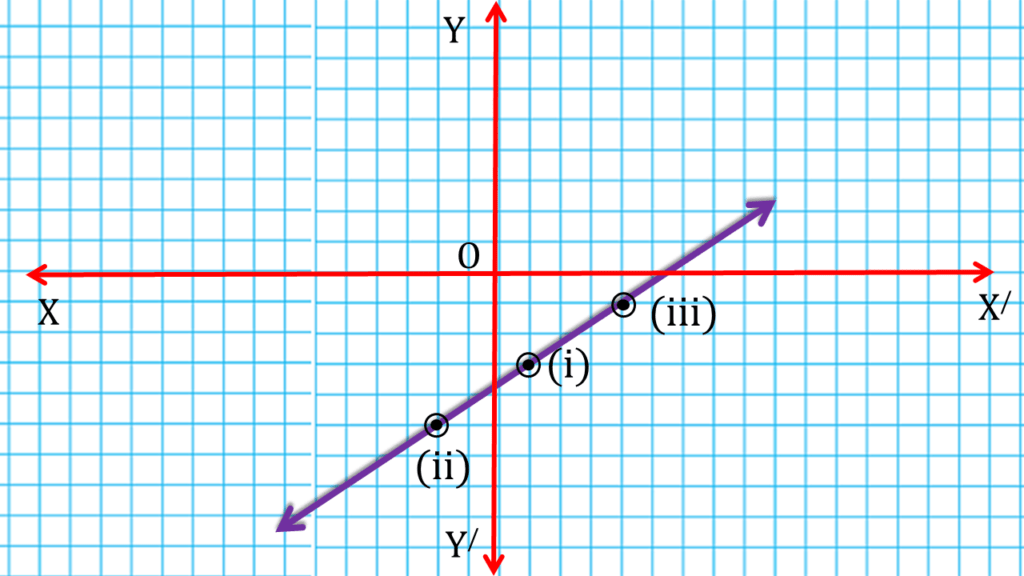
(vii) \(\frac{x}{3} + \frac{y}{4} = 0\)

সমাধানঃ-

\(\frac{x}{3} + \frac{y}{4} = 0\)
x = y = \(-\frac{4x}{3}\)স্থানাঙ্ক
00(i) (0,0)
3-4(ii) (3,-4)
-34(iii) (-3,4)
5.vii

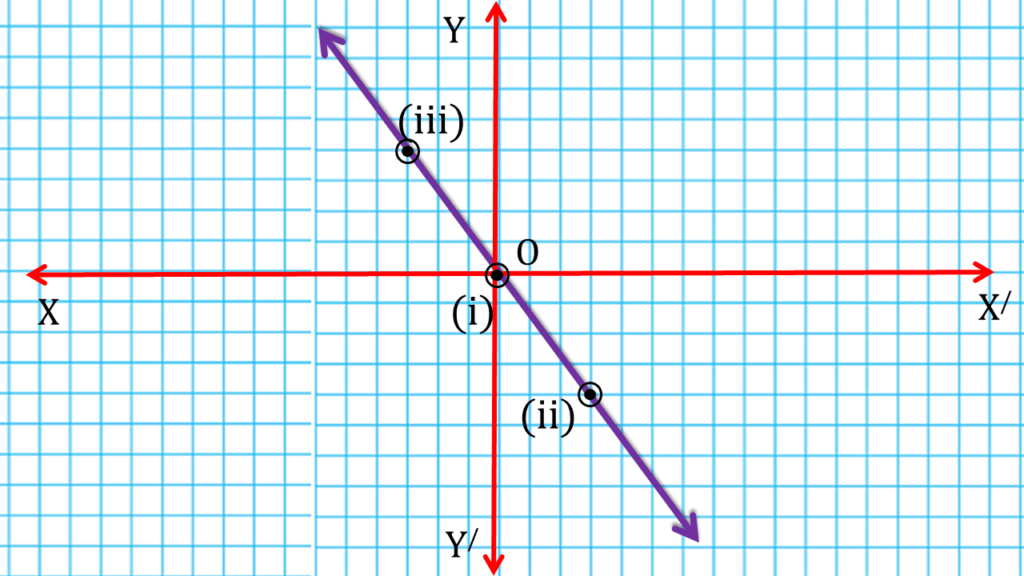
(viii) 6x-7y= 12

সমাধানঃ-

6x-7y= 12
x = y = \(\frac{6x-12}{7}\)স্থানাঙ্ক
20(i) (2,0)
96(ii) (9,6)
-5-6(iii) (-5,-6)
5.viii

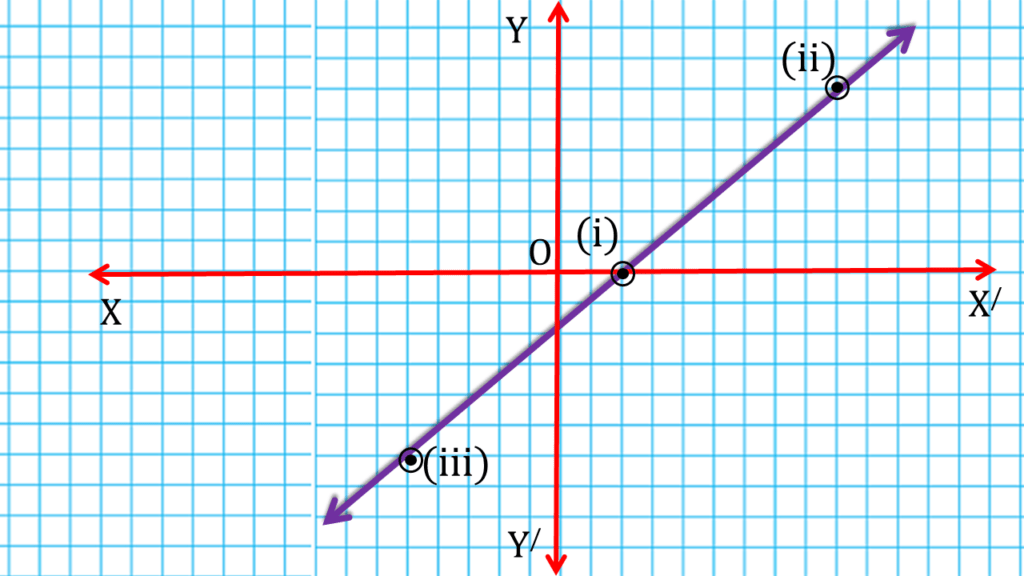
(ix) x + y – 10 = 0

সমাধানঃ-

x + y – 10 = 0
x = y = 10 – xস্থানাঙ্ক
55(i) (5,5)
64(ii) (6,4)
28(iii) (2,8)
5.ix

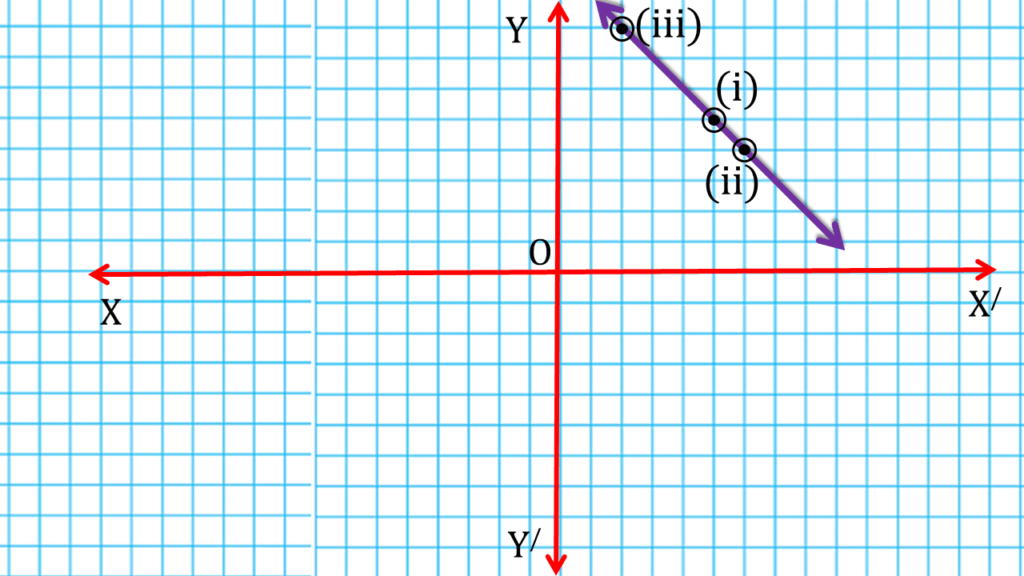
(x) y = 5x-3

সমাধানঃ-

y = 5x-3
x = y = 5x-3স্থানাঙ্ক
0-3(i) (0,-3)
12(ii) (1,2)
27(iii) (2,7)
5.x

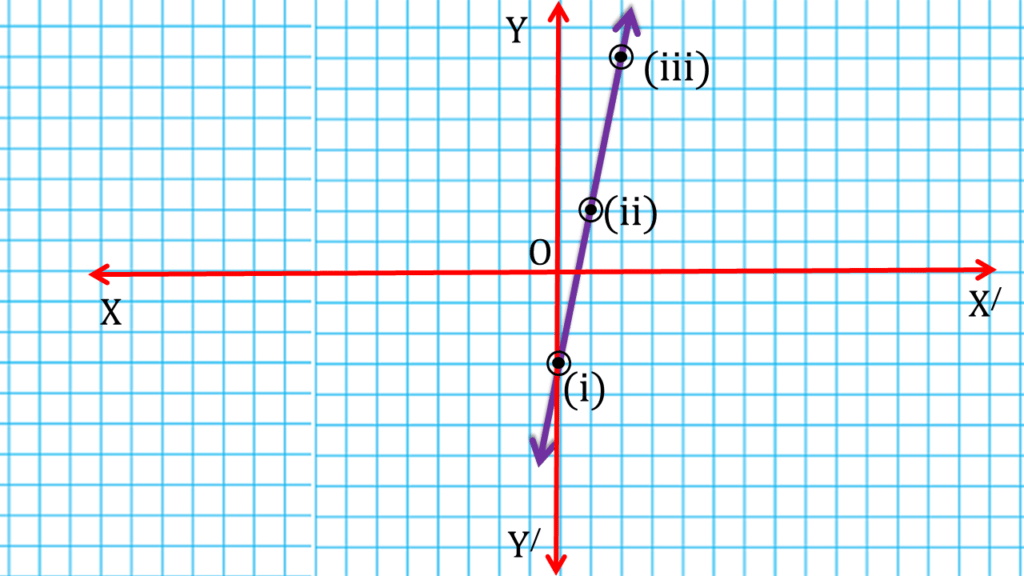
(xi) y=0

সমাধানঃ-

y=0 হল x -অক্ষের সমীকরণ ।

6. নীচের বক্তব্যগুলি রৈখিক সহসমীকরণ আকারে প্রকাশ করি ও সমীকরণগুলির লেখচিত্র অঙ্কন করে সমাধান করি।

(i) বর্তমানে রজতের মামা রজতের চেয়ে 16 বছরের বড়ো। 8 বছর পরে তার মামার বয়স তার বয়সের 2 গুণ হবে। বর্তমানে রজতের বয়স ও রজতের মামার বয়স লেখচিত্রের সাহায্যে নির্ণয় করি।

সমাধানঃ-

ধরি রজতের ও রজতের মামার বর্তমান বয়স যথাক্রমে x বছর ও y বছর।

বক্ত্যব্য রৈখিক সমীকরণ
বর্তমানে রজতের মামা রজতের চেয়ে 16 বছরের বড়োy = x + 16
8 বছর পরে তার মামার বয়স তার বয়সের 2 গুণ হবেy+8 = 2(x+8)
বা, y = 2x + 16 -8
বা, y = 2x + 8
y = x + 16
x = y = x + 16স্থানাঙ্ক
-79(i) (-7,9)
-88(ii) (-8,8)
-115(iii) (-11,5)
y = 2x + 8
x = y = 2x + 8স্থানাঙ্ক
08(iv) (0,8)
-24(v) (-2,4)
-40(vi) (-4,0)
6.i 2
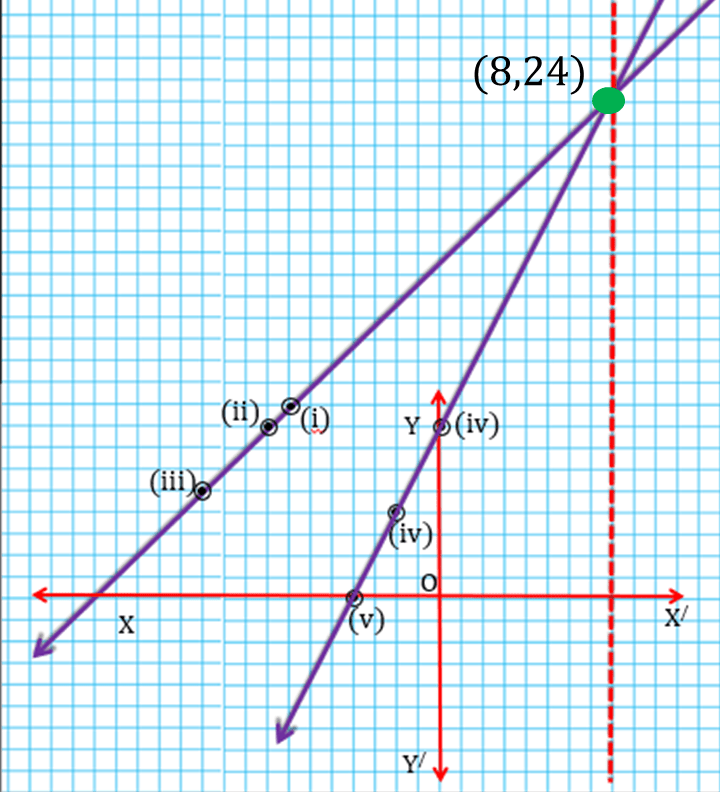
∴ রজতের ও রজতের মামার বর্তমান বয়স যথাক্রমে 8 বছর ও 24 বছর।

(ii) দুটি সংখ্যার সমষ্টি 15 এবং অন্তর 3; লেখচিত্রের সাহায্যে সমীকরণগুলি সমাধান করে সংখ্যা দুটি লিখি।

সমাধানঃ-

ধরি সংখ্যা দুটি x ও y.

বক্ত্যব্য রৈখিক সমীকরণ
দুটি সংখ্যার সমষ্টি 15 x + y = 15
দুটি সংখ্যার অন্তর 3x – y = 3
x + y = 15
x = y = 15 – xস্থানাঙ্ক
78(i) (7,8)
87(ii) (8,7)
105(iii) (10,5)
x – y = 3
x = y = x – 3স্থানাঙ্ক
63(iv) (6,3)
30(v) (3,0)
0-3(vi) (0,-3)
6.ii 1
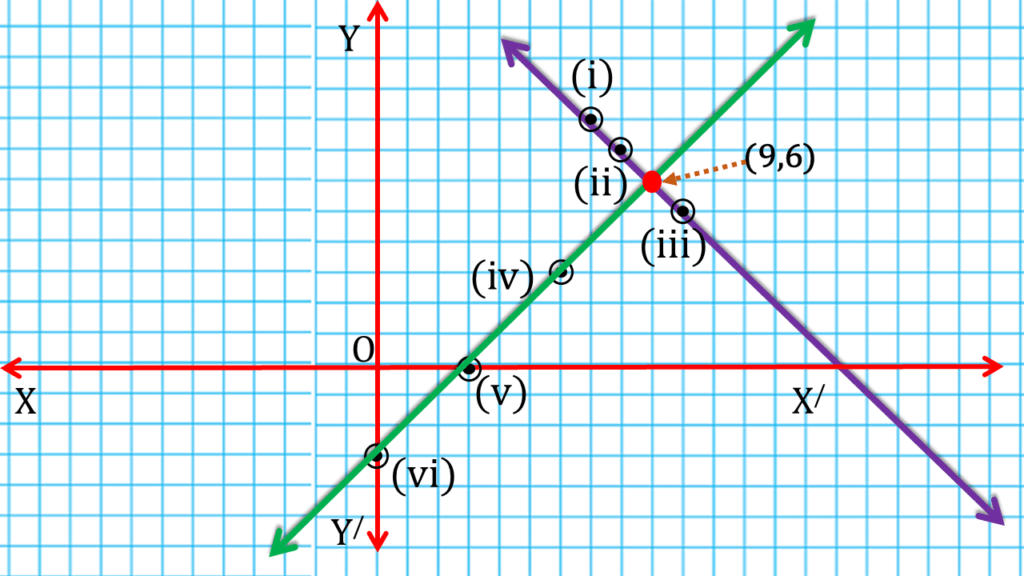
∴ সংখ্যা দুটি হল – 9 ও 6 ।

(iii) একটি ভগ্নাংশের লব থেকে 3 বিয়োগ এবং হরের সঙ্গে 2 যোগ করলে ভগ্নাংশটি \(\frac{1}{3}\) হয় এবং লব থেকে 4 এবং হর থেকে 2 বিয়োগ করলে ভগ্নাংশটি \(\frac{1}{2}\) হয়। বক্তব্যটির সমীকরণ গঠন করি ও লেখচিত্রের সাহায্যে সমাধান করে ভগ্নাংশটি লিখি।

সমাধানঃ-

ধরি ভগ্নাংশটির লব =x এবং হর = y

বক্ত্যব্য রৈখিক সমীকরণ
ভগ্নাংশের লব থেকে 3 বিয়োগ এবং হরের সঙ্গে 2 যোগ করলে ভগ্নাংশটি 1/3 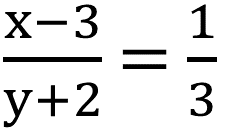6.iii 1
বা, 3(x-3) = y+2
বা, 3x – y = 11
লব থেকে 4 এবং হর থেকে 2 বিয়োগ করলে ভগ্নাংশটি ½ হয়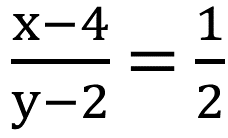6.iii 2 1
বা, 2(x-4) = y – 2
বা, 2x – y = 6
3x – y = 11
x = y = 3x – 11স্থানাঙ্ক
2-5(i) (2,-5)
3-2(ii) (3,-2)
41(iii) (4,1)
2x – y = 6
x = y = 2x – 6স্থানাঙ্ক
30(iv) (3,0)
2-2(v) (2,-2)
1-4(vi) (1,-4)
6.iii 1

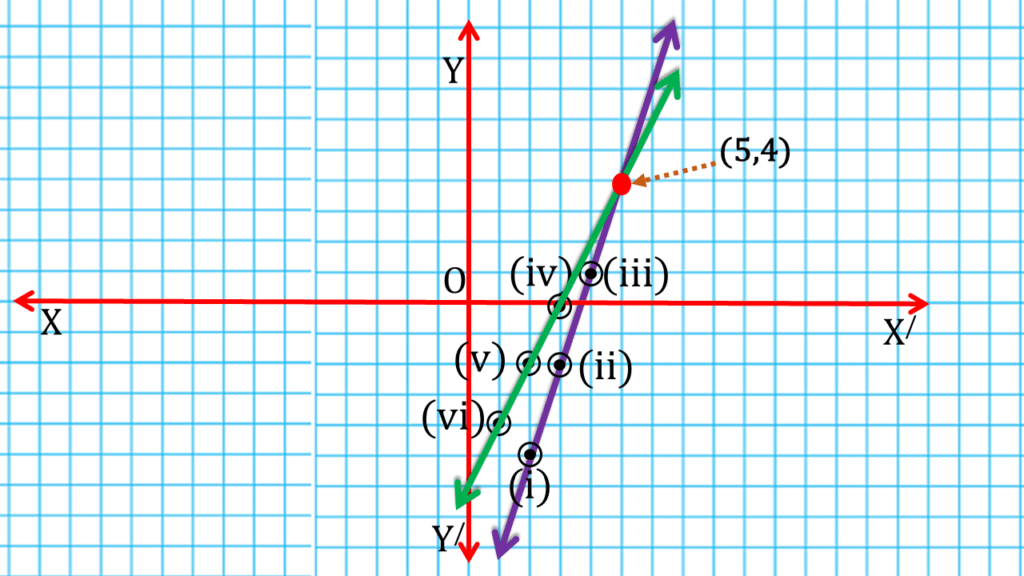
অতএব ভগ্নাংশটি হল- \(\frac{5}{4}\)

∴ ভগ্নাংশটি হল- \(\frac{5}{4}\)

(iv) রোহিতের আয়তাকার বাগানের পরিসীমা 60 মিটার। বাগানের দৈর্ঘ্য 2 মিটার বেশি ও প্রস্থ 2 মিটার কম হলে, বাগানটির ক্ষেত্রফল 24 বর্গমিটার কম হয়। লেখচিত্রের সাহায্যে সমাধান করে আয়তাকার বাগানটির দৈর্ঘ্য ও প্রস্থ লিখি।

সমাধানঃ-

ধরি বাগানের দৈর্ঘ্য = x মিটার এবং প্রস্থ=y মিটার

বক্ত্যব্য রৈখিক সমীকরণ
আয়তাকার বাগানের পরিসীমা 60 মিটার2(x+y)=60
বা, x + y = 30
বাগানের দৈর্ঘ্য 2 মিটার বেশি ও প্রস্থ 2 মিটার কম হলে, বাগানটির ক্ষেত্রফল 24 বর্গমিটার কম হয়(x + 2)(y – 2) = xy – 24
বা, xy+2y-2x-4 = xy -24
বা, 2y-2x = -20
বা, x – y = 10
x + y = 30
x = y = 30 – xস্থানাঙ্ক
1515(i) (15,15)
1812(ii) (18,12)
2010(iii) (20,10)
x – y = 10
x = y = x – 10স্থানাঙ্ক
122(iv) (12,2)
155(v) (15,5)
188(vi) (18,8)
6.iv

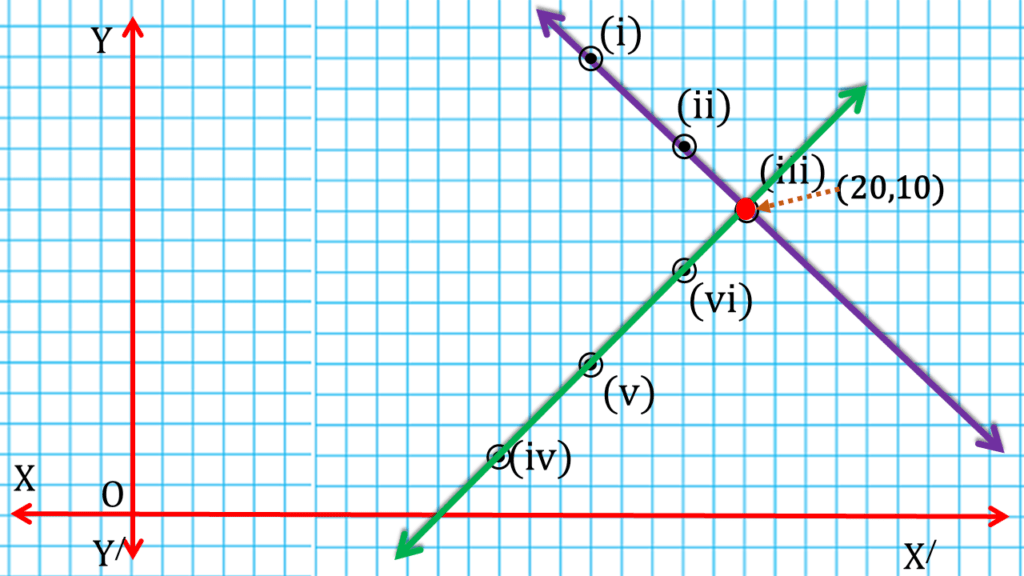
অতএব বাগানের দৈর্ঘ্য = 20 মিটার এবং প্রস্থ=10 মিটার

∴ বাগানের দৈর্ঘ্য = 20 মিটার এবং প্রস্থ=10 মিটার

(v) একটি নৌকা স্রোতের অনুকূলে 16 ঘণ্টায় 96 কিমি. যায় এবং স্রোতের প্রতিকূলে 8 ঘণ্টায় 16 কিমি যায়। লেখচিত্রের সাহায্যে সমাধান করে, স্থির জলে নৌকার বেগ ও স্রোতের বেগ লিখি।

সংকেত : ধরি, স্থির জলে নৌকার বেগ x কিমি./ঘন্টা এবং স্রোতের বেগ y কিমি/ ঘণ্টা। স্রোতের অনুকূলে নৌকাটি ঘণ্টায় যায় (x + y) কিমি. এবং স্রোতের প্রতিকূলে নৌকাটি 1 ঘণ্টায় যায় (x – y) কিমি.)

সমাধানঃ-

ধরি, স্থির জলে নৌকার বেগ x কিমি./ঘন্টা এবং স্রোতের বেগ y কিমি/ ঘণ্টা। স্রোতের অনুকূলে নৌকাটি ঘণ্টায় যায় (x + y) কিমি. এবং স্রোতের প্রতিকূলে নৌকাটি 1 ঘণ্টায় যায় (x – y) কিমি.)

বক্ত্যব্য রৈখিক সমীকরণ
স্রোতের অনুকূলে 16 ঘণ্টায় 96 কিমি. যায়\(\frac{96}{x+y} = 16\)
বা, x+y = 6
স্রোতের প্রতিকূলে 8 ঘণ্টায় 16 কিমি যায়\(\frac{16}{x-y}=8\)
বা, x-y = 2
x + y = 6
x = y = 6 – xস্থানাঙ্ক
60(i) (6,0)
15(ii) (1,5)
51(iii) (5,1)
x – y = 2
x = y = x – 2স্থানাঙ্ক
20(iv) (2,0)
1-1(v) (1,-1)
31(vi) (3,1)

∴ স্থির জলে নৌকার বেগ 4 কিমি./ঘন্টা এবং স্রোতের বেগ 2 কিমি/ ঘণ্টা

7. নীচের সহসমীকরণগুলির লেখচিত্র অঙ্কন করি ও ছেদবিন্দুর স্থানাঙ্ক নির্ণয় করি।

(i) x = 0 এবং 2x + 3y = 15

সমাধানঃ-

x = 0

2x + 3y = 15
x = y = \(\frac{15 – 2x}{3}\)স্থানাঙ্ক
33(i) (3,3)
61(ii) (6,1)
-37(iii) (-3,7)
∴ ছেদবিন্দুর স্থানাঙ্ক (0,5)

(ii) y = 5 এবং 2x + 3y = 11

সমাধানঃ-

2x + 3y = 11
x = y = \(\frac{11 – 2x}{3}\)স্থানাঙ্ক
-25(i) (-2,5)
7-1(ii) (7,-1)
41(iii) (4,1)
7.ii 2
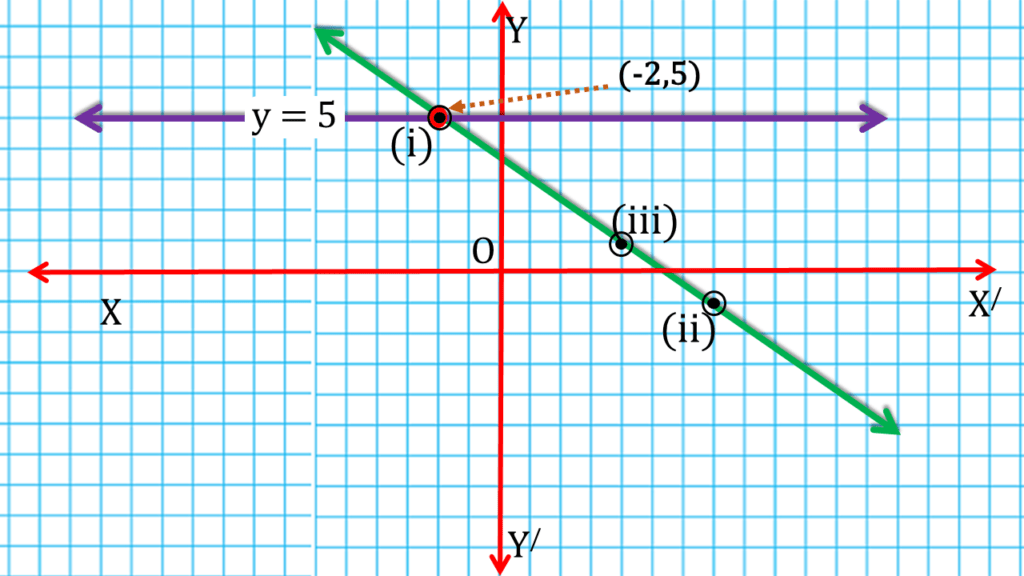
∴ ছেদবিন্দুর স্থানাঙ্ক (-2,5)

(iii) x + y = 12 এবং x – y = 2

সমাধানঃ-

x + y = 12
x = y = 12-xস্থানাঙ্ক
66(i) (6,6)
39(ii) (3,9)
75(iii) (7,5)
x – y = 2
x = y = x – 2স্থানাঙ্ক
20(iv) (2,0)
1-1(v) (1,-1)
31(vi) (3,1)
7.iii 1
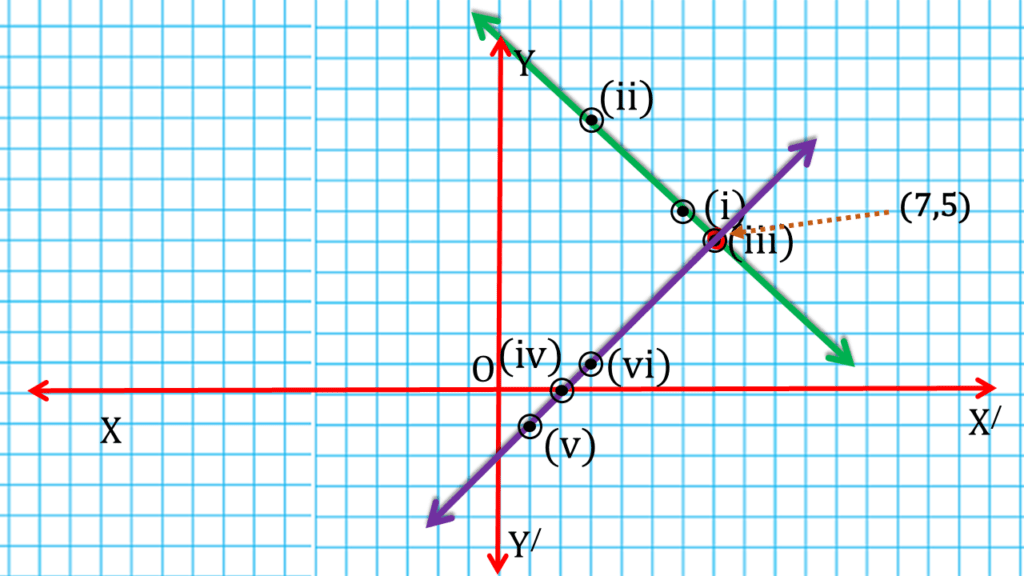
∴ ছেদবিন্দুর স্থানাঙ্ক (7,5)

(iv) 3x – 5y = 16 এবং 2x – 9y = 5

সমাধানঃ-

3x – 5y = 16
x = y = \(\frac{3x-16}{5y}\)স্থানাঙ্ক
2-2(i) (2,-2)
71(ii) (7,1)
-3-5(iii) (-3,-5)
2x – 9y = 5
x = y = \(\frac{5 – 2x}{9}\)স্থানাঙ্ক
-2-1(iv) (-2,-1)
71(v) (7,1)
-11-3(vi) (-11,-3)
7.iv 2
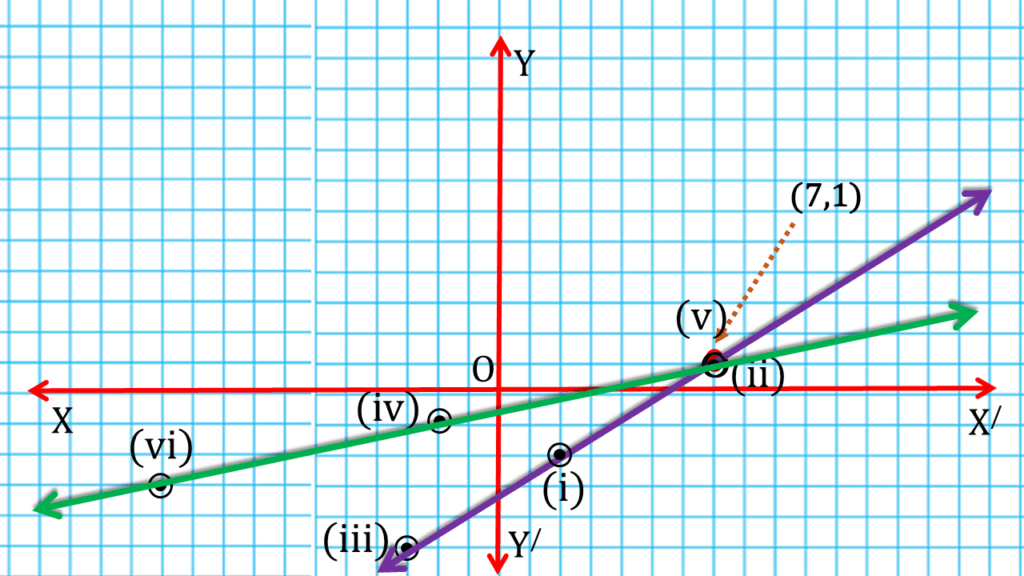
∴ ছেদবিন্দুর স্থানাঙ্ক (7,1)

8. লেখচিত্রের সাহায্যে নীচের সমীকরণগুলি সমাধান করি।

(i) 4x – y = 3; 2x + 3y = 5

সমাধানঃ-

4x – y = 3
x = y = 4x-3স্থানাঙ্ক
11(i) (1,1)
0-3(ii) (0,-3)
25(iii) (2,5)
2x + 3y = 5
x = y = \(\frac{5 – 2x}{3}\)স্থানাঙ্ক
11(iv) (1,1)
-23(v) (-2,3)
4-1(vi) (4,-1)
8.i 3
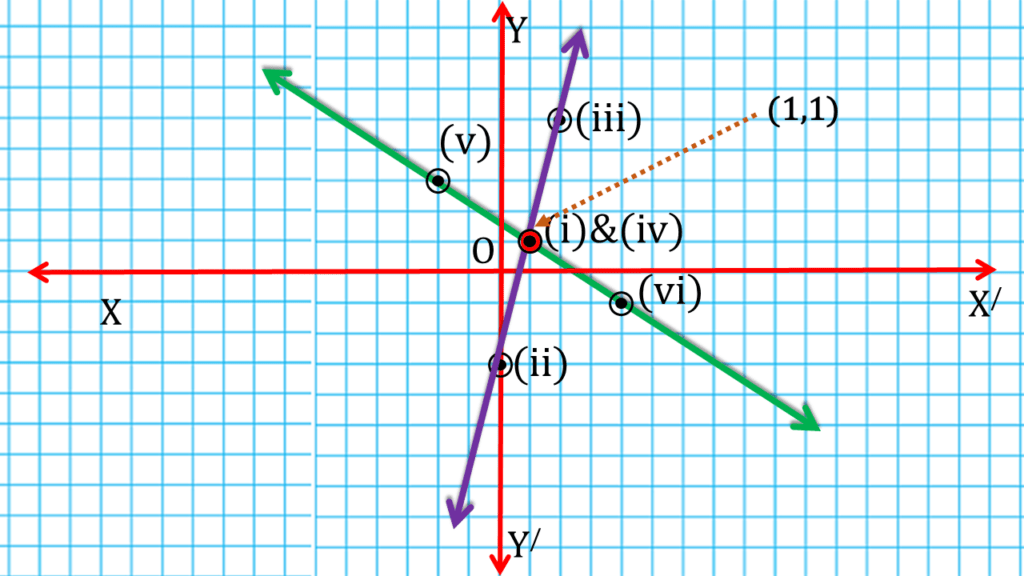
∴ x = 1 , y = 1

(ii) 3x – y = 5; 4x + 3y = 11

সমাধানঃ-

3x – y = 5
x = y = 3x-5স্থানাঙ্ক
0-5(i) (0,-5)
1-2(ii) (1,-2)
21(iii) (2,1)
4x + 3y = 11
x = y = \(\frac{11-4x}{3}\)স্থানাঙ্ক
-15(iv) (-1,5)
21(v) (2,1)
5-3(vi) (5,-3)
8.ii 2
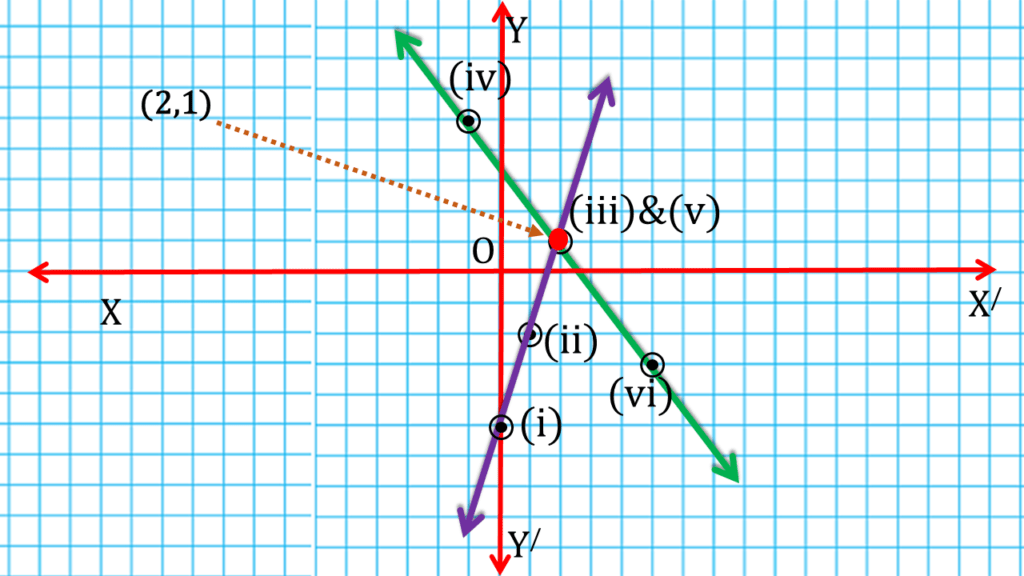
∴ x = 2 , y = 1

(iii) 3x – 2y = 1; 2x – y = 3

সমাধানঃ-

3x – 2y = 1
x = y = \(\frac{3x-1}{2}\)স্থানাঙ্ক
11(i) (1,1)
34(ii) (3,4)
-1-2(iii) (-1,-2)
2x – y = 3
x = y = 2x-3স্থানাঙ্ক
0-3(iv) (0,-3)
1-1(v) (1,-1)
21(vi) (2,1)
8.iii 1
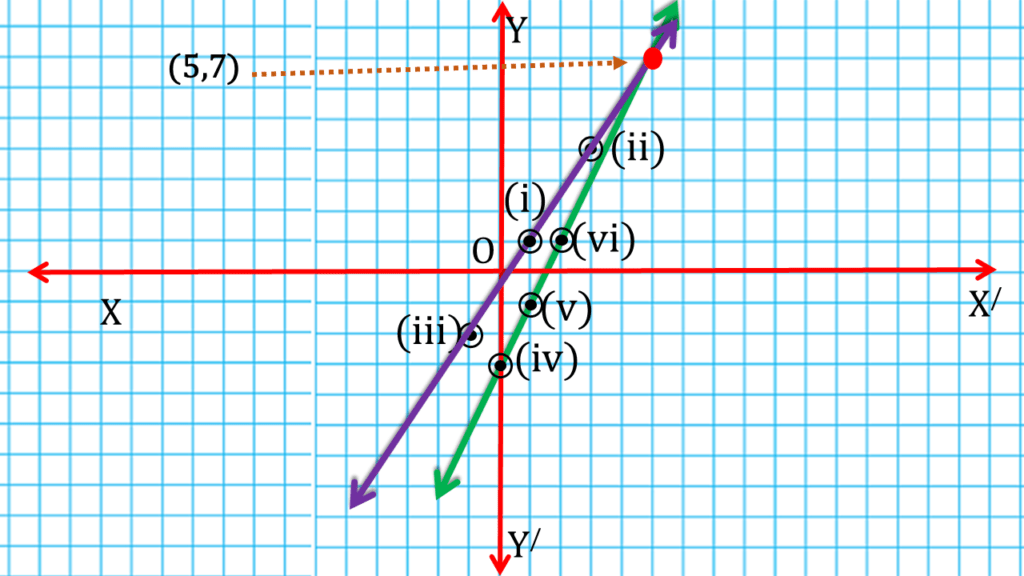
∴ x = 5 , y = 7

(iv) 2x + 3y = 12; 2x = 3y

সমাধানঃ-

2x + 3y = 12
x = y = \(\frac{12-2x}{3}\)স্থানাঙ্ক
32(i) (3,2)
-36(ii) (-3,6)
04(iii) (0,4)
2x = 3y
x = y = \(\frac{2x}{3}\)স্থানাঙ্ক
00(iv) (0,0)
32(v) (3,2)
-3-2(vi) (-3,-2)
8.iv 1
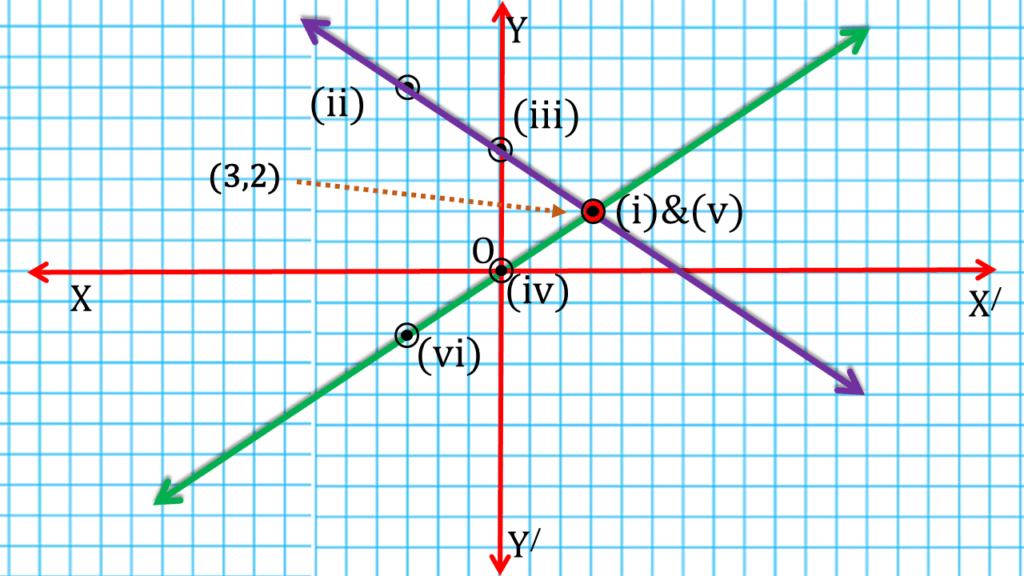
∴ x = 3 , y = 2

(v) 5x – 2y = 1; 3x + 5y = 13

সমাধানঃ-

5x – 2y = 1
x = y = \(\frac{5x-1}{2}\)স্থানাঙ্ক
12(i) (1,2)
-1-3(ii) (-1,-3)
37(iii) (3,7)
3x + 5y = 13
x = y = \(\frac{13-3x}{5}\)স্থানাঙ্ক
12(iv) (1,2)
-45(v) (-4,5)
6-1(vi) (6,-1)
8.v
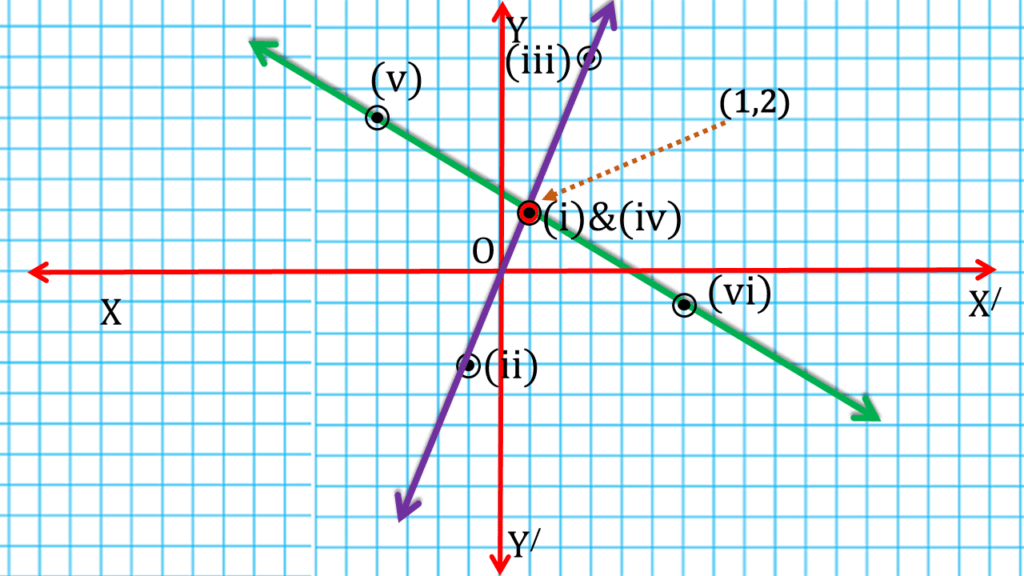
∴ x = 1 , y = 2

9. লেখচিত্রের সাহায্যে প্রদত্ত সমীকরণ দুটির সমাধান নির্ণয় করি ।

3x + 2y = 12, 12 = 9x – 2y

সমাধানঃ-

3x + 2y = 12
x = y = \(\frac{12-3x}{2}\)স্থানাঙ্ক
06(i) (0,6)
23(ii) (2,3)
40(iii) (4,0)
12 = 9x – 2y
x = y = \(\frac{9x-12}{2}\)স্থানাঙ্ক
0-6(iv) (0,-6)
23(v) (2,3)
412(vi) (4,12)
9 4
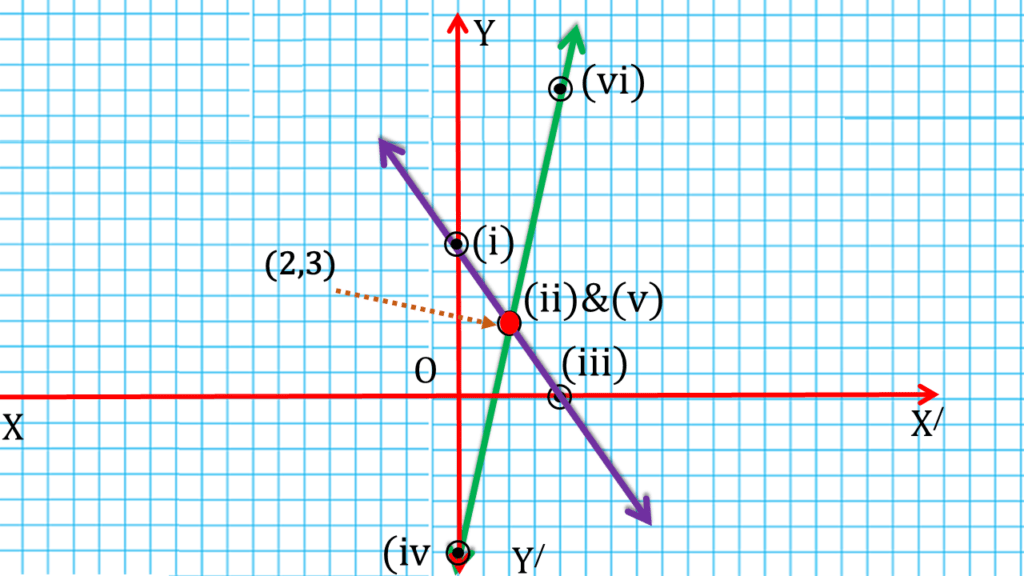
∴ x = 2 , y = 3

10. \(\frac{x}{3} + \frac{y}{4} = 2\) সমীকরণটির লেখচিত্র অঙ্কন করি এবং সমীকরণের লেখচিত্রটি অক্ষদ্বয়ের সঙ্গে যে ত্রিভুজ উৎপন্ন করেছে তার ক্ষেত্রফল হিসাব করে লিখি।

সমাধানঃ-

\(\frac{x}{3} + \frac{y}{4} = 2\)
x = y = \(\frac{4(6-x)}{3}\)স্থানাঙ্ক
34(i) (3,4)
08(ii) (0,8)
60(iii) (6,0)
10 3

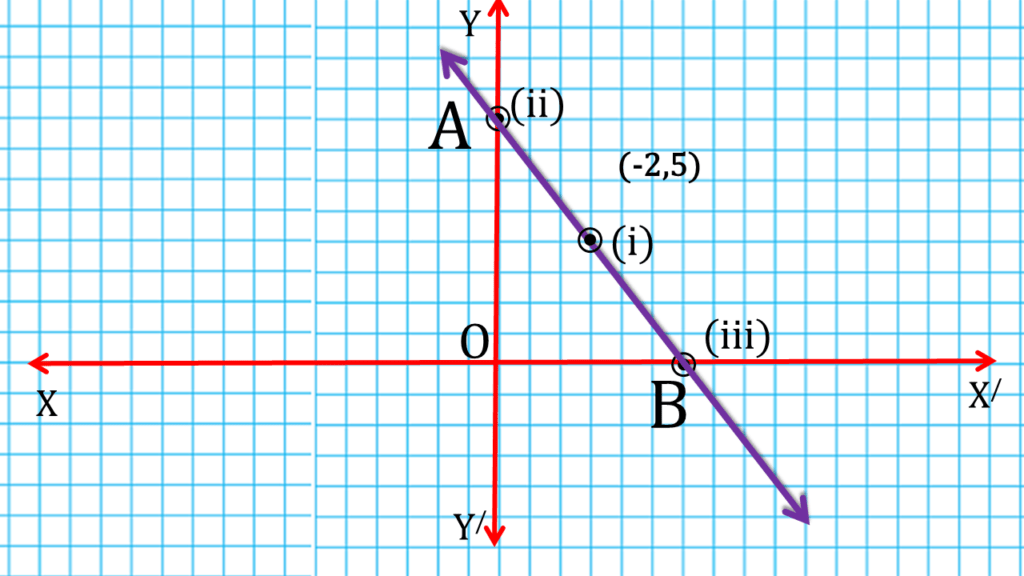
উক্ত সমীকরণ টি x-অক্ষ এবং y-অক্ষ কে যথাক্রমে B ও A বিন্দুতে ছেদ করেছে এবং ▲AOB একটি সমকোণী ত্রিভুজ।

যেখানে OB=6 একক

এবং

OA = 8 একক

▲AOB এর ক্ষেত্রফল

= ½×ভূমি × উচ্চতা

= ½×6×8

= 24 বর্গএকক

∴ সমীকরণের লেখচিত্রটি অক্ষদ্বয়ের সঙ্গে যে ত্রিভুজ উৎপন্ন করেছে তার ক্ষেত্রফল = 24 বর্গএকক

11. x = 4, y = 3 এবং 3x + 4y = 12 সমীকরণ তিনটির লেখচিত্র অঙ্কন করি এবং লেখচিত্রগুলি দ্বারা উৎপন্ন ত্রিভুজটির ক্ষেত্রফল নির্ণয় করি।

সমাধানঃ-

3x + 4y = 12
x = y = \(\frac{12-3x}{4}\)স্থানাঙ্ক
03(i) (0,3)
40(ii) (4,0)
8-3(iii) (8,-3)
11 1

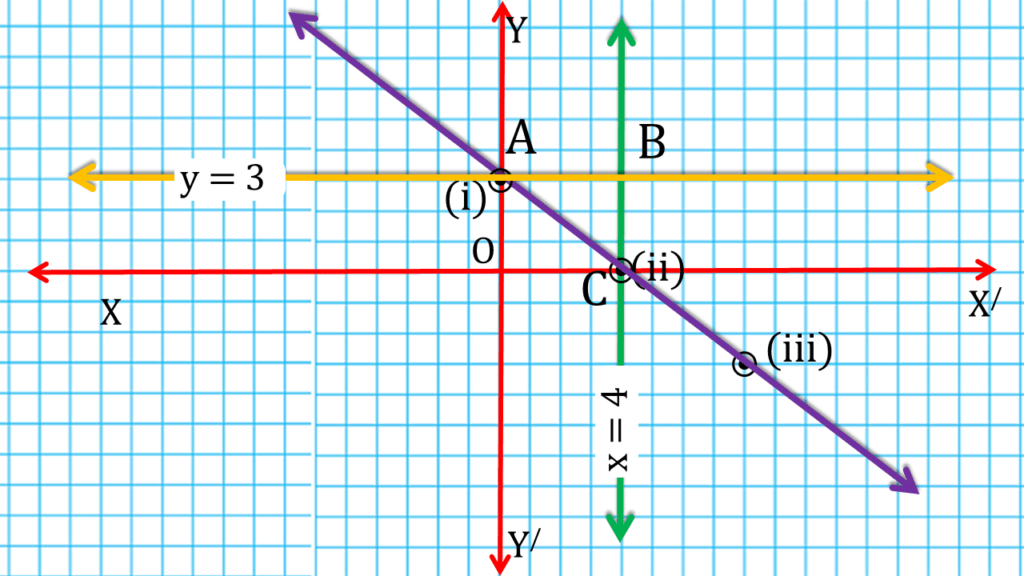
x = 4, y = 3 এবং 3x + 4y = 12 সমীকরণ তিনটির লেখচিত্র দ্বারা ABC সমকোণী ত্রিভুজ উৎপন্ন হয়েছে।

▲ABC এর

AB = 4 একক

BC = 3 একক

যদি ▲ABC এর BC কে ভূমি ধরা হয় তাহলে

▲ABC এর ক্ষেত্রফল

= ½×ভূমি × উচ্চতা

= ½×3×4

= 6 বর্গএকক

∴ লেখচিত্রগুলি দ্বারা উৎপন্ন ত্রিভুজটির ক্ষেত্রফল = 6 বর্গএকক ।

12. \(y=\frac{x+2}{3}\) সমীকরণটির লেখচিত্র অঙ্কন করি। সেই লেখচিত্র থেকে x= -2 -এর জন্য y -এর মান এবং x-এর কোন মানের জন্য y -এর মান 3 হবে, তা নির্ণয় করি।

সমাধানঃ-

\(y=\frac{x+2}{3}\)
x = \(y=\frac{x+2}{3}\)স্থানাঙ্ক
-20(i) (-2,0)
73(ii) (7,3)
-5-1(iii) (-5,-1)
12 1
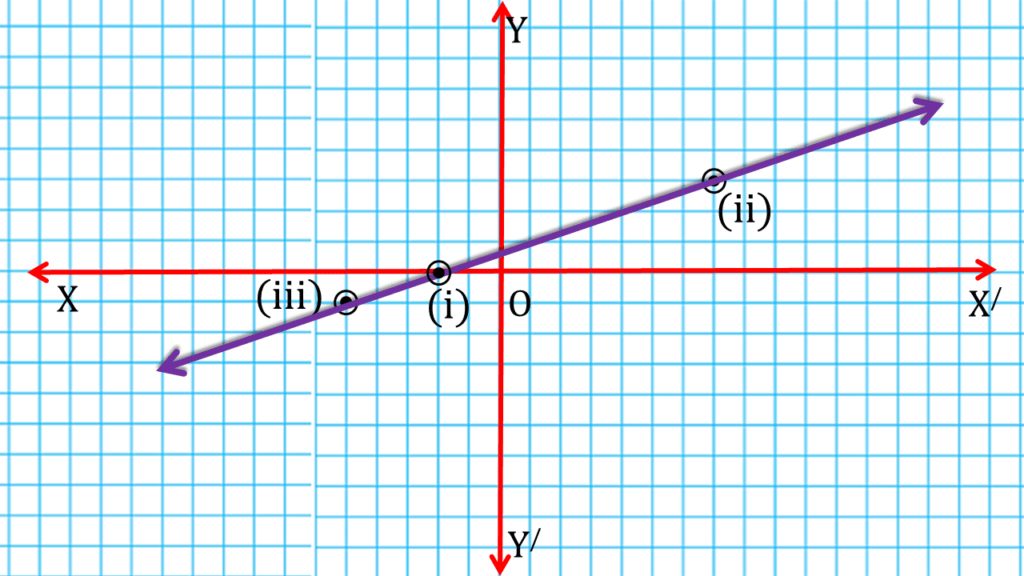
∴ x= -2 -এর জন্য y=0 এবং x=7 এর জন্য y -এর মান 3 হবে ।

13. লেখচিত্রের সাহায্যে সমাধান করি:

\(\frac{3x-1}{2} = \frac{2x+6}{3}\)

সংকেত : \(y = \frac{3x-1}{2}\) এবং \(y=\frac{2x + 6}{3}\) সমীকরণ দুটির লেখচিত্র অঙ্কন করে ছেদবিন্দুর স্থানাঙ্ক নির্ণয় করি। ছেদবিন্দুর x স্থানাঙ্কই হবে নির্ণের সমাধান।।

সমাধানঃ-

\(y = \frac{3x-1}{2}\)
x = \(y = \frac{3x-1}{2}\)স্থানাঙ্ক
11(i) (1,1)
-1-2(ii) (-1,-2)
34(iii) (3,4)
\(y = \frac{2x+6}{3}\)
x = \(y = \frac{2x+6}{3}\)স্থানাঙ্ক
02(iv) (0,2)
34(v) (3,4)
-30(vi) (-3,0)
13
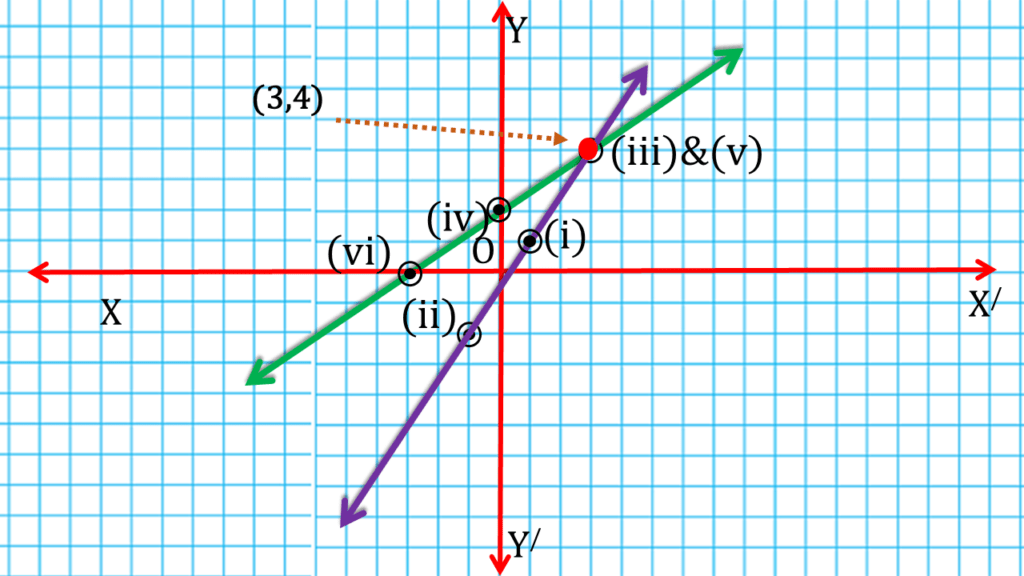
∴ x = 3

14. বহুমুখী বিকল্পীয় প্রশ্ন (M.C.Q.):

(i) 2x + 3 = 0 সমীকরণের লেখচিত্রটি

উত্তরঃ-
(b) y-অক্ষের সমান্তরাল
[ কারণ-
2x + 3 = 0
বা, x = -\(\frac{3}{2}\) = একটি ধ্রুবক ]

(ii) ay + b = (a ও b ধ্রুবক এবং a ≠0, b ≠0) সমীকরণের লেখচিত্রটি

উত্তরঃ- (a) x-অক্ষের সমান্তরাল
[ কারণ-
ay + b = 0
বা, y = -\(\frac{b}{a}\) = একটি ধ্রুবক ]

(iii) 2x + 3y = 0 সমীকরণের লেখচিত্রটি

উত্তরঃ- (c) মূলবিন্দুগামী
[ কারণ-
x=0 এবং y=0, উক্ত সমীকরণ কে সিদ্ধ করে। ]

(iv) cx + d = 0 ( c ও d ধ্রুবক, c ≠ 0 সমীকরণের লেখচিত্রটি y-অক্ষের সমীকরণ হবে যখন

উত্তরঃ- (c) d = 0
[ কারণ-
cx+d=0
বা, x = -\(\frac{d}{c}\)
এখন x = -\(\frac{d}{c}\) এই সমীকরণ টিতে x=0 হবে যখন \(\frac{d}{c}\)=0 হবে বা, d=0 হবে। ]

(v) ay + b = 0 ( a ও b ধ্রুবক, a≠0) সমীকরণের লেখচিত্রটি x-অক্ষের সমীকরণ হবে যখন

উত্তরঃ-(d) b = 0
[ কারণ-
ay+b=0
বা, y = -\(\frac{b}{a}\)
এখন y = -\(\frac{b}{a}\) এই সমীকরণ টিতে y=0 হবে যখন \(\frac{b}{a}\)=0 হবে বা, b=0 হবে। ]

15. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ

(i) 2x + 3y = 12 সমীকরণের লেখচিত্রটি x – অক্ষকে যে বিন্দুতে ছেদ করে তার স্থানাঙ্ক লিখি।

সমাধানঃ-
2x + 3y = 12 সমীকরণের লেখচিত্রটি x -অক্ষকে যে বিন্দুতে ছেদ করবে সেখানে y এর স্থানাঙ্ক শূন্য হবে।
অতএব সমীকরণটিতে y=0 বসিয়ে পাই,
2x + 3.0 = 12
বা, 2x = 12
বা, x = 6

∴ 2x + 3y = 12 সমীকরণের লেখচিত্রটি x -অক্ষকে যে বিন্দুতে ছেদ করে তার স্থানাঙ্ক (6,0)

(ii) 2x – 3y = 12 সমীকরণের লেখচিত্রটি y-অক্ষকে যে বিন্দুতে ছেদ করে তার স্থানাঙ্ক লিখি।

সমাধানঃ-
2x – 3y = 12 সমীকরণের লেখচিত্রটি y -অক্ষকে যে বিন্দুতে ছেদ করবে সেখানে x এর স্থানাঙ্ক শূন্য হবে।
অতএব সমীকরণটিতে x=0 বসিয়ে পাই,
2.0 – 3y = 12
বা, 3y = -12
বা, y = -4

∴ 2x – 3y = 12 সমীকরণের লেখচিত্রটি y-অক্ষকে যে বিন্দুতে ছেদ করে তার স্থানাঙ্ক (0,-4)

(iii) 3x + 4y = 12 সমীকরণের লেখচিত্রটি ও অক্ষদ্বয় দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল কত তা লিখি।

সমাধানঃ-
3x + 4y = 12 সমীকরণে x=0 বসিয়ে পাই,
3.0 + 4y = 12
বা, y = 3
আবার ,
3x + 4y = 12 সমীকরণে y=0 বসিয়ে পাই,
3x + 4.0 = 12
বা, x = 4
∴ সমীকরণ টি x-অক্ষকে (4,0) এবং y-অক্ষকে (0,3) বিন্দুতে ছেদ করবে।
ত্রিভুজের ক্ষেত্রফল
= ½×4×3
= 6 বর্গএকক

3x + 4y = 12 সমীকরণের লেখচিত্রটি ও অক্ষদ্বয় দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল 6 বর্গএকক

(iv) ( 6, -8 ) বিন্দুটির x-অক্ষ থেকে দূরত্ব ও y-অক্ষ থেকে দূরত্ব কত তা লিখি ।

উত্তরঃ-
( 6, -8 ) বিন্দুটির x-অক্ষ থেকে দূরত্ব= 8 একক ও y-অক্ষ থেকে দূরত্ব = 6 একক ।

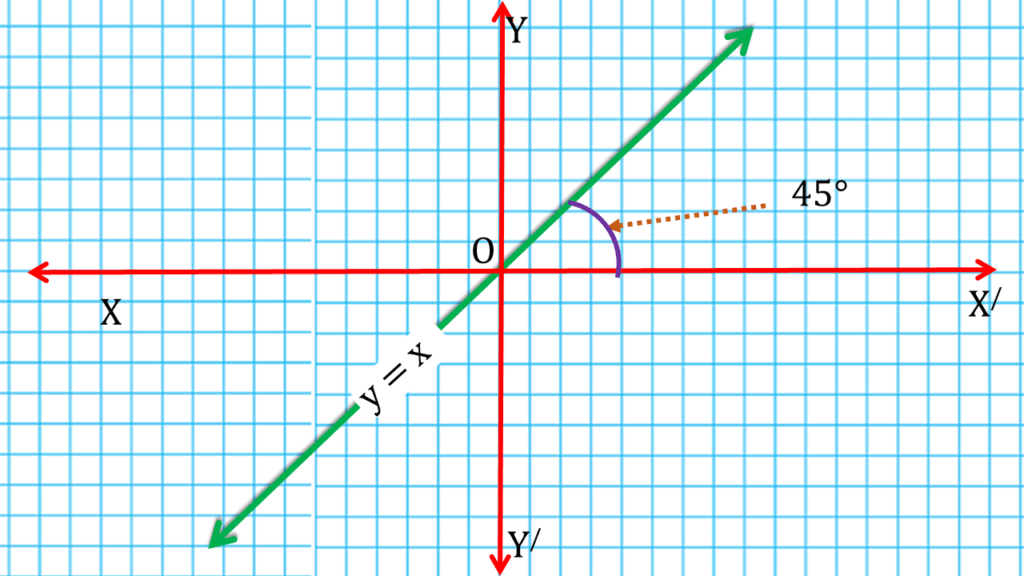
(v) x = y সমীকরণের লেখচিত্র x-অক্ষের ধনাত্মক দিকের সঙ্গে যে কোণ উৎপন্ন করে তার মান লিখি।

উত্তরঃ-
x = y সমীকরণের লেখচিত্র x-অক্ষের ধনাত্মক দিকের সঙ্গে 45° কোণ উৎপন্ন করে

15.v
WB Class 9 এর গণিত প্রকাশের সমস্ত অধ্যায়ের সমাধান-
অধ্যায়সমাধান
1. বাস্তব সংখ্যা (Real Numbers)কষে দেখি 1.1
কষে দেখি 1.2
কষে দেখি 1.3
2. সূচকের নিয়মাবলি (Laws of Indices)
কষে দেখি 2
3. লেখচিত্র (Graph)কষে দেখি 3.1
কষে দেখি 3.2
4. স্থানাঙ্ক জ্যামিতি : দূরত্ব নির্ণয় (Co-ordinate Geometry: Distance Formula)
কষে দেখি 4
5. রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) (Linear Simultaneous Equations)কষে দেখি 5.1
কষে দেখি 5.2
কষে দেখি 5.3
কষে দেখি 5.4
কষে দেখি 5.5
কষে দেখি 5.6
কষে দেখি 5.7
6. সামান্তরিকের ধর্ম (Properties of Parallelogram)
কষে দেখি 6
7. বহুপদী সংখ্যামালা (Polynomial)কষে দেখি 7.1
কষে দেখি 7.2
কষে দেখি 7.3
কষে দেখি 7.4
8. উৎপাদকে বিশ্লেষণ (Factorisation)কষে দেখি 8.1
কষে দেখি 8.2
কষে দেখি 8.3
কষে দেখি 8.4
কষে দেখি 8.5
9. ভেদক ও মধ্যবিন্দু সংক্রান্ত উপপাদ্য (Transversal & Mid-Point Theorem).
কষে দেখি 9
10. লাভ ও ক্ষতি (Profit and Loss)কষে দেখি 10.1
কষে দেখি 10.2
11. রাশিবিজ্ঞান (Statistics) কষে দেখি 11.1
কষে দেখি 11.2
12. ক্ষেত্রফল সংক্রান্ত উপপাদ্য (Theorems on Area)
কষে দেখি 12
13. সম্পাদ্য : ত্রিভুজের সমান ক্ষেত্রফল বিশিষ্ট সামান্তরিক অঙ্কন
কষে দেখি 13

14. সম্পাদ্য : চতুর্ভুজের সমান ক্ষেত্রফল বিশিষ্ট ত্রিভুজ অঙ্কন
কষে দেখি 14
15. ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল (Area & Perimeter of Triangle & Quadrilateral)কষে দেখি 15.1
কষে দেখি 15.2
কষে দেখি 15.3
16. বৃত্তের পরিধি (Circumference of Circle)কষে দেখি 16
17. সমবিন্দু সংক্রান্ত উপপাদ্য (Theorems on concurrence)
কষে দেখি 17
18. বৃত্তের ক্ষেত্রফল (Area of Circle)
কষে দেখি 18
19. স্থানাঙ্ক জ্যামিতি: সরলরেখাংশের অন্তর্বিভক্ত ও বহিঃবিভক্ত (Co-ordinate Geometry: Internal and External Division of Straight-Line Segment)
কষে দেখি 19
20. স্থানাঙ্ক জ্যামিতি: ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল (Co-ordinate Geometry: Area of Triangular Region)
কষে দেখি 20
21. লগারিদম (Logarithm)
কষে দেখি 21
Request For Share
সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো।
Let’s Study Together………….
Share

[Sassy_Social_Share]

এই কষে দেখি Class 9|Koshe Dekhi Class 9 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।

share

এখানে তোমরা তোমাদের নবম শ্রেণীতে| Class 9 এ কি কি পড়ানো হয়, মানে তোমাদের নবম শ্রেণী| Class 9 সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

নবম শ্রেণীর বই
নবম শ্রেণীর সিলেবাস
নবম শ্রেণীতে সরকারি সুবিধা


Leave a Comment