শ্রেণী-নবম ; অধ্যায় – রাশিবিজ্ঞান ; কষে দেখি 11.1
কষে দেখি 11.1 Class 9 এর সুচিপত্রঃ-
কষে দেখি 11.1 Class 9 এর অংকের সমাধান গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ
এই কষে দেখি 11.1 পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদ | WBBSE বোর্ডের অন্তর্গত তোমাদের নবম|Class 9 এর রাশিবিজ্ঞান অধ্যায়ের প্রথম অনুশীলনী। এই Koshe Dekhi 11.1 Class 9 এ যে সমস্ত অংক গুলো আমরা করবো সেগুলি করতে গেলে কিছু জিনিস তোমাদের জানতে হবে।সেগুলি নীচে আলোচনা করা হলো-
তোমাদের Class 9 এর এই কষে দেখি 11.1 অংকগুলি সাধারণত পরিসংখ্যার হিসাব নিয়ে আলোচনা। যেমন- কোনো গ্রামে 50 টি পরিবার আছে। এবার সরকারি কোনো কাজে ওই পরিবারের দৈনিক খরচ কত হয় সেটা দরকার। এই দরকারি হিসাবটি আমরা যে উপায়ে খুব সহজে বের করতে পারবো সেটাই হলো পরিসংখ্যার হিসাব।
এখন এই কষে দেখি 11.1 এর অংকতে পরিসংখ্যার হিসাব জানতে আমাদের জানতে হবে-
- চল কি এবং কত প্রকার?
- গুণ-লক্ষণ বা গুণ কি?
- কোনো রাশিতথ্যের প্রসার কাকে বলে?
- শ্রেণি অন্তর কি?
- পরিসংখ্যা ঘনত্ব কি?
- আপেক্ষিক পরিসংখ্যা কি?
চল কি ও কত প্রকার?
সংখ্যাগত লক্ষণকে চল বলে। যেমন- পরিবারের দৈনিক খরচ একটি চল।
চল দুই প্রকার যথা বিচ্ছিন্ন চল ও অবিচ্ছিন্ন চল।
যেমন-
| বিচ্ছিন্ন চলঃ দেশে নদির সংখ্যা, পরিবারের সদস্য সংখ্যা ইত্যাদি বিচ্ছিন্ন চল। |
| অবিচ্ছিন্ন চলঃ ছাত্রের ওজন, উচ্চতা ইত্যাদি অবিচ্ছিন্ন চল। |
গুণ-লক্ষণ/গুণ কি?
যা পরিমাপ করা যায় না, রাশিবিজ্ঞানে এমন পরিবর্তনশীল লক্ষণকে গুণ লক্ষণ বা গুণ বলে।
যেমন- কোনো বাড়িতে যতগুলি ইলেকট্রিক সুইচ থাকে তার দুটি অবস্থা – জ্বালানো অ নিভানো।
কোনো রাশিতথ্যের প্রসার কাকে বলে?
কোনো প্রদত্ত রাশিতথ্যের চলের সর্বচ্চ ও সর্বনিম্ন মানের অন্তর হলো প্রসার।
শ্রেণি অন্তর কি?
বিস্তৃত প্রসার আছে এইরকম চলের মানগুলিকে কতকগুলি শ্রেণি বা বিভাগে ভাগ করা যায়। এরকম প্রত্যেকটি ভাগ শ্রেণিকে শ্রেণি অন্তর বলা হয়।
শ্রেণি-পরিসংখ্যা কি?
কোনো শ্রেণীর অন্তর্গত মানগুলির সংখ্যাকে শ্রেণি-পরিসংখ্যা বলে।
পরিসংখ্যা ঘনত্ব কি?
পরিসংখ্যা ঘনত্ব হলো-
![]()
আপেক্ষিক পরিসংখ্যা কি?
আপেক্ষিক পরিসংখ্যা হলো-
![]()
আগামিতে এই কষে দেখি 11.1 Class 9 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 11.1 Class 9 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 11.1 Class 9 তারপর 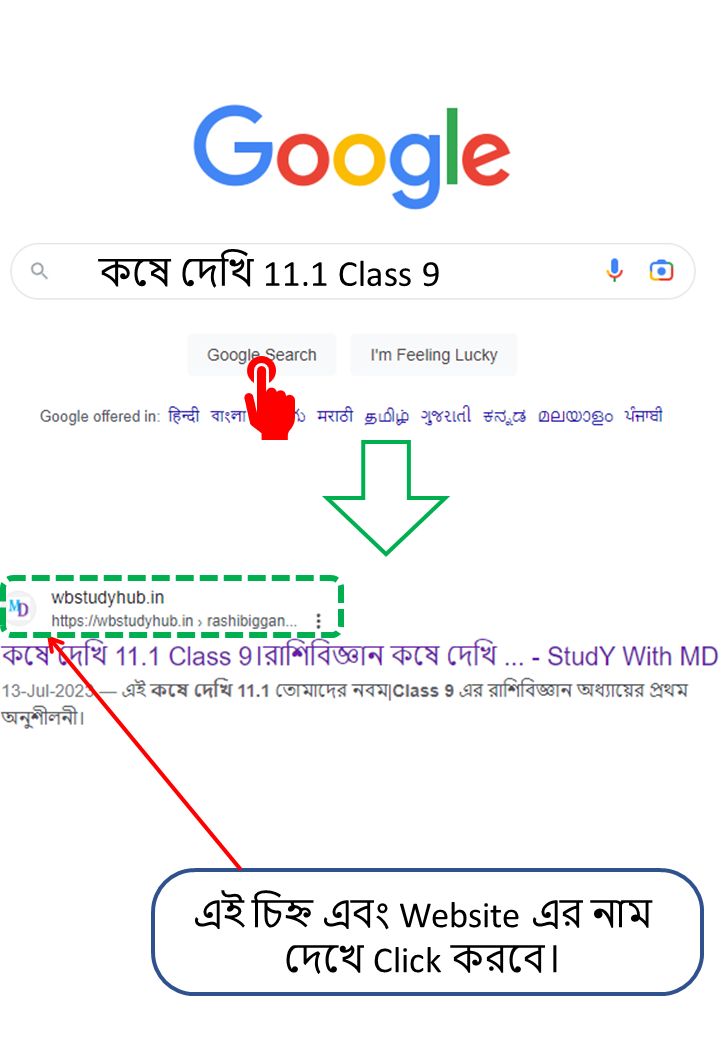 |
কষে দেখি 11.1 | Koshe Dekhi 11.1
1.পাড়ার 40টি পরিবারের প্রত্যেকটি পরিবারের শিশুসংখ্যার তথ্য নীচে লিখেছি
আমি উপরের তথ্যটির পরিসংখ্যা বিভাজন ছক তৈরি করি যার শ্রেণিগুলি হলো 0-2, 2-4…… ইত্যাদি।
এই পরিসংখ্যা বিভাজন ছক থেকে (i) শ্রেণি-অন্তর (ii) শ্রেণি-দৈর্ঘ্য (iii) শ্রেণি পরিসংখ্যা (iv) শ্রেণি-সীমা বলতে কী বুঝি লিখি।
সমাধানঃ-
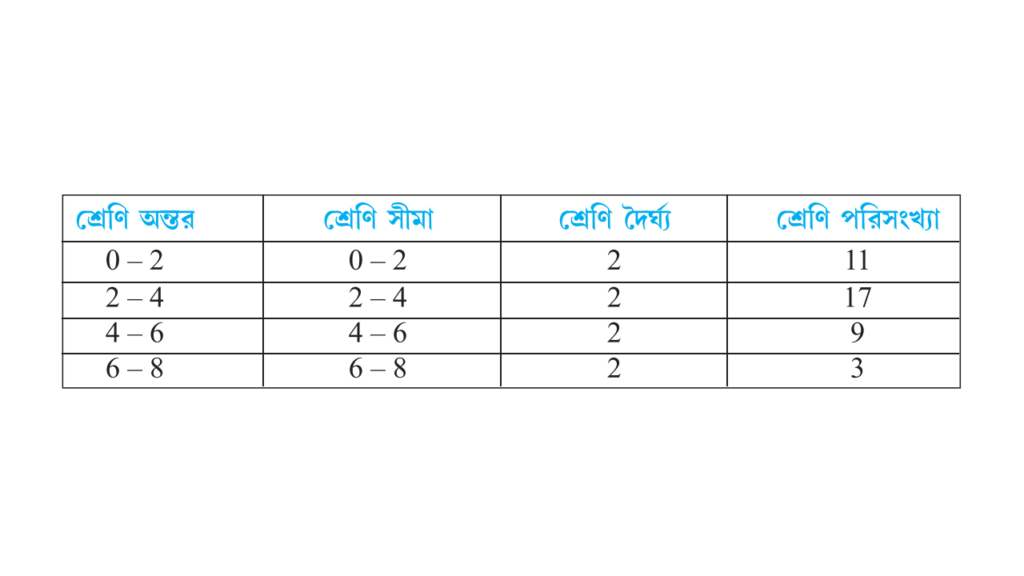
- (i) শ্রেণি-অন্তরঃ উপরের ছকে 0-2, 2-4, …… যে শ্রেণি করা হয়েছে এগুলিকে শ্রেণি অন্তর বলে।
- (ii) শ্রেণি-দৈর্ঘ্যঃ উপরের ছকে 0-2, 2-4, প্রতিটি শ্রেণীর দৈর্ঘ্য হলো – 2
- (iii) শ্রেণি-পরিসংখ্যাঃ শ্রেণি পরিসংখ্যা হলো কোনো শ্রেণীর অন্তর্গত মানগুলির সংখ্যাকে শ্রেণি পরিসংখ্যা বলে। এখানে প্রথম শ্রেণীর শ্রেণি পরিসংখ্যা হলো- 11
- (iv) শ্রেণি-সীমাঃ কোনো শ্রেণীর প্রান্থস্থ মানদ্বয়কে শ্রেণি-সীমা বলে। এখানে যেমন প্রথম শ্রেণীর শ্রেণি সীমা হলো 0 ও 2 ।
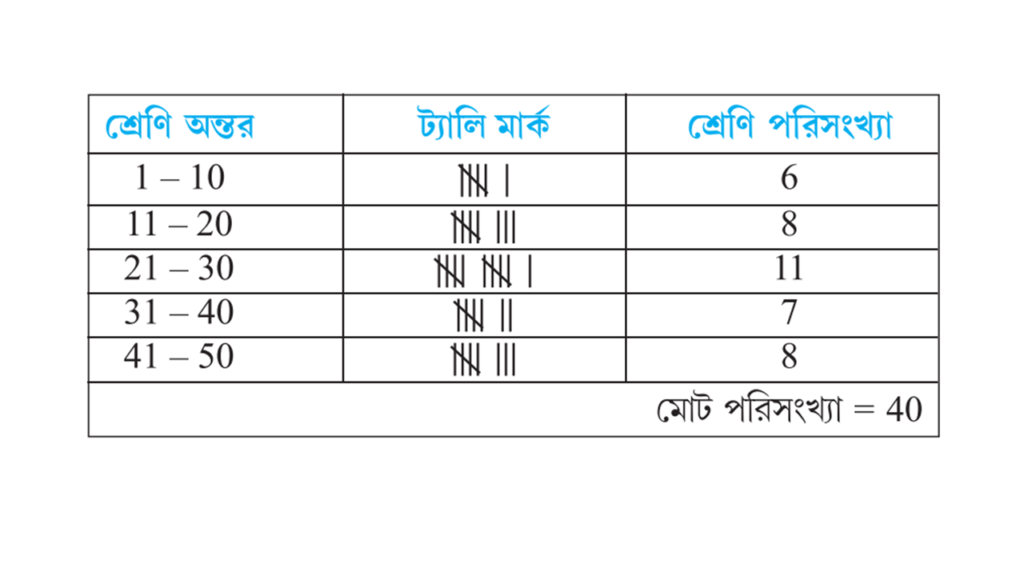
2. স্কুলের কোনো এক পরীক্ষায় 40 জন ছাত্রের প্রাপ্ত নম্বরের তালিকা নীচে প্রদত্ত হলো :
1-10, 11-20, …….., 41-50 শ্রোণিগুলি নিয়ে নম্বরগুলির একটি পরিসংখ্যা বিভাজন ছক প্রস্তুত করি।
সমাধানঃ-
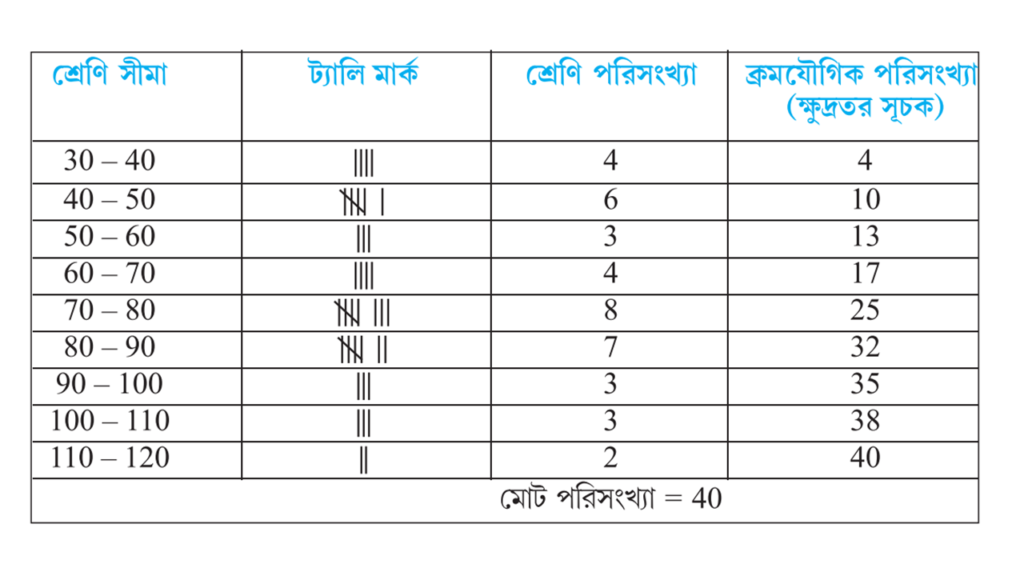
3. একটি ঝুড়িতে অনেকগুলি কমলালেবু রাখা আছে। এই এক ঝুড়ি কমলালেবু থেকে লক্ষ্যহীনভাবে 40টি কমলালেবু নিয়ে তাদের ওজন (গ্রামে) নীচে লিখলাম।
45, 35, 30, 55, 70, 100, 80, 110, 80.75, 85, 70, 75, 85, 90, 75, 90, 30, 55, 45, 40, 65, 60, 50, 40, 100, 65, 60, 40, 100, 75, 110, 30, 45, 84, 70, 80, 95, 85, 70.
এবার আমি উপরের তথ্যের একটি পরিসংখ্যা বিভাজন ছক এবং একটি ক্ষুদ্রতর-সুচক ক্রমযৌগিক পরিসংখ্যা বিভাজন ছক তৈরি করি।
সমাধানঃ-
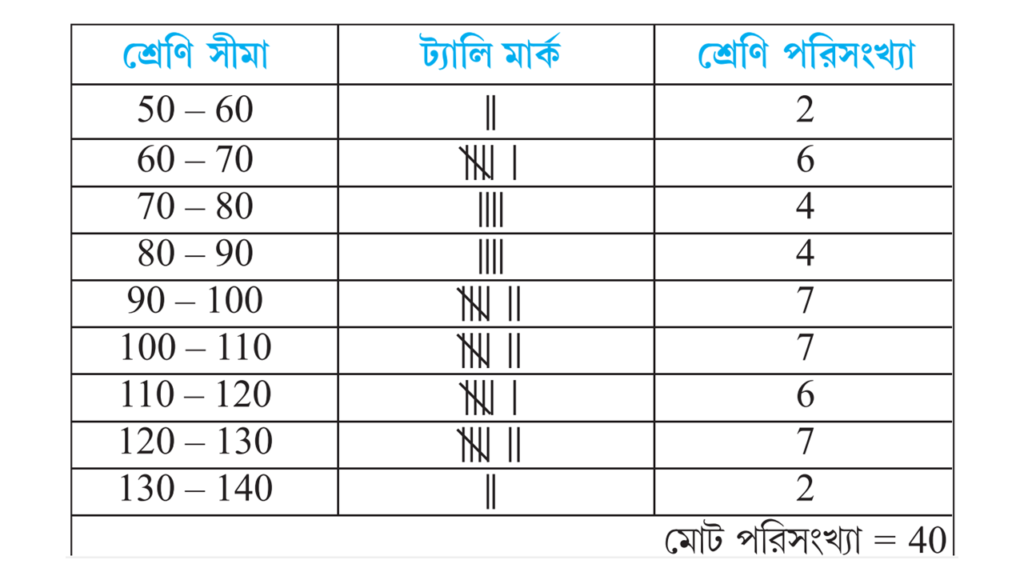
4. মিতালী ও মহিদুল গ্রামের এটি বাড়ির এই মাসের ইলেকট্রিক বিলের টাকার পরিমাণ নীচে লিখল।
116, 127, 100, 82, 80, 101, 91, 65, 95, 89, 75, 92, 129, 78, 87, 101, 65, 52, 59, 65, 95, 108, 115, 121, 128, 63, 76, 130, 116, 108, 118, 61, 129, 127, 91, 130, 125, 101, 116, 105, 92, 75, 98, 65,110.
আমি উপরের তথ্যের একটি পরিসংখ্যা বিভাজন তালিকা তৈরি করি।
সমাধানঃ-
5. মারিয়া একটি হাসপাতালের 300 জন রোগীর বয়স নীচের ছকে লিখল।
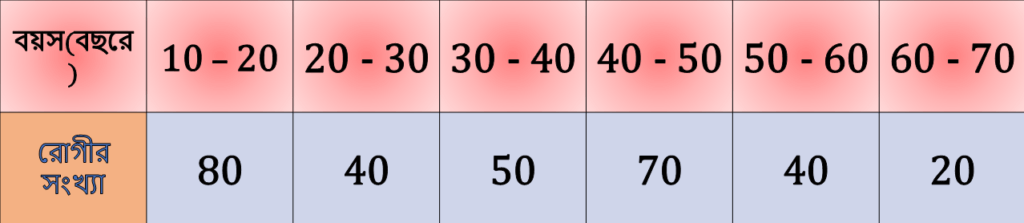
আমি উপরের তথ্যের বৃহত্তর-সূচক ক্রমযৌগিক পরিসংখ্যা বিভাজন তালিকা তৈরি করি।
সমাধানঃ-
| রোগীর বয়স | রোগীর সংখ্যা |
|---|---|
| 10 অথবা 10 এর থেকে বেশী | 80+40+50+70+40+20 = 300 |
| 20 অথবা 20 এর থেকে বেশী | 40+50+70+40+20 = 220 |
| 30 অথবা 30 এর থেকে বেশী | 50+70+40+20 = 180 |
| 40 অথবা 40 এর থেকে বেশী | 70+40+20 = 130 |
| 50 অথবা 50 এর থেকে বেশী | 40+20 = 60 |
| 60 অথবা 60 এর থেকে বেশী | 20 |
6. নীচের ক্রমযৌগিক পরিসংখ্যা বিভাজন ছকটি দেখি এবং একটি পরিসংখ্যা বিভাজন ছক তৈরি করি।
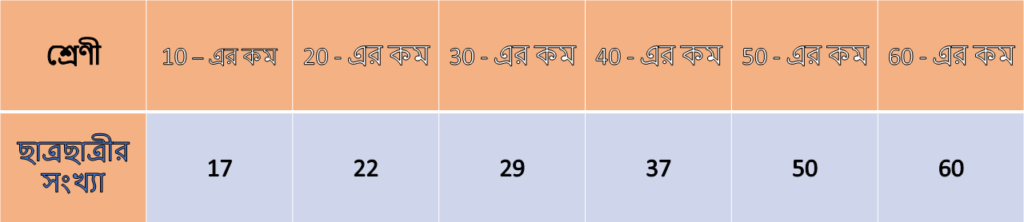
সমাধানঃ-
| শ্রেণী / প্রাপ্ত নম্বর | ছাত্রছাত্রীর সংখ্যা |
|---|---|
| 10 – এর কম | 17 |
| 10 – 20 | 22 – 17 = 5 |
| 20 – 30 | 29 – 22 = 7 |
| 30 – 40 | 37 – 29 = 8 |
| 40 – 50 | 50 – 37 = 13 |
| 50 – 60 | 60 – 50 = 10 |
7. নীচের ক্রমযৌগিক পরিসংখ্যা বিভাজন ছকটি দেখি এবং একটি পরিসংখ্যা বিভাজন ছক তৈরি করি।
| প্রাপ্ত নম্বর | ছাত্রছাত্রীর সংখ্যা |
|---|---|
| 60 -এর বাশি | 0 |
| 50 -এর বাশি | 16 |
| 40 -এর বাশি | 40 |
| 30 -এর বাশি | 75 |
| 20 -এর বাশি | 87 |
| 10 -এর বাশি | 92 |
| 0 -এর বাশি | 100 |
সমাধানঃ-
| শ্রেণী / প্রাপ্ত নম্বর | ছাত্রছাত্রীর সংখ্যা |
|---|---|
| 0 – 10 | 100 – 92 = 8 |
| 10 – 20 | 92 – 87 = 5 |
| 20 – 30 | 87 – 75 = 12 |
| 30 – 40 | 75 – 40 = 35 |
| 40 – 50 | 40 – 16 = 24 |
| 50 – 60 | 16 – 0 = 16 |
| 60 এর বেশী | 0 |
8. বহু বিকল্পীয় প্রশ্ন (M.C.Q.):
i) নিম্নের কোনটি তথ্যের চিত্র উপস্থাপন
উত্তরঃ (a)
(ii) 12, 25, 15, 18, 17, 20, 22, 26, 6, 16, 11, 8, 19, 10, 30, 20, 32 তথ্যের প্রসার
উত্তরঃ (d)
সমাধানঃ-
32 – 6 = 26
iii) 1-5, 6-10, ………. শ্রেণীর শ্রেণী-দৈর্ঘ্য
উত্তরঃ (b)
সমাধানঃ-
5.5 – .5 = 5
iv) একটি পরিসংখ্যা বিভাজন তালিকার শ্রেণির মধ্যবিন্দু যথাক্রমে 15, 20, 25, 30, ……….। যে শ্রেণির মধ্যবিন্দু 20 সেটি হলো,
উত্তরঃ (b)
v) একটি পরিসংখ্যা বিভাজন তালিকায় একটি শ্রেণির মধ্যবিন্দু 10 এবং প্রতিটি শ্রেণির শ্রেণি-দৈর্ঘ্য 6; শ্রেণিটির নিম্নসীমা
উত্তরঃ (b)
সমাধানঃ-
ধরি, শ্রেণিটির নিম্নসীমা = x
∴ শ্রেণিটির উর্ধসীমা = 6 + x
শর্তে,
| \(\frac{6 + x + x}{2}\) = 10 |
| বা, 6 + 2x = 20 |
| বা, 2x = 14 |
| বা, x = 7 |
9. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ
a) একটি অবিচ্ছিন্ন পরিসংখ্যা বিভাজন তালিকার একটি শ্রেণির মধ্যবিন্দু m এবং উচ্চশ্রেণি-সীমানা u হলে নিম্নশ্রেণি সীমানাটি কত তা বের করি।
সমাধানঃ-
ধরি শ্রেণিটির নিম্নশ্রেনি সিমানা = x
শর্তে,
| \(\frac{x + u}{2}\) = m |
| বা, x + u = 2m |
| বা, x = 2m – u |
∴ শ্রেণিটির নিম্নশ্রেনি সিমানা = 2m-u
b) একটি অবিচ্ছিন্ন পরিসংখ্যা বিভাজন তালিকায় একটি শ্রেণির মধ্যবিন্দু 42 এবং শ্রেণি-দৈর্ঘ্য 10 হলে শ্রেণিটির উচ্চ ও নিম্ন সীমা কত তা লিখি।
সমাধানঃ-
ধরি, শ্রেণীটির উচ্চসীমা ও নিম্নসীমা যথাক্রমে x ও y ।
মধ্যবিন্দু = \(\frac{x + y}{2}\)
এবং
শ্রেণী দৈর্ঘ্য = y – x
শর্তে,
| \(\frac{x + y}{2}\) = 42 বা, x + y = 84 ——-( i ) | y – x = 10 ——( ii ) |
(i) ও (ii) নং যোগ করে পাই,
| x + y + y – x = 84 + 10 |
| বা, 2y = 94 |
| বা, y = 47 |
y = 47, (i) নং সমীকরণে বসিয়ে পাই,
x = 84 – 47 = 37
∴শ্রেণিটির নিম্নসিমা=37 এবং উচ্চসীমা=47
c)
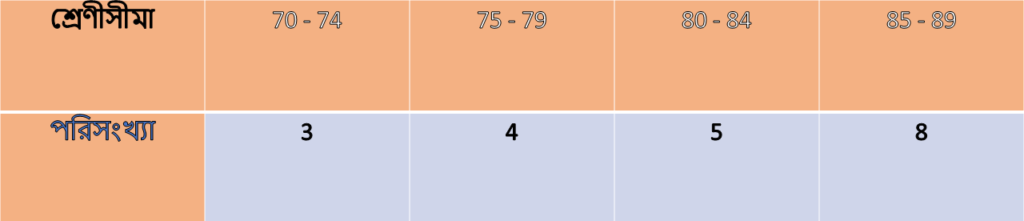
উপরের পরিসংখ্যা বিভাজন তালিকার প্রথম শ্রেণির পরিসংখ্যা ঘনত্ব কত তা লিখি।
সমাধানঃ-
আমরা জানি,

এখানে শ্রেণী দৈর্ঘ্য
= 74.5 – 69.5 = 5
∴ প্রথম শ্রেণীর পরিসংখ্যার ঘনত্ব
= \(\frac{3}{5}\) = 0.6
d) (c) প্রশ্নের শেষ শ্রেণির আপেক্ষিক পরিসংখ্যা কত তা লিখি
সমাধানঃ-
আমরা জানি,
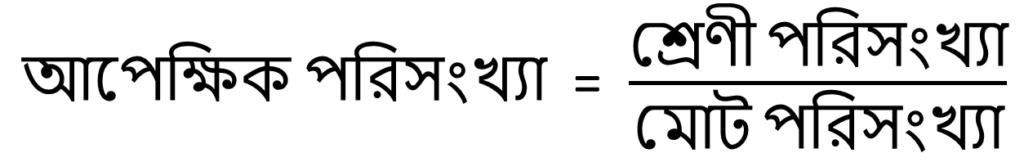
এখানে মোট পরিসংখ্যা
= 3 + 4 + 5 + 8
= 20
∴ শেষ শ্রেণীর আপেক্ষিক পরিসংখ্যা
= \(\frac{8}{20}\) = 0.4
e) নীচের উদাহরনগুলিতে কোনগুলি গুণ এবং কোনগুলি চল নির্দেশ করে লিখি :
সমাধানঃ-
| চল | গুণ |
|---|---|
| (i) (ii) (iv) | (iii) (v) |
| WB Class 9 এর গণিত প্রকাশের সমস্ত অধ্যায়ের সমাধান- | |
|---|---|
| অধ্যায় | সমাধান |
| 1. বাস্তব সংখ্যা (Real Numbers) | কষে দেখি 1.1 |
| কষে দেখি 1.2 | |
| কষে দেখি 1.3 | |
| 2. সূচকের নিয়মাবলি (Laws of Indices) | কষে দেখি 2 |
| 3. লেখচিত্র (Graph) | কষে দেখি 3.1 |
| কষে দেখি 3.2 | |
| 4. স্থানাঙ্ক জ্যামিতি : দূরত্ব নির্ণয় (Co-ordinate Geometry: Distance Formula) | কষে দেখি 4 |
| 5. রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) (Linear Simultaneous Equations) | কষে দেখি 5.1 |
| কষে দেখি 5.2 | |
| কষে দেখি 5.3 | |
| কষে দেখি 5.4 | |
| কষে দেখি 5.5 | |
| কষে দেখি 5.6 | |
| কষে দেখি 5.7 | |
| 6. সামান্তরিকের ধর্ম (Properties of Parallelogram) | কষে দেখি 6 |
| 7. বহুপদী সংখ্যামালা (Polynomial) | কষে দেখি 7.1 |
| কষে দেখি 7.2 | |
| কষে দেখি 7.3 | |
| কষে দেখি 7.4 | |
| 8. উৎপাদকে বিশ্লেষণ (Factorisation) | কষে দেখি 8.1 |
| কষে দেখি 8.2 | |
| কষে দেখি 8.3 | |
| কষে দেখি 8.4 | |
| কষে দেখি 8.5 | |
| 9. ভেদক ও মধ্যবিন্দু সংক্রান্ত উপপাদ্য (Transversal & Mid-Point Theorem). | কষে দেখি 9 |
| 10. লাভ ও ক্ষতি (Profit and Loss) | কষে দেখি 10.1 |
| কষে দেখি 10.2 | |
| 11. রাশিবিজ্ঞান (Statistics) | কষে দেখি 11.1 |
| কষে দেখি 11.2 | |
| 12. ক্ষেত্রফল সংক্রান্ত উপপাদ্য (Theorems on Area) | কষে দেখি 12 |
| 13. সম্পাদ্য : ত্রিভুজের সমান ক্ষেত্রফল বিশিষ্ট সামান্তরিক অঙ্কন | কষে দেখি 13 |
| 14. সম্পাদ্য : চতুর্ভুজের সমান ক্ষেত্রফল বিশিষ্ট ত্রিভুজ অঙ্কন | কষে দেখি 14 |
| 15. ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল (Area & Perimeter of Triangle & Quadrilateral) | কষে দেখি 15.1 |
| কষে দেখি 15.2 | |
| কষে দেখি 15.3 | |
| 16. বৃত্তের পরিধি (Circumference of Circle) | কষে দেখি 16 |
| 17. সমবিন্দু সংক্রান্ত উপপাদ্য (Theorems on concurrence) | কষে দেখি 17 |
| 18. বৃত্তের ক্ষেত্রফল (Area of Circle) | কষে দেখি 18 |
| 19. স্থানাঙ্ক জ্যামিতি: সরলরেখাংশের অন্তর্বিভক্ত ও বহিঃবিভক্ত (Co-ordinate Geometry: Internal and External Division of Straight-Line Segment) | কষে দেখি 19 |
| 20. স্থানাঙ্ক জ্যামিতি: ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল (Co-ordinate Geometry: Area of Triangular Region) | কষে দেখি 20 |
| 21. লগারিদম (Logarithm) | কষে দেখি 21 |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
এই কষে দেখি 11.1 Class 9|Koshe Dekhi 11.1 Class 9 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।

এখানে তোমরা তোমাদের নবম শ্রেণীতে| Class 9 এ কি কি পড়ানো হয়, মানে তোমাদের নবম শ্রেণী| Class 9 সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

