কষে দেখি 6 Class 9 ।সামান্তরিকের ধর্ম কষে দেখি 6 | Koshe Dekhi 6 Class 9 WBBSE.

শ্রেণী-নবম ; অধ্যায় -সামান্তরিকের ধর্ম ; কষে দেখি 6

---

কষে দেখি 6 Class 9 এর সুচিপত্রঃ-

কষে দেখি 6 Class 9 এর অংকের সমাধান গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ

কষে দেখি 6|Koshe Dekhi 6  WBBSE বোর্ডের অন্তর্গত তোমাদের নবম|Class 9 এর সামান্তরিকের ধর্ম অধ্যায়ের অনুশীলনী।

এই কষে দেখি 6 Class 9 এর অংক গুলি সম্পূর্ণ ভাবে সামান্তরিকের কিছু নিয়ম কে কাজে লাগিয়ে সমাধান করতে হবে।

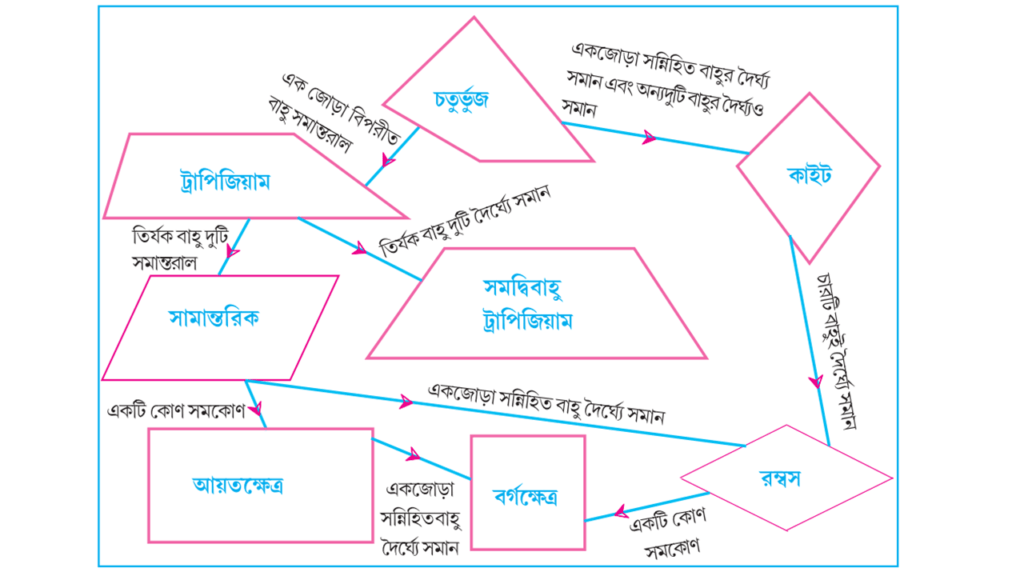
এই Koshe Dekhi 6 Class 9 এর অংকগুলি সমাধান করার জন্যে যে যে উপপাদ্য গুলি লাগবে সেগুলি হল-

উপপাদ্য 14
সামান্তরিকের, (i) প্রতিটি কর্ণ সামান্তরিককে দুটি সর্বসম ত্রিভুজে বিভক্ত করে। (ii) বিপরীত বাহুগুলির দৈর্ঘ্য সমান । (iii) বিপরীত কোণগুলি মানে সমান ।

উপপাদ্য 15
সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে।

উপপাদ্য 16
কোনো চতুর্ভুজের বিপরীত বাহুগুলির দৈর্ঘ্য সমান হলে চতুর্ভুজটি একটি সামান্তরিক হবে।

উপপাদ্য 17
কোনো চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সমান হলে চতুর্ভুজটি একটি সামান্তরিক হবে।

উপপাদ্য 18
কোনো চতুর্ভুজের একজোড়া বিপরীত বাহু সমান ও সমান্তরাল হলে চতুর্ভুজটি একটি সামান্তরিক হবে।

উপপাদ্য 19
কোনো চতুর্ভুজের দুটি কর্ণ পরস্পরকে সমদ্বিখণ্ডিত করলে চতুর্ভুজটি একটি সামান্তরিক হবে।

---

আগামিতে এই কষে দেখি 6 Class 9 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?

আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে?
কষে দেখি 6 Class 9 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 6 Class 9 তারপর এই চিহ্ন দেখে Click করলে আবার তোমরা এখানে এসে যাবে।

কষে দেখি 6 Class 9 এর Youtube Video:

Part 1

Part 2

Part 3

---

কষে দেখি 6 | Koshe Dekhi 6

1. প্রমাণ করি যে, একটি সামান্তরিকের কর্ণদ্বয়ের দৈর্ঘ্য সমান হলে, সামান্তরিকটি একটি আয়তাকার চিত্র।

সমাধানঃ-

প্রদত্তঃ

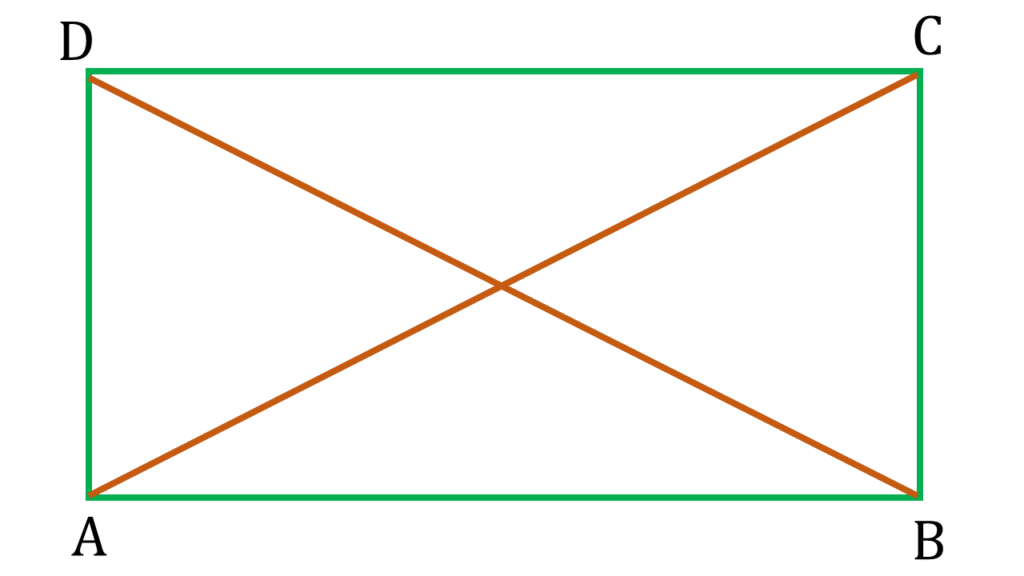
ABCD একটি সামান্তরিক যার AC ও BD কর্ণদ্বয়ের দৈর্ঘ্য সমান ।

প্রামাণ্যঃ

প্রমান করতে হবে,

ABCD একটি আয়তক্ষেত্র ।

প্রমাণঃ

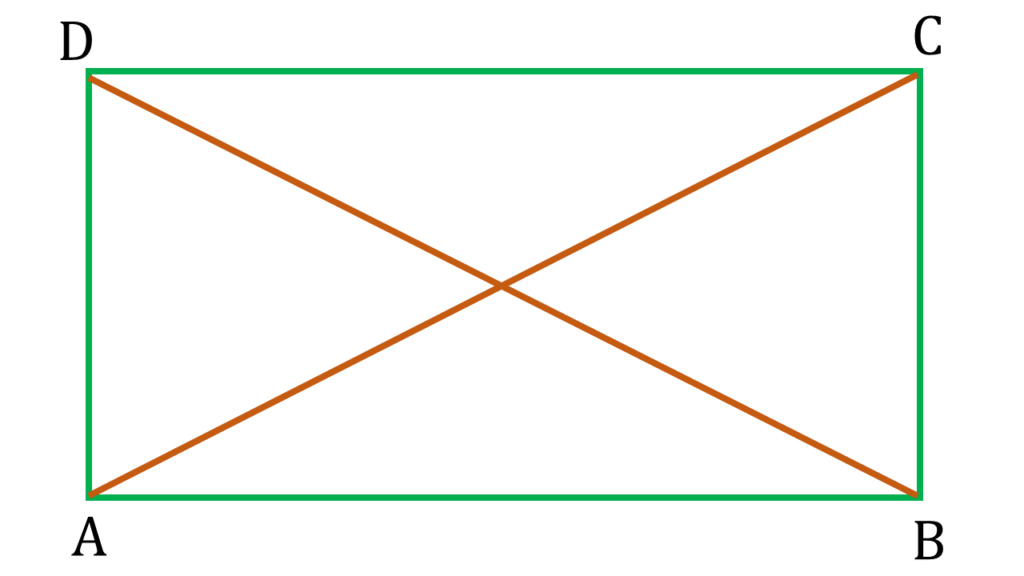
▲BAD ও ▲ABC এর মধ্যে,
BD=AC [∵ সামান্তরিকের কর্ণদ্বয় পরস্পর সমান ]
AD=BC
AB সাধারণ বাহু
∴ ▲BAD ≅ ▲ABC
⇒ ∠BAD=∠ABC [ সর্বসম ত্রিভুজের অনুরূপ কোণ ]

আবার, AD||BC এবং AB ভেদক

অতএব,

∠BAD+∠ABC = 180°

বা, ∠BAD + ∠BAD = 180°

বা, 2∠BAD = 180°

বা, ∠BAD = 90°

অতএব ABCD সামান্তরিকের একটি কোণ সমকোণ।

সুতরাং , ABCD একটি আয়তক্ষেত্র।

∴ ABCD একটি আয়তক্ষেত্র প্রমাণিত ।

---

---

2. প্রমাণ করি যে, একটি সামান্তরিকের কর্ণদ্বয়ের দৈর্ঘ্য সমান হলে এবং কর্ণদ্বয় পরস্পরকে লম্বভাবে ছেদ করলে, সামান্তরিকটি একটি বর্গাকার চিত্র।

সমাধানঃ-

প্রদত্তঃ

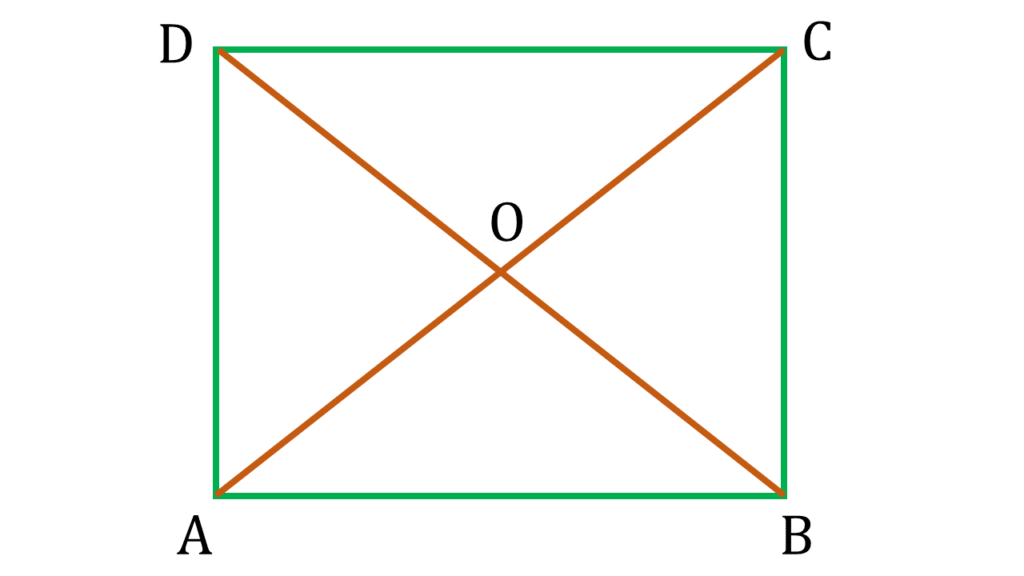
ABCD একটি সামান্তরিক যার AC ও BD কর্ণদ্বয়ের দৈর্ঘ্য সমান এবং কর্ণদ্বয় পরস্পরকে লম্বভাবে ছেদ করেছে ।

প্রামাণ্যঃ

প্রমান করতে হবে,

ABCD একটি বর্গাকার চিত্র ।

প্রমাণঃ

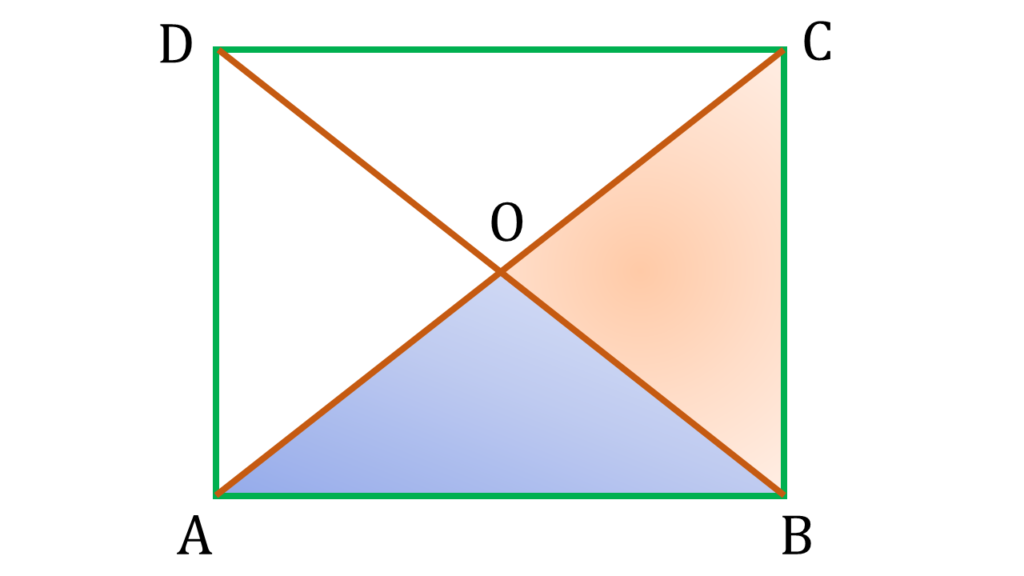
▲AOB ও ▲BOC এর মধ্যে,
AO=OC [ ∵ সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে ]
∠AOB=∠BOC
OB সাধারণ বাহু
∴ ▲AOB ≅ ▲BOC
⇒ AB=BC [ সর্বসম ত্রিভুজের অনুরূপ বাহু ]

অতএব, DC=AB=BC=AD ——(i)

আবার,

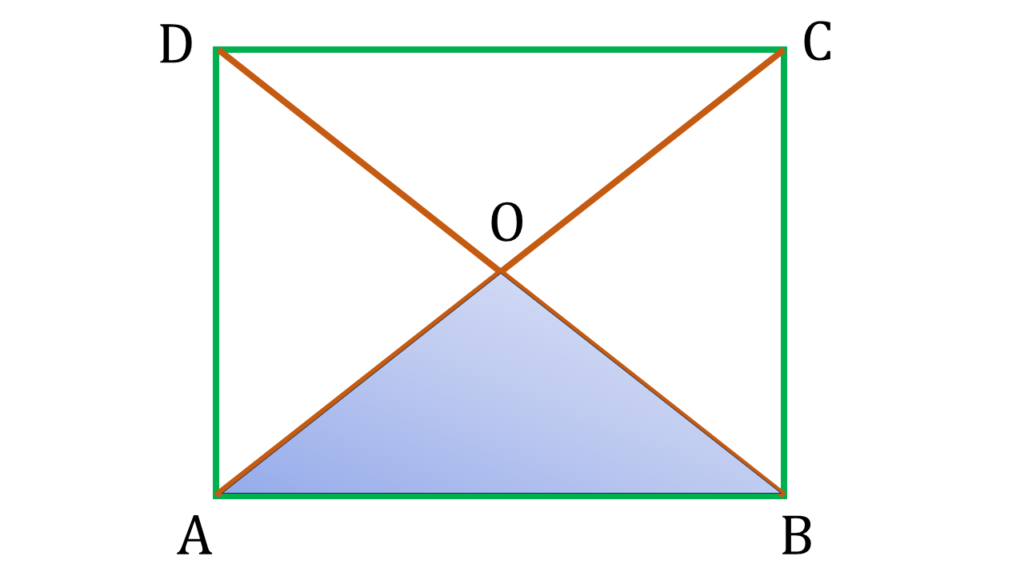
▲AOB এর মধ্যে,
AO=OB [ ∵ ABCD সামান্তরিকের কর্ণদ্বয় পরস্পর সমান ও পরস্পরকে লম্বভাবে সমদ্বিখণ্ডিত করে ]
∴ ∠OAB=∠OBA
আবার,
∠OAB+∠ABO+∠AOB=180°
বা, ∠OAB+∠OAB+90° = 180°
বা, 2∠OAB = 90°
বা, ∠OAB=45°

একইরকম ভাবে ▲AOD থেকে পাই,

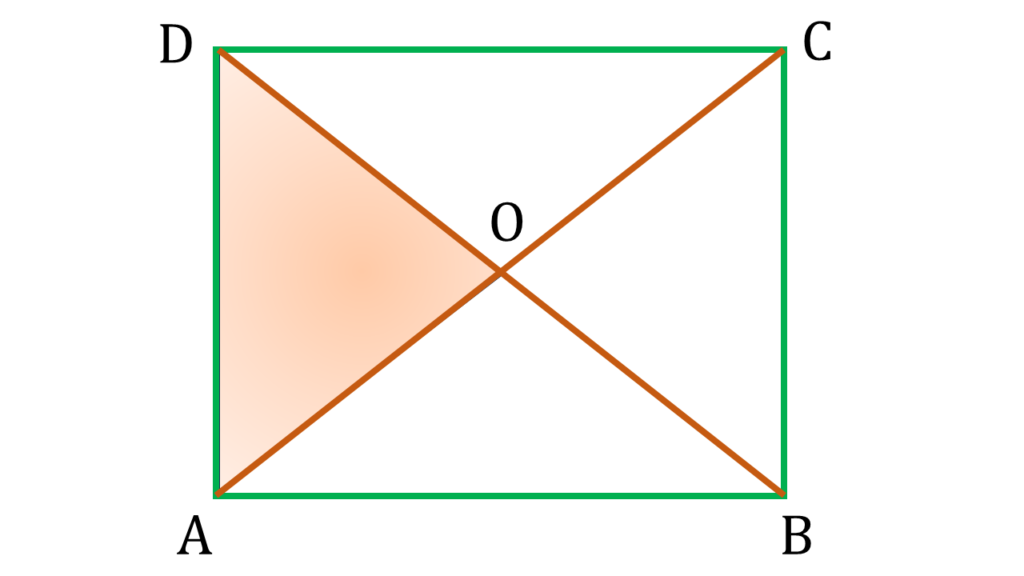
∠OAD = 45°

অতএব,

∠BAD

= ∠OAD + ∠OAB

= 45° + 45°

= 90°

সুতরাং , ABCD একটি বরগাকার চিত্র।

∴ ABCD একটি বরগাকার চিত্র প্রমাণিত ।

---

3. প্রমাণ করি যে, একটি সামান্তরিকের কর্ণদ্বয় পরস্পরকে লম্বভাবে ছেদ করলে, সামান্তরিকটি একটি রম্বস।

সমাধানঃ-

প্রদত্তঃ

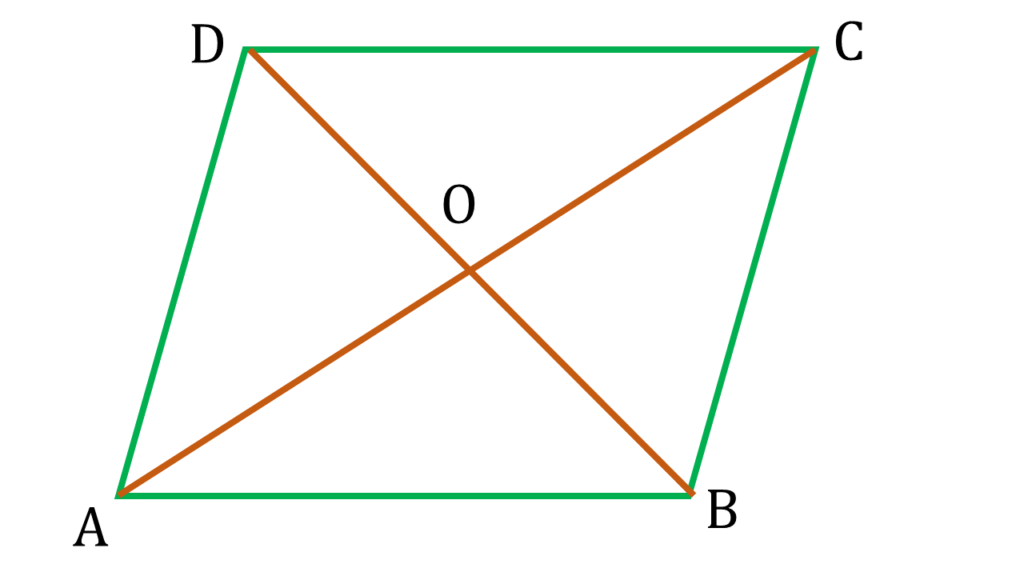
ABCD একটি সামান্তরিকের AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে লম্বভাবে ছেদ করেছে।

প্রামাণ্যঃ

প্রমান করতে হবে,

ABCD একটি রম্বস ।

প্রমাণঃ

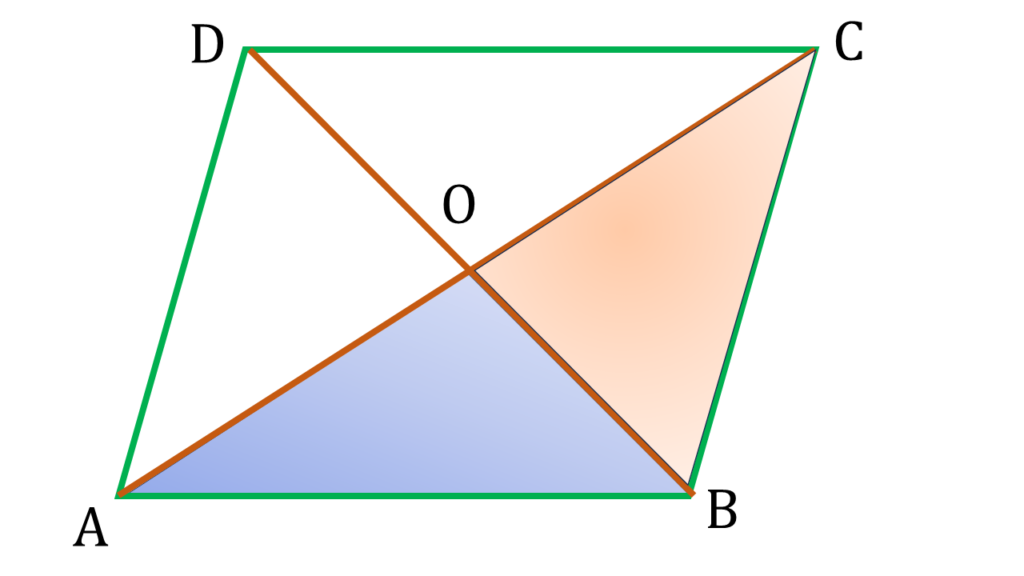
▲AOB ও ▲BOC এর মধ্যে,
AO=OC [ ∵ সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে ]
∠AOB=∠BOC
OB সাধারণ বাহু
∴ ▲AOB ≅ ▲BOC
⇒ AB=BC [ সর্বসম ত্রিভুজের অনুরূপ বাহু ]

∴ DC=AB=BC=AD

∴ ABCD একটি রম্বস প্রমাণিত ।

---

---

4. ABCD সামান্তরিকের AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করেছে। O বিন্দুগামী যেকোনো সরলরেখা AB ও DC বাহুকে যথাক্রমে P ও Q বিন্দুতে ছেদ করেছে। প্রমাণ করি যে OP = OQ

সমাধানঃ-

প্রদত্তঃ

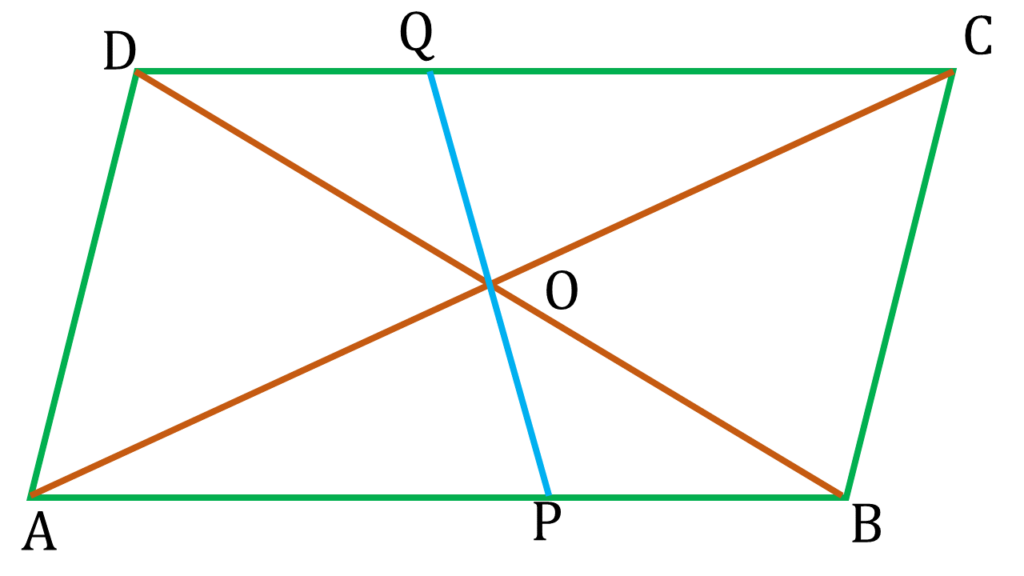
ABCD সামান্তরিকের AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করেছে। O বিন্দুগামী যেকোনো সরলরেখা AB ও DC বাহুকে যথাক্রমে P ও Q বিন্দুতে ছেদ করেছে।

প্রামাণ্যঃ

প্রমান করতে হবে,

OP=OQ ।

প্রমাণঃ

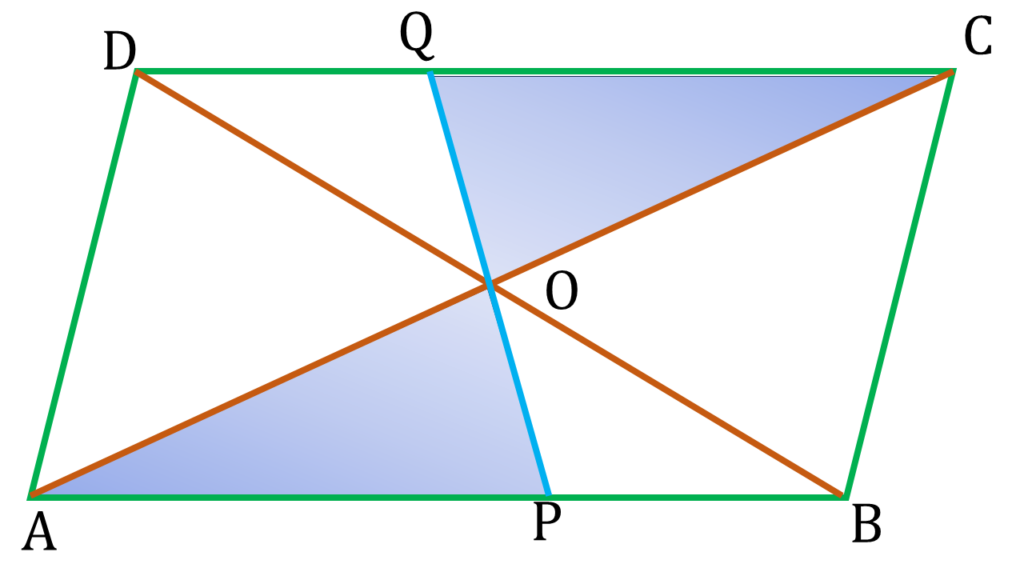
▲AOP ও ▲QOC এর মধ্যে,
AO=OC [ ∵ সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে ]
∠PAO=একান্তর∠QCO
∠AOP=বিপ্রতীপ∠QOC
∴ ▲AOP ≅ ▲QOC
⇒ OP=OQ [ সর্বসম ত্রিভুজের অনুরূপ বাহু ]

∴ OP=OQ প্রমাণিত ।

---

5. প্রমাণ করি যে, একটি সমদ্বিবাহু ট্রাপিজিয়ামের যে-কোনো সমান্তরাল বাহুসংলগ্ন দুটি কোণ পরস্পর সমান।

সমাধানঃ-

প্রদত্তঃ

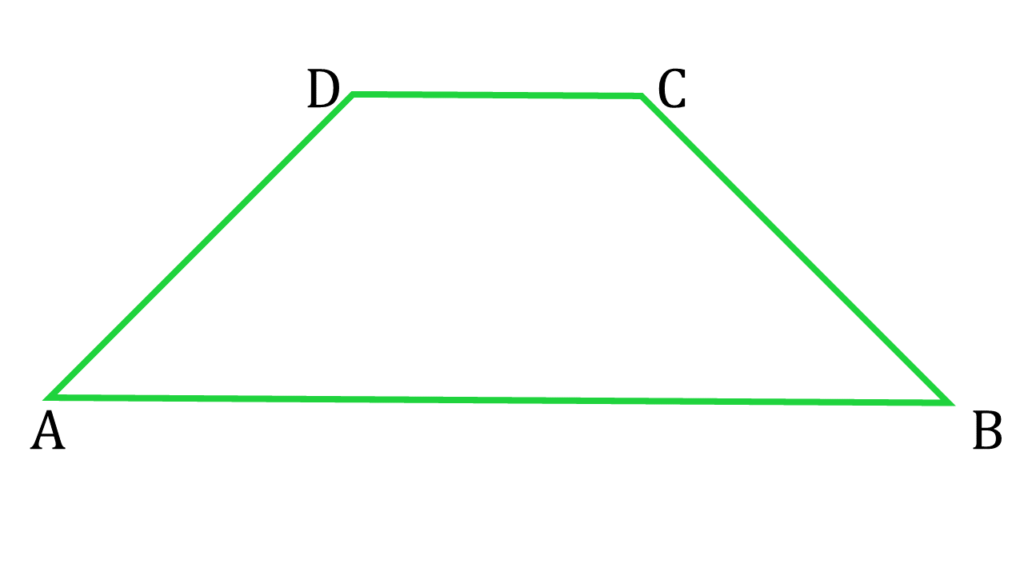
ABCD একটি সমদ্বিবাহু ট্রাপিজিয়াম যার AD=BC এবং AB||DC ।

প্রামাণ্যঃ

প্রমান করতে হবে,

∠ADC=∠BCD

এবং

∠DAC=∠ABC

অঙ্কনঃ

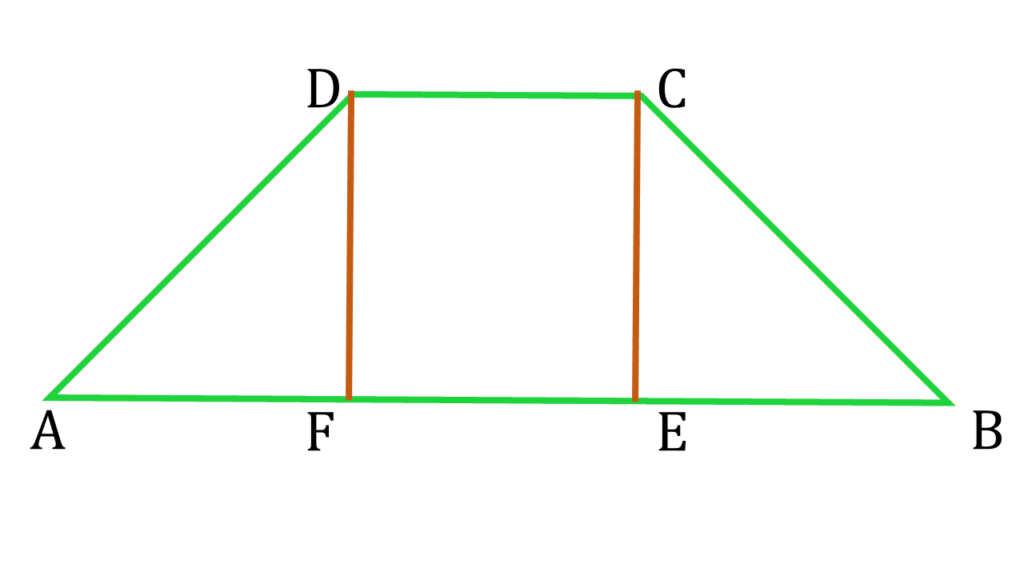
C ও D বিন্দু থেকে AB বাহুর উপর লম্ব অঙ্কন করলাম যারা AB বাহুকে যথাক্রমে E ও F বিন্দুতে ছেদ করেছে।

প্রমাণঃ

যেহেতু AB||DC এবং DF ও CE, AB বাহুর উপর লম্ব

অতএব, DF=CE

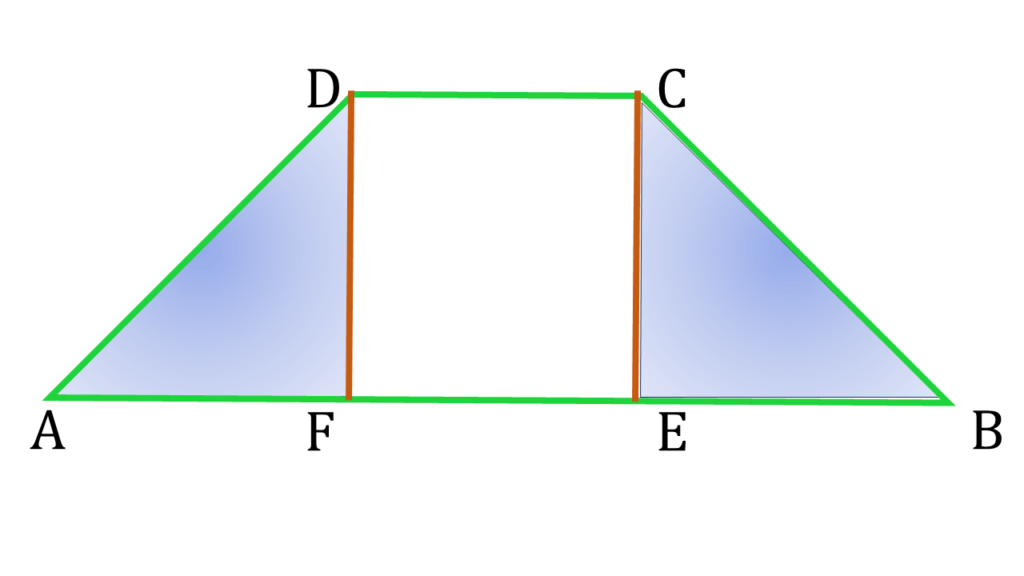
▲AFD ও ▲BCE এর মধ্যে,
AD=BC [ প্রদত্ত ]
DF=CE [ অঙ্কন থেকে পাই ]
∠AFD=∠BEC [ অঙ্কন থেকে পাই ]
∴ ▲AFD ≅ ▲BCE
⇒ ∠CBE=∠FAD ——(i) [ সর্বসম ত্রিভুজের অনুরূপ কোণ ]

আবার,

AB||DC এবং AD ও BC দুটি ভেদক।

অতএব,

∠FAD+∠ADC=180° ——(iii)

এবং

∠EBC+∠BCD=180° ——-(iv)

(iii) নং ও (iv) নং সমান করে পাই,

∠FAD+∠ADC=∠EBC+∠BCD

বা, ∠ADC=∠BCD [ (i) নং থেকে পাই ]

∴ একটি সমদ্বিবাহু ট্রাপিজিয়ামের যে-কোনো সমান্তরাল বাহুসংলগ্ন দুটি কোণ পরস্পর সমান প্রমাণিত ।

---

6. ABCD বর্গাকার চিত্রে BC বাহুর উপর P যে-কোনো একটি বিন্দু। B বিন্দু থেকে AP-এর উপর অঙ্কিত লম্ব DC বাহুকে Q বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, AP = BQ

সমাধানঃ-

প্রদত্তঃ

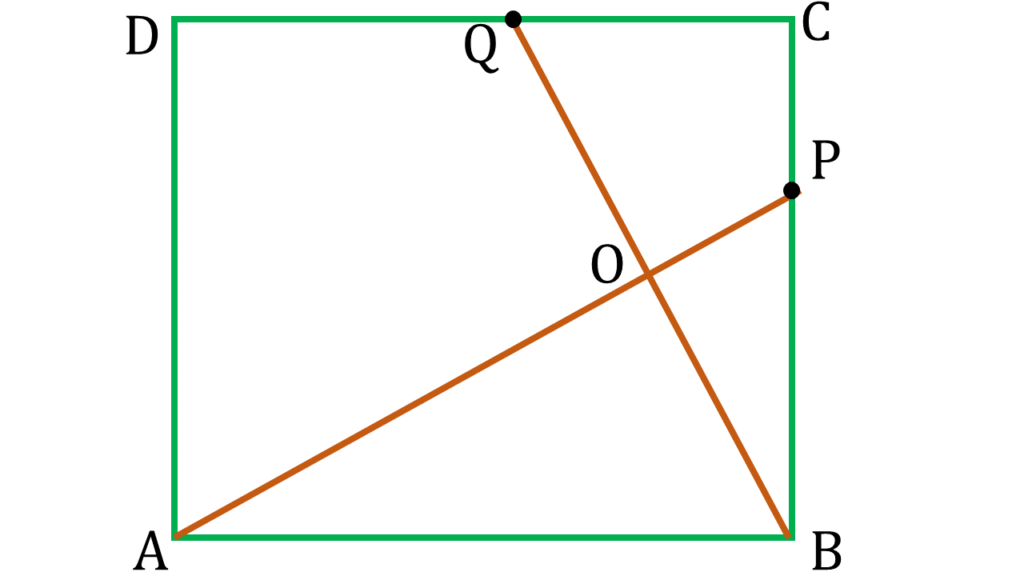
ABCD বর্গাকার চিত্রে BC বাহুর উপর P যে-কোনো একটি বিন্দু। B বিন্দু থেকে AP-এর উপর অঙ্কিত লম্ব DC বাহুকে Q বিন্দুতে ছেদ করেছে।

প্রামাণ্যঃ

প্রমান করতে হবে,

AP = BQ

প্রমাণঃ

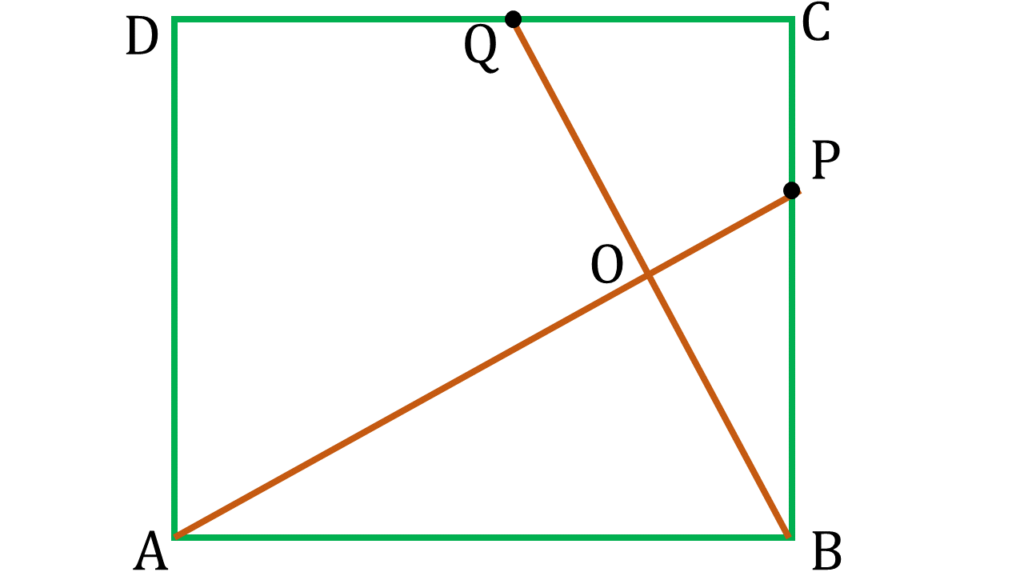
চতুর্ভুজ OPCQ এর মধ্যে,
∠OPC+∠PCQ+∠CQO+∠QOP=360°
বা, ∠OPC+90°+∠CQO+90°=360°
বা, ∠OPC+∠CQO=360°-90°-90°
বা, ∠OPC+∠CQO=180° ——-(i)

আবার, DC সরলরেখা থেকে পাই,

∠OQD+∠OQC=180° ——(ii)

(i) নং থেকে (ii) নং বিয়োগ করে পাই,

∠OPC+∠CQO-∠OQD-∠OQC =180°-180°

বা, ∠OPC-∠OQD=0

বা, ∠OPC=∠OQD

বা, 180°-∠OPC=180°-∠OQD

বা, ∠OPB=∠OQC

বা, ∠APB=∠BQC ——(iii)

এখন,

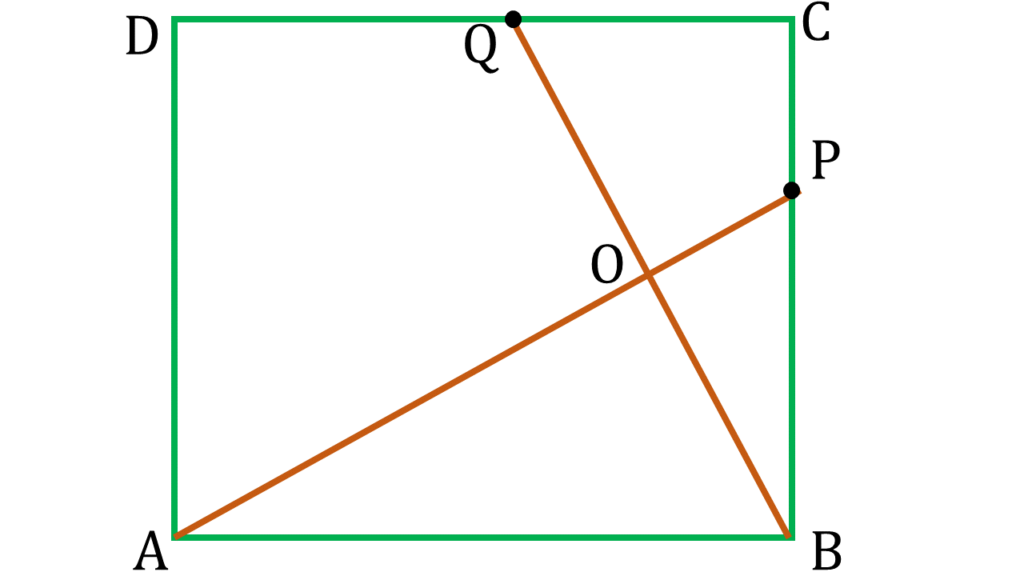
▲ABP এবং ▲BQC এর মধ্যে,
∠ABP=∠BCQ [ ∵ বর্গক্ষেত্রের প্রতিটি কোণ সমকোণ ]
∠APB=∠BQC [ (iii) নং থেকে পাই ]
AB=BC [∵ বর্গক্ষেত্রের প্রতিটি বাহু সমান ]
∴ ▲ABP ≅ ▲BQC
⇒ AP=BQ [ সর্বসম ত্রিভুজের অনুরূপ বাহু ]

∴ AP=BQ প্রমাণিত ।

---

---

7. প্রমাণ করি যে, একটি চতুর্ভুজের দুটি বিপরীত কোণ পরস্পর সমান ও দুটি বিপরীত বাহু পরস্পর সমান্তরাল হলে, চতুর্ভুজটি একটি সামান্তরিক।

সমাধানঃ-

প্রদত্তঃ

মনে করি ABCD একটি চতুর্ভুজ যার দুটি বিপরীত কোণ যথা ∠ABC এবং ∠ADC সমান এবং দুটি বিপরীত বাহু যথা AB ও CD পরস্পর সমান্তরাল।

অর্থাৎ,

∠ABC=∠ADC এবং AB||CD

প্রামাণ্যঃ

প্রমান করতে হবে,

চতুর্ভুজ ABCD একটি সামান্তরিক।

অঙ্কনঃ

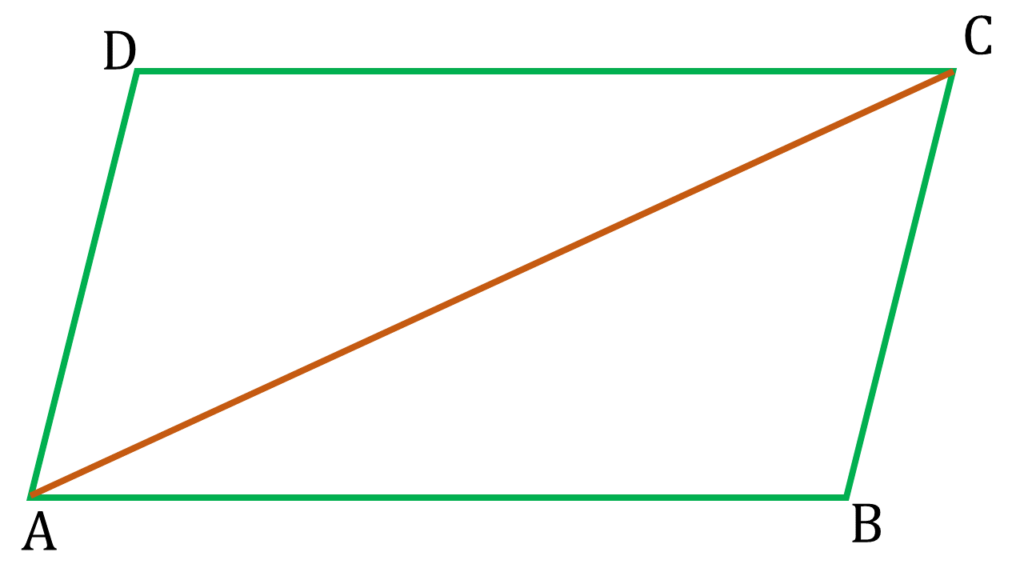
AC যুক্ত করলাম ।

প্রমাণঃ

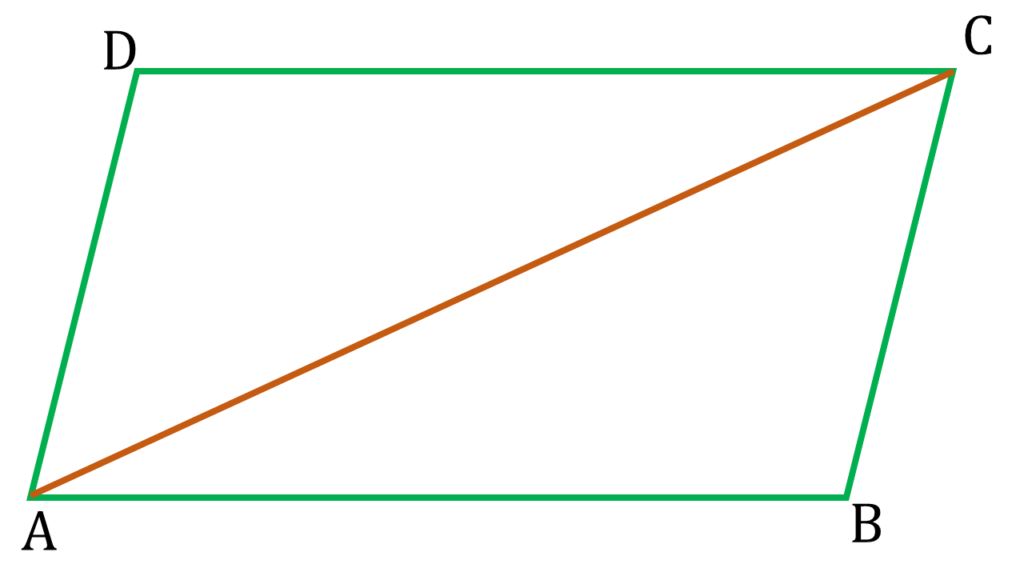
▲ADC এবং ▲ABC এর মধ্যে,
∠ABC=∠ADC
∠BAC=একান্তর∠ACD [ ∵ AB||DC এবং AC একটি ছেদক ]
AC সাধারণ বাহু
∴ ▲ADC ≅ ▲ABC
⇒ AB=DC [ সর্বসম ত্রিভুজের অনুরূপ বাহু ]

অতএব ABCD চতুর্ভুজের একজোড়া বিপরীত বাহু পরস্পর সমান ও সমান্তরাল।

সুতরাং, চতুর্ভুজ ABCD একটি সামান্তরিক।

∴ চতুর্ভুজ ABCD একটি সামান্তরিক প্রমাণিত ।

---

8. ▲ABC-এর BP ও CQ মধ্যমা দুটি যথাক্রমে R ও S বিন্দু পর্যন্ত এমনভাবে বর্ধিত করা হল যে, BP = PR এবং CQ = QS হয়। প্রমাণ করি যে, S, A, R বিন্দু তিনটি সমরেখ।

সমাধানঃ-

প্রদত্তঃ

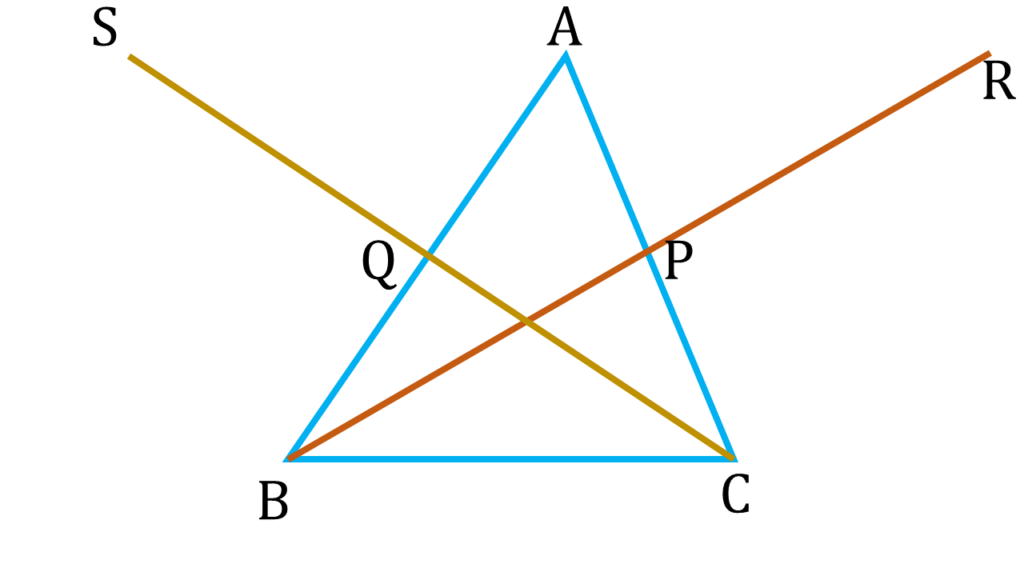
▲ABC-এর BP ও CQ মধ্যমা দুটি যথাক্রমে R ও S বিন্দু পর্যন্ত এমনভাবে বর্ধিত করা হল যে, BP = PR এবং CQ = QS হয়।

অতএব, AP=PC এবং AQ=BQ ।

প্রামাণ্যঃ

প্রমান করতে হবে,

S, A, R বিন্দু তিনটি সমরেখ।

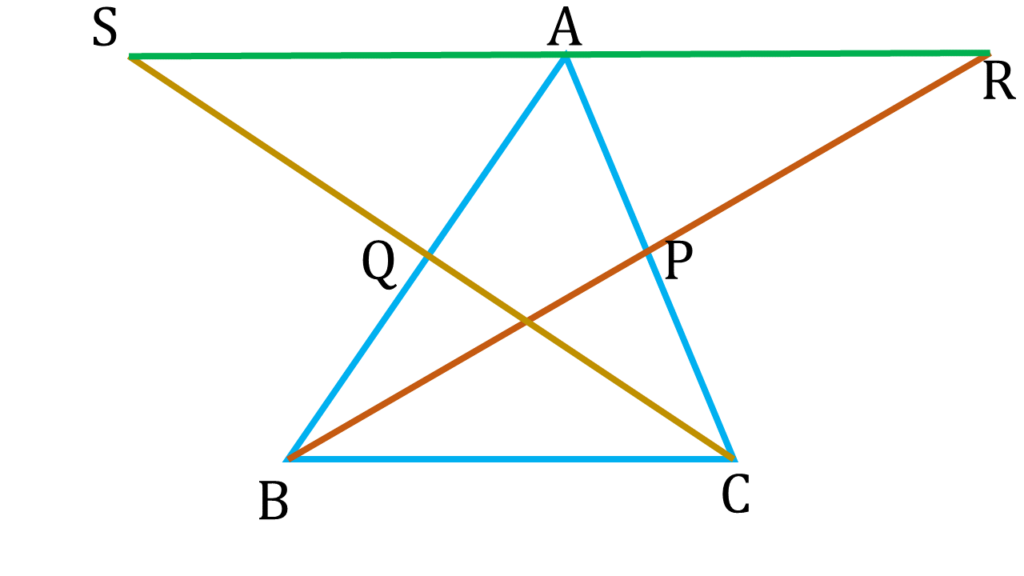
অঙ্কনঃ

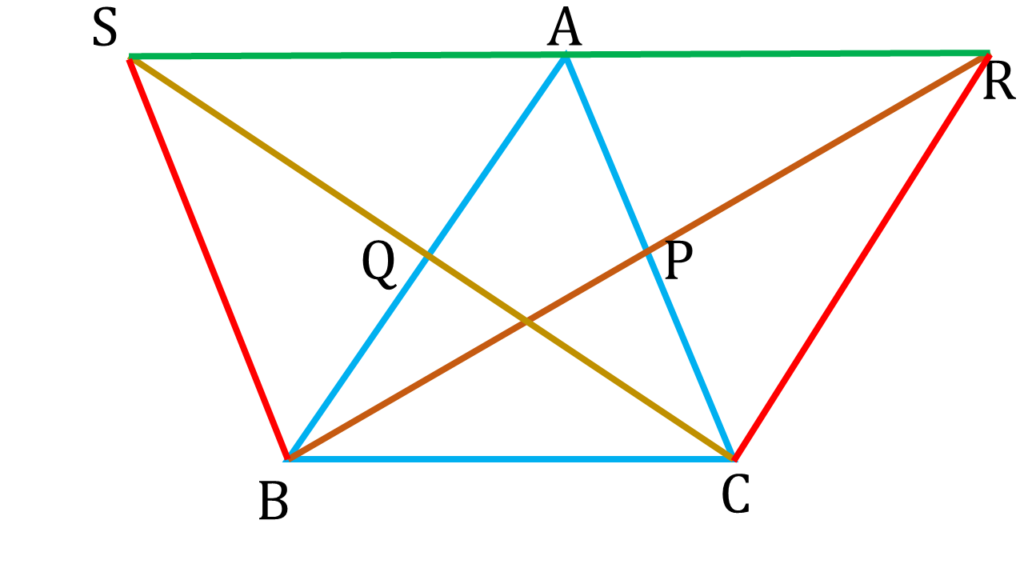
BS ও CR যুক্ত করলাম।

প্রমাণঃ

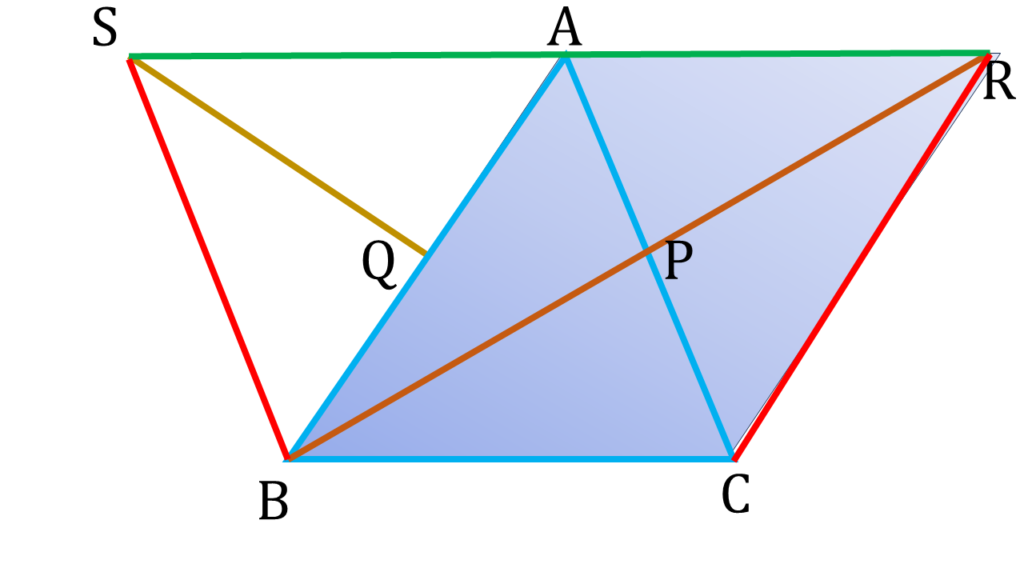
চতুর্ভুজ ABCR এর
AC ও BR দুটি কর্ণ
এবং
AP=PC এবং BP=PR
∴ চতুর্ভুজ ABCR এর দুটি কর্ণ পরস্পরকে সমদ্বিখণ্ডিত করে।
সুতরাং চতুর্ভুজ ABCR একটি সামান্তরিক।
⇒ BC||AR

আবার,

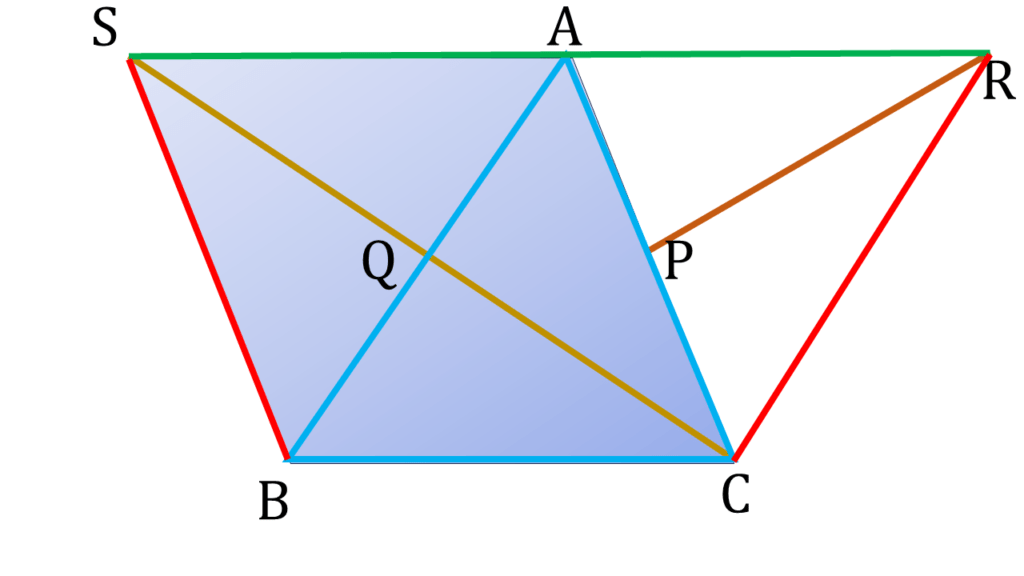
চতুর্ভুজ ACBS এর
AB ও SC দুটি কর্ণ
এবং
AQ=QB এবং CQ=QS
∴ চতুর্ভুজ ACBS এর দুটি কর্ণ পরস্পরকে সমদ্বিখণ্ডিত করে।
সুতরাং চতুর্ভুজ ACBS একটি সামান্তরিক।
⇒ BC||SA

যেহেতু, BC||AR এবং BC||SA

অতএব AR||SA

আবার যেহেতু A বিন্দুটি SA ও AR দুটি সরলরেখাংশতেই আছে, সুতরাং SA ও AR একই সরলরেখায় আছে।

সুতরাং, S, A ও R বিন্দু তিনটি সমরেখ।

∴ S, A ও R বিন্দু তিনটি সমরেখ প্রমাণিত ।

---

9. PQRS সামান্তরিকের SQ কর্ণ K ও L বিন্দুতে সমান তিনভাগে বিভক্ত হয়েছে। PK, SR-কে M বিন্দুতে এবং RL, PQ কে N বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, PMRN একটি সামান্তরিক।

সমাধানঃ-

প্রদত্তঃ

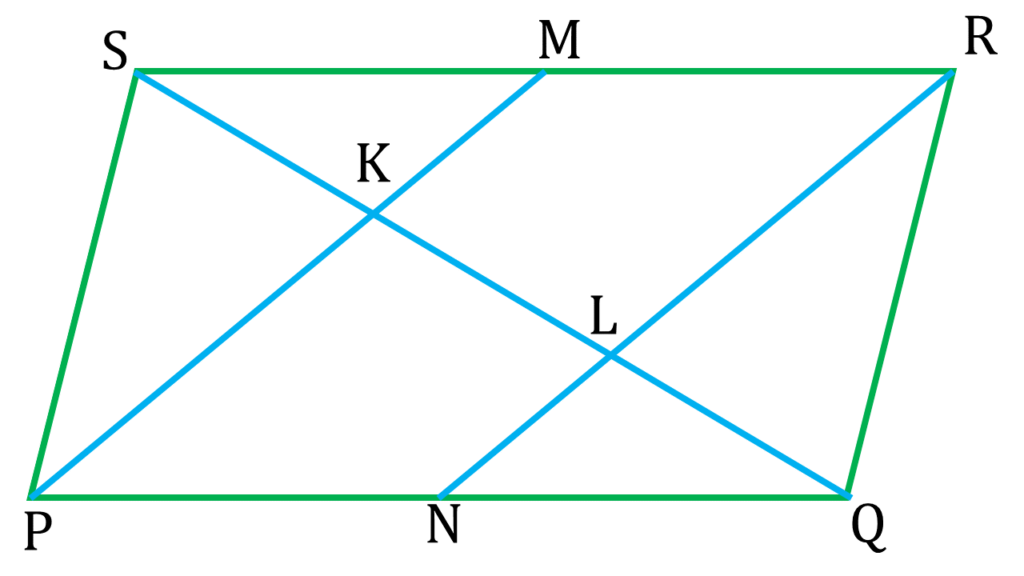
PQRS সামান্তরিকের SQ কর্ণ K ও L বিন্দুতে সমান তিনভাগে বিভক্ত হয়েছে। PK, SR-কে M বিন্দুতে এবং RL, PQ কে N বিন্দুতে ছেদ করেছে।

অতএব

SK=KL=LQ

প্রামাণ্যঃ

প্রমান করতে হবে,

PMRN একটি সামান্তরিক।

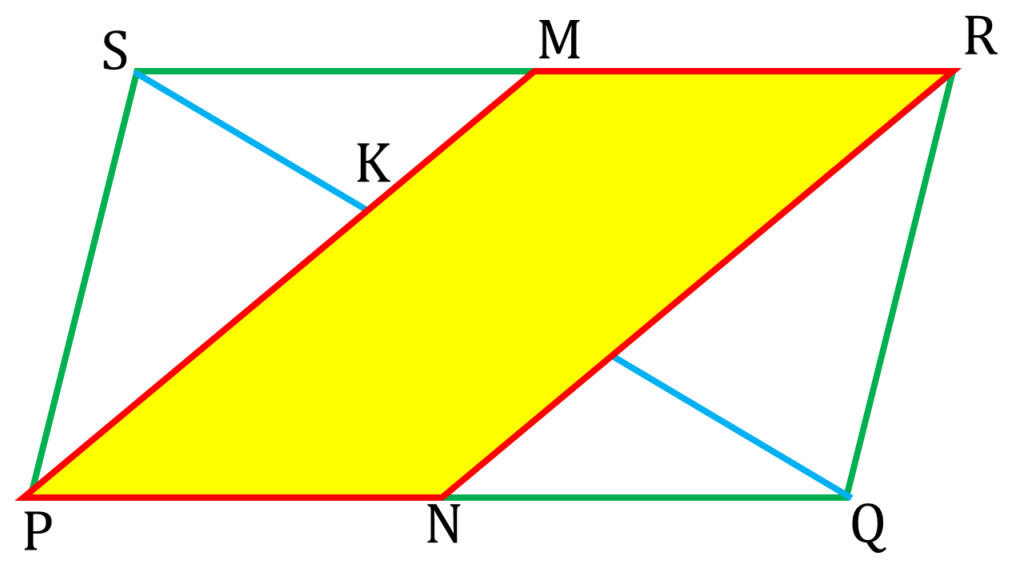
প্রমাণঃ

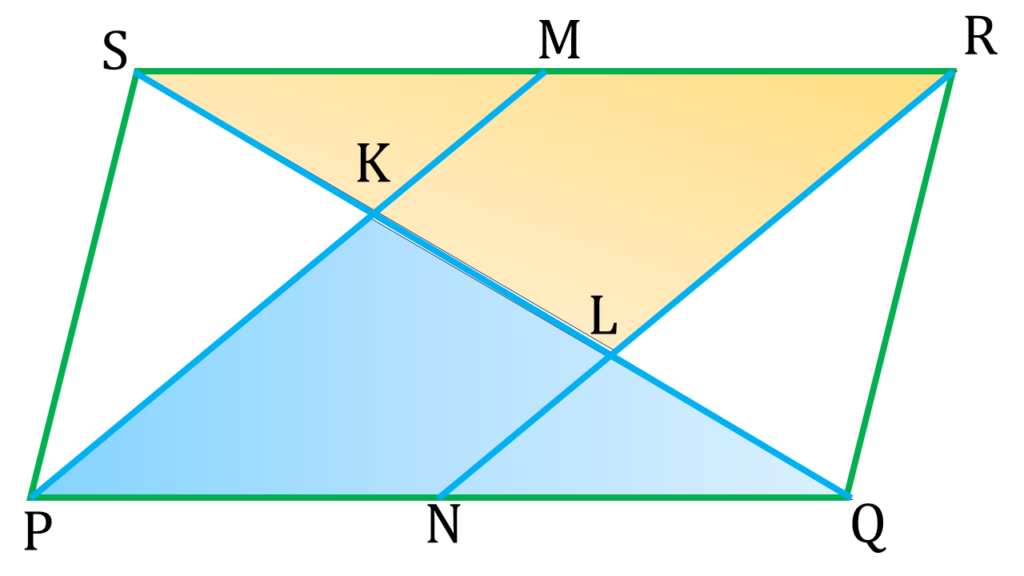
▲PKQ ও ▲SLR এর মধ্যে,
KQ=SL
SR=PQ [ ∵ PQRS একটি সামান্তরিক ]
∠PQK=একান্তর∠LSR
∴ ▲PKQ ≅ ▲SLR
⇒ ∠PKQ=∠SLR [ সর্বসম ত্রিভুজের অনুরূপ কোণ ] ———-(i)

এখন,

PM ও NR দুটি সরলরেখার KL একটি ছেদক এবং (i) নং থেকে পেলাম

∠PKQ=∠SLR

অতএব PM||NR —–(ii)

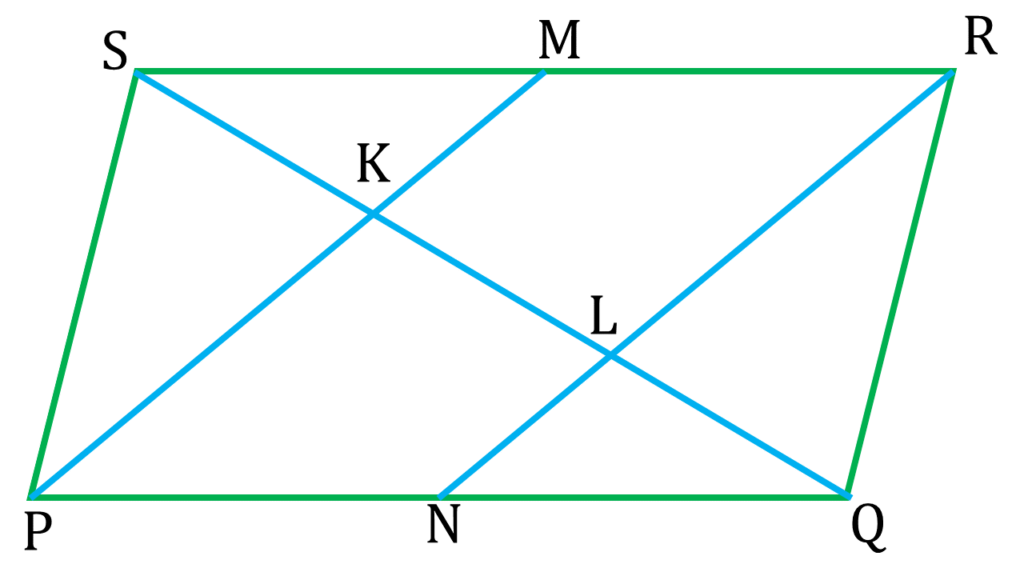
আবার, PQ||SR

⇒ ∠MRN=একান্তর∠RNQ=অনুরূপ∠MPN

বা, ∠MRN=∠MPN —–(iii)

আবার,

∠RNQ=অনুরূপ∠MPN=একান্তর∠SMK

বা, ∠RNQ=∠SMK

এখন ,

∠PNR		=180°-∠RNQ
		=180°-∠SMK
		=∠KMR
∴ ∠PNR=∠KMR

অতএব চতুর্ভুজ PNRM এর বিপরীত কোণগুলি পরস্পর সমান।

∴ PMRN একটি সামান্তরিক প্রমাণিত ।

---

---

10. ABCD ও AECF দুটি সামান্তরিকেরই AC একটি কর্ণ। B, E, D, F বিন্দুগুলি সমরেখ না হলে, প্রমাণ করি যে, BEDF একটি সামান্তরিক।

সমাধানঃ-

প্রদত্তঃ

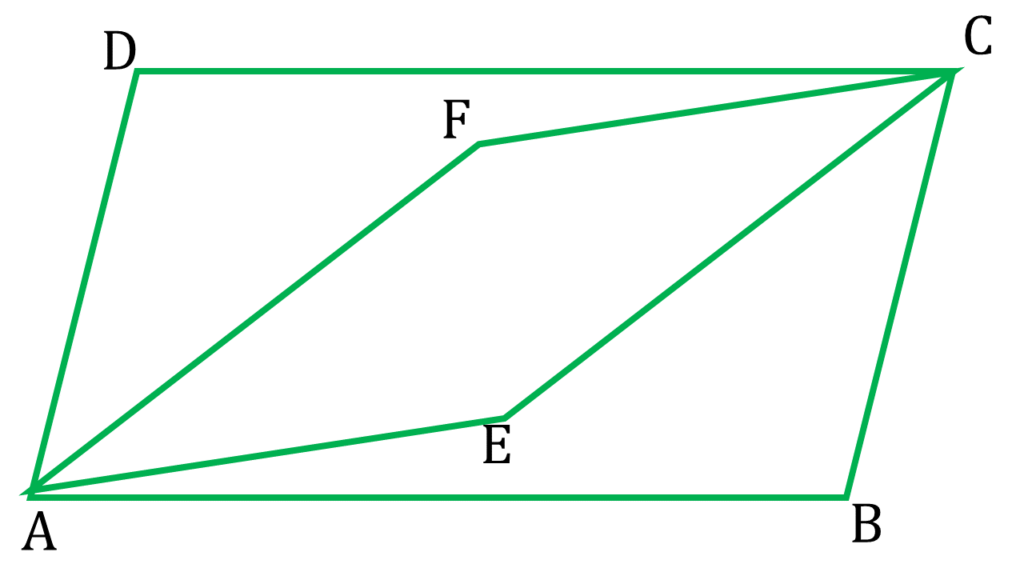
ABCD ও AECF দুটি সামান্তরিকেরই AC একটি কর্ণ।

প্রামাণ্যঃ

প্রমান করতে হবে,

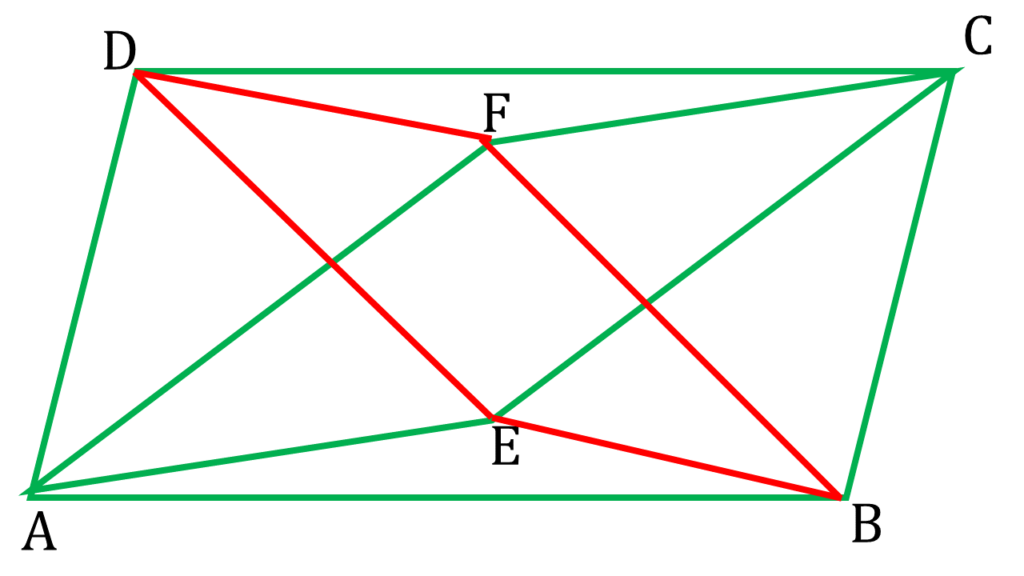
BEDF একটি সামান্তরিক।

অঙ্কনঃ

AF বাহুকে বর্ধিত করলাম যা DC বাহুকে M বিন্দুতে ছেদ করেছে এবং CE বাহুকে বর্ধিত করলাম যা AB বাহুকে N বিন্দুতে ছেদ করেছে।

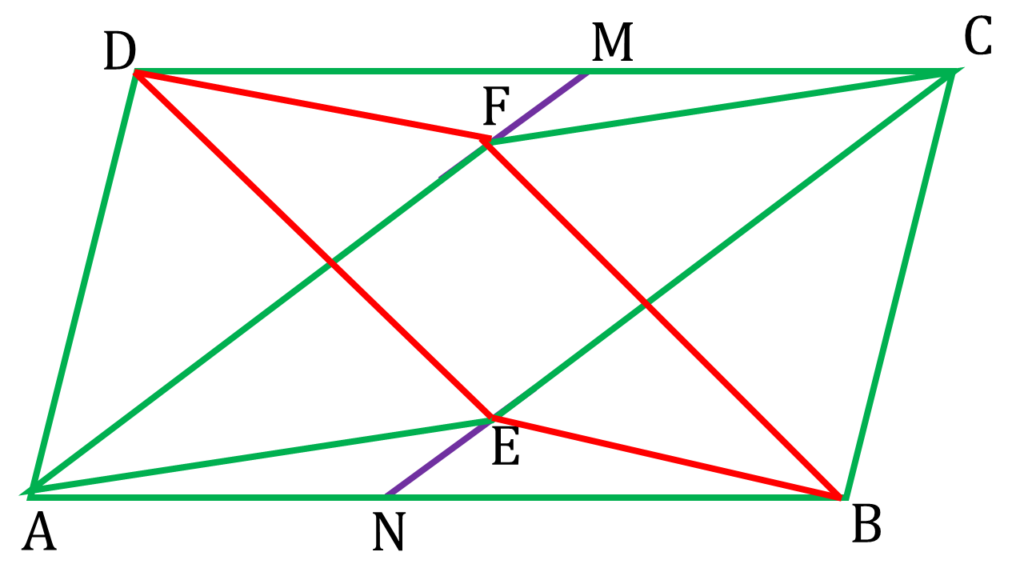
যার ফলে ANCM একটি সামান্তরিক তৈরি হলো।

প্রমাণঃ

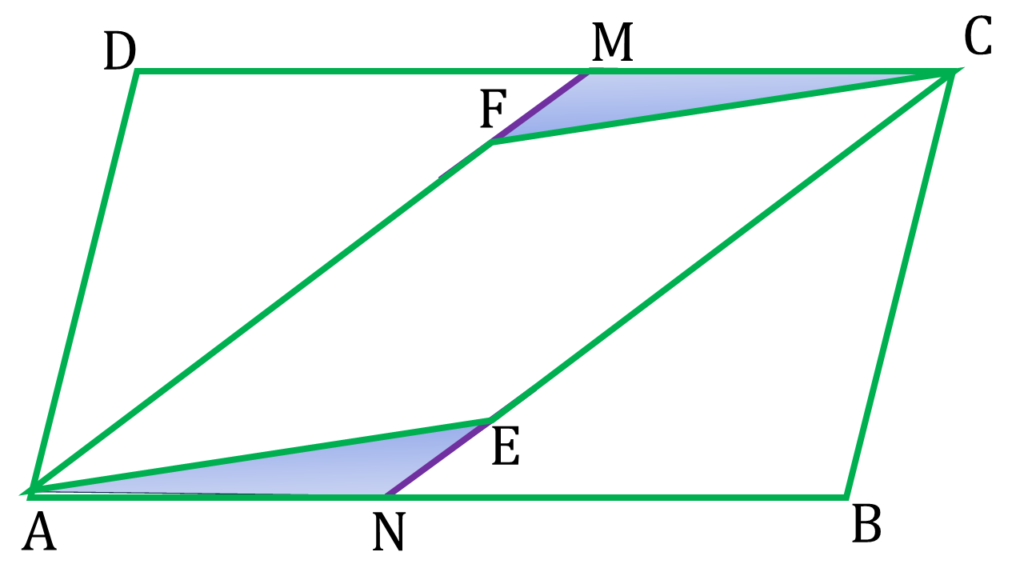
▲CFM ও ▲ANE এর মধ্যে,
AN=CM [ ∵ ANCM একটি সামান্তরিক ]
CF=AE [ ∵ AECF একটি সামান্তরিক ]
∠ANE=∠FMC [ ANCM সামান্তরিকের বিপরীত কোণ সমান ]
∴ ▲CFM ≅ ▲ANE
⇒ NE=FM [ সর্বসম ত্রিভুজের অনুরূপ বাহু ] ——-(i)
⇒ ∠FCM=∠EAN [ সর্বসম ত্রিভুজের অনুরূপ কোণ ] ——-(ii)
⇒ AN=CM [ সর্বসম ত্রিভুজের অনুরূপ বাহু ] ——-(iiii)

ABCD সামান্তরিকের,

AB=CD

বা, AN+BN=DM+CM

বা, BN=DM [ (iii) নং থেকে পাই ] ———-(iv)

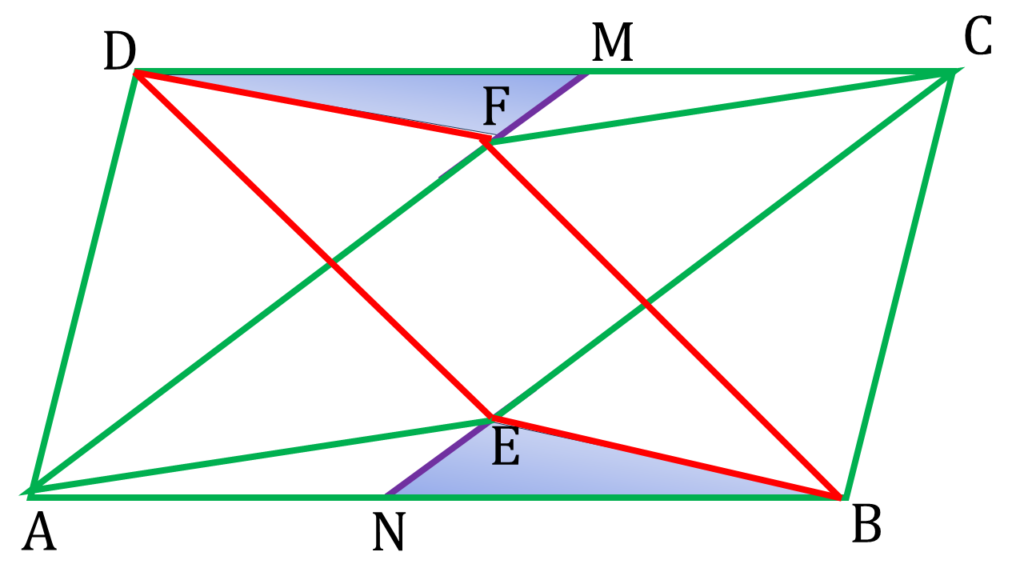
▲BNE ও ▲DFM এর মধ্যে,
BN=DM [ ∵ ANCM একটি সামান্তরিক ]
NE=FM [ (i) নং থেকে পাই ]
∠BNE=একান্তর∠FMC=অনুরূপ∠DMF
∴ ▲BNE ≅ ▲DFM
⇒ BE=DF [ সর্বসম ত্রিভুজের অনুরূপ বাহু ]

আবার,

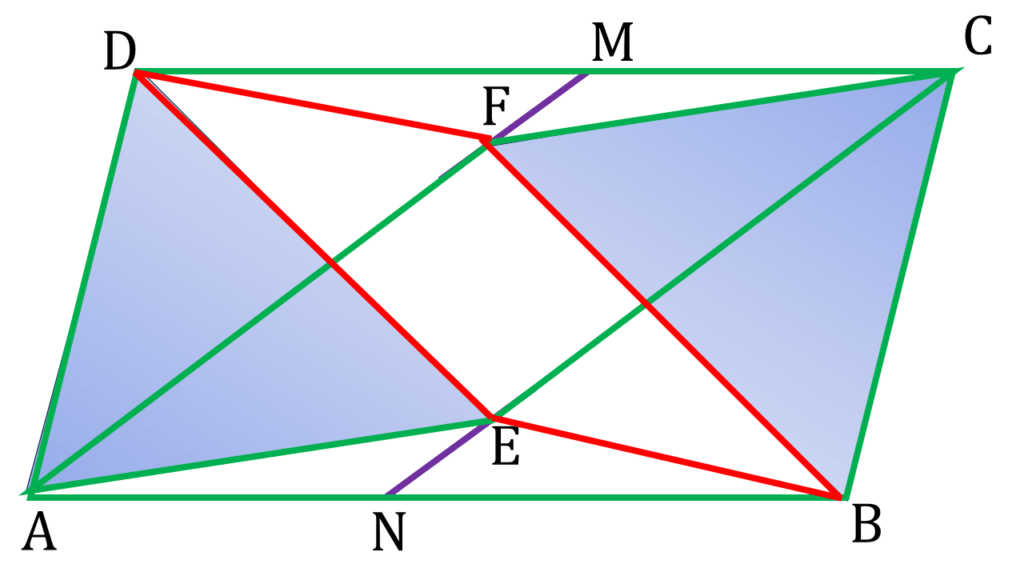
▲BFC ও ▲ADE এর মধ্যে,
AD=BC [ ∵ ABCD একটি সামান্তরিক ]
AE=CF [ ∵ AECF একটি সামান্তরিক ]
∠DAE	=∠DAB-∠NAE
	=∠BCD-∠FCM [ ∵ (ii) নং এবং সামান্তরিক ABCD থেকে পাই ]
	=∠BCF
∴ ▲BFC ≅ ▲ADE
⇒ DE=BF [ সর্বসম ত্রিভুজের অনুরূপ বাহু ]

অতএব চতুর্ভুজ BEDF এর বিপরীত বাহুগুলি পরস্পর সমান।

সুতরাং, BEDF একটি সামান্তরিক।

∴ BEDF একটি সামান্তরিক প্রমাণিত ।

---

11. ABCD একটি চতুর্ভুজ। ABCE ও BADF দুটি সামান্তরিক অঙ্কন করা হলো। প্রমাণ করি যে, CD ও EF পরস্পরকে সমদ্বিখণ্ডিত করে।

সমাধানঃ-

প্রদত্তঃ

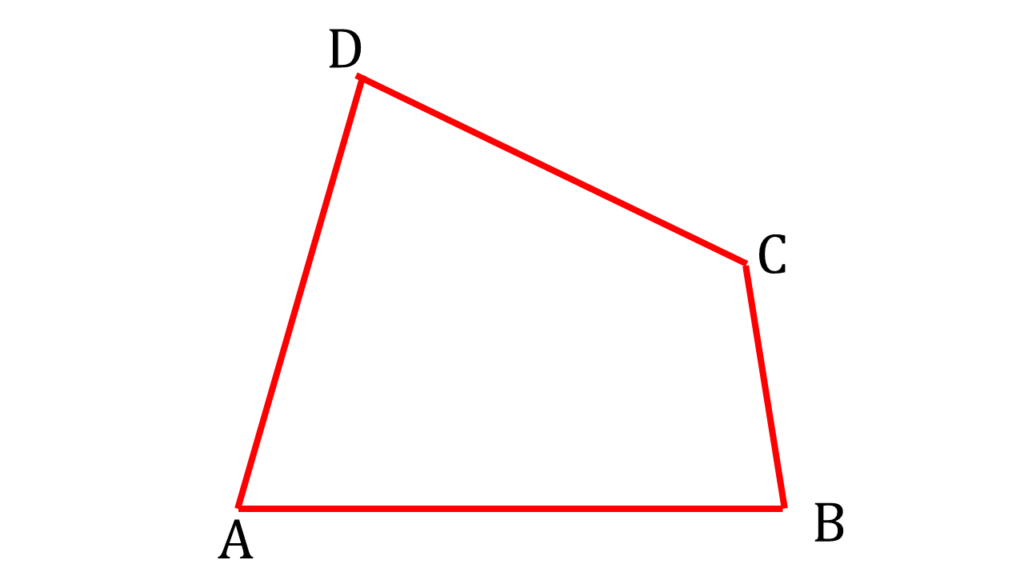
ABCD একটি চতুর্ভুজ। ABCE ও BADF দুটি সামান্তরিক অঙ্কন করা হলো।

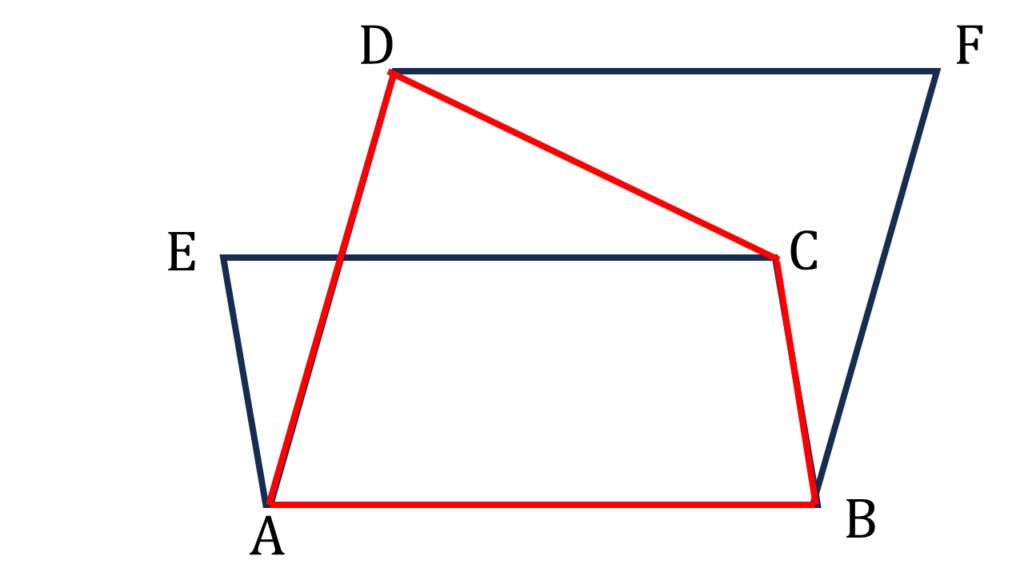
ABCE ও BADF দুটি সামান্তরিক থেকে পাই,
(i)	AB=EC এবং AB||EC
(ii)	AB=DF এবং AB||DF

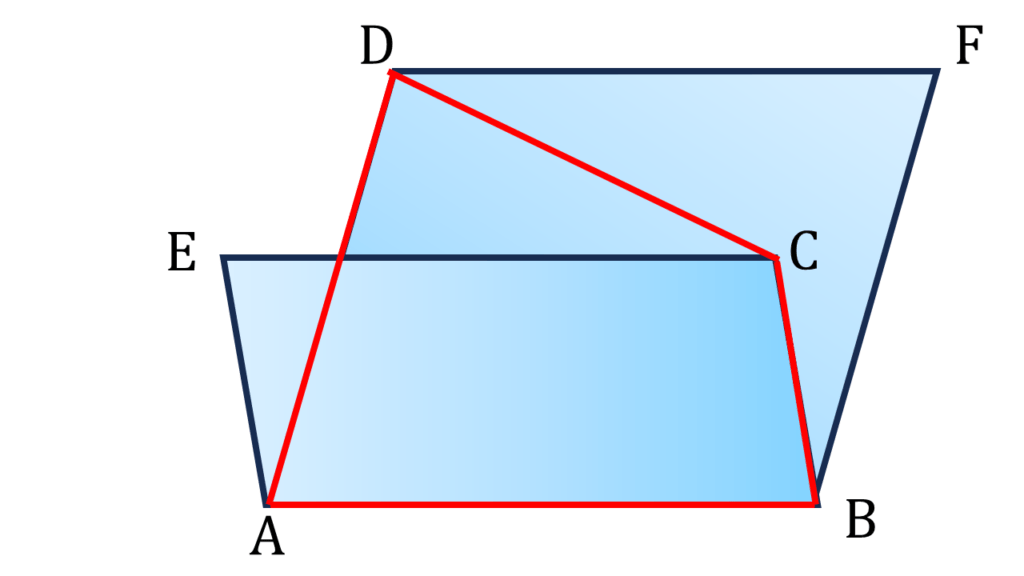
প্রামাণ্যঃ

প্রমান করতে হবে,

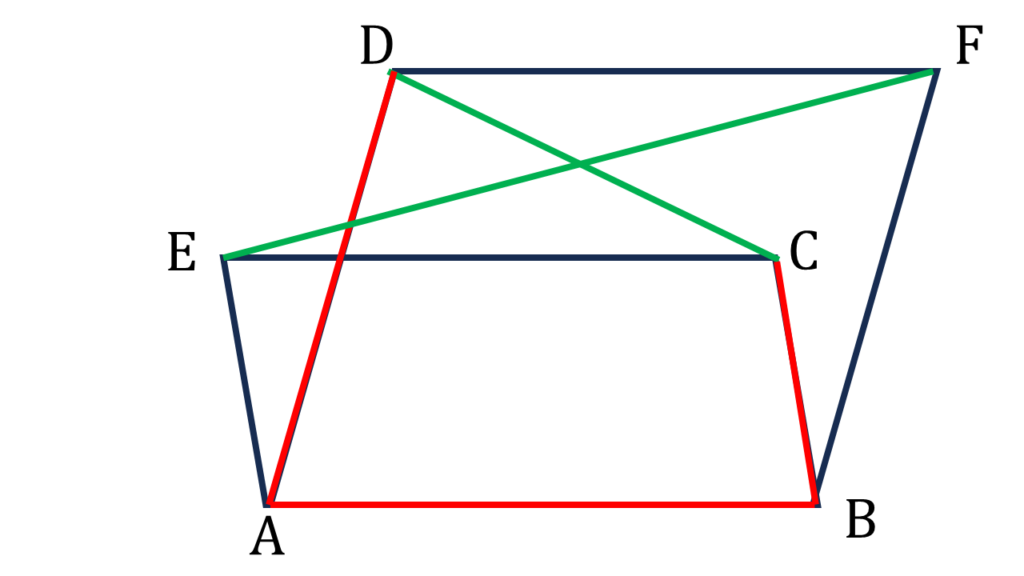
CD ও EF পরস্পরকে সমদ্বিখণ্ডিত করে।

অঙ্কনঃ

ED এবং CF যুক্ত করলাম।

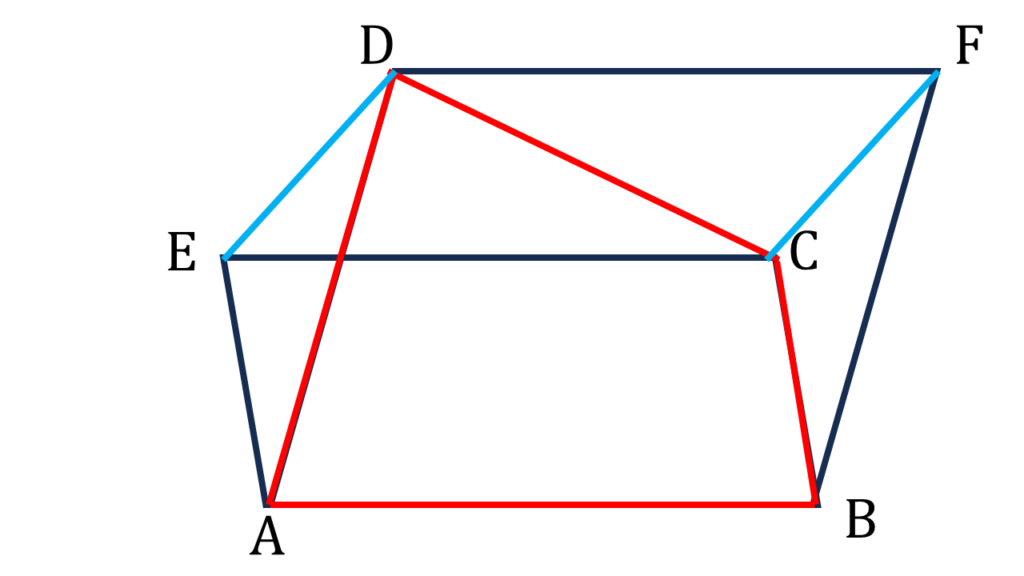
প্রমাণঃ

(i) ও (ii) নং থেকে পাই,

চতুর্ভুজ ECFD এর,

CE=DF এবং CE||DF

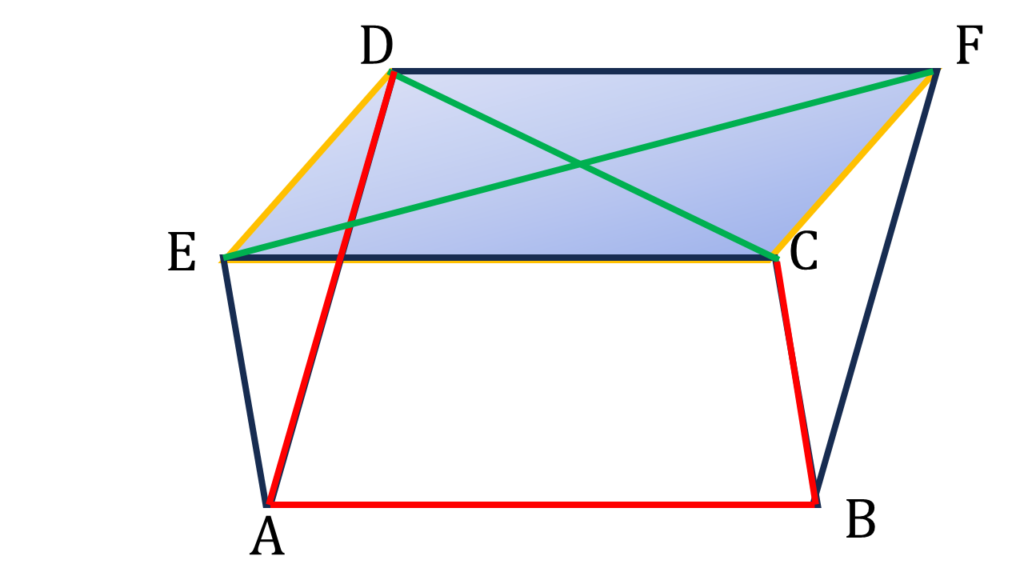
অতএব চতুর্ভুজ ECFD একটি সামান্তরিক।

এখন,

CD ও EF হল ECFD সামান্তরিকের দুটি কর্ণ।

অতএব CD ও EF পরস্পরকে সমদ্বিখণ্ডিত করে।

∴ CD ও EF পরস্পরকে সমদ্বিখণ্ডিত করে প্রমাণিত ।

---

12. ABCD সামান্তরিকের AB = 2 AD; প্রমাণ করি যে ∠BAD ও ∠ABC -এর সমদ্বিখণ্ডকদ্বয় DC বাহুর মধ্যবিন্দুতে সমকোণে মিলিত হয়।

সমাধানঃ-

প্রদত্তঃ

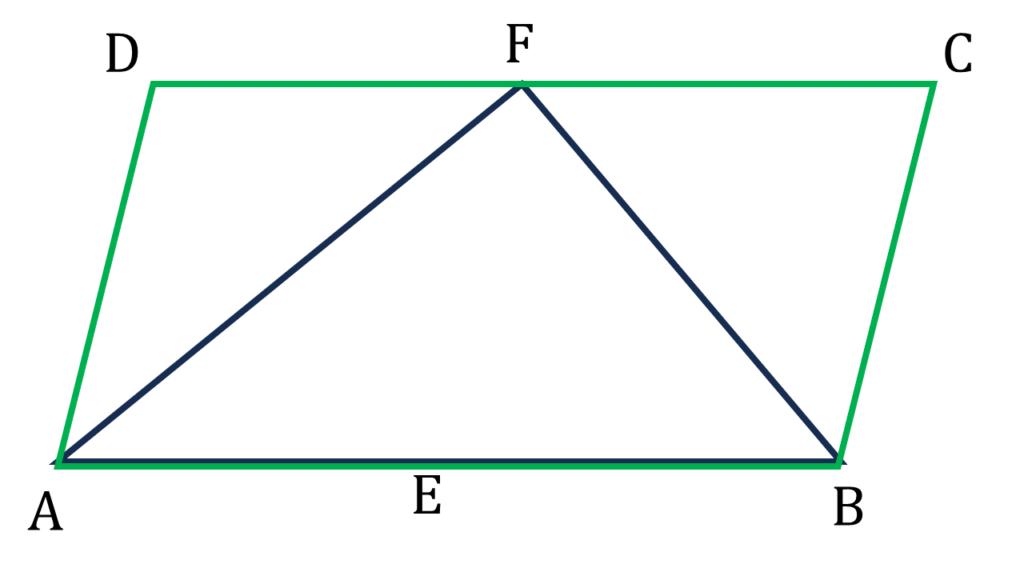
ABCD সামান্তরিকের AB = 2 AD, ∠BAD ও ∠ABC -এর সমদ্বিখণ্ডকদ্বয় DC বাহুর F বিন্দুতে মিলিত হয়েছে।

ধরি, AB বাহুর মধ্যবিন্দু হলো E ।

ABCD সামান্তরিক এবং AB = 2 AD থেকে পাই,
(i)	AD=AE=EB=BC
(ii)	∠ADF+∠BCD=180°

∠BAD ও ∠ABC -এর সমদ্বিখণ্ডকদ্বয় থেকে পাই,
(iii)	∠DAE=∠FAE
(iv)	∠EBF=∠CBF

প্রামাণ্যঃ

প্রমান করতে হবে,

∠BAD ও ∠ABC -এর সমদ্বিখণ্ডকদ্বয় DC বাহুর মধ্যবিন্দুতে সমকোণে মিলিত হয়।

প্রমাণঃ

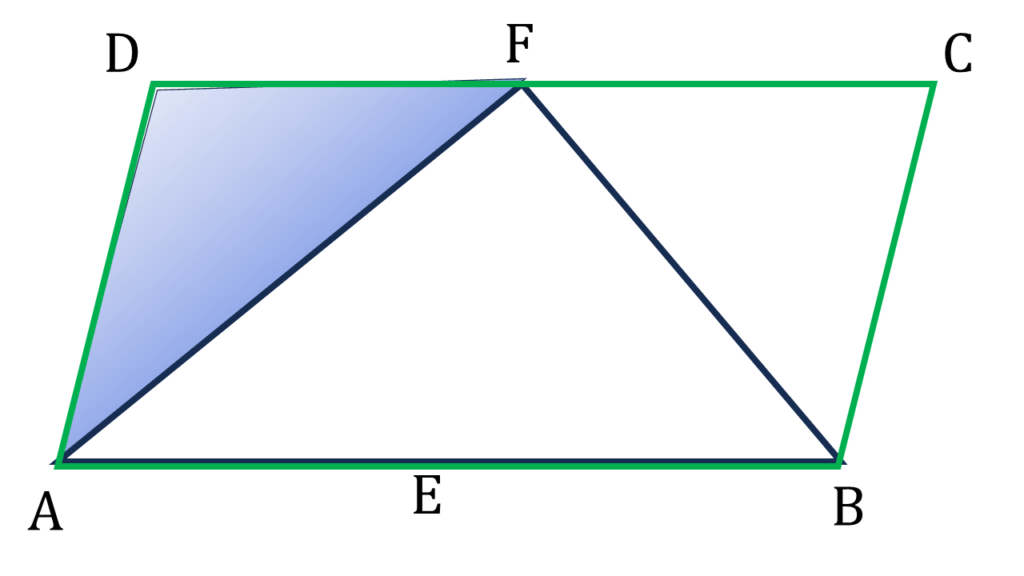
▲ADF এর মধ্যে,
∠DFA=একান্তর∠FAE=∠DAF [ ∵ DF||AE ও AF ছেদক এবং (iii) নং থেকে পাই]
∴ ▲ADF একটি সমদ্বিবাহু ত্রিভুজ যার, AD=DF
সুতরাং , DF=AE

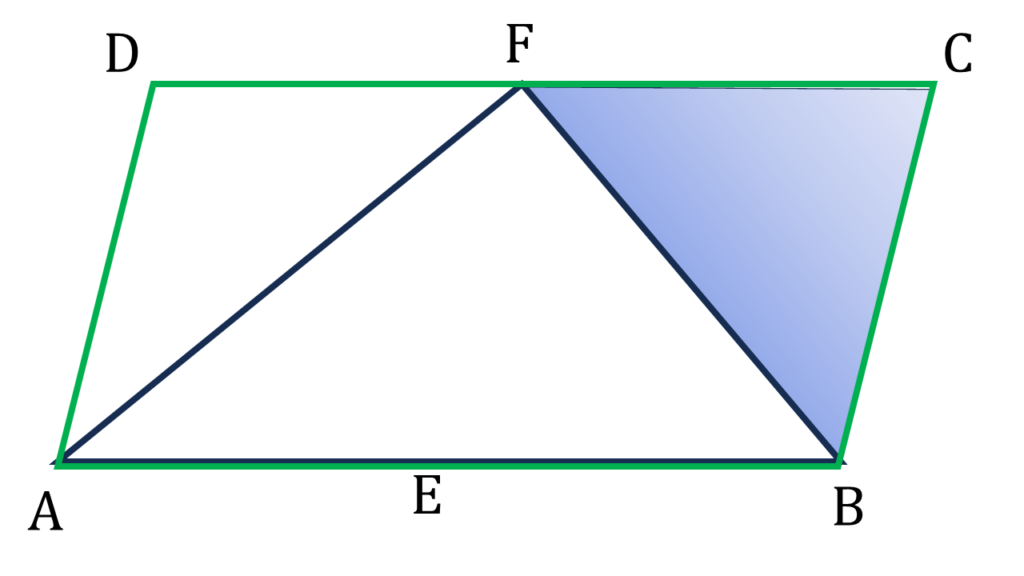
▲BFC এর মধ্যে,
∠BFC=একান্তর∠EBF=∠FBC [ ∵ FC||EB ও FB ছেদক এবং (iv) নং থেকে পাই]
∴ ▲BFC একটি সমদ্বিবাহু ত্রিভুজ যার, FC=BC
সুতরাং , FC=EB

যেহেতু, AB এর মধ্যবিন্দু E এবং AB=DC

সেহেতু, DF=AE এবং FC=EB থেকে পাই,

DC এর মধ্যবিন্দু হলো F ।

আবার,

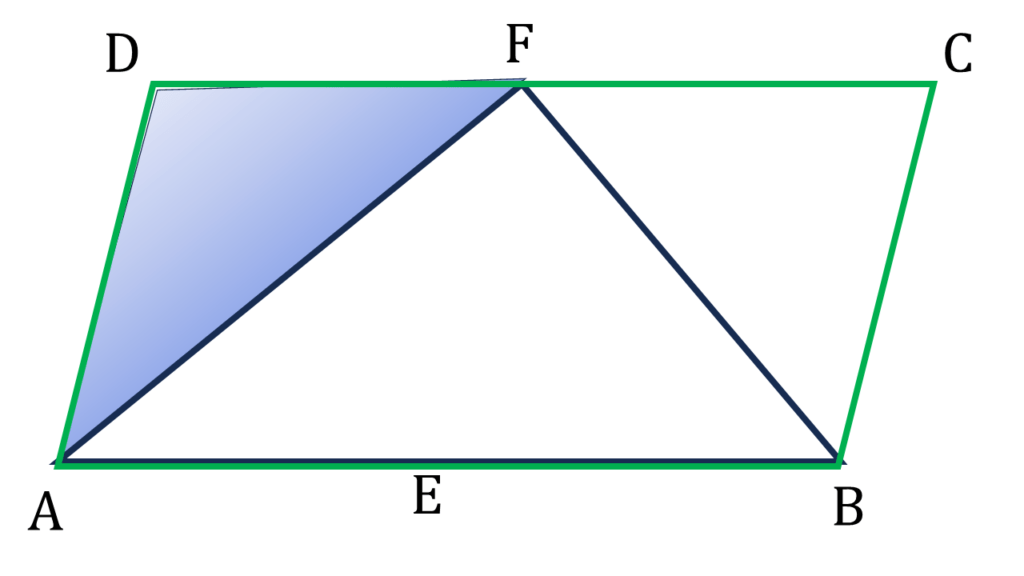
▲ADF এর
∠DAF+∠AFD+∠ADF=180°
বা, ∠AFD+∠AFD+∠ADF=180° [ ∵ ∠DFA=∠DAF]
বা, 2∠AFD+∠ADF=180°
বা, 2∠AFD=180°-∠ADF
বা, ∠AFD=90°-½∠ADF ——-(v)

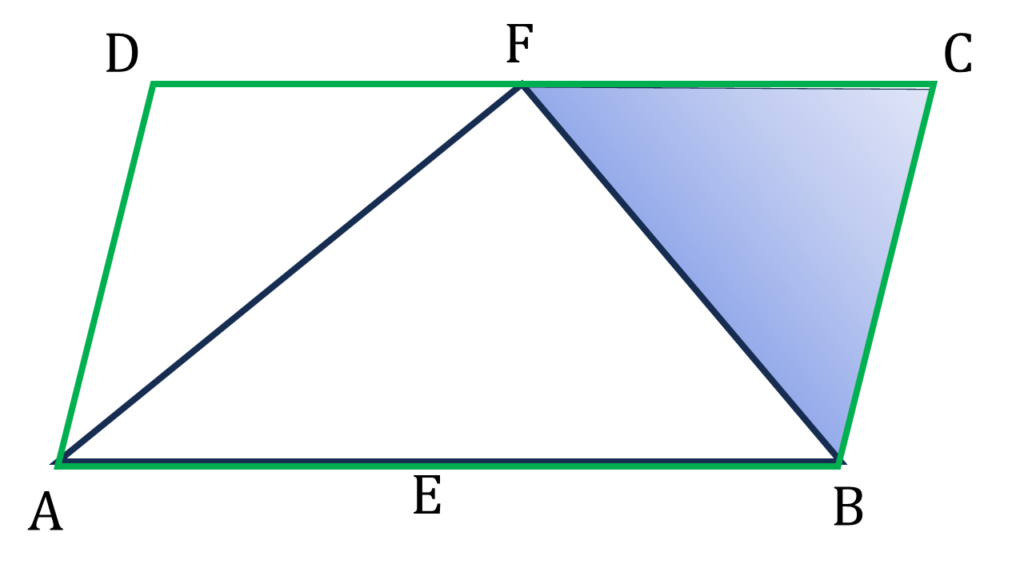
▲BFC এর
∠BFC+∠FBC+∠BCF=180°
বা, ∠BFC+∠BFC+∠BCF=180° [ ∵ ∠BFC=∠FBC]
বা, 2∠BFC+∠BCF=180°
বা, 2∠BFC=180°-∠BCF
বা, ∠BFC=90°-½∠BCF ——-(vi)

এখন,

∠AFD+∠AFB+∠BFC=180°

বা, ∠AFB=180°-(∠AFD+∠BFC)

বা, ∠AFD=180°-(90°-½∠ADF+90°-½∠BCF) [ (v) ও (vi) থেকে পাই]

বা, ∠AFD=180°-180°+½(∠ADF+∠BCF)

বা, ∠AFD=½×180° [ (ii) নং থেকে পাই ]

বা, ∠AFD=90°

∴ ∠BAD ও ∠ABC -এর সমদ্বিখণ্ডকদ্বয় DC বাহুর মধ্যবিন্দুতে সমকোণে মিলিত হয় প্রমাণিত ।

---

13. ABCD সামান্তরিকের AB ও AD বাহুর উপর যথাক্রমে ABPQ ও ADRS বর্গাকার চিত্র অঙ্কন করা হলো যারা সামান্তরিকটির বাইরে অবস্থিত। প্রমাণ করি যে, PRC ত্রিভুজটি সমদ্বিবাহু।

সমাধানঃ-

প্রদত্তঃ

ABCD সামান্তরিকের AB ও AD বাহুর উপর যথাক্রমে ABPQ ও ADRS বর্গাকার চিত্র অঙ্কন করা হলো যারা সামান্তরিকটির বাইরে অবস্থিত।

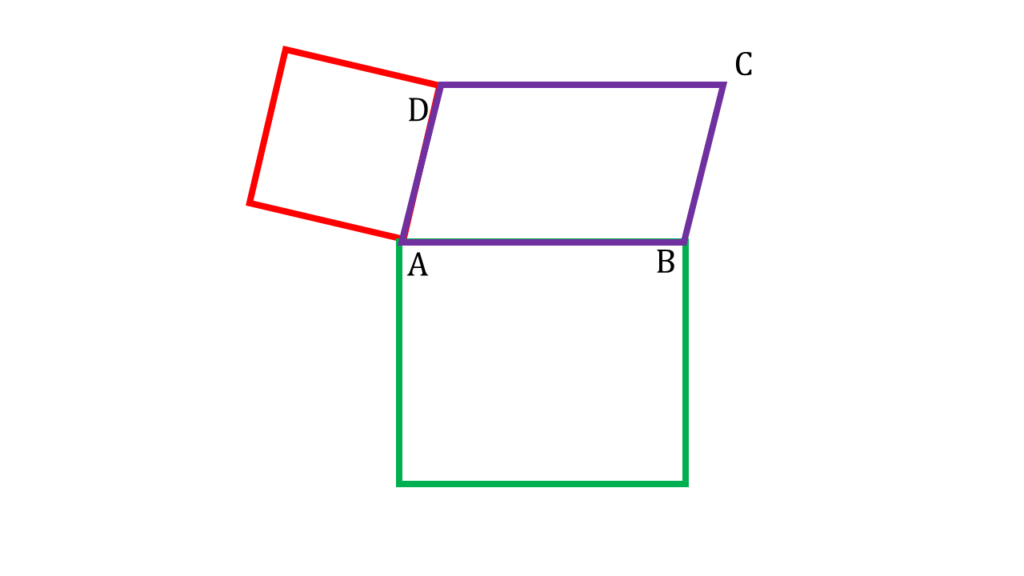
ABCD সামান্তরিক থেকে পাই,
(i)	AD=BC
(ii)	AB=DC
(iii)	∠ADC = ∠ABC

ABCD সামান্তরিক এবং বর্গক্ষেত্র ADRS থেকে পাই,
(iv)	RS=SA=RD=AD=BC

ABCD সামান্তরিক এবং বর্গক্ষেত্র AQPB থেকে পাই,
(v)	AQ=QP=PB=AB=DC

বর্গক্ষেত্র AQPB এবং বর্গক্ষেত্র ADRS থেকে পাই,
(vi)	∠ADR=∠ABP=90°

প্রামাণ্যঃ

প্রমান করতে হবে,

PRC ত্রিভুজটি সমদ্বিবাহু।

প্রমাণঃ

▲RDC ও ▲PBC এর মধ্যে,
RD=BC [(iv) নং থেকে পাই]
DC=PB [ (v) নং থেকে পাই]
∠RDC	=360°-(∠ADR+∠ADC)
	=360°-(∠ABP+∠ABC) [(iii) ও (vi) নং থেকে পাই,]
	=∠PBC
∴ ▲RDC ≅ ▲PBC
∴ RC=PC [ সর্বসম ত্রিভুজের অনুরূপ বাহু ]

∴ PRC ত্রিভুজটি সমদ্বিবাহু প্রমাণিত ।

---

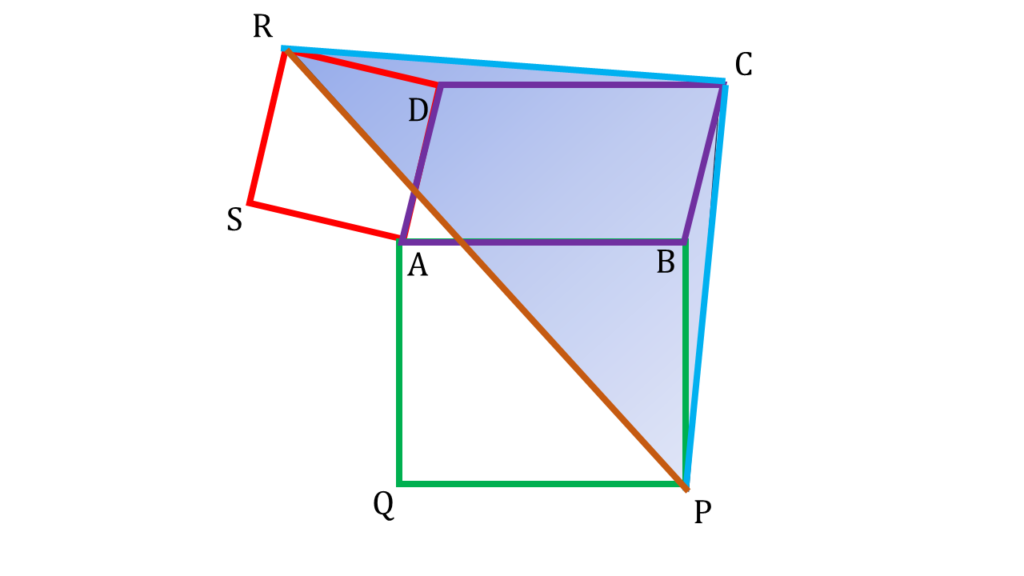
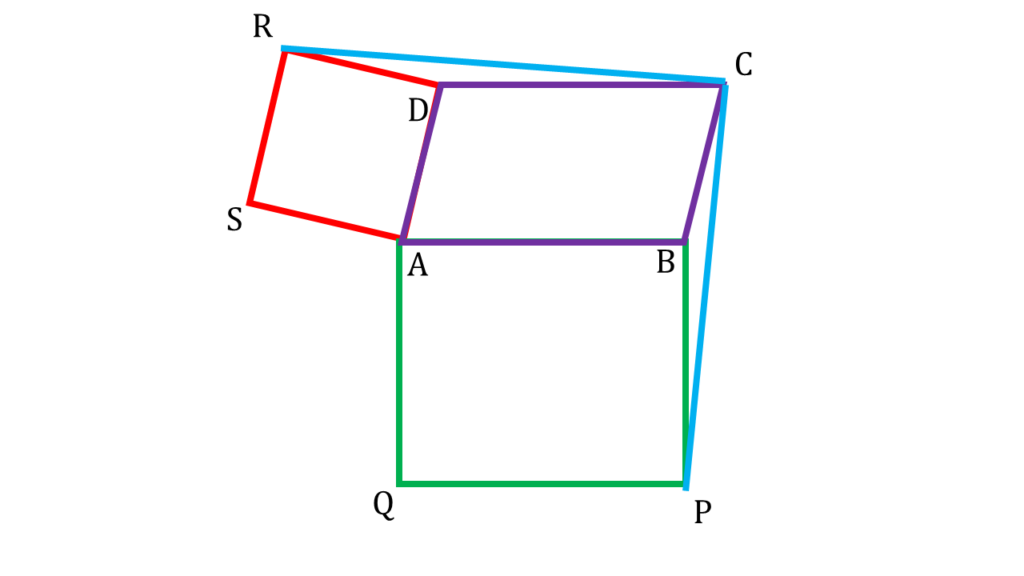
14. ABCD সামান্তরিকের ∠BAD স্থূলকোণ; AB ও AD বাহুর উপর দুটি সমবাহু ত্রিভুজ ABP ও ADQ অঙ্কন করা হলো যারা সামান্তরিকের বাইরে অবস্থিত। প্রমাণ করি যে, CPQ একটি সমবাহু ত্রিভুজ।

সমাধানঃ-

প্রদত্তঃ

ABCD সামান্তরিকের ∠BAD স্থূলকোণ; AB ও AD বাহুর উপর দুটি সমবাহু ত্রিভুজ ABP ও ADQ অঙ্কন করা হলো যারা সামান্তরিকের বাইরে অবস্থিত।

ABCD সামান্তরিক থেকে পাই,
(i)	AD=BC
(ii)	AB=DC
(iii)	∠ADC = ∠ABC
(iv)	∠BAD+∠ABC=180°

ABCD সামান্তরিক এবং সমবাহু ত্রিবুজ ADQ থেকে পাই,
(v)	QD=AQ=AD=BC

ABCD সামান্তরিক এবং সমবাহু ত্রিবুজ APB থেকে পাই,
(vi)	AP=PB=AB=DC

আবার,

সমবাহু ত্রিবুজ ADQ এবং সমবাহু ত্রিবুজ APB থেকে পাই,
(vii)	∠AQD=∠ADQ=∠QAD =∠PAB=∠APB=∠PBA =60°

প্রামাণ্যঃ

প্রমান করতে হবে,

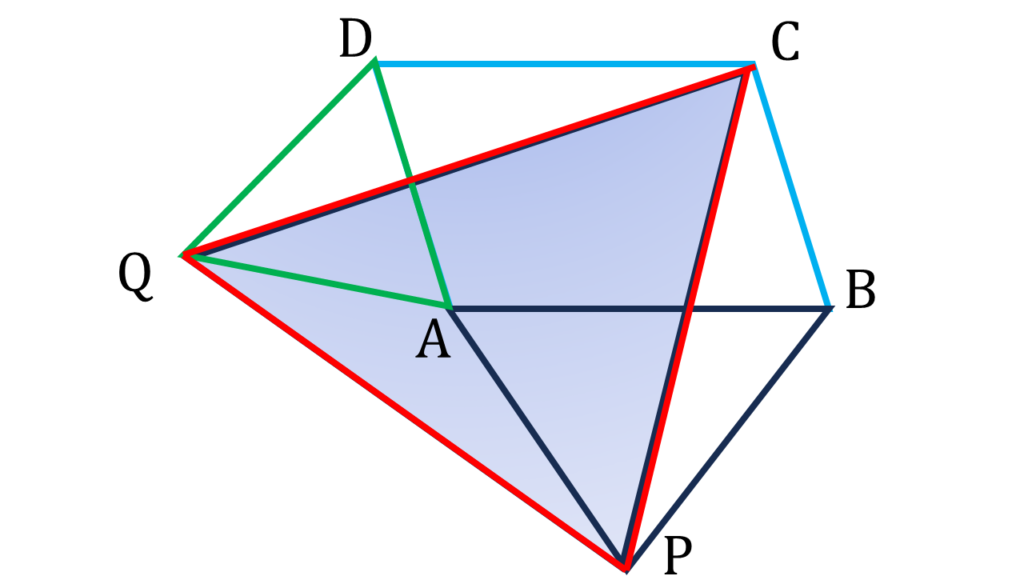
CPQ একটি সমবাহু ত্রিভুজ ।

প্রমাণঃ

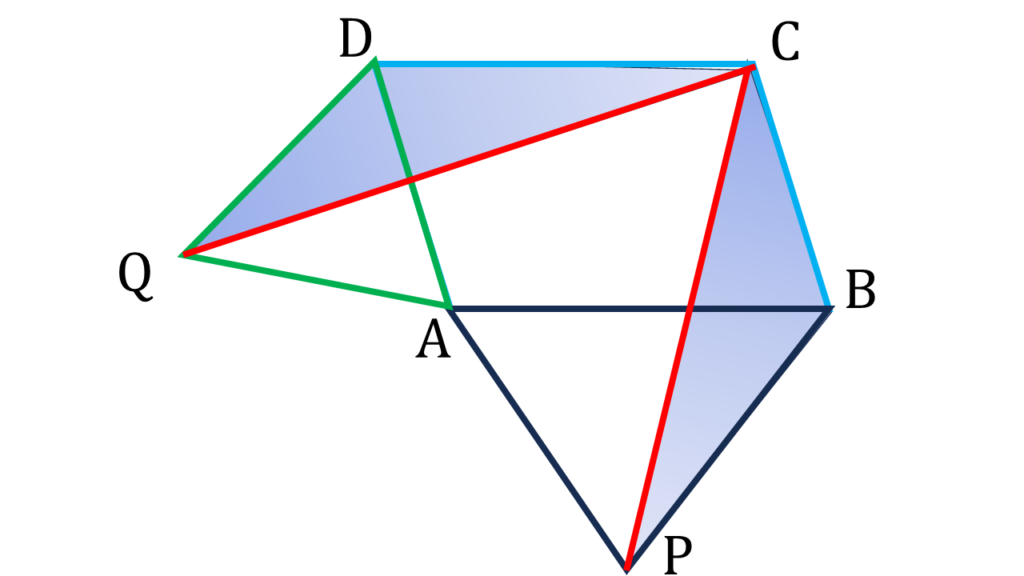
▲QDC ও ▲PBC এর মধ্যে,
QD=BC [(v) নং থেকে পাই]
DC=PB [ (vi) নং থেকে পাই]
∠ADQ+∠ADC=∠PBA+ABC বা, ∠QDC=∠PBC [ (iii) ও (vii) নং থেকে পাই]
∴ ▲QDC ≅ ▲PBC
∴ PC=QC [ সর্বসম ত্রিভুজের অনুরূপ বাহু ]

আবার,

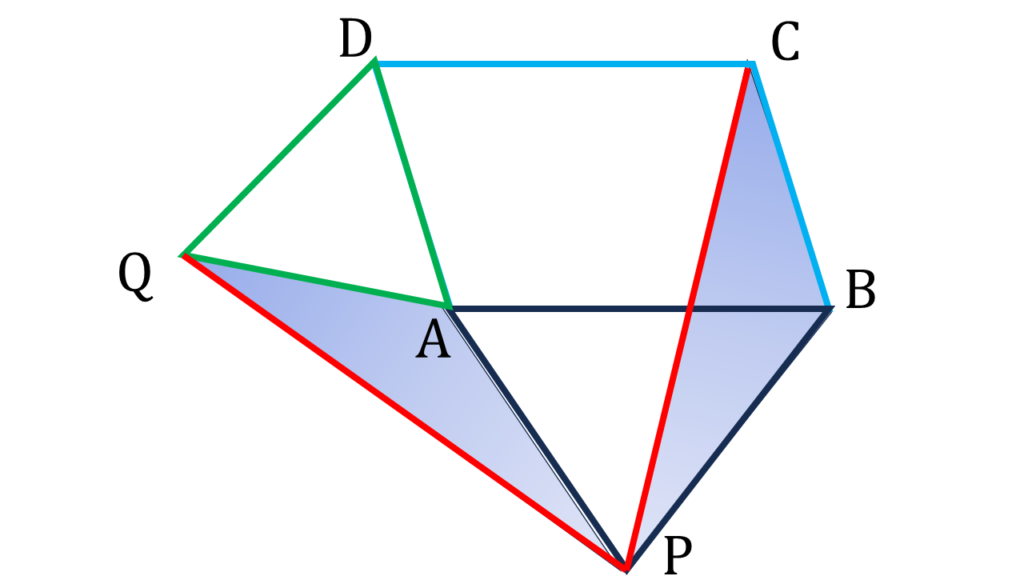
▲QAP ও ▲PBC এর মধ্যে,
QA=BC [(v) নং থেকে পাই]
AP=PB [ (vi) নং থেকে পাই]
∠QAP	=360°-(∠DAQ+∠BAD+∠BAP)
	=360°-(60°+60°+∠BAD)
	=360°-(120°+∠BAD)
	=360°-(120°+180°-∠ABC) [ (iv) নং থেকে পাই]
	=360°-300°+∠ABC
	=60°+∠ABC
	=∠PBA+∠ABC
	=∠PBC
∴ ▲QAP ≅ ▲PBC
∴ QP=PC [ সর্বসম ত্রিভুজের অনুরূপ বাহু ]

সুতরাং,

QC=QP=PC

∴ CPQ একটি সমবাহু ত্রিভুজ প্রমাণিত ।

---

---

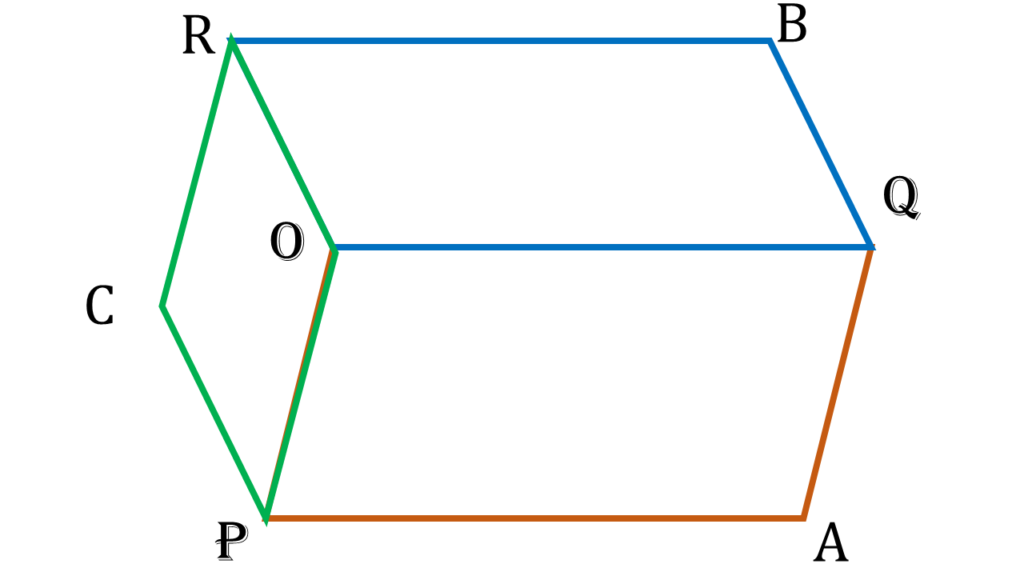
15. OP, OQ ও OR তিনটি সরলরেখাংশ। OPAQ, OQBR এবং ORCP সামান্তরিক তিনটি অঙ্কন করা হলো। প্রমাণ করি যে, AR, BP ও CQ পরস্পরকে সমদ্বিখণ্ডিত করে।

সমাধানঃ-

প্রদত্তঃ

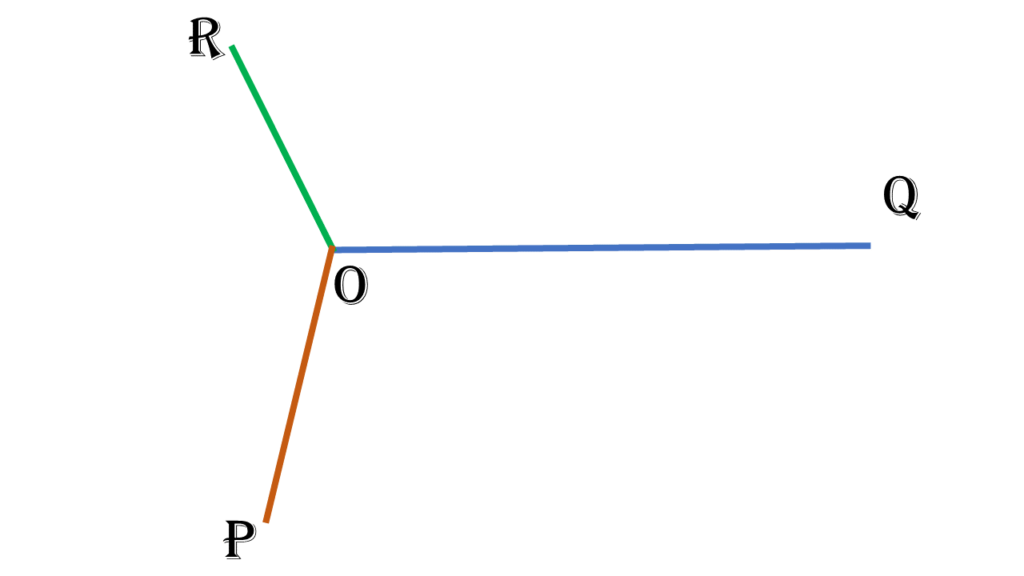
OP, OQ ও OR তিনটি সরলরেখাংশ। OPAQ, OQBR এবং ORCP সামান্তরিক তিনটি অঙ্কন করা হলো।

প্রামাণ্যঃ

প্রমান করতে হবে,

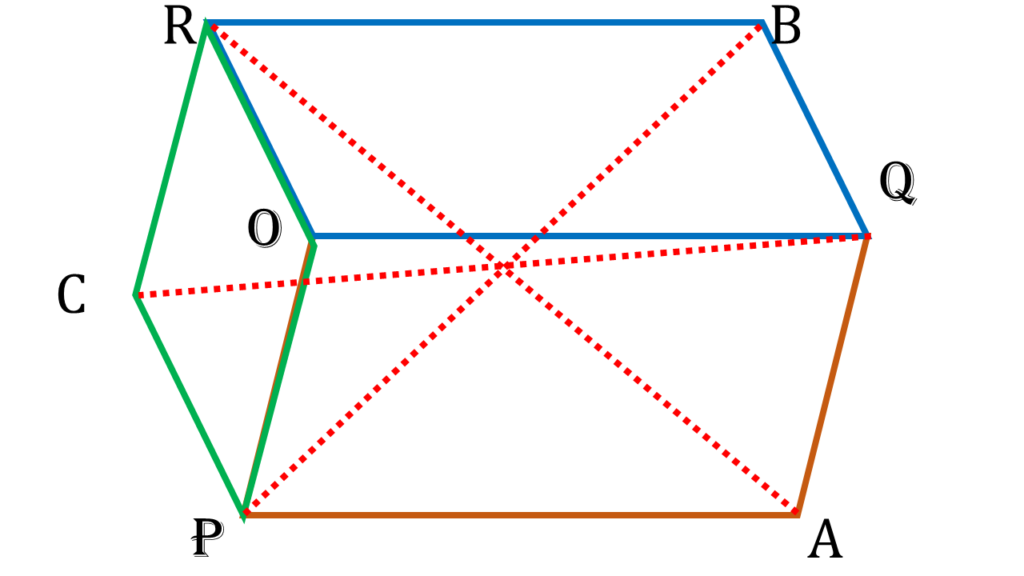
AR, BP ও CQ পরস্পরকে সমদ্বিখণ্ডিত করে

অঙ্কনঃ

P ও R বিন্দু, A ও B বিন্দু, C ও B বিন্দু এবং P ও Q বিন্দু যোগ করলাম।

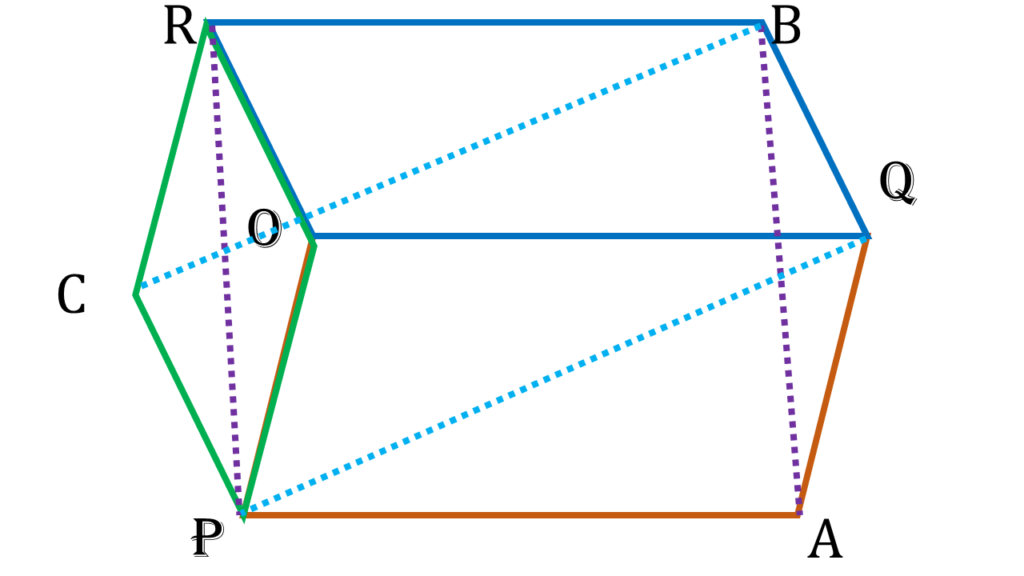
প্রমাণঃ

চতুর্ভুজ PABR এর
AP = BR [ কারণ- OPAQ সামান্তরিকের AP=OQ এবং OQBR সামান্তরিকের OQ=BR ∴ AP=OQ=BR ]
AP||BR [ কারণ- OPAQ সামান্তরিকের AP||OQ এবং OQBR সামান্তরিকের OQ||BR ∴ AP||OQ||BR ]
সুতরাং, PABR চতুর্ভুজের একজোড়া বিপরীত বাহু AP ও BR পরস্পর সমান ও সমান্তরাল।
∴ PABR একটি সামান্তরিক ।

এখন, AR ও PB হলো PABR সামান্তরিকের দুটি কর্ণ।

অতএব AR ও PB পরস্পরকে সমদ্বিখণ্ডিত করে।

আবার,

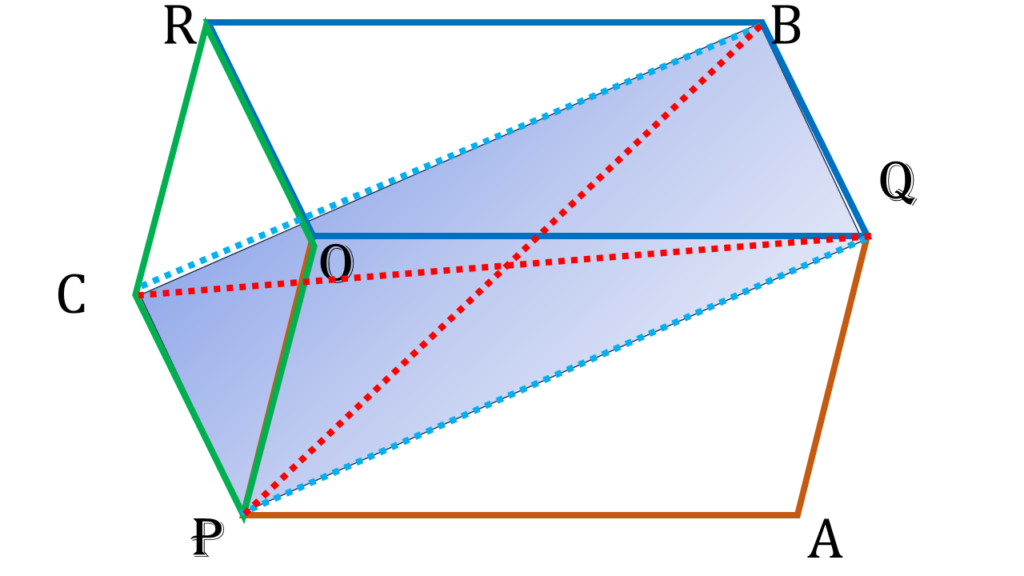
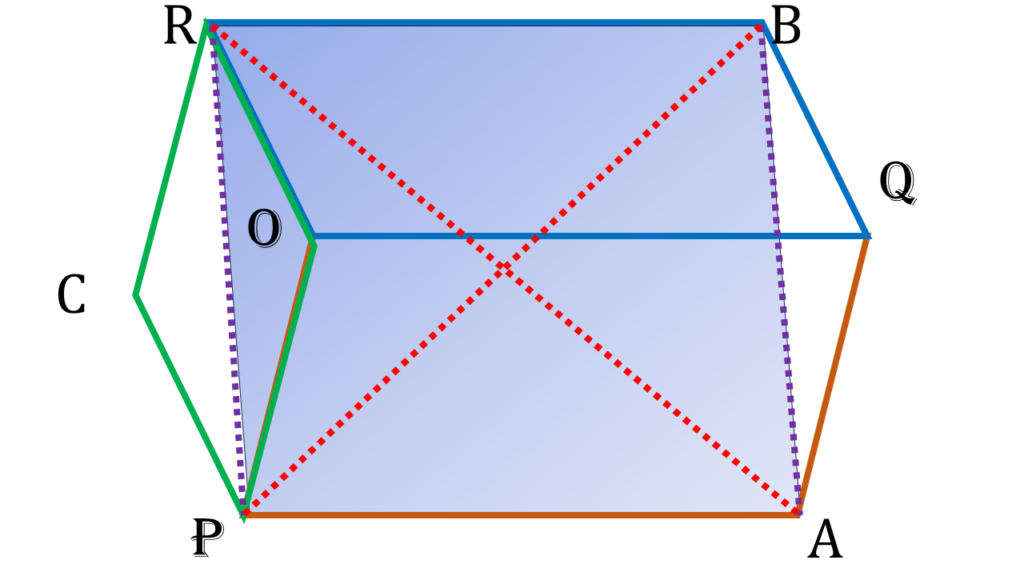
চতুর্ভুজ PQBC এর
PC = BQ [ কারণ- OQBR সামান্তরিকের OR=BQ এবং OPCR সামান্তরিকের OR=PC ∴ OR=BQ=PC ]
BQ||CP [ কারণ- OQBR সামান্তরিকের OR||BQ এবং OPCR সামান্তরিকের OR||PC ∴ OR||BQ||PC ]
সুতরাং, PQBC চতুর্ভুজের একজোড়া বিপরীত বাহু PC ও BQ পরস্পর সমান ও সমান্তরাল।
∴ PQBC একটি সামান্তরিক ।

এখন, PB ও CQ হলো PQBC সামান্তরিকের দুটি কর্ণ।

অতএব, PB ও CQ পরস্পরকে সমদ্বিখণ্ডিত করে।

∴ AR, BP ও CQ পরস্পরকে সমদ্বিখণ্ডিত করে প্রমাণিত ।

---

16. বহু বিকল্পীয় প্রশ্ন (M. C. Q.):

সমাধানঃ-

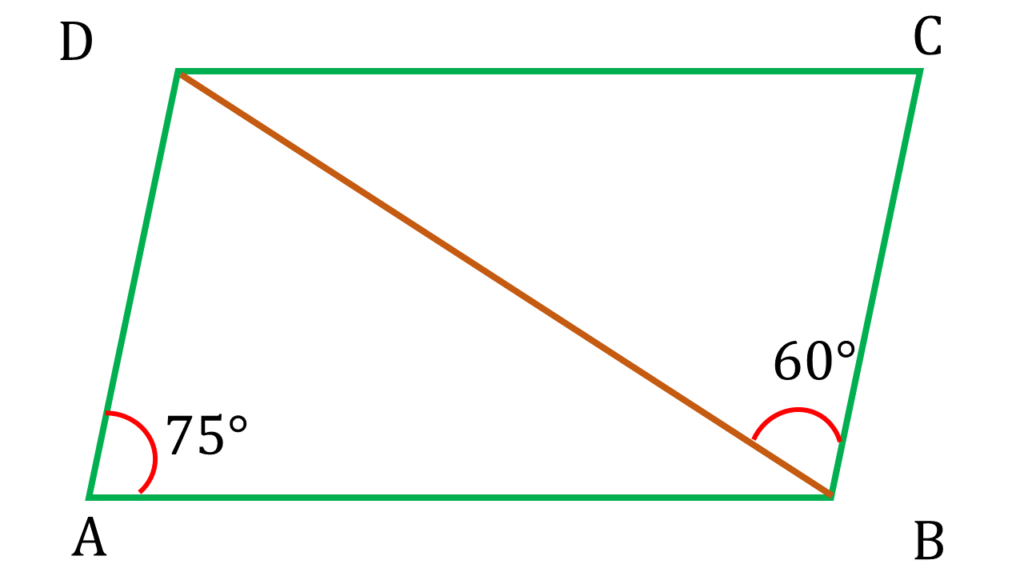
AD||BC এবং AB ভেদক ।

অতএব,

∠BAD+∠ABC = 180°

বা, ∠ABC=180°-75°

বা, ∠ABC=105°

বা, ∠ABD+∠CBD=105°

বা, ∠CBD=105°-60°

বা, ∠CBD=45°

∠BDC=একান্তর∠ABD=45°

---

---

---

---

সমাধানঃ-

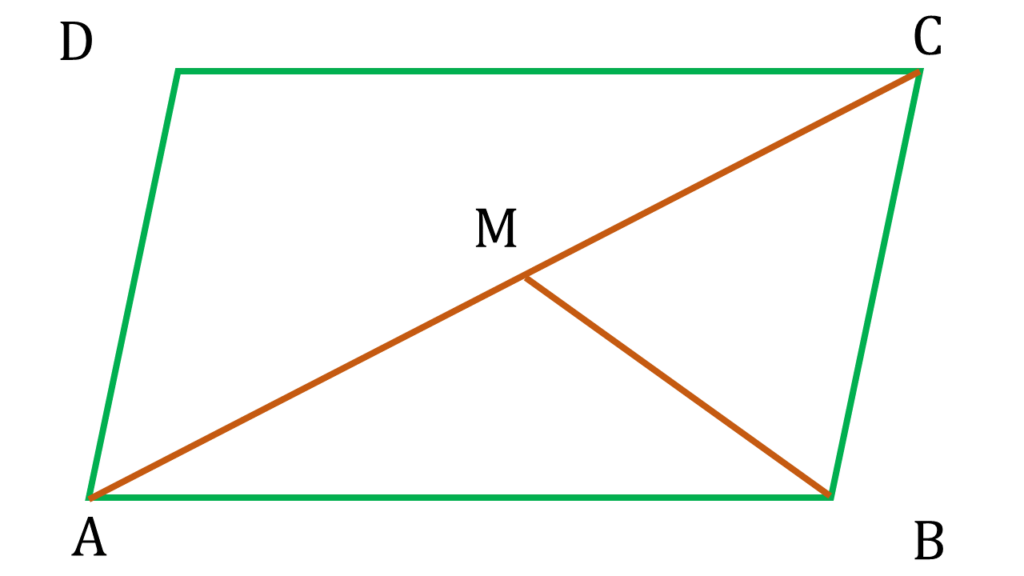
▲ABM ও ▲BMC এর মধ্যে,
AM=CM
BM সাধারণ বাহু [ ∵ PQRS একটি সামান্তরিক ]
∠ABM=∠CBM
∴ ▲ABM ≅ ▲BMC
⇒ ∠AMB=∠BMC [ সর্বসম ত্রিভুজের অনুরূপ ]

আবার,

∠AMB+∠BMC=180°

বা, ∠AMB+∠AMB=180°

বা, 2∠AMB=180°

বা, ∠AMB=90°

---

সমাধানঃ-

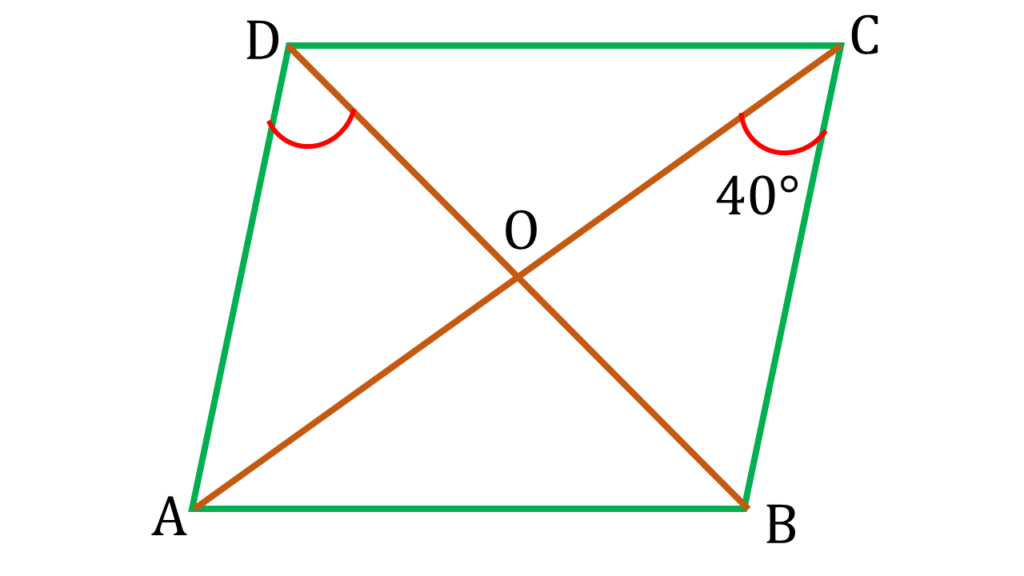
▲BOC এর

∠OBC+∠BCO+∠BOC=180°

বা, ∠OBC+40°+90°=180°

বা, ∠OBC = 50°

---

17. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন:

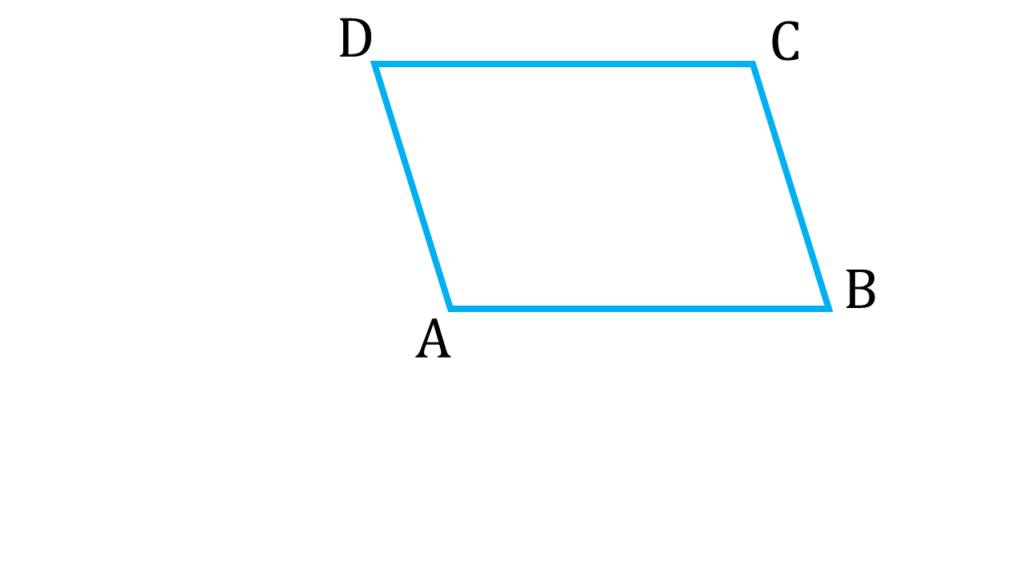
(i) ABCD সামান্তরিকের ∠A : ∠B = 3:2 হলে, সামান্তরিকটির কোণগুলির পরিমাপ লিখি ।

সমাধানঃ-

ABCD সামান্তরিকের ∠A : ∠B = 3:2

ধরি, ∠A=3x এবং ∠B=2x

অতএব ,

3x+2x=180°

বা, x=36°

অতএব,

∠C=∠A=3×36°=108°

এবং

∠D=∠B=2×36°=72°

---

---

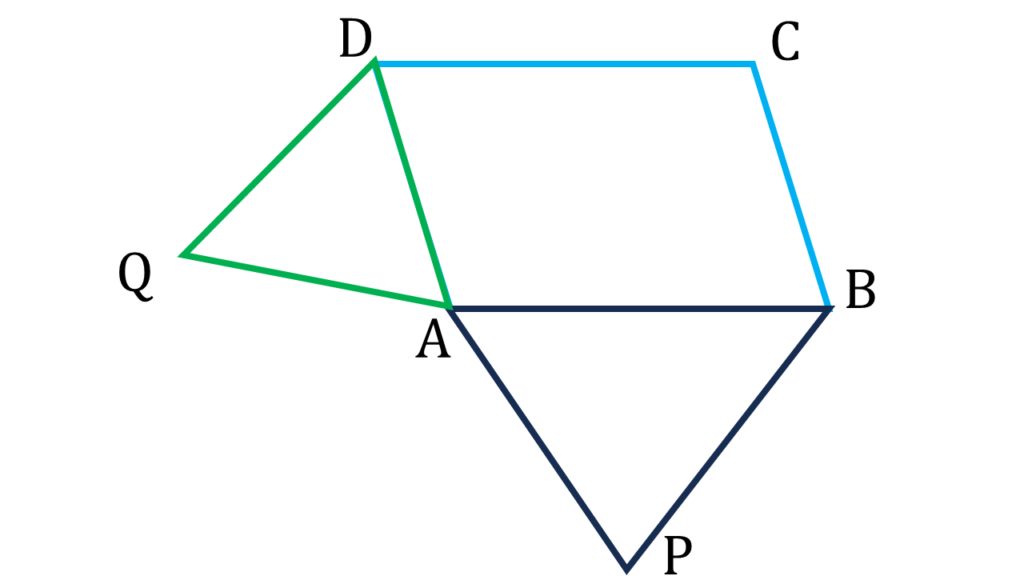
(ii) ABCD সামান্তরিকের ∠A ও ∠B-এর সমদ্বিখণ্ডদ্বয় CD বাহুর উপর E বিন্দুতে মিলিত হয়। BC বাহুর দৈর্ঘ্য 2 সেমি. হলে, AB বাহুর দৈর্ঘ্য কত তা লিখি।

সমাধানঃ-

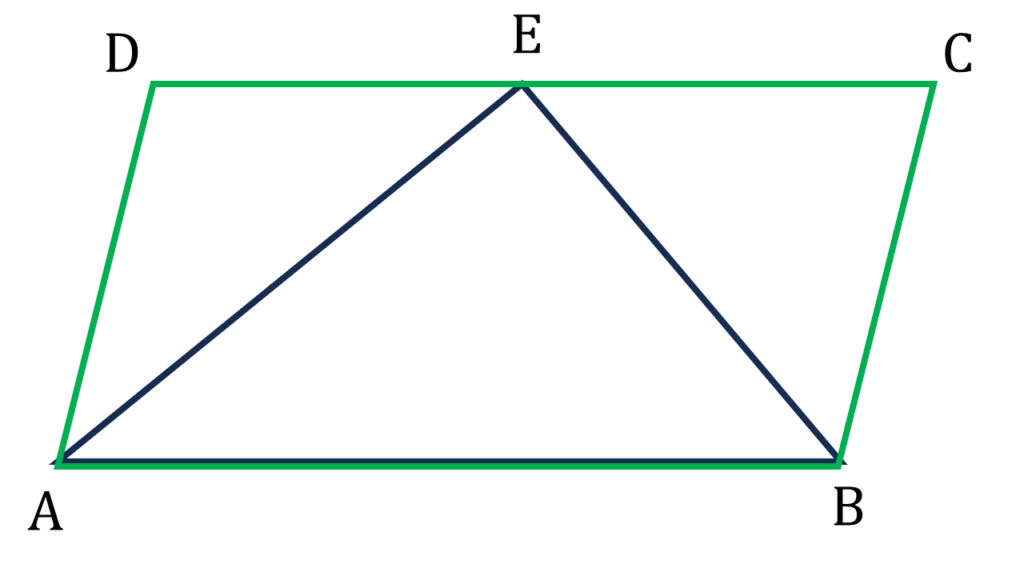
∠CBE=∠ABE=একান্তর∠BEC

অতএব BC=EC=2 সেমি

আবার,

∠DAE=∠BAE=একান্তর∠DEA

অতএব DE=AD=BC=2 সেমি

আবার,

AB=DC=DE+EC=2+2=4 সেমি

---

(iii) ABCD বর্গাকার চিত্রের ভিতর সমবাহু ত্রিভুজ AOB অবস্থিত। ∠COD -এর পরিমাপ লিখি ।

সমাধানঃ-

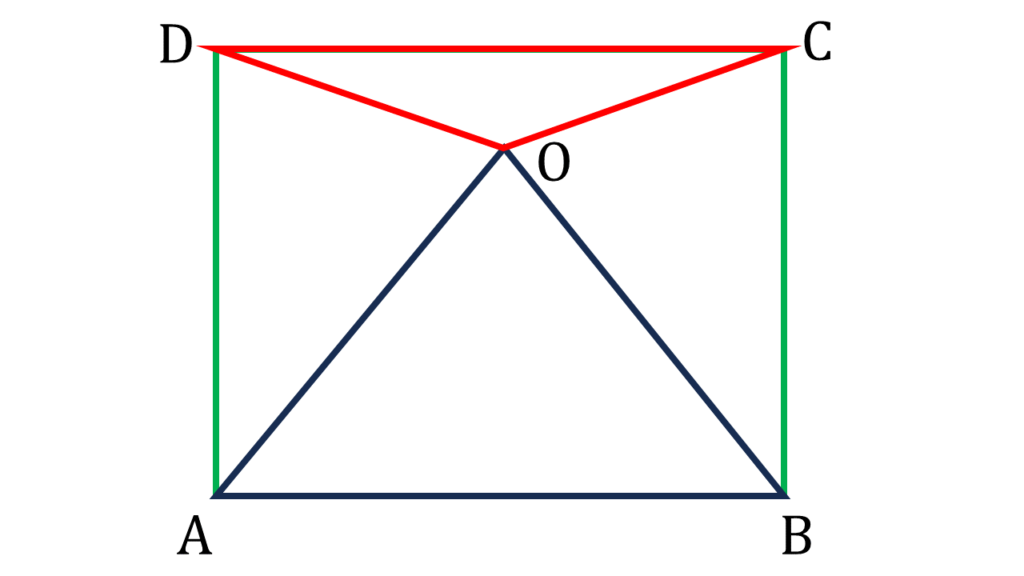
▲AOB সমবাহু ত্রিভুজ

অতএব, ∠AOB=∠OAB=∠ABO=60°

আবার,

▲OBC এর

OB=BC

এবং

∠OCB=∠BOC

আবার, ∠OBC=90°-60°=30°

অতএব ▲BOC এর

∠BOC+∠OCB+∠OBC=180°

বা, 2∠BOC=180°-30°

বা, ∠BOC=75°

একইরকম ভাবে,

▲AOB এর

∠AOD=75°

এখন,

∠COD+∠AOD+∠AOB+∠BOC=360°

বা, ∠COD = 360°-75°-75°-60°

বা, ∠COD = 150°

---

(iv) ABCD বর্গাকার চিত্রের AD বাহুর উপর M একটি বিন্দু যাতে ∠CMD = 30° হয়। কর্ণ BD, CM-কে P বিন্দুতে ছেদ করলে, ∠DPC-এর পরিমাপ কত তা লিখি ।

সমাধানঃ-

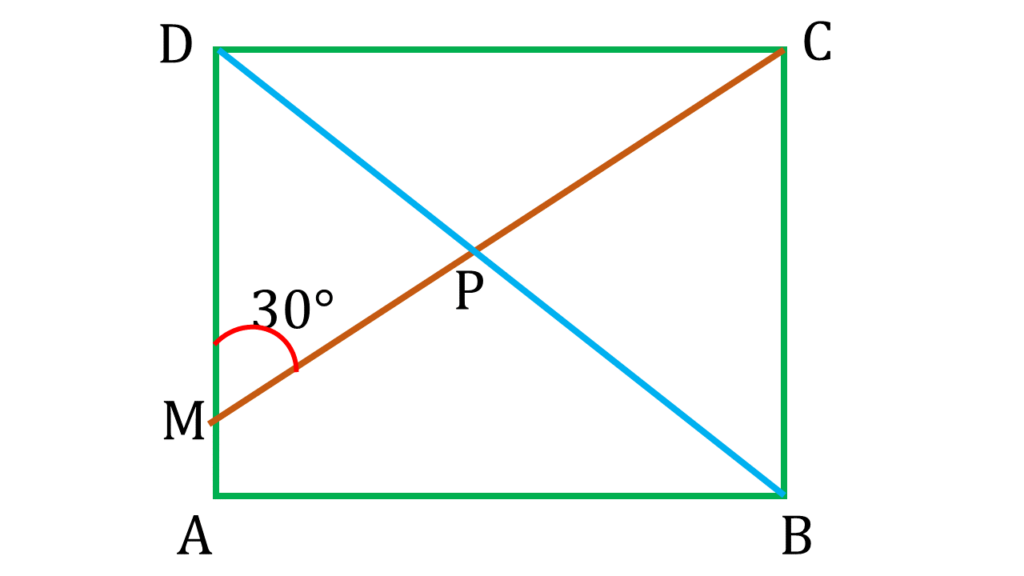
ABCD বর্গক্ষেত্রের AD||BC এবং CM ভেদক ।

অতএব,

∠DMC=একান্তর∠PCB=30°

আবার,

∠BCD=90°

বা, ∠PCD+∠PCB=90°

বা, ∠PCD=90°-30°=60°

আবার, ∠PDC=45°

অতএব ▲DPC এর

∠PDC+∠DPC+∠PCD=180°

বা, ∠DPC=180°-60°-45°

বা, ∠DPC=75°

---

(v) ABCD রম্বসের AB বাহুর দৈর্ঘ্য 4 সেমি. এবং ∠BCD = 60° হলে, কর্ণ BD -এর দৈর্ঘ্য কত তা লিখি।

সমাধানঃ-

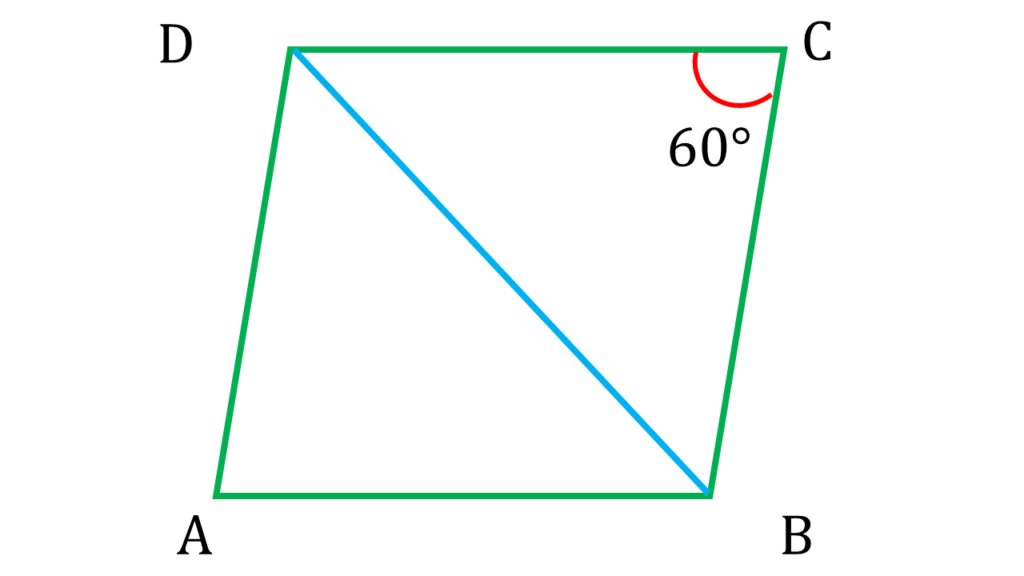
▲BCD এর

BC=CD

অতএব ∠CBD=∠CDB

আবার,

∠CBD+∠CDB+∠BCD=180°

বা, 2∠CBD+60°=180°

বা, ∠CBD = (180°-60°)/2

বা, ∠CBD=60°

∴ ∠CBD=∠CDB=∠BCD=60°

অতএব ▲BCD একটি সমবাহু ত্রিভুজ।

সুতরাং BD=BC=CD=4 সেমি।

---

WB Class 9 এর গণিত প্রকাশের সমস্ত অধ্যায়ের সমাধান-
অধ্যায়	সমাধান
1. বাস্তব সংখ্যা (Real Numbers)	কষে দেখি 1.1
	কষে দেখি 1.2
	কষে দেখি 1.3
2. সূচকের নিয়মাবলি (Laws of Indices)	কষে দেখি 2
3. লেখচিত্র (Graph)	কষে দেখি 3.1
	কষে দেখি 3.2
4. স্থানাঙ্ক জ্যামিতি : দূরত্ব নির্ণয় (Co-ordinate Geometry: Distance Formula)	কষে দেখি 4
5. রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) (Linear Simultaneous Equations)	কষে দেখি 5.1
	কষে দেখি 5.2
	কষে দেখি 5.3
	কষে দেখি 5.4
	কষে দেখি 5.5
	কষে দেখি 5.6
	কষে দেখি 5.7
6. সামান্তরিকের ধর্ম (Properties of Parallelogram)	কষে দেখি 6
7. বহুপদী সংখ্যামালা (Polynomial)	কষে দেখি 7.1
	কষে দেখি 7.2
	কষে দেখি 7.3
	কষে দেখি 7.4
8. উৎপাদকে বিশ্লেষণ (Factorisation)	কষে দেখি 8.1
	কষে দেখি 8.2
	কষে দেখি 8.3
	কষে দেখি 8.4
	কষে দেখি 8.5
9. ভেদক ও মধ্যবিন্দু সংক্রান্ত উপপাদ্য (Transversal & Mid-Point Theorem).	কষে দেখি 9
10. লাভ ও ক্ষতি (Profit and Loss)	কষে দেখি 10.1
	কষে দেখি 10.2
11. রাশিবিজ্ঞান (Statistics)	কষে দেখি 11.1
	কষে দেখি 11.2
12. ক্ষেত্রফল সংক্রান্ত উপপাদ্য (Theorems on Area)	কষে দেখি 12
13. সম্পাদ্য : ত্রিভুজের সমান ক্ষেত্রফল বিশিষ্ট সামান্তরিক অঙ্কন	কষে দেখি 13
14. সম্পাদ্য : চতুর্ভুজের সমান ক্ষেত্রফল বিশিষ্ট ত্রিভুজ অঙ্কন	কষে দেখি 14
15. ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল (Area & Perimeter of Triangle & Quadrilateral)	কষে দেখি 15.1
	কষে দেখি 15.2
	কষে দেখি 15.3
16. বৃত্তের পরিধি (Circumference of Circle)	কষে দেখি 16
17. সমবিন্দু সংক্রান্ত উপপাদ্য (Theorems on concurrence)	কষে দেখি 17
18. বৃত্তের ক্ষেত্রফল (Area of Circle)	কষে দেখি 18
19. স্থানাঙ্ক জ্যামিতি: সরলরেখাংশের অন্তর্বিভক্ত ও বহিঃবিভক্ত (Co-ordinate Geometry: Internal and External Division of Straight-Line Segment)	কষে দেখি 19
20. স্থানাঙ্ক জ্যামিতি: ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল (Co-ordinate Geometry: Area of Triangular Region)	কষে দেখি 20
21. লগারিদম (Logarithm)	কষে দেখি 21

Request For Share
সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share]

---

এই কষে দেখি 6 Class 9|Koshe Dekhi 6 Class 9 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।

---

এখানে তোমরা তোমাদের নবম শ্রেণীতে| Class 9 এ কি কি পড়ানো হয়, মানে তোমাদের নবম শ্রেণী| Class 9 সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

---