শ্রেণী-নবম ; অধ্যায় -ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল ; কষে দেখি 15.3
কষে দেখি 15.3 Class 9 এর সূচিপত্র:-
কষে দেখি 15.3 Class 9 এর অংকের সমাধান গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ
এই কষে দেখি 15.3 পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদ | WBBSE এর অন্তর্গত Class 9|নবম শ্রেণীর গণিত বই এর 15 নম্বর অধ্যায় ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল এর তৃতীয় অনুশীলনী।
আগামিতে এই কষে দেখি 15.3 Class 9 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 15.3 Class 9 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 15.3 Class 9 তারপর  |
কষে দেখি 15.3| Koshe Dekhi 15.3
সমাধানঃ-
1. রাতুল একটি সামান্তরিক এঁকেছে যার ভূমির দৈর্ঘ্য 5 সেমি. এবং উচ্চতা 4 সেমি.। রাতুলের আঁকা সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল হিসাব করি।
সমাধানঃ-

রাতুলের আঁকা সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল
= 5×4 = 20 বর্গ সেমি.
2. একটি সামান্তরিকের ভূমি তার উচ্চতার দ্বিগুণ। যদি সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল 98 বর্গ সেমি. হয়, তাহলে সামান্তরিকটির দৈর্ঘ্য ও উচ্চতার পরিমাপ হিসাব করি।
সমাধানঃ-
ধরি, সামান্তরিকের উচ্চতা = a সেমি.
অতএব ভূমির দৈর্ঘ্য = 2a সেমি.

সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল
= a × 2a = 2a2 বর্গ সেমি.
এখন
| 2a2 = 98 |
| বা, a2 = \(\frac{98}{2}\) |
| বা, a2 = 49 |
| বা, a = 7 |
অতএব,
| সামান্তরিকের ভূমি = | 14 সেমি. |
| সামান্তরিকের উচ্চতা = | 7 সেমি. |
3. আমাদের বাড়ির পাশে একটি সামান্তরিক আকারের জমি আছে যার সন্নিহিত বাহুদ্বয়ের দৈর্ঘ্য যথাক্রমে 15 মিটার ও 13 মিটার। যদি এই জমির একটি কর্ণের দৈর্ঘ্য 14 মিটার হয়, তবে হিসাব করে সামান্তরিক আকারের জমির ক্ষেত্রফল লিখি।
সমাধানঃ-
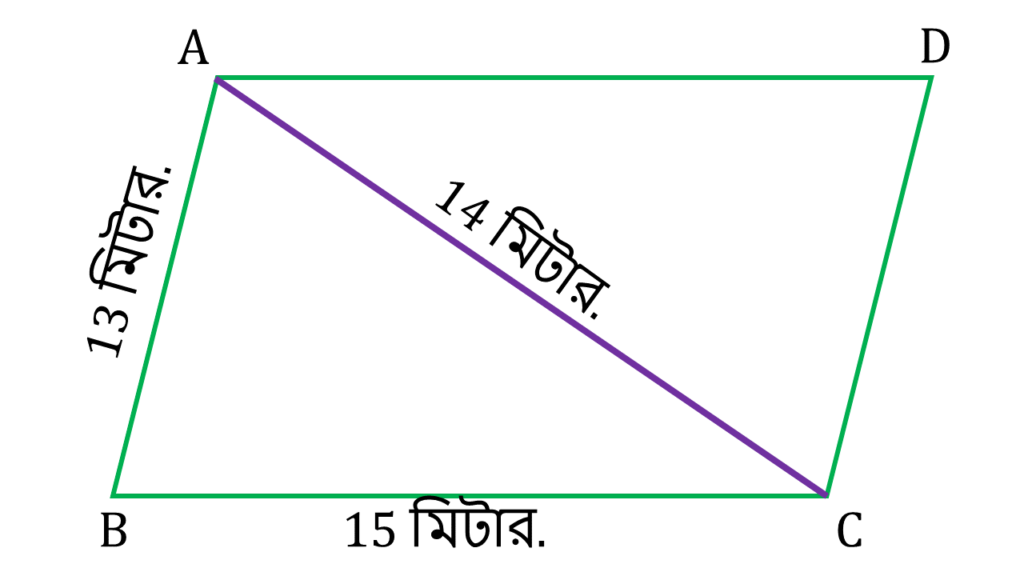
ABCD সামান্তরিকের AB = 13 মিটার., BC = 15 মিটার. এবং AC = 14 মিটার.
▲ABC এর s = \(\frac{13+15+14}{2}\) = 21

▲ABC এর ক্ষেত্রফল
= \(\sqrt{21(21-15)(21-14)(21-13)}\)
= \(\sqrt{21×6×7×8}\)
= 7×3×4 = 84 বর্গ মিটার
ধরি, BC বাহুকে ভূমি ধরে ▲ABC এর উচ্চতা = a মিটার.
BC বাহুকে ভূমি ধরে ▲ABC এর ক্ষেত্রফল
= ½×BC×a
= ½×15a
| ∴ \(\frac{15a}{2}\) = 84 |
| বা, a = 11.2 |
[ এই উচ্চতাটায় হলো সামান্তরিকের উচ্চতা ]
সামান্তরিক ABCD এর ক্ষেত্রফল
= 15 × 11.2
= 168 বর্গ মিটার.
4. পৃথা একটি সামান্তরিক এঁকেছে যার সন্নিহিত বাহুগুলির দৈর্ঘ্য 25 সেমি. ও 15 সেমি. এবং একটি কর্ণের দৈর্ঘ্য 20 সেমি.। হিসাব করে 25 সেমি, বাহুর উপর সামান্তরিকের উচ্চতার পরিমাপ লিখি ।
সমাধানঃ-
ABCD সামান্তরিকের AB = 15 মিটার., BC = 25 মিটার. এবং AC = 20 মিটার.
▲ABC এর s = \(\frac{15+25+20}{2}\) = 30

▲ABC এর ক্ষেত্রফল
= \(\sqrt{30(30-15)(30-25)(30-20)}\)
= \(\sqrt{30×15×5×10}\)
= 15×10 = 150 বর্গ মিটার
ধরি, BC বাহুকে ভূমি ধরে ▲ABC এর উচ্চতা = a মিটার.
BC বাহুকে ভূমি ধরে ▲ABC এর ক্ষেত্রফল
= ½×BC×a
= ½×25a
| ∴ \(\frac{25a}{2}\) = 150 |
| বা, a = 12 |
∴ নির্ণেয় উচ্চতা = 12 মিটার.
5. একটি সামান্তরিকের দুটি সন্নিহিত বাহুর দৈর্ঘ্য 15 সেমি. ও 12সেমি.। ক্ষুদ্রতর বাহু দুটির দূরত্ব 7.5 সেমি- হলে, বৃহত্তর বাহু দুটির দূরত্ব হিসাব করি।
সমাধানঃ-
ABCD একটি সামান্তরিকের দুটি সন্নিহিত বাহু BC ও AB যাদের দৈর্ঘ্য যথাক্রমে 15 সেমি. ও 12সেমি.।
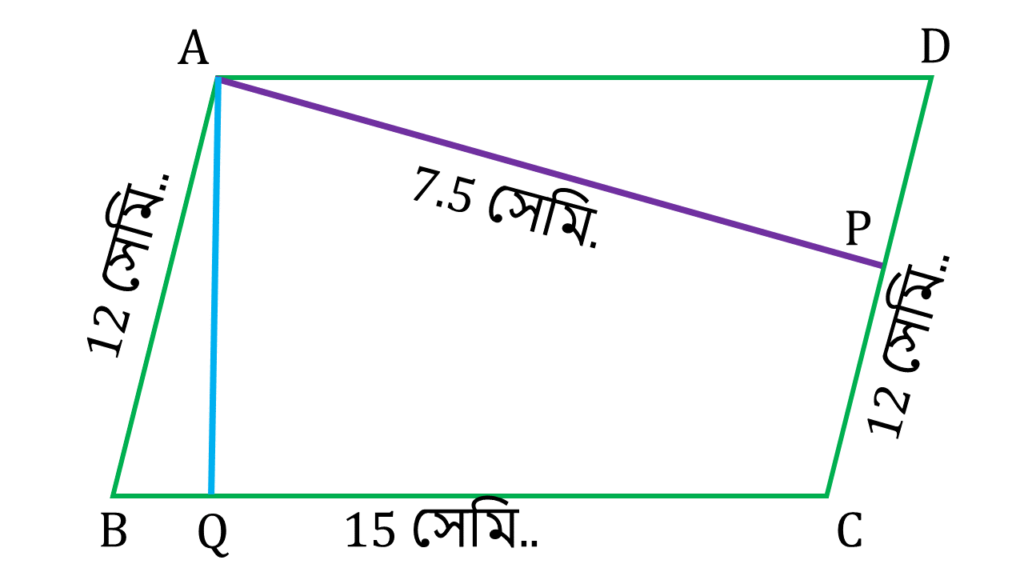
ক্ষুদ্রতর বাহু AB ও DC বাহু দুটির দূরত্ব AP = 7.5 সেমি.
এখন DC বাহুকে ভূমি ধরলে ▲ADC এর উচ্চতা হয় AP
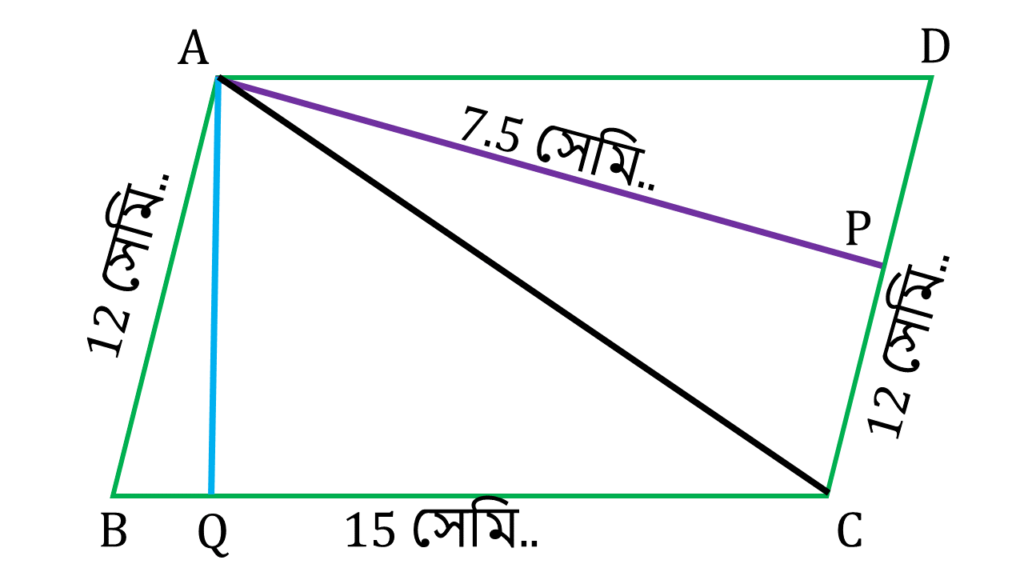
অতএব ▲ADC এর ক্ষেত্রফল
= ½×DC×AP
= ½×7.5×12 = 45 বর্গ মিটার
আবার, সামান্তরিক ABCD এর AC একটি কর্ণ
⇒ ▲ABC = ▲ADC
⇒ ½×BC×AQ = 45
⇒ 15×AQ = 45×2
⇒ AQ = \(\frac{45 \times 2}{15}\) = 6
∴ বৃহত্তর বাহু দুটির দূরত্ব = 6 সেমি.
6. একটি রম্বসের কর্ণদ্বয়ের পরিমাপ 15 মিটার ও 20 মিটার হলে, উহার পরিসীমা, ক্ষেত্রফল ও উচ্চতা হিসাব করে লিখি।
সমাধানঃ-
ABCD একটি রম্বস যার কর্ণদ্বয় AC ও BD এর পরিমাপ যথাক্রমে 15 মিটার ও 20 মিটার এবং পরস্পরকে O বিন্দুতে ছেদ করেছে।
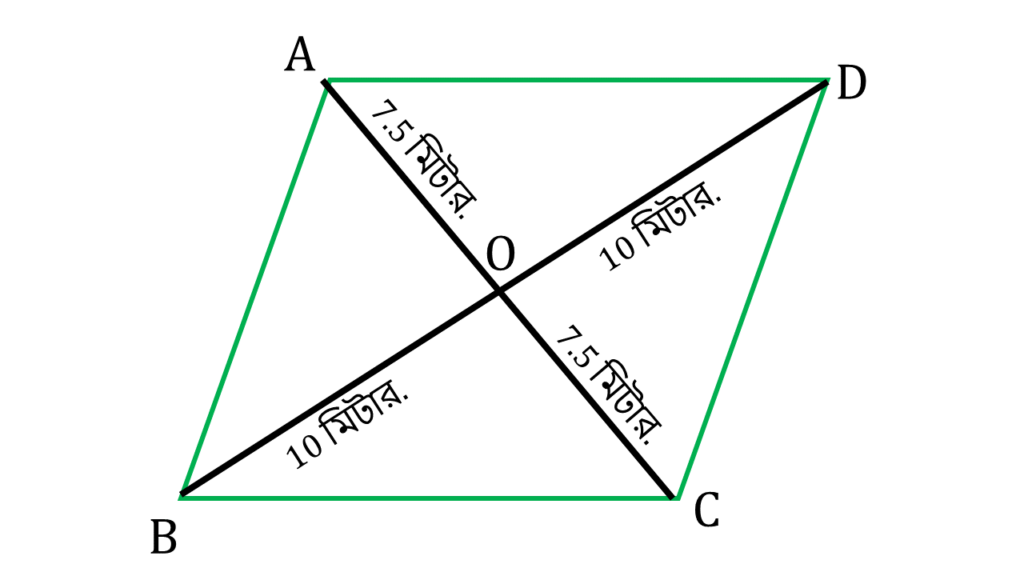
আমরা জানি রম্বসের কর্ণদ্বয় পরস্পরকে লম্ব সমদ্বিখণ্ডিত করে।
অর্থাৎ,
∠BOC = ∠DOC = ∠AOD = ∠AOB = 90°
| ▲BOC সমকোণী ত্রিভুজ এর |
|---|
 |
| BC2 = BO2 + OC2 |
| বা, BC2 = 102 + 7.52 |
| বা, BC2 = 100 + 56.25 = 156.25 |
| বা, BC = 12.5 |
- রম্বসের পরিসিমাঃ
পরিসীমা = 4×BC = 4×12.5 = 50 মিটার
- রম্বসের ক্ষেত্রফলঃ

খেত্রফল = ½×15×20 = 150 বর্গ মিটার.
- রম্বসের উচ্চতাঃ
যেহেতু রম্বস একটি সামান্তরিক, আমরা জানি একটি

ভূমি × উচ্চতা = 150
বা, উচ্চতা = \(\frac{150}{12.5}\) = 12 মিটার
7. একটি রম্বসের পরিসীমা 440 মিটার এবং সমান্তরাল বাহুদুটির মধ্যে দূরত্ব 22 মিটার হলে, রম্বস আকার ক্ষেত্রের ক্ষেত্রফল হিসাব করে লিখি।
সমাধানঃ-
ধরি, রম্বসের বাহুর দৈর্ঘ্য = a মিটার.
অতএব 4a = 440
বা, a = 110 মিটার.
যেহেতু রম্বস একটি সামান্তরিক

সুতরাং রম্বসের খেত্রফল
= 110×22
= 2420 বর্গ মিটার.
8. যদি একটি রম্বসের পরিসীমা 20 সেমি. এবং একটি কর্ণের দৈর্ঘ্য 6 সেমি. হয়, তবে ওই রম্বসের ক্ষেত্রফল হিসাব করে লিখি।
সমাধানঃ-
ABCD একটি রম্বস যার পরিসীমা 20 সেমি. এবং একটি কর্ণ AC এর দৈর্ঘ্য = 6 সেমি.
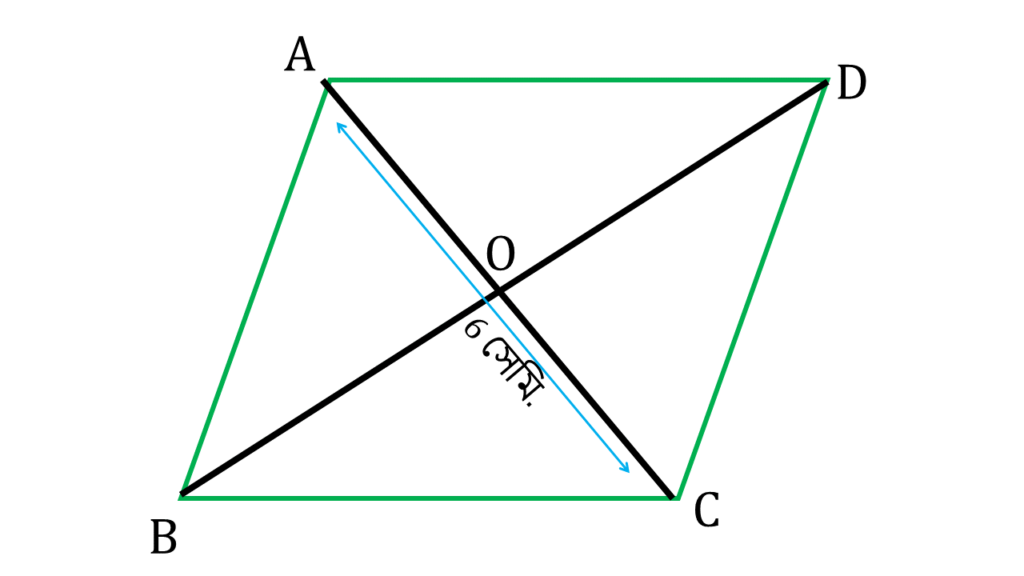
ধরি, রম্বসের বাহুর দৈর্ঘ্য = a মিটার.
অতএব 4a = 20
বা, a = 5 মিটার.
আমরা জানি রম্বসের কর্ণদ্বয় পরস্পরকে লম্ব সমদ্বিখণ্ডিত করে।
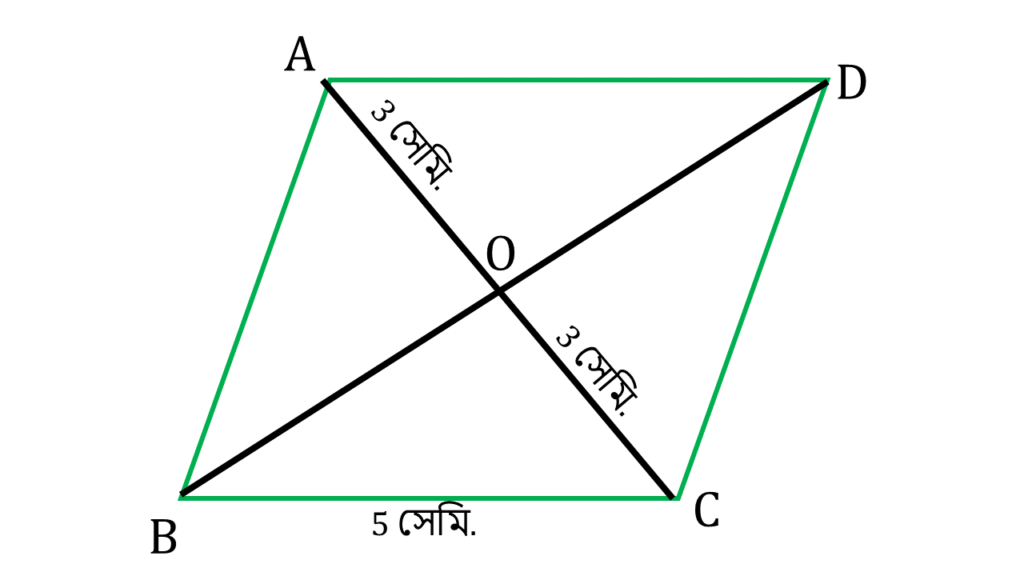
অর্থাৎ,
∠BOC = ∠DOC = ∠AOD = ∠AOB = 90°
| ▲BOC সমকোণী ত্রিভুজ এর |
|---|
 |
| BC2 = BO2 + OC2 |
| বা, BO2 = BC2 – OC2 |
| বা, BO2 = 52 – 32 |
| বা, BO2 = 25 – 9 = 16 |
| বা, BO = 4 |
| ∴ BD = 2BO = 2×4 = 8 |
এখন

= ½×6×8 = 24 বর্গ সেমি.
9. একটি ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল 1400 বর্গ ডেকামিটার। উহার সমান্তরাল বাহুদ্বয়ের মধ্যে লম্ব দূরত্ব 20 ডেকামিটার এবং সমান্তরাল বাহুদ্বয়ের দৈর্ঘ্যের অনুপাত 3:4 হলে, ওই বাহুদ্বয়ের দৈর্ঘ্য হিসাব করে লিখি।
সমাধানঃ-
ধরি, সমান্তরাল বাহুদ্বয়ের দৈর্ঘ্য 3x ডেকামিটার., ও 4x ডেকামিটার.
আমরা জানি,

অতএব,
| ½×(3x+4x)×20 = 1400 |
| বা, 7x = \(\frac{1400 \times 2}{20}\) |
| বা, 7x = 140 |
| বা, x = 20 |
∴ বাহুদ্বয়ের দৈর্ঘ্য
| 3×20 = 60 ডেকা মিটার. | 4×20 = 80 ডেকা মিটার. |
10. 8 সেমি বাহুবিশিষ্ট সুষম ষড়ভুজাকার ক্ষেত্রের ক্ষেত্রফল হিসাব করে লিখি (সংকেত : সুষম ষড়ভুজের কর্ণগুলি আঁকা হলে ছয়টি সর্বসম সমবাহু ত্রিভুজ পাব)
সমাধানঃ-
ABCDEF একটি সুষম ষড়ভুজ যার প্রতিটি বাহুর দৈর্ঘ্য = 8 সেমি. এবং যার কর্ণগুলি G বুন্দুতে পরস্পরকে ছেদ করেছে। যার ফলে ছয়টি সর্বসম সমবাহু ত্রিভুজ উৎপন্ন হয়েছে।
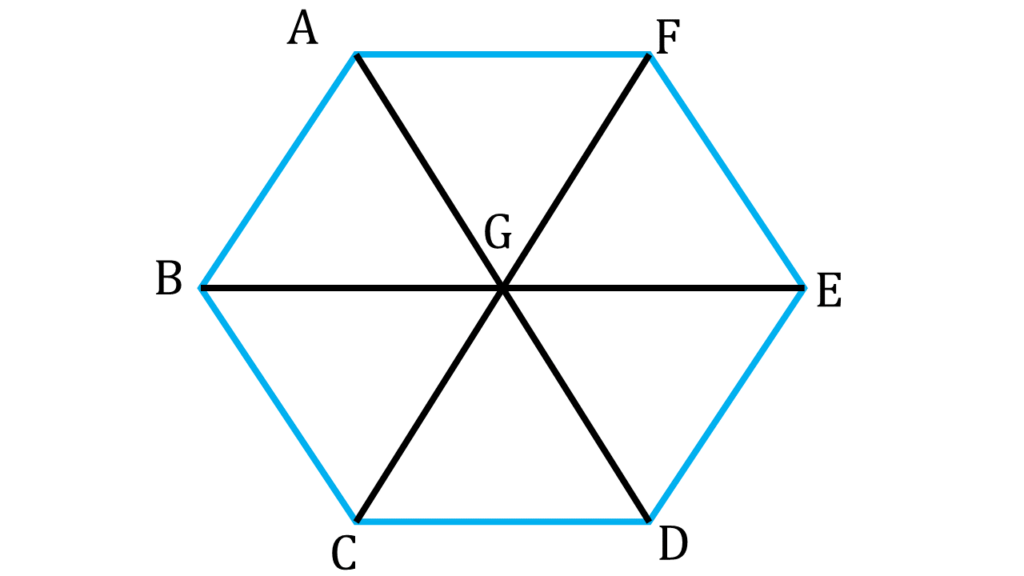
এখন,
| ষড়ভুজ ABCDEF = ▲AGF + ▲AGB + ▲BGC + ▲DGC + ▲GDE + ▲GEF |
| বা, ষড়ভুজ ABCDEF = ▲AGF + ▲AGF + ▲AGF + ▲AGF + ▲AGF + ▲AGF |
| বা, ষড়ভুজ ABCDEF = 6▲AGF |
| বা, ষড়ভুজ ABCDEF = 6×\(\frac{\sqrt3}{4}\)×82 |
| বা, ষড়ভুজ ABCDEF = 96√3 বর্গ সেমি. |
11. ABCD চতুর্ভুজের AB = 5 মিটার, BC= 12মিটার, CD = 14 মিটার, DA = 15 মিটার এবং ∠ABC = 90° হলে, ABCD চতুর্ভুজাকার ক্ষেত্রের ক্ষেত্রফল হিসাব করে লিখি।
সমাধানঃ-
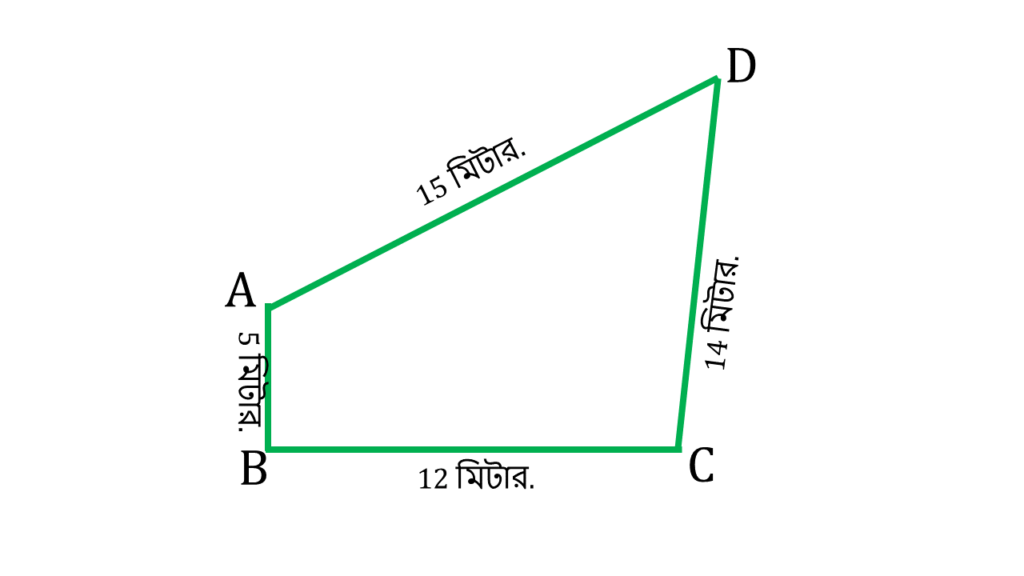
ABCD চতুর্ভুজের AB = 5 মিটার, BC= 12মিটার, CD = 14 মিটার, DA = 15 মিটার এবং ∠ABC = 90°
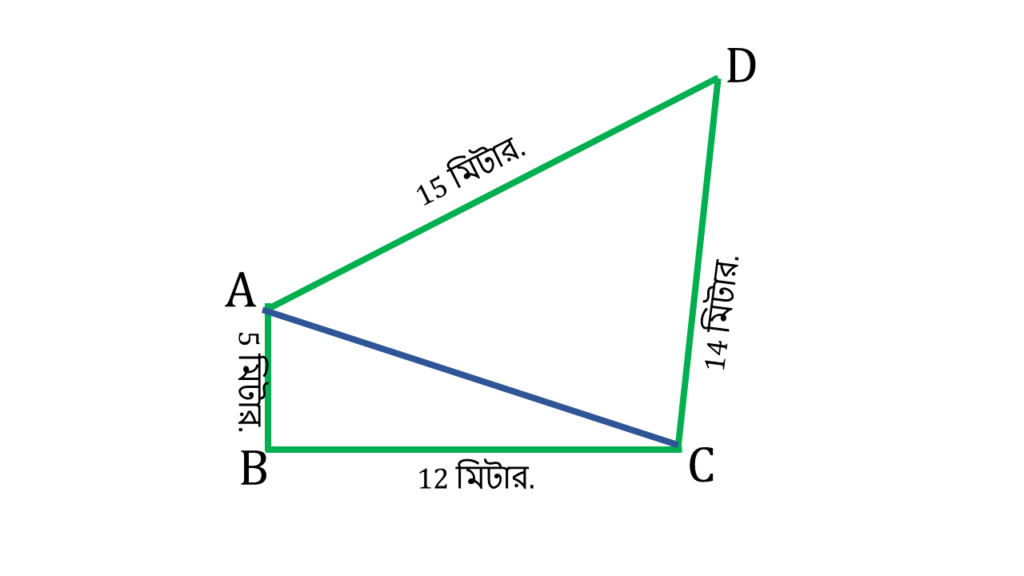
| চতুর্ভুজ ABCD এর ক্ষেত্রফল |
| = (▲ABC + ▲ACD) এর ক্ষেত্রফল |
এখন,
| ▲BOC সমকোণী ত্রিভুজ এর |
|---|
 |
| AC2 = AB2 + AC2 |
| বা, AB2 = 52 + 122 |
| বা, AB2 = 25 + 144 = 169 |
| বা, AB = 13 |
- ▲ABC এর ক্ষেত্রফলঃ
▲ABC একটি সমকোণী ত্রিভুজ।
ক্ষেত্রফল
= ½×BC×AB
= ½×12×5 = 30 বর্গ মিটার.
- ▲ACD এর ক্ষেত্রফলঃ
▲ACD এর s = \(\frac{13+14+15}{2}\) = 21
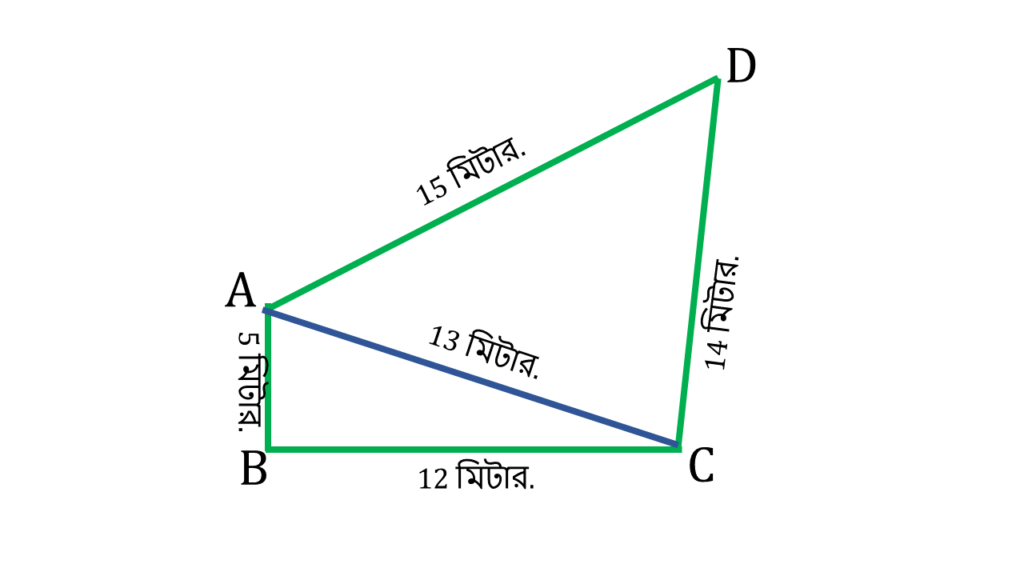

ক্ষেত্রফল
= \(\sqrt{21(21-13)(21-14)(21-15)}\)
= \(\sqrt{21×8×7×6}\)
= 7×3×4 = 84 বর্গ মিটার.
অতএব,
| চতুর্ভুজ ABCD এর ক্ষেত্রফল |
| = (▲ABC + ▲ACD) এর ক্ষেত্রফল |
| = 30 + 84 = 114 বর্গ মিটার. |
12. সাহিন ABCD একটি ট্রাপিজিয়াম এঁকেছে, যার BD কর্ণের দৈর্ঘ্য 11 সেমি. এবং A ও C বিন্দু থেকে BD কর্ণের উপর দুটি লম্ব এঁকেছে যাদের দৈর্ঘ্য যথাক্রমে 5 সেমি ও 11 সেমি.। হিসাব করে ট্রাপিজিয়াম আকার ক্ষেত্র ABCD -এর ক্ষেত্রফল লিখি।
সমাধানঃ-
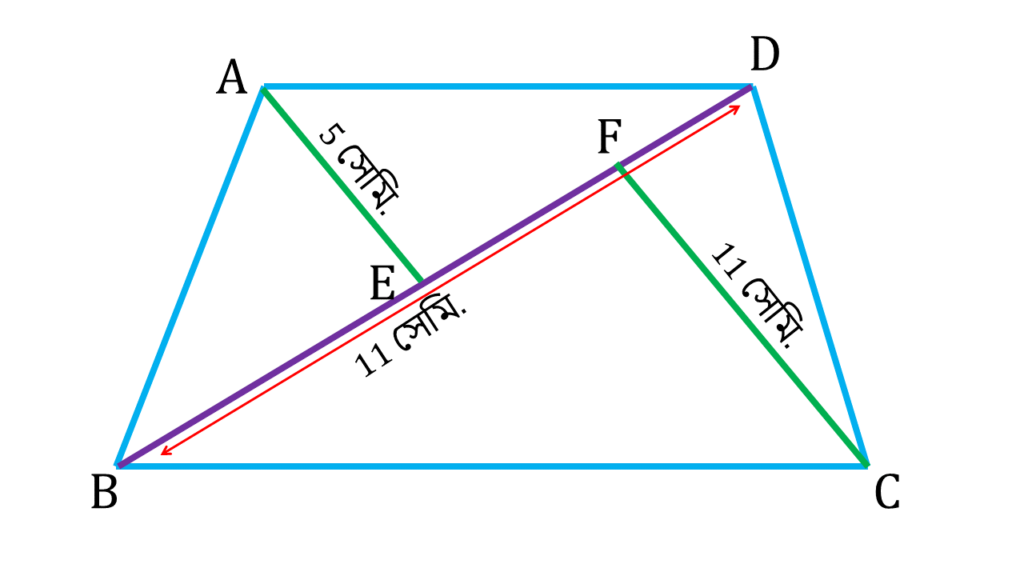
| ট্রাপিজিয়াম আকার ক্ষেত্র ABCD -এর ক্ষেত্রফল |
| = (▲BDC + ▲ABD) এর ক্ষেত্রফল |
 |
| = ½×BD×CF + ½×BD×AE |
| = ½×11×11 + ½×11×5 |
| = \(\frac{121+55}{2}\) |
| = \(\frac{176}{2}\)= 88 বর্গ সেমি. |
13. ABCDE একটি পঞ্চভুজ যার BC বাহুটি AD কর্ণের সমান্তরাল। EP, BC -এর উপর লম্ব এবং EP AD -কে Q বিন্দুতে ছেদ করেছে। BC = 7 সেমি., AD=13 সেমি., PE= 9 সেমি., এবং PQ = 4/9 PE হলে, ABCDE পঞ্চভুজাকার ক্ষেত্রের ক্ষেত্রফল হিসাব করে লিখি।
সমাধানঃ-
PQ = \(\frac{4}{9}\) PE
এখন
| PQ + QE = PE |
| বা, QE = PE – PQ |
| বা, QE = PE – \(\frac{4}{9}\)PE |
| বা, QE = \(\frac{(9-4)}{4}\)PE |
| বা, QE = \(\frac{5}{9}\)PE |
| বা, QE = \(\frac{5}{9} \times 9\) = 5 সেমি. |
| আবার, PQ = \(\frac{4}{9}\)PE |
| বা, PQ = \(\frac{4}{9} \times 9\) = 4 সেমি. |
আবার,
| ABCDE পঞ্চভুজাকার ক্ষেত্রের ক্ষেত্রফল |
| = (ট্রাপিজিয়াম ABCD + ▲ADE) এর ক্ষেত্রফল |
- ট্রাপিজিয়াম ABCD এর ক্ষেত্রফলঃ

ক্ষেত্রফল
= ½×(BC+AD)×PQ
= ½×(7+13)×4
= ½×20×4
= 40 বর্গ সেমি.
- ▲ADE এর ক্ষেত্রফলঃ

ক্ষেত্রফল
= ½×AD×QE
= ½×13×5 = 32.5 বর্গ সেমি.
অতএব
| ABCDE পঞ্চভুজাকার ক্ষেত্রের ক্ষেত্রফল |
| = (ট্রাপিজিয়াম ABCD + ▲ADE) এর ক্ষেত্রফল |
| = (40 + 32.5) = 72.5 বর্গ সেমি. |
14. একটি রম্বসের বাহুর দৈর্ঘ্য ও একটি বর্গক্ষেত্রের বাহুর দৈর্ঘ্য সমান এবং বর্গক্ষেত্রটির কর্ণের দৈর্ঘ্য 40√2 সেমি.। যদি রম্বসের কর্ণদ্বয়ের দৈর্ঘ্যের অনুপাত 3:4 হয়, তাহলে রম্বস আকার ক্ষেত্রের ক্ষেত্রফল হিসাব করে লিখি।
সমাধানঃ-
ধরি, বর্গক্ষেত্রের বাহুর দৈর্ঘ্য = a সেমি.
⇒ বর্গক্ষেত্রের কর্ণ = a√2 সেমি.
| ∴ a√2 = 40√2 |
| বা, a = 40 |
অতএব রম্বসের বাহুর দৈর্ঘ্য = 40 সেমি.
রম্বসের কর্ণদ্বয়ের দৈর্ঘ্যের অনুপাত 3:4
ধরি, রম্বসের কর্ণদ্বয়ের দৈর্ঘ্য 3x সেমি. ও 4x সেমি.
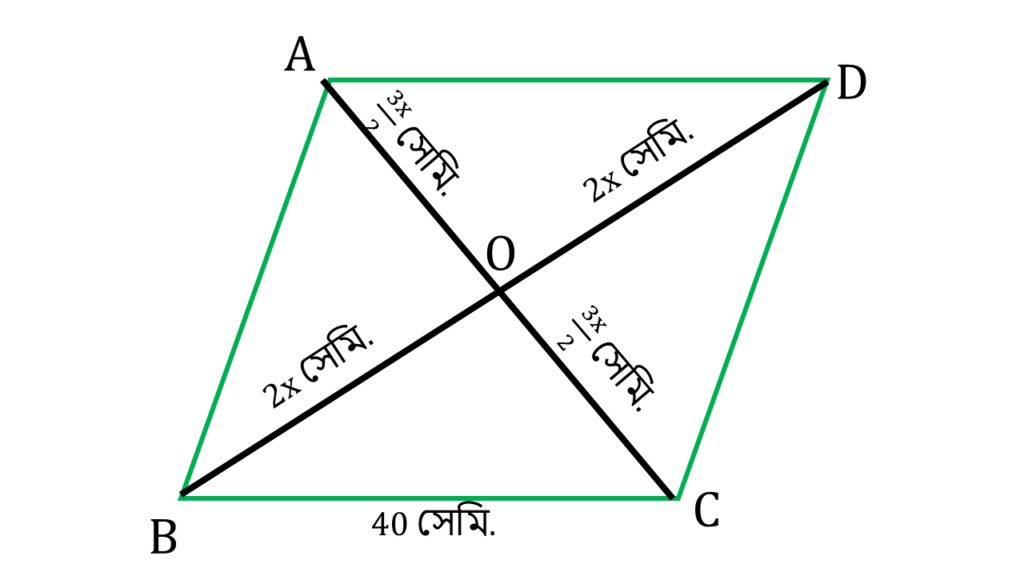
| ▲BOC সমকোণী ত্রিভুজ এর |
|---|
 |
| BC2 = BO2 + OC2 |
| বা, 402 = (2x)2 + (\(\frac{3x}{2}\))2 |
| বা, 4x2 + \(\frac{9x^2}{4}\) = 1600 |
| বা, \(\frac{16x^2 + 9x^2}{4}\) = 1600 |
| বা, 25x2 = 1600×4 |
| বা, x2 = \(\frac{6400}{25}\) = 4×64 = 16×16 |
| বা, x = 16 |
অতএব রম্বসের কর্ণদ্বয়ের দৈর্ঘ্য
| 3x = 3×16 = 48 সেমি. | 4x = 4×16 = 64 সেমি. |
- রম্বসের ক্ষেত্রফলঃ
আমরা জানি,

ক্ষেত্রফল
= ½×48×64
= 1536 বর্গ সেমি.
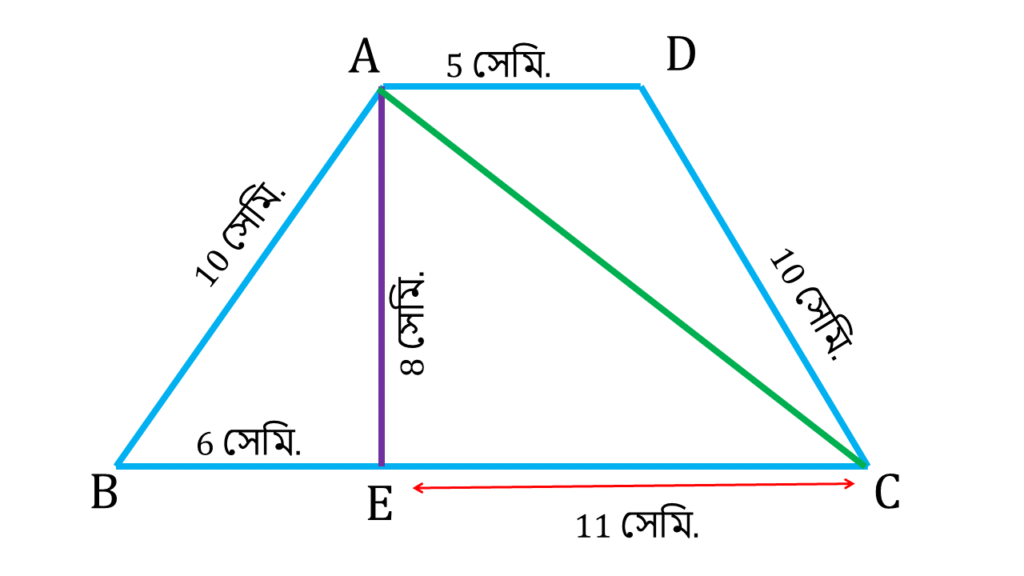
15 . একটি সমদ্বিবাহু ট্রাপিজিয়ামের তির্যক বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য 10 সেমি. এবং সমান্তরাল বাহুদুটির দৈর্ঘ্য যথাক্রমে 5 সেমি. ও 17 সেমি.। ট্রাপিজিয়াম আকার ক্ষেত্রের কর্ণের দৈর্ঘ্য ও ক্ষেত্রফল হিসাব করে লিখি।
সমাধানঃ-
ABCD একটি সমদ্বিবাহু ট্রাপিজিয়ামের তির্যক বাহুদ্বয় AB ও DC প্রত্যেকটির দৈর্ঘ্য 10 সেমি. এবং সমান্তরাল AD ও BC বাহুদুটির দৈর্ঘ্য যথাক্রমে 5 সেমি. ও 17 সেমি.।
A ও D বিন্দু থেকে BC বাহুর উপর AE ও DF লম্ব অঙ্কন করলাম.
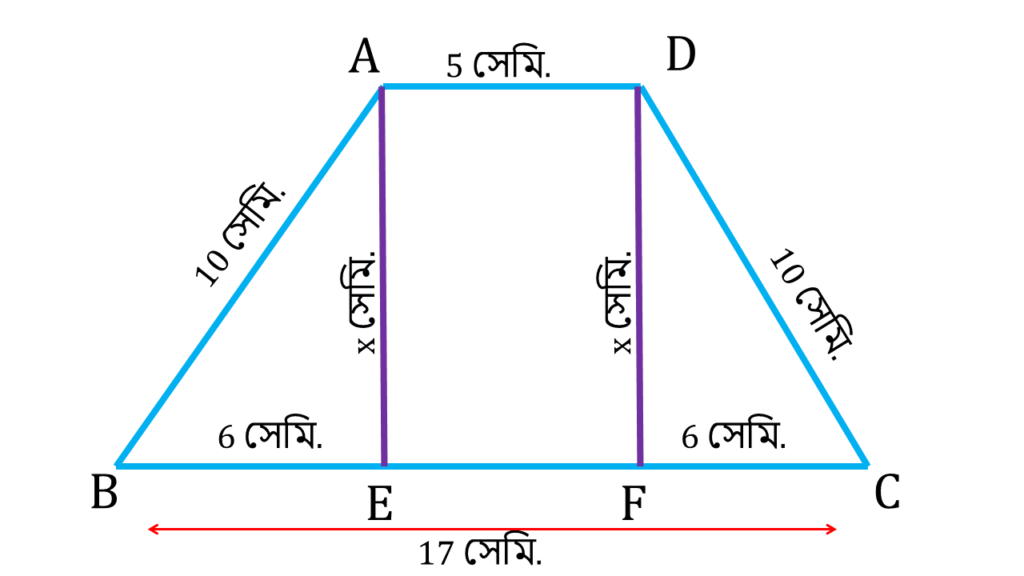
ধরি, AE = DF = x সেমি.
| ▲AEB ও ▲FDC এর মধ্যে, |
|---|
| AB = DC [প্রদত্ত] |
| ∠AEB = ∠DDC = 90° |
| AE = DF = x |
| ∴ ▲AEB ≅ ▲ FDC |
| ⇒ BE=FC [সর্বসম ত্রিভুজের অনুরূপ বাহু ] |
এখন
| BE + EF + FC = BC |
| বা, BE + 5 + BE = 17 |
| বা, 2BE = 12 |
| বা, BE = 6 = FC |

| ▲AEB সমকোণী ত্রিভুজ এর |
|---|
 |
| AB2 = BE2 + AE2 |
| বা, 62 + x2 = 102 |
| বা, x2 = 100 – 36 |
| বা, x2 = 64 |
| বা, x = 8 |
- BD কর্ণের দৈর্ঘ্যঃ
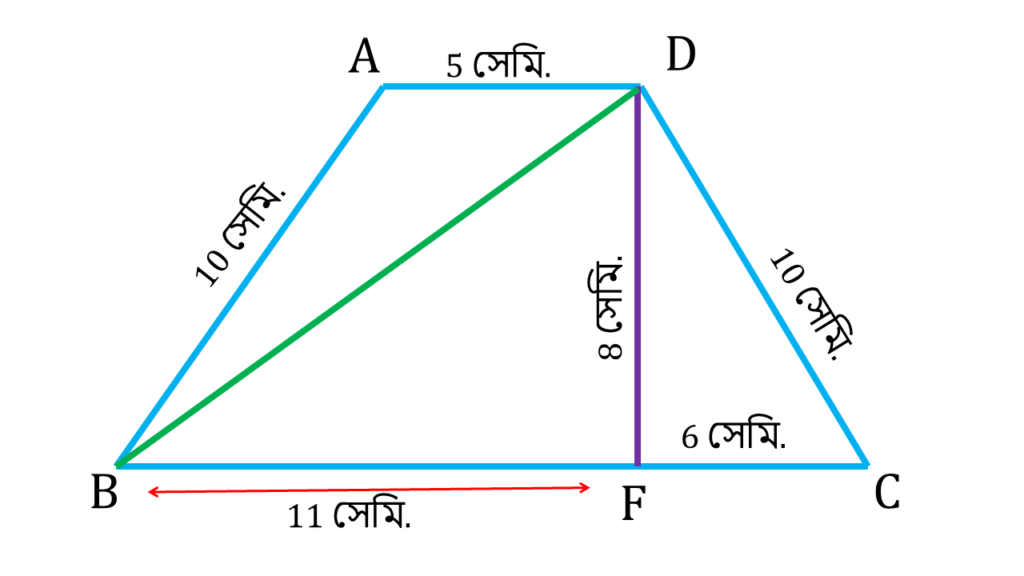
| ▲AEB সমকোণী ত্রিভুজ এর |
|---|
 |
| BD2 = DF2 + BF2 |
| বা, BD2 = 82 + 112 |
| বা, BD2 = 64 + 121 |
| বা, BD2 = 185 |
| বা,BD = \(\sqrt{185}\) |
- AC কর্ণের দৈর্ঘ্যঃ
| ▲AEC সমকোণী ত্রিভুজ এর |
|---|
 |
| AC2 = AE2 + EC2 |
| বা, AC2 = 82 + 112 |
| বা, AC2 = 64 + 121 |
| বা, AC2 = 185 |
| বা, AC = \(\sqrt{185}\) |
- ট্রাপিজিয়াম ABCD এর ক্ষেত্রফলঃ

খেত্রফল
= ½×(17+5)×8
= 4×22 = 88 বর্গ সেমি.
16. একটি ট্রাপিজিয়ামের সমান্তরাল বাহুদ্বয়ের দৈর্ঘ্য 19 সেমি. ও 9 সেমি. এবং তির্যক বাহুদ্বয়ের দৈর্ঘ্য 8 সেমি. ও 6 সেমি.। ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল হিসাব করি।
সমাধানঃ-
ABCD একটি ট্রাপিজিয়ামের সমান্তরাল বাহুদ্বয়ের দৈর্ঘ্য 19 সেমি. ও 9 সেমি. এবং তির্যক বাহুদ্বয়ের দৈর্ঘ্য 8 সেমি. ও 6 সেমি.
A ও D বিন্দু থেকে BC বাহুর উপর AE ও DF লম্ব অঙ্কন করলাম.
ধরি, AE = DF = x সেমি.
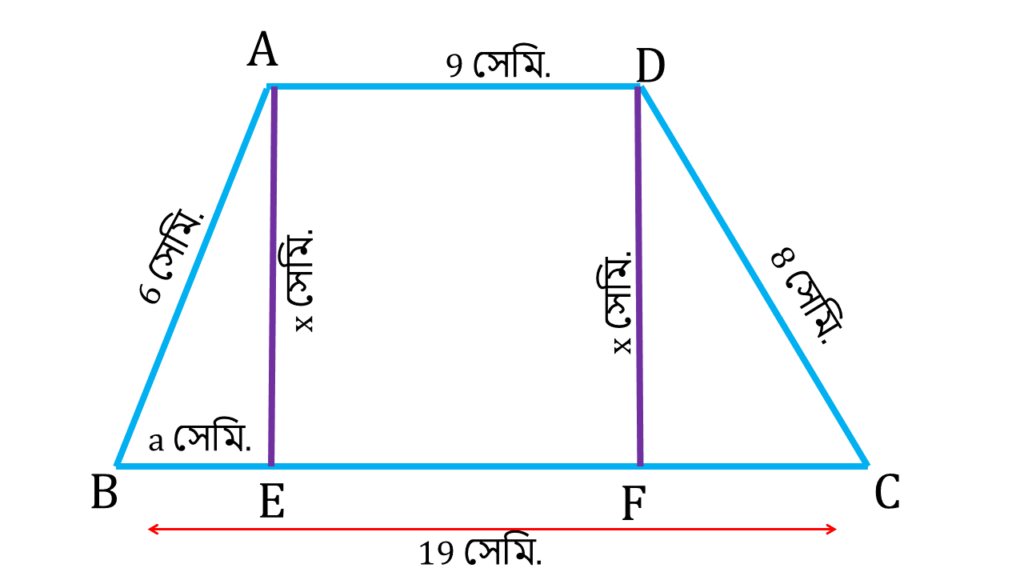
| BE + EF + FC = BC |
| বা, a + 9 + FC = 19 |
| বা, FC = 10 – a |
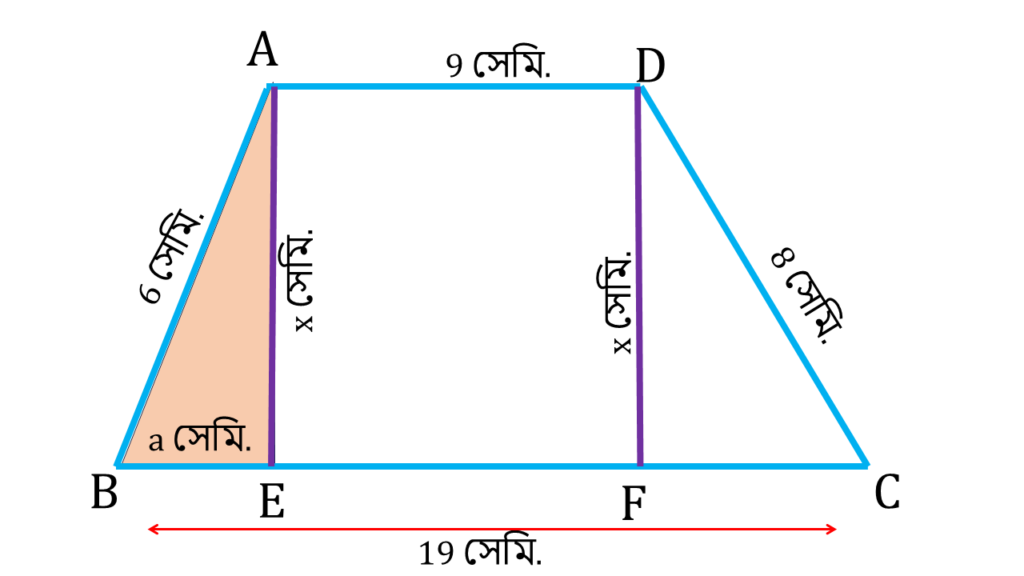
| ▲AEB সমকোণী ত্রিভুজ এর |
|---|
 |
| AB2 = AE2 + BE2 |
| বা, x2 + a2 = 62 |
| বা, x2 = 36 – a2 ——–(i) |
আবার,
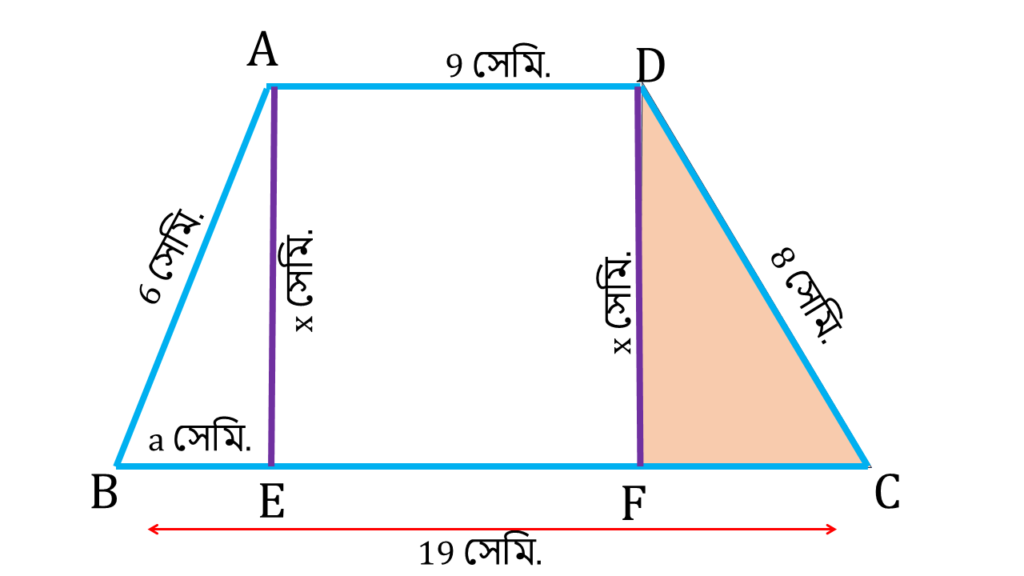
| ▲DFC সমকোণী ত্রিভুজ এর |
|---|
 |
| DC2 = FD2 + FC2 |
| বা, x2 + (10-a)2 = 82 |
| বা, x2 = 64 – (10-a)2 |
| বা, x2 = 64 – 100 + 20a – a2 |
| বা, x2 = -36 + 20a – a2 ——–(ii) |
(i) ও (ii) সমান করে পাই,
| 36 – a2 = -36 + 20a – a2 |
| বা, 20a = 36 + 36 |
| বা, a = \(\frac{72}{20}\) = \(\frac{18}{5}\) |
a = \(\frac{13}{5}\) (i) নং সমীকরণে বসিয়ে পাই,
| x2 = 36 – (\(\frac{18}{5}\))2 |
| বা, x2 = 36 – \(\frac{324}{25}\) |
| বা, x2 = \(\frac{(36 \times 25 – 324)}{25}\) |
| বা, x2 = \(\frac{576}{25}\) |
| বা, x = \(\frac{24}{5}\) |
- ট্রাপিজিয়াম ABCD এর ক্ষেত্রফলঃ

ক্ষেত্রফল
= ½×(19+9)×\(\frac{24}{5}\)
= 67.2 বর্গ সেমি.
17. বহু বিকল্পীয় প্রশ্ন (M.C.Q.)
(i) একটি সামান্তরিকের উচ্চতা ভূমির এক-তৃতীয়াংশ। সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল 192 বর্গসেমি. হলে, সামান্তরিকটির উচ্চতা
(b) 8 সেমি.
সমাধানঃ-
ধরি, সামান্তরিকের ভূমি = a সেমি.
উচ্চতা = \(\frac{a}{3}\) সেমি.
ক্ষেত্রফল
a × \(\frac{a}{3}\) = 192
বা, a2 = 576
বা, a = 24
অতএব, উচ্চতা = \(\frac{24}{3}\) = 8 সেমি.
(ii) একটি রম্বসের একটি বাহুর দৈর্ঘ্য 6সেমি. এবং একটি কোণের পরিমাপ 60° হলে, রম্বস আকার ক্ষেত্রের ক্ষেত্রফল
(b) 18√3 বর্গ সেমি.
সমাধানঃ- ABCD রম্বসের ∠ABC = 60°
▲ABC এর AB = BC
অতএব
∠BAC = ∠ACB
আবার,
∠BAC + ∠ACB + ∠ABC = 180°
বা, 2∠BAC = 180°-60°
বা, ∠BAC = 60° = ∠ACB
অতএব, ▲ABC একটি সর্বসম ত্রিভুজ।
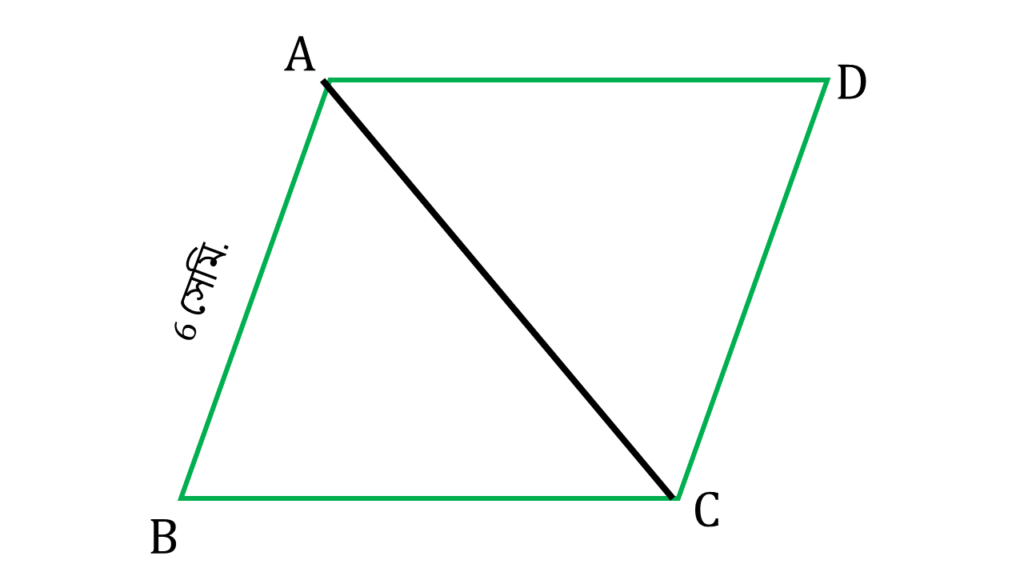
⇒ AB = BC = AC = 6 সেমি
সমকোণী ত্রিভুজ AOB এর
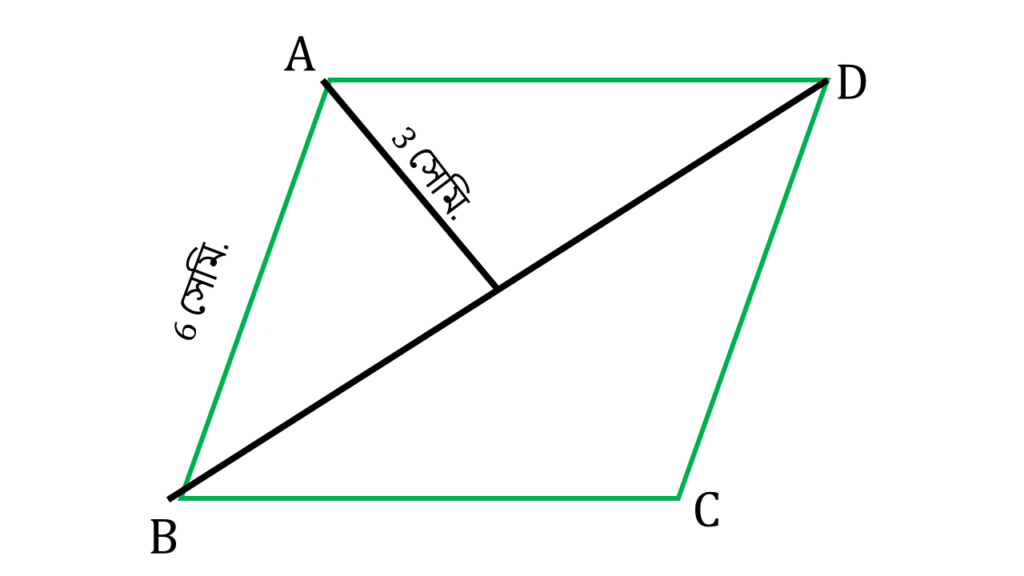
AO2 + BO2 = AB2
বা, BO2 = AB2 – AO2
বা, BO2 = 62 – 32
বা, BO2 = 36 – 9
বা, BO2 = 27
বা, BO = 3√3
⇒ BD = 2BO = 6√3
রম্বসের ক্ষেত্রফল
= ½×6×6√3
= 18√3 বর্গ সেমি.
(iii) একটি রম্বসের একটি কর্ণের দৈর্ঘ্য অপর কর্ণটির দৈর্ঘ্যের তিনগুণ। যদি রম্বস আকার ক্ষেত্রের ক্ষেত্রফল 96 বর্গ সেমি হয়, তাহলে বড় কর্ণটির দৈর্ঘ্য
(d) 24 সেমি.
সমাধানঃ-
ধরি, ছোটো কর্ণের দৈর্ঘ্য = a সেমি.
বড়ো কর্ণের দৈর্ঘ্য = 3a সেমি.
অতএব,
½×3a×a = 96
বা, a2 = \(\frac{96 \times 2}{3}\)
বা, a = 8
অতএব বড়ো কর্ণের দৈর্ঘ্য = 24 সেমি.
(iv) একটি রম্বস ও একটি বর্গক্ষেত্র একই ভূমির উপর অবস্থিত। বর্গক্ষেত্রের ক্ষেত্রফল x2 বর্গ একক এবং রম্বস আকার ক্ষেত্রের ক্ষেত্রফল y বর্গ একক হলে,
(b) y < x2
সমাধানঃ-
ধরি রম্বসের উচ্চতা FH = h<AB=x
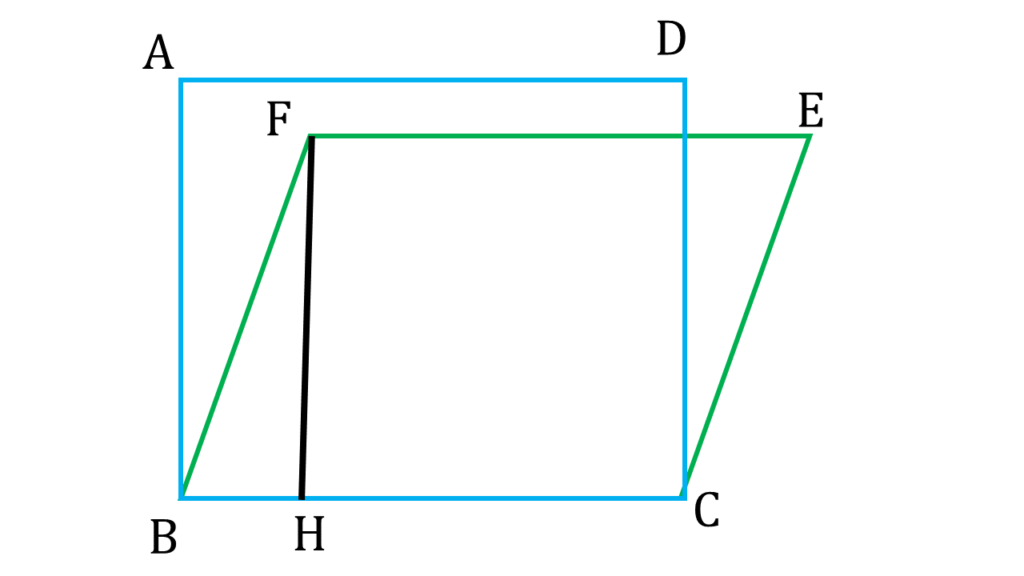
অতএব
| h < x বা, hx < x2 |
| বা, y < x2 |
(v) একটি ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল 162 বর্গ সেমি. এবং উচ্চতা 6 সেমি.। ট্রাপিজিয়ামটির একটি সমান্তরাল বাহুর দৈর্ঘ্য 23 সেমি. হলে, অপর সমান্তরাল বাহুর দৈর্ঘ্য
(b) 31 সেমি.
সমাধানঃ-
ধরি, অপর বাহুটির দৈর্ঘ্য = x সেমি.
| ½×(x + 23)×6 = 162 |
| বা, x + 23 = \(\frac{162 \times 2}{6}\) |
| বা, x = 54 – 23 = 31 |
18. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন
(i) ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল 96 বর্গ সেমি. ও BD কর্ণের দৈর্ঘ্য 12 সেমি । A বিন্দু থেকে BD কর্ণের উপর লম্বের দৈর্ঘ্য কত?
সমাধানঃ-
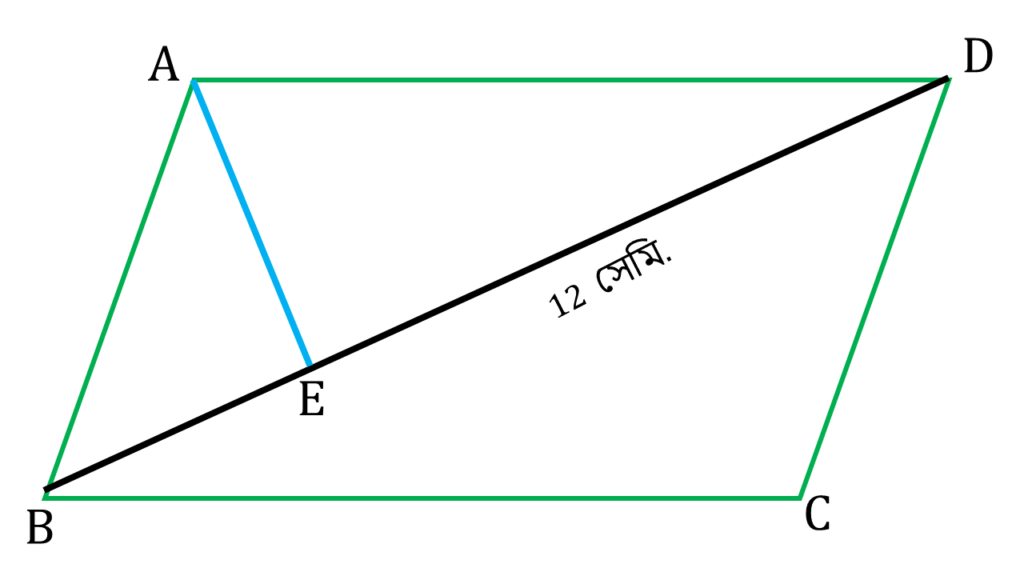
| 2▲ABD = সামান্তরিক ABCD |
| বা, 2× ½ × BD × AE = 96 |
| বা, 12×AE = 96 |
| বা, AE = 8 |
- ∴ A বিন্দু থেকে BD কর্ণের উপর লম্বের দৈর্ঘ্য = 8 সেমি.
(ii) একটি সামান্তরিকের সন্নিহিত বাহুদ্বয়ের দৈর্ঘ্য 5 সেমি এবং 3 সেমি.। বৃহত্তর বাহুদ্বয়ের মধ্যে দূরত্ব 2 সেমি. হলে, ক্ষুদ্রতর বাহুদ্বয়ের মধ্যে দূরত্ব কত?
সমাধানঃ-
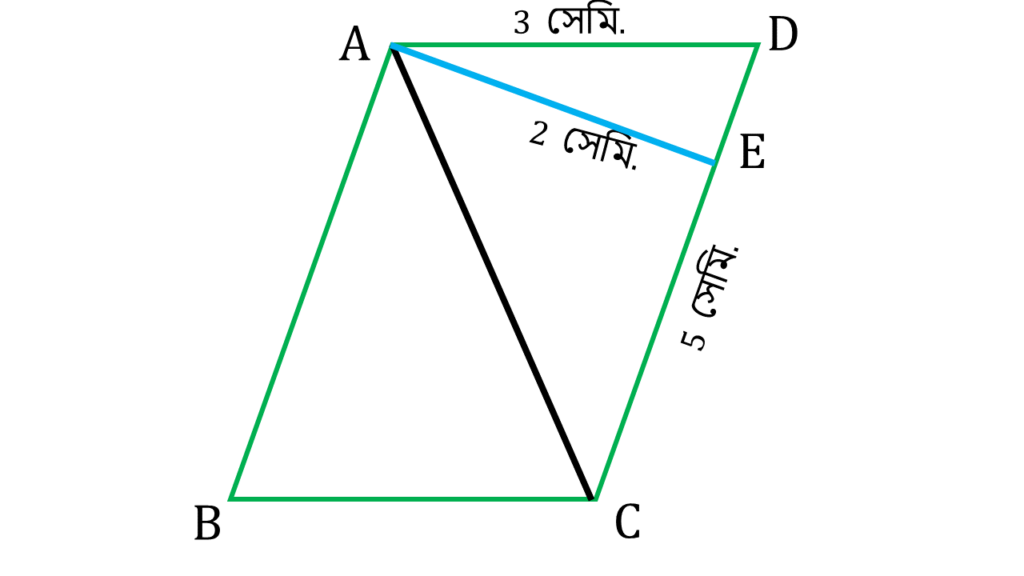
DC বাহুকে ভূমি ধরে ▲ADC এর ক্ষেত্রফল
= ½×DC×AE
= ½×5×2
= 5 বর্গ সেমি.
এখন ▲ADC এর AD বাহুকে ভূমি ধরে যে উচ্চতা পাবো সেটিই হলো সামান্তরিকের ক্ষুদ্রতম বাহুর মধ্যের দূরত্ব।
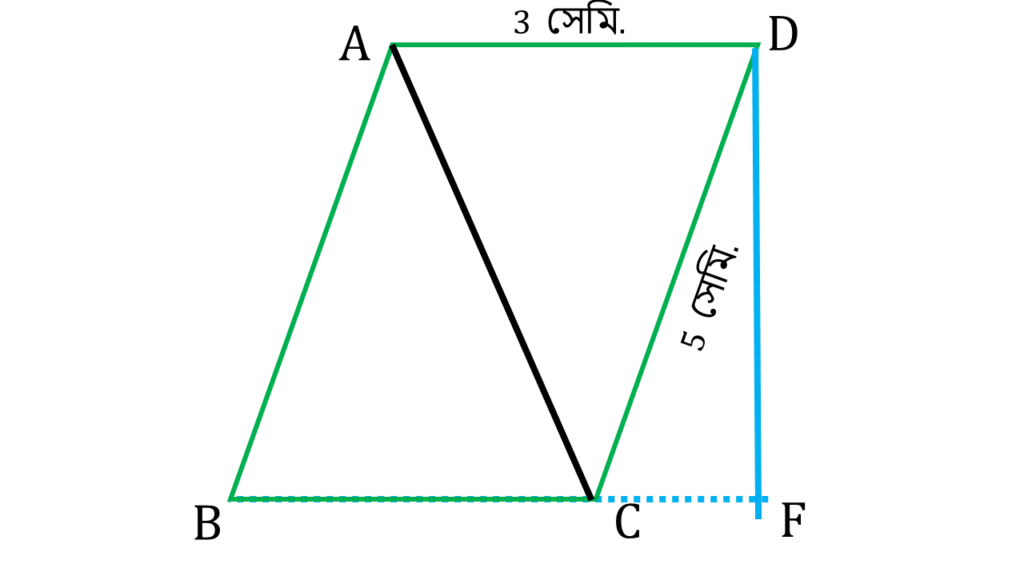
AD বাহুকে ভূমি ধরে ▲ADC এর ক্ষেত্রফল
= ½×AD×DF
= ½×3DF
অতএব,
½×3DF = 5
বা, DF = \(\frac{10}{3}\)
- ∴ ক্ষুদ্রতর বাহুদ্বয়ের মধ্যে দূরত্ব = \(\frac{10}{3}\) সেমি.
(iii) একটি রম্বসের উচ্চতা 4 সেমি. এবং বাহুর দৈর্ঘ্য 5 সেমি । রম্বস আকার ক্ষেত্রের ক্ষেত্রফল কত?
সমাধানঃ-
যেহেতু রম্বস একটি সামান্তরিক

ক্ষেত্রফল = 5×4 = 20 বর্গ সেমি.
(iv) একটি সমদ্বিবাহু ট্রাপিজিয়ামের যেকোনো সমান্তরাল বাহু সংলগ্ন একটি কোণ 45°; ট্রাপিজিয়ামের তির্যক বাহুর দৈর্ঘ্য 62 সেমি. হলে, সমান্তরাল বাহুদ্বয়ের মধ্যে দূরত্ব কত?
সমাধানঃ-
ABCD ট্রাপিজিয়ামের ∠ABC = 45°
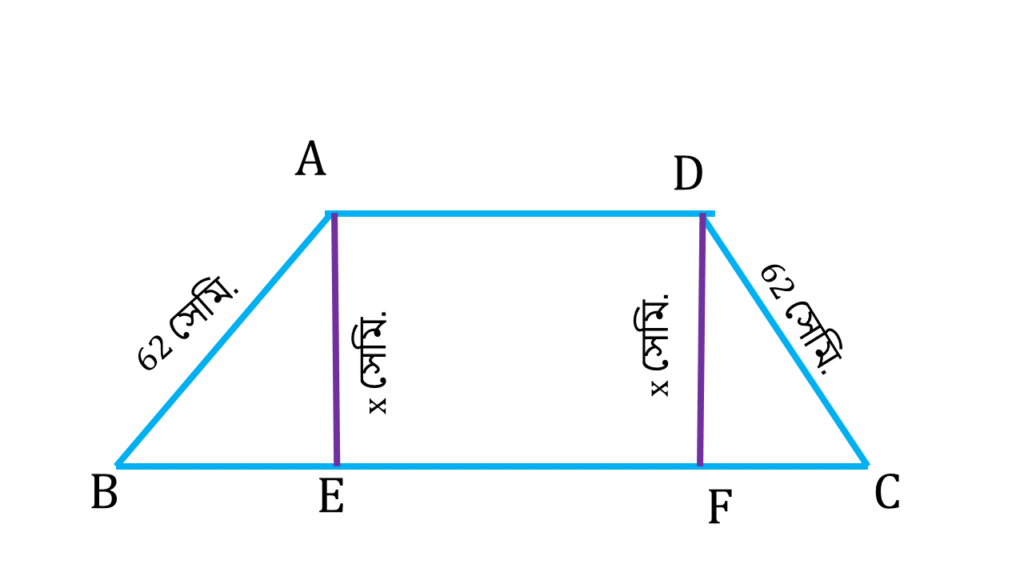
| ▲AEB সমকোণী ত্রিভুজ এর |
|---|
| ∠ABC + ∠AEB + ∠BAE = 180° |
| বা, ∠BAE = 180° – 90° – 45° |
| বা, ∠BAE = 45° |
| ∴ ▲AEB একটি সমকোণী সমদ্বিবাহু ত্রিভুজ যার AE=EB |
| আবার, |
| AE2 + BE2 = AB2 |
| বা, 2AE2 = 62×62 |
| বা, AE2 = 62×31 |
| বা, AE = 31√2 সেমি |
(v) ABCD সামান্তরিকের AB= 4 সেমি., BC = 6 সেমি. এবং ∠ABC = 30° হলে, ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল কত?
সমাধানঃ-
A বিন্দু থেকে BC বাহুর উপর AE লম্ব অঙ্কন করলাম এবং F পর্যন্ত এমনভাবে বর্ধিত করলাম যাতে AE = EF হয়।
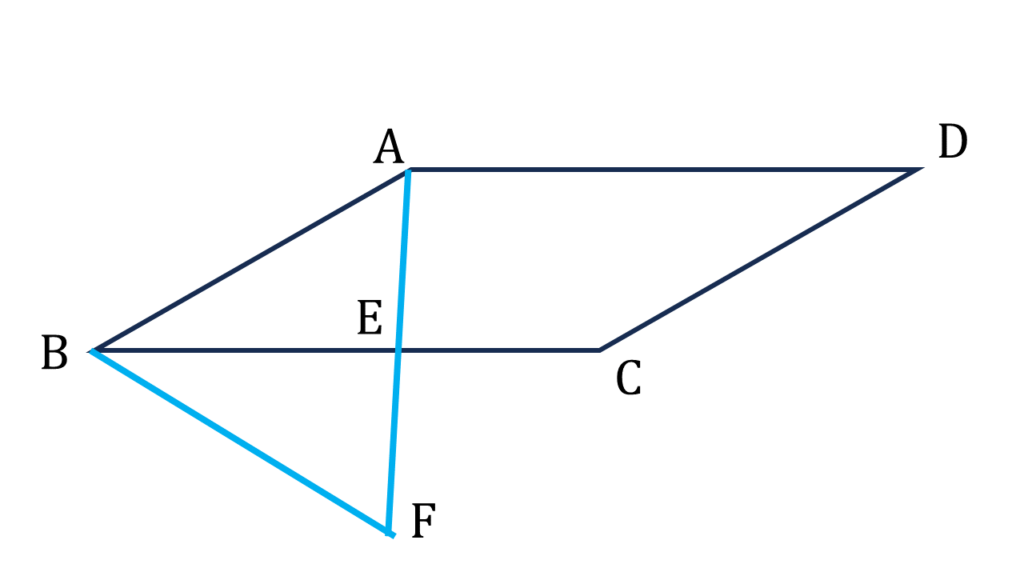
▲AEB এর
| ∠EAB |
| =180°-∠EBA-∠AEB |
| =180° – 30° – 90° = 60° |
এখন
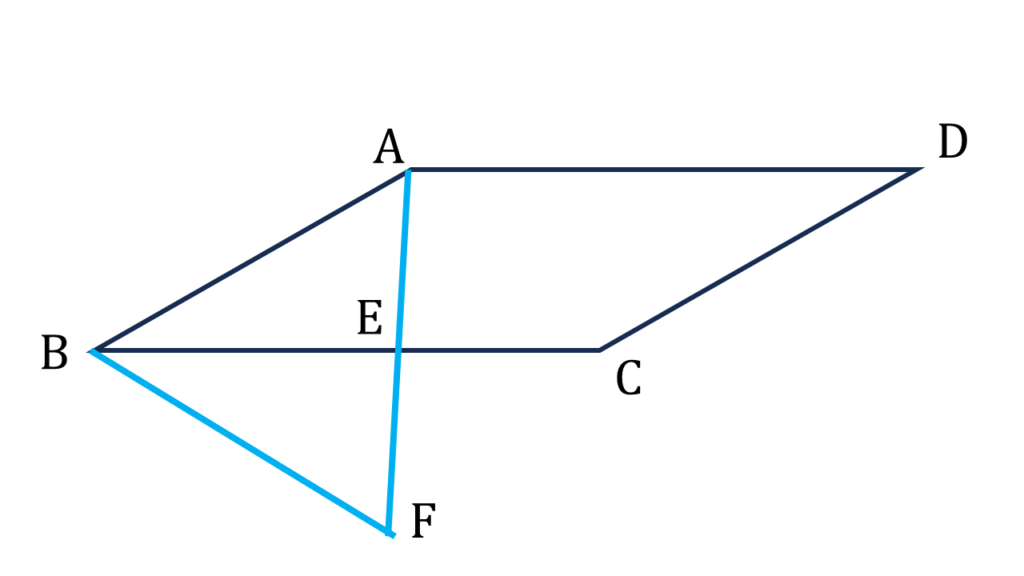
| ▲AEB ও ▲BEF এর মধ্যে, |
|---|
| AE = EF [অঙ্কন] |
| ∠AEB = ∠BEF = 90° |
| BE সাধারণ বাহু |
| ∴ ▲AEB ≅ ▲ BEF |
| ⇒ AB = BF [সর্বসম ত্রিভুজের অনুরূপ বাহু ] |
| এবং |
| ⇒ ∠BAE = ∠AFB [সর্বসম ত্রিভুজের অনুরূপ কোণ ] |
| এবং |
| ⇒ ∠EBF = ∠ABE [সর্বসম ত্রিভুজের অনুরূপ কোণ ] |
অতএব
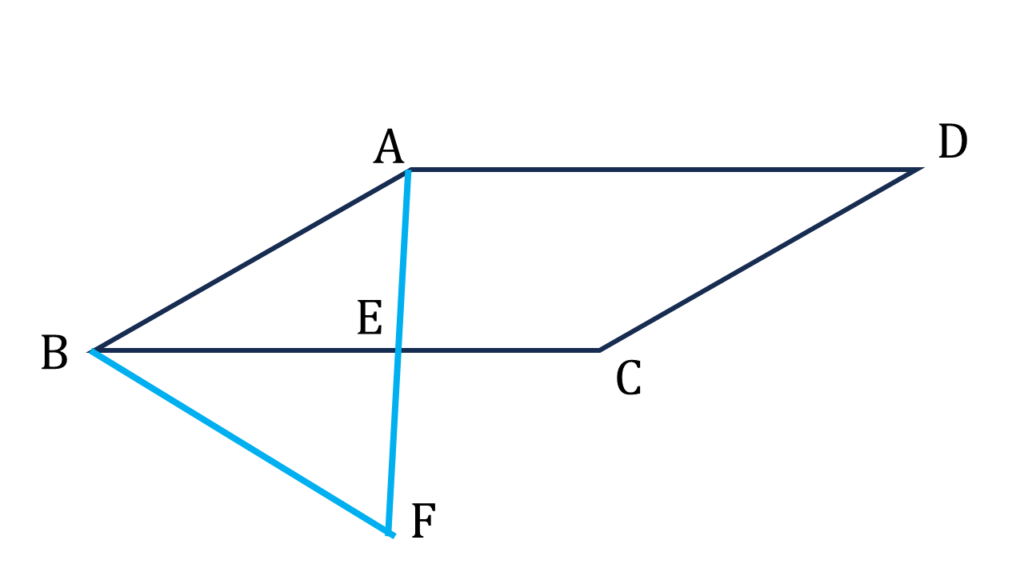
∠ABF = ∠FBE + ∠ABE = 30°+30°=60°
▲ABF এর
∠ABF = ∠BFA = ∠BAF = 60°
অতএব ▲ABF একটি সমবাহু ত্রিভুজ
AE = EF = \(\frac{4}{2}\) = 2 সেমি.
এখন

ক্ষেত্রফল = BC×AE = 6×2 = 12 বর্গ সেমি.
ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল অধ্যায়ের বাকি কষে দেখিঃ-
| WB Class 9 এর গণিত প্রকাশের সমস্ত অধ্যায়ের সমাধান- | |
|---|---|
| অধ্যায় | সমাধান |
| 1. বাস্তব সংখ্যা (Real Numbers) | কষে দেখি 1.1 |
| কষে দেখি 1.2 | |
| কষে দেখি 1.3 | |
| 2. সূচকের নিয়মাবলি (Laws of Indices) | কষে দেখি 2 |
| 3. লেখচিত্র (Graph) | কষে দেখি 3.1 |
| কষে দেখি 3.2 | |
| 4. স্থানাঙ্ক জ্যামিতি : দূরত্ব নির্ণয় (Co-ordinate Geometry: Distance Formula) | কষে দেখি 4 |
| 5. রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) (Linear Simultaneous Equations) | কষে দেখি 5.1 |
| কষে দেখি 5.2 | |
| কষে দেখি 5.3 | |
| কষে দেখি 5.4 | |
| কষে দেখি 5.5 | |
| কষে দেখি 5.6 | |
| কষে দেখি 5.7 | |
| 6. সামান্তরিকের ধর্ম (Properties of Parallelogram) | কষে দেখি 6 |
| 7. বহুপদী সংখ্যামালা (Polynomial) | কষে দেখি 7.1 |
| কষে দেখি 7.2 | |
| কষে দেখি 7.3 | |
| কষে দেখি 7.4 | |
| 8. উৎপাদকে বিশ্লেষণ (Factorisation) | কষে দেখি 8.1 |
| কষে দেখি 8.2 | |
| কষে দেখি 8.3 | |
| কষে দেখি 8.4 | |
| কষে দেখি 8.5 | |
| 9. ভেদক ও মধ্যবিন্দু সংক্রান্ত উপপাদ্য (Transversal & Mid-Point Theorem). | কষে দেখি 9 |
| 10. লাভ ও ক্ষতি (Profit and Loss) | কষে দেখি 10.1 |
| কষে দেখি 10.2 | |
| 11. রাশিবিজ্ঞান (Statistics) | কষে দেখি 11.1 |
| কষে দেখি 11.2 | |
| 12. ক্ষেত্রফল সংক্রান্ত উপপাদ্য (Theorems on Area) | কষে দেখি 12 |
| 13. সম্পাদ্য : ত্রিভুজের সমান ক্ষেত্রফল বিশিষ্ট সামান্তরিক অঙ্কন | কষে দেখি 13 |
| 14. সম্পাদ্য : চতুর্ভুজের সমান ক্ষেত্রফল বিশিষ্ট ত্রিভুজ অঙ্কন | কষে দেখি 14 |
| 15. ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল (Area & Perimeter of Triangle & Quadrilateral) | কষে দেখি 15.1 |
| কষে দেখি 15.2 | |
| কষে দেখি 15.3 | |
| 16. বৃত্তের পরিধি (Circumference of Circle) | কষে দেখি 16 |
| 17. সমবিন্দু সংক্রান্ত উপপাদ্য (Theorems on concurrence) | কষে দেখি 17 |
| 18. বৃত্তের ক্ষেত্রফল (Area of Circle) | কষে দেখি 18 |
| 19. স্থানাঙ্ক জ্যামিতি: সরলরেখাংশের অন্তর্বিভক্ত ও বহিঃবিভক্ত (Co-ordinate Geometry: Internal and External Division of Straight-Line Segment) | কষে দেখি 19 |
| 20. স্থানাঙ্ক জ্যামিতি: ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল (Co-ordinate Geometry: Area of Triangular Region) | কষে দেখি 20 |
| 21. লগারিদম (Logarithm) | কষে দেখি 21 |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
এই কষে দেখি 15.3 Class 9|Koshe Dekhi 15.3 Class 9 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।

এখানে তোমরা তোমাদের নবম শ্রেণীতে| Class 9 এ কি কি পড়ানো হয়, মানে তোমাদের নবম শ্রেণী| Class 9 সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

