শ্রেণী-নবম ; অধ্যায় -ক্ষেত্রফল সংক্রান্ত উপপাদ্য ; কষে দেখি 12
কষে দেখি 12 Class 9 এর সুচিপত্রঃ-
কষে দেখি 12 Class 9 এর অংকের সমাধান গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ
এই কষে দেখি 12 পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদ | WBBSE বোর্ডের অন্তর্গত তোমাদের Class 9 |নবম শ্রেণীর গণিত বই এর 12 নম্বর অধ্যায়-ক্ষেত্রফল সংক্রান্ত উপপাদ্য এর অনুশীলনী।
এই কষে দেখি 12 Class 9 এর অঙ্কগুলি উপপাদ্য ও প্রয়োগ এর অংক। তোমরা যারা উপপাদ্য দেখে ভয় করো তারা আমার নিম্নের এই নির্দেশিকা অনুসরণ করবে তাহলে উপপাদ্য লিখতে বা বুঝতে অসুবিধা হবেনা।
এই কষে দেখি 12 Class 9 এর অংক গুলি করার জন্যে তোমাদের যে যে উপপাদ্য গুলি ভালো করে জেনে নিতে হবে সেগুলি হলো-
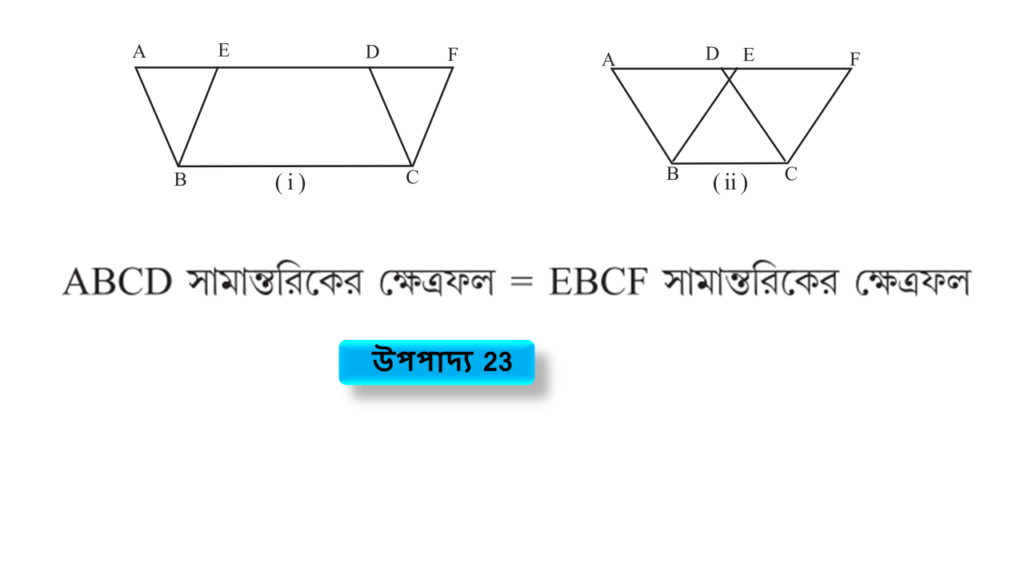
উপপাদ্য 23
যে সকল সামান্তরিক একই ভূমি একই সমান্তরাল সরলরেখা যুগলের মধ্যে অবস্থিত, তাদের ক্ষেত্রফল সমান।
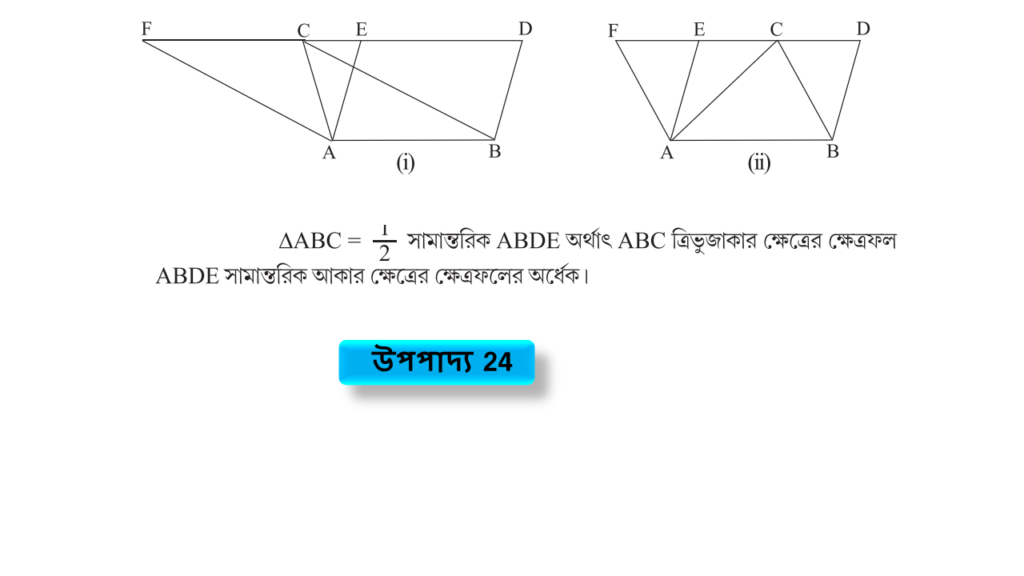
উপপাদ্য 24
ত্রিভুজ ও কোনো সামান্তরিক একই ভূমি ও একই সমান্তরলা সরলরেখাযুগলের মধ্যে অবস্থিত হলে, ত্রিভুজের ক্ষেত্রফল সামান্তরিক আঁকার ক্ষেত্রের ক্ষেত্রফলের অর্ধেক হবে।
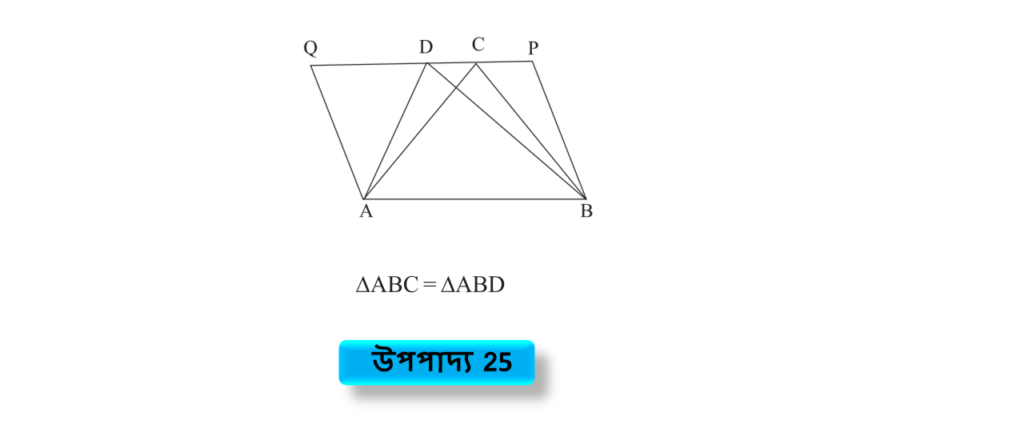
উপপাদ্য 25
একই ভূমি ও একই সমান্তরাল সরলরেখাযুগলের মধ্যে অবস্থিত ত্রিভুজাকার খেত্রগুলির ক্ষেত্রফল সমান।
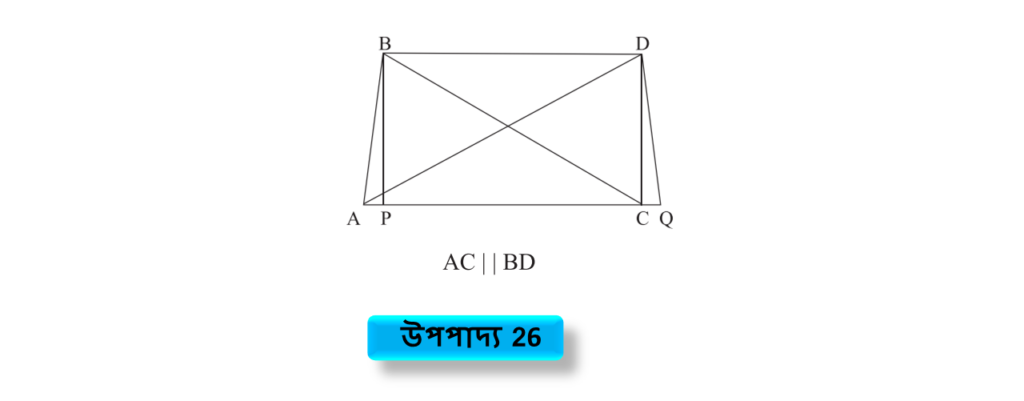
উপপাদ্য 26
সমান সমান ক্ষেত্রফলবিশিষ্ট ত্রিভুজাকার খেত্রগুলি একই ভূমির উপর এবং ভূমির একই পার্শে অবস্থিত হলে, তারা একই সমান্তরাল সরলরেখা যুগলের মধ্যে অবস্থিত হবে।
আগামিতে এই কষে দেখি 12 Class 9 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| আগামিতে আবার এই কষে দেওয়া অংকের প্রয়োজন হলে কি করবে? |
|---|
| কষে দেখি 12 Class 9 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 12 Class 9 তারপর 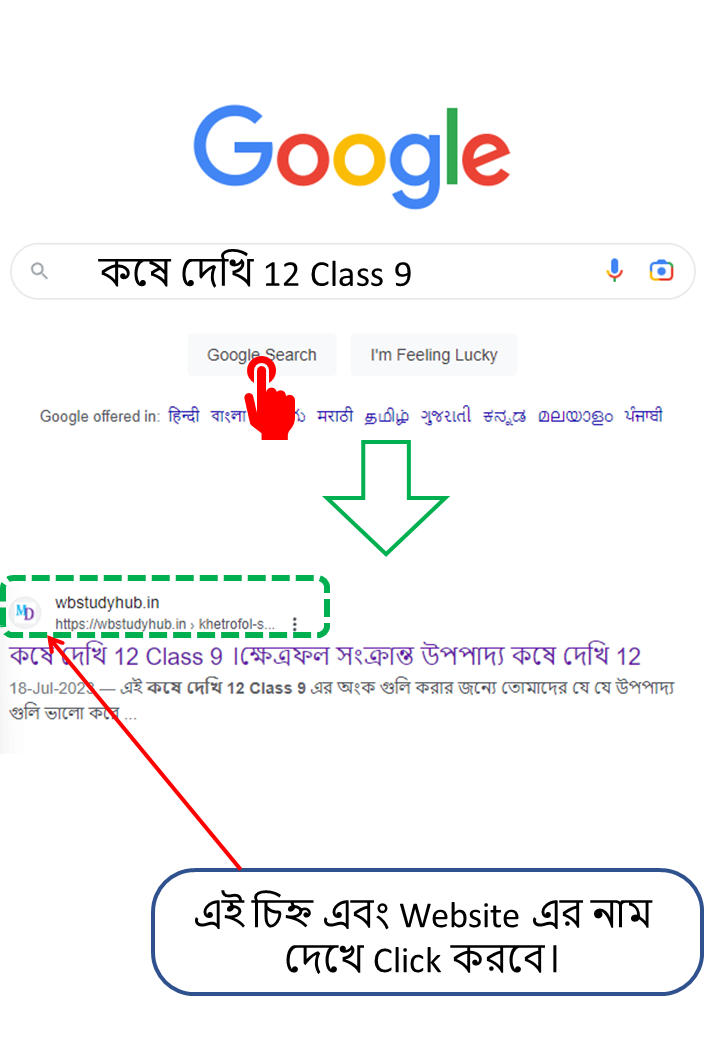 |
কষে দেখি 12 Class 9 এর Youtube Video-
Part 1
Part 2
Part 3
Part 4
কষে দেখি 12|Koshe Dekhi 12
1. ABCD সামান্তরিকের AB এবং DC বাহুর মধ্যবিন্দু যথাক্রমে P এবং Q; প্রমাণ করি যে, APCQ চতুর্ভুজাকার ক্ষেত্রের ক্ষেত্রফল = ½×ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল।
সমাধানঃ-
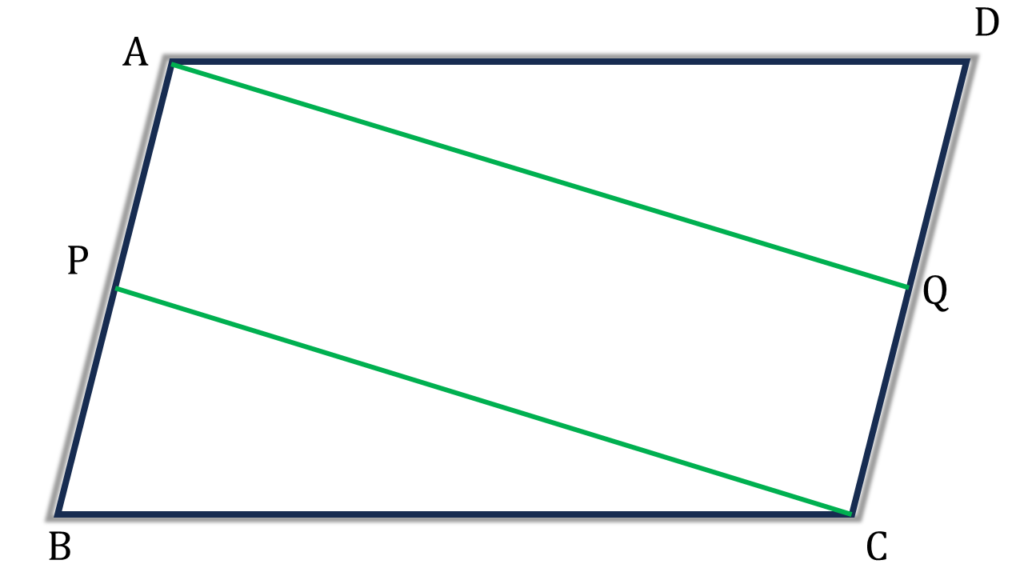
প্রদত্তঃ ABCD সামান্তরিকের AB এবং DC বাহুর মধ্যবিন্দু যথাক্রমে P এবং Q
প্রমাণ করতে হবেঃ APCQ চতুর্ভুজাকার ক্ষেত্রের ক্ষেত্রফল = ½×ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল।
অঙ্কনঃ AC যুক্ত করলাম।
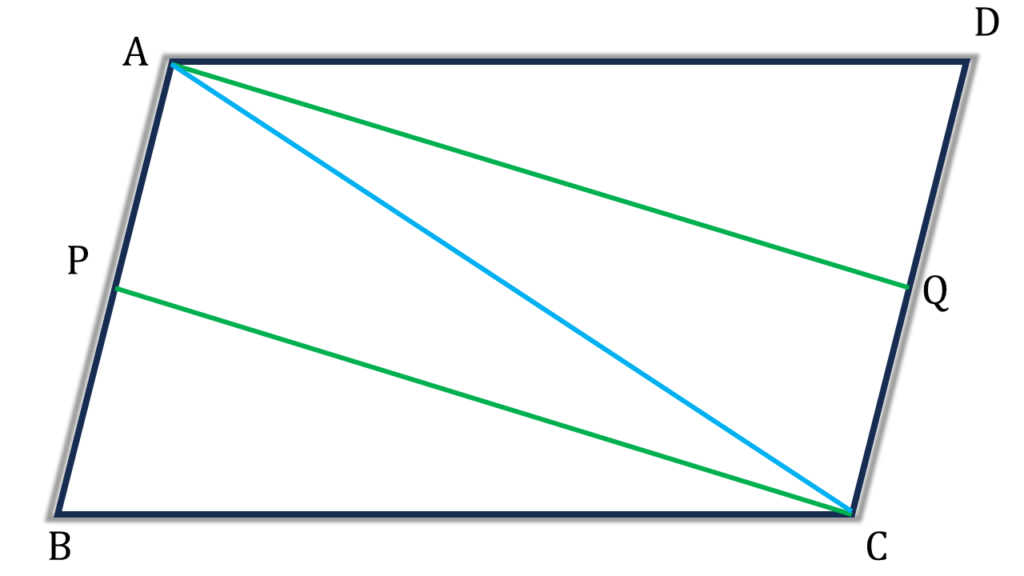
প্রমাণঃ
ABCD সামান্তরিকের AB এবং DC বাহুর মধ্যবিন্দু যথাক্রমে P এবং Q
∴ AP||QC এবং AP = QC
⇒ APCQ একটি সামান্তরিক।
∴ ▲ACQ = ½ সামান্তরিক APCQ —-(i)
আবার, ▲ACD এর Q, DC বাহুর মধ্যবিন্দু।
⇒ ▲ACQ = ½▲ACD
বা, ▲ACD = 2▲ACQ ——-(ii)
আবার, সামান্তরিক ABCD এর,
▲ACD = ½ সামান্তরিকABCD —— (iii)
(i), (ii), (iii) নং থেকে পাই,
APCQ চতুর্ভুজাকার ক্ষেত্রের ক্ষেত্রফল = ½×ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল (প্রমাণিত)
2. ABCD রম্বসের AB এবং DC বাহুর মধ্যে দূরত্ব PQ এবং AD ও BC বাহুর মধ্যে দূরত্ব RS প্রমাণ করি যে, PQ = RS
সমাধানঃ-
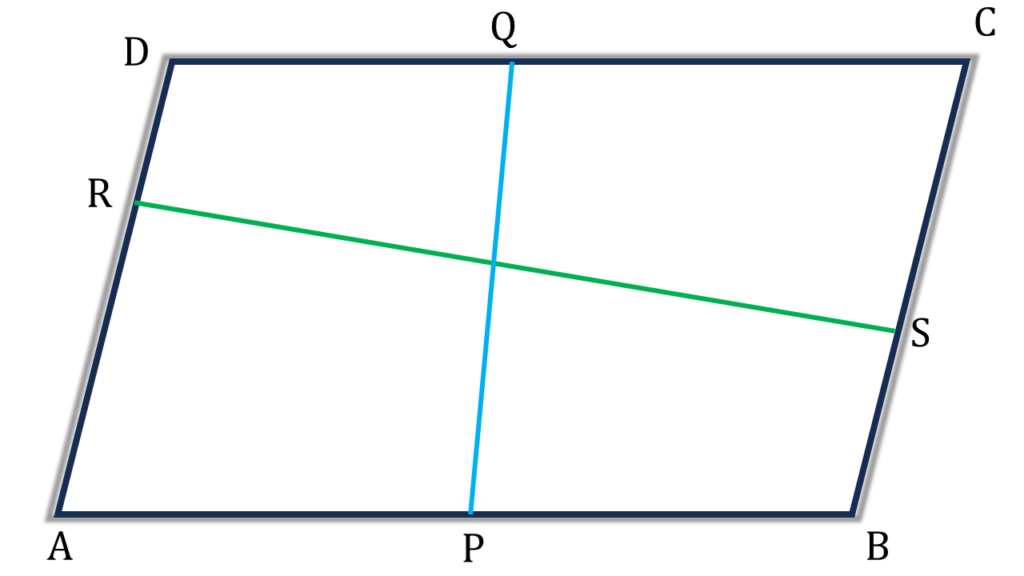
প্রদত্তঃ ABCD রম্বসের AB এবং DC বাহুর মধ্যে দূরত্ব PQ এবং AD ও BC বাহুর মধ্যে দূরত্ব RS
প্রমাণ করতে হবেঃ PQ = RS
অঙ্কনঃ
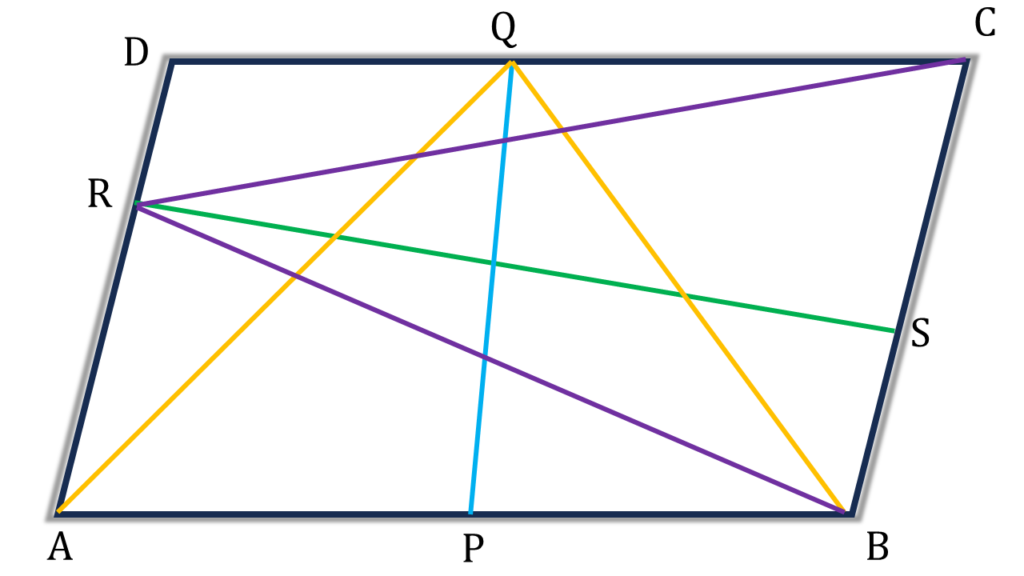
AQ, BQ, RC, BR যুক্ত করলাম।
প্রমাণঃ
ABCD রম্বসের AB এবং DC বাহুর মধ্যে দূরত্ব PQ
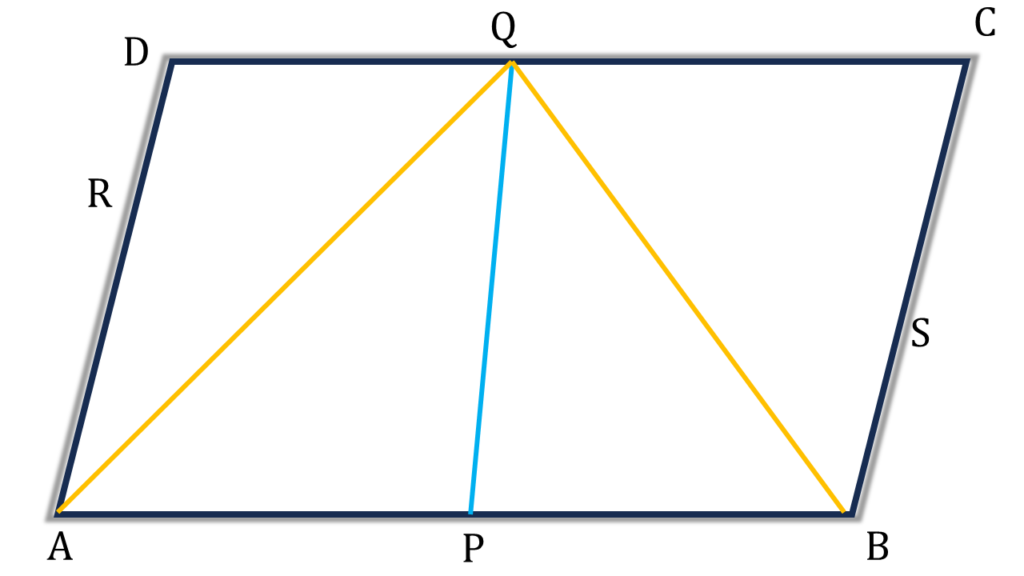
∴ ABCD রম্বসের ক্ষেত্রফল
= ভূমি × উচ্চতা
= AB × PQ ——-(i)
আবার, ABCD রম্বসের AD ও BC বাহুর মধ্যে দূরত্ব RS
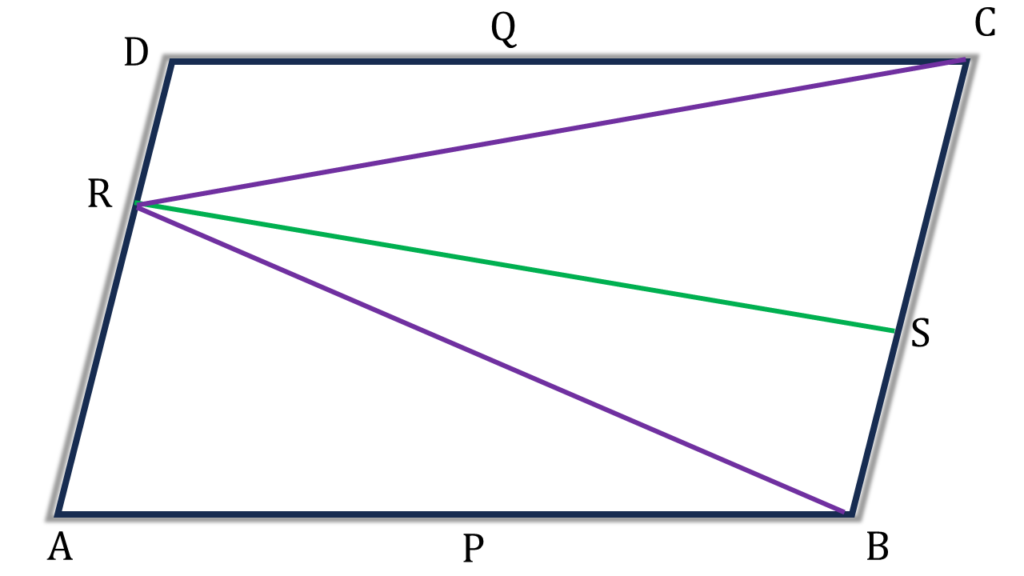
সেক্ষেত্রে ABCD রম্বসের ক্ষেত্রফল
= ভূমি × উচ্চতা
= BC × RS ——(ii)
(i) ও (ii) নং থেকে পাই,
| AB × PQ = BC × RS |
| বা, PQ = RS [ ∵ রম্বসের চারটি বাহু সমান ] (প্রমাণিত) |
3. ABCD সামান্তরিকের AB এবং DC বাহুর মধাবিন্দু যথাক্রমে P এবং Q; প্রমাণ করি যে, PBQD একটি সামান্তরিক এবং ▲PBC = ½সামান্তরিক PBQD.
সমাধানঃ-
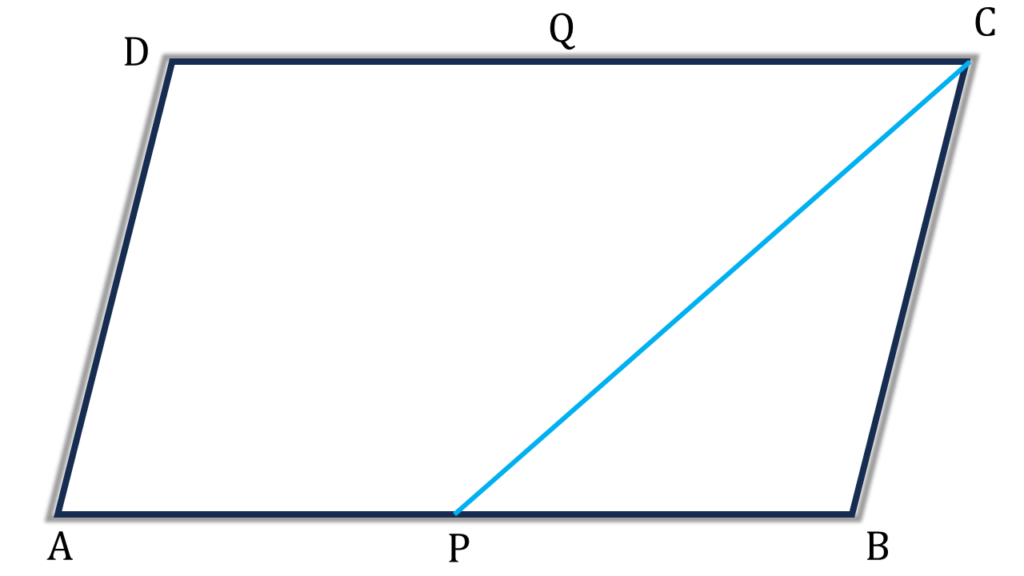
প্রদত্তঃ ABCD সামান্তরিকের AB এবং DC বাহুর মধাবিন্দু যথাক্রমে P এবং Q
প্রমাণ করতে হবেঃPBQD একটি সামান্তরিক এবং ▲PBC = ½সামান্তরিক PBQD
অঙ্কনঃ
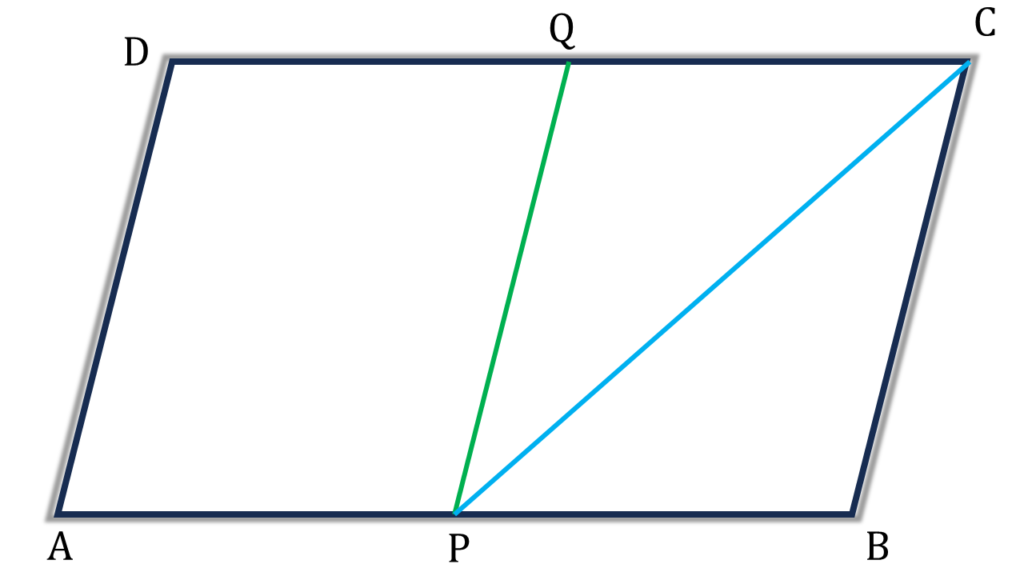
PQ যুক্ত করলাম
প্রমাণঃ
ABCD সামান্তরিকের AB এবং DC বাহুর মধাবিন্দু যথাক্রমে P এবং Q
⇒ PB = DQ এবং PB||DQ
⇒ PBQD একটি সামান্তরিক ( প্রমাণিত)
আবার, PB||DC
∴▲PBC = ½সামান্তরিক PBQD [ ∵ ত্রিভুজ ও কোনো সামান্তরিক একই ভূমি ও একই সমান্তরলা সরলরেখাযুগলের মধ্যে অবস্থিত হলে, ত্রিভুজের ক্ষেত্রফল সামান্তরিক আঁকার ক্ষেত্রের ক্ষেত্রফলের অর্ধেক হবে (উপপাদ্য 24) ]
প্রমাণিত ।
4. ABC সমদ্বিবাহু ত্রিভুজের AB=AC এবং বর্ধিত BC বাহুর উপর P যেকোন একটি বিন্দু। P বিন্দু থেকে AB এবং AC বাহুর উপর যথাক্রমে PQ ও PR লম্ব। B বিন্দু থেকে AC বাহুর উপর লম্ব BS; প্রমাণ করি যে, PQ-PR = BS.
সমাধানঃ-
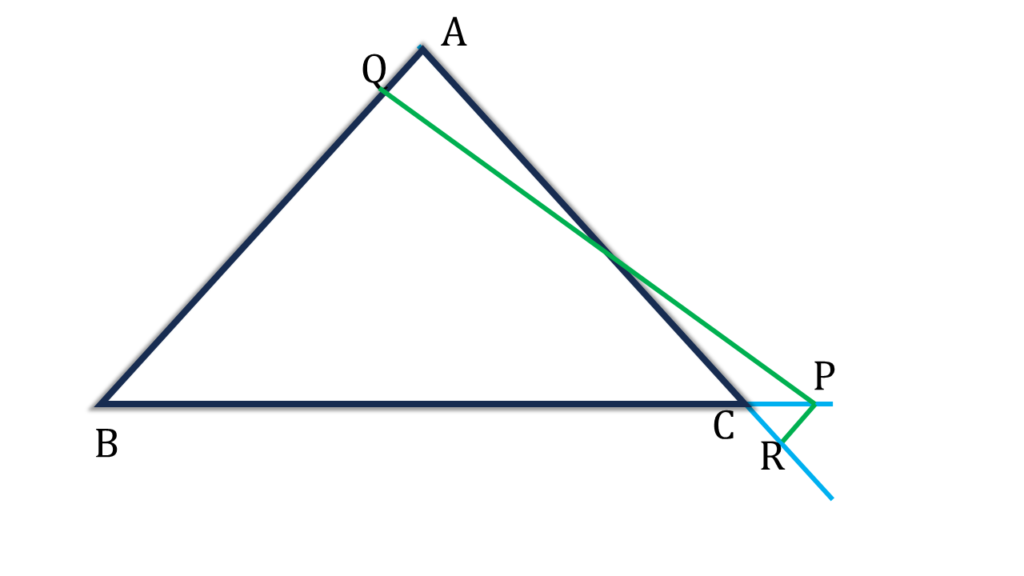
প্রদত্তঃ ABC সমদ্বিবাহু ত্রিভুজের AB=AC এবং বর্ধিত BC বাহুর উপর P যেকোন একটি বিন্দু। P বিন্দু থেকে AB এবং AC বাহুর উপর যথাক্রমে PQ ও PR লম্ব। B বিন্দু থেকে AC বাহুর উপর লম্ব BS
প্রমাণ করতে হবেঃ PQ-PR = BS
অঙ্কনঃ
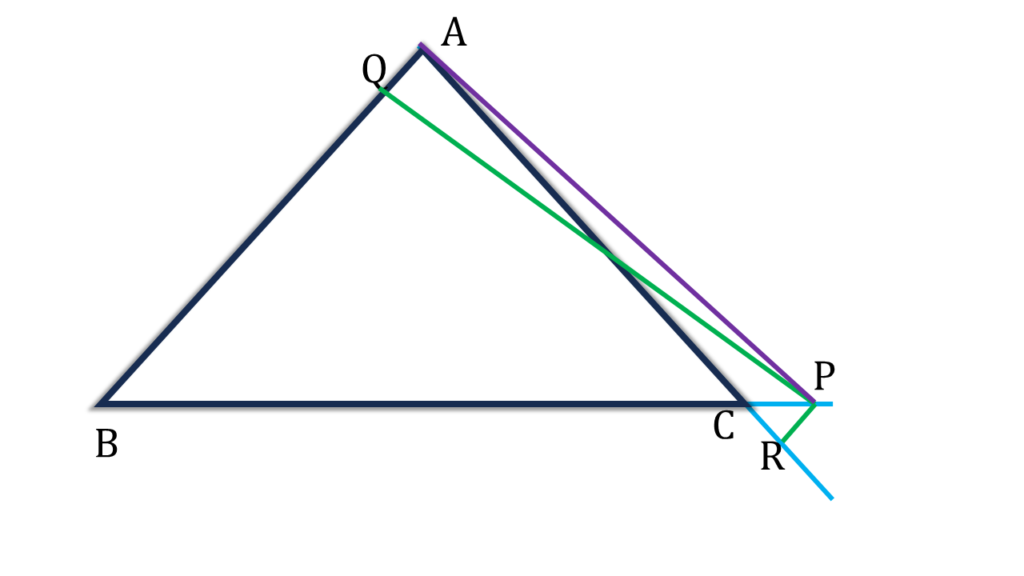
AP যুক্ত করলাম ।
প্রমাণঃ
| ▲ABC = ▲ABP – ▲ACP |
| বা, ½×AC×BS = ½×AB×PQ – ½×AC×PR |
| বা, ½×AC×BS = ½×AC×PQ – ½×AC×PR [ ∵ AB = AC ] |
| বা, ½×AC×BS = ½×AC× (PQ – PR) |
| বা, BS = PQ – PR (প্রমাণিত) |
5. ABC সমবাহু ত্রিভুজের বাইরে এবং ABC কৌণিক অঞ্চলের মধ্যে O যেকোন একটি বিন্দু। O বিন্দু থেকে AB, BC এবং CA বাহুর উপর লম্ব যথাক্রমে OP, OQ এবং OR; প্রমাণ করি যে, ত্রিভুজটির উচ্চতা = OP + OQ – OR.
সমাধানঃ-
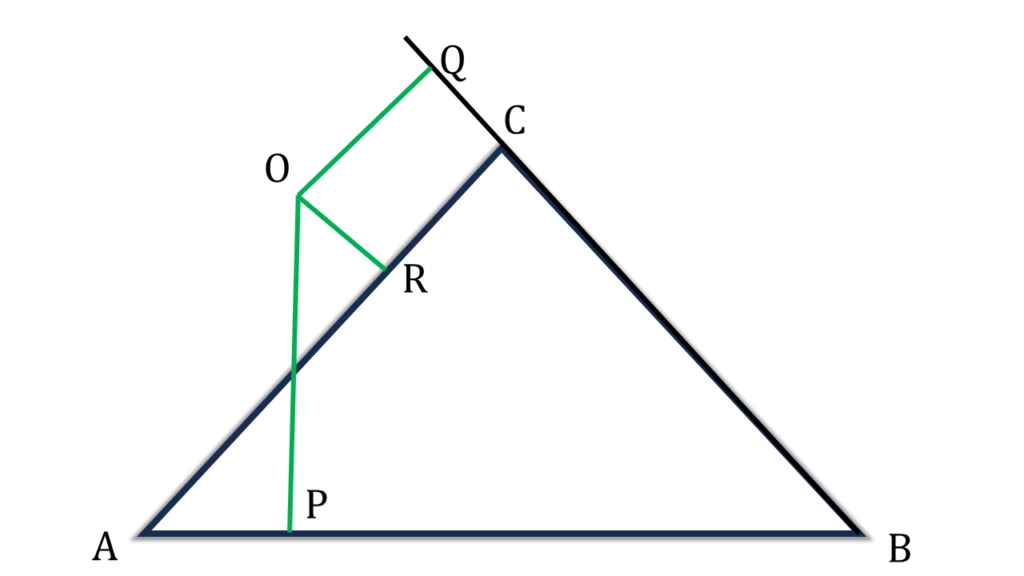
প্রদত্তঃ ABC সমবাহু ত্রিভুজের বাইরে এবং ABC কৌণিক অঞ্চলের মধ্যে O যেকোন একটি বিন্দু। O বিন্দু থেকে AB, BC এবং CA বাহুর উপর লম্ব যথাক্রমে OP, OQ এবং OR
প্রমাণ করতে হবেঃ ত্রিভুজটির উচ্চতা = OP + OQ – OR
অঙ্কনঃ
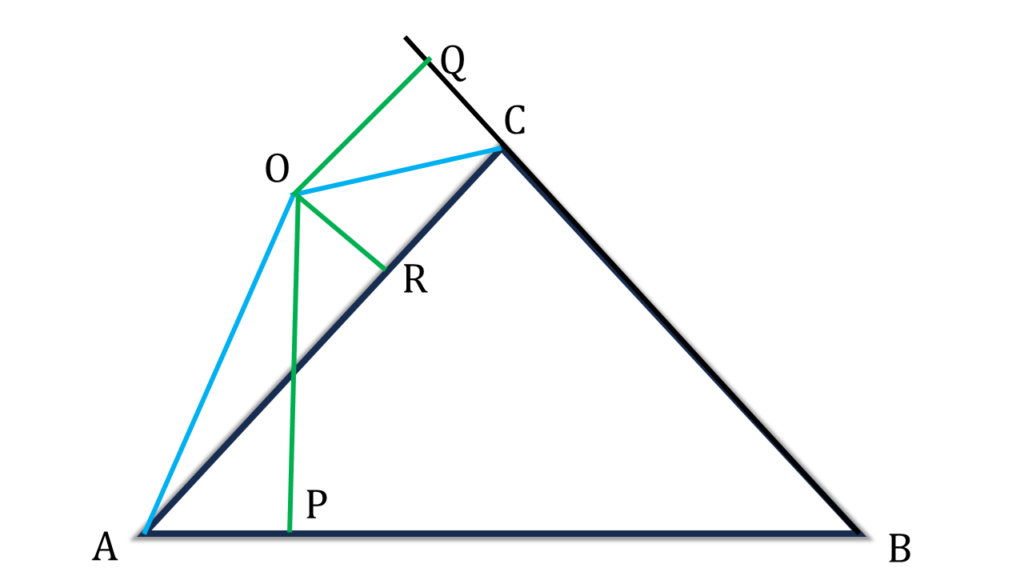
OA, OC যুক্ত করলাম।
প্রমাণঃ মনে করি ▲ABC এর উচ্চতা= h একক
| ▲ABC = চতুর্ভুজ ABCO – ▲AOC |
| বা, ▲ABC = ▲ABO + ▲BOC – ▲AOC |
| বা, ½×AB×h = ½×AB×OP + ½×BC×OQ – ½×AC×OR |
| বা, ½×AB×h = ½×AB×OP + ½×AB×OQ – ½×AB×OR [ ∵ ABC একটি সমবাহু ত্রিভুজ ] |
| বা, ½×AB×h = ½×AB× (OP + OQ – OR) |
| বা, h = OP + OQ – OR (প্রমাণিত ) |
6. ABCD সামান্তরিকের AB বাহুর সমান্তরাল সরলরেখা AD, AC এবং BC -কে বা তাদের বর্ধিত অংশকে যথাক্রমে E, F ও G বিন্দুতে ছেদ করে। প্রমাণ করি যে, ▲AEG=▲AFD.
সমাধানঃ-
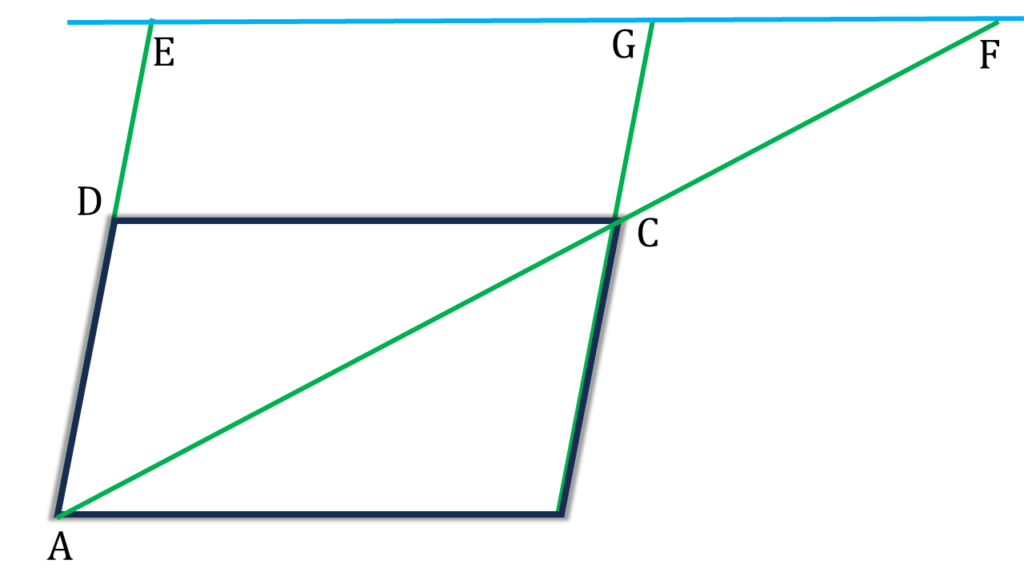
প্রদত্তঃ ABCD সামান্তরিকের AB বাহুর সমান্তরাল সরলরেখা AD, AC এবং BC -কে বা তাদের বর্ধিত অংশকে যথাক্রমে E, F ও G বিন্দুতে ছেদ করে।
প্রমাণ করতে হবেঃ ▲AEG=▲AFD
অঙ্কনঃ
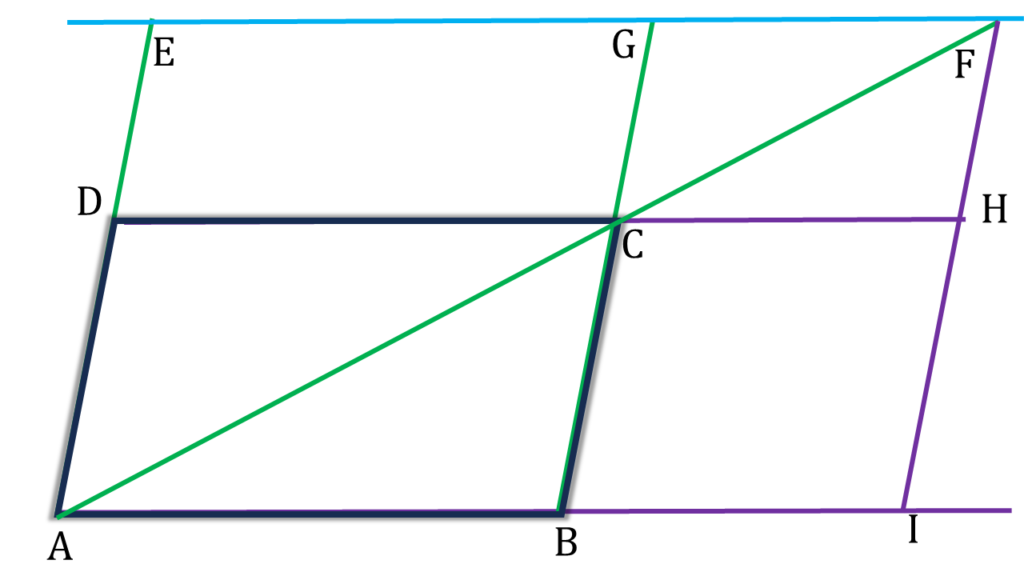
F বিন্দু দিয়ে BC সরলরেখার সমান্তরাল সরলরেখা অঙ্কন করলাম যা বর্ধিত DC ও AB কে যথাক্রমে H ও I বিন্দুতে ছেদ করেছে।
প্রমাণঃ

| ▲AEG |
| = ½ সামান্তরিক ABGE |
| = ½ (সামান্তরিক ABCD + সামান্তরিক DCGE) |
| = ½ (2▲ADC + সামান্তরিক DCGE) |
| = ▲ADC + ½সামান্তরিক DCGE |
| ∴ ▲AEG = ▲ADC + ½সামান্তরিক DCGE —————(i) |
আবার,

| ▲AEF |
| = ½ সামান্তরিক AIFE |
| = ½ (সামান্তরিক ABCD + সামান্তরিক BIHC + সামান্তরিক DHFE) |
| = ½ (2▲ADC + সামান্তরিক BIHC + 2▲DEF) |
| = ▲ADC + ½সামান্তরিক BIHC + ▲DEF |
| ∴ ▲AEF = ▲ADC + ½সামান্তরিক BIHC + ▲DEF |
| বা, ▲ADF + ▲DEF = ▲ADC + ½সামান্তরিক BIHC + ▲DEF |
| বা, ▲ADF = ▲ADC + ½সামান্তরিক BIHC ————(ii) |
সামান্তরিক AIFE, সামান্তরিক ABCD, সামান্তরিক CHFG থেকে পাই,

| ▲AIF = ▲AEF |
| ▲ABC = ▲ADC |
| ▲HCF = ▲GCF |
অতএব,
| ▲AIF = ▲AEF |
| বা, ▲AIF – ▲ABC = ▲AEF – ▲ADC |
| বা, ▲AIF – ▲ABC – ▲HCF = ▲AEF – ▲ADC – ▲GCF |
| সামান্তরিক DCGE = সামান্তরিক BIHC |
এখন (i) ও (ii) নং থেকে পাই,
| ▲AEG |
| = ▲ADC + ½সামান্তরিক DCGE |
| = ▲ADC + ½সামান্তরিক BIHC |
| = ▲AEF (প্রমাণিত) |
7. ABCD সামান্তরিকের DC বাহুর উপর E যেকোনো একটি বিন্দু। বর্ধিত AE বর্ধিত BC কে F বিন্দুতে ছেদ করে। D, F যুক্ত করা হলো। প্রমাণ করি যে
(i) ▲ADF = ▲ABE.
(ii) ▲DEF = ▲BEC
সমাধানঃ-
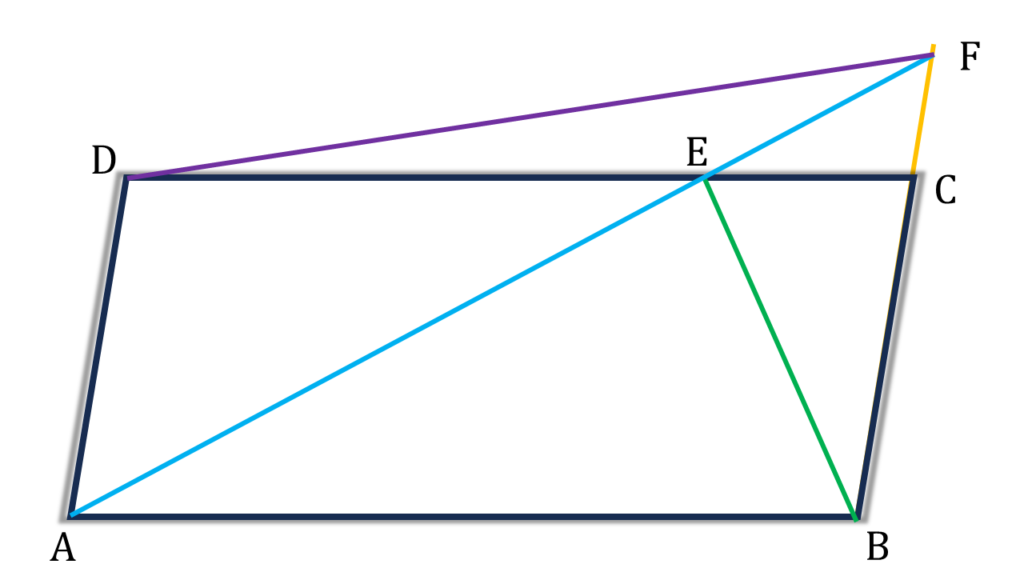
প্রদত্তঃ ABCD সামান্তরিকের DC বাহুর উপর E যেকোনো একটি বিন্দু। বর্ধিত AE বর্ধিত BC কে F বিন্দুতে ছেদ করে। D, E যুক্ত করা হলো।
প্রমাণ করতে হবেঃ
(i) ▲ADF = ▲ABE.
(ii) ▲DEF = ▲BEC
অঙ্কনঃ
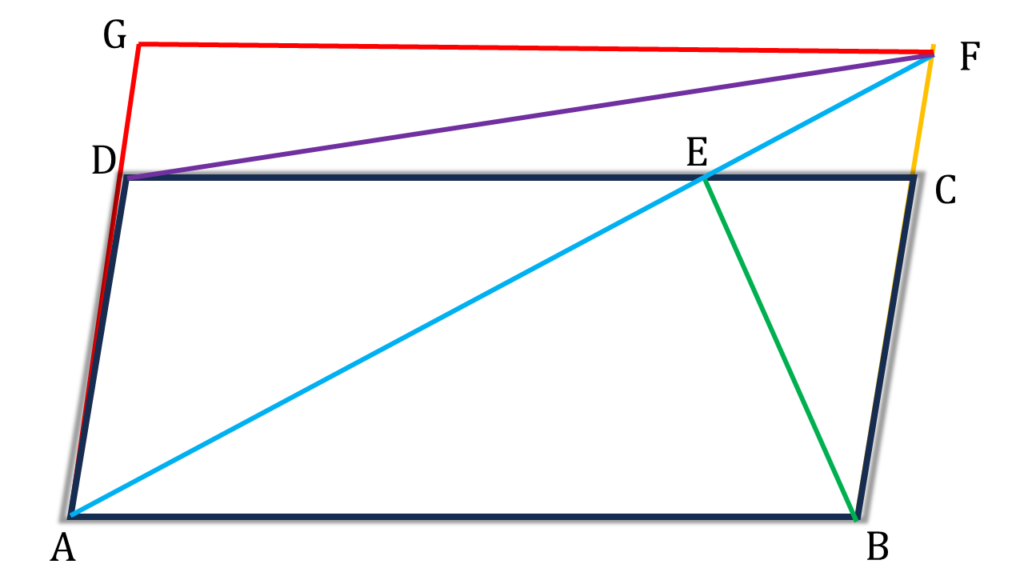
F বিন্দু দিয়ে DC বাহুর সমান্তরাল সরলরেখা অঙ্কন করলাম যা বর্ধিত AD কে G বিন্দুতে ছেদ করেছে।
প্রমাণঃ AB||DC||GF এবং DC=GF
⇒ ABFG একটি সামান্তরিক।
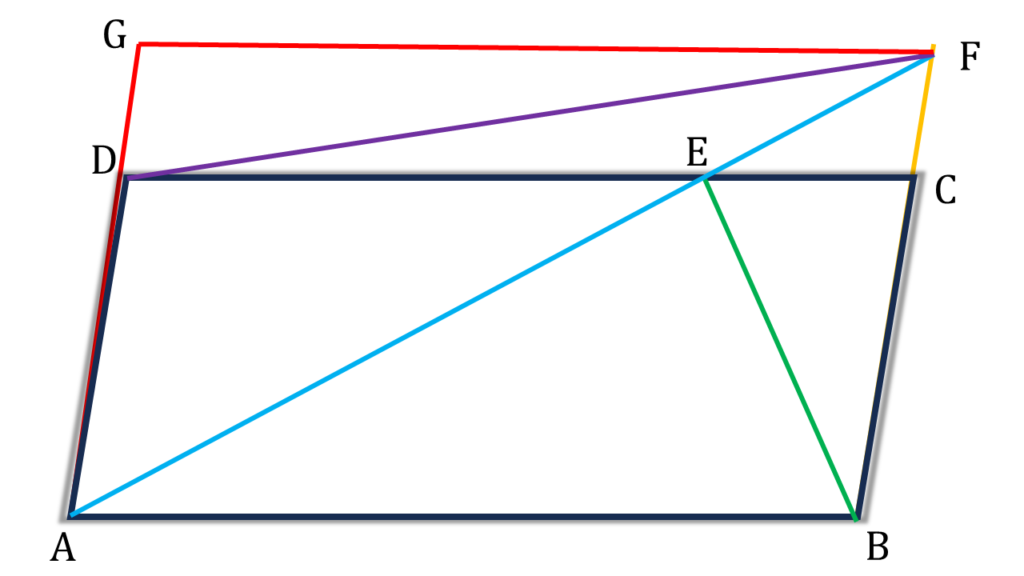
এখন ABFG সামান্তরিকের,
| ▲ABF = ½ সামান্তরিক ABFG |
| বা, ▲ABF = ½ (সামান্তরিকABCD + সামান্তরিক GDFC) |
| বা, ▲ABF = ½ (2▲ABE + 2▲DCF) [ ∵ সামান্তরিক ABCD এর ▲ABE = ½সামান্তরিক ABCD এবং সামান্তরিক GDFC এর ▲DCF = ½সামান্তরিক GDFC] |
| বা, ▲ABF = ▲ABE + ▲DCF —- (i) |
আবার, ▲ABF = ▲ABE + ▲BEF —–(ii)
(i) ও (ii) নং সমান করে পাই,
| ▲ABE + ▲DCF = ▲ABE + ▲BEF |
| বা, ▲DCF = ▲BEF —-(iii) |
আবার, সামান্তরিক GDCF এর ▲DCF = ▲GDF
∴ ▲GDF = ▲DCF = ▲BEF
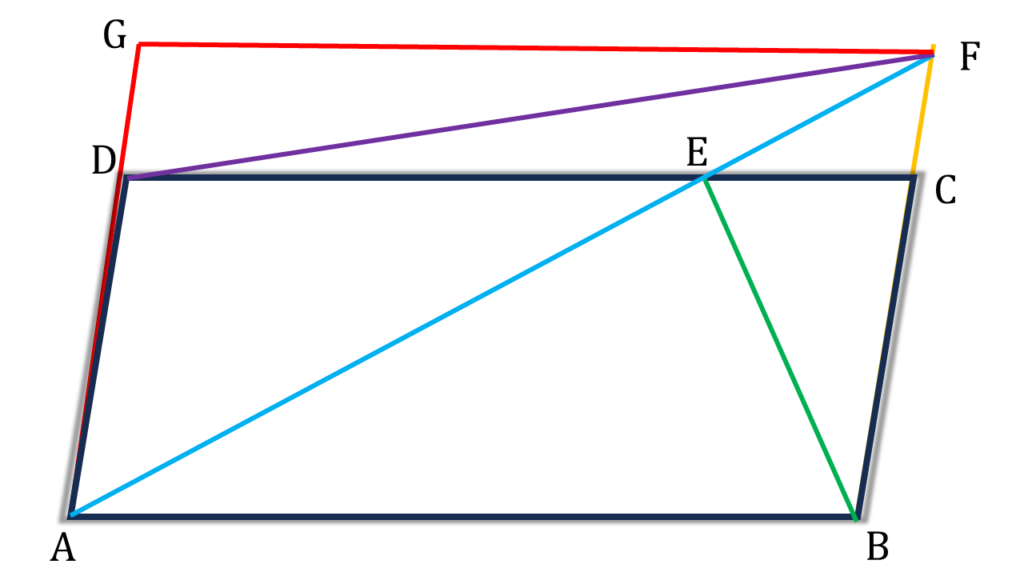
এখন, সামান্তরিক ABFG এর,
| ▲AGF = ▲ABF |
| বা, ▲ADF + ▲GDF = ▲ABE + ▲BEF |
| বা, ▲ADF = ▲ABE [ ∵ ▲GDF = ▲BEF] ( (i) নং প্রমাণিত ) |
আবার (iii) নং থেকে পাই,
| ▲DCF = ▲BEF |
| বা, ▲DEF + ▲CEF = ▲BCE + ▲CEF |
| বা, ▲DEF = ▲BEC (ii) নং প্রমাণিত |
8. সমান ক্ষেত্রফলবিশিষ্ট ABC এবং ABD দুটি ত্রিভুজাকার ক্ষেত্র AB বাহুর বিপরীত দিকে অবস্থিত। প্রমাণ করি যে, AB, CD-কে সমন্বিখণ্ডিত করে।
সমাধানঃ-
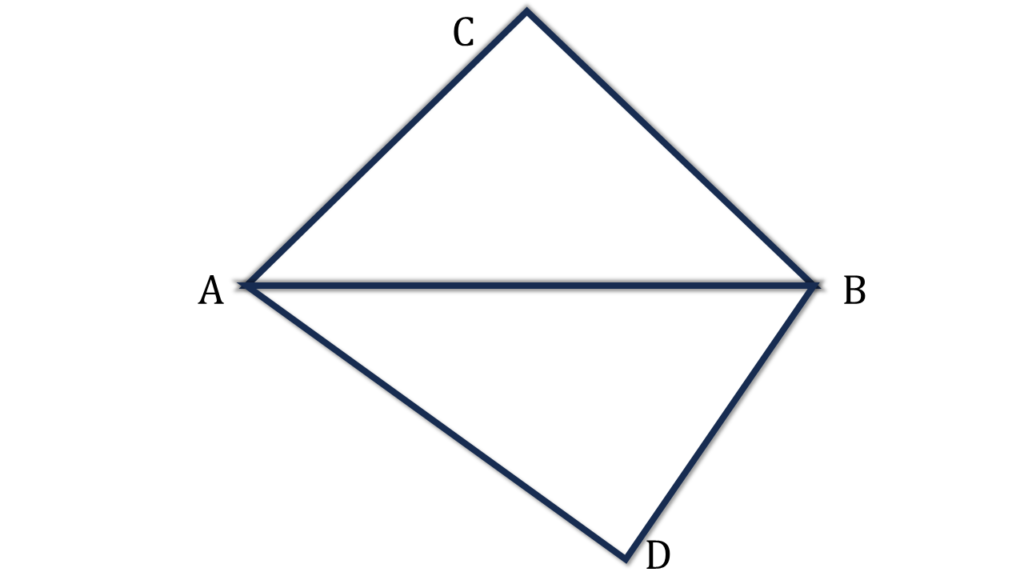
প্রদত্তঃ সমান ক্ষেত্রফলবিশিষ্ট ABC এবং ABD দুটি ত্রিভুজাকার ক্ষেত্র AB বাহুর বিপরীত দিকে অবস্থিত।
প্রমাণ করতে হবেঃAB, CD-কে সমন্বিখণ্ডিত করে।
অঙ্কনঃ
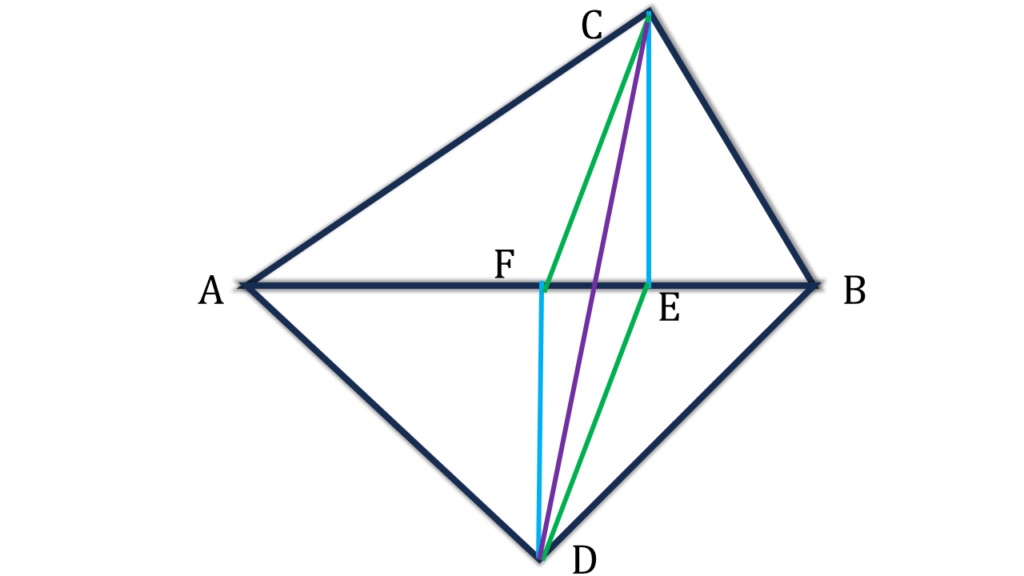
C বিন্দু থেকে AB বাহুর উপর লম্ব অঙ্কন করলাম যা AB বাহুকে E বিন্দুতে ছেদ করেছে। D বিন্দু থেকে AB বাহুর উপর লম্ব অঙ্কন করলাম যা AB বাহুকে F বিন্দুতে ছেদ করেছে।
CF, CD ও DE যুক্ত করলাম।
প্রমাণঃ
| ▲ABC = ▲ABD [ প্রদত্ত ] |
| বা, ½×AB×CE = ½×AB×DF |
| বা, CE = DF |
আবার, CE ও DF উভয়েই AB সরলরেখার উপর লম্ব ।
⇒ CE||DF
∴ CEDF চতুর্ভুজের CE=DF এবং CE||DF
⇒ CEDF একটি সামান্তরিক
⇒ CEDF সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে।
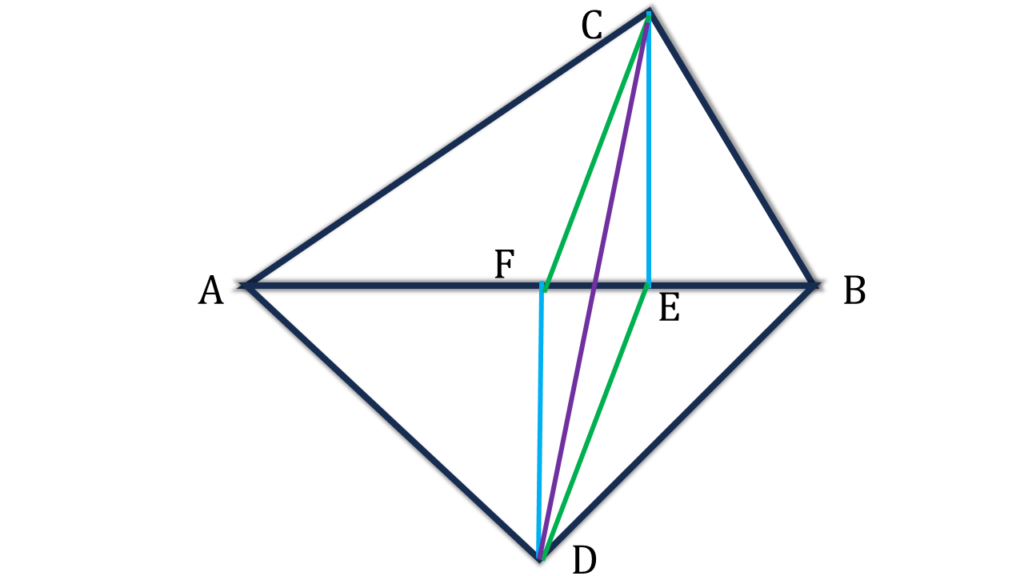
অর্থাৎ, FE, CD কে সমদ্বিখণ্ডিত করে।
⇒ AB, CD কে সমদ্বিখণ্ডিত করে। (প্রমাণিত)
9. ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D; CDEF সামান্তরিকটি BC বাহু এবং A বিন্দু দিয়ে BC বাহুর সমান্তরাল সরলরেখার মধ্যে অবস্থিত। প্রমাণ করি যে, ▲ABC = সামান্তরিক CDEF.
সমাধানঃ-
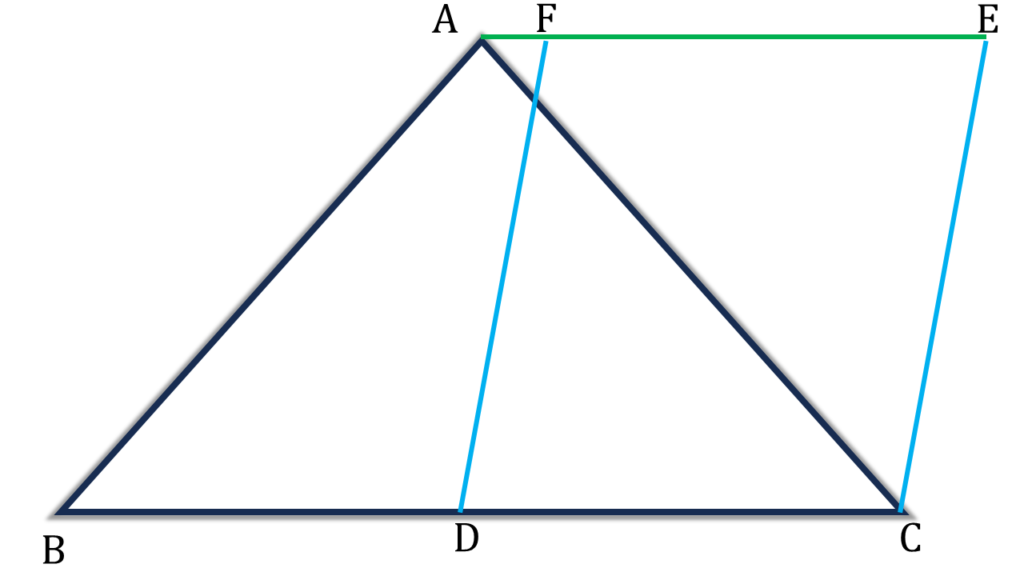
প্রদত্তঃ ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D; CDEF সামান্তরিকটি BC বাহু এবং A বিন্দু দিয়ে BC বাহুর সমান্তরাল সরলরেখার মধ্যে অবস্থিত।
প্রমাণ করতে হবেঃ ▲ABC = সামান্তরিক CDEF
অঙ্কনঃ
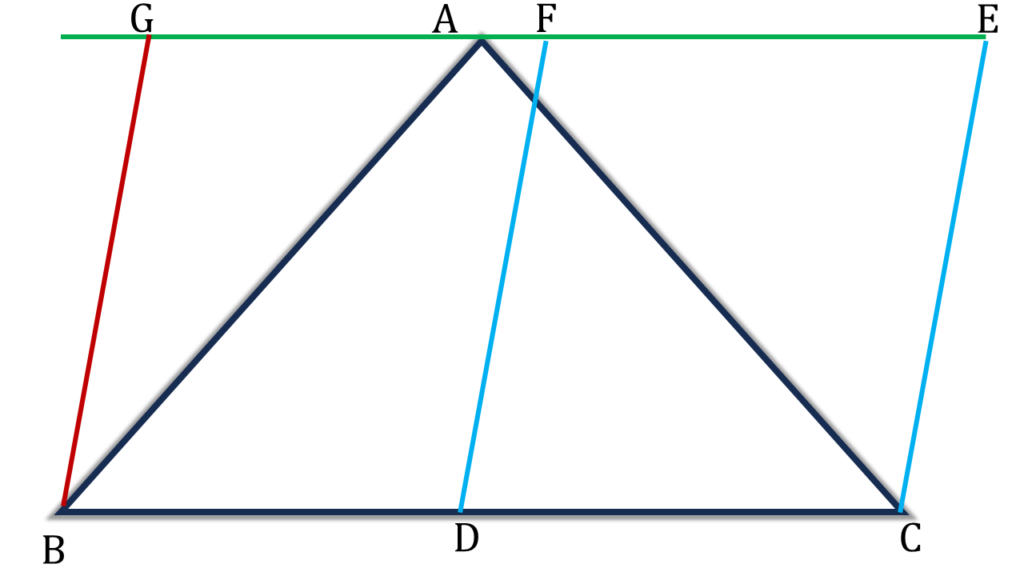
B বিন্দু দিয়ে DF এর সমান্তরাল সরলরেখা অঙ্কন করলাম যা বরধিত AE কে G বিন্দুতে ছেদ করেছে।
প্রমাণঃ
▲ABC এবং সামান্তরিক BCEG একই ভূমি এবং একই সমান্তরালযুগলের মধ্যে অবস্থিত।
⇒ ▲ABC = ½ সামান্তরিক BCEG
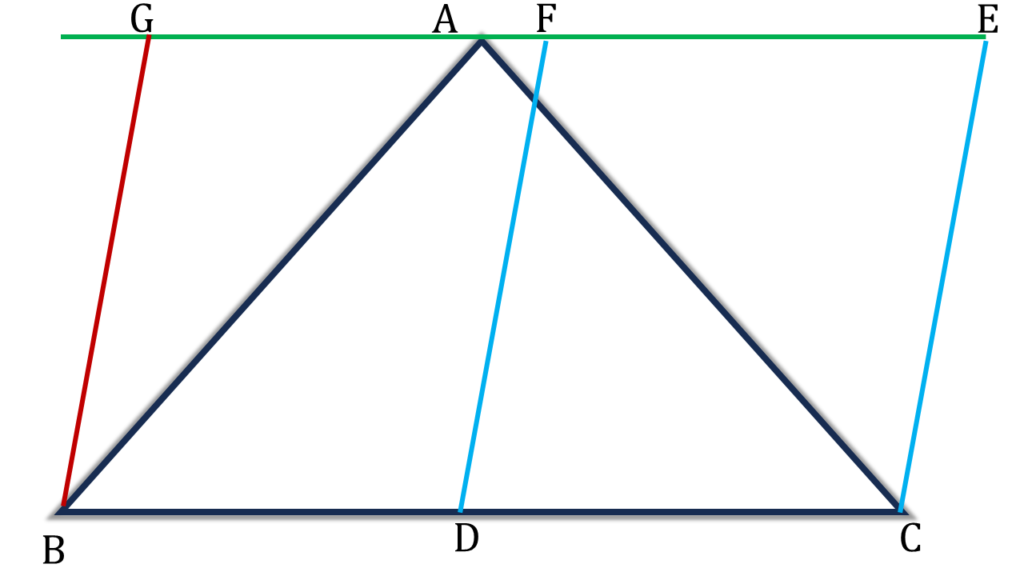
আবার,
| D, BC বাহুর মধ্যবিন্দু এবং DF||CE||BG |
| ⇒ সামান্তরিক DCEF = ½ সামান্তরিক BCEG |
| ∴ ▲ABC = ½ সামান্তরিক BCEG = সামান্তরিক DCEF |
10. ABCD সামান্তরিকের BD কর্ণের উপর P যেকোন একটি বিন্দু। প্রমাণ করি যে, ▲APD = ▲CPD.
সমাধানঃ-
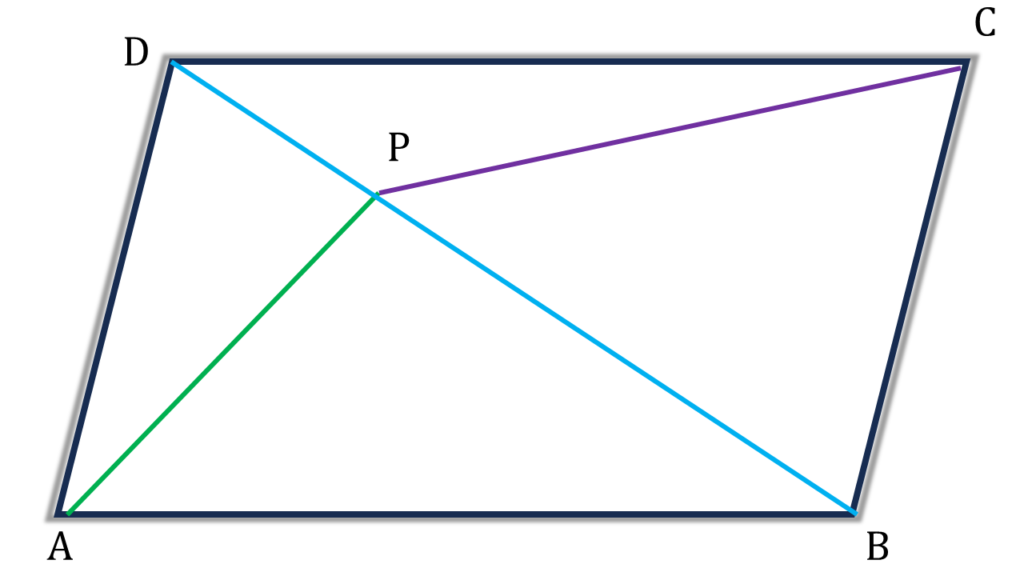
প্রদত্তঃ ABCD সামান্তরিকের BD কর্ণের উপর P যেকোন একটি বিন্দু।
প্রমাণ করতে হবেঃ ▲APD = ▲CPD
অঙ্কনঃ
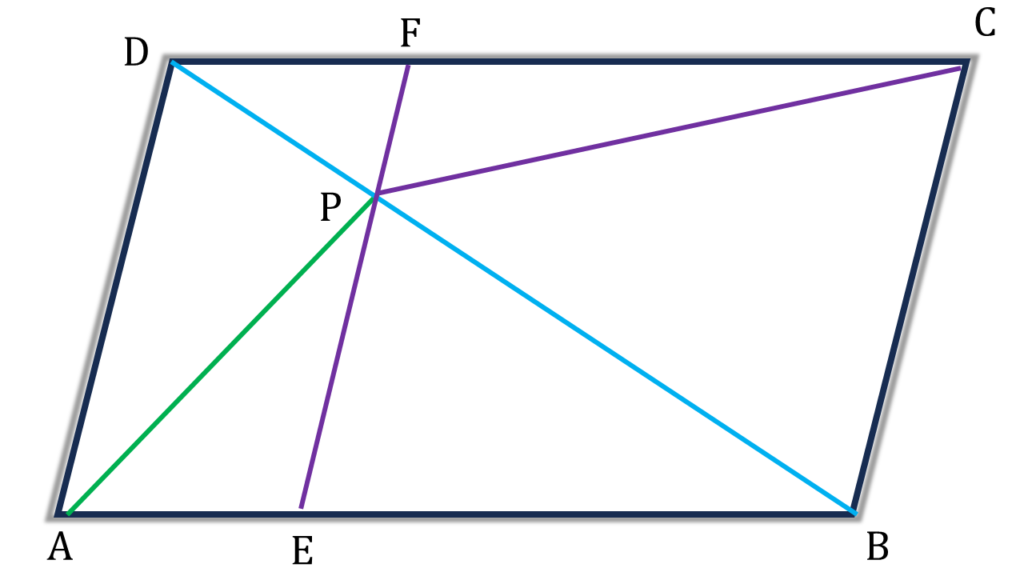
P বিন্দু দিয়ে BC এর সমান্তরাল সরলরেখা অঙ্কন করলাম যা AB ও CD বাহুকে যথাক্রমে E ও F বিন্দুতে ছেদ করেছে।
প্রমাণঃ
সামান্তরিক ABCD এর,
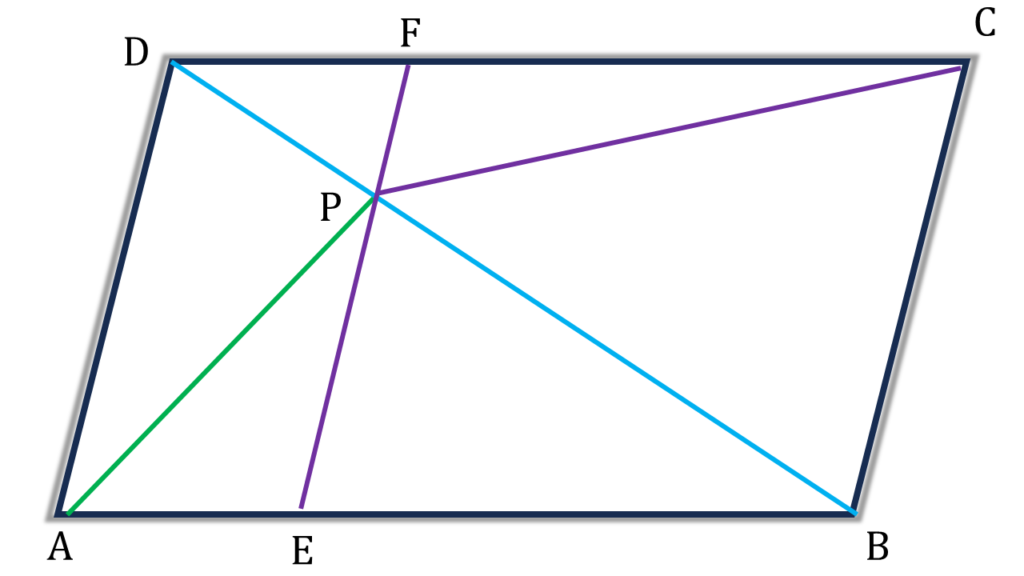
| ▲ABD |
| = ½ সামান্তরিক ABCD |
| = ½( সামান্তরিক AEFD + সামান্তরিক BEFC) |
| = ½সামান্তরিক AEFD + ½সামান্তরিক BEFC |
| = ▲APD + ▲BPC ———(i) |
আবার,▲ABD = ▲APD + ▲ABP ——-(ii)
(i) ও (ii) সমান করে পাই,
| ▲APD + ▲BPC = ▲APD + ▲ABP |
| বা, ▲BPC = ▲ABP ——-(iii) |
এখন সামান্তরিক ABCD এর
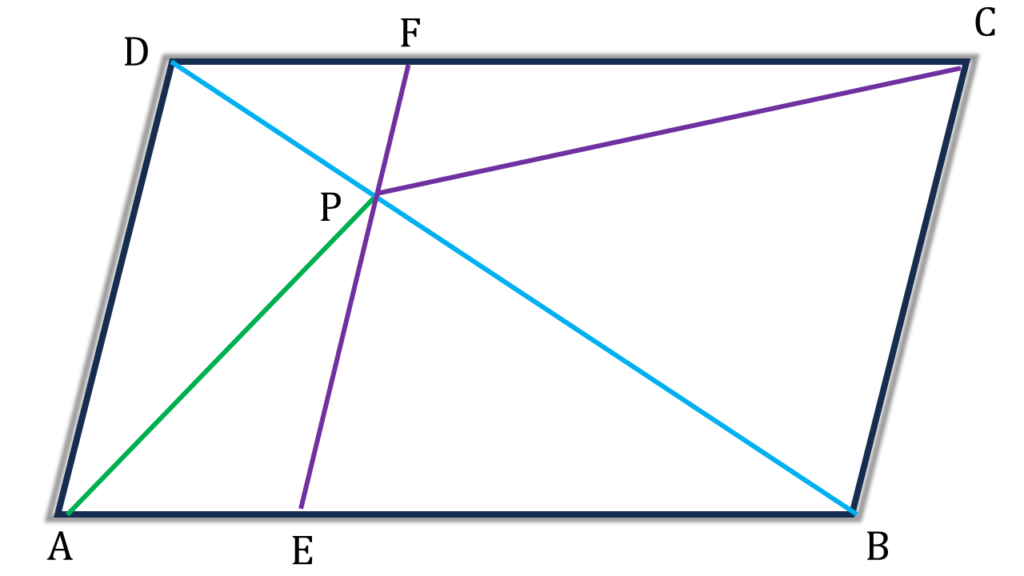
| ▲ABD = ▲BDC |
| বা, ▲ADP + ▲ABP = ▲BPC + ▲DPC |
| বা, ▲ADP = ▲DPC [ (iii) নং এ পেয়েছি ▲BPC = ▲ABP] (প্রমাণিত) |
11. ABC ত্রিভুজের AD এবং BE মধ্যমা। প্রমাণ করি যে, ▲ACD = ▲BCE
সমাধানঃ-
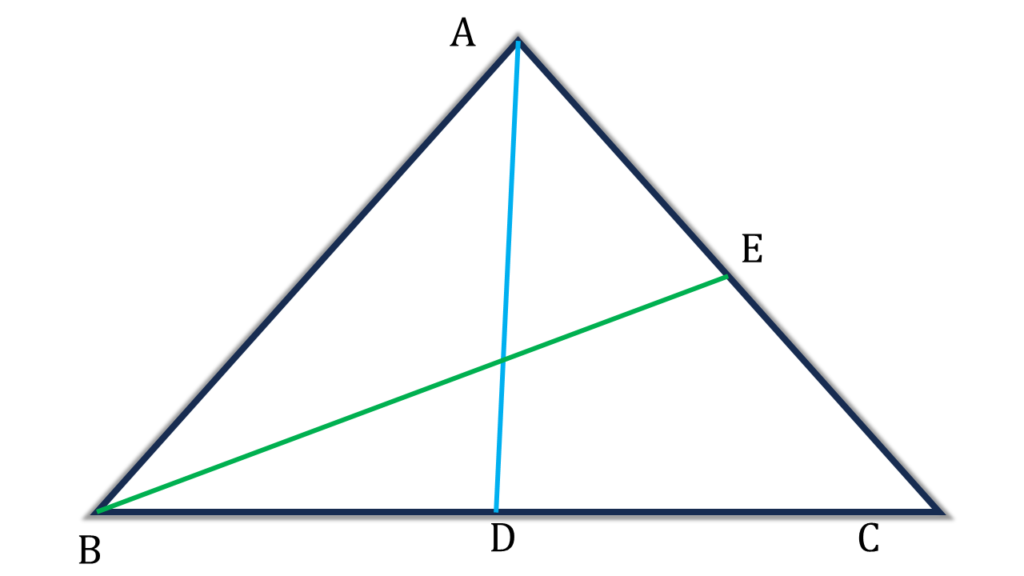
প্রদত্তঃ ABC ত্রিভুজের AD এবং BE মধ্যমা।
প্রমাণ করতে হবেঃ ▲ACD = ▲BCE
প্রমাণঃ
ABC ত্রিভুজের AD মধ্যমা
⇒ ▲ACD = ½▲ABC ———(i)
আবার, ABC ত্রিভুজের BE মধ্যমা
⇒ ▲BCE = ½▲ABC ———(ii)
(i) ও (ii) নং সমান করে পাই,
▲ACD = ▲BCE (প্রমাণিত)
12. ABC ত্রিভুজের BC বাহুর সমান্তরাল সরলরেখা AB এবং AC বাহুকে যথাক্রমে P এবং Q বিন্দুতে ছেদ করে। CP এবং BQ পরস্পরকে X বিন্দুতে ছেদ করে। প্রমাণ করি যে,
(i) ▲BPQ = ▲CPQ
(ii) ▲BCP = ▲BCQ
(iii) ▲ACP = ▲ABQ
(iv) ▲BXP = ▲CXQ
সমাধানঃ-
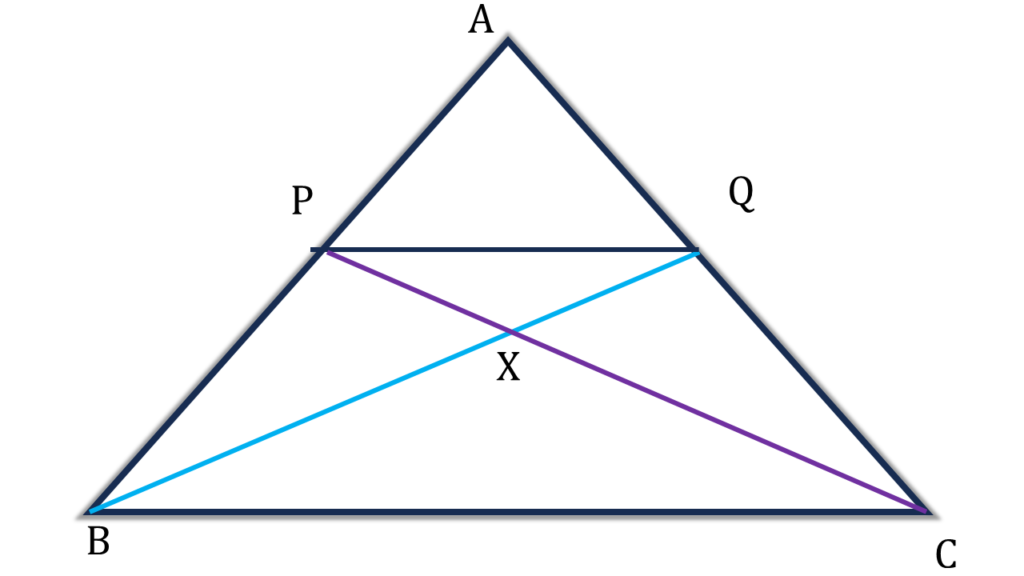
প্রদত্তঃ ABC ত্রিভুজের BC বাহুর সমান্তরাল সরলরেখা AB এবং AC বাহুকে যথাক্রমে P এবং Q বিন্দুতে ছেদ করে। CP এবং BQ পরস্পরকে X বিন্দুতে ছেদ করে।
প্রমাণ করতে হবেঃ
(i) ▲BPQ = ▲CPQ
(ii) ▲BCP = ▲BCQ
(iii) ▲ACP = ▲ABQ
(iv) ▲BXP = ▲CXQ
প্রমাণঃ
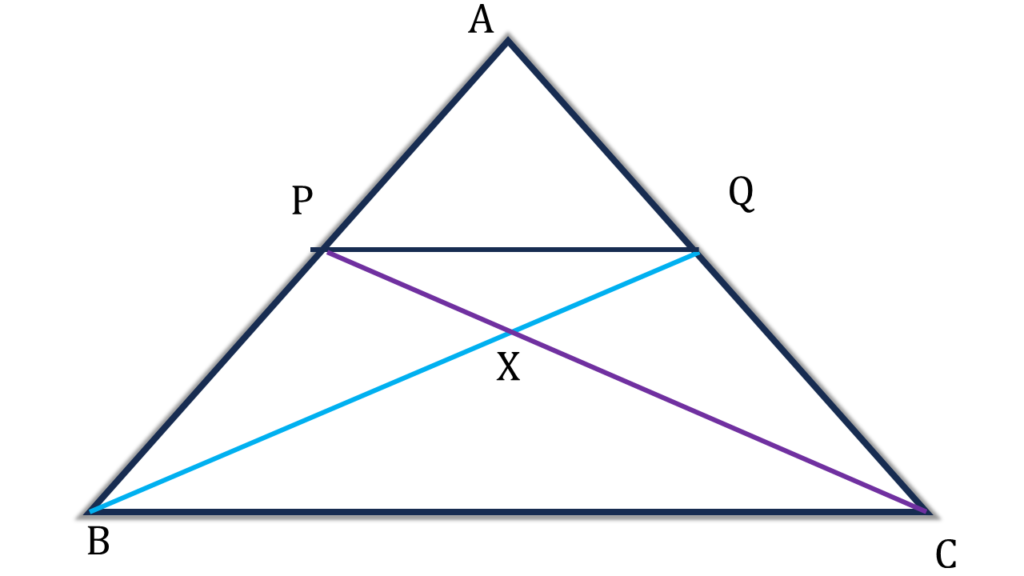
BC||PQ ⇒ ▲BCQ = ▲BCP [ একই সমান্তরালযুগল এর মধ্যে অবস্থিত]
(ii) নং প্রমাণিত
আবার,
| চতুর্ভুজ BCPQ – ▲BCQ = চতুর্ভুজ BCPQ – ▲BCP |
| বা, ▲BPQ = ▲CPQ |
| (i) নং প্রমাণিত |
আবার,
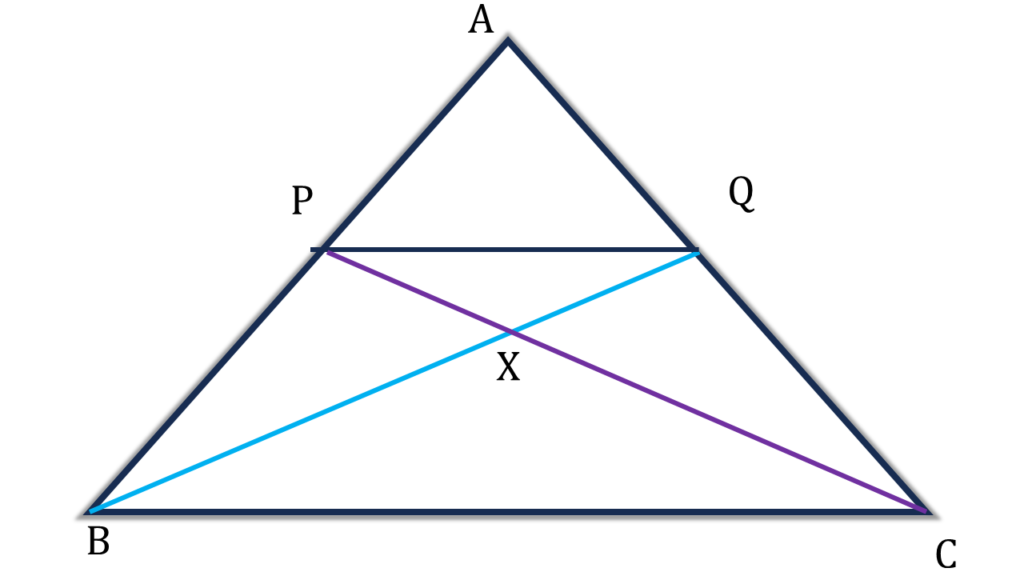
| ▲ABC – ▲BCQ = ▲ABC – ▲BCP |
| বা, ▲ABQ = ▲ACP |
| (iii) নং প্রমাণিত |
আবার,
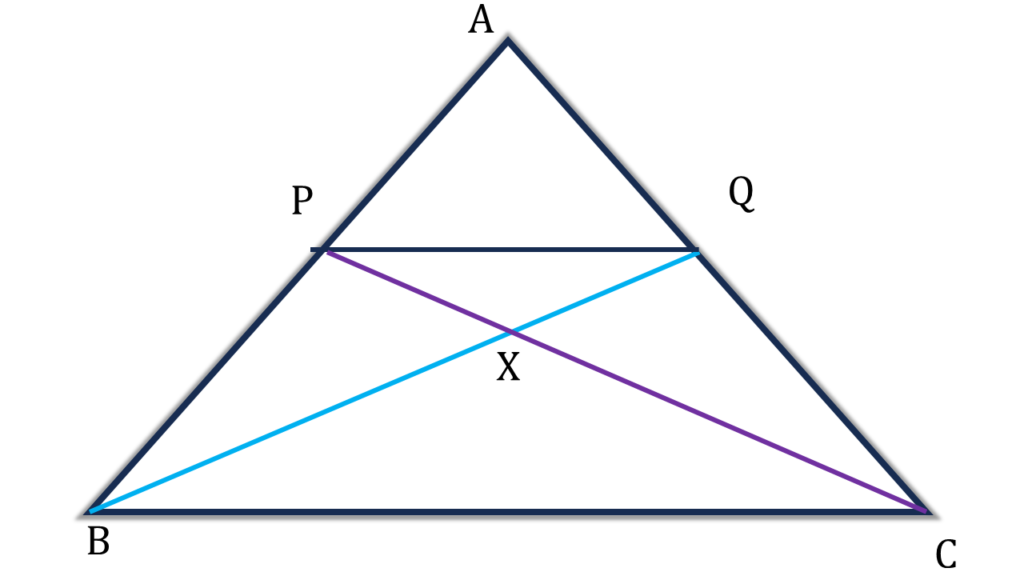
| ▲BCP = ▲BCQ |
| বা, ▲BCP – ▲BCX = ▲BCQ – ▲BCX |
| বা, ▲BXP = ▲CXQ |
| (iv) নং প্রমাণিত |
13. ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D এবং BC বাহুর উপর P যেকোন একটি বিন্দু। P, A যুক্ত করি। D বিন্দু দিয়ে PA সরলরেখাংশের সমাস্তরাল সরলরেখা AB বাহুকে Q বিন্দুতে ছেদ করে । প্রমাণ করি যে,
(i) ▲ADQ = ▲PDQ
(ii) ▲BPQ = ½▲ABC
সমাধানঃ-
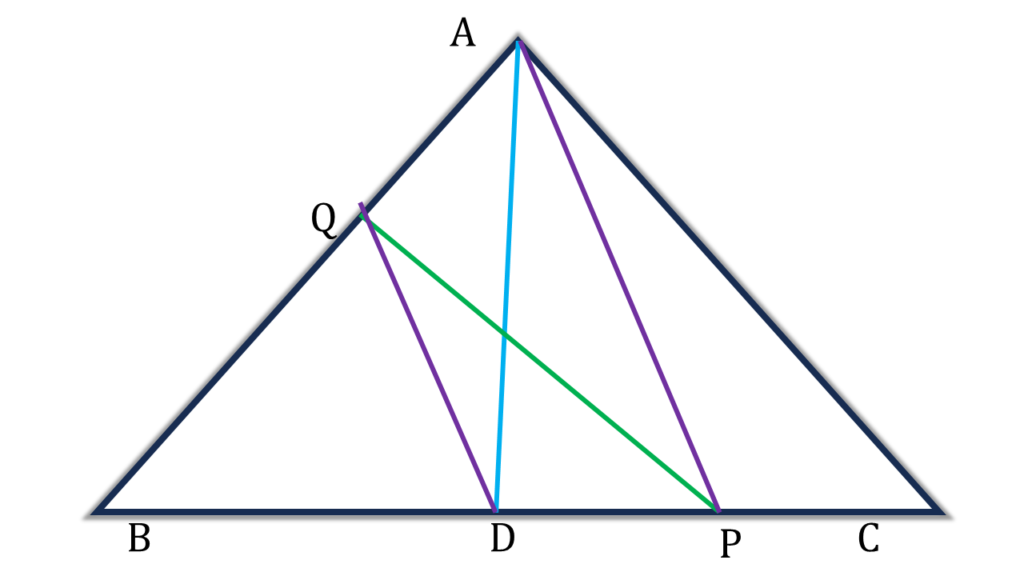
প্রদত্তঃ ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D এবং BC বাহুর উপর P যেকোন একটি বিন্দু। P, A যুক্ত করি। D বিন্দু দিয়ে PA সরলরেখাংশের সমাস্তরাল সরলরেখা AB বাহুকে Q বিন্দুতে ছেদ করে ।
প্রমাণ করতে হবেঃ
(i) ▲ADQ = ▲PDQ
(ii) ▲BPQ = ½▲ABC
প্রমাণঃ
PA||QD ⇒ ▲ADQ = ▲PDQ [ একই সমান্তরালযুগল এর মধ্যে অবস্থিত]
(i) নং প্রমাণিত
আবার, ▲ABC এর AD মধ্যমা
⇒ ▲ABD = ½▲ABC ——(1)
এখন
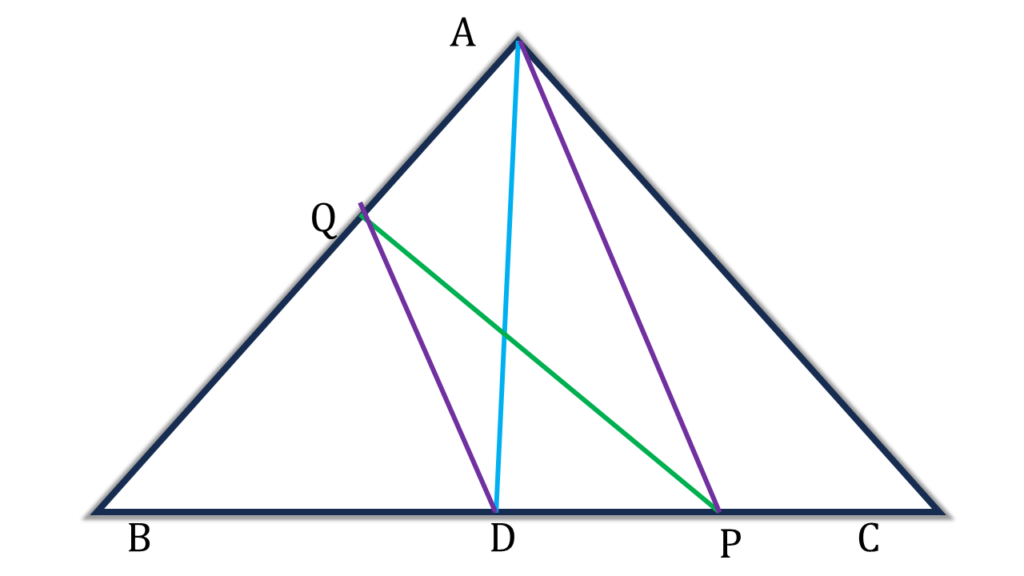
| ▲BPQ |
| = ▲BDQ + ▲PDQ |
| = ▲BDQ + ▲ADQ [ (i) নং থেকে পাই] |
| = ▲ABD |
| = ½▲ABC [ (1) নং থেকে পাই] |
| ∴ ▲BPQ = ½▲ABC (প্রমাণিত) |
14. ABC ত্রিভুজে AB = AC; B ও C বিন্দু থেকে AB ও AC বাহুর উপর লম্ব যথাক্রমে AC ও AB বাহুকে E ও F বিন্দুতে ছেদ করে। প্রমাণ করি যে, FE||BC
সমাধানঃ-
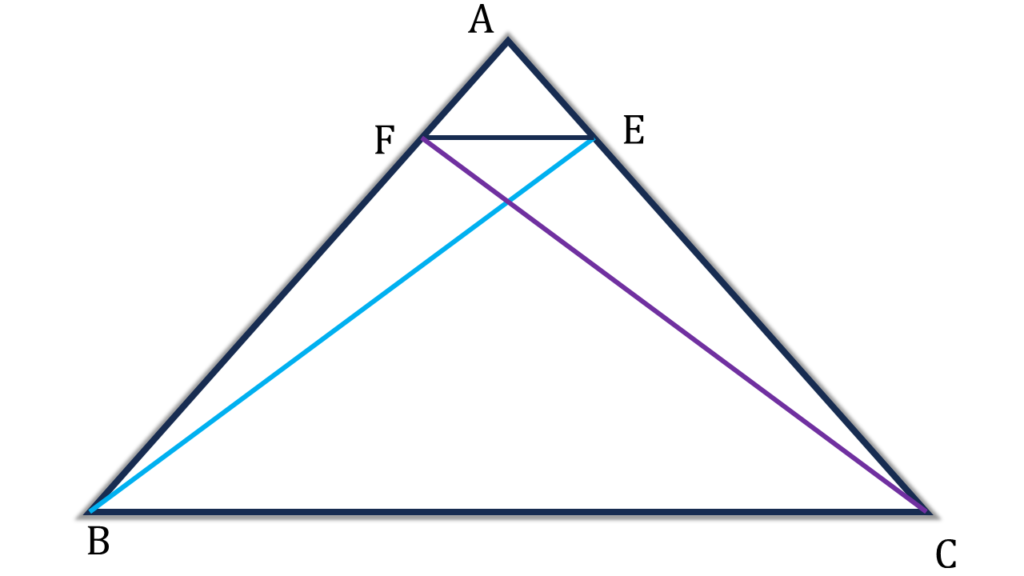
প্রদত্তঃ ABC ত্রিভুজে AB = AC; B ও C বিন্দু থেকে AB ও AC বাহুর উপর লম্ব যথাক্রমে AC ও AB বাহুকে E ও F বিন্দুতে ছেদ করে।
প্রমাণ করতে হবেঃ FE||BC
প্রমাণঃ AC বাহুকে ভূমি ধরে ▲ABC এর ক্ষেত্রফল = ½×AC×BE
আবার, AB বাহুকে ভূমি ধরে ▲ABC এর ক্ষেত্রফল = ½×AB×CF
∴ ½×AC×BE = ½×AB×CF
⇒ BE = CF ———(i)
এখন
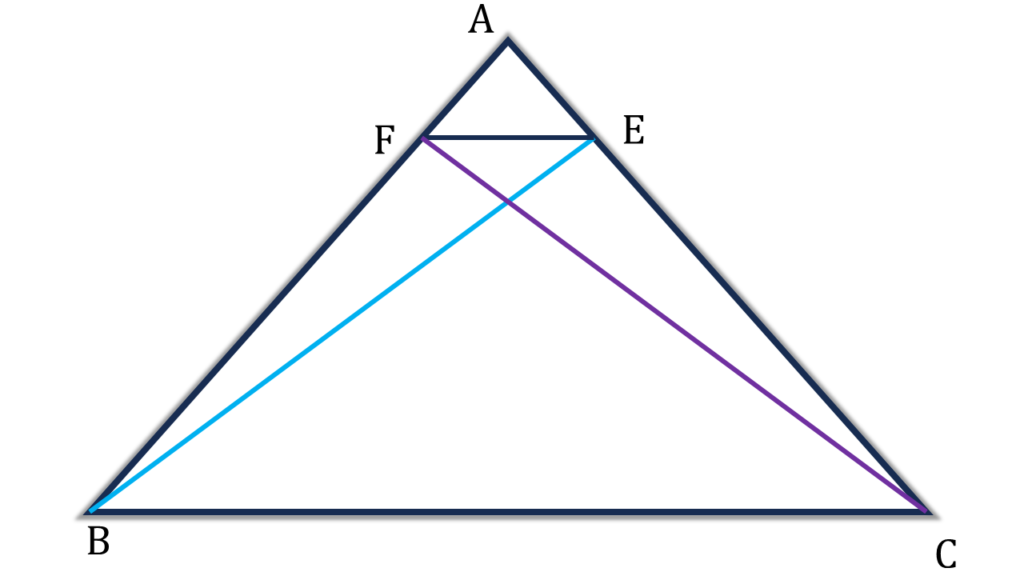
| ▲BCE ও ▲BCF এর মধ্যে, |
|---|
| BE = CF [(i) নং থেকে পেলাম] |
| ∠BFC = ∠BEC = 90° |
| BC সাধারণ ভূমি |
| ∴ ▲BCE ≅ ▲BCF |
| ⇒ ▲BCE ক্ষেত্রের ক্ষেত্রফল = ▲BCF ক্ষেত্রের ক্ষেত্রফল |
| ⇒ BC||FE [ উপপাদ্য 26 থেকে পাই ] (প্রমাণিত) |
15. ABC ত্রিভুজে ∠ABC = ∠ACB; ∠ABC ও ∠ACB কোণের সমদ্বিখণ্ডকদ্বয় AC এবং AB বাহুকে যথাক্রমে E ও F বিন্দুতে ছেদ করে। প্রমাণ করি যে, FE||BC
সমাধানঃ-
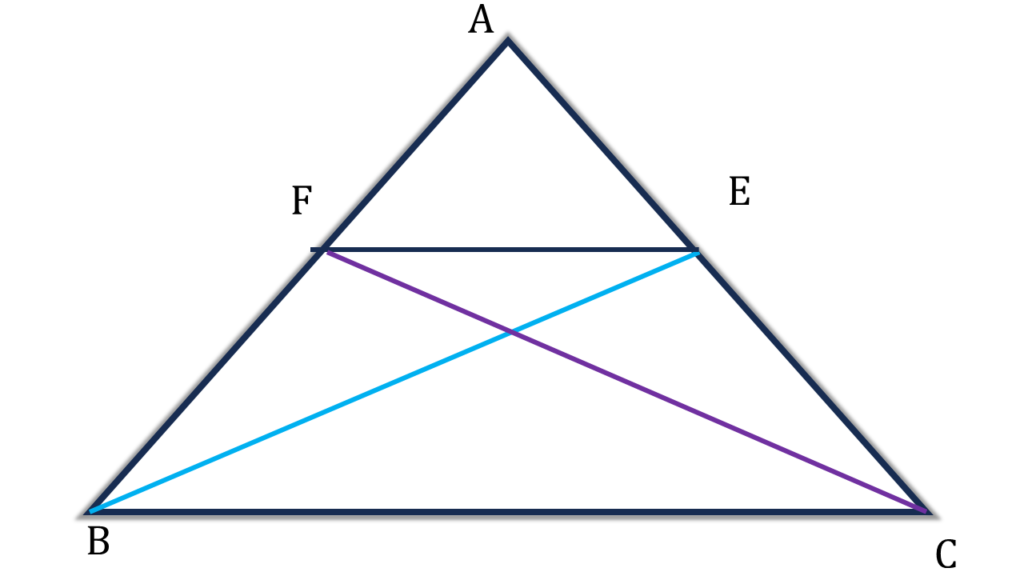
প্রদত্তঃ ABC ত্রিভুজে ∠ABC = ∠ACB; ∠ABC ও ∠ACB কোণের সমদ্বিখণ্ডকদ্বয় AC এবং AB বাহুকে যথাক্রমে E ও F বিন্দুতে ছেদ করে।
প্রমাণ করতে হবেঃ FE||BC
প্রমাণঃ
∠ABC ও ∠ACB কোণের সমদ্বিখণ্ডকদ্বয় যথাক্রমে BE ও CF.
⇒ ∠EBC = ½∠ABC=½∠ACB = ∠FCB —–(i)
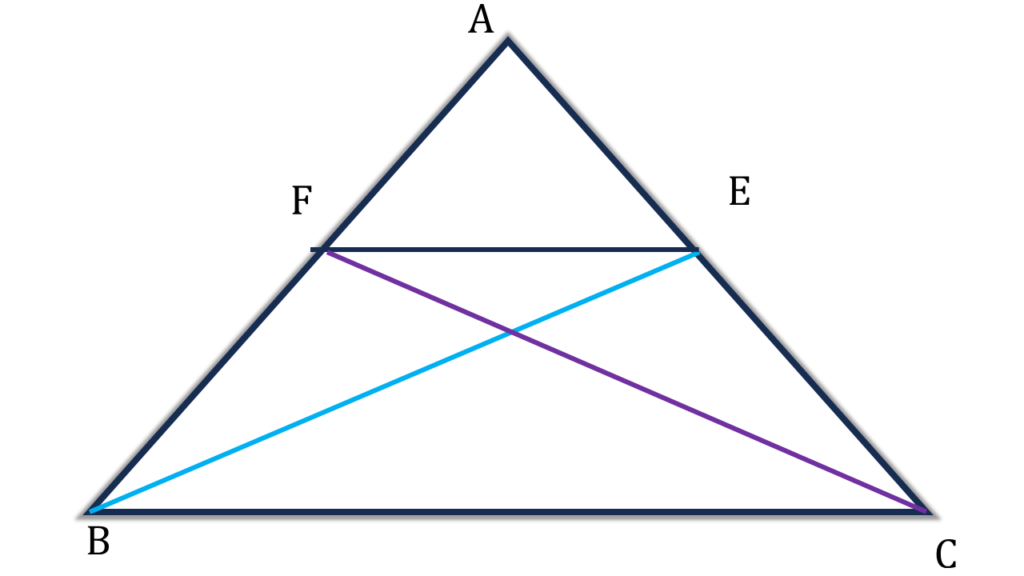
| ▲BCE ও ▲BCF এর মধ্যে, |
|---|
| ∠ECB = ∠FBC [ প্রদত্ত ] |
| ∠EBC = ∠FCB [ (i) নং থেকে পেলাম ] |
| BC সাধারণ ভূমি |
| ∴ ▲BCE ≅ ▲BCF |
| ⇒ ▲BCE ক্ষেত্রের ক্ষেত্রফল = ▲BCF ক্ষেত্রের ক্ষেত্রফল |
| ⇒ BC||FE [ উপপাদ্য 26 থেকে পাই ] (প্রমাণিত) |
16. সমান ক্ষেত্রফলবিশিষ্ট ABCD ও AEFG সামান্তরিক আকারের ক্ষেত্র দুটির ∠A সাধারণ এবং E,ABবাহুর উপর অবস্থিত। প্রমাণ করি যে. DE || FC
সমাধানঃ-
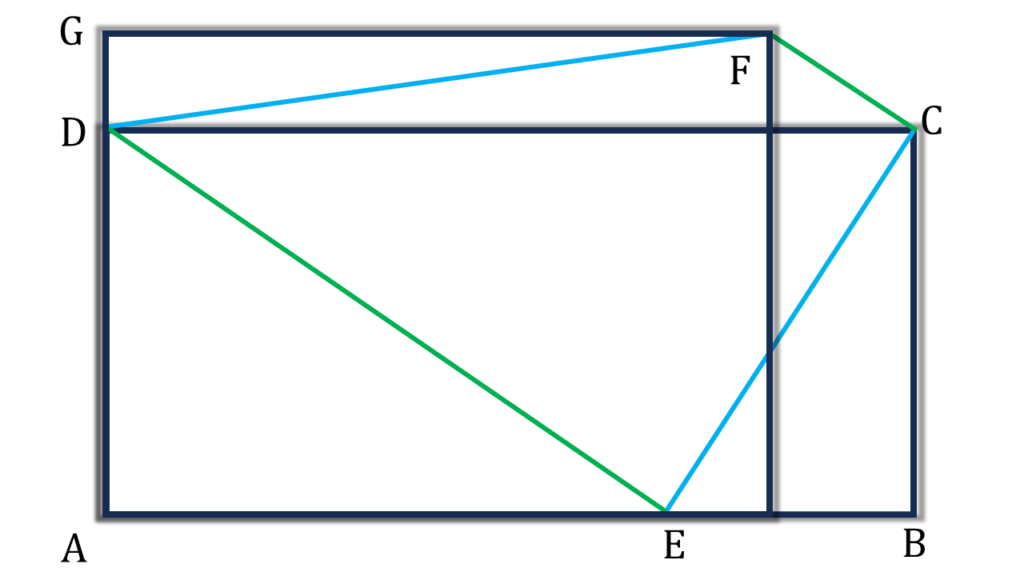
প্রদত্তঃ সমান ক্ষেত্রফলবিশিষ্ট ABCD ও AEFG সামান্তরিক আকারের ক্ষেত্র দুটির ZA সাধারণ এবং E,ABবাহুর উপর অবস্থিত।
প্রমাণ করতে হবেঃ DE || FC
প্রমাণঃ
সামান্তরিক ABCD এর,
▲DEC = ½ সামান্তরিক ABCD [ উপপাদ্য 24]
আবার, সামান্তরিক AEFG এর,
▲DEF = ½সামান্তরিক AEFG [ উপপাদ্য 24]
∴ ▲DEC = ▲DEF
⇒ DE||FC [ উপপাদ্য 26 থেকে পাই ]
17. ABCD একটি সামান্তরিক এবং ABCE একটি চতুর্ভুজ। AC কর্ণ ABCE চতুর্ভুজ আকারের ক্ষেত্রটিকে দুটি সমান অংশে বিভক্ত করে। প্রমাণ করি যে, AC || DE
সমাধানঃ-
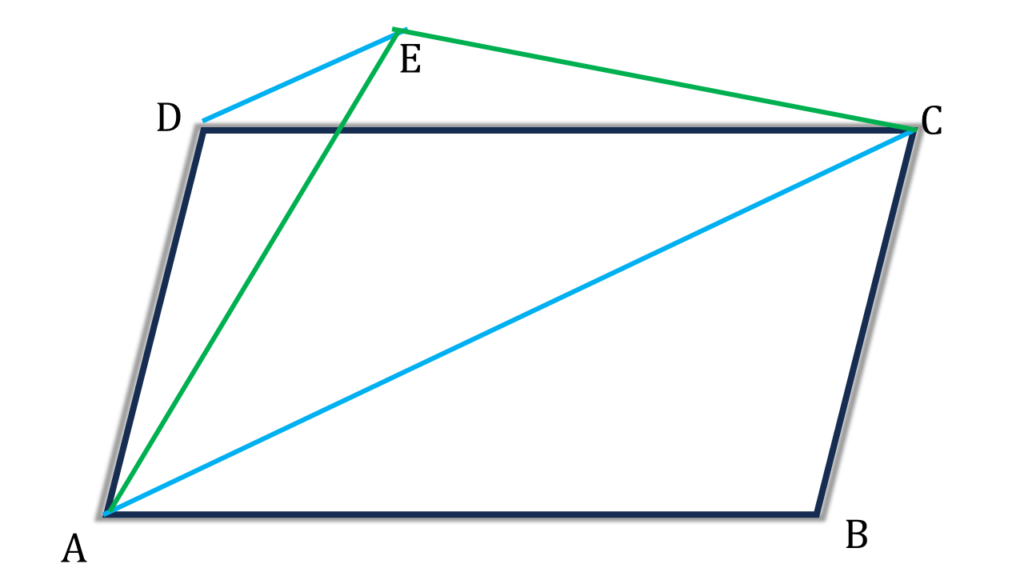
প্রদত্তঃ ABCD একটি সামান্তরিক এবং ABCE একটি চতুর্ভুজ। AC কর্ণ ABCE চতুর্ভুজ আকারের ক্ষেত্রটিকে দুটি সমান অংশে বিভক্ত করে।
প্রমাণ করতে হবেঃ AC || DE
প্রমাণঃ প্রদত্ত ▲ACE = ▲ABC
আবার, ABCD সামান্তরিকের, ▲ADC = ▲ABC
⇒ ▲ACE = ▲ADC
⇒ AC||DE [উপপাদ্য 26 থেকে পাই]
18. ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D; P এবং Q যথাক্রমে BC ও BA বাহুর উপর এমনভাবে অবস্থিত যে, ▲BPQ = ½ ▲ABC; প্রমাণ করি যে, DQ||PA
সমাধানঃ-
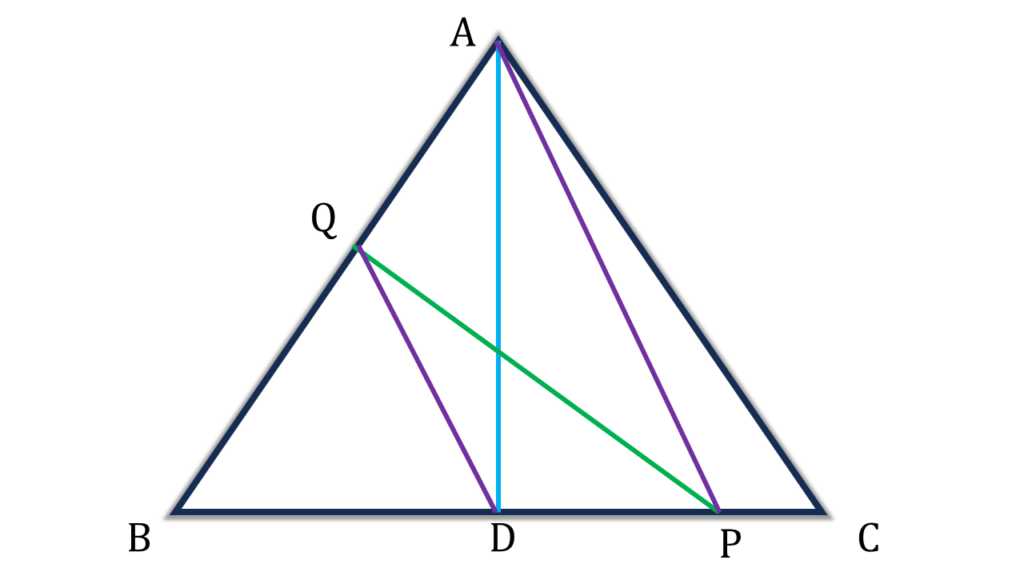
প্রদত্তঃ ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D; P এবং Q যথাক্রমে BC ও BA বাহুর উপর এমনভাবে অবস্থিত যে, ▲BPQ = ½ ▲ABC
প্রমাণ করতে হবেঃ DQ||PA
প্রমাণঃ
ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D
⇒ ▲ADB = ½ABC
আবার,প্রদত্ত ▲BPQ = ½▲ABC
| ∴ ▲ADB = ▲BPQ |
| বা, ▲AQD + ▲BDQ = ▲BDQ + ▲PDQ |
| বা, ▲PDQ = ▲AQD |
| ⇒ QD||PA [উপপাদ্য 26 থেকে পাই] |
19. ABCD সামান্তরিকের AB, BC, CD এবং DA বাহুর মধ্যবিন্দু যথাক্রমে E, F, G ও H; প্রমাণ করি যে,
(i) EFGH একটি সামান্তরিক
(ii) EFGH সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফলের অর্ধেক।
সমাধানঃ-
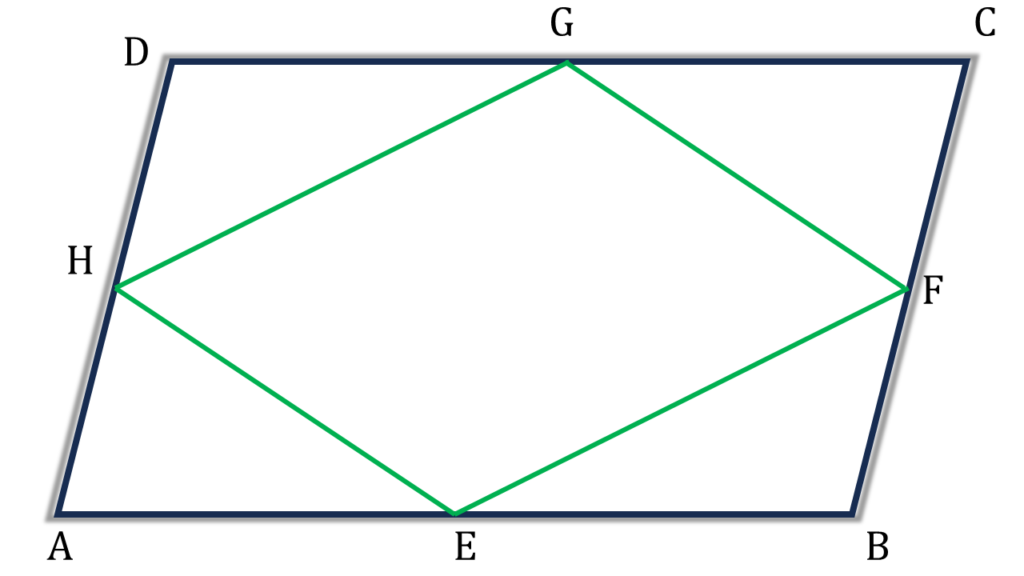
প্রদত্তঃ ABCD সামান্তরিকের AB, BC, CD এবং DA বাহুর মধ্যবিন্দু যথাক্রমে E, F, G ও H
প্রমাণ করতে হবেঃ
(i) EFGH একটি সামান্তরিক
(ii) EFGH সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফলের অর্ধেক।
অঙ্কনঃ
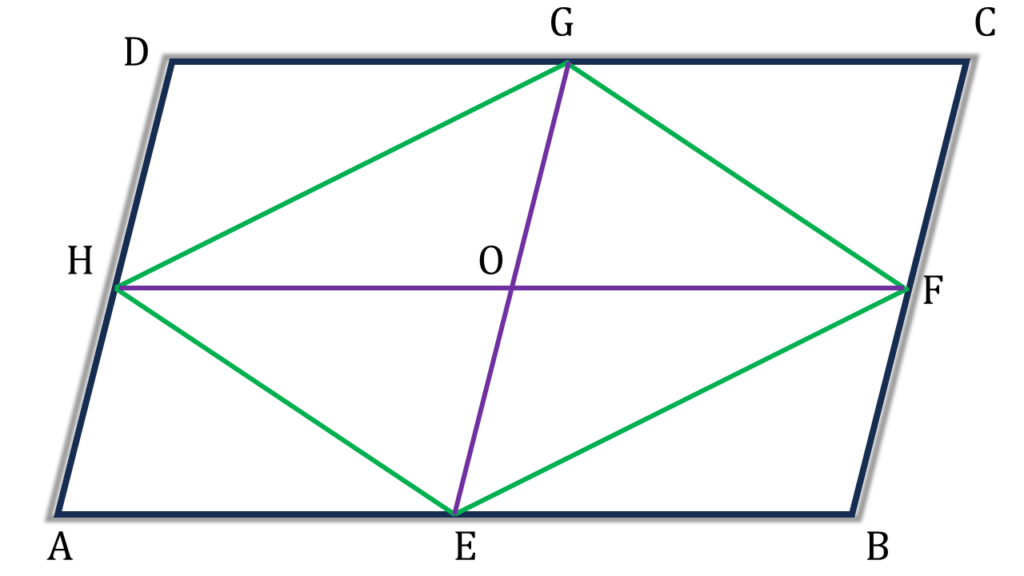
GE ও HF যুক্ত করলাম যারা পরস্পরকে O বিন্দুতে ছেদ করেছে।
প্রমাণঃ
ABFH চতুর্ভুজের, AH = BF এবং AH||BF
⇒ ABFH একটি সামান্তরিক
⇒ AB = HF এবং AB||HF ——–(i)
আবার, EBCG চতুর্ভুজের, EB=GC এবং EB||GC
⇒ EBCG একটি সামান্তরিক
⇒EG=BC এবং EG||BC ——–(ii)
(i) ও (ii) নং থেকে পাই,
OH = AE = EB = OF
এবং
OG = CF = FB = OE
∴ EFGH চতুর্ভুজের কর্ণ দুটি যথাক্রমে GE ও HF পরস্পরকে সমদ্বিখণ্ডিত করে।
⇒ EFGH একটি সামান্তরিক।[ (i) নং প্রমাণিত ]
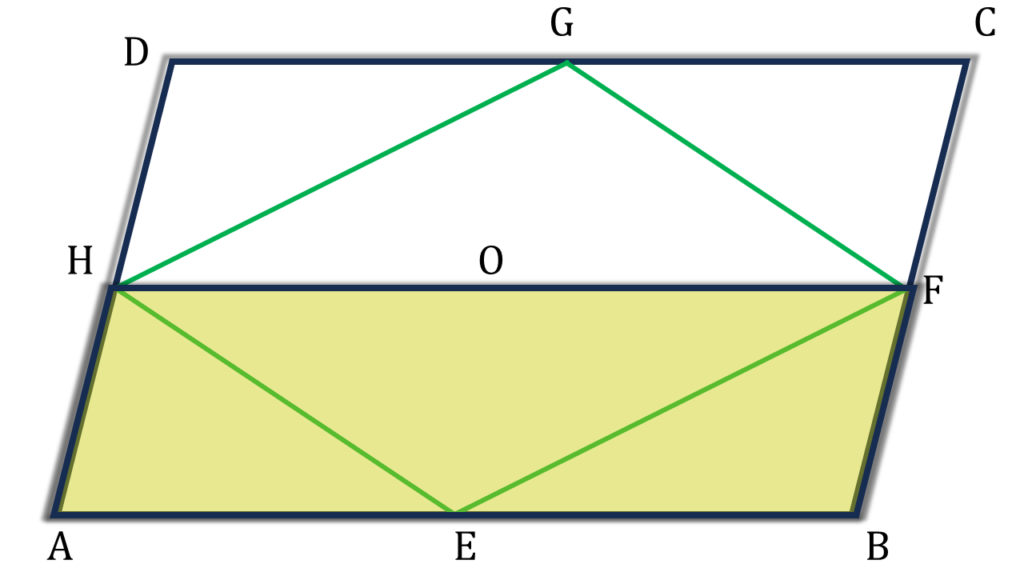
[ যেভাবে আমরা প্রমান করলাম EBCG একটি সামান্তরিক, একই ভাবে প্রমান করতে পারবো AEGD একটি সামান্তরিক ]
সামান্তরিক AEGD এর,
▲HEG = ½ সামান্তরিক AEGD
এবং
সামান্তরিক EBCG এর,
▲EFG = ½ সামান্তরিক EBCG
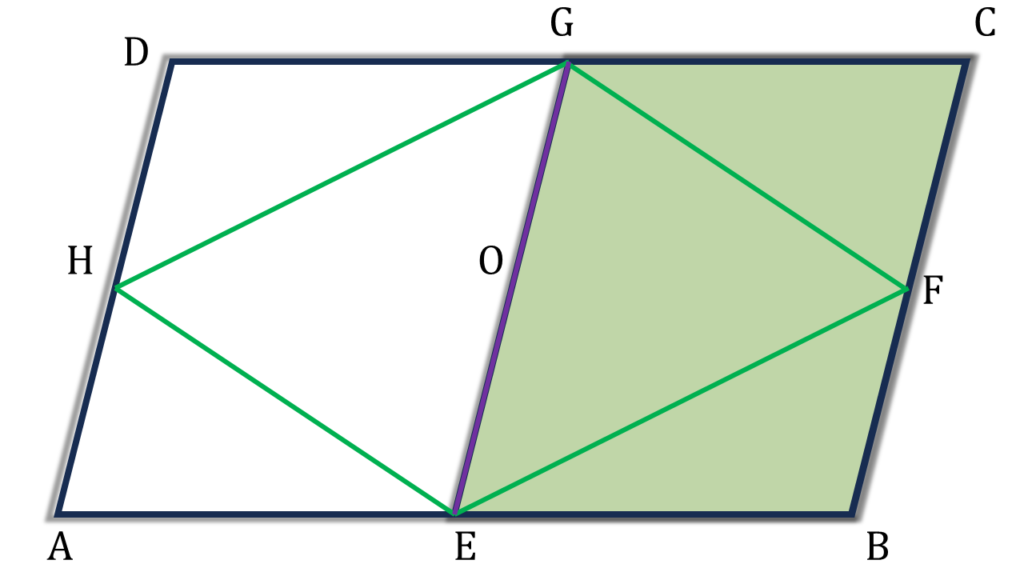
এখন
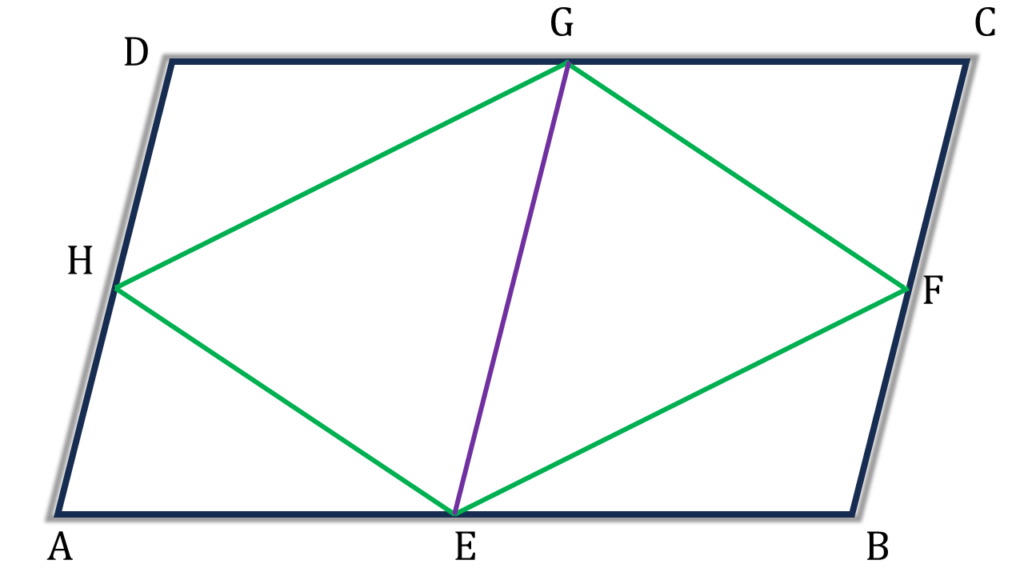
| সামান্তরিক HEFG |
| = ▲HEG + ▲EFG |
| = ½ সামান্তরিক AEGD + ½ সামান্তরিক EBCG |
| = ½ ( সামান্তরিক AEGD + ½ সামান্তরিক EBCG) |
| = ½ সামান্তরিক ABCD |
| (ii) নং প্রমাণিত |
20. ABCD ট্রাপিজিয়ামের AB || DC এবং BC বাহুর মধ্যবিন্দু E প্রমাণ করি যে, AED ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল =½ ABCD ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল।
সমাধানঃ-
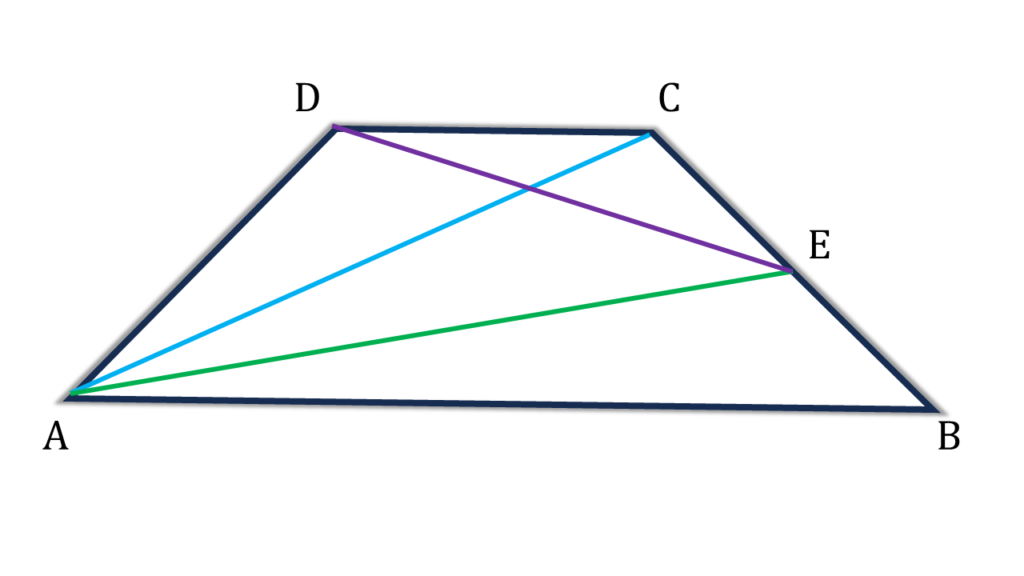
প্রদত্তঃ ABCD ট্রাপিজিয়ামের AB || DC এবং BC বাহুর মধ্যবিন্দু E
প্রমাণ করতে হবেঃ AED ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল =½ ABCD ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল।
প্রমাণঃ
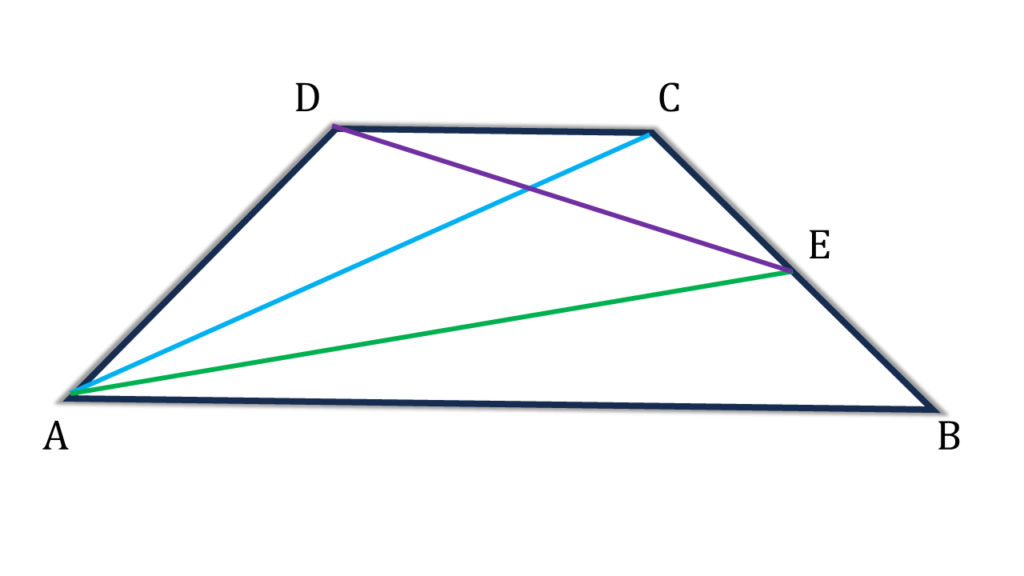
| ট্রাপিজিয়াম ABCD এর ক্ষেত্রফল |
| = ▲ABC + ▲ADC |
| = 2▲ABE + ▲BDC [ ∵ ▲ABC এর মধ্যমা AE এবং AB||DC ] |
| = 2▲ABE + 2▲DCE [ ∵ ▲BDC এর মধ্যমা DE ] |
| = 2(▲ABE + ▲DCE) |
| ∴ (▲ABE + ▲DCE) = ½ ট্রাপিজিয়াম ABCD এর ক্ষেত্রফল |
এখন
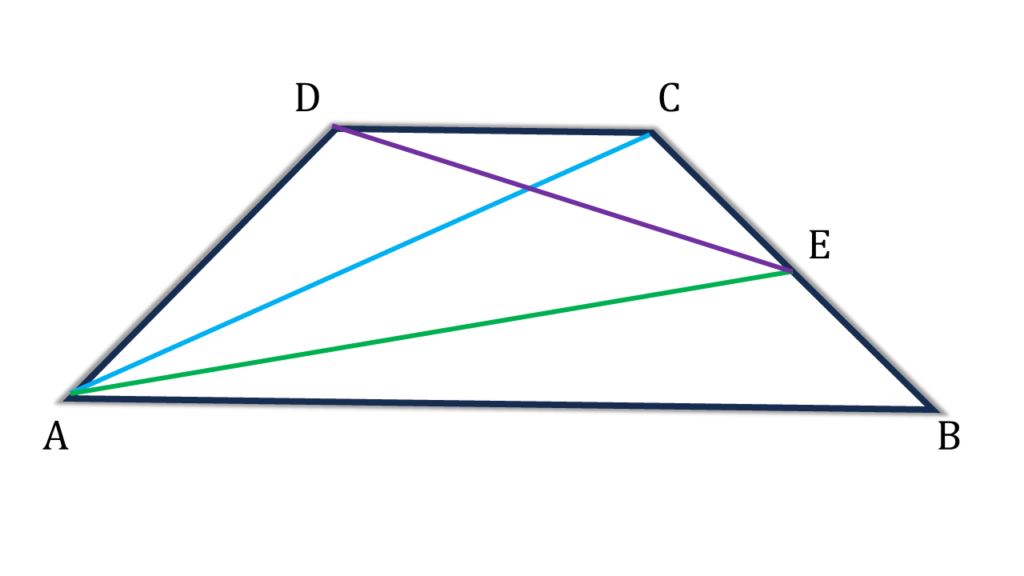
| AED ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল |
| = ট্রাপিজিয়াম ABCD এর ক্ষেত্রফল – (▲ABE + ▲DCE) |
| = ট্রাপিজিয়াম ABCD এর ক্ষেত্রফল – ½ ট্রাপিজিয়াম ABCD এর ক্ষেত্রফল |
| = ½ ট্রাপিজিয়াম ABCD এর ক্ষেত্রফল (প্রমাণিত) |
বহু বিকল্পীয় প্রশ্ন (M.C.Q.):
(i) ▲ABC এর BC, CA, এবং AB বাহুর মধ্যবিন্দু যথাক্রমে D, E ও F; যদি ▲ABC = 16 বৰ্গ সেমি. হয় তাহলে FBCE ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল
উত্তরঃ- (c) 12 বর্গ সেমি.
সমাধানঃ-
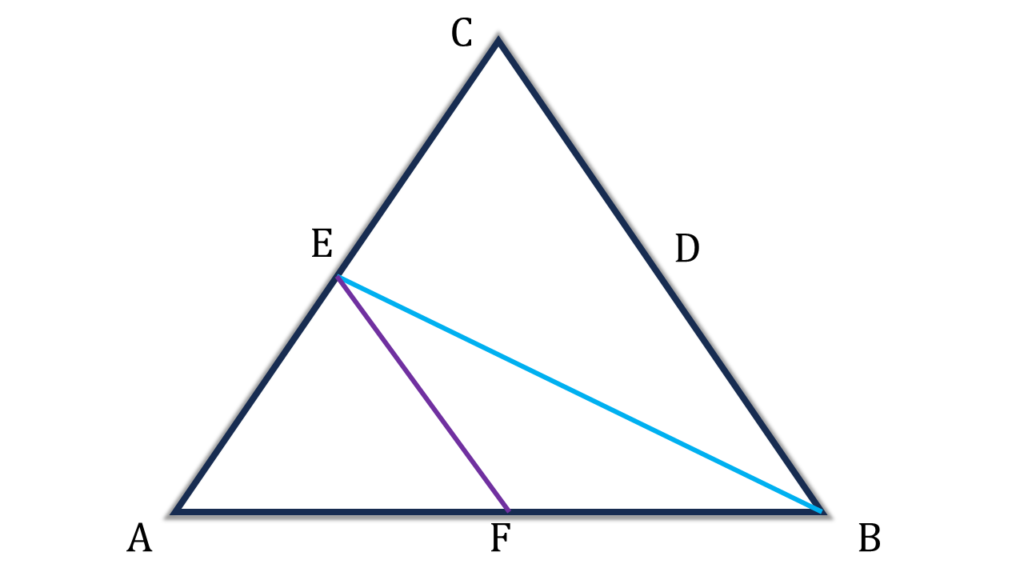
| FBCE ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল |
| = ▲ABC – ▲AEF |
| = ▲ABC – ½▲AEB |
| = ▲ABC – ½(½▲ABC) |
| = ▲ABC – ¼▲ABC |
| = ¾▲ABC |
| = ¾×16 |
| = 12 |
(ii) A, B, C, D যথাক্রমে PQRS সামান্তরিকের PQ QR, RS, SP বাহুর মধ্যবিন্দু। PQRS সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল = 36 বর্গ সেমি. হলে, ABCD ক্ষেত্রের ক্ষেত্রফল
উত্তরঃ- (b) 18 বর্গ সেমি.
সমাধানঃ-
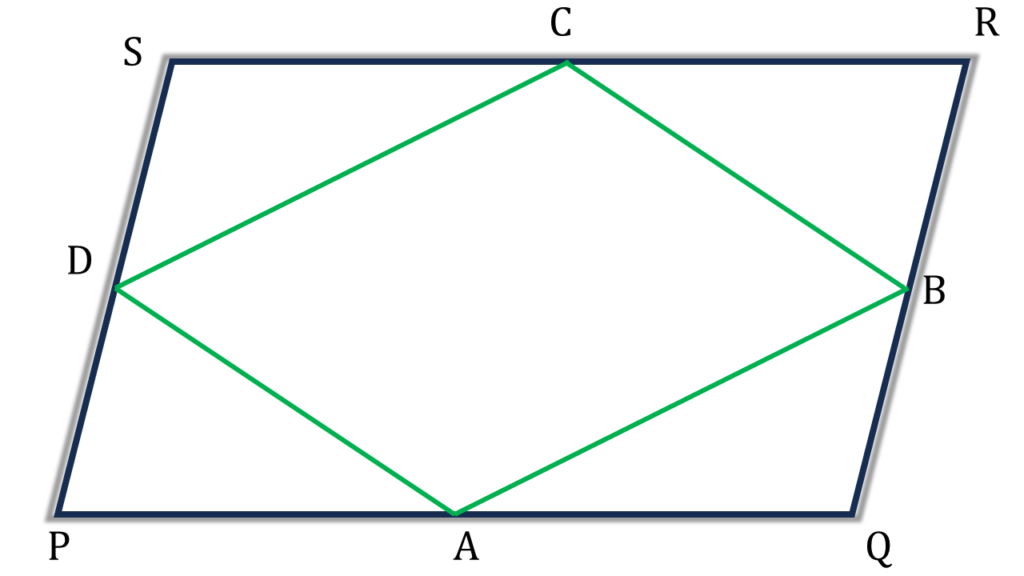
এই একই রকম অংক আমরা 19 নম্বর অংকতে করেছি।
সুতরাং,
| ABCD ক্ষেত্রের ক্ষেত্রফল |
| = ½ সামান্তরিক PQRS এর ক্ষেত্রফল |
| = ½ × 36 |
| = 18 |
(iii) ABCD সামান্তরিকের ভিতর O যে কোন একটি বিন্দু। ▲AOB + ▲COD = 16 বর্গ সেমি. হলে, ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল
উত্তরঃ- (c) 32 বর্গ সেমি.
সমাধানঃ-
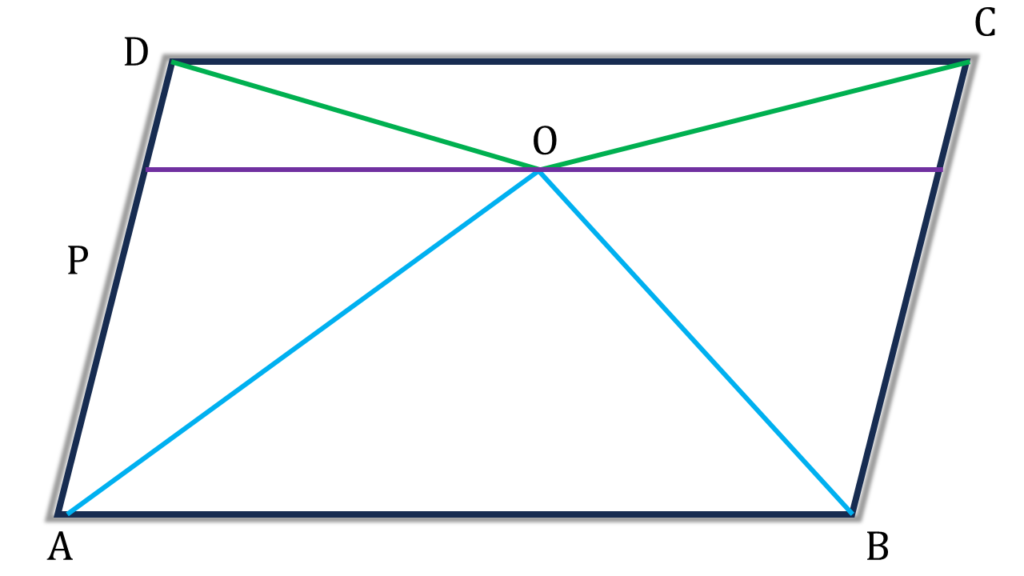
▲AOB = ½ সামান্তরিক ABFE
এবং
▲COD = ½ সামান্তরিক EFCD
| ∴ ▲AOB + ▲COD |
| = ½ (সামান্তরিক ABFE + সামান্তরিক EFCD) |
| = ½ সামান্তরিক ABCD |
∴ সামান্তরিক ABCD এর ক্ষেত্রফল
= 2(▲AOB + ▲COD)
= 2×16 = 32
(iv) ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D, BD বাহুর মধ্যবিন্দু E এবং AE-এর মধ্যবিন্দু O; BOE ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
উত্তরঃ- (d) 1/8×▲ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
সমাধানঃ-
| ▲BOE |
| = ½ ▲ABE |
| = ½ (½▲ABD) |
| = ¼▲ABD |
| = ¼(½▲ABC) |
| = \(\frac{1}{8}\) ▲ABC |
(v) একটি সামান্তরিক আকারের ক্ষেত্র, একটি আয়তক্ষেত্র এবং একটি ত্রিভুজাকার ক্ষেত্র একই ভূমি ও একই সমান্তরাল সরলরেখা যুগলের মধ্যে অবস্থিত এবং তাদের ক্ষেত্রফল যথাক্রমে P, R ও T হলে,
উত্তরঃ- (a) P = R = 2T
সমাধানঃ-
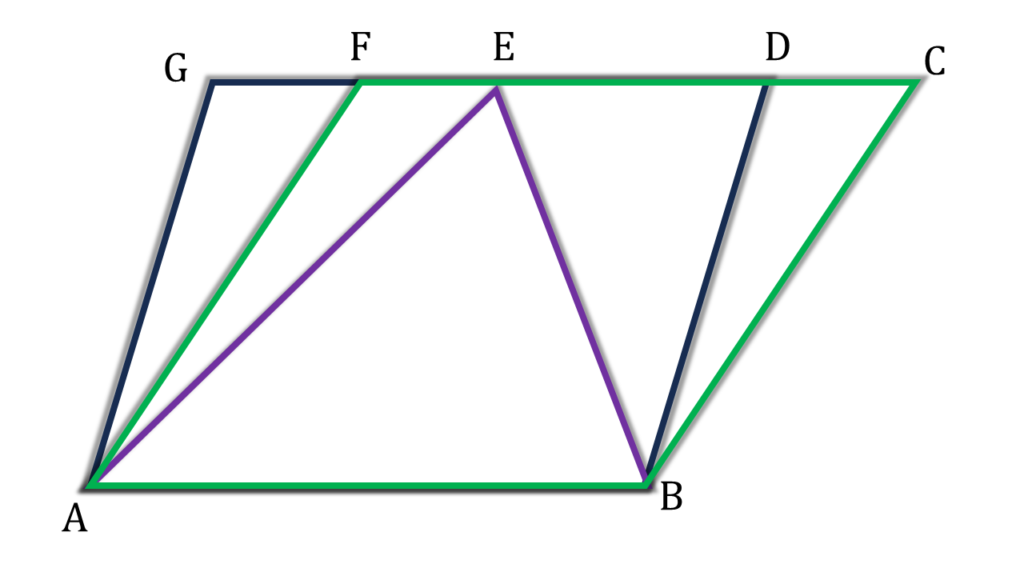
| ½ ABCD = ½ABDG = ▲AEB |
| ⇒ P = R = 2T |
সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন:
(i) ABCD সামান্তরিকের D বিন্দু থেকে AB বাহুর উপর লম্ব DE এবং B বিন্দু থেকে AD বাহুর উপর লম্ব BF; AB = 10 সেমি., AD = 8 সেমি. এবং DE = 6 সেমি. হলে, BF-এর দৈর্ঘ্য কত তা লিখি ।
সমাধানঃ-
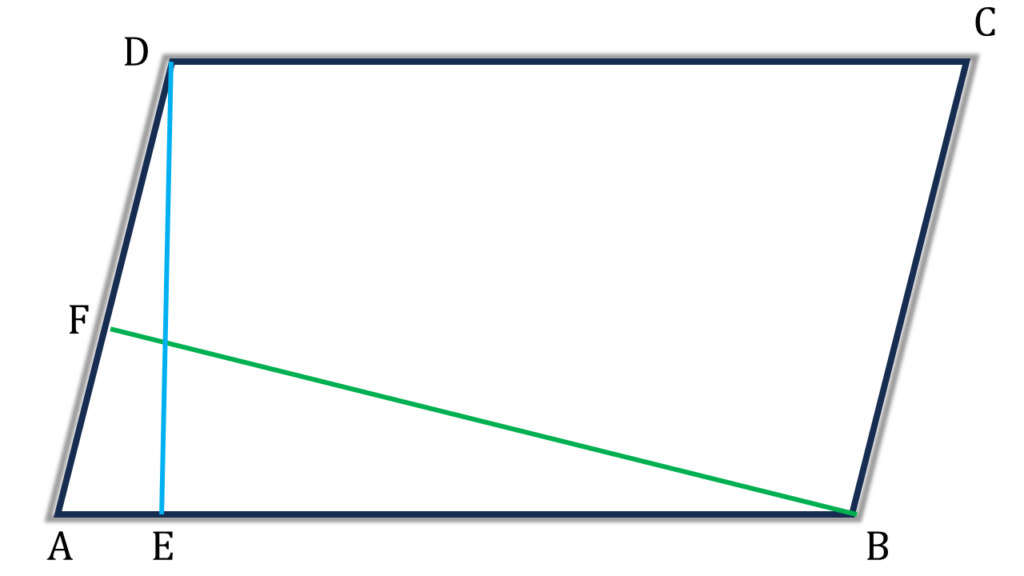
ABCD সামান্তরিকের,
| AD কে ভূমি ধরে ক্ষেত্রফল | = AD×BF |
| AB কে ভূমি ধরে ক্ষেত্রফল | = AB×DE |
∴ AD×BF = AB×DE
বা, BF = (AB×DE)/AD
বা, BF = \(\frac{10×6}{8} = \frac{15}{2}\)=7.5 সেমি.
(ii) ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল 100 বর্গ একক; BC বাহুর মধ্যবিন্দু P; ABPত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল কত তা লিখি।
সমাধানঃ-
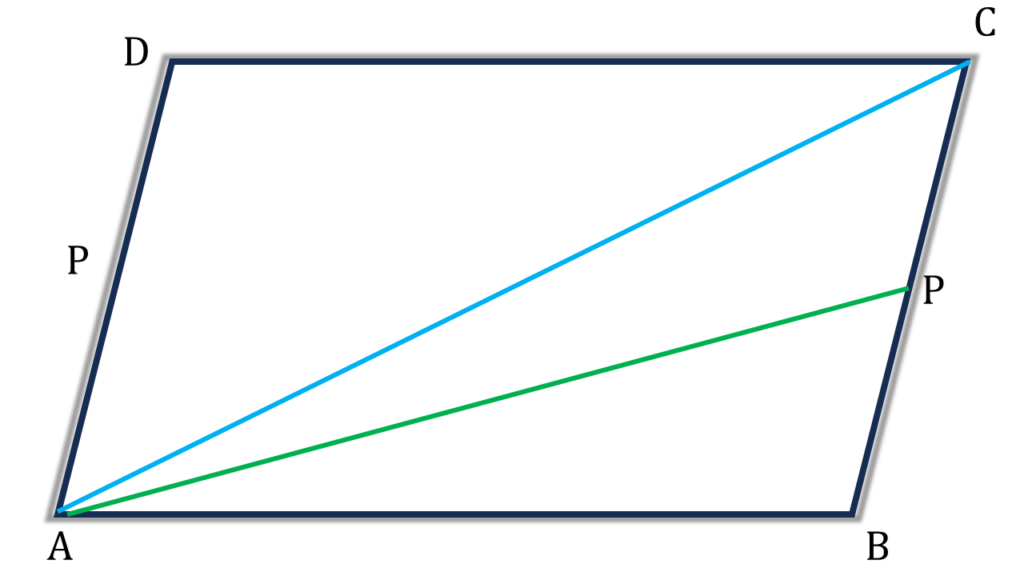
| ▲ABP |
| = ½ ▲ABC |
| = ½ (½ সামান্তরিক ABCD এর ক্ষেত্রফল) |
| = ¼ × 100 |
| = 25 বর্গ সেমি. |
(iii) ABC ত্রিভুজের AD মধ্যমা এবং AC বাহুর উপর P এমন একটি বিন্দু যাতে AADP -এর ক্ষেত্রফল: AABD -এর ক্ষেত্রফল = 2 : 3 হয়। ▲PDC-এর ক্ষেত্রফল : ▲ABC-এর ক্ষেত্রফল কত তা লিখি।
সমাধানঃ-
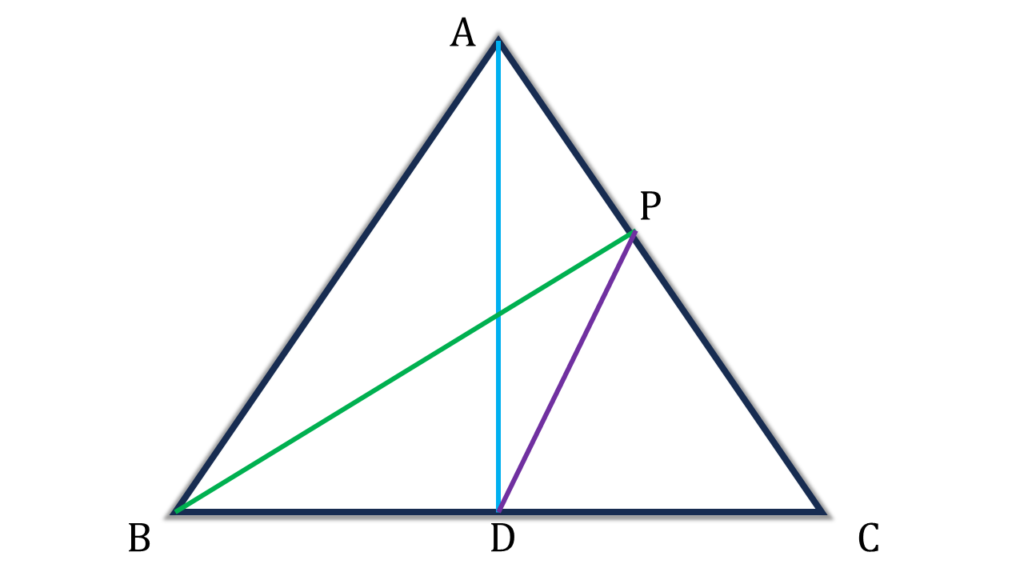
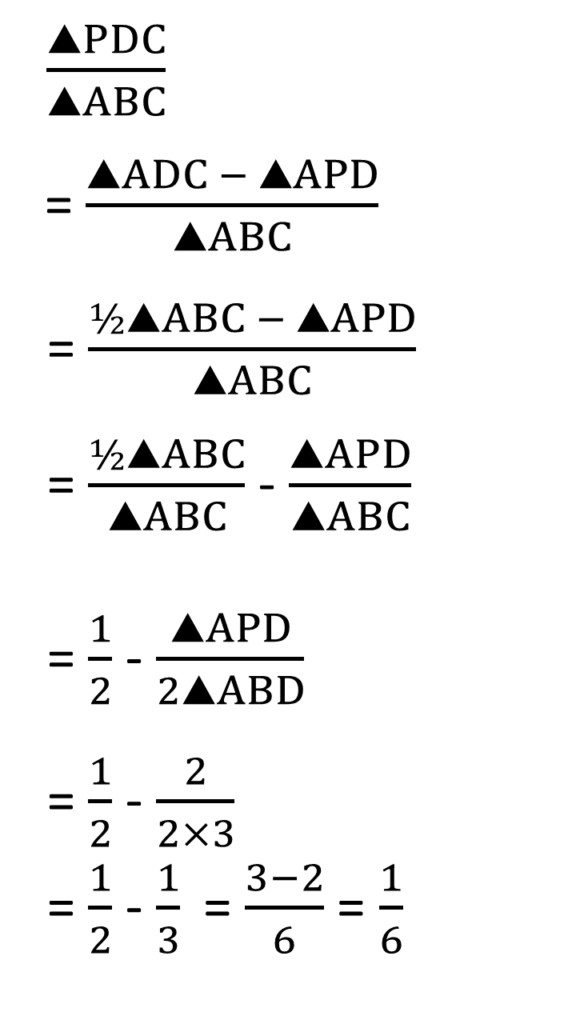
▲PDC-এর ক্ষেত্রফল : ▲ABC-এর ক্ষেত্রফল
= 1 : 6
(iv) ABDE একটি সামান্তরিক। F, ED বাহুর মধ্যবিন্দু। ABD ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল 20 বর্গ সেমি. হলে, AEF ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল কত তা লিখি।
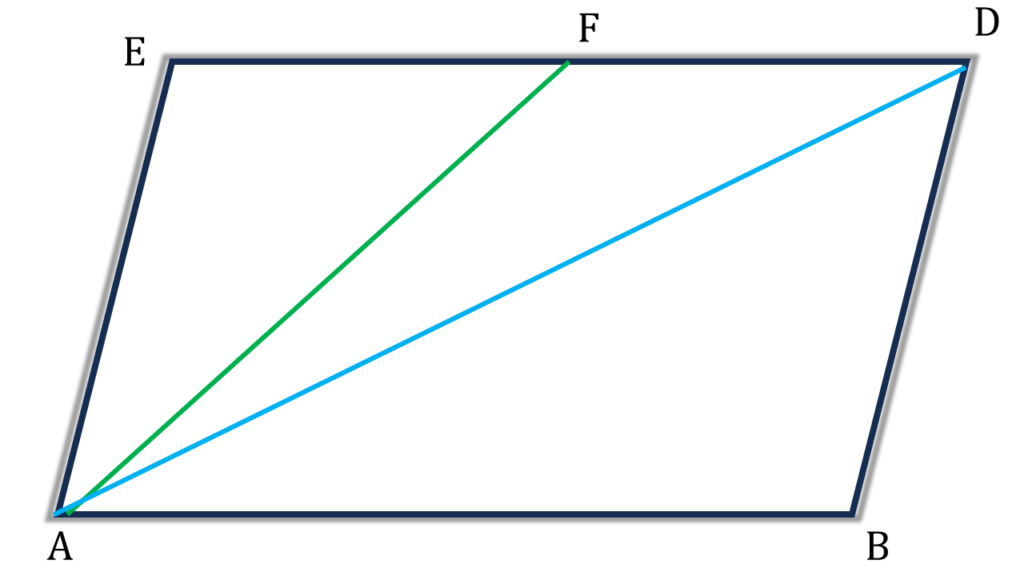
সমাধানঃ-
| ▲AEF |
| = ½ ▲AED |
| = ½ ▲ABD |
| = ½ × 20 = 10 বর্গ সেমি. |
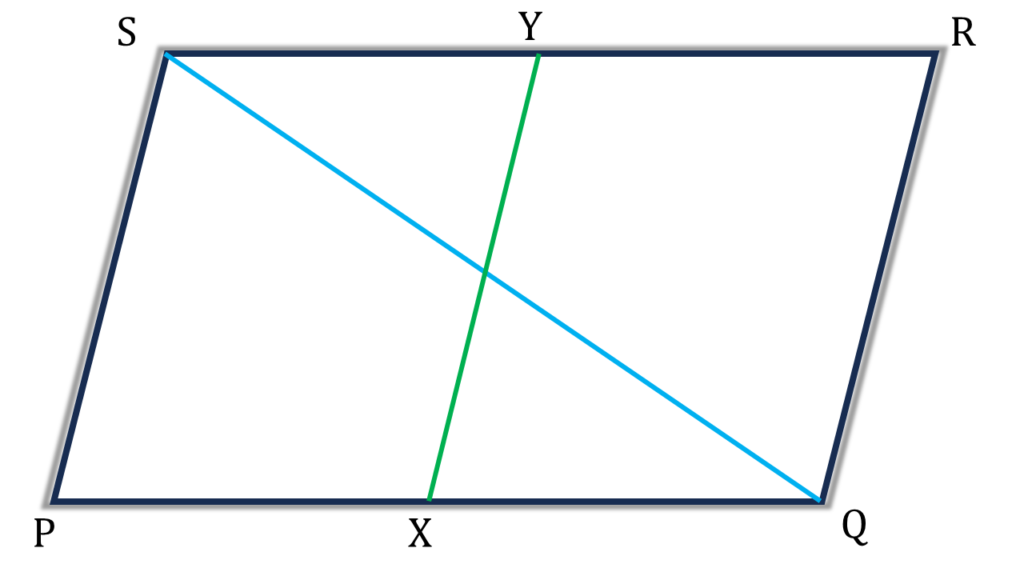
(v) PQRS একটি সামান্তরিক। X এবং Y যথাক্রমে PQ এবং SR বাহুর মধ্যবিন্দু। কর্ণ SQ যুক্ত করি। সামান্তরিক XQRY আকার ক্ষেত্রের ক্ষেত্রফল: QSR ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল কত তা লিখি।
সমাধানঃ-

| WB Class 9 এর গণিত প্রকাশের সমস্ত অধ্যায়ের সমাধান- | |
|---|---|
| অধ্যায় | সমাধান |
| 1. বাস্তব সংখ্যা (Real Numbers) | কষে দেখি 1.1 |
| কষে দেখি 1.2 | |
| কষে দেখি 1.3 | |
| 2. সূচকের নিয়মাবলি (Laws of Indices) | কষে দেখি 2 |
| 3. লেখচিত্র (Graph) | কষে দেখি 3.1 |
| কষে দেখি 3.2 | |
| 4. স্থানাঙ্ক জ্যামিতি : দূরত্ব নির্ণয় (Co-ordinate Geometry: Distance Formula) | কষে দেখি 4 |
| 5. রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) (Linear Simultaneous Equations) | কষে দেখি 5.1 |
| কষে দেখি 5.2 | |
| কষে দেখি 5.3 | |
| কষে দেখি 5.4 | |
| কষে দেখি 5.5 | |
| কষে দেখি 5.6 | |
| কষে দেখি 5.7 | |
| 6. সামান্তরিকের ধর্ম (Properties of Parallelogram) | কষে দেখি 6 |
| 7. বহুপদী সংখ্যামালা (Polynomial) | কষে দেখি 7.1 |
| কষে দেখি 7.2 | |
| কষে দেখি 7.3 | |
| কষে দেখি 7.4 | |
| 8. উৎপাদকে বিশ্লেষণ (Factorisation) | কষে দেখি 8.1 |
| কষে দেখি 8.2 | |
| কষে দেখি 8.3 | |
| কষে দেখি 8.4 | |
| কষে দেখি 8.5 | |
| 9. ভেদক ও মধ্যবিন্দু সংক্রান্ত উপপাদ্য (Transversal & Mid-Point Theorem). | কষে দেখি 9 |
| 10. লাভ ও ক্ষতি (Profit and Loss) | কষে দেখি 10.1 |
| কষে দেখি 10.2 | |
| 11. রাশিবিজ্ঞান (Statistics) | কষে দেখি 11.1 |
| কষে দেখি 11.2 | |
| 12. ক্ষেত্রফল সংক্রান্ত উপপাদ্য (Theorems on Area) | কষে দেখি 12 |
| 13. সম্পাদ্য : ত্রিভুজের সমান ক্ষেত্রফল বিশিষ্ট সামান্তরিক অঙ্কন | কষে দেখি 13 |
| 14. সম্পাদ্য : চতুর্ভুজের সমান ক্ষেত্রফল বিশিষ্ট ত্রিভুজ অঙ্কন | কষে দেখি 14 |
| 15. ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল (Area & Perimeter of Triangle & Quadrilateral) | কষে দেখি 15.1 |
| কষে দেখি 15.2 | |
| কষে দেখি 15.3 | |
| 16. বৃত্তের পরিধি (Circumference of Circle) | কষে দেখি 16 |
| 17. সমবিন্দু সংক্রান্ত উপপাদ্য (Theorems on concurrence) | কষে দেখি 17 |
| 18. বৃত্তের ক্ষেত্রফল (Area of Circle) | কষে দেখি 18 |
| 19. স্থানাঙ্ক জ্যামিতি: সরলরেখাংশের অন্তর্বিভক্ত ও বহিঃবিভক্ত (Co-ordinate Geometry: Internal and External Division of Straight-Line Segment) | কষে দেখি 19 |
| 20. স্থানাঙ্ক জ্যামিতি: ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল (Co-ordinate Geometry: Area of Triangular Region) | কষে দেখি 20 |
| 21. লগারিদম (Logarithm) | কষে দেখি 21 |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  [Sassy_Social_Share] |
এই কষে দেখি 12 Class 9|Koshe Dekhi 12 Class 9 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।

এখানে তোমরা তোমাদের নবম শ্রেণীতে | Class 9 এ কি কি পড়ানো হয়, মানে তোমাদের নবম শ্রেণী| Class 9 সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

