কষে দেখি 4 Class 10 ।আয়তঘন কষে দেখি Class 10| Koshe Dekhi Class 4 10 WBBSE.

শ্রেণী- দশম ; অধ্যায় – আয়তঘন ; কষে দেখি 4

---

কষে দেখি 4 Class 10 অংকের সূচিপত্র:-

কষে দেখি 4 Class 10 এর অংকের সমাধান গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ

এই কষে দেখি 4, পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদ | WBBSE এর অন্তর্গত দশম শ্রেণি|Class 10 এর চার নম্বর অধ্যায় আয়তঘন এর অনুশীলনী।

এই কষে দেখি 4 Class 10 এর অংকগুলি ভালোভাবে বোঝার জন্যে যে যে বিষয় গুলি তোমাদের জানতে হবে তা নীচে আলোচনা করা হলো-

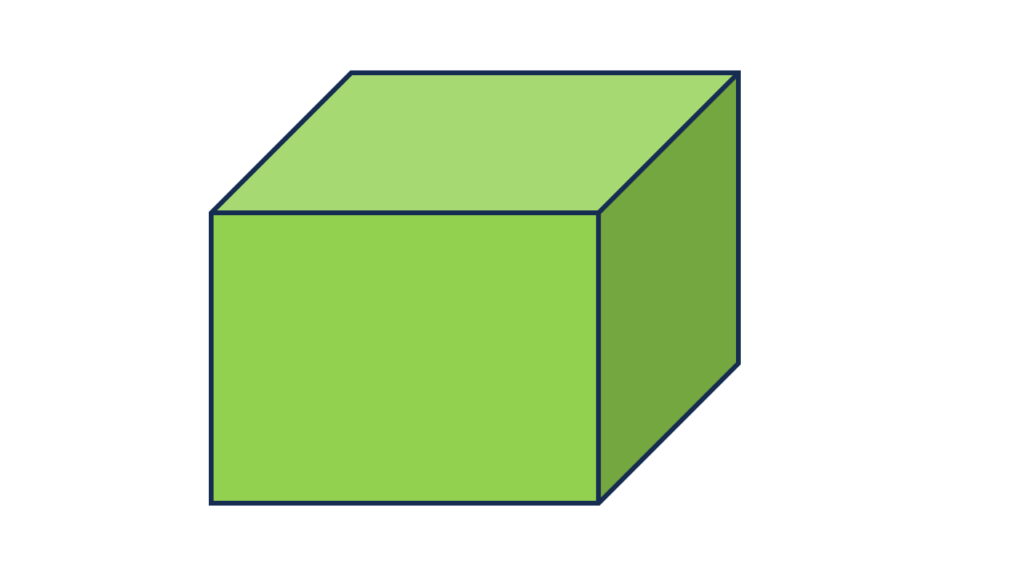
আয়তঘনের সমগ্রতলের ক্ষেত্রফলের সূত্রঃ

আয়তঘনের সমগ্রতলের ক্ষেত্রফল

= 2(দৈর্ঘ্য×প্রস্থ + প্রস্থ×উচ্চতা + দৈর্ঘ্য×উচ্চতা)

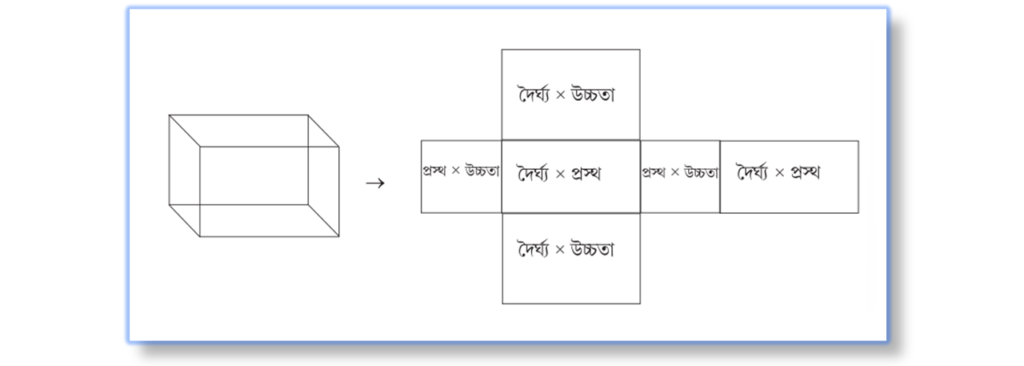
আয়তঘনের আয়তনের সূত্রঃ

আয়তঘনের আয়তন

= দৈর্ঘ্য × প্রস্থ × উচ্চতা

ঘনকের সমগ্রতলের ক্ষেত্রফলের সূত্রঃ

ঘনকের সমগ্রতলের ক্ষেত্রফল

= 6 × (ঘনকের একটি ধারের দৈর্ঘ্য)²

ঘনকের আয়তনের সূত্রঃ

ঘনকের আয়তন = (ঘনকের একটি ধারের দৈর্ঘ্য)³

---

আগামিতে এই কষে দেখি 4 Class 10 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?

কষে দেখি 4 Class 10 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 4 Class 10 তারপর এই চিহ্ন দেখে Click করলে আবার তোমরা এখানে এসে যাবে।

---

কষে দেখি 4 Class 10|Koshe Dekhi 4 Class 10

1. আমরা পরিবেশের 4 টি আয়তঘনাকার ও 4 টি ঘনক আকার বস্তুর নাম লিখি।

সমাধানঃ-

---

2. পাশের আয়তঘনাকার চিত্রের

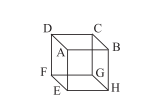
তলগুলি, ধারগুলি ও শীর্ষবিন্দুগুলির নাম লিখি।

সমাধানঃ-

তলগুলি	ABCD, EFGH, ADFE, DCGF, ABHE, BCGH
ধারগুলি	AB, BC, CD, DA, EF, FG, GH, HE, AE, DF, BH, CG
শীর্ষবিন্দু গুলি	A, B, C, D, E, F, G, H

---

3. একটি সমকোণী চৌপলাকার ঘরের দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 5 মি., 4 মি. ও 3 মি. হলে, ওই ঘরে সবচেয়ে লম্বা যে দণ্ড রাখা যাবে তার দৈর্ঘ্য হিসাব করে লিখি।

সমাধানঃ-

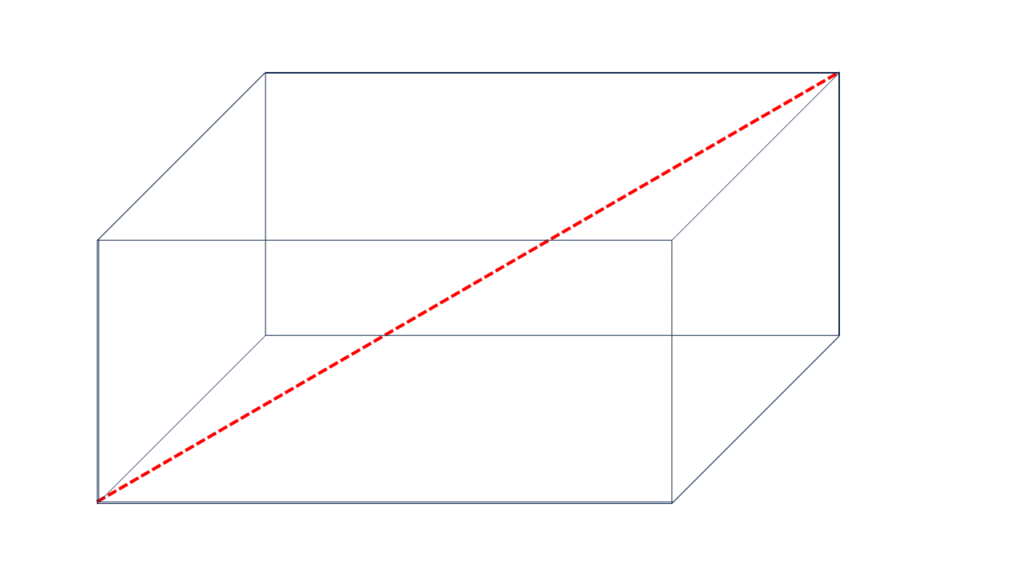
ওই ঘরে সবচেয়ে লম্বা যে দণ্ড রাখা যাবে সেটি ওই ঘরের কর্ণ বরাবর রাখতে হবে।

সমকোণী চৌপলাকার ঘরের কর্ণের দৈর্ঘ্য

= \(\sqrt{(দৈর্ঘ্য)^2+(প্রস্থ)^2+(উচ্চতা)^2}\)

= \(\sqrt{5^2+4^2+3^2}\)

= \(\sqrt{25+16+9}\)

= \(\sqrt{50}\)

= 5\(\sqrt{2}\) মি.

---

4. একটি ঘনকের একটি তলের ক্ষেত্রফল 64 বর্গ মিটার হলে, ঘনকটির আয়তন হিসাব করে লিখি।

সমাধানঃ-

ধরি, ঘনকটির একটি ধারের দৈর্ঘ্য = a মিটার।

তাহলে, a² = 64 বা, a = 8

অতএব ঘনকের একটি ধারের দৈর্ঘ্য = 8 মিটার.

ঘনকের আয়তন

a³

= 8×8×8

= 512 ঘন মিটার.

---

5. আমাদের বকুলতলা গ্রামে 2 মিটার চওড়া এবং 8 ডেসিমি. গভীর একটি খাল কাটা হয়েছে। যদি মোট 240 ঘন মিটার মাটি কাটা হয়ে থাকে তবে খালটি কত লম্বা হিসাব করে লিখি।

সমাধানঃ-

ধরি, খালটি লম্বা = a মিটার.

অতএব খালটির,

দৈর্ঘ্য	a মিটার
প্রস্থ	2 মিটার.
উচ্চতা	8 ডেসিমি. = 0.8 মিটার.

শর্তে,

a×2×0.8 = 240

বা, a = \(\frac{240}{2\times 0.8}\)

বা, a = 150 মিটার.

• খালটি 150 মিটার. লম্বা।

---

6. একটি ঘনকের কর্ণের দৈর্ঘ্য 4√3 সেমি. হলে, ঘনকটির সমগ্রতলের ক্ষেত্রফল হিসাব করে লিখি ।

সমাধানঃ-

ধরি, ঘনকের একটি ধারের দৈর্ঘ্য = a সেমি.

শর্তে,

a√3 = 4√3

বা, a = 4

ঘনকটির সমগ্রতলের ক্ষেত্রফল

= 6a²

= 6×4×4

= 96 বর্গ সেমি.

• ঘনকটির সমগ্রতলের ক্ষেত্রফল 96 বর্গ সেমি.

---

7. একটি ঘনকের ধারগুলির দৈর্ঘ্যের সমষ্টি 60 সেমি. হলে, ঘনকটির ঘনফল হিসাব করে লিখি।

সমাধানঃ-

একটি ঘনকের ধারের সংখ্যা = 12 টি।

অতএব প্রতিটি ধারের দৈর্ঘ্য = \(\frac{60}{12}\) = 5 সেমি.

ঘনকটির ঘনফল

= 5³

= 125 ঘন সেমি.

---

8. যদি একটি ঘনকের ছয়টি পৃষ্ঠতলের ক্ষেত্রফলের সমষ্টি 216 বর্গ সেমি. হয়, তবে ঘনকটির আয়তন কত হবে হিসাব করে লিখি ।

সমাধানঃ-

ধরি, ঘনকের একটি ধারের দৈর্ঘ্য = a সেমি.

শর্তে,

6a2 = 216

বা, a2 = 36

বা, a = 6

অতএব ঘনকটির আয়তন

a³

= 6×6×6

= 216 ঘন সেমি.

---

9. একটি সমকোণী চৌপলের আয়তন 432 ঘন সেমি.। তাকে সমান আয়তনবিশিষ্ট দুটি ঘনক-এ পরিণত করা হলে, প্রতিটি ঘনকের প্রত্যেক ধারের দৈর্ঘ্য কত হবে হিসাব করে লিখি।

সমাধানঃ-

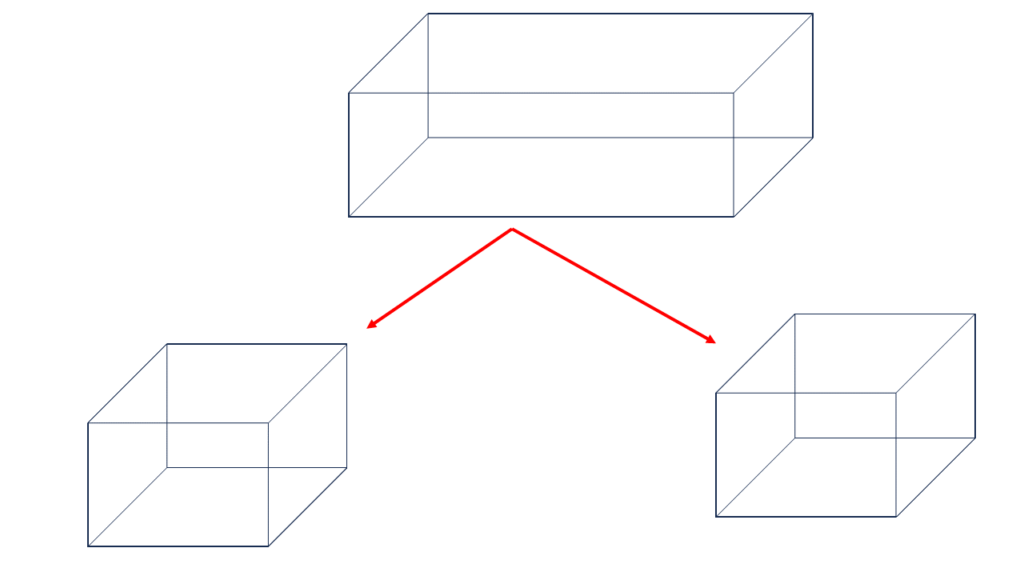
প্রতিটি ঘনকের আয়তন হবে \(\frac{432}{2}\)= 216 ঘন সেমি.

অতএব প্রতিটি ঘনকের প্রত্যেক ধারের দৈর্ঘ্য

= \(\sqrt[3]{216}\)

= 6 সেমি.

---

10. একটি ঘনকের প্রতিটি বাহুকে 50% কমানো হলো। মূল ঘনক ও পরিবর্তিত ঘনকের ঘনফলের অনুপাত কী হবে হিসাব করে লিখি।

সমাধানঃ-

ধরি, মূল ঘনকের প্রতিটি ধারের দৈর্ঘ্য = a মিটার.

পরিবর্তিত ঘনকের ধারের দৈর্ঘ্য হবে \(\frac{a}{2}\) মিটার.

মূল ঘনকের আয়তন	= a3 ঘন মিটার.
পরিবর্তিত ঘনকের আয়তন	= (\(\frac{a}{2}\))3 = \(\frac{a^3}{8}\) ঘন মিটার.

মূল ঘনক ও পরিবর্তিত ঘনকের ঘনফলের অনুপাত

= a3 : \(\frac{a^3}{8}\)

= 8 : 1

---

11. একটি সমকোণী চৌপল আকারের বাক্সের দৈর্ঘ্য, প্রস্থ ও উচ্চতার অনুপাত 3 : 2 : 1 এবং উহার আয়তন 384 ঘন সেমি. হলে, বাক্সটির সমগ্রতলের ক্ষেত্রফল কত হবে হিসাব করে লিখি।

সমাধানঃ-

ধরি, সমকোণী চৌপল আকারের বাক্সের

দৈর্ঘ্য	\(3x\) সেমি.
প্রস্থ	\(2x\) সেমি.
উচ্চতা	\(x\) সেমি.

সমকোণী চৌপল আকারের বাক্সের আয়তন = 384 ঘন সেমি.

বা, \(3x \times 2x \times x = 384\)

বা, \(6x^3 = 384\)

বা, \(x^3 = 64\)

বা, \(x = 4\)

অতএব সমকোণী চৌপল আকারের বাক্সের

দৈর্ঘ্য	3×4=12 সেমি.
প্রস্থ	2×4=8 সেমি.
উচ্চতা	4 সেমি.

বাক্সটির সমগ্রতলের ক্ষেত্রফল

= 2(12×8 + 8×4 + 4×12)

= 2(96 + 32 + 48)

= 2 × 176

= 352 বর্গ সেমি.

• বাক্সটির সমগ্রতলের ক্ষেত্রফল 352 বর্গ সেমি.

---

12. একটি চা-এর বাক্সের ভিতরের দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 7.5 ডেসিমি, 6 ডেসিমি. এবং 5.4 ডেসিমি.। চা ভর্তি বাক্সটির ওজন 52 কিগ্রা. 350 গ্রাম। কিন্তু খালি অবস্থায় বাক্সটির ওজন 3.75 কিগ্রা. হলে, 1 ঘন ডেসিমি, চা-এর ওজন কত হবে তা হিসাব করে লিখি।

সমাধানঃ-

চা এর বাক্সে চা ধরবে

= 7.5 × 6 × 5.4

= 243 ঘন ডেসিমি.

এখন বাক্সটিতে যা চা ধরবে সেই চা এর ওজন

= 52350 – 3750

= 48600 গ্রাম.

অতএব 243 ঘন ডেসিমি. চা এর ওজন 48600 গ্রাম

1 ঘন ডেসিমি. চা এর ওজন = \(\frac{48600}{243}\)

= 200 গ্রাম

• 1 ঘন ডেসিমি, চা-এর ওজন 200 গ্রাম।

---

13. একটি বর্গাকার ভূমিবিশিষ্ট পিতলের প্লেটের দৈর্ঘ্য x সেমি., বেধ। মিলিমি. এবং প্লেটটির ওজন 4725 গ্রাম। যদি 1 ঘন সেমি. পিতলের ওজন 8.4 গ্রাম হয়, তাহলে x এর মান কত হবে তা হিসাব করে লিখি।

সমাধানঃ-

বর্গাকার ভূমিবিশিষ্ট পিতলের প্লেটের

দৈর্ঘ্য এবং প্রস্থ	= \(x\) সেমি.
উচ্চতা	= 1 মিলিমি = .1 সেমি.

প্লেটটির আয়তন

= \(x \times x \times 0.1\)

= \(\frac{x^2}{10}\) ঘন সেমি.

এখন

1 ঘন সেমি. পিতলের ওজন 8.4 গ্রাম

\(\frac{x^2}{10}\) ঘন সেমি. পিতলের ওজন = \(\frac{84x^2}{100}\) গ্রাম

শর্তে,

\(\frac{84x^2}{100} = 4725 \)

বা, \( x^2 = \frac{4725\times 100}{84}

বা, \(x^2 = 5625\)

বা, \(x = 75\)

---

14. চাঁদমারির রাস্তাটি উঁচু করতে হবে। তাই রাস্তার দু-পাশে 30 টি সমান গভীর ও সমান মাপের আয়তঘনাকার গর্ত খুঁড়ে সেই মাটি দিয়ে রাস্তাটি উঁচু করা হয়েছে। যদি প্রতিটি গর্তের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 14 মি. এবং 8 মি. হয় এবং রাস্তাটি তৈরি করতে মোট 2520 ঘন মিটার মাটি লেগে থাকে, তবে প্রতিটি গর্তের গভীরতা হিসাব করে লিখি।

সমাধানঃ-

ধরি, প্রতিটি গর্তের গভীরতা = a মিটার.

এখন 30 টি গর্ত থেকে মাটি তলা হয়েছে

= 30 × 14 × 8 × a

= 336a ঘন মিটার.

শর্তে,

336a = 2520

বা, a = \(\frac{2520}{336}\)

বা, a = 7.5

অতএব, প্রতিটি গর্তের গভীরতা = 7.5 মিটার.

---

15. ঘনকাকৃতি একটি সম্পূর্ণ জলপূর্ণ চৌবাচ্চা থেকে সমান মাপের 64 বালতি জল তুলে নিলে চৌবাচ্চাটির \(\frac{1}{3}\) অংশ জলপূর্ণ থাকে। চৌবাচ্চার একটি ধারের দৈর্ঘ্য 1.2 মিটার হলে, প্রতিটি বালতিতে কত লিটার জল ধরে তা হিসাব করে লিখি।

সমাধানঃ-

চৌবাচ্চাটির আয়তন = (1.2)³ = 1.728 ঘন মিটার. = 1728 ঘন ডেসিমি.

জলপূর্ণ চৌবাচ্চা থেকে সমান মাপের 64 বালতি জল তুলে নিলে চৌবাচ্চাটির \(\frac{1}{3}\) অংশ জলপূর্ণ থাকে।

অতএব, 64 টি বালতিতে মোট জল উঠেছে

= 1728 × \(\frac{2}{3}\)

= 1152 ঘন ডেসিমি.

তাহলে প্রতিটি বালতিতে জল উঠেছে

= \(\frac{1152}{64}\)

= 18 ঘন ডেসিমি. = 18 লিটার.

---

16. এক গ্রোস দেশলাই বাক্সের একটি প্যাকেটের দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 2.8 ডেসিমি., 1.5 ডেসিমি ও 0.9 ডেসিমি. হলে, একটি দেশলাই বাক্সের আয়তন কত হবে হিসাব করি। [এক গ্রোস = 12 ডজন] কিন্তু যদি একটি দেশলাই বাক্সের দৈর্ঘ্য 5 সেমি এবং প্রস্থ 3.5 সেমি হয়, তবে তার উচ্চতা কত হবে হিসাব করে লিখি।

সমাধানঃ-

এক গ্রোস দেশলাই বাক্সের একটি প্যাকেটের

দৈর্ঘ্য	2.8 ডেসিমি. = 28 সেমি.
প্রস্থ	1.5 ডেসিমি. = 15 সেমি.
উচ্চতা	0.9 ডেসিমি. = 9 সেমি.

এক গ্রোস দেশলাই বাক্সের একটি প্যাকেটের আয়তন

= 28 × 15 × 9

= 3780 ঘন সিমি.

∴ একটি দেশলাই বাক্সের আয়তন

= \(\frac{3780}{12\times12}\)

= 26.25 ঘন সেমি.

আবার, যদি একটি দেশলাই বাক্সের দৈর্ঘ্য 5 সেমি এবং প্রস্থ 3.5 সেমি হয়, তবে তার উচ্চতা

= \(\frac{আয়তন}{দৈর্ঘ্য \times প্রস্থ}\)

= \(\frac{26.25}{5 \times 3.5}\)

= 1.5 সেমি.

---

17. 2.1 মিটার দীর্ঘ, 1.5 মিটার প্রশস্ত একটি আয়তঘনাকার চৌবাচ্চার অর্ধেক জলপূর্ণ আছে। ওই চৌবাচ্চায় আরও 630 লিটার জল ঢাললে জলের গভীরতা কতটা বৃদ্ধি পাবে হিসাব করে লিখি।

সমাধানঃ-

চৌবাচ্চার,

দৈর্ঘ্য	= 2.1 মিটার = 21 ডেসিমি.
প্রস্থ	= 1.5 মিটার = 15 ডেসিমি.

ধরি, ওই চৌবাচ্চায় আরও 630 লিটার জল ঢাললে জলের গভীরতা \(x\) মিটার. বৃদ্ধি পাবে।

সুতরাং,

চৌবাচ্চায় \(x\) মিটারে জলের পরিমাণ = 630 লিটার

বা, 21 × 15 × \(x\) = 630

বা, \(x = \frac{360}{21\times15}\)

বা,\( x = 2 \)

• চৌবাচ্চায় আরও 630 লিটার জল ঢাললে জলের গভীরতা 2 ডেসিমি. বৃদ্ধি পাবে।

---

18. গ্রামের আয়তক্ষেত্রাকার মাঠের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 20 মিটার এবং 15 মিটার। ওই মাঠের ভিতরে চারটি কোণে পিলার বসানোর জন্য 4 মিটার দৈর্ঘ্যবিশিষ্ট চারটি ঘনকাকৃতি গর্ত কেটে অপসারিত মাটি অবশিষ্ট জমির উপর ছড়িয়ে দেওয়া হলো। মাঠের তলের উচ্চতা কতটা বৃদ্ধি পেল হিসাব করে লিখি ।

সমাধানঃ-

ধরি, মাঠের তলের উচ্চতা a মিটার. বৃদ্ধি পেল ।

এখন 4 টি ঘনকাকৃতি গর্ত কেটে অপসারিত মাটির আয়তন

= 4 × 4³

= 4×64

= 256 ঘন মিটার.

আবার 4 টি গর্ত কাটার পর বাকি মাঠের ক্ষেত্রফল

= আয়তক্ষেত্রাকার মাঠের ক্ষেত্রফল – 4 × একটি গর্তের ক্ষেত্রফল

= 20 × 15 – 4 × 4²

= 300 – 64

= 236 বর্গ মিটার.

অতএব মাঠের তলের উচ্চতা বৃদ্ধি পাবে

= \(\frac{256}{236}\)

= \(1\frac{5}{59}\) মিটার.

---

19. 48 মিটার লম্বা এবং 31.5 মিটার চওড়া একখণ্ড নীচু জমিকে 6.5 ডেসিমি. উঁচু করার জন্য ঠিক করা হয়েছে পাশের 27 মিটার লম্বা এবং 18.2 মিটার চওড়া একটি জমি গর্ত করে মাটি তোলা হবে। গর্তটি কত মিটার গভীর করতে হবে হিসাব করে লিখি।

সমাধানঃ-

48 মিটার লম্বা এবং 31.5 মিটার চওড়া একখণ্ড নীচু জমিকে 6.5 ডেসিমি. উঁচু করার জন্য মাটি লাগবে

= 48 × 31.5 × .65

= 982.8 ঘন মিটার.

পাশের জমিতে গর্ত করতে হবে a মিটার।

শর্তে,

27 × 18.2 × a = 982.8

বা, a = \(\frac{982.8}{27\times 18.2}\)

বা, a = 2

• গর্তটি 2 মিটার গভীর করতে হবে।

---

20. বাড়ির তিনটি কেরোসিন তেলের ড্রামে যথাক্রমে 800 লিটার, 725 লিটার এবং 575 লিটার তেল ছিল। ওই তিনটি ড্রামের তেল একটি আয়তঘনাকার পাত্রে ঢালা হলো এবং এতে পাত্রে তেলের গভীরতা 7 ডেসিমি. হলো। ওই আয়তঘনাকার পাত্রের দৈর্ঘ্য ও প্রস্থের অনুপাত 4 : 3 হলে, পাত্রের দৈর্ঘ্য ও প্রস্থ হিসাব করে লিখি। যদি ওই আয়তঘনাকার পাত্রের গভীরতা 5 ডেসিমিটার হতো, তবে 1620 লিটার তেল ওই পাত্রে রাখা যেত কিনা হিসাব করে দেখি।

সমাধানঃ-

ধরি, আয়তঘনাকার পাত্রের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 4a ডেসিমি. ও 3a ডেসিমি.

শর্তে,

4a × 3a × 7 = 800 + 725 + 575

বা, 84a2 = 2100

বা, a2 = 25

বা, a = 5

∴ আয়তঘনাকার পাত্রের

• দৈর্ঘ্য = 4×5 = 20 ডেসিমি.
• প্রস্থ = 3×5 = 15 ডেসিমি.

---

21. আমাদের তিনতলা ফ্ল্যাটের তিনটি পরিবারের দৈনিক জলের চাহিদা যথাক্রমে 1200 লিটার, 1050 লিটার এবং 950 লিটার। এই চাহিদা মেটানোর পরও চাহিদার 25% জল মজুত থাকে এমন একটি ট্যাঙ্ক বসানোর জন্য মাত্র 2.5 মি. দীর্ঘ এবং 1.6 মিটার চওড়া একটি জায়গা পাওয়া গেছে। ট্যাঙ্কটি কত মিটার গভীর করতে হবে হিসাব করে লিখি। জায়গাটি যদি প্রস্থের দিকে আরও 4 ডেসিমি. বেশি হতো, তবে ট্যাঙ্কটি কতটা গভীর করতে হতো তা হিসাব করে লিখি।

সমাধানঃ-

তিনটি পরিবারের দৈনিক মোট জলের চাহিদা

= 1200 + 1050 + 950

= 3200 লিটার

মোট চাহিদার 25%

= 3200×\(\frac{25}{100}\)

= 32 × 25

= 800 লিটার.

মোট জলের চাহিদা মেটানোর পরও চাহিদার 25% জল মজুত থাকে এমন একটি ট্যাঙ্ক এ জল থাকতে হবে

= 3200 + 800

= 4000 লিটার .

ধরি, ট্যাঙ্কটি a ডেসিমিটার গভীর করতে হবে।

শর্তে,

25 × 16 × a = 4000

বা, a = \(\frac{4000}{25\times 16}\)

বা, a = 10

• ট্যাঙ্কটি 1 মিটার গভীর করতে হবে।

আবার, জায়গাটি যদি প্রস্থের দিকে আরও 4 ডেসিমি. বেশি হতো সেক্ষেত্রে দৈর্ঘ্য একই থেকে প্রস্থ হতো 16 + 4 = 20 ডেসিমি.

সেক্ষেত্রে,

25 × 20 × a = 4000

বা, a = 8

দ্বিতীয়ক্ষেত্রে ট্যাঙ্কটির গভীরতা হবে 8 ডেসিমি.

---

22. 5 সেমি. পুরু কাঠের তক্তায় তৈরি ঢাকনাসহ একটি কাঠের বাক্সের ওজন 115.5 কিগ্রা.। কিন্তু চাল ভর্তি বাক্সটির ওজন 880.5 কিগ্রা.। বাক্সটির ভিতরের দিকের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 12 ডেসিমি. এবং 8.5 ডেসিমি. এবং এক ঘন ডেসিমি, চালের ওজন 1.5 কিগ্রা.। বাক্সটির ভিতরের উচ্চতা কত হিসাব করে লিখি। প্রতি বর্গ ডেসিমি. 1.50 টাকা হিসাবে বাক্সটির বাইরের চারিপাশ রং করতে কত খরচ পড়বে হিসাব করে লিখি।

সমাধানঃ-

বাক্সটিতে যা চাল ধরবে সেই চালের ওজন

= 880.5 – 115.5

= 765 কিগ্রা.

এখন

1.5 কিগ্রা. চাল = 1 ঘন ডেসিমি চাল

765 কিগ্রা. চাল = \(\frac{765}{1.5}\) = 510 ঘন ডেসিমি চাল

ধরি, বাক্সটির উচ্চতা = a ডেসিমি.

শর্তে,

12 × 8.5 × a = 510

বা, a = \(\frac{510}{12\times 8.5}\)

বা, a = 5

অতএব, বাক্সটির উচ্চতা = 5 ডেসিমি.

এখন বাক্সটির বাইরের দিকের

দৈর্ঘ্য	12 + 2×.5 = 13 ডেসিমি.
প্রস্থ	8.5 + 2×.5 = 9.5 ডেসিমি.
উচ্চতা	5 + 2×.5 = 6 ডেসিমি.

বাক্সটির বাইরের সমগ্রতলের ক্ষেত্রফল

= 2 (13 × 9.5 + 9.5 × 6 + 6 × 13)

= 2(123.5 + 57 + 78)

= 2 × 258.5

= 517 বর্গ ডেসিমি.

517 বর্গ ডেসিমি. এ প্রতি বর্গ ডেসিমি. 1.50 টাকা হিসাবে বাক্সটির বাইরের চারিপাশ রং করতে খরচ

= 517 × 1.50

= 775.5 টাকা

---

23. 20 মি. দীর্ঘ এবং 18.5 মি. চওড়া একটি আয়তঘনাকার পুকুরে 3.2 মি. গভীর জল আছে। ঘণ্টায় 160 কিলোলিটার জলসেচ করতে পারে এমন একটি পাম্প দিয়ে কতক্ষণে পুকুরটির সমস্ত জলসেচ করা যাবে হিসাব করে লিখি। ওই জল যদি 59.2 মিটার দীর্ঘ এবং 40 মিটার চওড়া একটি আল দেওয়া ধান ক্ষেতে ফেলা হয়, তবে সেই জমিতে জলের গভীরতা কত হবে হিসাব করে লিখি। [1 ঘন মিটার = 1 কিলোলিটার]

সমাধানঃ-

পুকুরে জল আছে

= 20 × 18.5 × 3.2

= 1184 ঘন মিটার.

এখন

160 ঘন মিটার জল সেচ করতে সময় লাগে 1 ঘণ্টা

1184 ঘন মিটার জল সেচ করতে সময় লাগবে

= \(\frac{1184}{160}\)

= 7.4 ঘণ্টা

= 7 ঘণ্টা 24 মিনিট.

আবার এই 1184 ঘন মিটার জল পাশের জমিতে দিলে সেই জমির গভীরতা হবে

= \(\frac{1184}{59.2\times40}\)

= 0.5 মিটার.

---

24. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন :

(A) বহুবিকল্পীয় প্রশ্ন ( M.C.Q.) :

(i) একটি সমকোণী চৌপলাকৃতি বাক্সের ভিতরের আয়তন 440 ঘন সেমি. এবং ভিতরের ভূমিতলের ক্ষেত্রফল 88 বর্গ সেমি.। বাক্সটির ভিতরের উচ্চতা

উত্তরঃ- (b) 5 সেমি

সমাধানঃ-

বাক্সটির উচ্চতা

= \(\frac{{বাক্সের ভেতরের আয়তন}}{{বাক্সের মেঝের ক্ষেত্রফল}}\)

= \(\frac{440}{88}\)

= 5 সেমি.

---

(ii) একটি আয়তঘনাকার গর্তের দৈর্ঘ্য 40 মি., প্রস্থ 12 মি. এবং গভীরতা 16 মি.। ওই গর্তের মধ্যে 5. মি. দৈর্ঘ্য, 4 মি. প্রস্থ এবং 2 মি. পুরু তক্তা রাখা যাবে

উত্তরঃ- (b) 192 টি

সমাধানঃ-

ওই গর্তে তক্তা রাখা যাবে

= \(\frac{{গর্তের আয়তন}}{একটি তক্তার আয়তন}\)

= \(\frac{40\tmes 12 \tims 16}{5\times 4\times 2}\)

= 192 টি.

---

(iii) একটি ঘনকের পার্শ্বতলের ক্ষেত্রফল 256 বর্গ মিটার। ঘনকটির আয়তন

উত্তরঃ- (d) 512 ঘন মি

সমাধানঃ-

ধরি, ঘনকের একটি ধারের দৈর্ঘ্য = a মিটার.

অতএব,

6a² = 256

বা, a² = 64

বা, a = 8

সুতরাং, ঘনকের আয়তন

= 8 × 8 × 8

= 512 ঘন মিটার.

---

(iv) দুটি ঘনকের আয়তনের অনুপাত 1: 27 হলে, ঘনক দুটির সমগ্র তলের ক্ষেত্রফলের অনুপাত

উত্তরঃ- (c) 1:9

সমাধানঃ-

ধরি, দুটি ঘনকের একটি ধারের দৈর্ঘ্য যথাক্রমে a ও b একক।

দুটি ঘনকের আয়তনের অনুপাত = 1 : 27

বা, a3 : b3 = 1 : 27

বা, a : b = 1 : 3

বা, a2 : b2 = 1 : 9

এখন সমগ্র তলের ক্ষেত্রফলের অনুপাত

= 6a² : 6b²

= a² : b²

= 1 : 9

---

(v) একটি ঘনকের সমগ্রতলের ক্ষেত্রফল s বর্গ একক এবং কর্ণের দৈর্ঘ্য d একক হলে s এবং d-এর সম্পর্ক

উত্তরঃ- (d) d² = \(\frac{S}{2}\)

সমাধানঃ-

ধরি ঘনকের প্রতিটি ধারের দৈর্ঘ্য = a একক.

ঘনকের
সমগ্রতলের ক্ষেত্রফল	s = 6a2
কর্ণের দৈর্ঘ্য	d = a√3

d2

= 3a2

= 3 × \(\frac{s}{6}\)

= \(\frac{s}{2}\)

---

(B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি :

(i) একটি ঘনকের প্রতিটি ধারের দৈর্ঘ্য দ্বিগুণ হলে, ঘনকটির আয়তন প্রথম ঘনকের 4 গুণ হবে।

উত্তরঃ- মিথ্যা

(ii) বর্ষার সময় 2 হেক্টর জমিতে বৃষ্টিপাত 5 সেমি উচ্চতার হলে, বৃষ্টির জলের আয়তন 1000 ঘন মিটার।

উত্তরঃ- সত্য

[উত্তর সংকেত : 1 আর = 100 বর্গ মি., 1 হেক্টর = 100 আর]

(c) শূন্যস্থান পূরণ করি :

(i) একটি সমকোণী চৌপলের কর্ণের সংখ্যা

উত্তরঃ- 4 টি.

(ii) একটি ঘনকের একটি তলের কর্ণের দৈর্ঘ্য = …….. × একটি ধারের দৈর্ঘ্য।

উত্তরঃ- √2

(iii) সমকোণী চৌপলের দৈর্ঘ্য, প্রস্থ ও উচ্চতা সমান হলে সেই ঘনবস্তুর বিশেষ নাম,

উত্তরঃ- ঘনক

---

25. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) :

(i) একটি আয়তঘনের তল সংখ্যা = x, ধার সংখ্যা = y, শীর্ষবিন্দুর সংখ্যা = z এবং কর্ণের সংখ্যা = p হলে, x – y + z+ p-এর মান কত তা লিখি ।

সমাধানঃ-

একটি আয়তঘন এর

তল সংখ্যা	x = 6
ধার সংখ্যা	y = 12
শীর্ষবিন্দুর সংখ্যা	z = 8
কর্ণের সংখ্যা	p = 4

x – y + z + p

= 6 – 12 + 8 + 4

= 6

---

(ii) দুটি আয়তঘনের মাত্রাগুলির দৈর্ঘ্য যথাক্রমে 4, 6, 4 একক এবং 8, ( 2h – 1), 2 একক। যদি আয়তঘন দুটির ঘনফল সমান হয়, তাহলে h-এর মান কত তা লিখি।

সমাধানঃ-

দুটি আয়তঘন এর ঘনফল সমান, অর্থাৎ

8 × (2h – 1) × 2 = 4 × 6 × 4

বা, 2h – 1 = 6

বা, 2h = 7

বা, h = 3.5

---

(ii) একটি ঘনকের প্রত্যেকটি ধারের দৈর্ঘ্য 50% বৃদ্ধি পেলে, ঘনকটির সমগ্রতলের ক্ষেত্রফল শতকরা কত বৃদ্ধি হবে তা হিসাব করে লিখি।

সমাধানঃ-

ধরি, ঘনকের ধারের দৈর্ঘ্য = a মিটার.

ঘনকের প্রত্যেকটি ধারের দৈর্ঘ্য 50% বৃদ্ধি পেলে ঘনকের প্রতিটি ধারের দৈর্ঘ্য হয়

= a + \(\frac{a}{2}\)

= \(\frac{3a}{2}\)

ঘনকের সমগ্রতলের ক্ষেত্রফল
বৃদ্ধি করার আগে	6a2 বর্গ মিটার.
বৃদ্ধি করার পরে	6\((\frac{3a}{2})^2\) = \(\frac{27a^2}{2}\) ঘন মিটার.
আয়তন বৃদ্ধি হয়েছে	\(\frac{27a^2}{2} – 6a^2\) = \(\frac{15a^2}{2}\)

শতকরা আয়তন বৃদ্ধি হয়েছে

= \(\frac{\frac{15a^2}{2}}{6a^2}\) × 100

= 125

---

(iv) তিনটি নিরেট ঘনক যাদের প্রত্যেকটি ধারের দৈর্ঘ্য যথাক্রমে 3 সেমি, 4 সেমি. এবং 5 সেমি.। ঘনক তিনটিকে গলিয়ে একটি নতুন নিরেট ঘনক তৈরি করা হলো। নতুন ঘনকটির একটি ধারের দৈর্ঘ্য কত হবে তা লিখি।

সমাধানঃ-

তিনটি নিরেত ঘনকের আয়তনের যোগফল

= \( 3^3 + 4^3 + 5^3\)

= 27 + 64 + 125

= 216

= \(6^3\)

অতএব, নতুন ঘনকটির একটি ধারের দৈর্ঘ্য হবে 6 সেমি.

---

(v) একটি ঘরের দুটি সংলগ্ন দেয়ালের দৈর্ঘ্য যথাক্রমে 12 মি. এবং 8 মি.। ঘরটির উচ্চতা 4 মি. হলে, ঘরটির মেঝের ক্ষেত্রফল কত তা হিসাব করে লিখি।

সমাধানঃ-

ঘরের দুটি সংলগ্ন দেয়ালের দৈর্ঘ্য যথাক্রমে 12 মি. এবং 8 মি. ।

সুতরাং, মেঝের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 12 মি. এবং 8 মি.

মেঝের ক্ষেত্রফল

= 12 × 8

= 96 বর্গ মিটার.

---

Class 10 WBBSE এর বাকি অধ্যায়ের সমাধান-

অধ্যায়	সমাধান
1. একচলবিশিষ্ট দ্বিঘাত সমীকরণ (Quadratic Equations with one variable)	কষে দেখি 1.1
	কষে দেখি 1.2
	কষে দেখি 1.3
	কষে দেখি 1.4
	কষে দেখি 1.5
2. সরল সুদকষা (Simple Interest)	কষে দেখি 2
3. বৃত্ত সম্পর্কিত উপপাদ্য (Theorems related to circle)	কষে দেখি 3.1
	কষে দেখি 3.2
4. আয়তঘন (Rectangular Parallelopiped or Cuboid)	কষে দেখি 4
5. অনুপাত ও সমানুপাত ( Ratio and Proportion)	কষে দেখি 5.1
	কষে দেখি 5.2
	কষে দেখি 5.3
6. চক্রবৃদ্ধি সুদ ও সমহার বৃদ্ধি বা হ্রাস (Compound Interest and Uniform Rate of Increase or Decrease)	কষে দেখি 6.1
	কষে দেখি 6.2
7. বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য (Theorems related to Angles in a Circle)	কষে দেখি 7.1
	কষে দেখি 7.2
	কষে দেখি 7.3
8. লম্ব বৃত্তাকার চোঙ (Right Circular Cylinder)	কষে দেখি 8
9. দ্বিঘাত করণী (Quadratic Surd).	কষে দেখি 9.1
	কষে দেখি 9.2
	কষে দেখি 9.3
10. বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য (Theorems related to Cyclic Quadrilateral)	কষে দেখি 10
11. সম্পাদ্য : ত্রিভুজের পরিবৃত্ত ও অন্তবৃত্ত অঙ্কন	কষে দেখি 11
12. গোলক (Sphere)	কষে দেখি 12
13. ভেদ (Variation)	কষে দেখি 13
14. অংশীদারি কারবার (Partnership Business)	কষে দেখি 14
15. বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য (Theorems related to Tangent to a Circle)	কষে দেখি 15.1
	কষে দেখি 15.2
16. লম্ব বৃত্তাকার শঙ্কু (Right Circular Cone)	কষে দেখি 16
17. সম্পাদ্য : বৃত্তের স্পর্শক অঙ্কন (Construction: Construction of Tangent to a circle)	কষে দেখি 17
18. সদৃশতা (Similarity)	কষে দেখি 18.1
	কষে দেখি 18.2
	কষে দেখি 18.3
	কষে দেখি 18.4
19. বিভিন্ন ঘনবস্তু সংক্রান্ত বাস্তব সমস্যা (Real life Problems related to different Solid Objects)	কষে দেখি 19
20. ত্রিকোণমিতি : কোণ পরিমাপের ধারণা (Trigonometry: Concept of Measurment of Angle)	কষে দেখি 20
21. সম্পাদ্য : মধ্যসমানুপাতী নির্ণয় (Construction: Determination of Mean Proportional)	কষে দেখি 21
22. পিথাগোরাসের উপপাদ্য (Pythagoras Theorem)	কষে দেখি 22
23. ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি (Trigonometric Ratios and Trigonometric Identities)	কষে দেখি 23.1
	কষে দেখি 23.2
	কষে দেখি 23.3
24. পূরক কোণের ত্রিকোণমিতিক অনুপাত (Trigonometric Ratios of Complementrary angle)	কষে দেখি 24
25. ত্রিকোণমিতিক অনুপাতের প্রয়োগ : উচ্চতা ও দূরত্ব (Application of Trigonometric Ratios : Heights & Distances)	কষে দেখি 25
26. রাশিবিজ্ঞান : গড়, মধ্যমা, ওজাইভ, সংখ্যাগুরুমান (Statistics: Mean, Median, Ogive, Mode)	কষে দেখি 26.1
	কষে দেখি 26.2
	কষে দেখি 26.3
	কষে দেখি 26.4

Request For Share
সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together…………. [Sassy_Social_Share]

---

এই কষে দেখি 4 Class 10|Koshe Dekhi 4 Class 10 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।

---

এখানে তোমরা তোমাদের দশম শ্রেণীতে| Class 10 এ কি কি পড়ানো হয়, মানে তোমাদের দশম শ্রেণীতে| Class 10 সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

---