শ্রেণী- দশম ; অধ্যায় – ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি ; কষে দেখি 23.3
কষে দেখি 23.3 Class 10 অংকের সূচিপত্র:-
কষে দেখি 23.3 Class 10 এর অংকের সমাধান গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ
এই কষে দেখি 23.3, পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদ | WBBSE এর অন্তর্গত দশম শ্রেণি|Class 10 এর 23 নম্বর অধ্যায়|Chapter 23, ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি | Trigonometric Ratio and Trigometric Identities এর তৃতীয় অনুশীলনী।
এই কষে দেখি 23.3 Class 10 এর অঙ্ক গুলি বোঝার জন্যে যে যে বিষয় জানতে হবে তা আলোচনা করা হলো–
এই অঙ্কগুলি সমাধান করার জন্যে আমাদের কিছু সূত্র জানতে হবে যেগুলি হলো –
কোনো সমকোণী ত্রিভুজের \(\theta\) সূক্ষ্মকোণের জন্যে-
| (i) | \(\sin^2 \theta + \cos^2 \theta = 1\) |
| (ii) | \(\sec^2 \theta – \tan^2 \theta = 1\) |
| (iii) | \(\csc^2 \theta – \cot^2 \theta = 1\) |
- এখানে \(\csc\) মানে আমরা cosec ফাংশান কে বুঝবো ।
আগামিতে এই কষে দেখি 23.3 Class 10 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| কষে দেখি 23.3 Class 10 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 23.3 Class 10 তারপর  |
কষে দেখি 23.3 Class 10|Koshe Dekhi 23.3 Class 10

1.
(i) \(\sin \theta = \frac{4}{5}\) হলে, \(\frac{\csc \theta}{1 + \cot \theta}\)-এর মান নির্ণয় করে লিখি।
সমাধানঃ-
| \(\frac{\csc \theta}{1 + \cot \theta}\) |
| \(= \frac{\frac{1}{\sin \theta}}{1 + \frac{\cos \theta}{\sin \theta}}\) |
| \(= \frac{1}{\sin \theta + \cos \theta}\) |
| \(= \frac{1}{\sin \theta + \sqrt{1 – \sin^2 \theta}}\) \([∵ \sin^2 \theta + \cos^2 \theta = 1]\) |
| \(= \frac{1}{\frac{4}{5} + \sqrt{1-(\frac{4}{5})^2}}\) |
| \(= \frac{1}{\frac{4}{5} + \sqrt{1-\frac{16}{25}}}\) |
| \(= \frac{1}{\frac{4}{5} + \sqrt{\frac{9}{25}}}\) |
| \(= \frac{1}{\frac{4}{5} + \frac{3}{5}}\) |
| \(= \frac{1}{\frac{7}{5}}\) |
| \(= \frac{5}{7}\) |
(ii) যদি \(\tan\theta = \frac{3}{4}\) হয়, তবে দেখাই যে \(\sqrt{\frac{1 – \sin \theta}{1 + \sin \theta}} = \frac{1}{2}\)
সমাধানঃ-
| \(\tan\theta = \frac{3}{4}\) |
| বা, \(\tan^2 \theta = \frac{9}{16}\) |
| বা, \(1 + \tan^2 \theta = 1 + \frac{9}{16}\) |
| বা, \(\sec^2 \theta = \frac{25}{16} [∵ \sec^2 \theta – \tan^2 \theta = 1]\) |
| বা, \(\frac{1}{\cos^2 \theta} = \frac{25}{16}\) |
| বা, \(\cos^2 \theta = \frac{16}{25}\) |
| বা, \(1 – \cos^2 \theta = 1 – \frac{16}{25}\) |
| বা, \(\sin^2 \theta = \frac{9}{25} [∵ \sin^2 \theta + \cos^2 \theta = 1]\) |
| বা, \(\sin \theta = \frac{3}{5}\) |
| বা, \(\frac{1}{\sin \theta} = \frac{5}{3}\) |
| বা, \(\frac{1 – \sin \theta}{1 + \sin \theta} = \frac{5 – 3}{5 + 3}\) |
| বা, \(\frac{1 – \sin \theta}{1 + \sin \theta} = \frac{2}{8}\) |
| বা, \(\frac{1 – \sin \theta}{1 + \sin \theta} = \frac{1}{4}\) |
| বা, \(\sqrt{\frac{1 – \sin \theta}{1 + \sin \theta}} = \sqrt{\frac{1}{4}}\) |
| বা, \(\sqrt{\frac{1 – \sin \theta}{1 + \sin \theta}} = \frac{1}{2}\) |
(iii) \(\tan \theta = 1\) হলে, \(\frac{8\sin \theta + 5\cos \theta}{\sin^3 \theta – 2\cos^3 \theta + 7\cos \theta}\) -এর মান নির্ণয় করি।
সমাধানঃ-
| \(\tan \theta = 1\) |
| বা, \(\frac{\sin \theta}{\cos \theta} = 1\) |
| বা, \(\sin \theta = \cos \theta\) |
অতএব, \(\sin^2 \theta + \cos^2 \theta = 1\) থেকে পাই,
| \(\sin^2 \theta + \sin^2 \theta = 1\) |
| বা, \(2\sin^2 \theta = 1\) |
| বা, \(\sin \theta = \frac{1}{\sqrt2} = \cos \theta\) ——–(i) |
সুতরাং,
| \(\frac{8\sin \theta + 5\cos \theta}{\sin^3 \theta – 2\cos^3 \theta + 7\cos \theta}\) |
| \(= \frac{8 \times \frac{1}{\sqrt2} + 5 \times \frac{1}{\sqrt2}}{(\frac{1}{\sqrt2})^3 – 2(\frac{1}{\sqrt2})^3 + 7 \times \frac{1}{\sqrt2} }\) [(i) নং থেকে মান বসিয়ে পাই] |
| \(= \frac{\frac{8+5}{\sqrt2}}{\frac{1}{2\sqrt2} – \frac{2}{2\sqrt2} + \frac{7}{\sqrt2} }\) |
| \(= \frac{\frac{13}{\sqrt2}}{\frac{1-2+14}{2\sqrt2}}\) |
| \(= \frac{\frac{13}{\sqrt2}}{\frac{13}{2\sqrt2}}\) |
| \(= 2\) |
2.
(i) \(\csc \theta\) এবং \(\tan \theta\) -কে \(\sin \theta\) -এর মাধ্যমে প্রকাশ করি।
সমাধানঃ-
- \(\csc \theta = \frac{1}{\sin \theta}\)
এবং
| \(\tan \theta\) |
|---|
| \(= \frac{\sin \theta}{\cos \theta}\) |
| \(= \frac{\sin \theta}{\sqrt{1 – \sin^2 \theta}}\) \([∵ \sin^2 \theta – \cos^2 \theta = 1]\) |
(ii) \(\csc \theta \) এবং \(\tan \theta \) -কে \(\cos \theta\) -এর মাধ্যমে লিখি।
সমাধানঃ-
| \(\csc \theta \) |
|---|
| \(= \frac{1}{\sin \theta}\) |
| \(= \frac{1}{\sqrt{1 – \cos^2 \theta}}\) \([∵ \sin^2 \theta – \cos^2 \theta = 1]\) |
| \(\tan \theta\) |
|---|
| \(= \frac{\sin \theta}{\cos \theta}\) |
| \(= \frac{\sqrt{1 – \cos^2 \theta}}{\cos \theta}\) |
3.
(i) \(\sec\theta + \tan\theta = 2\) হলে, \(\sec\theta – \tan\theta\)-এর মান নির্ণয় করি।
সমাধানঃ-
আমরা জানি,
| \(\sec^2 \theta – \tan^2 \theta = 1\) |
| বা, \((\sec \theta + \tan \theta)(\sec \theta – \tan \theta) = 1\) |
| বা, \(2 \times (\sec \theta – \tan \theta) = 1\) |
| বা, \((\sec \theta – \tan \theta) = \frac{1}{2}\) |
(ii) \(\csc \theta – \cot \theta = \sqrt2 – 1\) হলে, \(\csc\theta+ \cot \theta\)-এর মান হিসাব করে লিখি।
সমাধানঃ-
আমরা জানি,
| \(\csc^2 \theta – \cot^2 \theta = 1\) |
| বা, \((\csc \theta + \cot \theta)(\csc \theta – \cot \theta) = 1\) |
| বা, \((\sec \theta + \tan \theta) \times (\sqrt2 – 1) = 1\) |
| বা, \((\csc \theta + \cot \theta) = \frac{1}{\sqrt2 – 1}\) |
| বা, \((\csc \theta + \cot \theta) = \frac{\sqrt2 + 1}{2 – 1}\) |
| বা, \((\csc \theta + \cot \theta) = \sqrt2 + 1\) |
(iii) \(\sin \theta + \cos\theta = 1\) হলে, \(\sin \theta \times \cos \theta\) -এর মান নির্ণয় করি।
সমাধানঃ-
আমরা জানি,
| \(\sin^2 \theta + \cos^2 \theta = 1\) |
| বা, \((\sin \theta + \cos \theta)^2 – 2\sin \theta \cos \theta = 1\) |
| বা, \(1^2 – 2\sin \theta \cos \theta = 1\) |
| বা, \(1 – 2\sin \theta \cos \theta = 1\) |
| বা, \(2\sin \theta \cos \theta = 0\) |
| বা, \(\sin \theta \cos \theta = 0\) |
(iv) \(\tan \theta + \cot \theta = 2\) হলে, \((\tan \theta – \cot \theta)\)-এর মান নির্ণয় করি।
সমাধানঃ-
| \((\tan \theta – \cot \theta)^2\) |
| \(= (\tan \theta + \cot \theta)^2 – 4 \tan \theta \cot \theta\) |
| \(= 2^2 – 4 \times 1\) |
| \(= 0 \) |
অতএব,
\((\tan \theta – \cot \theta)^2 = 0\)
বা, \((\tan \theta – \cot \theta) = 0\)
(v) \(\sin \theta – \cos \theta = \frac{7}{13}\) হলে, \(\sin\theta + \cos\theta\) -এর মান নির্ণয় করি।
সমাধানঃ-
| \(\sin \theta – \cos \theta = \frac{7}{13}\) |
| বা, \((\sin \theta – \cos \theta)^2 = (\frac{7}{13})^2\) |
| বা, \(\sin^2 \theta + \cos^2 \theta – 2\sin \theta \cos \theta = \frac{49}{169}\) |
| বা, \(1 – 2\sin \theta \cos \theta = \frac{49}{169}\) \([∵ \sin^2 \theta – \cos^2 \theta = 1]\) |
| বা, \(2\sin \theta \cos \theta = 1 – \frac{49}{169}\) |
| বা, \(2\sin \theta \cos \theta = \frac{169 – 49}{169}\) |
| বা, \(\sin \theta \cos \theta = \frac{60}{169}\) ——-(i) |
এখন,
| \((\sin\theta + \cos\theta)^2\) |
| \(= (\sin \theta – \cos \theta)^2 + 4\sin \theta \cos \theta\) |
| \(= (\frac{7}{13})^2 + 4 \times \frac{60}{169} \) [(i) নং থেকে মান বসিয়ে পাই] |
| \(= \frac{49}{169} + \frac{240}{169}\) |
| \(= \frac{49 + 240}{169}\) |
| \(= \frac{289}{169}\) |
| সুতরাং, |
| \((\sin\theta + \cos\theta)^2 = \frac{289}{169}\) |
| বা, \(\sin\theta + \cos\theta = \frac{17}{13}\) |
(vi) \(\sin\theta \cos \theta = \frac{1}{2}\) হলে, \(\sin\theta + \cos \theta\) -এর মান হিসাব করে লিখি ।
সমাধানঃ-
| \((\sin \theta + \cos \theta)^2\) |
| \(= \sin^2 \theta + \cos^2 \theta + 2\sin \theta \cos \theta\) \([∵ \sin^2 \theta – \cos^2 \theta = 1]\) |
| \(= 1 + 2 \sin \theta \cos \theta\) |
| \(= 1 + 2 \times \frac{1}{2}\) |
| \(= 1 + 1 = 2\) |
| অতএব, |
| \((\sin \theta + \cos \theta)^2 = 2\) |
| বা, \(\sin \theta + \cos \theta = \sqrt2\) |
(vii) \(\sec\theta – \tan\theta = \frac{1}{\sqrt3}\) হলে, \(\sec\theta\) এবং \(\tan\theta\) উভয়ের মান নির্ণয় করি।
সমাধানঃ-
দেওয়া আছ \(\sec\theta – \tan\theta = \frac{1}{\sqrt3}\) —–(i)
আবার,
| আমরা জানি, |
| \(\sec^2 \theta – \tan^2 \theta = 1\) |
| বা, \((\sec \theta + \tan \theta)(\sec \theta – \tan \theta) = 1\) |
| বা, \((\sec \theta + \tan \theta) \times \frac{1}{\sqrt3} = 1\) |
| বা, \((\sec \theta + \tan \theta) = \sqrt3\) ——–(ii) |
(i) ও (ii) যোগ করে পাই,
| \(\sec \theta – \tan \theta + \sec \theta + \tan \theta = \frac{1}{\sqrt3} + \sqrt3\) |
| বা, \(2\sec \theta = \frac{1 + 3}{\sqrt3}\) |
| বা, \(\sec \theta = \frac{2}{\sqrt3}\) |
\(\sec \theta = \frac{2}{\sqrt3}\) , (i) নং এ বসিয়ে পাই,
| \(\frac{2}{\sqrt3} – \tan \theta = \frac{1}{\sqrt3}\) |
| বা, \(\tan \theta = \frac{2}{\sqrt3} – \frac{1}{\sqrt3}\) |
| বা, \(\tan \theta = \frac{1}{\sqrt3}\) |
(viii) \(\csc\theta+ \cot\theta = \sqrt3\) হলে, \(\csc\theta\) এবং \(\cot\theta\) উভয়ের মান নির্ণয় করি।
সমাধানঃ-
দেওয়া আছ \(\csc\theta + \cot\theta = \sqrt3\) —–(i)
আবার,
| আমরা জানি, |
| \(\csc^2 \theta – \cot^2 \theta = 1\) |
| বা, \((\csc \theta – \cot \theta)(\csc \theta + \cot \theta) = 1\) |
| বা, \((\csc \theta – \cot \theta) \times \sqrt3 = 1\) |
| বা, \((\csc \theta – \cot \theta) = \frac{1}{\sqrt3}\) ——–(ii) |
(i) ও (ii) যোগ করে পাই,
| \(\csc \theta + \cot \theta + \csc \theta – \cot \theta = \sqrt3 + \frac{1}{\sqrt3}\) |
| বা, \(2\csc \theta = \frac{3+1}{\sqrt3}\) |
| বা, \(\csc \theta = \frac{2}{\sqrt3}\) |
\(\csc \theta = \frac{2}{\sqrt3}\) , (i) নং এ বসিয়ে পাই,
| \(\frac{2}{\sqrt3} + \cot \theta = \sqrt3\) |
| বা, \(\cot \theta = \sqrt3 – \frac{2}{\sqrt3} \) |
| বা, \(\cot \theta = \frac{3-2}{\sqrt3}\) |
| বা, \(\cot \theta = \frac{1}{\sqrt3}\) |
(ix) \(\frac{\sin\theta + \cos\theta}{\sin\theta – \cos\theta} = 7\) হলে, \(\tan\theta\)-এর মান হিসাব করে লিখি ।
সমাধানঃ-
| \(\frac{\sin\theta + \cos\theta}{\sin\theta – \cos\theta} = 7\) |
| বা, \(\frac{\sin\theta + \cos\theta + \sin \theta – \cos \theta}{\sin \theta + \cos \theta – \sin\theta + \cos\theta} = \frac{7+1}{7-1}\) [যোগ-ভাগ প্রক্রিয়া থেকে পাই] |
| বা, \(\frac{2\sin\theta}{2\cos\theta} = \frac{8}{6}\) |
| বা, \(\tan \theta = \frac{4}{3}\) |
(x) \(\frac{\csc\theta + \sin\theta}{\csc\theta -\sin\theta} = \frac{5}{2}\) হলে, \(\sin\theta\) -এর মান হিসাব করে লিখি ।
সমাধানঃ-
| \(\frac{\csc\theta + \sin\theta}{\csc\theta – \sin\theta} = \frac{5}{2}\) |
| বা, \(\frac{\csc\theta + \sin\theta + \csc \theta – \sin \theta}{\csc \theta + \sin \theta – \csc\theta + \sin\theta} = \frac{5+2}{5-2}\) [যোগ-ভাগ প্রক্রিয়া থেকে পাই] |
| বা, \(\frac{2\csc\theta}{2\sin\theta} = \frac{7}{3}\) |
| বা, \(\frac{1}{\sin^2 \theta} = \frac{7}{3}\) |
| বা, \(\sin^2 \theta = \frac{3}{7}\) |
| বা, \(\sin \theta = \sqrt{\frac{3}{7}}\) |
(xi) \(\sec\theta + \cos\theta = \frac{5}{2}\) হলে, \(\sec\theta – \cos\theta\) -এর মান হিসাব করে লিখি ।
সমাধানঃ-
| \(\sec\theta + \cos\theta = \frac{5}{2}\) |
| বা, \(\sec\theta + \frac{1}{\sec \theta} = \frac{5}{2}\) |
| বা, \(\frac{\sec^2 \theta + 1}{\sec \theta} = \frac{5}{2}\) |
| বা, \(2\sec^ \theta + 2 = 5\sec \theta\) |
| বা, \(2\sec^ \theta – 5\sec \theta + 2 = 0 \) |
| বা, \((2\sec^2 \theta – 4\sec \theta – \sec \theta + 2) = 0\) |
| বা, \(2\sec \theta (\sec \theta – 2) – (\sec \theta – 2) = 0\) |
| বা, \((2\sec \theta – 1)(\sec \theta – 2) = 0\) |
| অতএব, \(\sec \theta = \frac{1}{2} \) অথবা, \(\sec \theta = 2\) |
এখানে \(\sec \theta = \frac{1}{2}\) হবেনা কারণ \(\cos \theta < 1\)
সুতরাং, \(\sec \theta = 2\) এবং \(\cos \theta = \frac{1}{2}\)
অতএব,
\(\sec \theta – \cos \theta\)
\(= 2 – \frac{1}{2}\)
\(= \frac{3}{2}\)
(xii) \(5\sin^2\theta + 4\cos^2\theta = \frac{9}{2}\) সম্পর্কটি থেকে \(\tan\theta\)-এর মান নির্ণয় করি।
সমাধানঃ-
| \(5\sin^2\theta + 4\cos^2\theta = \frac{9}{2}\) |
| বা, \(10 \sin^2 \theta + 8\cos^2 \theta = 9 \times 1\) |
| বা, \(10 \sin^2 \theta + 8\cos^2 \theta = 9(\sin^2 \theta + \cos^2 \theta)\) \([∵ \sin^2 \theta – \cos^2 \theta = 1]\) |
| বা, \(10 \sin^2 \theta + 8\cos^2 \theta = 9\sin^2 \theta + 9\cos^2 \theta\) |
| বা, \(10 \sin^2 \theta – 9\sin^2 \theta = 9\cos^2 \theta – 8\cos^2 \theta\) |
| বা, \(\sin^2 \theta = \cos^2 \theta\) |
| বা, \(\frac{\sin^2 \theta}{\cos^2 \theta} = 1\) |
| বা, \((\frac{\sin \theta}{\cos\theta})^2 = 1\) |
| বা, \((\tan \theta)^2 = 1\) |
| বা, \(\tan \theta = 1\) |
(xiii) \(\tan^\theta + \cot^2\theta = \frac{10}{3}\) হলে, \(\tan\theta + \cot\theta\) এবং \(\tan\theta – \cot\theta\) -এর মান নির্ণয় করি এবং সেখান থেকে \(\tan\theta\)-এর মান হিসাব করে লিখি।
সমাধানঃ-
| \((\tan \theta + \cot \theta)^2\) |
| \(= \tan^2 \theta + \cot^2 \theta + 2\tan \theta \cot \theta\) |
| \(= \frac{10}{3} + 2 \times 1\) |
| \(= \frac{10 + 6}{3}\) |
| \(= \frac{16}{3}\) |
| অতএব, |
| \(\tan \theta + \cot \theta = \frac{4}{\sqrt3}\) ——(i) |
আবার,
| \((\tan \theta – \cot \theta)^2\) |
| \(= \tan^2 \theta + \cot^2 \theta – 2\tan \theta \cot \theta\) |
| \(= \frac{10}{3} – 2 \times 1\) |
| \(= \frac{10 – 6}{3}\) |
| \(= \frac{4}{3}\) |
| অতএব, |
| \(\tan \theta – \cot \theta = \pm \frac{2}{\sqrt3}\) —–(ii) |
- যখন \(\tan \theta – \cot \theta = \frac{2}{\sqrt3}\)
(i) ও (ii) যোগ করে পাই,
| \(\tan \theta + \cot \theta + \tan \theta – \cot \theta = \frac{4}{\sqrt3} + \frac{2}{\sqrt3}\) |
| বা, \(2\tan \theta = \frac{6}{\sqrt3}\) |
| বা, \(\tan \theta = \frac{3}{\sqrt3}\) |
| বা, \(\tan \theta = \sqrt3\) |
আবার,
- যখন \(\tan \theta – \cot \theta = – \frac{2}{\sqrt3}\)
(i) ও (ii) যোগ করে পাই,
| \(\tan \theta + \cot \theta + \tan \theta – \cot \theta = \frac{4}{\sqrt3} – \frac{2}{\sqrt3}\) |
| বা, \(2\tan \theta = \frac{2}{\sqrt3}\) |
| বা, \(\tan \theta = \frac{1}{\sqrt3}\) |
(xiv) \(\sec^2\theta + \tan^2\theta = \frac{13}{12}\) হলে, \(\sec^4\theta – \tan^4\theta\)-এর মান হিসাব করে লিখি।
সমাধানঃ-
| \(\sec^4\theta – \tan^4\theta\) |
| \(= (\sec^2 \theta + \tan^2 \theta)(\sec^2 \theta – \tan^2 \theta)\) |
| \(= \frac{13}{12} \times 1\) |
| \(= \frac{13}{12} \) |
4.
(i) PQR ত্রিভুজে ∠Q সমকোণ। PR= √5 একক এবং PQ – RQ = 1 একক হলে, \(\cos P – \cos R\) -এর মান নির্ণয় করি।
সমাধানঃ-
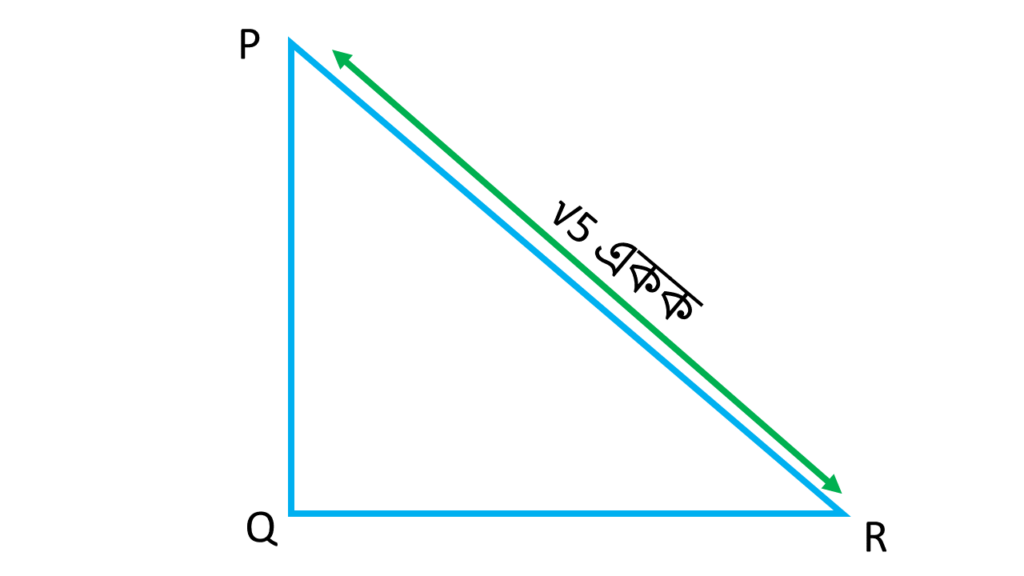
| \(\cos P – \cos R\) |
| \(= \frac{PQ}{PR} – \frac{QR}{PR}\) |
| \(= \frac{PQ – QR}{PR}\) |
| \(= \frac{1}{\sqrt5}\) |
(ii) XYZ ত্রিভুজে ∠Y সমকোণ। XY = 2√3 একক এবং XZ – YZ = 2 একক হলে, \((\sec X – \tan X)\) -এর মান নির্ণয় করি।
সমাধানঃ-
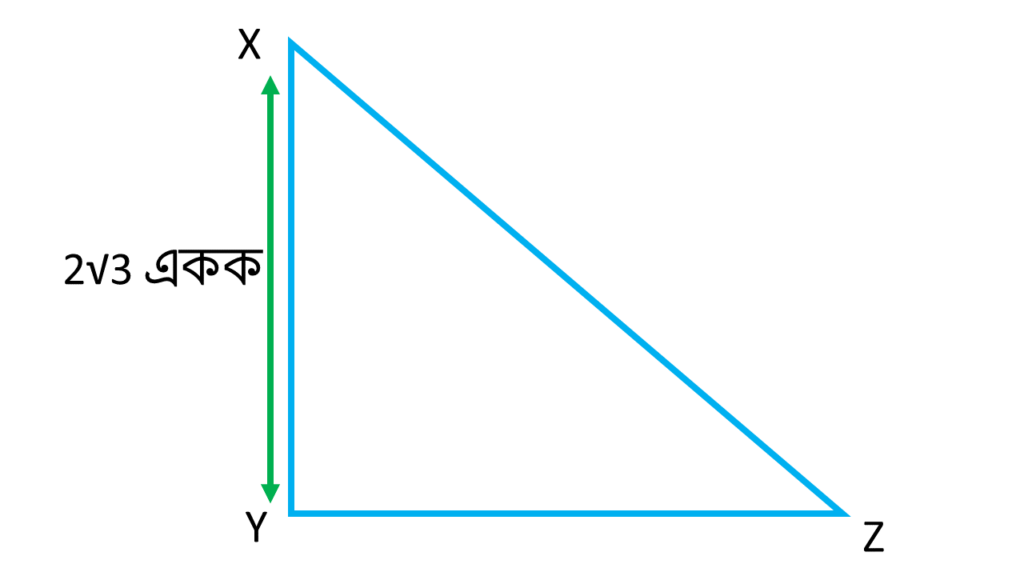
| \((\sec X – \tan X)\) |
| \(= \frac{XZ}{XY} – \frac{YZ}{XY}\) |
| \(= \frac{XZ – YZ}{XY}\) |
| \(= \frac{2}{2\sqrt3}\) |
| \(= \frac{1}{\sqrt3}\) |
5. সম্পর্কগুলি থেকে ‘\(\theta\)’ অপনয়ন করি :
(i) \(x = 2\sin\theta, y = 3\cos\theta\)
সমাধানঃ-
\(x = 2\sin \theta\)
বা, \(\sin \theta = \frac{x}{2}\)
এবং,
\(y = 3\cos\theta\)
বা, \(\cos \theta = \frac{y}{3}\)
| আমরা জানি, |
| \(\sin^2 \theta + \cos^2 \theta = 1\) |
| অতএব, |
| \((\frac{x}{2})^2 + (\frac{y}{3})^2 = 1\) |
| বা, \(\frac{x^2}{4} + \frac{y^2}{9} = 1\) |
(ii) \(5x = 3\sec\theta, y = 3\tan\theta\)
সমাধানঃ-
\(5x = 3\sec \theta\)
বা, \(\sec \theta = \frac{5x}{3}\)
এবং,
\(y = 3\tan\theta\)
বা, \(\tan \theta = \frac{y}{3}\)
| আমরা জানি, |
| \(\sec^2 \theta – \tan^2 \theta = 1\) |
| অতএব, |
| \((\frac{5x}{3})^2 – (\frac{y}{3})^2 = 1\) |
| বা, \(\frac{25x^2}{9} – \frac{y^2}{9} = 1\) |
| বা, \(25x^2 – y^2 = 9\) |
6.
(i) যদি \(\sin\alpha= \frac{5}{13}\) হয়, তাহলে দেখাই যে \(\tan\alpha + \sec\alpha = 1.5\)
সমাধানঃ-
| \(\tan\alpha + \sec\alpha \) |
| \(= \frac{\sin \alpha}{\cos \alpha} + \frac{1}{\cos \alpha}\) |
| \(= \frac{\sin \alpha + 1}{\cos \alpha}\) |
| \(= \frac{\sin \alpha + 1}{\sqrt{1 – \sin^2 \alpha}}\) |
| \(= \frac{\frac{5}{13} + 1}{\sqrt{1-(\frac{5}{13})^2}}\) |
| \(= \frac{\frac{5}{13} + 1}{\sqrt{1-\frac{25}{169}}}\) |
| \(= \frac{\frac{5+13}{13}}{\sqrt{\frac{169 – 25}{169}}}\) |
| \(= \frac{\frac{18}{13}}{\sqrt{\frac{144}{169}}}\) |
| \(= \frac{\frac{18}{13}}{\frac{12}{13}}\) |
| \(= \frac{18}{12}\) |
| \(= \frac{3}{2} = 1.5\) |
(ii) যদি \(\tan A = \frac{n}{m}\) হয়, তাহলে sinA ও secA উভয়ের মান নির্ণয় করি।
সমাধানঃ-
| \(\tan A = \frac{n}{m}\) |
| বা, \(\frac{\sin A}{\cos A} = \frac{n}{m}\) |
| বা, \(\frac{\sin A}{n} = \frac{\cos A}{m} = k\) (ধরি) |
| অতএব, \(\sin A = nk\) এবং \(\cos A = mk\) |
| এখন, \(\sin^2 A + \cos^2 A = 1\) থেকে পাই, |
| \((nk)^2 + (mk)^2 = 1\) |
| বা, \(m^2k^2 + n^2k^2 = 1\) |
| বা, \(k^2 = \frac{1}{m^2 + n^2}\) |
| বা, \(k = \frac{1}{\sqrt{m^2 + n^2}}\) |
অতএব,
| \(\sin A = \frac{n}{\sqrt{m^2 + n^2}}\) |
| এবং |
| \(\cos A = \frac{m}{\sqrt{m^2 + n^2}}\) বা, \(\sec A = \frac{\sqrt{m^2 + n^2}}{m}\) |
(iii) যদি \(\cos\theta = \frac{x}{\sqrt{x^2+y^2}}\) হয়, তাহলে দেখাই যে, \(x\sin\theta = y\cos\theta \)
সমাধানঃ-
| \(x\sin \theta\) |
| \(= x \sqrt{1 – \cos^2 \theta}\) |
| \(= x \sqrt{1 – (\frac{x}{\sqrt{x^2 + y^2}})^2}\) |
| \(= x \sqrt{1 – \frac{x^2}{x^2 + y^2}}\) |
| \(= x \sqrt{ \frac{x^2 + y^2 – x^2}{x^2 + y^2}}\) |
| \(= x \sqrt{ \frac{y^2}{x^2 + y^2}}\) |
| \(= x \times \frac{y}{\sqrt{x^2 + y^2}}\) |
| \(= y \times \frac{x}{\sqrt{x^2 + y^2}}\) |
| \(= y\cos \theta\) |
(iv) যদি \(\sin\alpha = \frac{a^2-b^2}{a^2+b^2}\) হয়, তাহলে দেখাই যে, \(\cot\alpha = \frac{2ab}{a^2 – b^2}\)
সমাধানঃ-
| \(\cot \alpha\) |
| \(= \frac{\cos \alpha}{\sin \alpha}\) |
| \(= \frac{\sqrt{1-\sin^2 \alpha}}{\sin \alpha}\) |
| \(= \frac{\sqrt{1-(\frac{a^2 – b^2}{a^2 + b^2})^2}}{\frac{a^2 – b^2}{a^2 + b^2}}\) |
| \(= \frac{\sqrt{1-\frac{(a^2 – b^2)^2}{(a^2 + b^2)^2}}}{\frac{a^2 – b^2}{a^2 + b^2}}\) |
| \(= \frac{\sqrt{\frac{(a^2+b^2)^2 – (a^2 – b^2)^2}{(a^2 + b^2)^2}}}{\frac{a^2 – b^2}{a^2 + b^2}}\) |
| \(= \frac{\sqrt{\frac{4a^2b^2}{(a^2 + b^2)^2}}}{\frac{a^2 – b^2}{a^2 + b^2}}\) |
| \(= \frac{\frac{2ab}{a^2 + b^2}}{\frac{a^2 – b^2}{a^2 + b^2}}\) |
| \(= \frac{2ab}{a^2 – b^2}\) |
(v) যদি \(\frac{\sin\theta}{x}= \frac{\cos\theta}{y}\) হয়, তাহলে দেখাই যে, \(\sin\theta – \cos\theta = \frac{x-y}{\sqrt{x^2+y^2}}\)
সমাধানঃ-
| বা, \(\frac{\sin \theta}{x} = \frac{\cos \theta}{y} = k\) (ধরি) |
| অতএব, \(\sin \theta = xk\) এবং \(\cos \theta = yk\) |
| এখন, \(\sin^2 \theta + \cos^2 \theta = 1\) থেকে পাই, |
| \((xk)^2 + (yk)^2 = 1\) |
| বা, \(x^2k^2 + y^2k^2 = 1\) |
| বা, \(k^2 = \frac{1}{x^2 + y^2}\) |
| বা, \(k = \frac{1}{\sqrt{x^2 + y^2}}\) |
অতএব,
| \(\sin \theta = \frac{x}{\sqrt{x^2 + y^2}}\) |
| এবং |
| \(\cos \theta = \frac{y}{\sqrt{x^2 + y^2}}\) |
সুতরাং,
| \(\sin \theta – \cos \theta\) |
| \(= \frac{x}{\sqrt{x^2+y^2}} – \frac{y}{\sqrt{x^2+y^2}}\) |
| \(= \frac{x-y}{\sqrt{x^2+y^2}}\) |
(vi) যদি \((1+ 4x^2) \cos A = 4x\) হয়, তাহলে দেখাই যে, \(\csc A + \cot A = \frac{1 + 2x}{1 – 2x}\)
সমাধানঃ-
\((1+ 4x^2) \cos A = 4x\)
বা, \(\cos A = \frac{4x}{1 + 4x^2}\) —(i)
এখন,
| \(\csc A + \cot A\) |
| \(= \frac{1}{\sin A} + \frac{\cos A}{\sin A}\) |
| \(= \frac{1 + \cos A}{\sin A}\) |
| \(= \frac{1 + \cos A}{\sqrt{1 – \cos^2 A}}\) |
| \(= \frac{1 + \frac{4x}{1 + 4x^2}}{\sqrt{1 – (\frac{4x}{1 + 4x^2})^2}}\) |
| \(= \frac{\frac{1 + 4x^2 + 4x}{1 + 4x^2}}{\sqrt{1 – \frac{(4x)^2}{(1 + 4x^2)^2}}}\) |
| \(= \frac{\frac{1 + 4x^2 + 4x}{1 + 4x^2}}{\sqrt{\frac{(1 + 4x^2)^2 – (4x)^2}{(1 + 4x^2)^2}}}\) |
| \(= \frac{\frac{1 + (2x)^2 + 2.2x}{1 + 4x^2}}{\sqrt{\frac{(1 + 4x^2)^2 – 4.4x^2}{(1 + 4x^2)^2}}}\) |
| \(= \frac{\frac{(1 + 2x)^2}{1 + 4x^2}}{\sqrt{\frac{(1 – 4x^2)^2}{(1 + 4x^2)^2}}}\) |
| \(= \frac{\frac{(1 + 2x)^2}{1 + 4x^2}}{\frac{1 – 4x^2}{1 + 4x^2}}\) |
| \(= \frac{(1 + 2x)^2}{1 – 4x^2}\) |
| \(= \frac{(1 + 2x)^2}{1 – (2x)^2}\) |
| \(= \frac{(1 + 2x)^2}{(1 + 2x)(1 – 2x)}\) |
| \(= \frac{1 + 2x}{1 – 2x}\) |
7. যদি \(x = a\sin\theta\) এবং \(y = b\tan\theta\) হয়, তাহলে প্রমাণ করি যে, \(\frac{a^2}{x^2} – \frac{b^2}{y^2} = 1\)
সমাধানঃ-
| \(x = a\sin\theta\) |
| বা, \(\csc \theta = \frac{a}{x}\) —-(i) |
| \(y = b\tan\theta\) |
| \(\cot \theta = \frac{b}{y}\) —–(ii) |
আমরা জানি, \(\csc^2 \theta – \cot^2 \theta = 1\)
অতএব, (i) ও (ii) নং থেকে পাই,
| \((\frac{a}{x})^2 – (\frac{b}{y})^2 = 1\) |
| বা, \(\frac{a^2}{x^2} – \frac{b^2}{y^2} = 1\) |
8. যদি \(\sin\theta + \sin^2\theta = 1\) হয়, তাহলে প্রমাণ করি যে, \(\cos^2\theta + \cos^4\theta = 1\)
সমাধানঃ-
দেওয়া আছে,
| \(\sin\theta + \sin^2\theta = 1\) |
| বা, \(\sin \theta = 1 – \sin^2 \theta\) |
| বা, \(\sin \theta = \cos^2 \theta\) —(i) |
সুতরাং,
| \(\cos^2\theta + \cos^4\theta\) |
| \(=\cos^2\theta + (\cos^2\theta)^2 \) [(i) নং থেকে মান বসিয়ে পাই] |
| \(= \sin \theta + \sin^2 \theta\) |
| \(= 1\) |
9. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) :
(i) যদি \(3x = \csc\alpha\) এবং \(\frac{3}{x} = \cot\alpha\) হয়, তাহলে \(3(x^2 – \frac{1}{x^2})\)-এর মান
উত্তরঃ (c) \(\frac{1}{3}\)
সমাধানঃ-
\(\csc^2 \alpha = 9x^2\) এবং \(\cot^2 \alpha = \frac{9}{x^2}\)
অতএব, \(\csc^2 \alpha – \cot^2 \alpha = 1\) থেকে পাই,
| \(9x^2 – \frac{9}{x^2} = 1\) |
| বা, \(3(x^2 – \frac{1}{x^2}) = \frac{1}{3}\) |
(ii) যদি \(2x = \sec A\) এবং \(\frac{2}{x} = \tan A\) হয়, তাহলে \(2(x^2 – \frac{1}{x^2} )\) -এর মান
উত্তরঃ (a) \(\frac{1}{2}\)
সমাধানঃ-
\(\sec^2 A = 4x^2\) এবং \(\tan^2 A = \frac{4}{x^2}\)
অতএব, \(\sec^2 A – \tan^2 A = 1\) থেকে পাই,
| \(4x^2 – \frac{4}{x^2} = 1\) |
| বা, \(2(x^2 – \frac{1}{x^2}) = \frac{1}{2}\) |
(iii) \(\tan\alpha + \cot\alpha = 2\) হলে, \((\tan^{13}\alpha + \cot^{13} \alpha)\)-এর মান
উত্তরঃ (c) 2
সমাধানঃ-
\(\tan\alpha + \cot\alpha = 2\) —-(i)
| \((\tan \alpha – \cot \alpha)^2\) |
| \(= (\tan \alpha + \cot \alpha)^2 – 4\tan \alpha \cot \alpha\) |
| \(= 2^2 – 4\) |
| \(= 4 – 4 = 0\) |
অতএব, \(\tan\alpha – \cot\alpha = 0\) —(ii)
(i) ও (ii) যোগ করে পাই,
| \(\tan \alpha + \cot \alpha + \tan \alpha – \cot \alpha = 2\) |
| বা, \(2\tan \alpha = 2\) |
| বা, \(\tan \alpha = 1\) |
| ⇒ \(\cot \alpha = 1\) |
সুতরাং,
| \(\tan^{13} \alpha + \cot^{13}\alpha\) |
| \(= 1^{13} + 1^{13}\) |
| \(= 1 + 1= 2\) |
(iv) যদি \(\sin\theta – \cos\theta = 0\) \(( 0^°\leq \theta \leq 90^° )\) এবং \(\sec\theta + \csc\theta = x\) হয়, তাহলে \(x\) এর মান
উত্তরঃ (d) 2√2
সমাধানঃ-
\(\sin \theta – \cos \theta = 0\) ⇒ \(\sin \theta = \cos \theta \) —–(i)
এখন,
| \(\sec\theta + \csc \theta = x\) |
| বা, \(\frac{1}{\cos \theta} + \frac{1}{\sin \theta} = x\) |
| বা, \(\frac{2}{\sin \theta} = x\) |
| বা, \(\sin \theta = \frac{2}{x} = \cos \theta\) |
\(\sin^2 \theta + \cos^2 \theta = 1\) থেকে পাই,
| \((\frac{2}{x})^2 + (\frac{2}{x})^2 = 1\) |
| বা, \(2 \times \frac{4}{x^2} = 1\) |
| বা, \(x^2 = 2\sqrt2\) |
(v) \(2\cos 3\theta = 1\) হলে, \(\theta\)-এর মান
উত্তরঃ (c) 20°
সমাধানঃ-
| \(2\cos 3\theta = 1\) |
| বা, \(\cos 3\theta = \frac{1}{2}\) |
| বা, \(\cos 3\theta = \cos 60^°\) |
| বা, \( 3\theta = 60^°\) |
| বা, \( \theta = 20^°\) |
(B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি :
(i) যদি, \(( 0^°\leq \alpha \leq 90^° )\) হয়, তাহলে \((\sec^2 \alpha + \cos^2 \alpha)\)-এর সর্বনিম্ন মান 2
উত্তরঃ সত্য
সমাধানঃ- কারণ,
| \(sec^2 \alpha + \cos^ \alpha\) |
| \(= (\sec\alpha + \cos \alpha)^2 – 2\sec \alpha \cos \alpha\) |
| \(= (\sec \alpha + \cos \alpha)^2 – 2\) |
(ii) \((\cos 0^° \times \cos 1^° \times \cos 2^° \times \cos 3^° \times ……….. \cos 90^°) \)-এর মান
উত্তরঃ মিথ্যা
সমাধানঃ- কারণ,
\(\cos 90^° = 0\)
(C) শূন্যস্থান পূরণ করি :
(i) \((\frac{4}{\sec^2 \theta} + \frac{1}{1 + \cot^2 \theta} + 3\sin^2 \theta)\) -এর মান ________
উত্তরঃ 4
সমাধানঃ-
| \(\frac{4}{\sec^2 \theta} + \frac{1}{1 + \cot^2 \theta} + 3\sin^2 \theta\) |
| \(= 4\cos^ \theta + \frac{1}{\csc^2 \theta} + 3\sin^2 \theta\) |
| \(= 4\cos^ \theta + \sin^2 \theta + 3\sin^2 \theta\) |
| \(= 4\cos^ \theta + 4\sin^2 \theta\) |
| \(= 4(\cos^ \theta + \sin^2 \theta)\) |
| \(= 4\) |
(ii) \(\sin (\theta – 30^°) = \frac{1}{2}\) হলে, \(\cos\theta\) -এর মান ________
উত্তরঃ \( \frac{1}{2}\)
সমাধানঃ-
| \(\sin (\theta – 30^°) = \frac{1}{2}\) |
| বা, \(\sin (\theta – 30^°) = \sin 30^°\) |
| বা, \(\theta – 30^° = 30^°\) |
| বা, \(\theta = 60^°\) |
অতএব, \(\cos \theta = \cos 60^° = \frac{1}{2}\)
(ii) \(\cos^2\theta – \sin^2 \theta = \frac{1}{2}\) হলে, \(\cos^4 \theta – \sin^4 \theta\) -এর মান –
উত্তরঃ \(= \frac{1}{2}\)
সমাধানঃ-
| \(\cos^4 \theta – \sin^4 \theta\) |
| \(= (\cos^2 \theta)^2 – (\sin^2 \theta)^2\) |
| \(= (\cos^2 \theta – \sin^2 \theta)(\cos^2 \theta + \sin^2 \theta)\) |
| \(= \frac{1}{2} \times 1\) |
| \(= \frac{1}{2}\) |
10.সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)
(i) যদি \(r\cos \theta = 2\sqrt3 , r\sin \theta = 2\) এবং\(( 0^°\leq \theta \leq 90^° )\) হয়, তাহলে \(r\) এবং \(\theta\) উভয়ের মান নির্ণয় করি।
সমাধানঃ-
\(r\cos \theta = 2\sqrt3\)
বা, \(r^2 \cos^2 \theta = 12\) —–(i)
এবং
\(r\sin \theta = 2\)
বা, \(r^2 \sin^2 \theta = 4\) —(ii)
(i) ও (ii) যোগ করে পাই,
| \(r^2\cos^2 \theta + r^2 \sin^2 \theta = 12 + 4\) |
| বা, \(r^2(\sin^2 \theta + \cos^2 \theta) = 16\) |
| বা, \(r^2 = 16\) |
| বা, \(r = 4\) |
এখন, \(r\sin \theta = 2\) তে \(r = 4\) বসিয়ে পাই,
| \(\sin \theta = \frac{1}{2}\) |
| বা, \(\sin \theta = \sin 30^°\) |
| বা, \(\theta = 30^°\) |
(ii) যদি sinA+ sinB=2 হয়, যেখানে \(( 0^°\leq A \leq 90^° )\) এবং \(( 0^°\leq B \leq 90^° )\), তাহলে (cosA + cosB) -এর মান নির্ণয় করি।
সমাধানঃ-
এখানে A এবং B উভয়েই 0° থেকে বড়ো এবং 90° অপেক্ষা ছোটো এবং কোণের এই মানের জন্যে \(\sin \theta\) এর মান কখনই 1 অপেক্ষা বড়ো হতে পারে না।
সুতরাং, sinA + sinB = 2 হবে কেবলমাত্র যদি, sinA = 1 এবং sinB = 1 হয়।
অতএব, sinA = sinB = 1
| sinA + sinB = 2 |
| ⇒ sinA + sinA = 2 |
| ⇒ 2sinA = 2 |
| ⇒ sinA = 1 |
| ⇒ sinA = sin90° |
| ⇒ A = 90° = B |
অতএব,
| cosA + cosB |
| = cos90° + cos90° |
| = 0 + 0 = 0 |
(iii) যদি \(( 0^° < \theta < 90^° )\) হয়, তাহলে \((9\tan^2 \theta + 4\cot^2 \theta)\) -এর সর্বনিম্ন মান নির্ণয় করি।
সমাধানঃ-
| \((9\tan^2 \theta + 4\cot^2 \theta)\) |
| \(= (3\tan \theta)^2 + (2\cot \theta)^2\) |
| \(= (3\tan \theta + \cot \theta)^2 – 2 \times 3\tan \theta \times 2\cot \theta\) |
| \(= (3\tan \theta + \cot \theta)^2 – 12\) |
এখন, \((3\tan \theta + \cot \theta)^2\) একটি পূর্ণ বর্গ সংখ্যা যার সর্বনিম্ন মান শুন্য এবং \((9\tan^2 \theta + 4\cot^2 \theta) (3\tan \theta)^2 + (2\cot \theta)^2\) দুটি বর্গের সমষ্টি কখনই ঋণাত্মক হতে পারে না।
সুতরাং, \((9\tan^2 \theta + 4\cot^2 \theta)\) এর সরবনিম্ন মান 12
(iv) \((\sin^6 \alpha + \cos^6 \alpha + 3\sin^2 \alpha \cos^2 \alpha)\)-এর মান নির্ণয় করি।
সমাধানঃ-
| \((\sin^6 \alpha + \cos^6 \alpha + 3\sin^2 \alpha \cos^2 \alpha)\) |
| \(= (\sin^2 \alpha)^3 + (\cos^2 \alpha)^3 + 3\sin^2 \alpha \cos^2 \alpha)\) |
| \(= (\sin^2 \alpha + \cos^2 \alpha)^3 – 3 \sin^2 \alpha \cos^2 \alpha(\sin^2 \alpha + \cos^2 \alpha) + 3\sin^2 \alpha \cos^2 \alpha)\) |
| \(= (\sin^2 \alpha + \cos^2 \alpha)^3 – 3 \sin^2 \alpha \cos^2 \alpha + 3\sin^2 \alpha \cos^2 \alpha)\) |
| \(= 1^3 = 1\) |
(v) যদি \(\csc^2 \theta = 2\cot\theta\) এবং \(( 0^° < \theta < 90^° )\) হয়, তাহলে \(\theta\)-এর মান নির্ণয় করি।
সমাধানঃ-
| \(\csc^2 \theta = 2\cot\theta\) |
| বা, \(1 + \cot^2 \theta = 2\cot \theta\) |
| বা, \(1 – 2 \cot \theta + \cot^2 \theta = 0\) |
| বা, \((1 – \cot \theta)^2 = 0\) |
| বা, \(\cot \theta = 1\) |
| বা, \(\cot \theta = \cot 45^°\) |
| বা, \(\theta = 45^°\) |
Class 10 WBBSE এর বাকি অধ্যায়ের সমাধান-
| অধ্যায় | সমাধান |
| 1. একচলবিশিষ্ট দ্বিঘাত সমীকরণ (Quadratic Equations with one variable) | কষে দেখি 1.1 |
| কষে দেখি 1.2 | |
| কষে দেখি 1.3 | |
| কষে দেখি 1.4 | |
| কষে দেখি 1.5 | |
| 2. সরল সুদকষা (Simple Interest) | কষে দেখি 2 |
| 3. বৃত্ত সম্পর্কিত উপপাদ্য (Theorems related to circle) | কষে দেখি 3.1 |
| কষে দেখি 3.2 | |
| 4. আয়তঘন (Rectangular Parallelopiped or Cuboid) | কষে দেখি 4 |
| 5. অনুপাত ও সমানুপাত ( Ratio and Proportion) | কষে দেখি 5.1 |
| কষে দেখি 5.2 | |
| কষে দেখি 5.3 | |
| 6. চক্রবৃদ্ধি সুদ ও সমহার বৃদ্ধি বা হ্রাস (Compound Interest and Uniform Rate of Increase or Decrease) | কষে দেখি 6.1 |
| কষে দেখি 6.2 | |
| 7. বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য (Theorems related to Angles in a Circle) | কষে দেখি 7.1 |
| কষে দেখি 7.2 | |
| কষে দেখি 7.3 | |
| 8. লম্ব বৃত্তাকার চোঙ (Right Circular Cylinder) | কষে দেখি 8 |
| 9. দ্বিঘাত করণী (Quadratic Surd). | কষে দেখি 9.1 |
| কষে দেখি 9.2 | |
| কষে দেখি 9.3 | |
| 10. বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য (Theorems related to Cyclic Quadrilateral) | কষে দেখি 10 |
| 11. সম্পাদ্য : ত্রিভুজের পরিবৃত্ত ও অন্তবৃত্ত অঙ্কন | কষে দেখি 11 |
| 12. গোলক (Sphere) | কষে দেখি 12 |
| 13. ভেদ (Variation) | কষে দেখি 13 |
| 14. অংশীদারি কারবার (Partnership Business) | কষে দেখি 14 |
| 15. বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য (Theorems related to Tangent to a Circle) | কষে দেখি 15.1 |
| কষে দেখি 15.2 | |
| 16. লম্ব বৃত্তাকার শঙ্কু (Right Circular Cone) | কষে দেখি 16 |
| 17. সম্পাদ্য : বৃত্তের স্পর্শক অঙ্কন (Construction: Construction of Tangent to a circle) | কষে দেখি 17 |
| 18. সদৃশতা (Similarity) | কষে দেখি 18.1 |
| কষে দেখি 18.2 | |
| কষে দেখি 18.3 | |
| কষে দেখি 18.4 | |
| 19. বিভিন্ন ঘনবস্তু সংক্রান্ত বাস্তব সমস্যা (Real life Problems related to different Solid Objects) | কষে দেখি 19 |
| 20. ত্রিকোণমিতি : কোণ পরিমাপের ধারণা (Trigonometry: Concept of Measurment of Angle) | কষে দেখি 20 |
| 21. সম্পাদ্য : মধ্যসমানুপাতী নির্ণয় (Construction: Determination of Mean Proportional) | কষে দেখি 21 |
| 22. পিথাগোরাসের উপপাদ্য (Pythagoras Theorem) | কষে দেখি 22 |
| 23. ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি (Trigonometric Ratios and Trigonometric Identities) | কষে দেখি 23.1 |
| কষে দেখি 23.2 | |
| কষে দেখি 23.3 | |
| 24. পূরক কোণের ত্রিকোণমিতিক অনুপাত (Trigonometric Ratios of Complementrary angle) | কষে দেখি 24 |
| 25. ত্রিকোণমিতিক অনুপাতের প্রয়োগ : উচ্চতা ও দূরত্ব (Application of Trigonometric Ratios : Heights & Distances) | কষে দেখি 25 |
| 26. রাশিবিজ্ঞান : গড়, মধ্যমা, ওজাইভ, সংখ্যাগুরুমান (Statistics: Mean, Median, Ogive, Mode) | কষে দেখি 26.1 |
| কষে দেখি 26.2 | |
| কষে দেখি 26.3 | |
| কষে দেখি 26.4 |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  |
এই কষে দেখি 23.3 Class 10|Koshe Dekhi 23.3 Class 10 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।

এখানে তোমরা তোমাদের দশম শ্রেণীতে| Class 10 এ কি কি পড়ানো হয়, মানে তোমাদের দশম শ্রেণীতে| Class 10 সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

