শ্রেণী- দশম ; অধ্যায় – চক্রবৃদ্ধি সুদ ও সমাহার বৃদ্ধি বা হ্রাস ; কষে দেখি 6.2
কষে দেখি 6.2 Class 10 অংকের সূচিপত্র:-
কষে দেখি 6.2 Class 10 এর অংকের সমাধান গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ
এই কষে দেখি 6.2, পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদ | WBBSE এর অন্তর্গত দশম শ্রেণি|Class 10 এর ছয় নম্বর অধ্যায়|Chapter 6 চক্রবৃদ্ধি সুদ ও সমাহার বৃদ্ধি বা হ্রাস | Compound Interest and Uniform Rate of Increase or Decrease এর দ্বিতীয় অনুশীলনী।
এই কষে দেখি 6.2 Class 10 এর অংকগুলি করার জন্যে তোমাদের জানতে হবে-
সমাহার বৃদ্ধি ও সমাহার হ্রাস কাকে বলে?
সমাহারে বৃদ্ধি ঘটলে তাকে সমাহার বৃদ্ধি[Uniform rate growth] এবং সমাহারে হ্রাস ঘটলে তাকে সমাহার হ্রাস [Ubiform rate of decrease or depreciation] বলা হয়।
- জনসংখ্যা বৃদ্ধি, শিক্ষার্থীর সংখ্যা বৃদ্ধি, কৃষি ও শিল্পের উৎপাদন বৃদ্ধি প্রভৃতি সমাহার বৃদ্ধির অন্তর্গত।
- আবার ক্রমাগত চলার ফলে যন্ত্রের ক্ষয়, অনেকদিনের ঘরবাড়ি, আসবাবপত্র, যানবাহন ইত্যাদি অস্থাবর সম্পতির মূল্য হ্রাস, সচেতনতা বৃদ্ধির ফলে রোগ ব্যাধির হ্রাস প্রভৃতি সসমাহার হ্রাসের অন্তর্গত।
কষে দেখি 6.2 Class 10 এর অংকের জন্যে একটি সমাহার বৃদ্ধির উদাহরণঃ
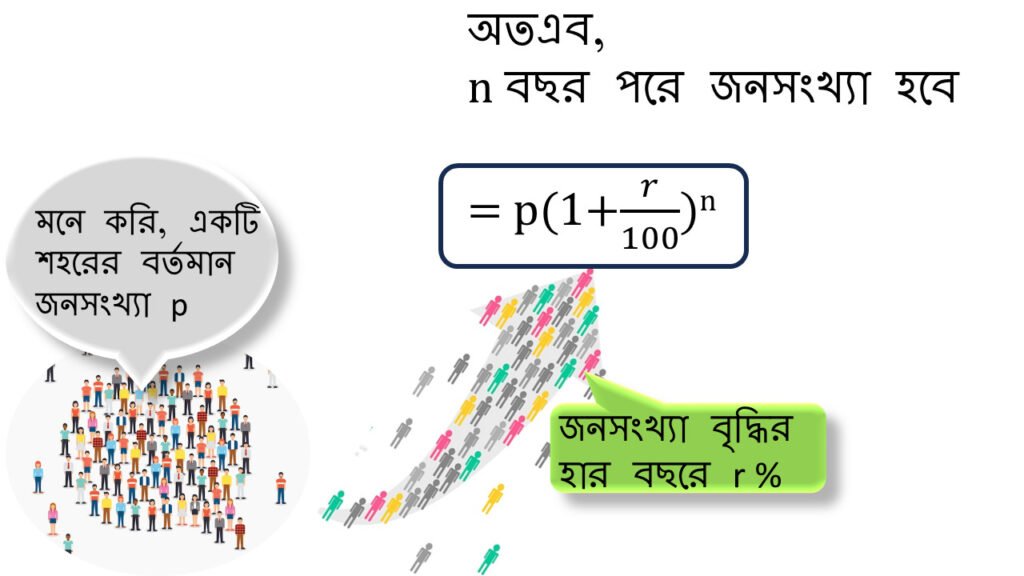
| মনে করি, একটি শহরের বর্তমান জনসংখ্যা \(p\) এবং জনসংখ্যা বৃদ্ধির হার বছরে \(r\)% অতএব, \(n \)বছর পরে জনসংখ্যা হবে = \(p(1+\frac{r}{100})^n\) |
এই কষে দেখি 6.2 Class 10 এর অংকগুলি করার সময় খেয়াল রাখতে হবে যে,
সমাহারে বৃদ্ধির সূত্র এবং চক্রবৃদ্ধি সুদের সূত্র একইরকম।
আগামিতে এই কষে দেখি 6.2 Class 10 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| কষে দেখি 6.2 Class 10 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 6.2 Class 10 তারপর  |
কষে দেখি 6.2 Class 10|Koshe Dekhi 6.2 Class 10

1. পহলমপুর গ্রামের বর্তমান লোকসংখ্যা 10000; ওই গ্রামে প্রতি বছর জনসংখ্যা বৃদ্ধির হার 3% হলে, 2 বছর পরে ওই গ্রামের জনসংখ্যা কত হবে, তা হিসাব করে লিখি।
সমাধানঃ-

ধরি,
| \(p\) | = 10000 জন |
| \(r\) | = 3 |
| \(n\) | = 2 বছর |
অতএব, 2 বছর পরে জনসংখ্যা হবে
= \(10000(1+\frac{3}{100})^2\)
= \(10000(\frac{103}{100})^2\)
= 10609 জন
2. কোনো একটি রাজ্যের প্রতি বছর জনসংখ্যা বৃদ্ধির হার 2%; বর্তমান জনসংখ্যা 80000000 হলে, 3 বছর পরে ওই রাজ্যের জনসংখ্যা কত হবে, তা নির্ণয় করি।
সমাধানঃ-
ধরি,
| \(p\) | = 80000000 জন |
| \(r\) | = 2 |
| \(n\) | = 3 বছর |
অতএব, 3 বছর পরে জনসংখ্যা হবে
= \(80000000(1+\frac{2}{100})^3\)
= \(80000000(\frac{102}{100})^3\)
= 84896640 জন
3. পাড়ার একটি লেদ কারখানার একটি মেশিনের মূল্য প্রতি বছর 10% হ্রাস প্রাপ্ত হয়। মেশিনটির বর্তমান মূল্য 100000 টাকা হলে, 3 বছর পরে ওই মেশিনটির মূল্য কত হবে, তা হিসাব করে লিখি।
সমাধানঃ-
ধরি,
| \(p\) | = 100000 জন |
| \(r\) | = 10 |
| \(n\) | = 3 বছর |
অতএব, 3 বছর পর মেশিনটির মূল্য হবে
= \(100000(1-\frac{10}{100})^3\)
= \(100000(1-\frac{1}{10})^3\)
= \(100000(\frac{9}{10})^3\)
= \(72900\) টাকা
4. সর্বশিক্ষা অভিযানের ফলে বিদ্যালয় ছেড়ে চলে যাওয়া শিক্ষার্থীদের পুনরায় বিদ্যালয়ে ভর্তির ব্যবস্থা করা হয়েছে। এরূপ শিক্ষার্থীদের ভর্তির হার প্রতি বছর তার পূর্ববর্তী বছর অপেক্ষা 5% বৃদ্ধি পেয়েছে। কোনো এক জেলায় বর্তমান বছরে যদি 3528 জন এরূপ শিক্ষার্থী নতুন করে ভর্তি হয়ে থাকে, তবে 2 বছর পূর্বে এরূপ কত জন শিক্ষার্থী ভর্তি হয়েছিল, তা হিসাব করে লিখি।
সমাধানঃ-
ধরি, 2 বছর পূর্বে এরূপ \(p\) জন শিক্ষার্থী ভর্তি হয়েছিল।
প্রতি বছর তার পূর্ববর্তী বছর অপেক্ষা 5% বৃদ্ধিতে 2 বছর পরে শিক্ষার্থীর সংখ্যা হবে
= \(p(1+\frac{5}{100})^2\)
= \(p(\frac{105}{100})^2\)
শর্তে,
| \(p(\frac{105}{100})^2 = 3528\) |
| বা, \(p = 3528 \times (\frac{100}{105})^2\) |
| বা, \(p = \frac{3528\times 10000}{11025}\) |
| বা, \(p = 3200\) |
- 2 বছর পূর্বে এরূপ 3200 জন শিক্ষার্থী ভর্তি হয়েছিল।
5. পুরুলিয়া জেলায় পথ নিরাপত্তা সংক্রান্ত প্রচার অভিযানের মাধ্যমে পথ দুর্ঘটনা প্রতি বছর তার পূর্ব বছরের তুলনায় 10% হ্রাস পেয়েছে। বর্তমান বছরে এই জেলায় 8748 টি পথ দুর্ঘটনা ঘটে থাকলে, 3 বছর আগে পথ দুর্ঘটনার সংখ্যা কত ছিল, তা নির্ণয় করি।
সমাধানঃ-
ধরি, 3 বছর আগে পথ দুর্ঘটনার সংখ্যা ছিল \(p\) টি।
প্রতি বছর তার পূর্ব বছরের তুলনায় 10% হ্রাসে 3 বছর পরে পথ দুর্ঘটনার সংখ্যা হবে
= \(p(1-\frac{10}{100})^3\)
= \(p(1-\frac{1}{10})^3\)
= \(p(\frac{9}{10})^3\)
শর্তে,
| \(p(\frac{9}{10})^3 = 8748\) |
| বা, \(p = 8748 \times (\frac{10}{9})^3\) |
| বা, \(p = \frac{8748\times 1000}{729}\) |
| বা, \(p = 12000\) |
- 3 বছর আগে পথ দুর্ঘটনার সংখ্যা ছিল 12000 টি।
6. একটি মৎস্যজীবী সমবায় সমিতি উন্নত প্ৰথায় মাছ চাষ করার জন্য এরূপ একটি পরিকল্পনা গ্রহণ করেছে যে কোনো বছরের মাছের উৎপাদন পূর্ববর্তী বছরের তুলনায় 10% বৃদ্ধি করবে। বর্তমান বছরে যদি ওই সমবায় সমিতি 400 কুইন্টাল মাছ উৎপাদন করে, তবে 3 বছর পরে সমবায় সমিতির মাছের উৎপাদন কত হবে, তা হিসাব করে লিখি।
সমাধানঃ-
ধরি,
| \(p\) | = 400 কুইন্টাল |
| \(r\) | = 10 |
| \(n\) | = 3 বছর |
প্রতি বছর 10% বৃদ্ধিতে 3 বছর পরে সমবায় সমিতির মাছের উৎপাদন হবে
= \(400(1+\frac{10}{100})^3\)
= \(400(1+\frac{1}{10})^3\)
= \(400(\frac{11}{10})^3\)
= \(532.4\) কুইন্টাল
7. একটি গাছের উচ্চতা প্রতি বছর 20% হারে বৃদ্ধি পায়। গাছটির বর্তমান উচ্চতা 28.8 মিটার হলে, 2 বছর আগে গাছটির উচ্চতা কত ছিল, তা নির্ণয় করি।
সমাধানঃ-
ধরি,
| 2 বছর আগের উচ্চতা | = \(p\) মিটার |
| \(r\) | = 20 |
| \(n\) | = 2 বছর |
প্রতি বছর 20% হারে বৃদ্ধিতে 2 বছর পরে গাছের উচ্চতা হবে
= \(p(1+\frac{20}{100})^2\)
= \(p(1+\frac{1}{5})^2\)
= \(p(\frac{6}{5})^2\)
শর্তে,
| \(p(\frac{6}{5})^2 = 28.8 \) |
| বা, \(p = 28.8 \times (\frac{5}{6})^2\) |
| বা, \(p = \frac{28.8 \times 25}{36}\) |
| বা, \(p = 20\) |
- 2 বছর আগে গাছটির উচ্চতা ছিল 20 মিটার।
8. কোনো একটি পরিবার আজ থেকে 3 বছর পূর্বে বিদ্যুৎ অপচয় বন্ধ করতে ইলেকট্রিক বিলের খরচ পূর্ববর্তী বছরের তুলনায় 5% হ্রাস করার পরিকল্পনা গ্রহণ করে। 3 বছর পূর্বে ওই পরিবারকে বছরে 4000 টাকার ইলেকট্রিক বিল দিতে হয়েছিল। বর্তমান বছরে ইলেকট্রিক বিলে বিদ্যুৎ খরচ কত হবে, তা হিসাব করে লিখি।
সমাধানঃ-
ধরি,
| 3 বছর আগের ইলেকট্রিক বিল \(p\) | = 4000 টাকা |
| \(r\) | = 5 |
| \(n\) | = 3 বছর |
প্রতি বছর বিদ্যুৎ বিল 5% হ্রাসে 3 বছর পর ইলেকট্রিক বিল হবে
= \(4000(1-\frac{5}{100})^3\)
= \(4000(1-\frac{1}{20})^3\)
= \(4000(\frac{19}{20})^3\)
= \(3429.50 \) টাকা
9. শোভনবাবুর ওজন 80 কিগ্রা.। ওজন কমানোর জন্য তিনি নিয়মিত হাঁটা শুরু করলেন। তিনি ঠিক করলেন যে প্রতি বছরের প্রারম্ভে যা ওজন থাকবে তার 10% হ্রাস করবেন। 3 বছর পরে শোভনবাবুর ওজন কত হবে, তা হিসাব করে লিখি।
সমাধানঃ-
ধরি,
| শোভনবাবুর ওজন \(p\) | = 80 কিগ্রা. |
| \(r\) | = 10 |
| \(n\) | = 3 বছর |
প্রতি বছর 10% হ্রাসে 3 বছর পরে শোভনবাবুর ওজন হবে
= \(80(1-\frac{10}{100})^3\)
= \(80(1-\frac{1}{10})^3\)
= \(80(\frac{9}{10})^3\)
= \(58.32\) কিগ্রা.
10. কোনো এক জেলার সমস্ত মাধ্যমিক শিক্ষাকেন্দ্রের (M.S.K) বর্তমান শিক্ষার্থীর সংখ্যা 3993 জন। প্রতি বছর বিগত বছরের তুলনায় যদি 10% শিক্ষার্থী বৃদ্ধি পেয়ে থাকে, তবে 3 বছর পূর্বে ওই জেলার সকল মাধ্যমিক শিক্ষাকেন্দ্রের শিক্ষার্থীর সংখ্যা কত ছিল, তা নির্ণয় করি।
সমাধানঃ-
ধরি,
| 3 বছর পূর্বে ওই জেলার সকল মাধ্যমিক শিক্ষাকেন্দ্রের শিক্ষার্থীর সংখ্যা | = \(p\) জন |
| \(r\) | = 10 |
| \(n\) | = 3 বছর |
প্রতি বছর 10% বৃদ্ধিতে 3 বছর পরে শিক্ষার্থীর সংখ্যা হবে
= \(p(1+\frac{10}{100})^3\)
= \(p(1+\frac{1}{10})^3\)
= \(p(\frac{11}{10})^3\)
শর্তে,
| \(p(\frac{11}{10})^3 = 3993\) |
| বা, \(p = 3993 \times (\frac{10}{11})^3\) |
| বা, \(p = \frac{3993 \times 1000}{1331}\) |
| বা, \(p = 3000\) |
- 3 বছর পূর্বে ওই জেলার সকল মাধ্যমিক শিক্ষাকেন্দ্রের শিক্ষার্থীর সংখ্যা ছিল 3000 জন।
11. কৃষিজমিতে কেবলমাত্র রাসায়নিক সার ও কীটনাশক ব্যবহারের কুফল সম্পর্কে সচেতনতা বৃদ্ধির ফলে রসুলপুর গ্রামে কেবলমাত্র রাসায়নিক সার ও কীটনাশক ব্যবহারকারী কৃষকের সংখ্যা পূর্ববর্তী বছরের তুলনায় 20% হ্রাস পায়। 3 বছর পূর্বে রসুলপুর গ্রামের ওরকম কৃষকের সংখ্যা 3000 জন হলে, বর্তমানে ওই গ্রামে ওরকম কৃষকের সংখ্যা কত হবে, তা নির্ণয় করি।
সমাধানঃ-
ধরি,
| 3 বছর পূর্বে রসুলপুর গ্রামের ওরকম কৃষকের সংখ্যা \(p\) | = 3000 জন |
| \(r\) | = 20 |
| \(n\) | = 3 বছর |
প্রতি বছর 20% হ্রাসে 3 বছর পরে কৃষকের সংখ্যা হবে
= \(3000(1-\frac{20}{100})^3\)
= \(3000(1-\frac{1}{5})^3\)
= \(3000(\frac{4}{5})^3\)
= \(1536\) জন
12. একটি কারখানার একটি মেশিনের মূল্য 180000 টাকা। মেশিনটির মূল্য প্রতি বছর 10% হ্রাস প্রাপ্ত হয়। 3 বছর পরে ওই মেশিনটির মূল্য কত হবে, তা হিসাব করে লিখি ।
সমাধানঃ-
ধরি,
| মেশিনের মূল্য \(p\) | = 180000 টাকা |
| \(r\) | = 10 |
| \(n\) | = 3 বছর |
প্রতি বছর 10% হ্রাসে 3 বছর পর ওই মেশিনটির মূল্য হবে
= \(180000(1-\frac{10}{100})^3\)
= \(180000(1-\frac{1}{10})^3\)
= \(180000(\frac{9}{10})^3\)
= \(131220\) টাকা
13. বকুলতলা গ্রামের পঞ্চায়েত সমিতি যেসব পরিবারে বিদ্যুৎ সংযোগ নেই তাদের বাড়িতে বিদ্যুৎ পৌঁছানোর পরিকল্পনা গ্রহণ করে। এই গ্রামে 1200 পরিবারের বিদ্যুৎ সংযোগ নেই। প্রতি বছর যদি পূর্ব বছরের তুলনায় 75% বিদ্যুৎহীন পরিবারে বিদ্যুৎ পৌঁছানোর ব্যবস্থা করা হয়, তবে 2 বছর পরে বকুলতলা গ্রামে বিদ্যুৎহীন পরিবারের সংখ্যা কত হবে, তা হিসাব করে লিখি।
সমাধানঃ-
ধরি,
| গ্রামে বিদ্যুৎ সংযোগ নেই ,\(p\) | = 1200 টি পরিবারের |
| \(r\) | = 75 |
| \(n\) | = 2 বছর |
প্রতি বছর 75% হ্রাসে 2 বছর পর ওই গ্রামে বিদ্যুৎহিন পরিবারের সংখ্যা হবে
= \(1200(1-\frac{75}{100})^2\)
= \(1200(1-\frac{3}{4})^2\)
= \(1200(\frac{1}{4})^2\)
= \(75\) টি
14. বোতল ভর্তি ঠান্ডা পানীয় ব্যবহারের উপর বিরূপ প্রতিক্রিয়া প্রচারের ফলে প্রতি বছর তার পূর্ববর্তী বছরের তুলনায় ওই ঠান্ডা পানীয় ব্যবহারকারীর সংখ্যা 25% হ্রাস পায়। 3 বছর পূর্বে কোনো শহরে ঠান্ডা পানীয় ব্যবহারকারীর সংখ্যা 80000 হলে, বর্তমান বছরে ঠান্ডা পানীয় ব্যবহারকারীর সংখ্যা কত হবে, তা হিসাব করে লিখি।
সমাধানঃ-
ধরি,
| 3 বছর পূর্বে ঠান্ডা পানীয় ব্যবহারকারীর সংখ্যা\(p\) | = 80000 জন |
| \(r\) | = 25 |
| \(n\) | = 3 বছর |
প্রতি বছর 25% হ্রাসে 3 বছর পরে ওই শহরে ঠান্ডা পানীয় ব্যবহারকারীর সংখ্যা হবে
= \(80000(1-\frac{25}{100})^3\)
= \(80000(1-\frac{1}{4})^3\)
= \(80000(\frac{3}{4})^3\)
= \(33750\) জন
15. ধূমপান বিরোধী প্রচারের ফলে প্রতি বছর ধূমপায়ীর সংখ্যা \(6\frac{1}{4}\)% হারে হ্রাস পায়। বর্তমানে কোনো শহরে 33750 জন ধূমপায়ী থাকলে, 3 বছর পূর্বে ওই শহরে কত জন ধূমপায়ী ছিল, তা হিসাব করে লিখি ।
সমাধানঃ-
ধরি,
| 3 বছর পূর্বে ওই শহরে ধূমপায়ী ছিল | = \(p\) জন |
| \(r\) | = \(6\frac{1}{4}\) = \(\frac{25}{4}\) |
| \(n\) | = 3 বছর |
প্রতি বছর \(\frac{25}{4}\)% হ্রাসে 3 বছর পর ধূমপায়ীর সংখ্যা হবে
= \(p(1-\frac{\frac{25}{4}}{100})^3\)
= \(p(1-\frac{25}{4\times 100})^3\)
= \(p(1-\frac{1}{4\times 4})^3\)
= \(p(1-\frac{1}{16})^3\)
= \(p(\frac{15}{16})^3\)
| \(p(\frac{15}{16})^3 = 33750\) |
| বা, \(p = 33750 \times (\frac{16}{15})^3\) |
| বা, \(p = \frac{33750 \times 4096}{3375}\) |
| বা, \(p = 40960\) |
- 3 বছর পূর্বে ওই শহরে 40960 জন ধূমপায়ী ছিল ।
16. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) :
(i) চক্রবৃদ্ধি সুদের ক্ষেত্রে প্রতি বছর বার্ষিক চক্রবৃদ্ধি সুদের হার
উত্তরঃ (c) সমান অথবা অসমান উভয়ই
(ii) চক্রবৃদ্ধি সুদের ক্ষেত্রে
উত্তরঃ (b) প্রতি বছর আসল পরিবর্তিত হয়
(iii) একটি গ্রামের বর্তমান জনসংখ্যা p এবং প্রতি বছর জনসংখ্যা বৃদ্ধির হার 2r% হলে, n বছর পর জনসংখ্যা হবে
উত্তরঃ (b) \(p(1+\frac{r}{50})^n\)
(iv) একটি মেশিনের বর্তমান মূল্য 2p টাকা এবং প্রতি বছর মেশিনটির দাম 21% হ্রাস হলে 2n বছর পরে মেশিনের দাম হবে
উত্তরঃ (d) \(2p(1-\frac{r}{50})^2n\)
(v) এক ব্যক্তি একটি ব্যাংকে 100 টাকা জমা রেখে, 2 বছর পর সমূল চক্রবৃদ্ধি পেলেন 121 টাকা। বার্ষিক চক্রবৃদ্ধি সুদের হার
উত্তরঃ (a) 10%
(b) 20%
(c) 5%
(d) 10%
সমাধানঃ-
ধরি, চক্রবৃদ্ধি সুদের হার = r %
শর্তে,
\(100(1+\frac{r}{100})^2 = 121\)
বা, \((1+\frac{r}{100})^2= \frac{121}{100}\)
বা, \(1+\frac{r}{100}= \frac{11}{10}\)
বা, \(\frac{r}{100}= \frac{11}{10}-1\)
বা, \(\frac{r}{100}= \frac{1}{10}\)
বা, \(\r= \frac{100}{10} = 10\)
(B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি :
(i) নির্দিষ্ট পরিমাণ টাকার বার্ষিক নির্দিষ্ট শতকরা হার সুদে নির্দিষ্ট সময়ের জন্য চক্রবৃদ্ধি সুদ সরল সুদের থেকে কম হবে।
উত্তরঃ মিথ্যা
(ii) চক্রবৃদ্ধি সুদের ক্ষেত্রের নির্দিষ্ট সময় অন্তর সুদ আসলের সঙ্গে যোগ হয়। সেই কারণে আসলের পরিমাণ ক্রমাগত বাড়তে থাকে।
উত্তরঃ সত্য
(C) শূন্যস্থান পূরণ করি :
(i) নির্দিষ্ট পরিমাণ টাকার বার্ষিক নির্দিষ্ট শতকরা হার সুদে 1 বছরে চক্রবৃদ্ধি সুদের পরিমাণ এবং সরল সুদের পরিমাণ
উত্তরঃ সমান
(ii) সময়ের সঙ্গে কোনো কিছুর নির্দিষ্ট হারে বৃদ্ধি হলে সেটি
উত্তরঃ সমাহার বৃদ্ধি
(iii) সময়ের সঙ্গে কোনো কিছুর নির্দিষ্ট হারে হ্রাস হলে সেটি সমহার
উত্তরঃ হ্রাস
7. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)
i) 400 টাকার 2 বছরে সমূল চক্রবৃদ্ধি 441 টাকা হলে, বার্ষিক শতকরা চক্রবৃদ্ধি সুদের হার কত তা লিখি ।
সমাধানঃ-
ধরি, চক্রবৃদ্ধি সুদের হার = \(r\) %
শর্তে,
| 400 টাকার \(r\)% হারে 2 বছরে সমূল চক্রবৃদ্ধি = 441 টাকা |
| বা, \(400(1+\frac{r}{100})^2 = 441\) |
| বা, \((1+\frac{r}{100})^2 = \frac{441}{400}\) |
| বা, \((1+\frac{r}{100})^2 = (\frac{21}{20})^2\) |
| বা, \(1+\frac{r}{100} = \frac{21}{20}\) |
| বা, \(\frac{r}{100} = \frac{21}{20}-1\) |
| বা, \(\frac{r}{100} = \frac{1}{20}\) |
| বা, \(r = \frac{100}{20} = 5\) |
ii) বার্ষিক নির্দিষ্ট শতকরা চক্রবৃদ্ধি হার সুদে কিছু টাকা n বছরে দ্বিগুণ হলে, কত বছরে 4 গুণ হবে তা লিখি।
সমাধানঃ-
ধরি, \(p\) টাকা \(r\)% হার চক্রবৃদ্ধি সুদে \(n\) বছরে \(2p\) টাকা হয়।
অতএব,
\(p(1+\frac{r}{100})^n = 2p\)
বা, \(1+\frac{r}{100} = 2^{\frac{1}{n}}\) —-(i)
এখন ধরি, ওই টাকা \(x\) বছরে 4 গুণ হবে।
শর্তে,
| \(p(1+\frac{r}{100})^x=4p\) |
| বা, \((1+\frac{r}{100})^x=4\) |
| বা, \((2^{\frac{1}{n}})^x=2^2\) |
| বা, \(2^{\frac{x}{n}=2^2}\) |
| বা, \(\frac{x}{n}=2\) |
| বা, \(x = 2n\) |
iii) বার্ষিক 5% চক্রবৃদ্ধি হার সুদে কিছু টাকার 2 বছরে চক্রবৃদ্ধি সুদ 615 টাকা হলে, আসল নির্ণয় করি।
সমাধানঃ-
ধরি, আসল = \(p\) টাকা।
শর্তে,
| \(p(1+\frac{5}{100})^2-p = 615\) |
| বা, \(p(1+\frac{1}{20})^2-p = 615\) |
| বা, \(p[(1+\frac{1}{20})^2-1] = 615\) |
| বা, \(p[1+2\times \frac{1}{20}+(\frac{1}{20})^2-1] = 615\) |
| বা, \(p[\frac{1}{10}+\frac{1}{400}] = 615\) |
| বা, \(p\frac{40+1}{400}=615\) |
| বা, \(p = \frac{400\times615}{41}\) |
| বা, \(p = 6000\) |
iv) প্রতি বছর r% হ্রাসপ্রাপ্ত হলে, n বছর পর একটি মেশিনের মূল্য হয় v টাকা। n বছর পূর্বে মেশিনটির মূল্য কত ছিল তা নির্ণয় করি।
সমাধানঃ-
ধরি, n বছর পূর্বে মেশিনটির মূল্য ছিল \(p\) টাকা।
শর্তে,
| \(p(1-\frac{r}{100})^n=v\) |
| বা, \(p= v(1-\frac{r}{100})^{-n}\) |
v) প্রতি বছর জনসংখ্যা r% বৃদ্ধি হলে n বছর পর জনসংখ্যা হয় p; n বছর পূর্বে জনসংখ্যা কত ছিল তা নির্ণয় করি।
সমাধানঃ-
ধরি, n বছর পূর্বে জনসংখ্যা ছিল \(x\) জন
শর্তে,
| \(x(1+\frac{r}{100})^n=p\) |
| বা, \(x=p(1+\frac{r}{100})^{-n}\) |
Class 10 WBBSE এর বাকি অধ্যায়ের সমাধান-
| অধ্যায় | সমাধান |
| 1. একচলবিশিষ্ট দ্বিঘাত সমীকরণ (Quadratic Equations with one variable) | কষে দেখি 1.1 |
| কষে দেখি 1.2 | |
| কষে দেখি 1.3 | |
| কষে দেখি 1.4 | |
| কষে দেখি 1.5 | |
| 2. সরল সুদকষা (Simple Interest) | কষে দেখি 2 |
| 3. বৃত্ত সম্পর্কিত উপপাদ্য (Theorems related to circle) | কষে দেখি 3.1 |
| কষে দেখি 3.2 | |
| 4. আয়তঘন (Rectangular Parallelopiped or Cuboid) | কষে দেখি 4 |
| 5. অনুপাত ও সমানুপাত ( Ratio and Proportion) | কষে দেখি 5.1 |
| কষে দেখি 5.2 | |
| কষে দেখি 5.3 | |
| 6. চক্রবৃদ্ধি সুদ ও সমহার বৃদ্ধি বা হ্রাস (Compound Interest and Uniform Rate of Increase or Decrease) | কষে দেখি 6.1 |
| কষে দেখি 6.2 | |
| 7. বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য (Theorems related to Angles in a Circle) | কষে দেখি 7.1 |
| কষে দেখি 7.2 | |
| কষে দেখি 7.3 | |
| 8. লম্ব বৃত্তাকার চোঙ (Right Circular Cylinder) | কষে দেখি 8 |
| 9. দ্বিঘাত করণী (Quadratic Surd). | কষে দেখি 9.1 |
| কষে দেখি 9.2 | |
| কষে দেখি 9.3 | |
| 10. বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য (Theorems related to Cyclic Quadrilateral) | কষে দেখি 10 |
| 11. সম্পাদ্য : ত্রিভুজের পরিবৃত্ত ও অন্তবৃত্ত অঙ্কন | কষে দেখি 11 |
| 12. গোলক (Sphere) | কষে দেখি 12 |
| 13. ভেদ (Variation) | কষে দেখি 13 |
| 14. অংশীদারি কারবার (Partnership Business) | কষে দেখি 14 |
| 15. বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য (Theorems related to Tangent to a Circle) | কষে দেখি 15.1 |
| কষে দেখি 15.2 | |
| 16. লম্ব বৃত্তাকার শঙ্কু (Right Circular Cone) | কষে দেখি 16 |
| 17. সম্পাদ্য : বৃত্তের স্পর্শক অঙ্কন (Construction: Construction of Tangent to a circle) | কষে দেখি 17 |
| 18. সদৃশতা (Similarity) | কষে দেখি 18.1 |
| কষে দেখি 18.2 | |
| কষে দেখি 18.3 | |
| কষে দেখি 18.4 | |
| 19. বিভিন্ন ঘনবস্তু সংক্রান্ত বাস্তব সমস্যা (Real life Problems related to different Solid Objects) | কষে দেখি 19 |
| 20. ত্রিকোণমিতি : কোণ পরিমাপের ধারণা (Trigonometry: Concept of Measurment of Angle) | কষে দেখি 20 |
| 21. সম্পাদ্য : মধ্যসমানুপাতী নির্ণয় (Construction: Determination of Mean Proportional) | কষে দেখি 21 |
| 22. পিথাগোরাসের উপপাদ্য (Pythagoras Theorem) | কষে দেখি 22 |
| 23. ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি (Trigonometric Ratios and Trigonometric Identities) | কষে দেখি 23.1 |
| কষে দেখি 23.2 | |
| কষে দেখি 23.3 | |
| 24. পূরক কোণের ত্রিকোণমিতিক অনুপাত (Trigonometric Ratios of Complementrary angle) | কষে দেখি 24 |
| 25. ত্রিকোণমিতিক অনুপাতের প্রয়োগ : উচ্চতা ও দূরত্ব (Application of Trigonometric Ratios : Heights & Distances) | কষে দেখি 25 |
| 26. রাশিবিজ্ঞান : গড়, মধ্যমা, ওজাইভ, সংখ্যাগুরুমান (Statistics: Mean, Median, Ogive, Mode) | কষে দেখি 26.1 |
| কষে দেখি 26.2 | |
| কষে দেখি 26.3 | |
| কষে দেখি 26.4 |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  |
এই কষে দেখি 6.2 Class 10|Koshe Dekhi 6.2 Class 10 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।

এখানে তোমরা তোমাদের দশম শ্রেণীতে| Class 10 এ কি কি পড়ানো হয়, মানে তোমাদের দশম শ্রেণীতে| Class 10 সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।


