শ্রেণী- দশম ; অধ্যায় – একচলবিশিষ্ট দ্বিঘাত সমীকরণ ; কষে দেখি 1.4
কষে দেখি 1.4 Class 10 অংকের সূচিপত্র:-
কষে দেখি 1.4 Class 10 এর অংকের সমাধান গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ
এই কষে দেখি 1.4, পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদ | WBBSE এর অন্তর্গত দশম শ্রেণি|Class 10 এর প্রথম অধ্যায় একচল বিশিষ্ট দ্বিঘাত সমীকরণ এর চতুর্থ অনুশীলনী।
এই কষে দেখি 1.4 Class 10 এর অংকগুলি ভালোভাবে বোঝার জন্যে তোমাদের শ্রীধর আচার্যের সূত্রটি জানতে হবে।
শ্রীধর আচার্যের সূত্রঃ
ax2 + bx + c = 0 , দ্বিঘাত সমীকরণের দুটি বীজ হলো-
\( x = \frac{-b\pm \sqrt {b^2 – 4ac}}{2a}\)
আগামিতে এই কষে দেখি 1.4 Class 10 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| কষে দেখি 1.4 Class 10 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 1.4 Class 10 তারপর 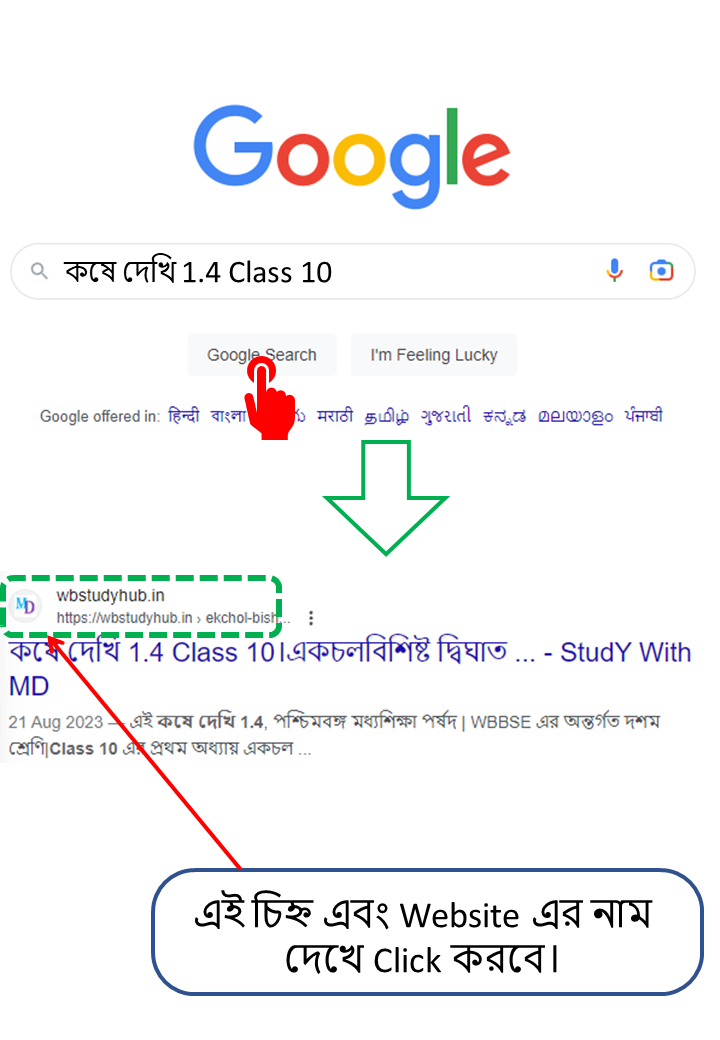 |

কষে দেখি 1.4|Koshe Dekhi 1.4
সমাধানঃ-
1.
(i) 4x2 + (2x-1)(2x+1) = 4x(2x-1) -এই সমীকরণটি সমাধানে শ্রীধর আচার্যের সূত্র প্রয়োগ সম্ভব কিনা বুঝে লিখি।
সমাধানঃ-
| 4x2 + (2x-1)(2x+1) = 4x(2x-1) |
| বা, 4x2 + 4x2 – 1 = 8x2 – 4x |
| বা, 4x – 1 = 0 |
| এটি একটি x চলরাশির একঘাত সমীকরণ। |
সুতরাং, এই সমীকরণটি সমাধানে শ্রীধর আচার্যের সূত্র প্রয়োগ সম্ভব নয়।
(ii) শ্রীধর আচার্যের সূত্রের সাহায্যে আমরা কোন ধরনের সমীকরণের সমাধান করতে পারি বুঝে লিখি
সমাধানঃ-
শ্রীধর আচার্যের সূত্রের সাহায্যে আমরা একচলবিশিষ্ট দ্বিঘাত সমীকরণের সমাধান করতে পারি।
(iii) 5x2 + 2x – 7 = 0 এই সমীকরণে শ্রীধর আচার্যের সূত্র প্রয়োগ করে x = \(\frac{k \pm 12}{10}\)পাওয়া গেলে k-এর মান কী হবে হিসাব করে লিখি।
সমাধানঃ-
\( x = \frac{-b\pm \sqrt {b^2 – 4ac}}{2a}\) এর সঙ্গে তুলনা করে পাই,
x = – 2
2. নীচের দ্বিঘাত সমীকরণগুলির বাস্তব বীজ থাকলে শ্রীধর আচার্যের সূত্রের সাহায্যে নির্ণয় করি।
(i) 3x2 + 11x – 4 = 0
সমাধানঃ-
∴ শ্রীধর আচার্যের সূত্র প্রয়োগ করে পাই,
\( x = \frac{-b\pm \sqrt {b^2 – 4ac}}{2a}\)
বা, \( x = \frac{- 11 \pm \sqrt {11^2 – 4.3(-4)}}{2.3}\)
বা, \( x = \frac{- 11 \pm \sqrt {121 + 48}}{6}\)
বা, \( x = \frac{- 11 \pm \sqrt {169}}{6}\)
বা, \( x = \frac{- 11 \pm 13}{6}\)
অতএব হয়
\( x = \frac{-11+13}{6}\) = \(\frac{1}{3}\)
অথবা,
\( x = \frac{-11-13}{6} = 4 \)
- 3x2 + 11x – 4 = 0 সমীকরণের বীজদ্বয় 4 ও \(\frac{1}{3}\)
(ii) (x – 2) (x+4) +9=0
সমাধানঃ-
| (x – 2) (x+4) +9=0 |
| বা, x2 + 2x + 1 = 0 |
∴ শ্রীধর আচার্যের সূত্র প্রয়োগ করে পাই,
\( x = \frac{-b\pm \sqrt {b^2 – 4ac}}{2a}\)
বা, \( x = \frac{- 2 \pm \sqrt {2^2 – 4.1.1}}{2.1}\)
বা, \( x = \frac{- 2 \pm \sqrt {4 – 4}}{2}\)
বা, \(x =\) – 1 ও – 1
(iii) (4x – 3)2 – 2(x + 3) = 0
সমাধানঃ-
| (4x – 3)2 – 2(x + 3) = 0 |
| বা, 16x2 – 2.4x.3 + 9 – 2x – 6 = 0 |
| বা, 16x2 – 24x – 2x + 3 = 0 |
| বা, 16x2 – 26x + 3 = 0 |
∴ শ্রীধর আচার্যের সূত্র প্রয়োগ করে পাই,
\( x = \frac{-b\pm \sqrt {b^2 – 4ac}}{2a}\)
বা, \( x = \frac{-(-26)\pm \sqrt {(-26)^2 – 4.16.3}}{2.16}\)
বা, \( x = \frac{26\pm \sqrt {676 – 192}}{32}\)
বা, \( x = \frac{26\pm \sqrt {484}}{32}\)
বা, \( x = \frac{26\pm 22}{32}\)
অতএব হয়
\( x = \frac{26 + 22}{32} = \frac{3}{2}\)
অথবা,
\( x = \frac{26 – 22}{32} = \frac{1}{8}\)
- (4x – 3)2 – 2(x + 3) = 0 সমীকরণের বীজদ্বয় \(\frac{3}{2}\) ও \(\frac{1}{8}\)
(iv) 3x2 + 2x – 1 = 0
সমাধানঃ-
∴ শ্রীধর আচার্যের সূত্র প্রয়োগ করে পাই,
\( x = \frac{-b\pm \sqrt {b^2 – 4ac}}{2a}\)
বা, \( x = \frac{-2\pm \sqrt {2^2 – 4.3(-1)}}{2.3}\)
বা, \( x = \frac{-2\pm \sqrt {4 + 12}}{6}\)
বা, \( x = \frac{-2\pm \sqrt {16}}{6}\)
বা, \( x = \frac{-2\pm 4}{6}\)
অতএব হয়
\( x = \frac{-2 + 4}{6} = \frac{1}{3}\)
অথবা,
\( x = \frac{-2 – 4}{6} = -1 \)
- 3x2 + 2x – 1 = 0 সমীকরণের বীজদ্বয় – 1 ও \(\frac{1}{3}\)
(v) 3x2 + 2x + 1 = 0
সমাধানঃ-
\({b^2 – 4ac}\)
= \(2^2 – 4.3.1\)
= \(4 – 12\)
= -8 < 0
- সুতরাং 3x2 + 2x + 1 = 0 সমীকরণের কোনো বাস্তব বীজ নেই।
(vi) 10x2 – x – 3 = 0
সমাধানঃ-
∴ শ্রীধর আচার্যের সূত্র প্রয়োগ করে পাই,
\( x = \frac{-b\pm \sqrt {b^2 – 4ac}}{2a}\)
বা, \( x = \frac{-(-1)\pm \sqrt {(-1)^2 – 4.10(-3)}}{2.10}\)
বা, \( x = \frac{1\pm \sqrt {1 + 120}}{20}\)
বা, \( x = \frac{1\pm \sqrt {121}}{20}\)
বা, \( x = \frac{1\pm 11}{20}\)
অতএব হয়
\( x = \frac{1 + 11}{20} = \frac{3}{5}\)
অথবা,
\( x = \frac{1 – 11}{20} = – \frac{1}{2}\)
- 10x2 – x – 3 = 0 সমীকরণের বীজদ্বয় \(\frac{3}{5}\) ও \(- \frac{1}{2}\)
(vii) 10x2 – x + 3 =0
সমাধানঃ-
\({b^2 – 4ac}\)
= \((-1)^2 – 4.10.3\)
= \(1 – 120\)
= -119 < 0
- সুতরাং 10x2 – x + 3 =0 সমীকরণের কোনো বাস্তব বীজ নেই।
(viii) 25x2 – 30x + 7 = 0
সমাধানঃ-
∴ শ্রীধর আচার্যের সূত্র প্রয়োগ করে পাই,
\( x = \frac{-b\pm \sqrt {b^2 – 4ac}}{2a}\)
বা, \( x = \frac{-(-30)\pm \sqrt {(-30)^2 – 4.25.7}}{2.25}\)
বা, \( x = \frac{30\pm \sqrt {900 – 700}}{50}\)
বা, \( x = \frac{30\pm \sqrt {200}}{50}\)
বা, \( x = \frac{30\pm 10 \sqrt {2}}{50}\)
অতএব হয়
\( x = \frac{30 + 10 \sqrt {2}}{50} = \frac{3 + \sqrt {2}}{5} \)
অথবা,
\( x = \frac{30 – 10 \sqrt {2}}{50} = \frac{3 – \sqrt {2}}{5} \)
(ix) (4x-2)2 + 6x = 25
সমাধানঃ-
| (4x-2)2 + 6x = 25 |
| বা, 16x2 – 2.4x.2 + 4 + 6x = 25 |
| বা, 16x2 – 16x + 6x + 4 – 25 = 0 |
| বা, 16x2 – 10x – 21 = 0 |
∴ শ্রীধর আচার্যের সূত্র প্রয়োগ করে পাই,
\( x = \frac{-(-10)\pm \sqrt {(-10)^2 – 4.16(-21)}}{2.16}\)
বা, \( x = \frac{10\pm \sqrt {100 + 1344}}{32}\)
বা, \( x = \frac{10\pm \sqrt {1444}}{32}\)
বা, \( x = \frac{10\pm 38}{32}\)
অতএব হয়
\( x = \frac{10 + 38}{32} = \frac{3}{2}\)
অথবা, \( x = \frac{10 – 38}{32} = -\frac{7}{8}\)
- (4x-2)2 + 6x = 25 সমীকরণের বীজদ্বয় \(\frac{3}{2}\) ও \(-\frac{7}{8}\)
3 . নিম্নলিখিত গাণিতিক সমস্যাগুলি একচলবিশিষ্ট দ্বিঘাত সমীকরণে প্রকাশ করি এবং শ্রীধর আচার্যের সূত্র প্রয়োগ করে বা উৎপাদকের সাহায্যে সমাধান করি।
(i) সাথি একটি সমকোণী ত্রিভুজ অঙ্কন করেছে যার অতিভুজের দৈর্ঘ্য ক্ষুদ্রতম বাহুর দ্বিগুণ অপেক্ষা 6 সেমি. বেশি। যদি তৃতীয় বাহুর দৈর্ঘ্য অতিভুজের দৈর্ঘ্যের থেকে 2 সেমি. কম হয়, তবে সাথির আঁকা সমকোণী ত্রিভুজের বাহু তিনটির দৈর্ঘ্য হিসাব করে লিখি।
সমাধানঃ-
ধরি, ক্ষুদ্রতম বাহুর দৈর্ঘ্য = x সেমি.
তাহলে,
| অতিভুজের দৈর্ঘ্য | 2x + 6 সেমি. |
| তৃতীয় বাহুর দৈর্ঘ্য | 2x + 4 সেমি. |
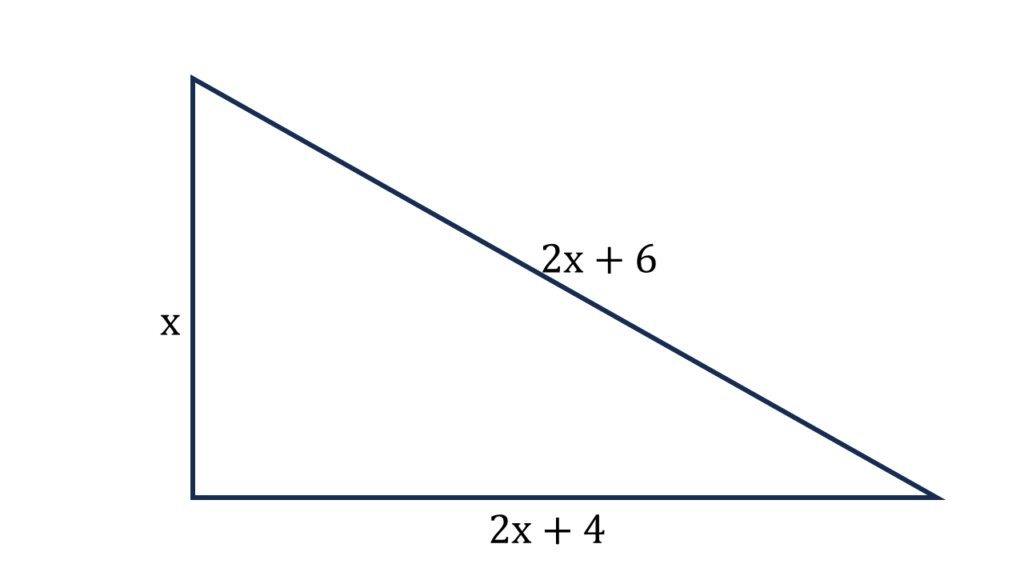
পিথাগোরাসের উপপাদ্য প্রয়গ করে পাই,
| (লম্ব)2 + (ভূমি)2 = (অতিভুজ)2 |
| বা, x2 + (2x + 4)2 = (2x + 6)2 |
| বা, x2 + 4x2 + 16x + 16 = 4x2 + 24x + 36 |
| বা, x2 – 8x – 20 = 0 |
∴ শ্রীধর আচার্যের সূত্র প্রয়োগ করে পাই,
\( x = \frac{-b\pm \sqrt {b^2 – 4ac}}{2a}\)
বা, \( x = \frac{-(-8)\pm \sqrt {(-8)^2 – 4.1(-20)}}{2.1}\)
বা, \( x = \frac{8\pm \sqrt {64 + 80}}{2}\)
বা, \( x = \frac{8\pm \sqrt {144}}{2}\)
বা, \( x = \frac{8\pm 12}{2}\)
অতএব হয়
\( x = \frac{8 + 12}{2} = 10\)
অথবা,
\( x = \frac{8 – 12}{2} = – 2\)
যেহেতু বাহুর দৈর্ঘ্য ঋণাত্মক হয়না সেহেতু x = 10
- সমকোণী ত্রিভুজের বাহুর দৈর্ঘ্য-
| ক্ষুদ্রতম বাহুর দৈর্ঘ্য | 10 সেমি. |
| অতিভুজের দৈর্ঘ্য | 2×10 + 6 = 26 সেমি. |
| তৃতীয় বাহুর দৈর্ঘ্য | 2×10 + 4 = 24 সেমি. |
(ii) যদি দুই অঙ্কের একটি ধনাত্মক সংখ্যাকে উহার এককের ঘরের অঙ্ক দিয়ে গুণ করলে গুণফল 189 হয় এবং দশকের ঘরের অঙ্ক এককের ঘরের অঙ্কের দ্বিগুণ হয়, তবে এককের ঘরের অঙ্কটি নির্ণয় করি।
সমাধানঃ-
ধরি, সংখ্যাটির এককের ঘরের অংক x , তাহলে দশকের ঘরের অংকটি হবে 2x ।
সংখ্যাটি হবে
10×2x + x = 21x
শর্তে,
| \(x \times 21x = 189\) |
| বা, \(x^2 = 9\) |
| বা, \(x = \pm 3 \) |
যেহেতু কোনো সংখ্যার অংক একটি ধনাত্মক সংখ্যা সেহেতু x = 3 হবে।
- এককের ঘরের অংকটি হলো 3
(iii) সালমার গতিবেগ অণিকের গতিবেগের থেকে 1 মি./সেকেন্ড বেশি। 180 মিটার দৌড়াতে গিয়ে সালমা অণিকের থেকে 2 সেকেন্ড আগে পৌঁছায়। অণিকের গতিবেগ প্রতি সেকেন্ডে কত মিটার হিসাব করে লিখি।
সমাধানঃ-
ধরি, অনিকের গতিবেগ \(v\) মি./সেকেন্ড, তাহলে সালমার গতিবেগ হবে \(v+1\) মি./সেকেন্ড
শর্তে,
| \(\frac{180}{v} – \frac{180}{v+1} = 2\) |
| বা, \(90 = v^2 + v\) |
| বা, \(v^ + v – 90 = 0\) |
| বা, \(v^2 + 10v – 9v – 90 = 0\) |
| বা, \(v(v + 10) – 9(v + 10) = 0\) |
| বা, \((v+10)(v – 9) = 0\) |
| ∴ \(v = 9\) অথবা -10 |
| যেহেতু গতিবেগ এখানে ধনাত্মক সেহেতু x = 9 |
- অনিকের গতিবেগ সেকেন্ডে 9 মিটার.
(iv) আমাদের পাড়ায় একটি বর্গক্ষেত্রাকার পার্ক আছে। ওই পার্কের একটি বাহুর দৈর্ঘ্যের থেকে 5 মিটার বেশি দৈর্ঘ্য বিশিষ্ট ও ওই পার্কের বাহুর দৈর্ঘ্য থেকে 3 মি. কম প্রস্থবিশিষ্ট একটি আয়তক্ষেত্রাকার পার্কের ক্ষেত্রফল ওই বর্গক্ষেত্রাকার পার্কের ক্ষেত্রফলের দ্বিগুণ অপেক্ষা 78 বর্গ মিটার কম হলে বর্গক্ষেত্রাকার পার্কের বাহুর দৈর্ঘ্য হিসাব করে লিখি।
সমাধানঃ-
ধরি, বর্গক্ষেত্রের বাহুর দৈর্ঘ্য = x মিটার.
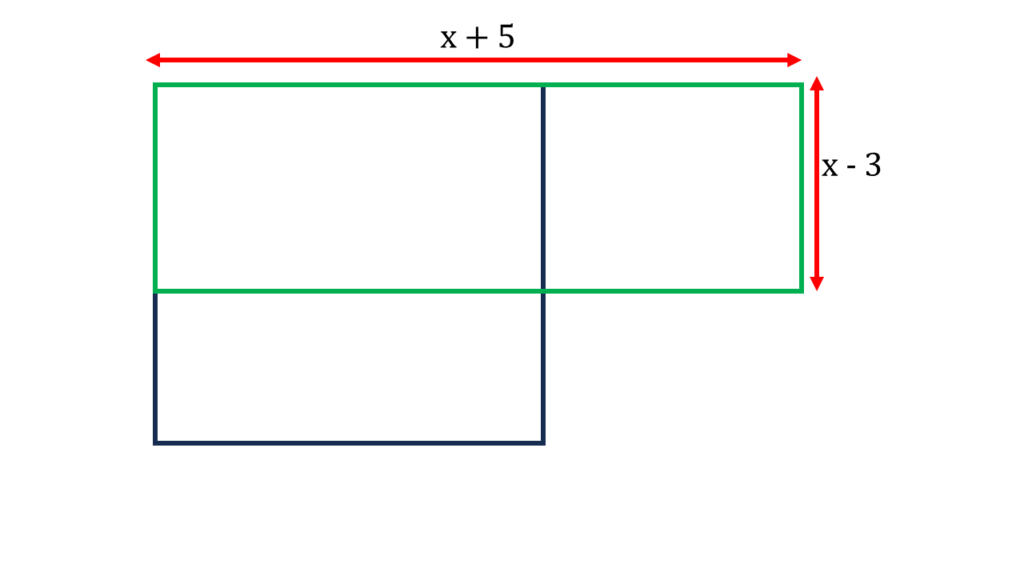
অতএব আয়তক্ষেত্রকার পার্কের,
| দৈর্ঘ্য | x + 5 মিটার. |
| প্রস্থ | x – 3 মিটার. |
| ক্ষেত্রফল | (x + 5) (x – 3) = x2 + 2x – 15 মিটার. |
শর্তে,
| x2 + 2x – 15 = 2x2 – 78 |
| বা, x2 – 2x – 63 = 0 |
| বা, x2 – 9x + 7x – 63 = 0 |
| বা, x(x – 9) + 7(x – 9) = 0 |
| বা, (x – 9)(x + 7) = 0 |
| অতএব x = 9 অথবা – 7 |
| যেহেতু বাহুর দৈর্ঘ্য ধনাত্মক সেহেতু x = 9 |
- ∴ বর্গক্ষেত্রাকার পার্কের বাহুর দৈর্ঘ্য 9 মিটার.
(v) আমাদের গ্রামে প্রলয়বাবু তার আয়তক্ষেত্রাকার জমিতে লাগানোর জন্য মোট 350টি লঙ্কার চারা কিনলেন। সারি ধরে চারাগাছ লাগাতে গিয়ে দেখলেন যে, প্রতিটি সারিতে সারির সংখ্যা থেকে 24টি করে বেশী গাছ লাগালে আরও 10টি গাছ অতিরিক্ত থাকে। সারির সংখ্যা হিসাব করে লিখি।
সমাধানঃ-
ধরি, সারির সংখ্যা = x টি।
শর্তে,
| x(x + 24) = 340 |
| বা, x2 + 24x – 340 = 0 |
| বা, x2 + 34x – 10x – 340 = 0 |
| বা, x(x + 34) – 10(x + 34) = 0 |
| বা, (x + 34)(x – 10) = 0 |
| অতএব x = – 34 অথবা 10 |
| যেহেতু সারির সংখ্যা ধনাত্মক সেহেতু x = 10 |
- নির্ণেয় সারির সংখ্যা = 10 টি.
(vi) জোসেফ এবং কুন্তল একটি কারখানায় কাজ করে। জোসেফ একটি জিনিস তৈরি করতে কুণ্ডলের চেয়ে 5 মিনিট কম সময় নেয়। ঘেণ্টা কাজ করে জোসেফ, কুন্তলের চেয়ে 6টি জিনিস বেশি তৈরি করে। কুন্তল ওই সময়ে কয়টি জিনিস তৈরি করে হিসাব করে লিখি।
সমাধানঃ-
ধরি, কুন্তলের একটি জিনিস করতে সময় লাগে x মিনিট, তাহলে জোসেফের একটি জিনিস করতে সময় লাগবে x – 5 মিনিট.
এখন কুন্তল
| x মিনিটে তৈরি করে 1 টি জিনিস |
| 6 ঘণ্টা= 360 মিনিটে তৈরি করে \(\frac{360}{x}\) টি জিনিস। |
অতএব 360 মিনিটে জোসেফ তৈরি করবে \(\frac{360}{x-5}\) টি জিনিস।
শর্তে,
| \(\frac{360}{x-5} – \frac{360}{x} = 6\) |
| বা, \(360(\frac{x – x + 5}{x(x – 5)} = 6\) |
| বা, \(60 \times 5 = x^2 – 5x\) |
| বা, \(x^2 – 5x – 300 = 0\) |
| বা, \(x^2 – 20x + 15x – 300 = 0\) |
| বা, \(x(x – 20) + 15(x – 20) = 0\) |
| বা, \((x – 20)(x + 15) = 0\) |
| অতএব x = 20 অথবা – 15 |
| যেহেতু জিনিসের সংখ্যা ধনাত্মক সেহেতু x = 20 |
সুতরাং ওই সময়ে কুন্তল জিনিস তৈরি করবে
= \(\frac{360}{20} = 18\) টি
(vii) স্থিরজলে একটি নৌকার গতিবেগ 8 কিমি/ঘণ্টা। নৌকাটি 5 ঘণ্টায় স্রোতের অনুকূলে 15 কিমি. এবং স্রোতের প্রতিকূলে 22 কিমি. গেলে, স্রোতের বেগ কত ছিল হিসাব করে লিখি।
সমাধানঃ-
ধরি, স্রোতের গতিবেগ = \(x\) কিমি/ঘণ্টা
শর্তে,
| \(\frac{15}{8 + x} + \frac{22}{8 – x} = 5\) |
| বা, \(\frac{15(8 – x) + 22(8 + x)}{(8-x)(8+x)} = 5) |
| বা, \(\frac{120 – 15x + 176 + 22x)}{(64-x^2)} = 5) |
| বা, \(\frac{296 + 7x}{(64-x^2)} = 5) |
| বা, \(296 + 7x = 320 – 5x^2\) |
| বা, \(5x^2 + 7x – 24 = 0\) |
| বা, \(5x^2 + 15x – 8x – 24 = 0\) |
| বা, \(5x(x + 3) – 8(x + 3) = 0\) |
| বা, \((x + 3)(5x – 8) = 0\) |
| অতএব x = -3 অথবা \(\frac{8}{5}\) |
| যেহেতু গতিবেগ ঋণাত্মক নয় সেহেতু x = \(\frac{8}{5} = 1\frac{3}{5}\) |
- স্রোতের বেগ = \(1\frac{3}{5}\ কিমি/ঘণ্টা
(viii) একটি সুপারফাস্ট ট্রেন একটি এক্সপ্রেস ট্রেনের থেকে ঘণ্টায় 15 কিমি. বেশি বেগে যায়। একইসঙ্গে একটি স্টেশন থেকে ছেড়ে 180 কিমি. দূরে অন্য একটি স্টেশনে সুপারফাস্ট ট্রেনটি 1 ঘণ্টা আগে পৌঁছাল। সুপারফাস্ট ট্রেনটির গতিবেগ ঘণ্টায় কত কিমি. ছিল নির্ণয় করি।
সমাধানঃ-
ধরি, এক্সপ্রেস ট্রেনের গতিবেগ ঘণ্টায় \(v\) কিমি. , তাহলে সুপারফাস্ট ট্রেনের গতিবেগ হবে \(v\) + 15 কিমি/ঘণ্টা.
শর্তে,
| \(\frac{180}{v} – \frac{180}{v + 15} = 1\) |
| বা, \(180(\frac{v + 15 – v}{v(v + 15}) = 1\) |
| বা, \(180\times 15 = v^2 + 15v\) |
| বা, \(v^2 + 15v – 2700 = 0\) |
| বা, \(v^2 + 60v – 45v – 2700 = 0\) |
| বা, \(v(v + 60) – 45(v + 60) = 0\) |
| বা, \((v + 60)(v – 45) = 0\) |
| অতএব \(v = 45\) |
- সুতরাং সুপারফাস্ট ট্রেনের গতিবেগ = 45 + 15 = 60 কিমি/ঘণ্টা.
(ix) রেহানা বাজারে গিয়ে দেখল প্রতি কিগ্রা মাছের যা দাম, ডালের দাম তা থেকে প্রতি কিগ্রা 20 টাকা কম এবং চালের দাম প্রতি কিগ্রা. 40 টাকা কম। রেহানা 240 টাকার মাছ ও 240 টাকার ডাল কিনে মোটা যে পরিমাণ মাছ ও ডাল পেল তা 280 টাকায় চাল কেনার পরিমাণের সমান। রেহানা প্রতি কিগ্রা মাছ কী দামে কিনেছিল হিসাব করি।
সমাধানঃ-
ধরি, প্রতি কিগ্রা মাছের দাম = \(x \) টাকা
শর্তে,
\(\frac{240}{x} + \frac{240}{x-20} = \frac{280}{x-40}\)
বা, \(24(\frac{x-10+x}{x(x-20)}) = \frac{28}{x-40}\)
বা, \(\frac{12(x – 10)}{x^2 – 20x} = \frac{7}{x-40}\)
বা, 12(x – 10)(x – 40) = 7(x2 – 20x)
বা, 12(x2 – 50x + 400) = 7x2 – 140x
বা, 12x2 – 600x + 4800 = 7x2 – 1400x
বা, 5x2 – 460x + 4800 = 0
বা, x2 – 92x + 960 = 0
বা, x2 – 80x – 12x + 960 = 0
বা, x(x – 80) – 12(x – 80) = 0
বা, (x – 80)(x – 12) = 0
অতএব x = 80 অথবা x = 12
এখানে x = 12 হলে চাল ও মাছের দাম ঋণাত্মক হয়ে যাবে যা বাস্তব নয়। সুতরাং x = 80
- সুতরাং প্রতি কিগ্রা মাছে দাম 80 টাকা.
| একচলবিশিষ্ট দ্বিঘাত সমীকরণ অধ্যায়ের বাকি কষে দেখি – | |
|---|---|
 | কষে দেখি 1.1 |
| কষে দেখি 1.2 | |
| কষে দেখি 1.3 | |
| কষে দেখি 1.5 | |
Class 10 WBBSE এর বাকি অধ্যায়ের সমাধান-
| অধ্যায় | সমাধান |
| 1. একচলবিশিষ্ট দ্বিঘাত সমীকরণ (Quadratic Equations with one variable) | কষে দেখি 1.1 |
| কষে দেখি 1.2 | |
| কষে দেখি 1.3 | |
| কষে দেখি 1.4 | |
| কষে দেখি 1.5 | |
| 2. সরল সুদকষা (Simple Interest) | কষে দেখি 2 |
| 3. বৃত্ত সম্পর্কিত উপপাদ্য (Theorems related to circle) | কষে দেখি 3.1 |
| কষে দেখি 3.2 | |
| 4. আয়তঘন (Rectangular Parallelopiped or Cuboid) | কষে দেখি 4 |
| 5. অনুপাত ও সমানুপাত ( Ratio and Proportion) | কষে দেখি 5.1 |
| কষে দেখি 5.2 | |
| কষে দেখি 5.3 | |
| 6. চক্রবৃদ্ধি সুদ ও সমহার বৃদ্ধি বা হ্রাস (Compound Interest and Uniform Rate of Increase or Decrease) | কষে দেখি 6.1 |
| কষে দেখি 6.2 | |
| 7. বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য (Theorems related to Angles in a Circle) | কষে দেখি 7.1 |
| কষে দেখি 7.2 | |
| কষে দেখি 7.3 | |
| 8. লম্ব বৃত্তাকার চোঙ (Right Circular Cylinder) | কষে দেখি 8 |
| 9. দ্বিঘাত করণী (Quadratic Surd). | কষে দেখি 9.1 |
| কষে দেখি 9.2 | |
| কষে দেখি 9.3 | |
| 10. বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য (Theorems related to Cyclic Quadrilateral) | কষে দেখি 10 |
| 11. সম্পাদ্য : ত্রিভুজের পরিবৃত্ত ও অন্তবৃত্ত অঙ্কন | কষে দেখি 11 |
| 12. গোলক (Sphere) | কষে দেখি 12 |
| 13. ভেদ (Variation) | কষে দেখি 13 |
| 14. অংশীদারি কারবার (Partnership Business) | কষে দেখি 14 |
| 15. বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য (Theorems related to Tangent to a Circle) | কষে দেখি 15.1 |
| কষে দেখি 15.2 | |
| 16. লম্ব বৃত্তাকার শঙ্কু (Right Circular Cone) | কষে দেখি 16 |
| 17. সম্পাদ্য : বৃত্তের স্পর্শক অঙ্কন (Construction: Construction of Tangent to a circle) | কষে দেখি 17 |
| 18. সদৃশতা (Similarity) | কষে দেখি 18.1 |
| কষে দেখি 18.2 | |
| কষে দেখি 18.3 | |
| কষে দেখি 18.4 | |
| 19. বিভিন্ন ঘনবস্তু সংক্রান্ত বাস্তব সমস্যা (Real life Problems related to different Solid Objects) | কষে দেখি 19 |
| 20. ত্রিকোণমিতি : কোণ পরিমাপের ধারণা (Trigonometry: Concept of Measurment of Angle) | কষে দেখি 20 |
| 21. সম্পাদ্য : মধ্যসমানুপাতী নির্ণয় (Construction: Determination of Mean Proportional) | কষে দেখি 21 |
| 22. পিথাগোরাসের উপপাদ্য (Pythagoras Theorem) | কষে দেখি 22 |
| 23. ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি (Trigonometric Ratios and Trigonometric Identities) | কষে দেখি 23.1 |
| কষে দেখি 23.2 | |
| কষে দেখি 23.3 | |
| 24. পূরক কোণের ত্রিকোণমিতিক অনুপাত (Trigonometric Ratios of Complementrary angle) | কষে দেখি 24 |
| 25. ত্রিকোণমিতিক অনুপাতের প্রয়োগ : উচ্চতা ও দূরত্ব (Application of Trigonometric Ratios : Heights & Distances) | কষে দেখি 25 |
| 26. রাশিবিজ্ঞান : গড়, মধ্যমা, ওজাইভ, সংখ্যাগুরুমান (Statistics: Mean, Median, Ogive, Mode) | কষে দেখি 26.1 |
| কষে দেখি 26.2 | |
| কষে দেখি 26.3 | |
| কষে দেখি 26.4 |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  |
এই কষে দেখি 1.4 Class 10|Koshe Dekhi 1.4 Class 10 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।

এখানে তোমরা তোমাদের দশম শ্রেণীতে| Class 10 এ কি কি পড়ানো হয়, মানে তোমাদের দশম শ্রেণীতে| Class 10 সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

