শ্রেণী- দশম ; অধ্যায় – বিভিন্ন ঘনবস্তু সংক্রান্ত সমস্যা ; কষে দেখি 19
কষে দেখি 19 Class 10 অংকের সূচিপত্র:-
কষে দেখি 19 Class 10 এর অংকের সমাধান গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ
এই কষে দেখি 19, পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদ | WBBSE এর অন্তর্গত দশম শ্রেণি|Class 10 এর 19 নম্বর অধ্যায়|Chapter 19, বিভিন্ন ঘনবস্তু সংক্রান্ত বাস্তব সমস্যা | Real Life Problems Related to Different Solid Objects এর অনুশীলনী।
এই কষে দেখি 19 Class 10 এর অঙ্ক গুলি বোঝার জন্যে যে যে বিষয় জানতে হবে তা আলোচনা করা হলো–
এই অনুশীলনীর অংক গুলি করার সময় তোমরা এর আগে যে আয়তঘন, গোলক, লম্ব বৃত্তাকার চোঙ ও শঙ্কু অধ্যায় গুলি পড়েছ সেগুলি একবার দেখে নেবে। যেমন- আয়তঘন এর আয়তন, গোলকের আয়তন, চোঙের আয়তন ইত্যাদির সূত্র।
আগামিতে এই কষে দেখি 19 Class 10 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| কষে দেখি 19 Class 10 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 19 Class 10 তারপর  |
কষে দেখি 19 Class 10|Koshe Dekhi 19 Class 10
1. আনোয়ারদের বাড়ির সামনে একটি নিরেট লোহার স্তম্ভ আছে যার নীচের অংশ লম্ব বৃত্তাকার চোঙ আকৃতির এবং উপরের অংশ শঙ্কু আকৃতির। এদের ভূমিতলের ব্যাসের দৈর্ঘ্য 20 সেমি., চোঙাকৃতি অংশের উচ্চতা 2.8 মিটার এবং শঙ্কু আকৃতি অংশের উচ্চতা 42 সেমি.। । ঘন সেমি. লোহার ওজন 7.5 গ্রাম হলে, লোহার স্তম্ভের ওজন কত হবে তা হিসাব করে লিখি।
সমাধানঃ-

লম্ব বৃত্তাকার চোঙাকৃতির,
| ভুমিতলের ব্যাসার্ধ | \(r\) = \(\frac{20}{2}\) = 10 সেমি. |
| উচ্চতা | \(h_1\) = 2.8 মিটার. = 280 সেমি. |
শঙ্কু আকৃতির,
| উচ্চতা | \(h_2\) = 42 সেমি. |
লোহার স্তম্ভটির আয়তন
| = লম্ব বৃত্তাকার চোঙাকৃতির আয়তন + শঙ্কু আকৃতির আয়তন |
| = \(πr^2h_1 + \frac{1}{3}πr^2h_2\) |
| = \(\frac{22}{7}\times (10)^2 \times 280 + \frac{1}{3}\times \frac{22}{7} \times (10)^2 \times 42\) |
| = 22×100×40 + 22×100×2 |
| = 88000 + 4400 |
| = 92400 ঘন সেমি. |
এখন 1 ঘন সেমি. লোহার ওজন 7.5 গ্রাম।
অতএব,
- 92400 ঘন সেমি. লোহার ওজন হবে
= 92400×7.5
= 693000 গ্রাম
= 693 কিগ্রা.
2. একটি নিরেট লম্ব বৃত্তাকার শঙ্কুর উচ্চতা 20 সেমি. এবং তির্যক উচ্চতা 25 সেমি । শঙ্কুটির সমান আয়তনবিশিষ্ট একটি নিরেট লম্ব বৃত্তাকার চোঙের উচ্চতা 15 সেমি. হলে, চোঙটির ভূমিতলের ব্যাসের দৈর্ঘ্য হিসাব করে লিখি।
সমাধানঃ-

লম্ব বৃত্তাকার শঙ্কুর,
| উচ্চতা | \(h_1\) = 20 সেমি. |
| তির্যক উচ্চতা | \(l\) = 25 সেমি. |
| অতএব, ভুমিতলের ব্যাসার্ধ | \(r = \sqrt{l^2-{h_1}^2}\) = \(\sqrt{625 – 400}\) = \(\sqrt{225}\) = 15 সেমি. |
লম্ব বৃত্তাকার চোঙের ,
| ভূমির ব্যাসার্ধ | \(p\) (ধরি) |
| উচ্চতা | \(h_2\) = 15 সেমি. |
প্রশ্নানুসারে,
| লম্ব বৃত্তাকার চোঙের আয়তন = লম্ব বৃত্তাকার শঙ্কুর আয়তন |
| বা, \(πP^2h_2 = \frac{1}{3}πr^2h_1\) |
| বা, \(p^2 \times 15 = \frac{1}{3}\times (15)^2 \times 20\) |
| বা, \(p^2 = \frac{225 \times 20}{3 \times 15}\) |
| বা, \(p^2 = 100\) |
| বা, \(p = 10\) |
| বা, \(2p = 20\) |
অতএব,
- চোঙটির ভূমিতলের ব্যাসের দৈর্ঘ্য = 20 সেমি.
3. 24 সেমি দৈর্ঘ্যের ব্যাসবিশিষ্ট একটি লম্ব বৃত্তাকার চোঙাকৃতি পাত্রে কিছু জল আছে। 6 সেমি. দৈর্ঘ্যের ভূমিতলের ব্যাস ও 4 সেমি উচ্চতাবিশিষ্ট 60 টি নিরেট শঙ্কু আকৃতির লোহার টুকরো ওই জলে সম্পূর্ণভাবে নিমজ্জিত করলে, জলতলের উচ্চতা কতটা বৃদ্ধি পাবে হিসাব করে লিখি।
সমাধানঃ-
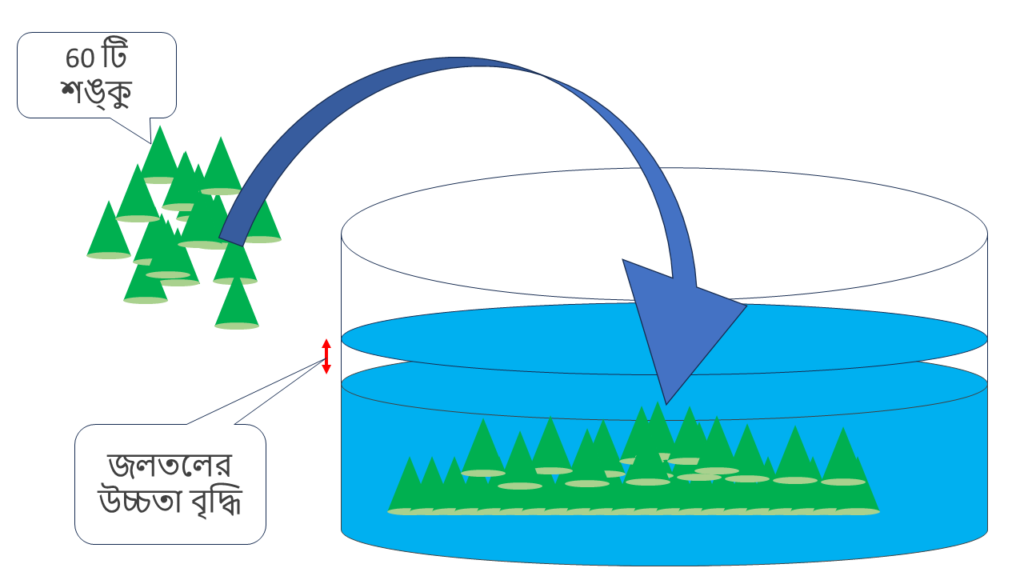
60 টি শঙ্কুর আয়তন
| \(= 60 \times \frac{1}{3} π\times (\frac{6}{2})^2 \times 4 \) |
| \(= 720π\) ঘন সেমি. |
এখন মনে করি 60 টি নিরেট শঙ্কু আকৃতির লোহার টুকরো ওই জলে সম্পূর্ণভাবে নিমজ্জিত করলে, জলতলের উচ্চতা \(h\)সেমি. বৃদ্ধি পাবে।
প্রশ্নানুসারে,
| লম্ব বৃত্তাকার চোঙে বৃদ্ধিপ্রাপ্ত জলের আয়তন = 60 টি শঙ্কুর আয়তন |
| বা, \(π(\frac{24}{2})^2 \times h = 720π\) |
| বা, \(h = \frac{720}{144}\) |
| বা, \( h = 5\) |
অতএব,
- জলতল 5 সেমি. বৃদ্ধি পাবে।
4. একই দৈর্ঘ্যের ভূমিতলের ব্যাসার্ধ এবং একই উচ্চতাবিশিষ্ট একটি নিরেট শঙ্কু ও একটি নিরেট লম্ব বৃত্তাকার চোঙের বক্রতলের ক্ষেত্রফলের অনুপাত 5:8 হলে, উহাদের ভূমির ব্যাসার্ধের দৈর্ঘ্য ও উচ্চতার অনুপাত নির্ণয় করি।
সমাধানঃ-
ধরি,
| ব্যাসার্ধ | = \(r\) (ধরি) |
| উচ্চতা | = \(h\) (ধরি) |
| শঙ্কুর তির্জক উচ্চতা | = \(l\)(ধরি) |
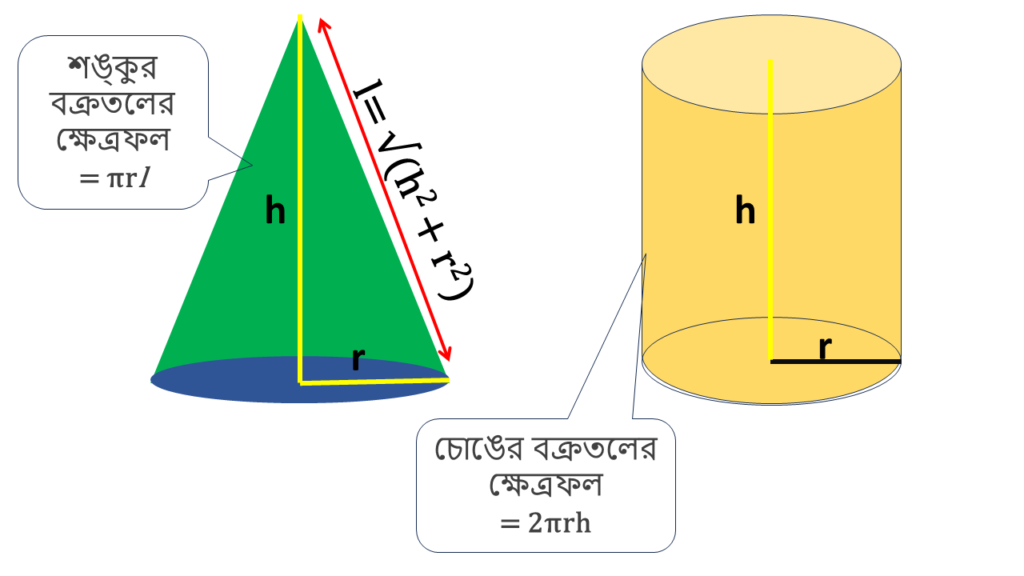
প্রশ্নানুসারে,
| \(πrl : 2πrh = 5 : 8\) |
| বা, \(\frac{l}{2h} = \frac{5}{8}\) |
| বা, \(\frac{l}{h}= \frac{5}{4}\) |
| বা, \(\frac{l^2}{h^2} = \frac{25}{16}\) |
| বা, \(\frac{r^2+h^2}{h^2}=\frac{25}{16}\) |
| বা, \(\frac{r^2}{h^2} + 1 = \frac{25}{16}\) |
| বা, \(\frac{r^2}{h^2} = \frac{25-16}{16}\) |
| বা, \(\frac{r^2}{h^2} = \frac{9}{16}\) |
| বা, \(\frac{r}{h} = \frac{3}{4}\) |
| বা, \(r : h = 3 : 4\) |
5. 8 সেমি. দৈর্ঘ্যের ব্যাসার্ধের একটি নিরেট লোহার গোলককে গলিয়ে 1 সেমি দৈর্ঘ্যের ব্যাসের কয়টি নিরেট গুলি পাওয়া যাবে হিসাব করে দেখি।
সমাধানঃ-

মনে করি, 8 সেমি. দৈর্ঘ্যের ব্যাসার্ধের একটি নিরেট লোহার গোলককে গলিয়ে 1 সেমি দৈর্ঘ্যের ব্যাসের \(n\) টি নিরেট গুলি পাওয়া যাবে।
প্রশ্নানুসারে,
| 1 সেমি দৈর্ঘ্যের ব্যাসের \(n\) টি নিরেট গুলির আয়তন = 8 সেমি. দৈর্ঘ্যের ব্যাসার্ধের নিরেট লোহার গোলকের আয়তন |
| বা, \(n \times \frac{4}{3}π(\frac{1}{2})^3=\frac{4}{3}π8^3\) |
| বা, \(\frac{n}{8} = 512\) |
| বা, \(n = 4096\) |
- 4096 টি নিরেট গুলি পাওয়া যাবে
6. একটি নিরেট লম্ব বৃত্তাকার লোহার দণ্ডের ভূমিতলের ব্যাসার্ধের দৈর্ঘ্য 32 সেমি. এবং দৈর্ঘ্য 35 সেমি.। দণ্ডটি গলিয়ে 8 সেমি. দৈর্ঘ্যের ব্যাসার্ধ ও 28 সেমি. উচ্চতাবিশিষ্ট কতগুলি নিরেট শঙ্কু তৈরি করা যাবে তা হিসাব করে লিখি।
সমাধানঃ-

ধরি, দণ্ডটি গলিয়ে 8 সেমি. দৈর্ঘ্যের ব্যাসার্ধ ও 28 সেমি. উচ্চতাবিশিষ্ট \(n\) সংখ্যক নিরেট শঙ্কু তৈরি করা যাবে।
প্রশ্নানুসারে,
| 8 সেমি. দৈর্ঘ্যের ব্যাসার্ধ ও 28 সেমি. উচ্চতাবিশিষ্ট \(n\) সংখ্যক নিরেট শঙ্কুর আয়তন = 32 সেমি. ব্যাসার্ধ এবং 35 সেমি. উচ্চতা বিশিষ্ট লম্ব বৃত্তাকার দণ্ডের আয়তন |
| বা, \(n \times \frac{1}{3}π\times 8^2 \times 28=π(32)^2 \times 35\) |
| বা, \(n = \frac{32 \times 32 \times 35 \times 3}{8 \times 8 \times 28}\) |
| বা, \(n = 60\) |
- 60 টি নিরেট শঙ্কু তৈরি করা যাবে
7. 4.2 ডেসিমি দৈর্ঘ্যের ধারবিশিষ্ট একটি নিরেট কাঠের ঘনক থেকে সবচেয়ে কম কাঠ নষ্ট করে যে নিরেট লম্ব বৃত্তাকার শঙ্কু পাওয়া যাবে তার আয়তন নির্ণয় করি।
সমাধানঃ-
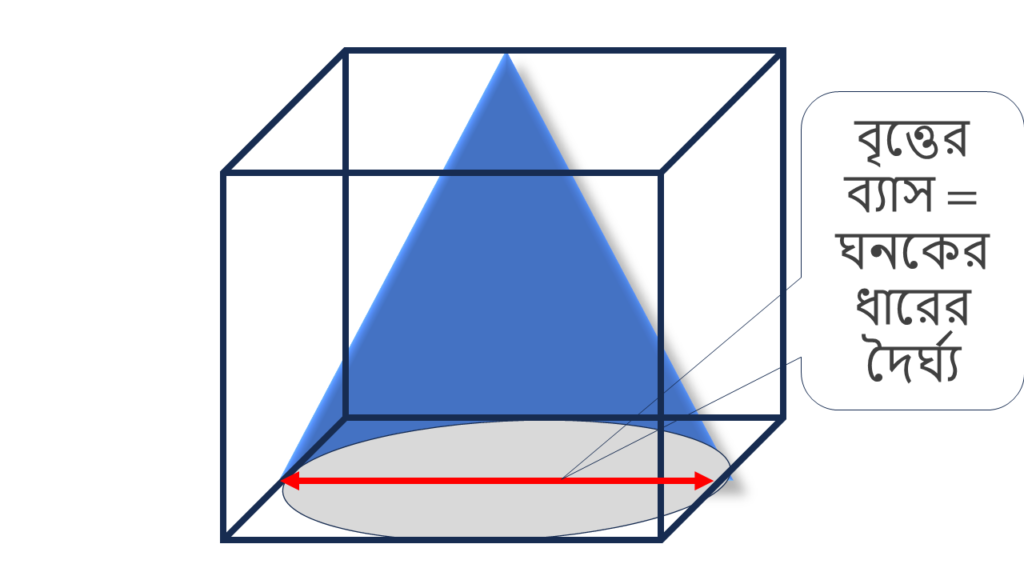
একটি ঘনক থেকে সবচেয়ে কম কাঠ নষ্ট করে যে লম্ব বৃত্তাকার শঙ্কুটি পাওয়া যাবে তার ভূমির ব্যাস এর দৈর্ঘ্য ওই ঘনকের একটি ধারের দৈর্ঘ্যের সমান হবে।
সুতরাং, লম্ব বৃত্তাকার শঙ্কুটির ব্যাসার্ধ = \(\frac{4.2}{2}\) = 2.1 ডেসিমি. এবং উচ্চচতা = 4.2 ডেসিমি.
অতএব, শঙ্কুটির আয়তন
= \(\frac{1}{3}π\times (2.1)^2 \times 4.2\)
= 19.404 ঘন ডেসিমি.
= 19404 ঘন সেমি.
8 . একটি নিরেট গোলক ও একটি নিরেট লম্ব বৃত্তাকার চোঙের ব্যাসার্ধের দৈর্ঘ্য সমান ও তাদের ঘনফলও সমান হলে, চোঙটির ব্যাসার্ধের দৈর্ঘ্য ও উচ্চতার অনুপাত হিসাব করে লিখি ।
সমাধানঃ-
ধরি, ব্যাসার্ধ = \(r\) একক এবং
চোঙের উচ্চতা = \(h\) একক.
প্রশ্নানুসারে,
| গোলকের আয়তন = লম্ব বৃত্তাকার চোঙের আয়তন |
| বা, \(\frac{4}{3}πr^3 = πr^2h\) |
| বা, \(\frac{r}{h} = \frac{3}{4}\) |
| বা, \(r : h = 3 : 4\) |
9. 6.6 ডেসিমি. দীর্ঘ, 4.2 ডেসিমি. প্রশস্ত এবং 1.4 ডেসিমি. পুরু একটি তামার নিরেট আয়তঘনাকার টুকরো গলিয়ে 2.1 ডেসিমি দৈর্ঘ্যের ব্যাসের কয়টি নিরেট গোলক ঢালাই করা যাবে এবং প্রতিটি গোলকে কত ঘন ডেসিমি. ধাতু থাকবে হিসাব করে দেখি।
সমাধানঃ-
2.1 ডেসিমি দৈর্ঘ্যের ব্যাসের নিরেট গোলকে ধাতু থাকবে
= \(\frac{4}{3}π (\frac{2.1}{2})^3\)
= \(\frac{4}{3}\times \frac{22}{7} \times (\frac{2.1}{2})^3\)
= 4.851 ঘন ডেসিমি.
অতএব, নিরেট গোলকের সংখ্যা
= \(\frac{আয়তঘনের আয়তন}{গোলকের আয়তন}\)
= \(\frac{6.6 \times 4.2 \times 1.4}{4.851}\)
= 8 টি.
10. 4.2 সেমি দৈর্ঘ্যের ব্যাসার্ধের একটি সোনার নিরেট গোলক পিটিয়ে 2.8 সেমি দৈর্ঘ্যের ব্যাসের একটি নিরেট লম্ব বৃত্তাকার দণ্ড তৈরি করা হলে, দণ্ডটির দৈর্ঘ্য নির্ণয় করি।
সমাধানঃ-
ধরি, লম্ব বৃত্তাকার দণ্ডটির দৈর্ঘ্য = \(h\) সেমি.
প্রশ্নানুসারে,
| 2.8 সেমি দৈর্ঘ্যের ব্যাস এবং \(h\) সেমি দৈর্ঘ্য বিশিষ্ট নিরেট লম্ব বৃত্তাকার দণ্ডের আয়তন = 4.2 সেমি দৈর্ঘ্যের ব্যাসার্ধের সোনার নিরেট গোলকের আয়তন |
| বা, \(π(\frac{2.8}{2})^2 \times h\) = \(\frac{4}{3}π(4.2)^3 \) |
| বা, \((1.4)^2 \times h\) = \(\frac{4}{3}(4.2)^3 \) |
| বা, \(h = \frac{4\times 4.2 \times 4.2 \times 4.2}{3 \times 1.4 \times 1.4}\) |
| বা, \(h = 50.4\) |
- দণ্ডটির দৈর্ঘ্য = 50.4 সেমি.
11. 6 ডেসিমি দৈর্ঘ্যের ব্যাসের একটি নিরেট রৌপ্য গোলক গলিয়ে 1 ডেসিমি. লম্বা একটি নিরেট লম্ব বৃত্তাকার দণ্ড তৈরি করা হলে, দণ্ডটির ব্যাসের দৈর্ঘ্য হিসাব করে লিখি ।
সমাধানঃ-
মনে করি, দণ্ডটির ব্যাসার্ধের দৈর্ঘ্য = \(r\) ডেসিমি.
প্রশ্নানুসারে,
| \(r\) ডেসিমি. ব্যাসার্ধ এবং 1 ডেসিমি. লম্বা দণ্ডটির আয়তন = 6 ডেসিমি দৈর্ঘ্যের ব্যাসের নিরেট রৌপ্য গোলকের আয়তন |
| বা, \(πr^2 \times 1 = \frac{4}{3}π(\frac{6}{2})^3\) |
| বা, \(r^2 = \frac{4}{3} \times 3^3\) |
| বা, \(r^2 = 4 \times 3^2\) |
| বা, \(r = 2 \times 3\) |
| বা, \(2r = 12\) |
- দণ্ডটির ব্যাসের দৈর্ঘ্য \(2r = 12\) ডেসিমি.
12. একটি নিরেট লম্ব বৃত্তাকার দণ্ডের প্রস্থচ্ছেদের ব্যাসার্ধের দৈর্ঘ্য 3.2 ডেসিমি.। সেই দণ্ডটি গলিয়ে 21টি নিরেট গোলক তৈরি করা হলো। গোলকগুলির ব্যাসার্ধের দৈর্ঘ্য যদি ৪ সেমি হয়, তবে দণ্ডটির দৈর্ঘ্য কত ছিল তা হিসাব করে লিখি।
সমাধানঃ-
লম্ব বৃত্তাকার দণ্ডের প্রস্থচ্ছেদের ব্যাসার্ধের দৈর্ঘ্য
= 3.2 ডেসিমি. = 32 সেমি.
ধরি, লম্ব বৃত্তাকার দণ্ডের দৈর্ঘ্য = \(h\) সেমি.
প্রশ্নানুসারে,
| 32 সেমি. ব্যাসার্ধ এবং \(h\) সেমি দৈর্ঘ্যের লম্ব বৃত্তাকার দণ্ডের আয়তন = 8 সেমি. ব্যাসার্ধের 21 টি গোলকের আয়তন |
| বা, \(π \times (32)^2 \times h = 21 \times \frac{4}{3}π \times 8^3\) |
| বা, \(h = \frac{21 \times 4 \times 8^3}{3 \times 32 \times 32}\) |
| বা, \(h = 14\) |
- লম্ব বৃত্তাকার দণ্ডের দৈর্ঘ্য \(h\) = 14 সেমি.
13. 21 ডেসিমি, দীর্ঘ, 11 ডেসিমি. প্রশস্ত এবং 6 ডেসিমি. গভীর একটি চৌবাচ্চা অর্ধেক জলপূর্ণ আছে। এখন সেই চৌবাচ্চায় যদি 21 সেমি দৈর্ঘ্যের ব্যাসের 100টি লোহার গোলক সম্পূর্ণ ডুবিয়ে দেওয়া হয়, তবে জলতল কত ডেসিমি. উঠবে তা হিসাব করে লিখি।
সমাধানঃ-
গোলক গুলির ব্যাসার্ধ
= \(\frac{21}{2}\) সেমি.
= 10.5 সেমি.
= 1.05 ডেসিমি.
ধরি, চৌবাচ্চায় 21 সেমি. দৈর্ঘ্যের ব্যাসের 100টি লোহার গোলক সম্পূর্ণ ডুবিয়ে দেওয়া হয়, তবে জলতল \(h\) ডেসিমি. উঠবে।
প্রশ্নানুসারে,
| 100 টি গোলক ডোবানোর পর চৌবাচ্চায় বৃদ্ধিপ্রাপ্ত জলের আয়তন = 1.05 ডেসিমি. ব্যাসার্ধের 100 টি গোলকের আয়তন |
| বা, \(21 \times 11 \times h = 100 \times \frac{4}{3} \times π (1.05)^3\) |
| বা, \(h = \frac{100 \times 4 \times 22 \times 1.05 \times 1.05 \times 1.05}{21 \times 11 \times 21}\) |
| বা, \(h = 2.1\) |
- জলতল 2.1 ডেসিমি. উঠবে
14. সমান ভূমিতলের ব্যাস এবং সমান উচ্চতাবিশিষ্ট একটি নিরেট শঙ্কু, একটি নিরেট অর্ধগোলক এবং একটি নিরেট চোঙের আয়তনের অনুপাত নির্ণয় করি।
সমাধানঃ-
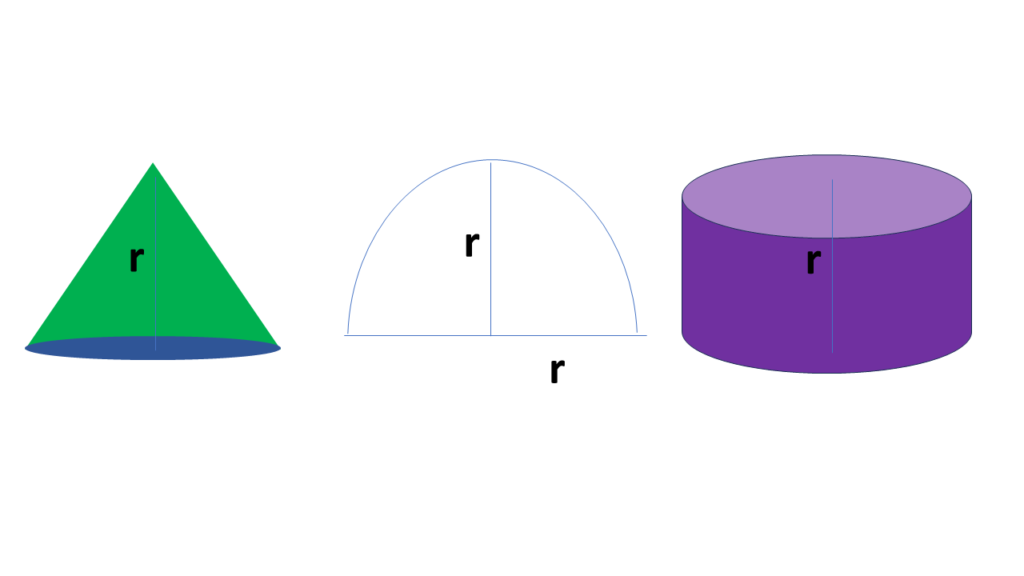
ধরি, ভুমিতলের ব্যাসার্ধ = \(r\) একক.
যেহেতু তিনটি আকৃতির উচ্চতা সমান সেহেতু লম্ব বৃত্তাকার চোঙ এবং লম্ব বৃত্তাকার শঙ্কুর উচ্চতা হবে \(r\) একক.
- নির্নেয় অনুপাত
= \(\frac{1}{3}πr^2.r : \frac{2}{3}πr^3 : πr^2.r\)
= \(\frac{1}{3} : \frac{2}{3} : 1\)
= \(1 : 2 : 3\)
15. 1 সেমি. পুরু সিসার পাতের তৈরি একটি ফাঁপা গোলকের বাহিরের ব্যাসার্ধের দৈর্ঘ্য 6 সেমি.। গোলকটি গলিয়ে 2 সেমি দৈর্ঘ্যের ব্যাসার্ধের একটি নিরেট লম্ব বৃত্তাকার দণ্ড তৈরি করা হলে, দণ্ডটির দৈর্ঘ্য কত হবে হিসাব করে লিখি ।
সমাধানঃ-
ধরি, দণ্ডটির দৈর্ঘ্য = \(h\) সেমি.
প্রশ্নানুসারে,
| 2 সেমি দৈর্ঘ্যের ব্যাসার্ধের এবং \(h\) সেমি. দৈর্ঘ্য বিশিষ্ট নিরেট লম্ব বৃত্তাকার দণ্ড এর আয়তন = 1 সেমি. পুরু এবং বাহিরের ব্যাসার্ধের দৈর্ঘ্য 6 সেমি. বিশিষ্ট ফাঁপা গোলকের আয়তন |
| বা, \(π.2^2.h = \frac{4}{3}π(6^3 – 5^3)\) |
| বা, \(h =\frac{6^3 – 5^3}{3}\) |
| বা, \(h = \frac{216 – 125}{3}\) |
| বা, \(h = \frac{91}{3}\) = \(30\frac{1}{3}\) |
- দণ্ডটির দৈর্ঘ্য = \(30\frac{1}{3}\) সেমি.
16. 2 মিটার লম্বা একটি আয়তঘনাকার কাঠের লগের প্রস্থচ্ছেদ বর্গাকার এবং তার প্রতিটি বাহুর দৈর্ঘ্য 14 ডেসিমি। সবচেয়ে কম কাঠ নষ্ট করে ওই লগটিকে যদি একটি লম্ব বৃত্তাকার গুঁড়িতে পরিণত করা যায়, তবে তাতে কত ঘন মিটার কাঠ থাকবে এবং কত ঘন মিটার কাঠ নষ্ট হবে হিসাব করি।
সমাধানঃ-
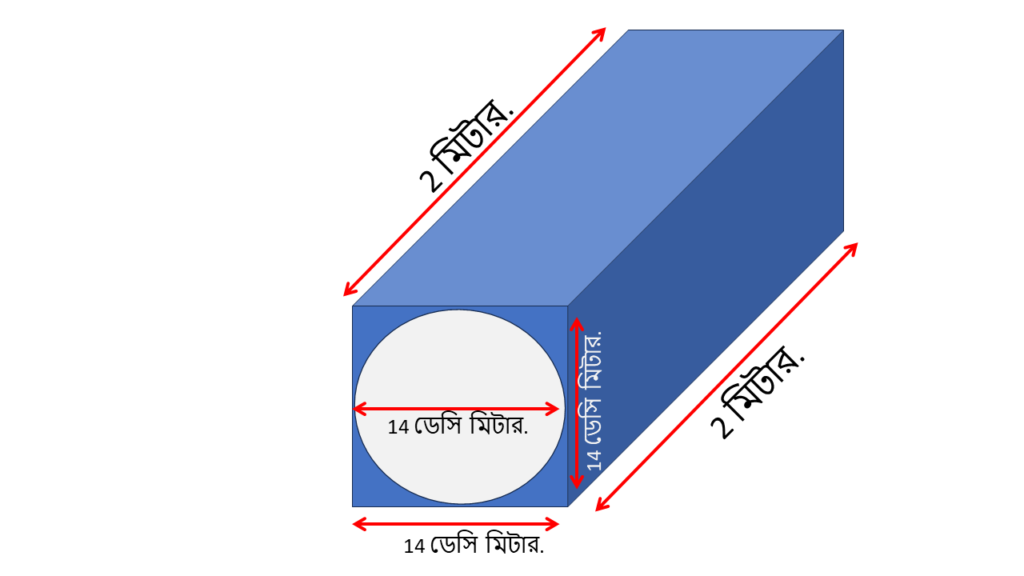
বর্গাকার প্রস্থচ্ছেদের প্রতিটি বাহুর দৈর্ঘ্য
= 14 ডেসিমি.
= 1.4 মিটার.
এখন এই বর্গাকার প্রস্থচ্ছেদের প্রতিটি বাহুর দৈর্ঘ্যই হলো লম্ব বৃত্তাকার গুঁড়ির ব্যাসের দৈর্ঘ্য।
অতএব, লম্ব বৃত্তাকার গুঁড়ির ব্যাসার্ধ
= \(\frac{1.4}{2}\)
= .7 মিটার.
সুতরাং, লম্ব বৃত্তাকার গুঁড়ির আয়তন
= \(\frac{22}{7} \times .7 \times .7 \times 2\)
= 3.08 ঘন মিটার.
আবার, 2 মিটার লম্বা আয়তঘনাকার কাঠের আয়তন
= 1.4×1.4×2
= 3.92 ঘন মিটার.
অতএব, কাঠ নষ্ট হয়েছে
= 3.92 – 3.08
= 0.84 ঘন মিটার.
17. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.)
(i) r একক দৈর্ঘ্যের ব্যাসার্ধবিশিষ্ট একটি নিরেট গোলককে গলিয়ে r একক উচ্চতার একটি নিরেট লম্ব বৃত্তাকার শঙ্কু তৈরি করা হলো। শঙ্কুটির ভূমির ব্যাসার্ধের দৈর্ঘ্য
উত্তরঃ (a) 2r একক
সমাধানঃ-
ধরি, শঙ্কুটির ভূমির ব্যাসার্ধ = \(p\) একক.
প্রশ্নানুসারে,
| শঙ্কুর আয়তন = গোলকের আয়তন |
| বা, \(\frac{1}{3}πp^2.r = \frac{4}{3}πr^3\) |
| বা, \(p^2 = 4r^2\) |
| বা, \(p = 2r\) |
(ii) একটি নিরেট লম্ব বৃত্তাকার শঙ্কুকে গলিয়ে একই দৈর্ঘ্যের ব্যাসার্ধবিশিষ্ট একটি নিরেট লম্ব বৃত্তাকার চোঙ তৈরি করা হলো যার উচ্চতা 5 সেমি. । শঙ্কুটির উচ্চতা
উত্তরঃ (b) 15 সেমি.
সমাধানঃ-
ধরি, শঙ্কুর উচ্চতা = \(h\) সেমি.
প্রশ্নানুসারে,
| শঙ্কুর আয়তন = চোঙের আয়তন |
| বা, \(\frac{1}{3}πr^2.h = πr^2 \times 5\) |
| বা, \(h = 3 \times 5\) |
| বা, \(h = 15\) |
(iii) একটি লম্ব বৃত্তাকার চোঙের ব্যাসার্ধের দৈর্ঘ্য r একক এবং উচ্চতা 2r একক। চোঙটির মধ্যে সর্ববৃহৎ যে গোলকটি রাখা যাবে তার ব্যাসের দৈর্ঘ্য
উত্তরঃ (b) 2r একক
সমাধানঃ-
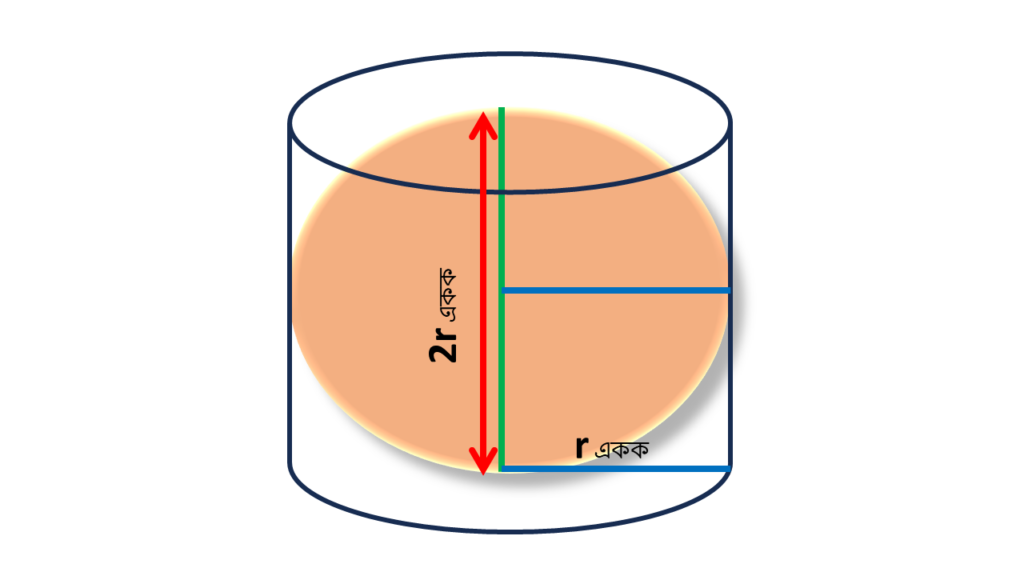
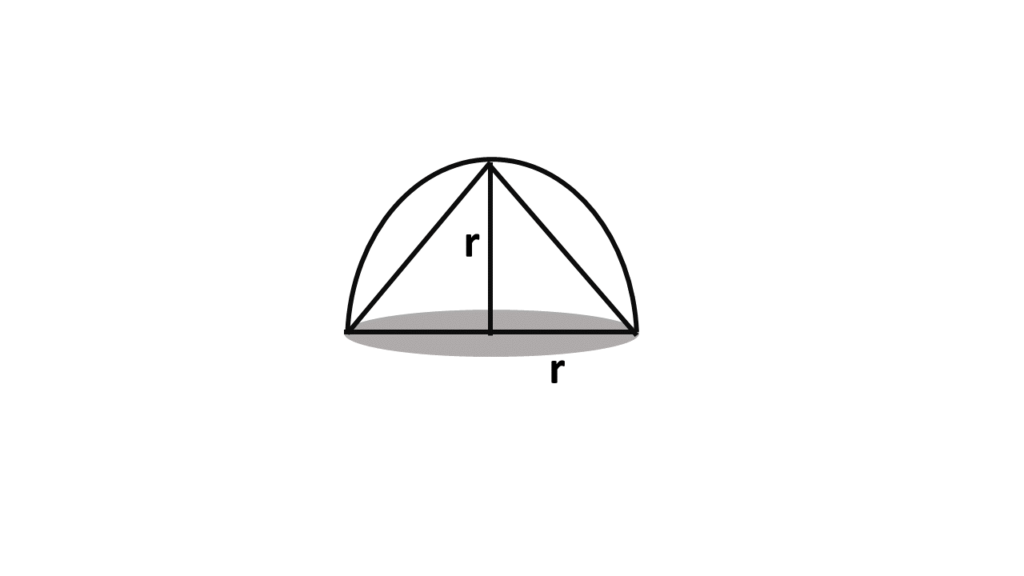
(iv) r একক দৈর্ঘ্যের ব্যাসার্ধবিশিষ্ট একটি নিরেট অর্ধগোলক থেকে সর্ববৃহৎ যে নিরেট শঙ্কু কোটে নেওয়া যাবে তার আয়তন
উত্তরঃ (d) \(\frac{πr^3}{3}\) ঘন একক
সমাধানঃ-
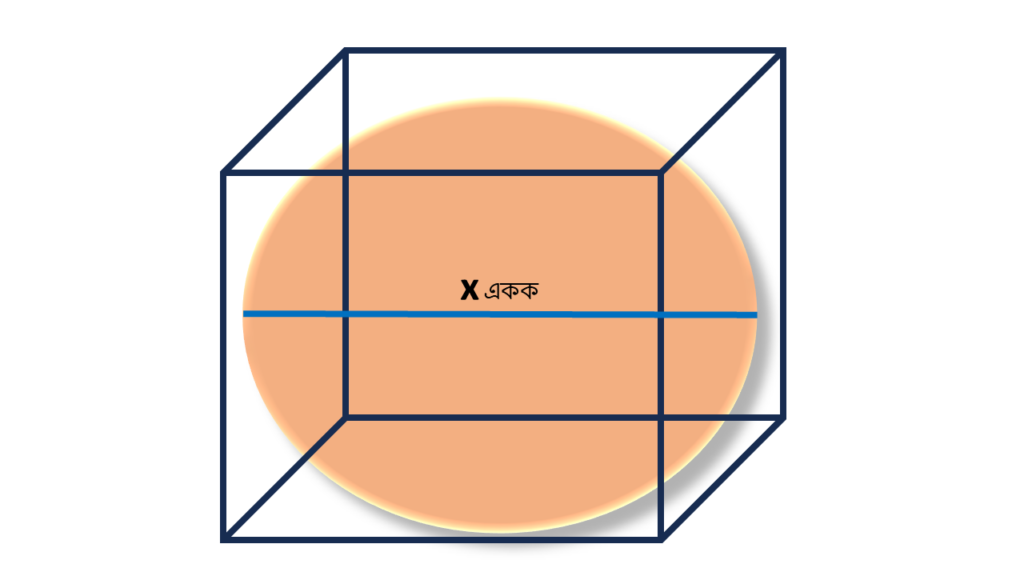
(v) x একক দৈর্ঘ্যের ধারবিশিষ্ট একটি নিরেট ঘনক থেকে সর্ববৃহৎ একটি নিরেট গোলক কেটে নেওয়া হলে, গোলকের ব্যাসের দৈর্ঘ্য
উত্তরঃ (a) x একক
সমাধানঃ-
(B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি :
(i) দুটি একই ধরনের নিরেট অর্ধগোলক যাদের ভূমিতলের প্রত্যেকের ব্যাসার্ধের দৈর্ঘ্য r একক এবং তা ভূমি বরাবর জোড়া হলে, মিলিত ঘনবস্তুর সমগ্রতলের ক্ষেত্রফল হবে 6πr2 বর্গ একক।
উত্তরঃ মিথ্যা
কারণ 2πr2 + 2πr2 = 4πr2
(ii) একটি নিরেট লম্ব বৃত্তাকার শঙ্কুর ভূমিতলের ব্যাসার্ধের দৈর্ঘ্য r একক এবং উচ্চতা h একক এবং তির্যক উচ্চতা \(l\) একক। শঙ্কুটির ভূমিতলকে একটি নিরেট লম্ব বৃত্তাকার চোঙের ভূমিতল বরাবর জুড়ে দেওয়া হলো। যদি চোঙের ও শঙ্কুর ভূমিতলের ব্যাসার্ধের দৈর্ঘ্য এবং উচ্চতা একই হয় তবে মিলিত ঘনবস্তুর সমগ্রতলের ক্ষেত্রফল (πrl + 2πrh + 2πr2) বর্গ একক।
উত্তরঃ মিথ্যা
(C) শূন্যস্থান পূরণ করি :
(i) একটি নিরেট লম্ব বৃত্তাকার চোঙ ও দুটি অর্ধগোলকের ভূমিতলের ব্যাসার্ধের দৈর্ঘ্য সমান। দুটি অর্ধগোলককে চোঙটির দুটি সমতলে আটকে দেওয়া হলে নতুন ঘনবস্তুর সমগ্রতলের ক্ষেত্রফল = একটি অর্ধগোলকের বক্রতলের ক্ষেত্রফল + _____ বক্রতলের ক্ষেত্রফল + অপর অর্ধগোলকটির বক্রতলের ক্ষেত্রফল।
উত্তরঃ চোঙের
(ii) একমুখ কাটা একটি পেনসিলের আকার শঙ্কু ও ________ সমন্বয় ।
উত্তরঃ চোঙের
(iii) একটি নিরেট গোলককে গলিয়ে একটি নিরেট লম্ব বৃত্তাকার চোঙ তৈরি করা হলো। গোলক ও চোঙের আয়তন ________ ।
উত্তরঃ সমান
18. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)
(i) একটি নিরেট লম্ব বৃত্তাকার শঙ্কুকে গলিয়ে একটি নিরেট লম্ব বৃত্তাকার চোঙ তৈরি করা হলো। উভয়ের ব্যাসার্ধের দৈর্ঘ্য সমান। যদি শঙ্কুর উচ্চতা 15 সেমি, হয়, তাহলে নিরেট চোঙের উচ্চতা কত হিসাব করে লিখি।
সমাধানঃ-
ধরি, চোঙের উচ্চতা = \(h\) সেমি.
প্রশ্নানুসারে,
| লম্ব বৃত্তাকার চোঙ এর আয়তন = লম্ব বৃত্তাকার শঙ্কুর আয়তন |
| বা, \(πr^2 .h = \frac{1}{3}πr^2 \times 15\) |
| বা, \(h = \frac{15}{3}\) |
| বা, \(h = 5\) সেমি. |
(ii) একটি নিরেট লম্ব বৃত্তাকার শঙ্কু এবং একটি নিরেট গোলকের ব্যাসার্ধের দৈর্ঘ্য সমান এবং আয়তন সমান। গোলকের ব্যাসের দৈর্ঘ্য এবং শঙ্কুর উচ্চতা অনুপাত কত তা হিসাব করে লিখি।
সমাধানঃ-
ধরি, ব্যাসার্ধ =\(r\) একক এবং
শঙ্কুর উচ্চতা = \(h\) একক.
প্রশ্নানুসারে,
| গোলকের আয়তন = শঙ্কুর আয়তন |
| বা, \(\frac{4}{3}πr^3 = \frac{1}{3}πr^2h\) |
| বা, \(4r = h\) |
| বা, \(2.2r = h\) |
| বা, \(2r : h = 1 : 2\) |
(iii) সমান দৈর্ঘ্যের ব্যাস এবং সমান উচ্চতাবিশিষ্ট নিরেট লম্ব বৃত্তাকার চোঙ, নিরেট লম্ব বৃত্তাকার শঙ্কু এবং নিরেট গোলকের আয়তনের অনুপাত কত তা লিখি।
সমাধানঃ-
নির্ণেয় অনুপাত
= \(πr^.2r : \frac{1}{3}πr^2.2r : \frac{4}{3}πr^3\)
= \(2 : \frac{2}{3} : \frac{4}{3}\)
= \(3 : 1 : 2\)
(iv) একটি ঘনবস্তুর নীচের অংশ অর্ধগোলক আকারের এবং উপরের অংশ লম্ব বৃত্তাকার শঙ্কু আকারের। যদি দুটি অংশের তলের ক্ষেত্রফল সমান হয়, তাহলে ব্যাসার্ধের দৈর্ঘ্য এবং শঙ্কুর উচ্চতার অনুপাত হিসাব করে লিখি।
সমাধানঃ-
ধরি, ব্যাসার্ধ = \(r\) একক এবং
শঙ্কুর তির্যক উচ্চতা এবং উচ্চতা যথাক্রমে \(l\) একক. এবং \(h\) একক.
প্রশ্নানুসারে,
| \(πrl = 2πr^2\) |
| বা, \(l = 2r\) |
| বা, \(l^2 = 4r^2\) |
| বা, \(r^2 + h^2 = 4r^2\) |
| বা, \(3r^2 = h^2\) |
| বা, \(r\sqrt3 = h\) |
| বা, \(\frac{r}{h} = \frac{1}{\sqrt3}\) |
| বা, \(r : h = 1 : \sqrt3+\) |
(v) একটি নিরেট লম্ব বৃত্তাকার শঙ্কুর, ভূমিতলের ব্যাসার্ধের দৈর্ঘ্য একটি নিরেট গোলকের ব্যাসার্ধের দৈর্ঘ্যের সমান। গোলকের আয়তন শঙ্কুর আয়তনের দ্বিগুণ হলে, শঙ্কুর উচ্চতা এবং ভূমিতলের ব্যাসার্ধের দৈর্ঘ্যের অনুপাত কত তা লিখি।
সমাধানঃ-
ধরি, ভুমিতলের ব্যাসার্ধ = \(r\) একক. এবং
শঙ্কুর উচ্চতা = \(h\) একক.
প্রশ্নানুসারে,
| \(2 \times \frac{1}{3}πr^2h = \frac{4}{3}πr^3\) |
| বা, \(h = 2r\) |
| বা, \(\frac{h}{r} = 2\) |
| বা, \(h : r = 2 : 1\) |
Class 10 WBBSE এর বাকি অধ্যায়ের সমাধান-
| অধ্যায় | সমাধান |
| 1. একচলবিশিষ্ট দ্বিঘাত সমীকরণ (Quadratic Equations with one variable) | কষে দেখি 1.1 |
| কষে দেখি 1.2 | |
| কষে দেখি 1.3 | |
| কষে দেখি 1.4 | |
| কষে দেখি 1.5 | |
| 2. সরল সুদকষা (Simple Interest) | কষে দেখি 2 |
| 3. বৃত্ত সম্পর্কিত উপপাদ্য (Theorems related to circle) | কষে দেখি 3.1 |
| কষে দেখি 3.2 | |
| 4. আয়তঘন (Rectangular Parallelopiped or Cuboid) | কষে দেখি 4 |
| 5. অনুপাত ও সমানুপাত ( Ratio and Proportion) | কষে দেখি 5.1 |
| কষে দেখি 5.2 | |
| কষে দেখি 5.3 | |
| 6. চক্রবৃদ্ধি সুদ ও সমহার বৃদ্ধি বা হ্রাস (Compound Interest and Uniform Rate of Increase or Decrease) | কষে দেখি 6.1 |
| কষে দেখি 6.2 | |
| 7. বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য (Theorems related to Angles in a Circle) | কষে দেখি 7.1 |
| কষে দেখি 7.2 | |
| কষে দেখি 7.3 | |
| 8. লম্ব বৃত্তাকার চোঙ (Right Circular Cylinder) | কষে দেখি 8 |
| 9. দ্বিঘাত করণী (Quadratic Surd). | কষে দেখি 9.1 |
| কষে দেখি 9.2 | |
| কষে দেখি 9.3 | |
| 10. বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য (Theorems related to Cyclic Quadrilateral) | কষে দেখি 10 |
| 11. সম্পাদ্য : ত্রিভুজের পরিবৃত্ত ও অন্তবৃত্ত অঙ্কন | কষে দেখি 11 |
| 12. গোলক (Sphere) | কষে দেখি 12 |
| 13. ভেদ (Variation) | কষে দেখি 13 |
| 14. অংশীদারি কারবার (Partnership Business) | কষে দেখি 14 |
| 15. বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য (Theorems related to Tangent to a Circle) | কষে দেখি 15.1 |
| কষে দেখি 15.2 | |
| 16. লম্ব বৃত্তাকার শঙ্কু (Right Circular Cone) | কষে দেখি 16 |
| 17. সম্পাদ্য : বৃত্তের স্পর্শক অঙ্কন (Construction: Construction of Tangent to a circle) | কষে দেখি 17 |
| 18. সদৃশতা (Similarity) | কষে দেখি 18.1 |
| কষে দেখি 18.2 | |
| কষে দেখি 18.3 | |
| কষে দেখি 18.4 | |
| 19. বিভিন্ন ঘনবস্তু সংক্রান্ত বাস্তব সমস্যা (Real life Problems related to different Solid Objects) | কষে দেখি 19 |
| 20. ত্রিকোণমিতি : কোণ পরিমাপের ধারণা (Trigonometry: Concept of Measurment of Angle) | কষে দেখি 20 |
| 21. সম্পাদ্য : মধ্যসমানুপাতী নির্ণয় (Construction: Determination of Mean Proportional) | কষে দেখি 21 |
| 22. পিথাগোরাসের উপপাদ্য (Pythagoras Theorem) | কষে দেখি 22 |
| 23. ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি (Trigonometric Ratios and Trigonometric Identities) | কষে দেখি 23.1 |
| কষে দেখি 23.2 | |
| কষে দেখি 23.3 | |
| 24. পূরক কোণের ত্রিকোণমিতিক অনুপাত (Trigonometric Ratios of Complementrary angle) | কষে দেখি 24 |
| 25. ত্রিকোণমিতিক অনুপাতের প্রয়োগ : উচ্চতা ও দূরত্ব (Application of Trigonometric Ratios : Heights & Distances) | কষে দেখি 25 |
| 26. রাশিবিজ্ঞান : গড়, মধ্যমা, ওজাইভ, সংখ্যাগুরুমান (Statistics: Mean, Median, Ogive, Mode) | কষে দেখি 26.1 |
| কষে দেখি 26.2 | |
| কষে দেখি 26.3 | |
| কষে দেখি 26.4 |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  |
এই কষে দেখি 19 Class 10|Koshe Dekhi 19 Class 10 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।

এখানে তোমরা তোমাদের দশম শ্রেণীতে| Class 10 এ কি কি পড়ানো হয়, মানে তোমাদের দশম শ্রেণীতে| Class 10 সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

