শ্রেণী- দশম ; অধ্যায় – পূরক কোণের ত্রিকোণমিতিক অনুপাত ; কষে দেখি 24
কষে দেখি 24 Class 10 অংকের সূচিপত্র:-
কষে দেখি 24 Class 10 এর অংকের সমাধান গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ
এই কষে দেখি 24, পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদ | WBBSE এর অন্তর্গত দশম শ্রেণি|Class 10 এর 24 নম্বর অধ্যায়|Chapter 24, পূরক কোণের ত্রিকোণমিতিক অনুপাত | Trigonometric Ratio of Complementary Angle এর অনুশীলনী।
এই কষে দেখি 24 Class 10 এর অঙ্ক গুলি বোঝার জন্যে যে যে বিষয় জানতে হবে তা আলোচনা করা হলো–
এই অঙ্কগুলি সমাধান করার জন্যে আমাদের কিছু সূত্র জানতে হবে যেগুলি হলো –
| (i) | \(sin \theta = \cos(90^° – \theta)\) এবং \(\cos \theta = \sin(90^° – \theta)\) |
| (ii) | \(\tan \theta = \cot (90^° – \theta)\) এবং \(\cot \theta = \tan (90^° – \theta)\) |
| (iii) | \(\sec \theta = \csc (90^° – \theta)\) এবং \(\csc \theta = \sec (90^° – \theta)\) |
আগামিতে এই কষে দেখি 24 Class 10 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| কষে দেখি 24 Class 10 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 24 Class 10 তারপর  |
কষে দেখি 24 Class 10|Koshe Dekhi 24 Class 10
1. মান নির্ণয় করি:
(i) \(\frac{\sin 38^°}{\cos 52^°}\)
সমাধানঃ-
| \(\frac{\sin 38^°}{\cos 52^°}\) |
| \(= \frac{\sin (90^° – 52^°)}{\cos 52^°}\) |
| \(= \frac{\cos 52^°}{\cos 52^°}\) |
| \(= 1\) |
(ii) \(\frac{\csc 79^°}{\sec 11^°}\)
সমাধানঃ-
| \(\frac{\csc 79^°}{\sec 11^°}\) |
| \(= \frac{\csc (90^° – 11^°)}{\sec 11^°}\) |
| \(\frac{\sec 11^°}{\sec 11^°}\) |
| \(= 1\) |
(iii) \(\frac{\tan 27^°}{\cot 63^°}\)
সমাধানঃ-
| \(\frac{\tan 27^°}{\cot 63^°}\) |
| \(= \frac{\tan (90^° – 63^°)}{\cot 63^°}\) |
| \(= \frac{\cot 63^°}{\cot 63^°}\) |
| \(= 1\) |
2.দেখাই যে:
(i) \(\sin 66^° – \cos 24^° = 0\)
সমাধানঃ-
| \(\sin 66^° – \cos 24^°\) |
| \(= \sin 66^° – \cos (90^°-66^°\) |
| \(= \sin 66^° – \sin 66^°\) |
| \(= 0 \) |
(ii) \(\cos^2 57^° + \cos^2 33^° = 1\)
সমাধানঃ-
| \(\cos^2 57^° + \cos^2 33^°\) |
| \(= \cos^2 (90^° – 33^°) + \cos^2 33^°\) |
| \(= \sin^2 33^° + \cos^2 33^°\) |
| \(= 1 \) [\(∵ \sin^2 \theta + \cos^2 \theta = 1\)] |
(iii) \(\cos^2 75^° – \sin^2 15^° = 0\)
সমাধানঃ-
| \(\cos^2 75^° – \sin^2 15^°\) |
| \(= \cos^2 75^° – \sin^2 (90^°-75^°)\) |
| \(= \cos^2 75^° – \cos^2 75^°\) |
| \(= 0\) |
(iv) \(\csc^2 48^° – \tan^2 42^° = 1\)
সমাধানঃ-
| \(\csc^2 48^° – \tan^2 42^°\) |
| \(= \csc^2 48^° – \tan^2 (90^°-48^°\) |
| \(= \csc^2 48^° – \cot^2 48^°\) |
| \(= 1\) [\(∵ \csc^2 \theta – \cot^2 \theta = 1] |
(v) \(\sec 70^° \sin 20^° + \cos 20^° \csc 70^° = 2\)
সমাধানঃ-
| \(\sec 70^° \sin 20^° + \cos 20^° \csc 70^°\) |
| \(= \sec 70^° \sin (90^° – 70^°) + \cos (90^°-70^°) \csc 70^°\) |
| \(= \sec 70^° \cos70^° + \sin 70^° \csc 70^°\) |
| \(= 1 + 1\) |
| \(= 2 \) |
3. যদি \(\alpha\) ও \(\beta\) কোণ দুটি পরস্পর পূরক কোণ হয়, তাহলে দেখাই যে,
\(\alpha\) ও \(\beta\) কোণ দুটি পরস্পর পূরক কোণ.
অর্থাৎ, \(\angle \alpha + \angle \beta = 90^°\)
(i) \(\sin^2 \alpha + \sin^2 \beta = 1\)
সমাধানঃ-
| \(\sin^2 \alpha + \sin^2 \beta\) |
| \(= \sin^2 \alpha + \sin^2 (90^° – \alpha)\) [\(∵ \alpha + \beta = 90^°\)] |
| \(= \sin^2 \alpha + \cos^2 \alpha\) |
| \(= 1 \) [\(∵ \sin^2 \theta + \cos^2 \theta = 1\)] |
(ii) \(\cot \beta + \cos \beta = \frac{\cos \beta}{\cos \alpha}(1 + \sin \beta)\)
সমাধানঃ-
| \(\frac{\cos \beta}{\cos \alpha}(1 + \sin \beta)\) |
| \(= \frac{\cos \beta}{\cos \alpha} + \frac{\cos \beta \sin \beta}{\cos \alpha}\) |
| \(= \frac{\cos \beta}{\cos (90^° – \beta)} + \frac{\cos \beta \sin \beta}{\cos (90^° – \beta)}\) [\(∵ \alpha + \beta = 90^°\)] |
| \(= \frac{\cos \beta}{\sin \beta} + \frac{\cos \beta \sin \beta}{\sin \beta}\) |
| \(= \cot \beta + \cos \beta\) |
(iii) \(\frac{\sec \alpha}{\cos \alpha} – \cot^2 \beta = 1\)
সমাধানঃ-
| \(\frac{\sec \alpha}{\cos \alpha} – \cot^2 \beta\) |
| \(= \frac{\sec (90^° – \beta)}{\cos (90^°- \beta)} – \cot^2 \beta\) [\(∵ \alpha + \beta = 90^°\)] |
| \(= \frac{\csc \beta}{\sin \beta} – \cot^2 \beta\) |
| \(= \csc \beta \csc \beta – \cot^2 \beta\) |
| \(= \csc^2 \beta – \cot^2 \beta\) |
| \(= 1 \) [\(∵ \csc^2 \theta – \cot^2 \theta = 1\) ] |
4. যদি \(\sin 17^° = \frac{x}{y}\) হয়, তাহলে দেখাই যে,
\(\sec 17^° – \sin 73^° = \frac{x^2}{y\sqrt{y^2 – x^2}}\)
সমাধানঃ-
| \(\sec 17^° – \sin 73^°\) |
| \(= \frac{1}{\cos 17^°} – \sin (90^° – 17^°)\) |
| \(= \frac{1}{\cos 17^°} – \cos17^°\) |
| \(= \frac{1 – \cos^2 17^°}{\cos 17^°}\) |
| \(= \frac{\sin^2 17^°}{\cos 17^°}\) |
| \(= \frac{\sin^2 17^°}{\sqrt{1 – \sin^2 17^°}}\) |
| \(= \frac{(\frac{x}{y})^2}{\sqrt{1 – (\frac{x}{y})^2}}\) |
| \(= \frac{\frac{x^2}{y2}}{\sqrt{1 – \frac{x^2}{y^2}}}\) |
| \(= \frac{\frac{x^2}{y2}}{\sqrt{\frac{y^2 – x^2}{y^2}}}\) |
| \(= \frac{x^2}{y^2} \times \frac{y}{\sqrt{y^2 – x^2}}\) |
| \(= \frac{x^2}{y\sqrt{y^2 – x^2}}\) |
5. দেখাই যে, \(\sec^2 12^° – \frac{1}{\tan^2 78^°}= 1\)
সমাধানঃ-
| \(\sec^2 12^° – \frac{1}{\tan^2 78^°}\) |
| \(= \sec^2 (90^° – 78^°) – \frac{1}{\tan^2 78^°}\) |
| \(= \csc^2 78^° – \cot^2 78^°\) |
| \(= 1\) [\(∵ \csc^2 \theta – \cot^2 \theta = 1\) ] |
6. \(\angle A + \angle B = 90^°\) হলে, দেখাই যে, \(1 + \frac{\tan A}{\tan B}= \sec^2 A\)
সমাধানঃ-
| \(1 + \frac{\tan A}{\tan B}\) |
| \(= 1 + \frac{\tan A}{\tan (90^° – A)}\) [\(∵\angle A + \angle B = 90^°\)] |
| \(= 1 + \frac{\tan A}{\cotA}\) |
| \(= 1 + \tan A \tan A\) |
| \(= 1 + \tan^2 A\) |
| \(= \sec^2 A\) [\(∵ \sec^2 \theta – \tan^2 \theta = 1\)] |
7. দেখাই যে, \(\csc^2 22^° \cot^2 68^° = \sin^2 22^° + \sin^2 68^° + \cot^2 68^°\)
সমাধানঃ-
| \(\sin^2 22^° + \sin^2 68^° + \cot^2 68^°\) |
| \(= \sin^2 22^° + \sin^2 (90^° – 22^°) + \cot^2 68^°\) |
| \(= \sin^2 22^° + \cos^2 22^° + \cot^2 68^°\) |
| \(= 1 + \frac{1}{\tan^2 68^°}\) |
| \(= \frac{\tan^2 68^° + 1}{\tan^2 68^°}\) |
| \(= \frac{\sec^2 68^°}{\tan^2 68^°}\) [\(∵ \sec^2 \theta – \tan^2 \theta = 1\)] |
| \(= \frac{\sec^2 (90^° – 22^°)}{\tan^2 68^°}\) |
| \(= \csc^2 22^° \cot^2 68^°\) |
8. যদি \(\angle P+ \angle Q = 90^°\) হয়, তবে দেখাই যে, \(\sqrt{\frac{\sin P}{\cos Q} – \sin P \cos Q} = \cos P\)
সমাধানঃ-
| \(\sqrt{\frac{\sin P}{\cos Q} – \sin P \cos Q} \) |
| \(= \sqrt{\frac{\sin P}{\cos (90^° – P)} – \sin P \cos (90^° – P)} \) [\(∵\angle P+ \angle Q = 90^°\)] |
| \(= \sqrt{\frac{\sin P}{\sinP} – \sin P \sin P} \) |
| \(= \sqrt{1 – \sin^2 P } \) |
| \(= \sqrt{\cos^2 P } \) [\(∵ \sin^2 \theta + \cos^2 \theta = 1\)] |
| \(= \cos P\) |
9. প্রমাণ করি যে,
\(\cot 12^° \cot 38^° \cot 52^° \cot 78^° \cot 60^° = \frac{1}{\sqrt3}\)
সমাধানঃ-
| \(\cot 12^° \cot 38^° \cot 52^° \cot 78^° \cot 60^°\) |
| \(= (\cot 12^° \cot 78^°) (\cot 38^° \cot 52^°) \cot 60^°\) |
| \(= (\cot 12^° \cot (90^° – 12^°)) (\cot 38^° \cot (90^° – 38^°)) \cot 60^°\) |
| \(= (\cot 12^° \tan12^°) (\cot 38^° \tan 38^°) \cot 60^°\) |
| \(= 1 \times 1 \times \frac{1}{\sqrt3}\) |
| \(= \frac{1}{\sqrt3}\) |
10. O কেন্দ্রীয় যে-কোনো একটি বৃত্তের AOB একটি ব্যাস এবং বৃত্তের উপর C যে-কোনো একটি বিন্দু।এবার A, C; B, C এবং O, C যুক্ত করে দেখাই যে,
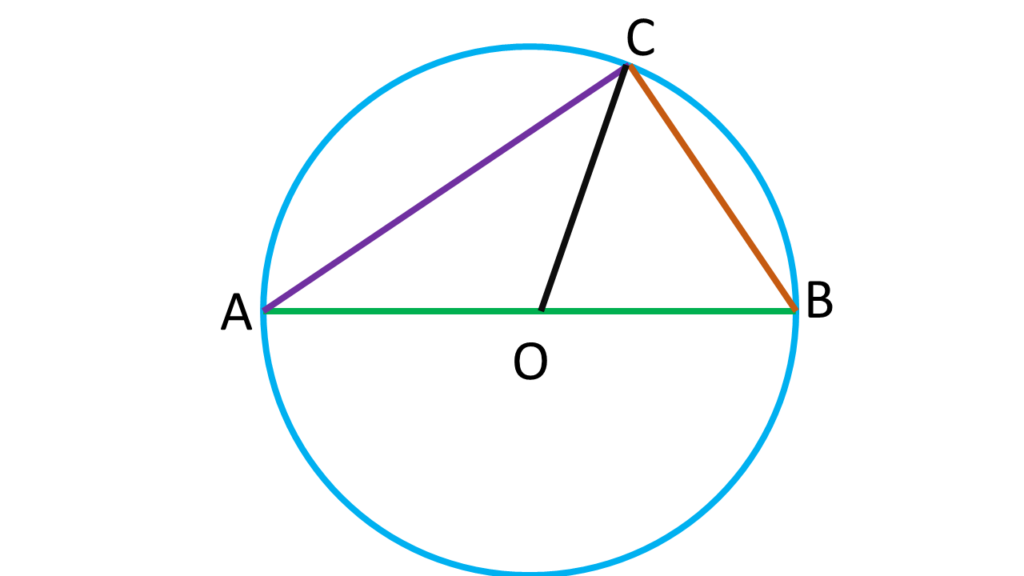
চিত্রানুযায়ী, আমরা যা যা পেলাম তা হলো –
| (i) | ∠BAC + ∠ABC = 90° [কারণ,▲ACB এর অর্ধবৃত্তস্থ ∠ACB = 90°, অতএব বাকি দুই কোণের সমষ্টি 90°] |
| (ii) | ∠ACO = ∠OAC [কারণ, ▲AOC এর OA = OC একই বৃত্তের ব্যাসার্ধ] |
| (iii) | ∠OCB = ∠OBC [কারণ, ▲OBC এর OB = OC একই বৃত্তের ব্যাসার্ধ] |
(i) \(\tan \angle ABC = \cot \angle ACO\)

সমাধানঃ-
| \(\tan \angle ABC\) |
| \(= \tan (90^° – \angle BAC)\) [∵ ∠BAC + ∠ABC = 90°] |
| \(= \cot \angle BAC\) |
| \(= \cot \angle ACO\) [∵ ∠ACO = ∠OAC] |
(ii) \(\sin^2 \angle BCO + \sin^2 \angle ACO = 1\)
সমাধানঃ-

| \(\sin^2 \angle BCO + \sin^2 \angle ACO\) |
| \(= \sin^2 \angle OBC + \sin^2 \angle BAC\) [∵∠ACO = ∠OAC এবং ∠OCB = ∠OBC] |
| \(= \sin^2 \angle ABC + \sin^2 (90^° – \angle ABC\) [∵∠BAC + ∠ABC = 90°] |
| \(= \sin^2 \angle ABC + \cos^2 \angle ABC\) |
| \(= 1 \) [\(∵ \sin^2 \theta + \cos^2 \theta = 1\)] |
(iii) \(\csc^2 \angle CAB – 1 = \tan^2 \angle ABC\)
সমাধানঃ-

| \(\csc^2 \angle CAB – 1 \) |
| \(= \csc^2 (90^° – \angle ABC) – 1 \) [∵∠BAC + ∠ABC = 90°] |
| \(= \sec^2 \angle ABC – 1 \) |
| \(= \tan^2 \angle ABC\) [\(∵ \sec^2 \theta – \tan^2 \theta = 1\)] |
11. ABCD একটি আয়তাকার চিত্র। A, C যুক্ত করে প্রমাণ করি যে,
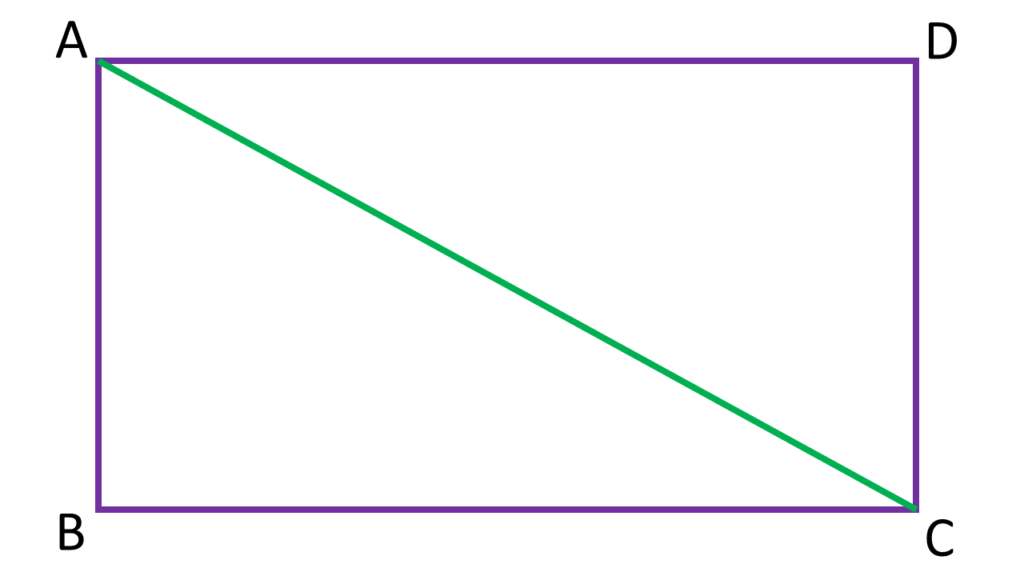
চিত্রানুযায়ী, আমরা যা যা পেলাম তা হলো –
| (i) | ∠BAC + ∠CAD = 90° [কারণ, আয়তক্ষেত্রের প্রতিটি কোণের মান 90°] |
| (ii) | ∠ACD + ∠ACB = 90° [কারণ, আয়তক্ষেত্রের প্রতিটি কোণের মান 90°] |
(i) \(\tan \angle ACD = \cot \angle ACB\)
সমাধানঃ-

| \(\tan \angle ACD\) |
| \(= \tan (90^° – \angle ACB)\) [∵∠ACD + ∠ACB = 90°] |
| \(= \cot \angle ACB\) |
(ii)\( \tan^2 \angle CAD + 1 = \frac{1}{\sin^2 \angle BAC}\)
সমাধানঃ-

| \( \tan^2 \angle CAD + 1\) |
| \( = \tan^2 (90^° – \angle BAC) + 1\) |
| \( = \cot^2 \angle BAC + 1\) |
| \( = \csc^2 \angle BAC\) [\(∵ \csc^2 \theta – \cot^2 \theta = 1\) ] |
| \(= \frac{1}{\sin^2 \angle BAC}\) |
12. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.):
(i) (sin 43° cos 47° + cos 43° sin 47°) -এর মান
উত্তরঃ (b) 1
সমাধানঃ-
| (sin 43° cos 47° + cos 43° sin 47°) |
| = sin 43° cos (90° – 43°) + cos 43° sin (90° – 43°) |
| = sin 43° sin 43° + cos 43° cos 43° |
| = sin243° + cos243° = 1 |
(ii)\(\frac{\tan 35^°}{\cot 55^°} + \frac{\cot 78^°}{\tan 12^°}\) -এর মান
উত্তরঃ (c) 2
সমাধানঃ-
| \(\frac{\tan 35^°}{\cot 55^°} + \frac{\cot 78^°}{\tan 12^°}\) |
| \(= \frac{\tan 35^°}{\cot (90^° – 35^°)} + \frac{\cot 78^°}{\tan (90^° – 78^°)}\) |
| \(= \frac{\tan 35^°}{\tan 35^°} + \frac{\cot 78^°}{\cot 78^°}\) |
| \(= 1 + 1\) |
| \(= 2\) |
(iii) {\(\cos (40^°+\theta)-\sin(50^°-\theta)\)}-এর মান
উত্তরঃ (c) 0
সমাধানঃ-
| \(\cos (40^°+\theta)-\sin(50^°-\theta)\) |
| \(= \cos (40^°+\theta)-\sin[90^° – (40^°+\theta)]\) |
| \(= \cos (40^°+\theta)-\cos (40^°+\theta)\) |
| \(= 0 \) |
(iv) ABC একটি ত্রিভুজ। \(\sin \frac{(B+C)}{2}\) =
উত্তরঃ (b) \(= \cos \frac{A}{2}\)
সমাধানঃ-
| \(\sin \frac{(B+C)}{2}\) |
| \(= \sin \frac{(180^° – A)}{2}\) [ত্রিভুজের তিনটি কোণের সমষ্টি 180°] |
| \(= \sin (90^° – \frac{A}{2}\) |
| \(= \cos \frac{A}{2}\) |
(v) A+B=90° এবং \(\tan A =\frac{3}{4}\) হলে, \(\cot B\) -এর মান
উত্তরঃ (a) \(= \frac{3}{4}\)
সমাধানঃ-
| \(\cot B\) |
| \(= \cot (90^° – A) \) |
| \(= \tan A\) |
| \(= \frac{3}{4}\) |
(B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি:
(i) cos 54° এবং sin 36°-এর মান সমান।
উত্তরঃ সত্য
(ii) (sin 12° – cos 78°) -এর সরলতম মান 1.
উত্তরঃ মিথ্যা
(C) শূন্যস্থান পূরণ করি:
(i) (tan 15°×tan 45°×tan 60°× tan 75°)-এর মান _______
উত্তরঃ \(\sqrt3\)
সমাধানঃ-
| (tan 15°×tan 45°×tan 60°× tan 75°) |
| = tan (90° – 75°)×tan 45°×tan 60°× tan 75° |
| = cot75°×tan 45°×tan 60°× tan 75° |
| = cot75° × tan 75°×tan 45°×tan 60° |
| = 1 × 1 × \(\sqrt3\) |
| = \(\sqrt3\) |
(ii) (sin 12°×cos 18º× sec 78° × cosec 72°)-এর মান _______
উত্তরঃ 1
সমাধানঃ-
| sin 12°cos 18º× sec 78° × cosec 72° |
| = sin (90° – 78°)×cos(90° – 72º)× sec 78° × cosec 72° |
| = cos 78° × sin 72º × sec 78° × cosec 72° |
| = cos 78° × sec 78° × sin 72° × cosec 72° |
| = 1 × 1 = 1 |
(iii) A এবং B পরস্পর পূরক কোণ হলে, sin A = ______
উত্তরঃ cos B
13. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.):
(i) \(\sin 10\theta = \cos 8\theta\) এবং \(10\theta\) ধনাত্মক সূক্ষ্মকোণ হলে, \(\tan 9\theta\)-এর মান নির্ণয় করি।
সমাধানঃ-
| \(\sin 10\theta = \cos 8\theta\) |
| বা, \(\sin 10\theta = \sin (90^° – 8\theta)\) |
| বা, \(10\theta = 90^° – 8\theta\) |
| বা, \(10\theta + 8\theta = 90^°\) |
| বা, \(18\theta = 90^°\) |
| বা, \(9\theta = 45^°\) |
| বা, \(\tan 9\theta = \tan 45^°\) |
| বা, \(\tan 9\theta = 1\) |
(ii) \(\tan 4\theta \times \tan 6\theta = 1\) এবং \(6\theta\) ধনাত্মক সূক্ষ্মকোণ হলে, \(\theta\)-এর মান নির্ণয় করি।
সমাধানঃ-
| \(\tan 4\theta \times \tan 6\theta = 1\) |
| বা, \(\tan 4\theta = \frac{1}{\tan 6\theat}\) |
| বা, \(\tan 4\theta = \cot 6\theat\) |
| বা, \(\tan 4\theta = \tan(90^° – 6\theat)\) |
| বা, \( 4\theta = 90^° – 6\theat)\) |
| বা, \( 4\theta + 6\theat = 90^°)\) |
| বা, \( 10\theat = 90^°)\) |
| বা, \( \theat = 9^°)\) |
(iii) \(\frac{2\sin^2 63^°+1+2sin^2 27°}{3\cos^2 17^°-2+3\cos^2 73^°}\) -এর মান নির্ণয় করি।
সমাধানঃ-
| \(\frac{2\sin^2 63^°+1+2sin^2 27°}{3\cos^2 17^°-2+3\cos^2 73^°}\) |
| \(= \frac{2\sin^2 63^°+1+2sin^2 (90^° – 63°)}{3\cos^2 (90^° – 73^°)-2+3\cos^2 73^°}\) |
| \(= \frac{2\sin^2 63^°+1+2cos^2 63°}{3\sin^2 73^°-2+3\cos^2 73^°}\) |
| \(= \frac{2(\sin^2 63^°+ cos^2 63°) + 1}{3(\sin^2 73^° + \cos^2 73^°) – 2}\) |
| \(= \frac{2 \times 1 + 1}{3 \times 1 – 2}\) |
| \(= \frac{3}{3 – 2} = 3\) |
(iv) (tan 1°× tan 2° x tan 3°……..tan 89°)-এর মান নির্ণয় করি।
সমাধানঃ-
| tan 1°× tan 2° x tan 3°……..tan 89° |
| = tan 1°× tan 2° x tan 3°………×tan44° × tan45° × tan46° ……× tan 87°× tan 88°× tan 89° |
| = tan 1°× tan 2° x tan 3°………×tan44° × tan45° × tan(90° – 44°) ……× tan (90°-3°)× tan (90°-2°)× tan (90°-1°) |
| = tan 1°× tan 2° x tan 3°………×tan44° × tan45° × cot44° ……× cot3°× cot2°× cot1° |
| = (tan1° × cot1°) × (tan2°×cot2°) × (tan3°×cot3°)…………(tan44°×cot44°) × tan45° |
| = 1 × 1 × 1 × ……..×1×1 |
| = 1 |
(v) sec5A = cosec(A+36°) এবং 5A ধনাত্মক সূক্ষ্মকোণ হলে, A-এর মান নির্ণয় করি।
সমাধানঃ-
| sec5A = cosec(A+36°) |
| বা, cosec (90° – 5A) = cosec (A + 36°) |
| বা, 90° – 5A = A + 36° |
| বা, 6A = 90° – 36° |
| বা, 6A = 54° |
| বা, A = 9° |
Class 10 WBBSE এর বাকি অধ্যায়ের সমাধান-
| অধ্যায় | সমাধান |
| 1. একচলবিশিষ্ট দ্বিঘাত সমীকরণ (Quadratic Equations with one variable) | কষে দেখি 1.1 |
| কষে দেখি 1.2 | |
| কষে দেখি 1.3 | |
| কষে দেখি 1.4 | |
| কষে দেখি 1.5 | |
| 2. সরল সুদকষা (Simple Interest) | কষে দেখি 2 |
| 3. বৃত্ত সম্পর্কিত উপপাদ্য (Theorems related to circle) | কষে দেখি 3.1 |
| কষে দেখি 3.2 | |
| 4. আয়তঘন (Rectangular Parallelopiped or Cuboid) | কষে দেখি 4 |
| 5. অনুপাত ও সমানুপাত ( Ratio and Proportion) | কষে দেখি 5.1 |
| কষে দেখি 5.2 | |
| কষে দেখি 5.3 | |
| 6. চক্রবৃদ্ধি সুদ ও সমহার বৃদ্ধি বা হ্রাস (Compound Interest and Uniform Rate of Increase or Decrease) | কষে দেখি 6.1 |
| কষে দেখি 6.2 | |
| 7. বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য (Theorems related to Angles in a Circle) | কষে দেখি 7.1 |
| কষে দেখি 7.2 | |
| কষে দেখি 7.3 | |
| 8. লম্ব বৃত্তাকার চোঙ (Right Circular Cylinder) | কষে দেখি 8 |
| 9. দ্বিঘাত করণী (Quadratic Surd). | কষে দেখি 9.1 |
| কষে দেখি 9.2 | |
| কষে দেখি 9.3 | |
| 10. বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য (Theorems related to Cyclic Quadrilateral) | কষে দেখি 10 |
| 11. সম্পাদ্য : ত্রিভুজের পরিবৃত্ত ও অন্তবৃত্ত অঙ্কন | কষে দেখি 11 |
| 12. গোলক (Sphere) | কষে দেখি 12 |
| 13. ভেদ (Variation) | কষে দেখি 13 |
| 14. অংশীদারি কারবার (Partnership Business) | কষে দেখি 14 |
| 15. বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য (Theorems related to Tangent to a Circle) | কষে দেখি 15.1 |
| কষে দেখি 15.2 | |
| 16. লম্ব বৃত্তাকার শঙ্কু (Right Circular Cone) | কষে দেখি 16 |
| 17. সম্পাদ্য : বৃত্তের স্পর্শক অঙ্কন (Construction: Construction of Tangent to a circle) | কষে দেখি 17 |
| 18. সদৃশতা (Similarity) | কষে দেখি 18.1 |
| কষে দেখি 18.2 | |
| কষে দেখি 18.3 | |
| কষে দেখি 18.4 | |
| 19. বিভিন্ন ঘনবস্তু সংক্রান্ত বাস্তব সমস্যা (Real life Problems related to different Solid Objects) | কষে দেখি 19 |
| 20. ত্রিকোণমিতি : কোণ পরিমাপের ধারণা (Trigonometry: Concept of Measurment of Angle) | কষে দেখি 20 |
| 21. সম্পাদ্য : মধ্যসমানুপাতী নির্ণয় (Construction: Determination of Mean Proportional) | কষে দেখি 21 |
| 22. পিথাগোরাসের উপপাদ্য (Pythagoras Theorem) | কষে দেখি 22 |
| 23. ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি (Trigonometric Ratios and Trigonometric Identities) | কষে দেখি 23.1 |
| কষে দেখি 23.2 | |
| কষে দেখি 23.3 | |
| 24. পূরক কোণের ত্রিকোণমিতিক অনুপাত (Trigonometric Ratios of Complementrary angle) | কষে দেখি 24 |
| 25. ত্রিকোণমিতিক অনুপাতের প্রয়োগ : উচ্চতা ও দূরত্ব (Application of Trigonometric Ratios : Heights & Distances) | কষে দেখি 25 |
| 26. রাশিবিজ্ঞান : গড়, মধ্যমা, ওজাইভ, সংখ্যাগুরুমান (Statistics: Mean, Median, Ogive, Mode) | কষে দেখি 26.1 |
| কষে দেখি 26.2 | |
| কষে দেখি 26.3 | |
| কষে দেখি 26.4 |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  |
এই কষে দেখি 24 Class 10|Koshe Dekhi 24 Class 10 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।

এখানে তোমরা তোমাদের দশম শ্রেণীতে| Class 10 এ কি কি পড়ানো হয়, মানে তোমাদের দশম শ্রেণীতে| Class 10 সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

