শ্রেণী- দশম ; অধ্যায় – ত্রিকোণমিতিঃ কোণ পরিমাপের ধারণা ; কষে দেখি 20
কষে দেখি 20 Class 10 অংকের সূচিপত্র:-
কষে দেখি 20 Class 10 এর অংকের সমাধান গুলি ভালোভাবে বোঝার জন্যে কিছু উপদেশঃ
এই কষে দেখি 20, পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদ | WBBSE এর অন্তর্গত দশম শ্রেণি|Class 10 এর 20 নম্বর অধ্যায়|Chapter 20, ত্রিকোণমিতিঃ কোণ পরিমাপের ধারণা | Trigonometry: Concept of Measurement of Angle এর অনুশীলনী।
এই কষে দেখি 20 Class 10 এর অঙ্ক গুলি বোঝার জন্যে যে যে বিষয় জানতে হবে তা আলোচনা করা হলো–
ত্রিকোণমিতিক কোণ পরিমাপের সাধারণভাবে দুটি পদ্ধতি হলো-
- ষষ্টিক পদ্ধতি (Sexagesimal System),
- বৃত্তীয় পদ্ধতি (Circular System)
ষষ্টিক পদ্ধতি:
দুটি পরস্পরছেদী সরলরেখা একে অপরের উপর লম্বভাবে দাঁড়ালে যে কোণ তৈরি হয় তাকে সমকোণ বলা হয়।
এই পদ্ধতিতে এক সমকোণকে 90টি সমান ভাগে বিভক্ত করা হয় এবং তার প্রতিটি ভাগকে এক ডিগ্রি (1) বলা হয় এবং এই কারণেই এক সমকোণ = 90° ; এক ডিগ্রিকে পুনরায় 60টি সমান যষ্টিক মিনিটে (Minutes ) ও প্রতি মিনিটকে সমান 60টি ষষ্টিক সেকেন্ডে (Seconds) বিভক্ত করা হয়।
- 1 সমকোণ = 90° (ডিগ্রি)
- 1° (ডিগ্রি) = 60′ (মিনিট)
- 1′ (মিনিট) = 60″ (সেকেন্ড)
বৃত্তীয় পদ্ধতি :
একটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্যের সমান দৈর্ঘ্যের বৃত্তচাপ ওই বৃত্তের কেন্দ্রে যে সম্মুখ কোণ উৎপন্ন করে তার পরিমাপকে এক রেডিয়ান [Radian] বলা হয় এবং লেখা হয় 1; যে-কোনো একটি বৃত্তের পরিধি এবং ব্যাসের দৈর্ঘ্যের অনুপাত ধ্রুবক। এই সম্পর্কটির উপর ভিত্তি করেই এই পদ্ধতির একক নির্ধারিত হয়েছে।
আগামিতে এই কষে দেখি 20 Class 10 এর অংক গুলির সমাধানের প্রয়োজন হলে কি করবে?
| কষে দেখি 20 Class 10 এর এই কষে দেওয়া অংক গুলি তোমাদের যদি আগামিতে আবার প্রয়োজন হয় তাহলে তোমরা Google এ গিয়ে Search করবে- কষে দেখি 20 Class 10 তারপর |
কষে দেখি 20 Class 10|Koshe Dekhi 20 Class 10
1. নিম্নলিখিতগুলিকে ডিগ্রি, মিনিট ও সেকেন্ডে প্রকাশ করি :
(i) 832′
সমাধানঃ-
| \(\frac{832}{60}\) |
| = 13 + \(\frac{52}{60}\) |
অতএব, 832′ = 13°52′
(ii) 6312″
সমাধানঃ-
| \(\frac{6312}{60}\) |
| = 105 + \(\frac{12}{60}\) |
অতএব, 6312” = 105’12”
আবার,
| \(\frac{105}{60}\) |
| = 1 + \(\frac{45}{60}\) |
অতএব, 105’12” = 1°45’12”
(iii) 375″
সমাধানঃ-
| \(\frac{375}{60}\) |
| = 6 + \(\frac{15}{60}\) |
অতএব, 375” = 6’15”
(iv) \(27\frac{1°}{12}\)
সমাধানঃ-
| \(27\frac{1°}{12}\) |
| = 27° + \(\frac{1°}{12}\) |
| = 27° + \((\frac{1 \times 60}{12})’\) |
| = 27° + 5′ |
| = 27°5′ |
(v) 72.04°
সমাধানঃ-
| \(72.04°\) |
| \(= 72° + (.04)°\) |
| \(= 72° + (\frac{4}{100})°\) |
| \(= 72° + (\frac{4 \times 60}{100})’\) |
| \(= 72° + (\frac{240}{100})’\) |
| \(= 72° + (2 + \frac{4}{10})’\) |
| \(= 72° + 2′ + (\frac{4}{10})’\) |
| \(= 72° + 2′ + (\frac{4}{10})’\) |
| \(= 72° + 2′ + (\frac{4 \times 60}{10})”\) |
| \(= 72° + 2′ + 24”\) |
| \(= 72°2’24”\) |
2. নিম্নলিখিতগুলির বৃত্তীয় মান নির্ণয় করি :
(i) 60°
সমাধানঃ- \(\frac{π}{3}\)
(ii) 135 °
সমাধানঃ-
যেহেতু \(π^c = 180°\)
সুতরাং,
| 135° |
| = \((\frac{π}{180} \times 135)^c\) |
| = \(\frac{3π}{4}\) |
(iii) – 150 °
সমাধানঃ-
যেহেতু \(π^c = 180°\)
সুতরাং,
| -150° |
| = – \((\frac{π}{180} \times 150)^c\) |
| = – \(\frac{5π}{6}\) |
(iv) 72°
সমাধানঃ-
যেহেতু \(π^c = 180°\)
সুতরাং,
| 72° |
| = \((\frac{π}{180} \times 72)^c\) |
| = \(\frac{2π}{5}\) |
(v) 22°30′
সমাধানঃ-
| 22°30′ |
| = 22° + 30′ |
| = \(22° + (\frac{1}{2})^°\) [∵ 1° = 60′] |
| = \((\frac{45}{2})^°\) |
যেহেতু \(π^c = 180°\)
সুতরাং,
| \((\frac{45}{2})^°\) |
| = \((\frac{π}{180} \times \frac{45}{2})^c\) |
| = \(\frac{π}{8}\) |
(vi) – 62°30′
সমাধানঃ-
| – 62°30′ |
| = -(62° + 30′) |
| = -\(62° + (\frac{1}{2})^°\) [∵ 1° = 60′] |
| = \(-(\frac{125}{2})^°\) |
যেহেতু \(π^c = 180°\)
সুতরাং,
| \(-(\frac{125}{2})^°\) |
| = -\((\frac{π}{180} \times \frac{125}{2})^c\) |
| = -\(\frac{25π}{72}\) |
(vii) 52° 52’30”
সমাধানঃ-
| 52° 52’30” |
| = 52° + 52′ + 30” |
| = \(52° + 52′ + (\frac{1}{2})’\) [∵ 1′ = 60”] |
| = \(52° + (\frac{105}{2})’\) |
| = \(52 + (\frac{105}{2\times 60})^°\) [∵ 1° = 60′] |
| = \(52 + (\frac{21}{24})^°\) |
| = \((\frac{1269}{24})^°\) |
যেহেতু \(π^c = 180°\)
সুতরাং,
| \(\frac{1269}{24})^°\) |
| = \((\frac{π}{180} \times \frac{1269}{24})^c\) |
| = \(\frac{47π}{160}\) |
(viii) 40°16’24”
সমাধানঃ-
| 40°16’24” |
| = 40° + 16′ + 24” |
| = \(40^° + 16′ + (\frac{24}{60})’\) [∵ 1′ = 60”] |
| = \(40^° + 16′ + (\frac{2}{5})’\) |
| = \(40^° + (\frac{82}{5})’\) |
| = \(40^° + (\frac{82}{5\times 60})^°\) [∵ 1° = 60′] |
| = \(40^° + (\frac{41}{150})^°\) |
| = \((\frac{6041}{150})^°\) |
যেহেতু \(π^c = 180°\)
সুতরাং,
| \((\frac{6041}{150})^°\) |
| = \((\frac{π}{180} \times \frac{6041}{150})^c\) |
| = \(\frac{6041π}{27000}\) |
3. ▲ABC-এর AC = BC এবং BC বাহুকে D পর্যন্ত বর্ধিত করলাম। যদি ∠ACD=144° হয়, তবে ABC ত্রিভুজের প্রতিটি কোণের বৃত্তীয় মান নির্ণয় করি।
সমাধানঃ-
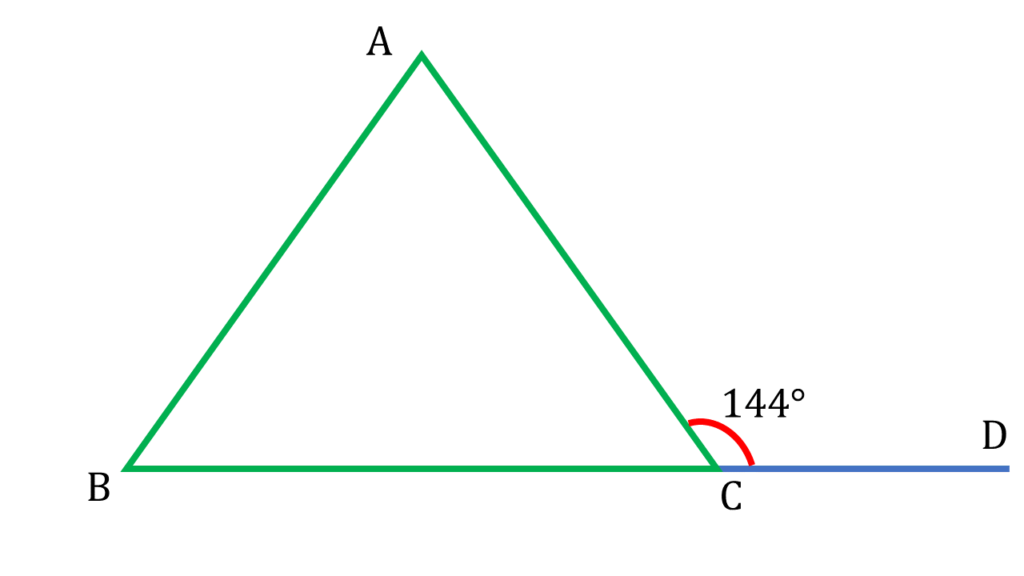
যেহেতু, AC = BC সেহেতু, ∠ABC = ∠BAC
আবার, ▲ABC এর বহিঃকোণ ∠ACD = 144°
অতএব,
| ∠ACD = ∠BAC + ∠ABC |
| বা, ∠BAC + ∠ABC = ∠ACD |
| বা, ∠BAC + ∠BAC = ∠ACD |
| বা, 2∠BAC = 144° |
| বা, ∠BAC = 72° = ∠BAC |
এখন, অবশিষ্ট কোণ
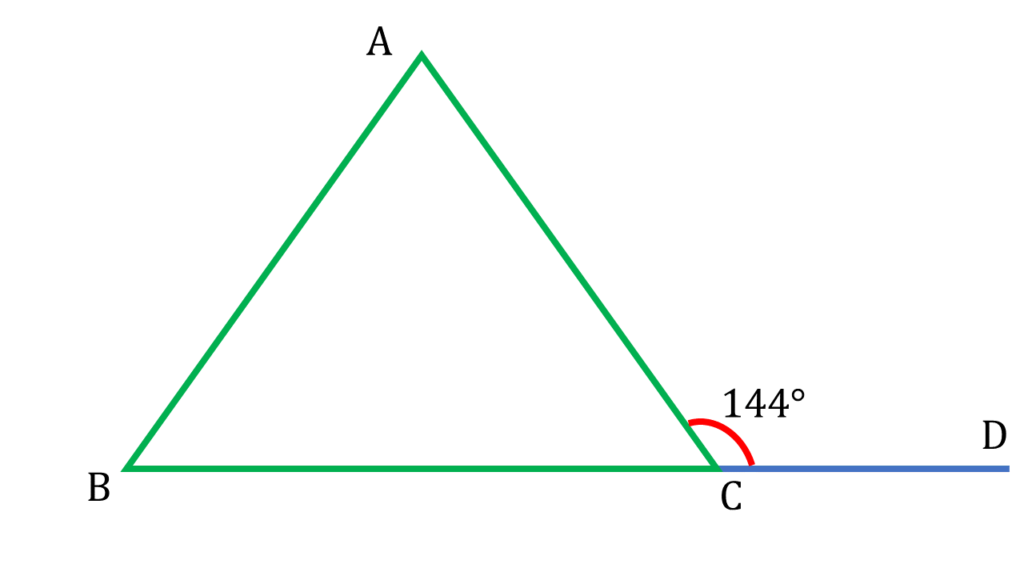
| ∠ACB |
| = 180° – (∠BAC + ∠ABC) |
| = 180° – (72°+72°) |
| = 180° – 144° |
| = 36° |
এখন কোণগুলির বৃত্তীয় মান গুলি হলো-
| কোণ | বৃত্তীয় মান |
|---|---|
| ∠ACB =36° | = \((36 \times \frac{π}{180})^c\) = \(\frac{π}{5}\) |
| ∠ABC = 72° | = \((72 \times \frac{π}{180})^c\) = \(\frac{2π}{5}\) |
| ∠BAC = 72° | = \((72 \times \frac{π}{180})^c\) = \(\frac{2π}{5}\) |
4. একটি সমকোণী ত্রিভুজের সূক্ষ্মকোণ দুটির অন্তর \(\frac{2π}{5}\) হলে, যষ্টিক পদ্ধতিতে ওই কোণদ্বয়ের মান লিখি ।
সমাধানঃ-
ধরি, সমকোণী ত্রিভুজটির দুটি সূক্ষ্মকোণ যথাক্রমে \(x^c\) ও \(y^c\)
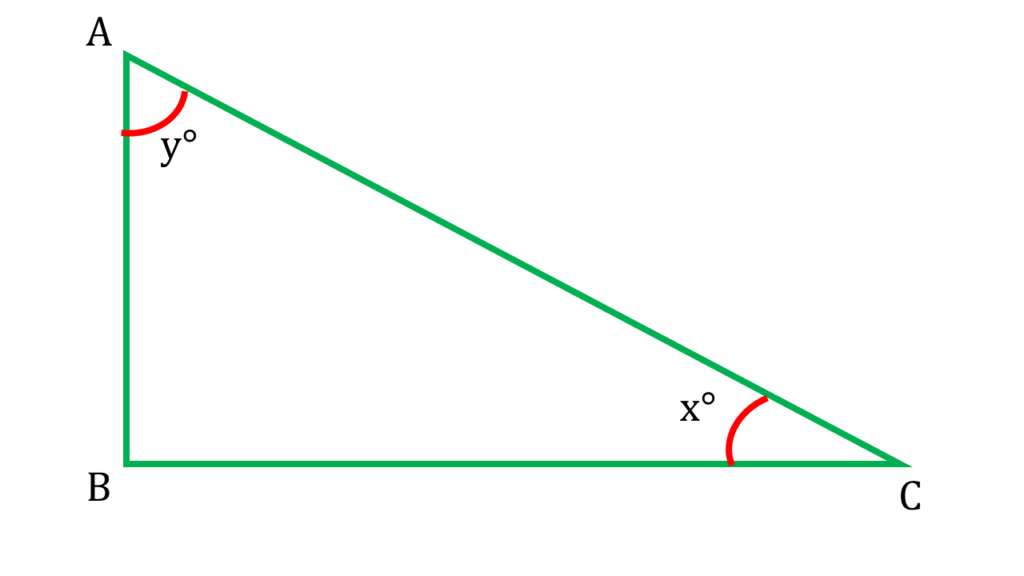
অতএব, \(x + y = \frac{π}{2}\) —-(i)
এবং দেওয়া আছে, \(x – y = \frac{2π}{5}\) -(ii)
(i) ও (ii) নং যোগ করে পাই,
| \(x + y + x – y = \frac{π}{2} + \frac{2π}{5}\) |
| বা, \( 2x = \frac{9π}{10}\) |
| বা, \( x = \frac{9π}{20}\) |
| বা, \(x = \frac{9 \times 180^°}{20}\) [∵π = 180°] |
| বা, \(x = 81^°\) |
(i) নং এ \( x = \frac{9π}{20}\) বসিয়ে পাই,
| \( \frac{9π}{20} + y = \frac{π}{2} \) |
| বা, \(y = \frac{π}{2} – \frac{9π}{20}\) |
| বা, \(y = \frac{π}{20}\) |
| বা, \(y = \frac{180°}{20}\) [∵π = 180°] |
| বা, \(y = 9^°\) |
5. একটি ত্রিভুজের একটি কোণের পরিমাপ 65° এবং দ্বিতীয়টির পরিমাপ \(\frac{π}{12}\) ; তৃতীয় কোণটির ষষ্টিক ও বৃত্তীয় মান হিসাব করে লিখি।
সমাধানঃ-
| কোণ | ষষ্টিক মান | বৃত্তীয় মান |
|---|---|---|
| প্রথম কোণ | 65° | |
| দ্বিতীয় কোণ | \(\frac{180°}{12}\) = 15° | \(\frac{π}{12}\) |
| তৃতীয় কোণ | = 180° – (65°+15°) = 180° – 80° = 100° | = \(100 \times \frac{π}{180}\) = \(\frac{5π}{9}\) |
6. দুটি কোণের সমষ্টি 135° এবং তাদের অন্তর \(\frac{π}{12}\)হলে, কোণ দুটির ষষ্টিক ও বৃত্তীয় মান হিসাব করে লিখি ।
সমাধানঃ-
ধরি, দুটি কোণ যথাক্রমে \(x^°\) ও \(y^°\)
অতএব,
| \(x + y = 135°\) ———(i) |
| এবং |
| \(x – y = \frac{180°}{12} = 15^°\) —–(ii) |
(i) ও (ii) নং যোগ করে পাই,
| \(x + y + x – y = 135 + 15\) |
| বা, \(2x = 150\) |
| বা, \(x = 75°\) |
এখন, \(x=75°\), (i) নং এ বসিয়ে পাই,
| \(75° + y = 135°\) |
| বা, \(y = 135° – 75°\) |
| বা, \(y = 60°\) |
এখন কোণগুলির বৃত্তীয় মানগুলি হলো-
| ষষ্টিক মান | বৃত্তীয় মান |
|---|---|
| \(x = 75°\) | \(75\times \frac{π}{180}\) = \(\frac{5π}{12}\) |
| \(y = 60°\) | \(60\times \frac{π}{180}\) = \(\frac{π}{3}\) |
7. একটি ত্রিভুজের কোণ তিনটির অনুপাত 2:3:4 হলে, ত্রিভুজটির বৃহত্তম কোণটির বৃত্তীয় মান হিসাব করে লিখি ।
সমাধানঃ-
মনে করি, কোণগুলির মান \(2x : 3x : 4x\) রেডিয়ান । যেখানে \(x\) সাধারণ গুণিতক এবং \(x\) > 0
অতএব,
| \(2x + 3x + 4x = π\) |
| বা, \(9x = π\) |
| বা, \(x = \frac{π}{9}\) |
অতএব, বৃহত্তর কোণটির বৃত্তীয় মান হবে, \(\frac{4π}{9}\)
8. একটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 28 সেমি.। এই বৃত্তে 5.5 সেমি. দৈর্ঘ্যের বৃত্তচাপ দ্বারা ধৃত কেন্দ্রীয় কোণটির বৃত্তীয় মান হিসাব করে লিখি ।
সমাধানঃ-
এখানে \(r= 28 \) সেমি. এবং \(s = 5.5\) সেমি.
ধরি, 5.5 সেমি. বৃত্তচাপ দ্বারা ধৃত কেন্দ্রস্থ কোণের বৃত্তীয় মান = \(\theta\)
| \(s = r\theta\) |
| বা, \(\theta = \frac{s}{r}\) |
| বা, \(\theta = \frac{5.5}{28}\) |
| বা, \(\theta = \frac{11}{56}\) |
অতএব, নির্নেয় কোণের বৃত্তীয় মান \(\frac{11}{56}\) রেডিয়ান বা, \(\frac{π^c}{16}\) [∵ π~\frac{22}{7}]
9. একটি বৃত্তের অসমান দৈর্ঘ্যের দুটি চাপ কেন্দ্রে যে কোণ ধারণ করে আছে তার অনুপাত 5:2 এবং দ্বিতীয় কোণটির ষষ্টিক মান 30° হলে, প্রথম কোণটির ষষ্টিক মান ও বৃত্তীয় মান হিসাব করে লিখি।
সমাধানঃ-
ধরি, প্রথম কোণটির ষষ্টিক মান = \(\theta^°\)
শর্তে,
| \(\frac{{\theta}^°}{30^°} = \frac{5}{2}\) |
| বা, \(\theta^° = 75^°\) |
75° এর বৃত্তীয় মান
= \(75 \times \frac{π}{180}\)
= \(\frac{5π}{12}\)
10. একটি ঘূর্ণায়মান রশ্মি –\(5\frac{1}{12}π\) কোণ উৎপন্ন করেছে। রশ্মিটি কোনদিকে কতবার পূর্ণ আবর্তন করেছে এবং তারপরে আরও কত ডিগ্রি কোণ উৎপন্ন করেছে তা হিসাব করে লিখি।
সমাধানঃ-
| –\(5\frac{1}{12}π\) |
| = –\(\frac{61}{12} \times 180°\) |
| = – 915° |
| = -(720° + 195°) |
| = -(2×360° + 195°) |
- রশ্মিটি ঘড়ির কাঁটার দিকে দুই বার পূর্ণ আবর্তন করেছে এবং তারপরে আরও 195 ডিগ্রি কোণ উৎপন্ন করেছে
11. ABC একটি সমদ্বিবাহু ত্রিভুজ অঙ্কন করেছি যার সমান বাহুদ্বয়ের অন্তর্ভূত কোণ ∠ABC = 45° ; ∠ABC-এর সমদ্বিখণ্ডক AC বাহুকে D বিন্দুতে ছেদ করেছে। ∠ABD, ∠BAD, ∠CBD এবং ∠BCD-এর বৃত্তীয় মান নির্ণয় করি।
সমাধানঃ-
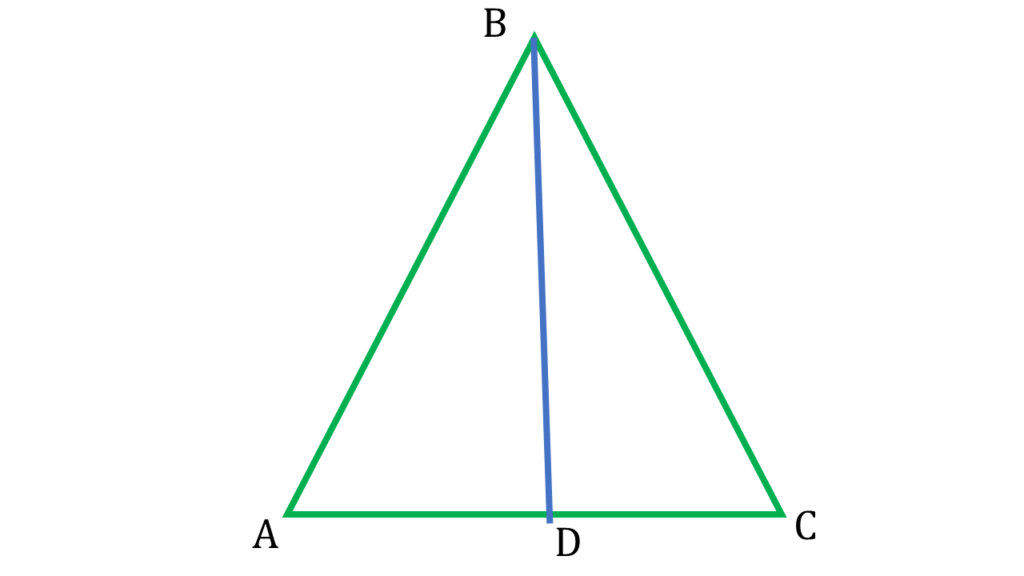
▲ABC এর
| ∠ABC + ∠BAC + ∠ACB = 180° |
| বা, 45° + ∠BAC + ∠BAC = 180° [∵AB=BC] |
| বা, 2∠BAC = 135° |
| বা, ∠BAC = \(\frac{135^°}{2}\) = ∠ACB |
আবার, BD, ∠ABC এর সমদ্বিখণ্ডক ।
সুতরাং, ∠ABD = ∠DBC = \(\frac{45^°}{2}\)
| কোণ | বৃত্তীয় মান |
|---|---|
| ∠ABD =∠DBC | \(\frac{45}{2} \times \frac{π}{180}\) = \(\frac{π}{8}\) |
| ∠BAC =∠ACB | \(\frac{135}{2} \times \frac{π}{180}\) = \(\frac{3π}{8}\) |
12. ABC সমবাহু ত্রিভুজের BC ভূমিকে E বিন্দু পর্যন্ত এমনভাবে বর্ধিত করলাম যেন CE = BC হয়। A, E যুক্ত করে ACE ত্রিভুজের কোণগুলির বৃত্তীয় মান নির্ণয় করি।
সমাধানঃ-
▲ACE এর , AC = CE [∵ ▲ABC একটি সমবাহু ত্রিভুজ এবং BC = CE]
অতএব, ∠AEC = ∠CAE
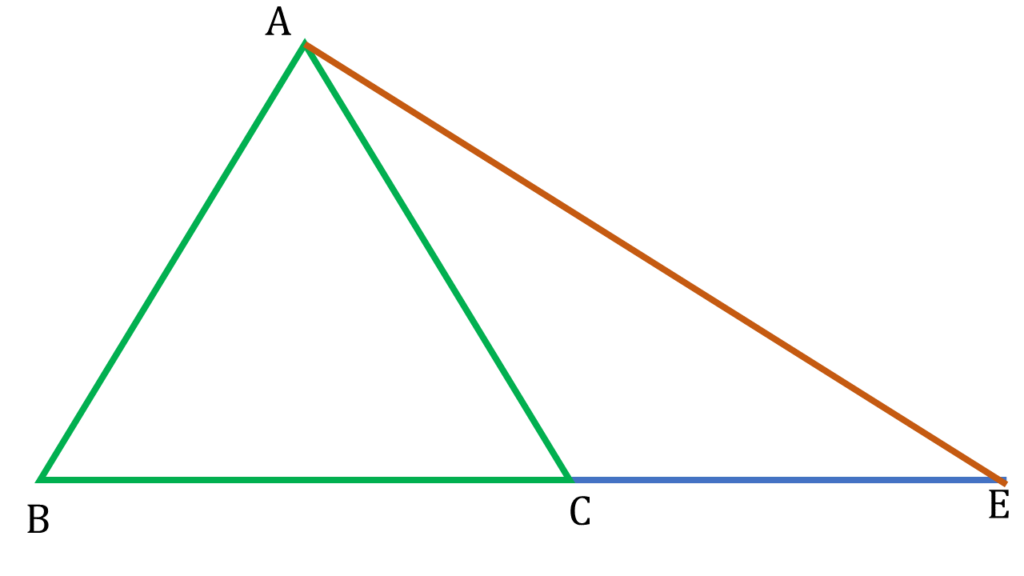
এখন ▲ACE এর তিনটি কোণের সমষ্টি 180°
| ∠ACE + ∠CAE + ∠AEC = 180° |
| বা, ∠ACE + ∠CAE + ∠CAE = 180° [∵∠AEC = ∠CAE] |
| বা, ∠ACE + 2∠CAE = 180° |
| বা, ∠BAC + ∠ABC + 2∠CAE = 180° [∵ ∠ACE, ▲ABC এর বহিঃকোণ] |
| বা, 60° + 60° + 2∠CAE = 180° |
| বা, 120° + 2∠CAE = 180° |
| বা, ∠CAE = 30° = ∠AEC |
| কোণ | বৃত্তীয় মান |
|---|---|
| ∠CAE = ∠AEC = 30° | \(\frac{π}{6}\) |
| ∠ACE = 120° | \(\frac{2π}{3}\) |
13. কোনো চতুর্ভুজের তিনটি কোণের পরিমাপ যথাক্রমে \(\frac{π}{3}, \frac{5π}{6}\), ও 90° হলে, চতুর্থ কোণটির যষ্টিক ও বৃত্তীয় মান হিসাব করে লিখি।
সমাধানঃ-
যেহেতু চতুর্ভুজের চারটি কোণের সমষ্টি 4 সমকন বা 2π রেডিয়ান।
সুতরাং,
চতুর্থ কোণের মান
| \(= 2π – (\frac{π}{3} + \frac{5π}{6} + \frac{π}{2})\) [∵\(\frac{π}{2} = 90^°\) ] |
| \(= 2π – (\frac{2π + 5π + 3π}{6})\) |
| \(= 2π – \frac{5π}{3}\) |
| \(=\frac{6π – 5π}{3}\) |
| \(= \frac{π}{3}\) |
অতএব, চতুর্থ কোণের ষষ্টিক মান = 60°
14. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
(A) বহুবিকল্পীয় প্রশ্ন (MCQ) :
(i) একটি ঘড়ির মিনিটের কাঁটার প্রান্তবিন্দু 1 ঘণ্টায় আবর্তন করে
উত্তরঃ (d) 2π রেডিয়ান
সমাধানঃ-

(ii) \(\frac{π}{6}\)রেডিয়ান সমান
উত্তরঃ (d) 30°
(iii) একটি সুষম ষড়ভুজের প্রতিটি অন্তঃকোণের বৃত্তীয় মান।
উত্তরঃ (b) \(\frac{2π}{3}\)
সমাধানঃ-
একটি অন্তঃকোণের মান
= \(\frac{2(6-2)\times 90^°}{6}\)
= 120°
(iv) \(s = r\theta\) সম্পর্কে \(\theta\)-এর পরিমাপ করা হয়
উত্তরঃ (b) বৃত্তীয় পদ্ধতিতে
(v) ABCD বৃত্তস্থ চতুর্ভুজের ∠A=120° হলে, ∠C-এর বৃত্তীয় মান
উত্তরঃ (a) \(\frac{π}{3}\)
সমাধানঃ-
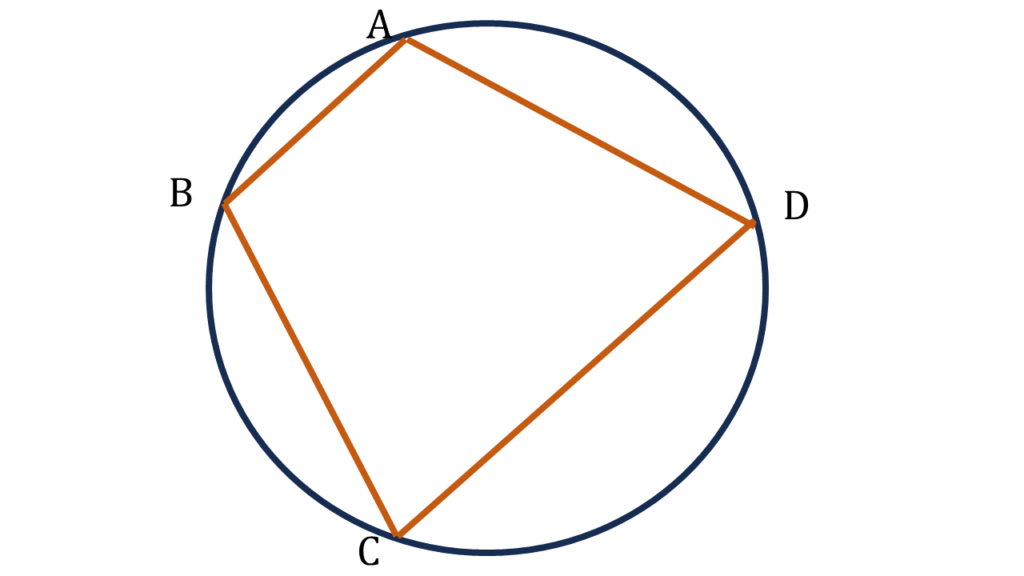
যেহেতু, বৃত্তস্থ চতুর্ভুজের বিপরীত কোণদ্বয়ের সমষ্টি 180°
সুতরাং, ∠C = 180° – 120° = 60° = \(\frac{π}{3}\)
(B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি :
(i) একটি রশ্মির প্রান্তবিন্দুকে কেন্দ্র করে রশ্মিটির ঘড়ির কাঁটার বিপরীত দিকে ঘোরার জন্য উৎপন্ন কোণটি ধনাত্মক।
উত্তরঃ সত্য
(ii) একটি রশ্মির প্রান্তবিন্দুকে কেন্দ্র করে রশ্মিটির ঘড়ির কাঁটার দিকে দু-বার পূর্ণ আবর্তনের জন্য 720° কোণ উৎপন্ন হয়।
উত্তরঃ মিথ্যা
(C) শূন্যস্থান পূরণ করি :
(i) রেডিয়ান একটি _______ কোণ।
উত্তরঃ ধ্রুবক
(ii) যষ্টিক পদ্ধতিতে 1 রেডিয়ান সমান _______ (প্রায়)।
উত্তরঃ 57°16’22”
(iii) \(\frac{3π}{8}\)পরিমাপের কোণটির সম্পূরক কোণের বৃত্তীয় মান _______।
উত্তরঃ \(\frac{5π}{8}\)
15. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
(i) একটি কোণের ডিগ্রিতে মান D এবং ওই কোণের রেডিয়ানে মান R হলে, \(\frac{R}{D}\) -এর মান নির্ণয় করি।
সমাধানঃ-
| \(D^° = (\frac{π}{180} \times D)^c\) |
অতএব,
| \(R = (\frac{π}{180} \times D)\) |
| বা, \(\frac{R}{D} = \frac{π}{180}\) |
ii) 63°35’15” পরিমাপের কোণটির পূরক কোণের মান লিখি।
সমাধানঃ-
| 90° = 89°59’60” |
অতএব,
| 89°59’60” – 63°35’15” |
| = 26°24’45” |
(iii) একটি ত্রিভুজের দুটি কোণের পরিমাপ 65°56’55” এবং 64°3’5″ হলে, তৃতীয় কোণটির বৃত্তীয় মান নির্ণয় করি।
সমাধানঃ-
তৃতীয় কোণটির ষষ্টিক মান
| = 180° – (65°56’55” + 64°3’5”) |
| = 180° – 129°59’60” |
| = 180° – 130° |
| = 50° |
- তৃতীয় কোণটির বৃত্তীয় মান
= \(50 \times \frac{π}{180} = \frac{5π}{18}\)
(iv) একটি বৃত্তে 220 সেমি দৈর্ঘ্যের বৃত্তচাপ বৃত্তের কেন্দ্রে 63° পরিমাপের কোণ উৎপন্ন করলে, বৃত্তের ব্যাসার্ধের দৈর্ঘ্য নির্ণয় করি।
সমাধানঃ-
\(63^° = 63\times \frac{π}{180} = \frac{7π}{20}\)
এখানে, \(s = 220\) সেমি. এবং \(\theta = \frac{7π}{20}\)
ধরি, ব্যাসার্ধ = \(r\) একক.
| \(s = r\theta\) |
| বা, \(220 = r \times \frac{7π}{20}\) |
| বা, \(r = \frac{20 \times 220}{7π}\) |
| বা, \(r = \frac{20 \times 220}{7 \times \frac{22}{7}}\) |
| বা, \(r = 200\) সেমি. |
(v) একটি ঘড়ির ঘণ্টার কাঁটার প্রান্তবিন্দু 1 ঘণ্টা আবর্তনে যে পরিমাণ কোণ উৎপন্ন করে তার বৃত্তীয় মান লিখি।
সমাধানঃ-
ঘণ্টার কাঁটার প্রান্তবিন্দু 1 ঘণ্টা আবর্তনে \(\frac{360°}{12} = 30^°\) কোণ উৎপন্ন করে যার বৃত্তীয় মান = \(\frac{π}{6}\)
Class 10 WBBSE এর বাকি অধ্যায়ের সমাধান-
| অধ্যায় | সমাধান |
| 1. একচলবিশিষ্ট দ্বিঘাত সমীকরণ (Quadratic Equations with one variable) | কষে দেখি 1.1 |
| কষে দেখি 1.2 | |
| কষে দেখি 1.3 | |
| কষে দেখি 1.4 | |
| কষে দেখি 1.5 | |
| 2. সরল সুদকষা (Simple Interest) | কষে দেখি 2 |
| 3. বৃত্ত সম্পর্কিত উপপাদ্য (Theorems related to circle) | কষে দেখি 3.1 |
| কষে দেখি 3.2 | |
| 4. আয়তঘন (Rectangular Parallelopiped or Cuboid) | কষে দেখি 4 |
| 5. অনুপাত ও সমানুপাত ( Ratio and Proportion) | কষে দেখি 5.1 |
| কষে দেখি 5.2 | |
| কষে দেখি 5.3 | |
| 6. চক্রবৃদ্ধি সুদ ও সমহার বৃদ্ধি বা হ্রাস (Compound Interest and Uniform Rate of Increase or Decrease) | কষে দেখি 6.1 |
| কষে দেখি 6.2 | |
| 7. বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য (Theorems related to Angles in a Circle) | কষে দেখি 7.1 |
| কষে দেখি 7.2 | |
| কষে দেখি 7.3 | |
| 8. লম্ব বৃত্তাকার চোঙ (Right Circular Cylinder) | কষে দেখি 8 |
| 9. দ্বিঘাত করণী (Quadratic Surd). | কষে দেখি 9.1 |
| কষে দেখি 9.2 | |
| কষে দেখি 9.3 | |
| 10. বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য (Theorems related to Cyclic Quadrilateral) | কষে দেখি 10 |
| 11. সম্পাদ্য : ত্রিভুজের পরিবৃত্ত ও অন্তবৃত্ত অঙ্কন | কষে দেখি 11 |
| 12. গোলক (Sphere) | কষে দেখি 12 |
| 13. ভেদ (Variation) | কষে দেখি 13 |
| 14. অংশীদারি কারবার (Partnership Business) | কষে দেখি 14 |
| 15. বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য (Theorems related to Tangent to a Circle) | কষে দেখি 15.1 |
| কষে দেখি 15.2 | |
| 16. লম্ব বৃত্তাকার শঙ্কু (Right Circular Cone) | কষে দেখি 16 |
| 17. সম্পাদ্য : বৃত্তের স্পর্শক অঙ্কন (Construction: Construction of Tangent to a circle) | কষে দেখি 17 |
| 18. সদৃশতা (Similarity) | কষে দেখি 18.1 |
| কষে দেখি 18.2 | |
| কষে দেখি 18.3 | |
| কষে দেখি 18.4 | |
| 19. বিভিন্ন ঘনবস্তু সংক্রান্ত বাস্তব সমস্যা (Real life Problems related to different Solid Objects) | কষে দেখি 19 |
| 20. ত্রিকোণমিতি : কোণ পরিমাপের ধারণা (Trigonometry: Concept of Measurment of Angle) | কষে দেখি 20 |
| 21. সম্পাদ্য : মধ্যসমানুপাতী নির্ণয় (Construction: Determination of Mean Proportional) | কষে দেখি 21 |
| 22. পিথাগোরাসের উপপাদ্য (Pythagoras Theorem) | কষে দেখি 22 |
| 23. ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি (Trigonometric Ratios and Trigonometric Identities) | কষে দেখি 23.1 |
| কষে দেখি 23.2 | |
| কষে দেখি 23.3 | |
| 24. পূরক কোণের ত্রিকোণমিতিক অনুপাত (Trigonometric Ratios of Complementrary angle) | কষে দেখি 24 |
| 25. ত্রিকোণমিতিক অনুপাতের প্রয়োগ : উচ্চতা ও দূরত্ব (Application of Trigonometric Ratios : Heights & Distances) | কষে দেখি 25 |
| 26. রাশিবিজ্ঞান : গড়, মধ্যমা, ওজাইভ, সংখ্যাগুরুমান (Statistics: Mean, Median, Ogive, Mode) | কষে দেখি 26.1 |
| কষে দেখি 26.2 | |
| কষে দেখি 26.3 | |
| কষে দেখি 26.4 |
| Request For Share |
|---|
| সমাধান গুলি ভালো লাগলে অবশ্যই বন্দুদের সাথে share করবে। নিজে শেখো ও অপরকে শিখতে সাহায্য করো। Let’s Study Together………….  |
এই কষে দেখি 20 Class 10|Koshe Dekhi 20 Class 10 এর সমাধান গুলি ভালো লাগলে অবশ্যই বন্ধুদের সাথে share করবে এবং wbstudyhub.in এই ওয়েবসাইট কে বুকমার্ক করে রাখবে যাতে যে কোনো অধ্যায়ের অংক আটকালে তোমরা তা এখানে এসে দেখে নিতে পারবে।

এখানে তোমরা তোমাদের দশম শ্রেণীতে| Class 10 এ কি কি পড়ানো হয়, মানে তোমাদের দশম শ্রেণীতে| Class 10 সিলেবাসে কি আছে তা জানার জন্যে তোমরা তোমাদের শ্রেণীর সিলেবাস এখানে দেখে নিতে পারবে ।

